Abstract
The development of protein variants with improved properties (thermostability, binding affinity, catalytic activity, etc.) has greatly benefited from the application of high-throughput screens evaluating large, diverse combinatorial libraries. At the same time, since only a very limited portion of sequence space can be experimentally constructed and tested, an attractive possibility is to use computational protein design to focus libraries on a productive portion of the space. We present a general-purpose method, called “Structure-based Optimization of Combinatorial Mutagenesis” (SOCoM), which can optimize arbitrarily large combinatorial mutagenesis libraries directly based on structural energies of their constituents. SOCoM chooses both positions and substitutions, employing a combinatorial optimization framework based on library-averaged energy potentials in order to avoid explicitly modeling every variant in every possible library. In case study applications to green fluorescent protein, β-lactamase, and lipase A, SOCoM optimizes relatively small, focused libraries whose variants achieve energies comparable to or better than previous library design efforts, as well as larger libraries (previously not designable by structure-based methods) whose variants cover greater diversity while still maintaining substantially better energies than would be achieved by representative random library approaches. By allowing the creation of large-scale combinatorial libraries based on structural calculations, SOCoM promises to increase the scope of applicability of computational protein design and improve the hit rate of discovering beneficial variants. While designs presented here focus on variant stability (predicted by total energy), SOCoM can readily incorporate other structure-based assessments, such as the energy gap between alternative conformational or bound states.
Keywords: combinatorial library, structure-based protein design, cluster expansion, high-throughput screening, protein design space
Introduction
Computational protein design focuses experimental effort on beneficial regions of sequence space, by modeling protein sequence-structure-function relationships and optimizing variants with desired properties. In contexts where a limited number of alternatives are to be experimentally tested, computational methods have yielded a wide range of novel proteins: new sequences for existing structures1,2 and new sequences for previously unobserved structures;3,4 enzymes with altered substrate specificity,5 grafted activity,6 and entirely new catalytic activity;6,7 variants with optimized binding affinity;8–10 new pairs of binding partners with targeted affinity and specificity;11 variants with improved thermostability12 or immunogenicity;13,14 and so on. In contexts where screening and selection techniques are available to assess larger libraries of diverse alternatives, computational methods have generated functionally enriched sets of candidates that likewise have led to the identification of a wide range of novel proteins, with altered activity;15,16 improved activity;17,18 targeted binding affinity and selectivity;19 and enhanced thermostability.20,21 We seek here the best of both worlds, bringing structure-based design techniques to bear in library-based experimental contexts.
The use of detailed structural modeling has been critical in many individual protein design studies, but unfortunately such modeling does not readily scale to the design of large combinatorial libraries, which can include millions or even billions of variants (with room for expansion, as stochastic library construction techniques already generate orders of magnitude more). It would thus be computationally very demanding to model at an atomistic level even the variants in a single library, much less over the space of possible libraries that must be considered in the design process. Consequently, computational structure-based approaches in library optimization have been limited to smaller mutagenesis libraries,15,22 for guiding the selection of degenerate codons encoding frequently occurring choices from individual protein designs,23 or indirect application in contact assessment for recombination libraries.17,24–26 However, modern library techniques are enabling larger library sizes, and it has been shown that large mutational loads can lead to beneficial variant properties.27,28 Thus the integration of structure-based design with large-scale library-based experiments promises mutual benefits: a high library hit rate due to enrichment of structurally stable variants, the ability to scale to large library size, and a tractable structure-based design objective of generating diverse stable variants (leaving more poorly understood and modeled objectives to the screening process).
This article presents a novel approach to structure-based protein library design that enables optimization of large combinatorial mutagenesis libraries (in library space) directly based on the structural properties of its members. Our method, Structure-based Optimization of Combinatorial Mutagenesis (SOCoM) builds from OCoM,29 a method to optimize combinatorial mutagenesis libraries based on a one- and two-body sequence potential derived from a multiple sequence alignment (MSA) for the target protein. The key enabling insight in the jump from OCoM to SOCoM is the use of Cluster Expansion (CE)11,30 to transform structure-based evaluation into a function of amino acid sequence that can be efficiently assessed and optimized. As shown in previous studies, CE improves calculation time by orders of magnitude without a significant loss in accuracy.31 It has been successfully applied in a number of significant individual protein design studies.11,30,31 However, even with CE-based efficient evaluation of variant energies, it is computationally infeasible to enumerate and explicitly evaluate every variant in every possible library. Instead, design must be performed in library space, treating libraries as “points” that can be efficiently represented, evaluated, and optimized. To address this issue, SOCoM leverages the OCoM-based formulation of library design, specifying a library in terms of choices of mutations at choices of positions and assessing it in terms of average variant quality, under the hypothesis that a better average leads to better individuals (shown to hold in the results presented here).
Results
Figure 1 summarizes the SOCoM approach. The library design space is defined in terms of possible positions at which to introduce mutations and possible choices of amino acids at those positions; the goal is to choose a subset of positions and substitutions to be “mixed and matched” in a library. As used in previous studies,29 each set of amino acid choices that make up these libraries is referred to as a “tube.” A tube can either specify any mixture of point mutations or, if extended to multisets, degenerate oligonucleotides. Using sets of tubes for library construction, the total number of variants within a library is equal to the product of the size of the tubes used (thus implicitly controlling the overall library size). For example, in the left-hand library in Figure 1, there are two sites, one incorporating {R,K,H} and the other {S,T}, leading to the six variants listed; in the middle library one site has {R,K} and the other {I,L}, leading to the four variants. The variants define a distribution of energies, but to enable efficient evaluation and optimization in library space, SOCoM assesses libraries in terms of their average CE-based energies without explicitly enumerating the variants. SOCoM employs an integer linear programming framework to select a specific library (positions and substitutions) that optimizes this library-averaged score. This library is predicted to be enriched in stable variants (each a combination of some of the mutations) that can be experimentally evaluated for other properties of interest.
Figure 1.
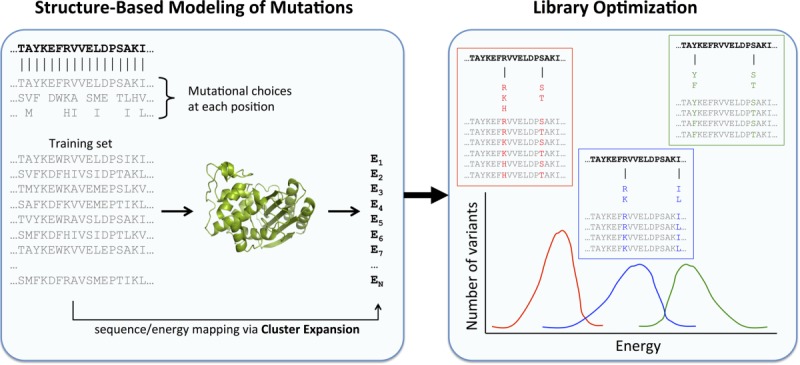
Overview of SOCoM. (Left) The library design space specifies possible positions that could be mutated and amino acids that could be incorporated at those positions. Each library is defined by choices for positions and amino acids. A Cluster Expansion model maps amino acid sequences of potential library variants to structural properties, here energies. (right) Library designs, specifying subsets of positions and amino acids, are optimized by an integer linear programming method. To enable efficient evaluation of large combinatorial libraries while optimizing over the massive design space, energy evaluation is based on library-averaged energy scores, computed without enumerating all variants.
Validation of the SOCoM method requires demonstrating that it meets the stated goal of generating library designs enriched in variants with good scores. Here we use Rosetta energy as the score. While our method can be applied with any structure-based score via CE decomposition, Rosetta has certainly proved its utility in structure-based protein design, particularly with diverse variants, as SOCoM now enables for structure-based libraries.
In order to assess SOCoM's ability to correctly optimize combinatorial mutagenesis libraries, we applied it to three different proteins previously targeted by library studies: green fluorescent protein (GFP), β-lactamase, and lipase A. We first performed smaller-scale focused design and compared SOCoM-optimized libraries with those from earlier library studies by Treynor et al.15 (GFP core), Hayes et al.32 (β-lactamase active site), and Sandström et al.33 (lipase A active site). Since library space is sufficiently large that experimental results provide little insight on our designs (and again, would reflect only on the scoring function employed), we focus on the demonstration that SOCoM does indeed produce libraries enriched in variants with good scores. We then allowed SOCoM to optimize larger libraries (previously unattainable by structure-based library design) and studied scalability and implications for library design, as well as how SOCoM-optimized libraries compared against representative randomly designed libraries.
Focused designs
For a direct comparison with the previous methods, in each case the same mutable positions were targeted as in the earlier studies; point mutation libraries were restricted to incorporate at most three mutations at a site in addition to wild-type, optimized by SOCoM by choosing from position-specific sets prefiltered for homology (i.e., for each position, all subsets of up to three mutations found sufficiently frequently in homologs); and the library size was restricted to generate the same number of variants. Libraries constructed using degenerate oligos are also presented. As a matter of general practice, mutations to/from proline and cysteine were not considered for the SOCoM designs, avoiding the need for more detailed modeling of their structural impact.
Green fluorescent protein
GFP has revolutionized microscopy and enabled significant advances in cell biology by highlighting patterns of gene expression, protein localization and protein association.34–37 Newly designed GFP variants have enabled the identification of new proteins38 as well as better visualization of subcellular structures in cells.39 The generation of a large library of stable variants to be screened/selected for desired activities could further expand the palette of applications.
Following Treynor et al.,15 512-member libraries were optimized for wild-type GFP from Aequorea victoria, allowing mutations at positions 57 to 72, which form the longest stretch of contiguous core residues.40 Targeting core positions could be disruptive;41,42 however, such mutations have a higher likelihood of directly affecting the fluorescence properties of the chromophore region43 and hence producing better-differentiated libraries.
Figure 2 summarizes the libraries and constituent variant energies designed by both SOCoM and the ORBIT methods applied by Treynor et al. The table in Figure 2(a) compares mutations selected by the methods. For example, position 57 and 67 remain unmutated by all methods, and all methods choose S72A. At position 63, both CORBIT and SOCoM-degenerate oligos opt for T63A, SOCoM-point mutations selects T63E, and DBISORBIT leaves it unmutated. Divergence between the ORBIT library plans and the SOCoM ones is observed at both T59, where the ORBIT plans choose the relatively conservative S while the SOCoM ones choose I or E, and similarly Q69, where ORBIT plans incorporate L but SOCoM uses E. We next explore the energetic implications of these choices.
Figure 2.
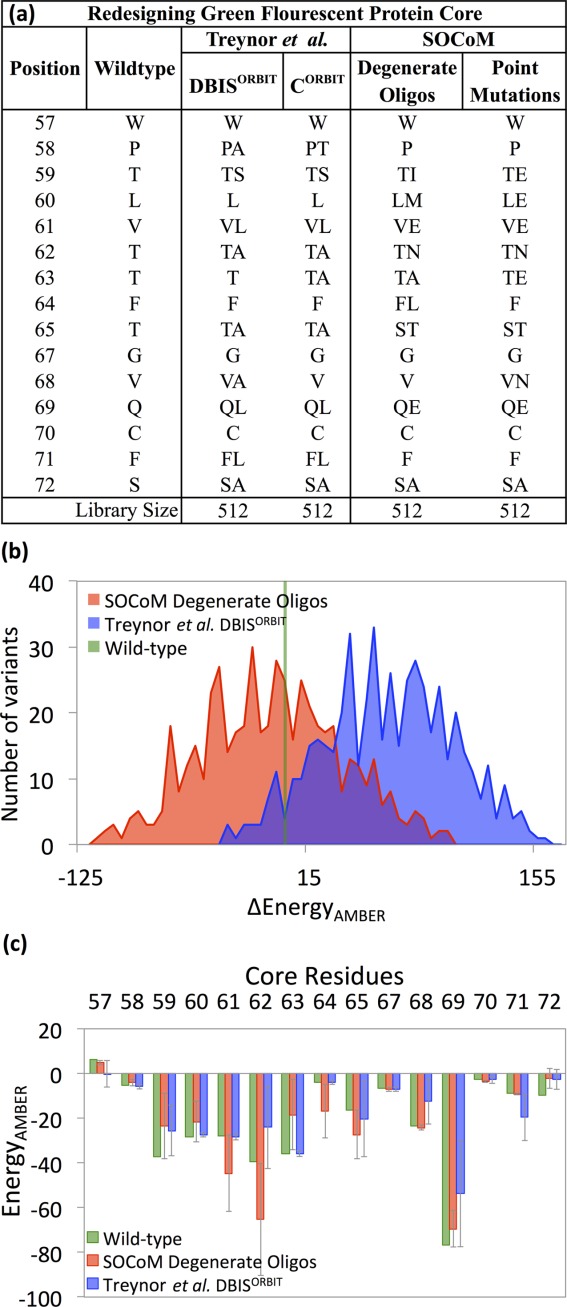
GFP core libraries. (a) Mutational choices made by previous methods (Treynor et al.) and by SOCoM. (b) Histograms of the AMBER energies (postminimization) of structural models built for the variants comprising the libraries. (c) Position-specific contributions to the AMBER energies, averaged over the libraries.
We enumerated all 512 variants in the DBISORBIT library and all 512 variants in the SOCoM degenerate oligo library, and used Rosetta to construct models for them all. Our designs score more favorably in terms of Rosetta energies (Supporting Information Fig. 1), but this is somewhat to be expected as SOCoM optimizes for Rosetta energy (albeit library averaged). Thus in order to provide a more unbiased comparison in assessing relative energetic favorability of the variants (predictive of stability, our goal), we subjected each model to energy minimization via Tinker44 according to the AMBER45 force field using the Generalized Born implicit solvent model. We present analyses based on these AMBER energies, as a somewhat distinct evaluation. Corresponding Rosetta-based evaluations are provided in the Supporting Information (Supporting Information Fig. 1(a)) and illustrate similar conclusions.
Figure 2(b) illustrates the distributions of AMBER energies over the two libraries. Clearly, SOCoM variants tend to have better energies, on average scoring more favorably by 71 kcal/mol relative to DBISORBIT variants; the difference in distributions is statistically significant (Wilcoxon P value <0.001). Further, whereas most SOCoM variants (59%) are scored with lower energies than the wild-type sequence, only 6% of the DBISORBIT variants are in this category. The standard deviation of the energies captures one aspect of library diversity, and we see that the SOCoM library is slightly more diverse under this notion, at 43 kcal/mol, compared with 40 kcal/mol for DBISORBIT.
SOCoM optimally selects mutations for the overall library score, summed over variants and positions. While Figure 2(b) broke the score down by variant, it is also interesting to characterize it by position-specific energy contributions. Figure 2(c) presents the energetic contributions for each position, averaged over all library variants. It also indicates the contributions from those positions in the wild-type. We see that SOCoM variants are also much better than DBISORBIT variants at this finer resolution, with SOCoM's variants aiding nine positions at an average of −7.8 kcal/mol energy with respect to wild-type, versus DBISORBIT's variants benefiting only eight positions at an average of only −2.9 kcal/mol. SOCoM variants tend to substantially improve energies involving positions 61, 62, 64, and 65, but only marginally those at 57, 67, 68, 70, and 71. Note that the improvements can be observed even at positions that are left wild-type, due to interactions with mutated residues; for example, the wild-type valine at position 68 has an energetic contribution of −23.3 kcal/mol, which is further enhanced among variants by an additional −0.98 kcal/mol.
β-lactamase
The family of β-lactamases comprises a diverse group of enzymes that hydrolyze the β-lactam ring of penicillin-like drugs, providing bacteria with antibiotic resistance46 and thus forming an important drug target.47 β-lactamase may also be put to productive use, for example, in anti-cancer ADEPT therapies13 and in measuring gene expression levels in cells.48 β-lactamases have been widely used as model systems in the development of combinatorial library construction methods29,49 due to inexpensive, high-throughput activity screens. β-lactamase libraries can provide insights on hydrolysis activity of β-lactam derivatives. As such, site saturation studies have helped to characterize functional and stability contributions of active site residues.50 Also, site-saturation methods are widely popular for understanding diversity in the spectrum of substrate recognition.51
We follow the general specification of Hayes et al.,32 designing libraries targeting the active site of TEM-1 β-lactamase from Escherichia coli, thereby potentially altering enzyme activity and substrate specificity.52,53 Specifically, the mutable positions include a total of 19 residues within 5Å of β-lactamase active site residues S70, K73, S130, E166, and K234. Mutations at catalytic residue sites (S70, K73, S130, and E166) themselves were not considered. For a direct comparison with the Hayes et al. library, at most four mutations were allowed at each position in addition to wild-type, optimally selected by SOCoM from prefiltered position-specific sets of allowed mutations.
Figure 3 summarizes the library designs by both SOCoM and the Protein Design Automation (PDA) method employed by Hayes et al.32 (panel a), AMBER energies of sampled sets of library members (panel b), and position-specific contributions among those library members (panel c). Since the libraries contain too many members to allow explicit structural modeling of each, 1000 were randomly chosen from each library. Considering all 19 positions, SOCoM provides an average stabilizing effect of −2.4 kcal/mol (with 11 of 19 being stabilized) whereas PDA provides an average destabilizing effect of 0.5 kcal/mol (though 10 of 19 are stabilized). Positions with major differences (>10 kcal/mol) in the stability effects include 69M, F72, Y105, N132, N170, D214, and S235. Some of the mutated residues have similar stabilizing (Y105N, I127L, and G236S) and destabilizing (K234I) trends within SOCoM and PDA, with respect to the wild-type.
Figure 3.
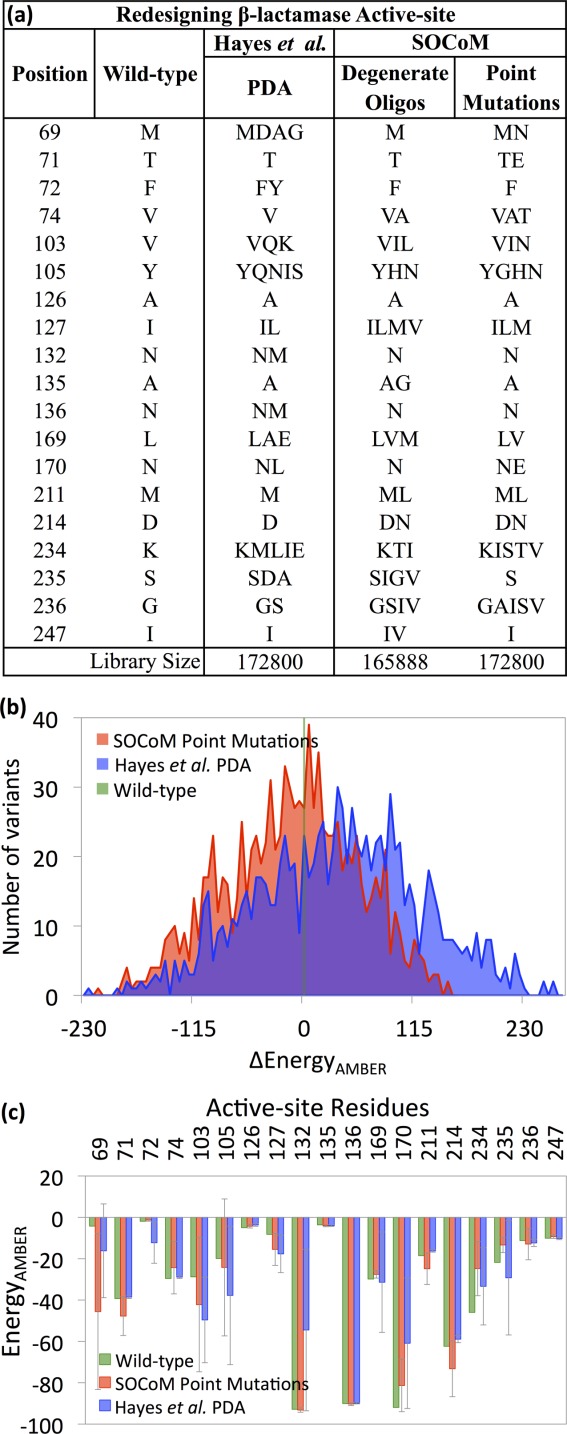
β-lactamase active site libraries. (a) Mutational choices made by previous methods (Hayes et al.) and by SOCoM. (b) Histograms of the AMBER energies (postminimization) of structural models built for the variants comprising the libraries. (c) Position-specific contributions to the AMBER energies, averaged over the libraries.
The energy distributions in Figure 3(b) show that SOCoM has better scoring β-lactamase variants than PDA does. The wild-type β-lactamase AMBER energy is referenced at 0 kcal/mol, and in comparison, ∼58% of the SOCoM variants are better while only ∼36% of the PDA ones are. The mean (±SD) Δenergy of SOCoM library is −16 (±69) kcal/mol, whereas the PDA library's mean Δenergy is 32 (±86) kcal/mol and the distributions are significantly different with a P value of less than 0.001. As discussed for GFP, these results are with respect to the minimized AMBER energy (not the objective function for either method). The Rosetta energies optimized by SOCoM (via cluster expansion and library averaging) display similar trends (Supporting Information Fig. 1(b)).
Lipase A
Candida antarctica lipase A is a thermostable enzyme that exhibits many different properties such as activity towards tertiary alcohols,54 high enantioselectivity towards β-amino acids,55 and sn-2 fatty acid preference of triglycerides.56 Recent studies have shown that combinatorial reshaping of Lipase A substrate pocket leads to highly active enantioselectivite variants. Such enzymes can be employed in industrial processes under mild reaction conditions providing beneficial outcomes for production of pharmaceuticals.57
The Lipase A library design was focused on the residues targeted in the Sandström et al.33 enantioselective library: F149, I150, P215, T221, L225, F233, A234, G237, and F431. These active site proximal residues were identified from ibuprofen ester binding and include all nonconserved residues within 4 Å from the bound ester, that is, those with a higher chance of influencing lipase A catalytic properties.58 Our conservation analysis identified ∼4 allowed mutations at each of these sites.
Figure 4 summarizes the designs and constituent variant energies. Sandström et al. constructed their combinatorial library using a knowledge-based approach, and it was surprising to note that SOCoM, without such prior knowledge, captured some of the mutations identified as being important for enantioselectivity, including F149Y and I150N.59 Other similar mutations selected by Sandström et al. and SOCoM libraries include L225V (degenerate oligos) and G237A (point mutations). Analyzing the localized AMBER energies shows that in general SOCoM mutations are more stabilizing at five out of nine positions, and make an average stability contribution of −20.75 kcal/mol versus −11.48 kcal/mol in the Sandström et al. library. The wild-type residue at position 149 exhibits a low energy state which Sandström et al. improve by incorporating tyrosine (knowledge-based), while SOCoM improves further by providing additional sets of stabilizing mutations (i.e., asparagine and tryptophan). While SOCoM avoids mutations to/from proline, interestingly the P215A mutation of Sandström et al. seems to have little effect.
Figure 4.
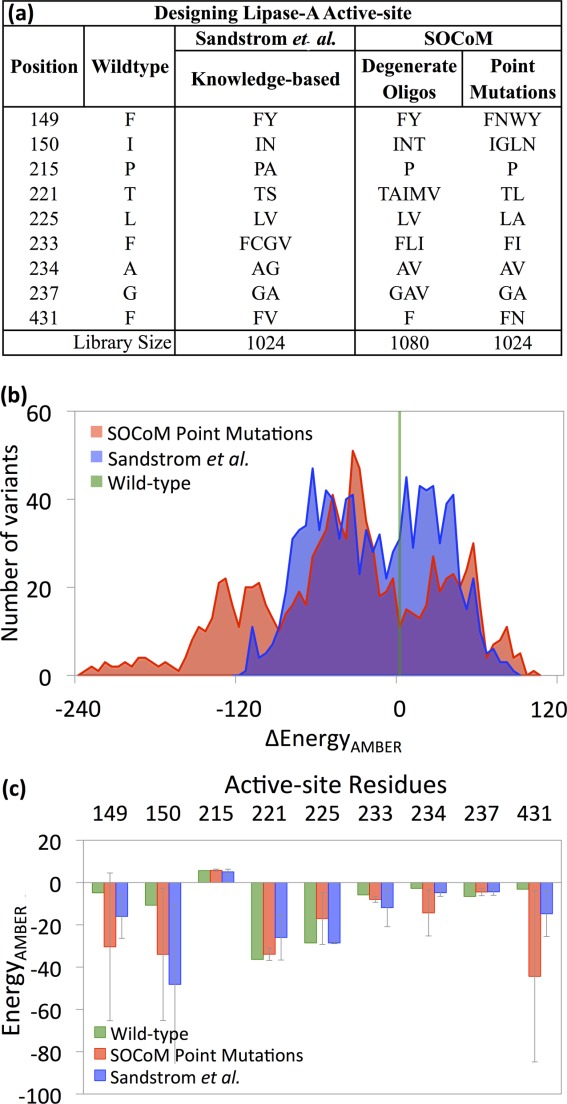
Lipase A active site libraries. (a) Mutational choices made by previous methods (Sandström et al.) and by SOCoM. (b) Histograms of the AMBER energies (postminimization) of structural models built for the variants comprising the libraries. (c) Position-specific contributions to the AMBER energies, averaged over the libraries.
The library energy distributions [Fig. 4(b)] clearly show that SOCoM yields more variants predicted to be more stable. The distributions are significantly different with a Wilcoxon P value <0.001. Wild-type lipase A has an AMBER Δenergy of −44 kcal/mol and 72% of SOCoM variants are better, as compared with 59% of the Sandström et al. ones. It is also interesting to observe that most of the stabilized variants from Sandström et al. overlap with the bimodal tail region of SOCoM variants, suggesting that SOCoM provides equal quality but with a higher deviation yielding greater diversity. Supporting Information Figure 1(c) shows that the same trends hold under the Rosetta energy.
Complete designs
In addition to the smaller-scale focused library designs, a set of larger-scale libraries was also designed considering mutations at any position, over the range of 10, 15, 20, 25, and 30 mutated sites. Such scalability is not computationally tractable by any other structure-based design method, but when an appropriate screen/selection is available, a scale up improves the chances to find beneficial variants, either at higher mutational loads themselves,27,28 or even just as different subsets of the larger (but targeted) sequence space being explored experimentally.
Figure 5 shows the trends in average library energy at different numbers of mutated sites (optimally selected by SOCoM throughout the entire protein). A stabilizing trend is observed when increasing the number of sites from 10 to 30. However, the average stabilizing contribution at each position decreases when increasing the number of mutations. For example, a 10-site β-lactamase library provides an average stability of 1 kcal/mol while a 30-site library provides only 0.8 kcal/mol on average per mutation. Also, the average energetic favorability of point mutations over degenerate codon GFP libraries is ∼4 kcal/mol.
Figure 5.
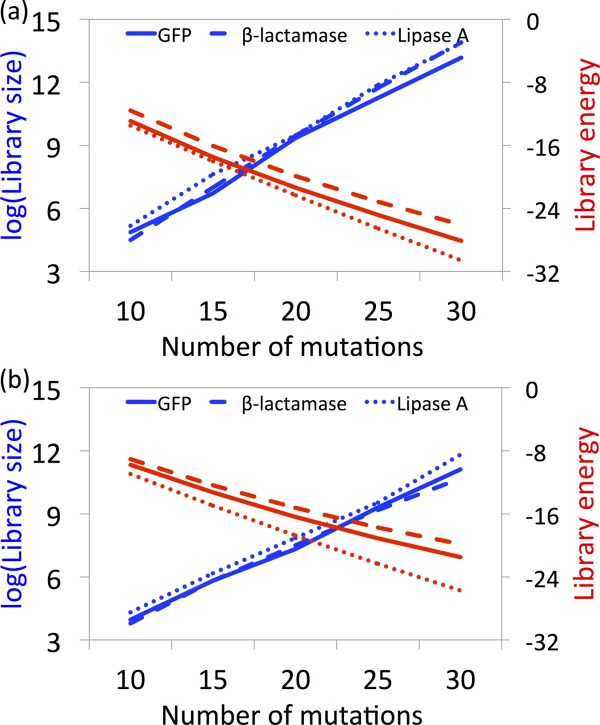
Trends in energies and sizes of SOCoM-based complete library designs over different numbers of mutated sites using (a) point mutations and (b) degenerate oligos.
These optimally constructed libraries were tested for stability by library enumeration. The average number of sequences over all three proteins' point mutation libraries is 8.4 × 104 for the 10-site library, 2.8 × 109 for the 20-site, and 5.7 × 1013 for the 30-site. Due to computational infeasibility of complete library enumeration, we chose 1000 variants for each of libraries for each of the proteins and compared them with 20 mutated-site random libraries representative of approaches regularly employed in library-based protein engineering. As such, 20 random positions with Shannon entropy scores between 1 and 2 were chosen60 from the MSA. Given these positions, we evaluated libraries composed of (A) all 20 amino acids at each of the 20 positions, mimicking NNK-based libraries;61 (B) only those amino acids represented in the MSA, representing more finely-targeted random libraries. For a direct comparison with SOCoM optimized libraries, we picked 1000 random variants from each and computed the CE-based energies.
Figure 6 illustrates the distributions of energies (with wild-type reference energy 0) for the various libraries. For all three proteins, the optimized libraries display a stabilizing trend while the variants of the random libraries have higher energy scores with respect to the wild-type. Apparently, entropy-based mutagenesis libraries produce few beneficial variants in terms of predicted stability, whereas SOCoM designed libraries provide many more and much better variants.
Figure 6.
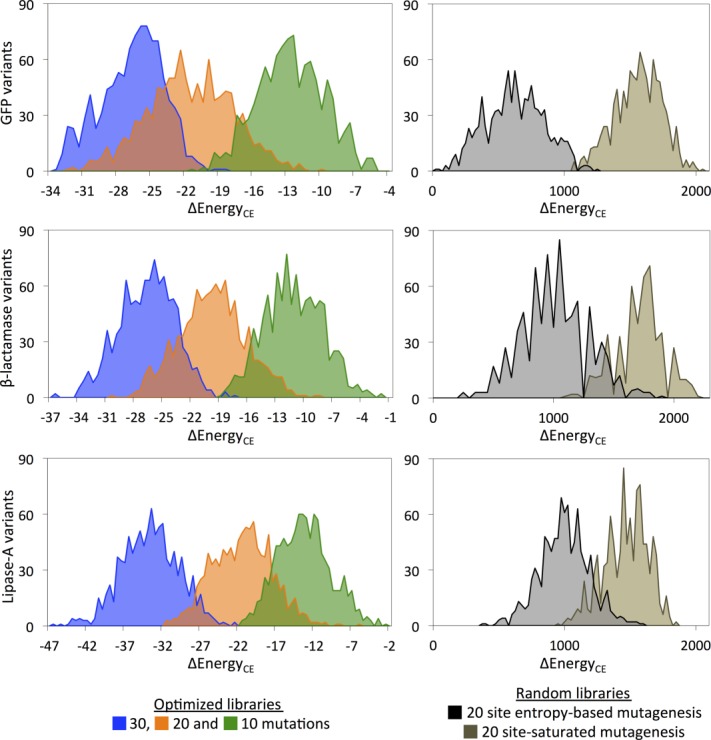
Histograms of the AMBER energies (postminimization) of structural models built for sampled variants from different complete library designs.
Calculation time
SOCoM is fast, requiring only minutes on commodity hardware (an off-the-shelf 2012 Macbook Pro) to optimize each library presented so far. This excludes the time for Rosetta modeling and CE training, which requires far more CPU time, but then the resulting model may be used repeatedly by all subsequent library designs. Tens of thousands of models must be generated by Rosetta in order to properly fit the CE parameters. Supporting Information Table 1 provides details on the resulting design space scalability and calculation times. For example, constructing all 30,000 Rosetta models for Lipase-A would require 810,000 CPU minutes. This task was accomplished in 13.5 h on a 25 node cluster (having four cores in each node). Interestingly, the optimization time does depend on the number of positions being considered and the number of choices at each. For example, 10-site complete design libraries required 1 min for GFP, 3 min for β-lactamase, and 29 min for lipase A. While we expected an increasing calculation time with increasing numbers of mutated sites, the differences were only of a few milliseconds. Consequently SOCoM can readily scale to design massive libraries. For example, as proof of principle we designed a 30-site GFP library, with 1 trillion unique variants, in less than a minute.
Discussion
We have introduced a novel method for optimization of combinatorial mutagenesis libraries, the first such method to perform large-library structure-based design. SOCoM works directly in library space, choosing positions and mutations to produce a set of variants enriched, on average, in a defined structure-based property. This stands in contrast to typical approaches, which work primarily at the level of individual variants and then generate a library from them, without care for the overall quality of the library members.
We have applied our method to a number of proteins that have been previously targeted via combinatorial mutagenesis, including green fluorescent protein, β-lactamase and Candida antarctica lipase A. We demonstrated the ability of SOCoM to effectively optimize libraries over a range of scenarios that would be appropriate in different contexts: with point mutations or degenerate codons, under different numbers of mutated sites, with or without focusing on particular positions, and controlling the overall library size. Comparison of results reveals that SOCoM can efficiently generate better libraries than other existing methods. Our results also suggest that higher numbers of mutated sites enable spreading out the energetically favorable mutations more broadly, while generating a diverse group of variants better than random libraries. In a study of scalability, we have found that we can optimize billion-member libraries in only a few minutes.
Our method is general, enabling the optimization of arbitrary structure-based properties of members of combinatorial mutagenesis libraries, constrained by key criteria such as library size and composition. Further, because it is expressed as an integer linear program, SOCoM enables the incorporation of additional constraints such as diversity,62 potentially set in the Pareto optimization framework63 enabling simultaneous optimization of multiple such criteria. Ultimately, designing libraries in this fashion promises to result in improved success rates in discovering beneficial variants.
Methods
Given a target protein, the goal is to design combinatorial mutagenesis libraries optimizing the structural energy of the constituent variants (Fig. 1). A preprocessing phase identifies allowed mutations and constructs energy-based potentials by which to score possible libraries. Then an optimization phase identifies the best protein library in terms of its average score over library members. The key input to SOCoM is a structure of the target protein; a multiple sequence alignment (MSA) of its homologs can be used to help identify allowed mutations. Additional parameters for preprocessing refine and control the allowed mutations and the terms to be included in the potentials. Parameters for optimization specify the number of sites to mutate, whether to use point mutations or degenerate oligos, the allowed number of mutations per site, and the total library size. Default values for these parameters, used in the presented results, are indicated.
Algorithm
Allowed mutations
In can be helpful both computationally and experimentally to prefilter the mutations to be considered at each position, rather than considering all 19 other amino acids. For example, a multiple sequence alignment of homologs may reveal which positions are highly conserved (and to which amino acids); this information may complement the structure-based analysis by encoding information about function,64 allosteric pathways,65 folding,66 etc. The prefiltering also helps keep under control the potential combinatorial explosion in the design space.
SOCoM includes preprocessing scripts to aid the specification of a position-specific list of allowed mutations defining the choices to consider for inclusion in a library. Ultimately it is up to the user to define which sites and amino acids to consider for library optimization, but the following approaches are generally useful.
A standard approach to prefiltering mutations is to select those of sufficient frequency in an MSA of homologs, assuming that evolutionarily-accepted mutations are likely to be favorable. Here, an MSA is preprocessed to identify sequences that are not too gappy (default at most 25%), that are sufficiently similar to the wild type (default at least 35% identity), and are sufficiently different from each other (default at most 95% identity). A background distribution (default McCaldon and Argos67) provides thresholds, potentially scaled to be more/less conservative (default unscaled); a substitution at a position is deemed acceptable if its MSA frequency exceeds the background threshold for the amino acid type.
Structure-based allowed mutations (in addition to homology-based allowed mutations) are those whose secondary structure Chou-Fasman propensities68 are similar enough (default propensity cutoff of 1.50 or more) to those of the corresponding wild-type residues in the target structure. In addition, by default mutations to and from proline and cysteine are excluded, due to their larger structural impact.
Target-based positions and allowed mutations are those manually indicated based on previous experimental results or insights into structure and function (e.g., to avoid or to focus on active site regions, depending on goals).
Energy-based potential
As discussed in the introduction, Cluster Expansion (CE) provides an efficient yet accurate representation of a given protein property, expressed as a sequence potential (i.e., a function of the amino acid sequence). SOCoM applies CE to derive an up to two-body potential Ψ(S) characterizing the energy of the structure adopted by sequence S = {s1, s2, …, sN}, where si represents the amino acid at position i and N is the total number of amino acids:
| 1 |
Here ψi(si) is the energetic contribution of amino acid si at position i and ψi,j(si, sj) is the contribution due to the pair-wise interaction between amino acid si at position i and sj at j. (The constant contribution from CE is distributed among self terms.31) To derive the terms in this potential, CE starts with a large training set of sequence:energy pairs, and considers which possible “clusters” (positions i for terms ψi and position pairs i, j for terms ψi,j) to include in the model (the rest are 0). Here we train CE based on structures and energies predicted by Rosetta69 for a large set of randomly sampled sequences; any method or force field (and indeed any structural properties) can be used for energy calculation and subsequently for CE training. Only those sequences with sufficiently good energies (below a desired energy cutoff value, e.g., 0 kcal/mol) are included in the training set. It is recommended to generate a set of low-energy sequences numbering at least (# one-body terms) × (# AAs) + 2 × (# two-body terms) × (# AAs)2, where the number of amino acids represents the average number of choices considered per site. This corresponds to ∼25,000 variants for a protein of 200 or so residues with approximately four allowed amino acids at each mutable position and ∼800 contact-derived two-body terms. All single-position clusters and all pair clusters between residues deemed to be in sufficient contact are considered. Inter-residue contacts are quantified by placing all rotamers of all amino acids at both positions, discarding rotamers with backbone clashes, and counting the fraction of remaining rotamer pairs with closest heavy-atom distances below 3 Å. The rotamer library by Lovell et al.70 is used, and if this fraction is above 0.05, the two positions are considered in contact. CE terms are then optimized as previously described.71 The potential Ψ enables the rapid calculation of the overall energy of any given sequence S, and the predictive quality of the potential can be assessed by cross-validation before proceeding to use the potential prospectively. We show below how to build on the CE-based model to enable efficient evaluation of a combinatorial library of variants.
As discussed in the Introduction, with sufficient training data the CE approach yields remarkably good predictions of structural properties based on amino acid sequence. It is particularly appropriate for library optimization, as the accuracy is certainly good enough to be used to guide library screening, and yet it is many orders of magnitude more efficient than atomistic evaluation of individual variants, and thus enables optimization of massive libraries over massive design spaces.
Tube-based library representation and evaluation
As illustrated in the right panel of Figure 1, a combinatorial mutagenesis library is specified in terms of particular amino acids (including wild-type) at particular mutation sites; all combinations are to be constructed. The illustrated libraries have two mutated sites each, with a choice from a set of two or three amino acids incorporated at each site. More generally, if there are M sites to be mutated with amino acids T1 = {a11, a12, …} to be used at the first position, T2 = {a21, a22, …} at the second, …, TM = {aM1, aM2, …} at the Mth, then the variants comprising the library are T1 × T2 × … × TM = {{a11, a21, …, aM1}, …, {a11, a21, …, aM2}, {a11, a22, …, aM1}, …, {a12, a22, …, aM2}, …}. The amino acid sets Ti can specify point mutations or, if extended to multisets, degenerate oligonucleotides (i.e., a codon mixture can include multiple “copies” of the same amino acid encoded by different codons). Thus for short we call these amino acid (multi-)sets “tubes,” as introduced previously in the OCoM method.29
Using the tube-based representation of a library, library design can be formulated as selecting a set of positions and corresponding set of tubes, from predetermined position-specific sets of allowed tubes. Thus it is analogous to single variant design, except using a tube alphabet rather than an amino acid or rotamer alphabet. The allowed tubes are predetermined based on possible mutations. One allowed tube contains just the wild-type, that is, no mutations at the site. When using point mutations, SOCoM enumerates for each position all available amino acid combinations that include the wild-type plus one or more allowed mutations, up to a user-specified maximum number of amino acids per tube (the prefiltering of allowed amino acids for each position keeps the combinatorics of this enumeration under control). When using degenerate oligos, SOCoM considers all degenerate codons that include the wild-type and no stop codons. Degenerate codons that include additional amino acids beyond the desired ones are eliminated if there are too many undesired ones; the default, used in this study, is to allow only desired amino acids. When multiple tubes encode the same proportions of amino acids, only the smallest one is used.
The previous section presented an energy-based potential for evaluating individual variants. Considering that this evaluation must be done throughout optimization, it would be extremely inefficient to enumerate all the variants in a combinatorial library and separately score them, in order to compute an aggregate score for the library. Instead, following the tube potential approach of OCoM29 (which was in turn based on analogous evaluations of recombination-based libraries24,26), SOCoM computes an average score over the variants in a library by summing position-specific tube-averaged potentials. The intuition is that each amino acid in a tube occurs the same number of times in the library (in the same combinations with the amino acids in the other tubes). To compute an average one-body score in the library, a sum can be taken of the position-specific amino acid contributions for each variant, and an average can then be taken over the variants. But since each amino acid at a position occurs in the same number of variants, the sum and average can be rearranged to instead sum position-specific average amino acid contributions. The same idea works for two-body terms. The tube-averaged potentials are thus computed as follows.
| 2 |
| 3 |
An entire library T = {T1, T2, …, TM} can then be evaluated by summing the tube-averaged potentials.
| 4 |
Library optimization
The tube-based library representation and evaluation provides the means for specifying a library optimization problem: given position-specific sets of allowed tubes and a desired library size (number of mutated positions and total number of variants), choose positions and tubes yielding a set of variants with optimal average energy. Since the energy includes two-body terms, it has the same form as the side-chain packing problem which has been shown to be NP-hard72 and can be readily reduced to this problem. Following the lead of OCoM,29 SOCoM formulates the optimization as an integer linear program for optimization via the IBM ILOG CPLEX solver. We present here only the single optimal design for each problem specification, though we note that SOCoM can readily generate a series of suboptimal library designs by invoking the optimizer once per identified design, adding constraints in subsequent rounds to ensure uniqueness of solutions.
The choice of tubes comprising a library is represented by a set of binary variables: xi,t indicates whether or not tube t is present at position i. In order to account for the two-body terms in the potential, pairwise binary variable yi,j,t,u are derived from these single position binary variables, indicating whether or not both tube t is at i and u is at j. Using these two sets of binary variables to represent the composition of a library, Eq. 4 can be rewritten as:
| 5 |
This is the objective function, to be minimized. To ensure a valid library, the following constraints impose the selection of exactly one tube at a position (Eq. 6) and consistency of the pairwise variables with the single-position ones (Eqs. 7 and 8).
| 6 |
| 7 |
| 8 |
The number of mutated positions and total library size are constrained to user-specified ranges. Equation 9 ensures that between µ and M positions have a selected tube that is not just the wild-type residue. Equation 10 ensures that the product of the number of amino acids in the selected tubes (expressed as the sum of the logs, so as to be linear) is between λ and Λ.
| 9 |
| 10 |
SOCoM is implemented in Python, and the source code is freely available for academic use. It interfaces to the CPLEX IP solver, which is freely available from IBM for academic use.
Data processing
Green fluorescent protein
We targeted wild-type GFP from Aequorea victoria (Uniprot ID GFP_AEQVI), using the structure with PDB ID 1GFL.73 The allowed mutations were derived from 243 homologs in Pfam PF01353, filtered to 44 non-gappy, diverse representatives. The Chou-Fasman secondary structure propensities were also used to generate allowed mutational choices. The CE-based energy potential was derived using training sets of ∼6000 randomly mutated sequences for focused design and ∼24,000 for complete design (following the formula in the methods) that were repacked and minimized in Rosetta. Correlation coefficients of more than 0.8 and 0.7, respectively, were achieved on predicted energies of new randomly chosen structures (chosen to not overlap with the training dataset and to constitute approximately 15% of its size). For the focused design studies, the preprocessing resulted in an average of about three degenerate oligos and 11-point mutation tube choices at each mutable position; for the complete design studies, the averages were about four degenerate oligos and 14-point mutation tube choices.
β-lactamase
Our target is TEM-1 β-lactamase from Escherichia coli, with PDB 1BT574 and an MSA from Pfam PF13354. Filtering 148 MSA sequences leaves 42 nongappy, diverse homologs, as used in our previous combinatorial recombination work.26 Allowed mutations were based on these along with Chou-Fasman. Structural energy scores were derived by CE using training sets of ∼6000 randomly mutated sequences for focused design and ∼36,000 for complete design. A nonoverlapping set of new variant test cases yielded correlation coefficients of more than 0.8 and 0.7, respectively. For focused designs, point mutation libraries were relaxed to at most three allowed mutations per tube in addition to wild-type. The additional choices allowed us to generate a bigger library for a direct comparison with Hayes et al. β-lactamase library. On an average, about three degenerate oligo and eight-point mutation tube choices were available for optimization at each mutable position for focused designs; and about four degenerate oligo and 19-point mutation tube choices for complete designs.
Lipase A
Our target is wild-type structure 2VEO from Candida Antarctica. The sequence was used to gather 500 similar sequences from three PSI-BLAST iterations; these were multiply aligned and used, in combination with Chou Fasman, to identify allowed mutations. CE training was based on ∼18,000 sequences for focused design and ∼30,000 for complete design, and yielded correlation coefficients of more than 0.7 for both sets using nonoverlapping new variants. The preprocessing resulted in about five degenerate oligo and 24-point mutation tube choices per site for focused designs and about four degenerate oligo and 17-point mutation tube choices for each site for complete designs.
Acknowledgments
The authors thank Dr. Yoonjoo Choi for valuable insights and assistance. In addition to his academic affiliation with Dartmouth College, C.B.K. is affiliated with Stealth Biologics, LLC, a company that engineers proteins to optimize functionality and minimize immunogenicity. Dartmouth has worked with him to manage all potential conflicts of interest arising from this affiliation.
Supporting Information
Additional Supporting Information may be found in the online version of this article.
Supplementary Information Figure 1.
Supplementary Information Table 1.
References
- Dahiyat BI, Mayo SL. De novo protein design: fully automated sequence selection. Science. 1997;278:82–87. doi: 10.1126/science.278.5335.82. [DOI] [PubMed] [Google Scholar]
- Socolich M, Lockless SW, Russ WP, Lee H, Gardner KH, Ranganathan R. Evolutionary information for specifying a protein fold. Nature. 2005;437:512–518. doi: 10.1038/nature03991. [DOI] [PubMed] [Google Scholar]
- Kuhlman B, Dantas G, Ireton GC, Varani G, Stoddard BL, Baker D. Design of a novel globular protein fold with atomic-level accuracy. Science. 2003;302:1364–1368. doi: 10.1126/science.1089427. [DOI] [PubMed] [Google Scholar]
- Koga N, Tatsumi-Koga R, Liu G, Xiao R, Acton TB, Montelione GT, Baker D. Principles for designing ideal protein structures. Nature. 2012;491:222–227. doi: 10.1038/nature11600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen C-Y, Georgiev I, Anderson AC, Donald BR. Computational structure-based redesign of enzyme activity. Proc Natl Acad Sci USA. 2009;106:3764–3769. doi: 10.1073/pnas.0900266106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zanghellini A, Jiang L, Wollacott AM, Cheng G, Meiler J, Althoff EA, Röthlisberger D, Baker D. New algorithms and an in silico benchmark for computational enzyme design. Protein Sci. 2006;15:2785–2794. doi: 10.1110/ps.062353106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siegel JB, Zanghellini A, Lovick HM, Kiss G, Lambert AR, St Clair JL, Gallaher JL, Hilvert D, Gelb MH, Stoddard BL, Houk KN, Michael FE, Baker D. Computational design of an enzyme catalyst for a stereoselective bimolecular Diels-Alder reaction. Science. 2010;329:309–313. doi: 10.1126/science.1190239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lippow SM, Wittrup KD, Tidor B. Computational design of antibody-affinity improvement beyond in vivo maturation. Nat Biotechnol. 2007;25:1171–1176. doi: 10.1038/nbt1336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roberts KE, Cushing PR, Boisguerin P, Madden DR, Donald BR. Computational design of a PDZ domain peptide inhibitor that rescues CFTR activity. PLoS Comput Biol. 2012;8:e1002477. doi: 10.1371/journal.pcbi.1002477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tinberg CE, Khare SD, Dou J, Doyle L, Nelson JW, Schena A, Jankowski W, Kalodimos CG, Johnsson K, Stoddard BL, Houk KN, Michael FE, Baker D. Computational design of ligand-binding proteins with high affinity and selectivity. Nature. 2013;501:212–216. doi: 10.1038/nature12443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grigoryan G, Reinke AW, Keating AE. Design of protein-interaction specificity gives selective bZIP-binding peptides. Nature. 2009;458:859–864. doi: 10.1038/nature07885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Korkegian A, Black ME, Baker D, Stoddard BL. Computational thermostabilization of an enzyme. Science. 2005;308:857–860. doi: 10.1126/science.1107387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Osipovitch DC, Parker AS, Makokha CD, Desrosiers J, Kett WC, Moise L, Bailey-Kellogg C, Griswold KE. Design and analysis of immune-evading enzymes for ADEPT therapy. Protein Engin Des Sel. 2012;25:613–623. doi: 10.1093/protein/gzs044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salvat RS, Parker AS, Guilliams A, Choi Y, Bailey-Kellogg C, Griswold KE. Computationally Driven Deletion of Broadly Distributed T cell Epitopes in a Biotherapeutic Candidate. Cell Mol Life Sci. 2014;71:4869–4880. doi: 10.1007/s00018-014-1652-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Treynor TP, Vizcarra CL, Nedelcu D, Mayo SL. Computationally designed libraries of fluorescent proteins evaluated by preservation and diversity of function. Proc Natl Acad Sci USA. 2007;104:48–53. doi: 10.1073/pnas.0609647103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perez-Aguilar JM, Xi J, Matsunaga F, Cui X, Selling B, Saven JG, Liu R. A computationally designed water-soluble variant of a G-protein-coupled receptor: the human mu opioid receptor. PloS One. 2013;8:e66009. doi: 10.1371/journal.pone.0066009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meyer MM, Hochrein L, Arnold FH. Structure-guided SCHEMA recombination of distantly related beta-lactamases. Protein Engin Des Sel. 2006;19:563–570. doi: 10.1093/protein/gzl045. [DOI] [PubMed] [Google Scholar]
- Chen MMY, Snow CD, Vizcarra CL, Mayo SL, Arnold FH. Comparison of random mutagenesis and semi-rational designed libraries for improved cytochrome P450 BM3-catalyzed hydroxylation of small alkanes. Protein Engin Des Sel. 2012;25:171–178. doi: 10.1093/protein/gzs004. [DOI] [PubMed] [Google Scholar]
- Miller BR, Demarest SJ, Lugovskoy A, Huang F, Wu X, Snyder WB, Croner LJ, Wang N, Amatucci A, Michaelson JS, et al. Stability engineering of scFvs for the development of bispecific and multivalent antibodies. Protein Engin Des Sel. 2010;23:549–557. doi: 10.1093/protein/gzq028. [DOI] [PubMed] [Google Scholar]
- Wijma HJ, Floor RJ, Jekel PA, Baker D, Marrink SJ, Janssen DB. Computationally designed libraries for rapid enzyme stabilization. Protein Engin Des Sel. 2014;27:49–58. doi: 10.1093/protein/gzt061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chica RA, Moore MM, Allen BD, Mayo SL. Generation of longer emission wavelength red fluorescent proteins using computationally designed libraries. Proc Natl Acad Sci USA. 2010;107:20257–20262. doi: 10.1073/pnas.1013910107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saraf MC, Moore GL, Goodey NM, Cao VY, Benkovic SJ, Maranas CD. IPRO: an iterative computational protein library redesign and optimization procedure. Biophys J. 2006;90:4167–4180. doi: 10.1529/biophysj.105.079277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mena MA, Daugherty PS. Automated design of degenerate codon libraries. Protein Engin Des Sel. 2005;18:559–561. doi: 10.1093/protein/gzi061. [DOI] [PubMed] [Google Scholar]
- Zheng W, Friedman AM, Bailey-Kellogg C. Algorithms for joint optimization of stability and diversity in planning combinatorial libraries of chimeric proteins. J Comput Biol. 2008;16:1151–1168. doi: 10.1089/cmb.2009.0090. [DOI] [PubMed] [Google Scholar]
- Pantazes RJ, Saraf MC, Maranas CD. Optimal protein library design using recombination or point mutations based on sequence-based scoring functions. Protein Engin Des Sel. 2007;20:361–373. doi: 10.1093/protein/gzm030. [DOI] [PubMed] [Google Scholar]
- Ye X, Friedman AM, Bailey-Kellogg C. Hypergraph model of multi-residue interactions in proteins: sequentially-constrained partitioning algorithms for optimization of site-directed protein recombination. J Comput Biol. 2007;14:777–790. doi: 10.1089/cmb.2007.R016. [DOI] [PubMed] [Google Scholar]
- Zaccolo M, Gherardi E. The effect of high-frequency random mutagenesis on in vitro protein evolution: a study on TEM-1 beta-lactamase. J Mol Biol. 1999;285:775–783. doi: 10.1006/jmbi.1998.2262. [DOI] [PubMed] [Google Scholar]
- Drummond DA, Iverson BL, Georgiou G, Arnold FH. Why high-error-rate random mutagenesis libraries are enriched in functional and improved proteins. J Mol Biol. 2005;350:806–816. doi: 10.1016/j.jmb.2005.05.023. [DOI] [PubMed] [Google Scholar]
- Parker AS, Griswold KE, Bailey-Kellogg C. Optimization of combinatorial mutagenesis. J Comput Biol. 2011;18:1743–1756. doi: 10.1089/cmb.2011.0152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grigoryan G, Zhou F, Lustig SR, Ceder G, Morgan D, Keating AE. Ultra-fast evaluation of protein energies directly from sequence. PLoS Comput Biol. 2006;2:e63. doi: 10.1371/journal.pcbi.0020063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou F, Grigoryan G, Lustig SR, Keating AE, Ceder G, Morgan D. Coarse-graining protein energetics in sequence variables. Physical Rev Lett. 2005;95:148103. doi: 10.1103/PhysRevLett.95.148103. [DOI] [PubMed] [Google Scholar]
- Hayes RJ, Bentzien J, Ary ML, Hwang MY, Jacinto JM, Vielmetter J, Kundu A, Dahiyat BI. Combining computational and experimental screening for rapid optimization of protein properties. Proc Natl Acad Sci USA. 2002;99:15926–15931. doi: 10.1073/pnas.212627499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sandström AG, Wikmark Y, Engström K, Nyhlén J, Bäckvall J-E. Combinatorial reshaping of the Candida antarctica lipase A substrate pocket for enantioselectivity using an extremely condensed library. Proc Natl Acad Sci USA. 2012;109:78–83. doi: 10.1073/pnas.1111537108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huh W-K, Falvo JV, Gerke LC, Carroll AS, Howson RW, Weissman JS, O'Shea EK. Global analysis of protein localization in budding yeast. Nature. 2003;425:686–691. doi: 10.1038/nature02026. [DOI] [PubMed] [Google Scholar]
- Heim R, Prasher DC, Tsien RY. Wavelength mutations and posttranslational autoxidation of green fluorescent protein. Proc Natl Acad Sci USA. 1994;91:12501–12504. doi: 10.1073/pnas.91.26.12501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soboleski MR, Oaks J, Halford WP. Green fluorescent protein is a quantitative reporter of gene expression in individual eukaryotic cells. FASEB J. 2005;19:440–442. doi: 10.1096/fj.04-3180fje. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang J, Campbell RE, Ting AY, Tsien RY. Creating new fluorescent probes for cell biology. Nature Rev. 2002;3:906–918. doi: 10.1038/nrm976. [DOI] [PubMed] [Google Scholar]
- Rolls MM, Stein PA, Taylor SS, Ha E, McKeon F, Rapoport TA. A visual screen of a GFP-fusion library identifies a new type of nuclear envelope membrane protein. J Cell Biol. 1999;146:29–44. doi: 10.1083/jcb.146.1.29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cutler SR, Ehrhardt DW, Griffitts JS, Somerville CR. Random GFP::cDNA fusions enable visualization of subcellular structures in cells of Arabidopsis at a high frequency. Proc Natl Acad Sci USA. 2000;97:3718–3723. doi: 10.1073/pnas.97.7.3718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jain RK, Ranganathan R. Local complexity of amino acid interactions in a protein core. Proc Natl Acad Sci USA. 2004;101:111–116. doi: 10.1073/pnas.2534352100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rennell D, Bouvier SE, Hardy LW, Poteete AR. Systematic mutation of bacteriophage T4 lysozyme. J Mol Biol. 1991;222:67–88. doi: 10.1016/0022-2836(91)90738-r. [DOI] [PubMed] [Google Scholar]
- Markiewicz P, Kleina LG, Cruz C, Ehret S, Miller JH. Genetic studies of the lac repressor. XIV. Analysis of 4000 altered Escherichia coli lac repressors reveals essential and non-essential residues, as well as “spacers” which do not require a specific sequence. J Mol Biol. 1994;240:421–433. doi: 10.1006/jmbi.1994.1458. [DOI] [PubMed] [Google Scholar]
- Arpino JAJ, Rizkallah PJ, Jones DD. Crystal structure of enhanced green fluorescent protein to 1.35 Å resolution reveals alternative conformations for Glu222. PloS One. 2012;7:e47132. doi: 10.1371/journal.pone.0047132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lab JP. TINKER—software tools for molecular design. MO: St. Louis; . TINKER version 6.0, released in year 2011. [Google Scholar]
- Ponder JW, Case DA. Force fields for protein simulations. Adv Prot Chem. 2003;66:27–85. doi: 10.1016/s0065-3233(03)66002-x. [DOI] [PubMed] [Google Scholar]
- Wallmark G. The production of penicillinase in Staphylococcus aureus pyogenes and its relation to penicillin resistance. Acta Path Microbiol Scand. 1954;34:182–190. doi: 10.1111/j.1699-0463.1954.tb00815.x. [DOI] [PubMed] [Google Scholar]
- Harding FA, Liu AD, Stickler M, Razo OJ, Chin R, Faravashi N, Viola W, Graycar T, Yeung VP, Aehle W, et al. A beta-lactamase with reduced immunogenicity for the targeted delivery of chemotherapeutics using antibody-directed enzyme prodrug therapy. Mol Cancer Therapeut. 2005;4:1791–1800. doi: 10.1158/1535-7163.MCT-05-0189. [DOI] [PubMed] [Google Scholar]
- Zlokarnik G. Fusions to beta-lactamase as a reporter for gene expression in live mammalian cells. Methods Enzymol. 2000;326:221–244. doi: 10.1016/s0076-6879(00)26057-6. [DOI] [PubMed] [Google Scholar]
- Meyer MM, Hiraga K, Arnold FH. Combinatorial recombination of gene fragments to construct a library of chimeras. Curr Protocols Prot Sci Chapter. 2006;26 doi: 10.1002/0471140864.ps2602s44. :Unit 26.2. [DOI] [PubMed] [Google Scholar]
- Schultz SC, Richards JH. Site-saturation studies of beta-lactamase: production and characterization of mutant beta-lactamases with all possible amino acid substitutions at residue 71. Proc Natl Acad Sci USA. 1986;83:1588–1592. doi: 10.1073/pnas.83.6.1588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Wals P-Y, Doucet N, Pelletier JN. High tolerance to simultaneous active-site mutations in TEM-1 beta-lactamase: distinct mutational paths provide more generalized beta-lactam recognition. Protein Sci. 2009;18:147–160. doi: 10.1002/pro.25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matagne A, Lamotte-Brasseur J, Frère JM. Catalytic properties of class A beta-lactamases: efficiency and diversity. Biochem J. 1998;330:581–598. doi: 10.1042/bj3300581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palzkill T, Botstein D. Identification of amino acid substitutions that alter the substrate specificity of TEM-1 beta-lactamase. J Bacteriol. 1992;174:5237–5243. doi: 10.1128/jb.174.16.5237-5243.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmidt M, Barbayianni E, Fotakopoulou I, Höhne M, Constantinou-Kokotou V, Bornscheuer UT, Kokotos G. Enzymatic removal of carboxyl protecting groups. 1. Cleavage of the tert-butyl moiety. J Organ Chem. 2005;70:3737–3740. doi: 10.1021/jo050114z. [DOI] [PubMed] [Google Scholar]
- Gedey S, Liljeblad A, Lázár L, Fülöp F, Kanerva LT. Preparation of highly enantiopure β-amino esters by Candida antarctica lipase A. Tetrahedron. 2001;12:105–110. [Google Scholar]
- Domínguez de María P, Carboni-Oerlemans C, Tuin B, Bargeman G, van der Meer A, van Gemert R. Biotechnological applications of Candida antarctica lipase A: state-of-the-art. J Mol Catal B. 2005;37:36–46. [Google Scholar]
- Tang WL, Zhao H. Industrial biotechnology: tools and applications. Biotechnol J. 2009;4:1725–1739. doi: 10.1002/biot.200900127. [DOI] [PubMed] [Google Scholar]
- Morley KL, Kazlauskas RJ. Improving enzyme properties: when are closer mutations better? Trends Biotechnol. 2005;23:231–237. doi: 10.1016/j.tibtech.2005.03.005. [DOI] [PubMed] [Google Scholar]
- Engström K, Nyhlén J, Sandström AG, Bäckvall J-E. Directed evolution of an enantioselective lipase with broad substrate scope for hydrolysis of alpha-substituted esters. J Am Chem Soc. 2010;132:7038–7042. doi: 10.1021/ja100593j. [DOI] [PubMed] [Google Scholar]
- Perelson AS, Weisbuch G, editors. Theoretical and experimental insights into immunology. Berlin: Springer-Verlag; 1992. , editors ( [Google Scholar]
- Nov Y. When second best is good enough: another probabilistic look at saturation mutagenesis. Appl Environ Microbiol. 2012;78:258–262. doi: 10.1128/AEM.06265-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng W, Ye X, Friedman AM, Bailey-Kellogg C. Algorithms for selecting breakpoint locations to optimize diversity in protein engineering by site-directed protein recombination. Comput Syst Bioinform. 2007;6:31–40. [PubMed] [Google Scholar]
- He L, Friedman AM, Bailey-Kellogg C. A divide-and-conquer approach to determine the Pareto frontier for optimization of protein engineering experiments. Proteins. 2012;80:790–806. doi: 10.1002/prot.23237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Verma D, Jacobs DJ, Livesay DR. Variations within class-A β-lactamase physiochemical properties reflect evolutionary and environmental patterns, but not antibiotic specificity. PLoS Comput Biol. 2013;9:e1003155. doi: 10.1371/journal.pcbi.1003155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang J-S, Seo SW, Jang S, Jung GY, Kim S. Rational engineering of enzyme allosteric regulation through sequence evolution analysis. PLoS Comput Biol. 2012;8:e1002612. doi: 10.1371/journal.pcbi.1002612. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matsuoka M, Kikuchi T. Sequence analysis on the information of folding initiation segments in ferredoxin-like fold proteins. BMC Struct Biol. 2014;14:15. doi: 10.1186/1472-6807-14-15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCaldon P, Argos P. Oligopeptide biases in protein sequences and their use in predicting protein coding regions in nucleotide sequences. Proteins. 1998;4:99–122. doi: 10.1002/prot.340040204. [DOI] [PubMed] [Google Scholar]
- Chou PY, Fasman GD. Prediction of protein conformation. Biochemistry. 1974;13:222–245. doi: 10.1021/bi00699a002. [DOI] [PubMed] [Google Scholar]
- Rohl CA, Strauss CEM, Misura KMS, Baker D. Protein structure prediction using Rosetta. Methods Enzymol. 2004;383:66–93. doi: 10.1016/S0076-6879(04)83004-0. [DOI] [PubMed] [Google Scholar]
- Lovell SC, Word JM, Richardson JS, Richardson DC. The penultimate rotamer library. Proteins. 2000;40:389–408. [PubMed] [Google Scholar]
- Hahn S, Ashenberg O, Grigoryan G, Keating AE. Identifying and reducing error in cluster-expansion approximations of protein energies. J Comput Chem. 2010;31:2900–2914. doi: 10.1002/jcc.21585. [DOI] [PubMed] [Google Scholar]
- Pierce NA, Winfree E. Protein design is NP-hard. Prot Engin Des Sel. 2002;15:779–782. doi: 10.1093/protein/15.10.779. [DOI] [PubMed] [Google Scholar]
- Yang F, Moss LG, Phillips GN. The molecular structure of green fluorescent protein. Nat Biotechnol. 1996;14:1246–1251. doi: 10.1038/nbt1096-1246. [DOI] [PubMed] [Google Scholar]
- Maveyraud L, Mourey L, Kotra LP, Pedelacq J-D, Guillet V, Mobashery S, Samama J-P. Structural basis for clinical longevity of carbapenem antibiotics in the face of challenge by the common class A β-lactamases from the antibiotic-resistant bacteria. J Am Chem Soc. 1998;120:9748–9752. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Information Figure 1.
Supplementary Information Table 1.


