Abstract
This study presents a framework for viscoelasticity where the free energy density depends on the stored energy of intact strong and weak bonds, where weak bonds break and reform in response to loading. The stress is evaluated by differentiating the free energy density with respect to the deformation gradient, similar to the conventional approach for hyperelasticity. The breaking and reformation of weak bonds is treated as a reaction governed by the axiom of mass balance, where the constitutive relation for the mass supply governs the bond kinetics. The evolving mass contents of these weak bonds serve as observable state variables. Weak bonds reform in an energy-free and stress-free state, therefore their reference configuration is given by the current configuration at the time of their reformation. A principal advantage of this formulation is the availability of a strain energy density function that depends only on observable state variables, also allowing for a separation of the contributions of strong and weak bonds. The Clausius-Duhem inequality is satisfied by requiring that the net free energy from all breaking bonds must be decreasing at all times. In the limit of infinitesimal strains, linear stress-strain responses and first-order kinetics for breaking and reforming of weak bonds, the reactive framework reduces exactly to classical linear viscoelasticity. For large strains, the reactive and classical quasilinear viscoelasticity theories produce different equations, though responses to standard loading configurations behave similarly. This formulation complements existing tools for modeling the nonlinear viscoelastic response of biological soft tissues under large deformations.
Keywords: Soft tissue mechanics, Viscoelasticity, Mixture theory, Reaction kinetics
1. Introduction
Many biological soft tissues exhibit viscoelastic responses (Fung, 1981), often with relaxation times that depend on the strain magnitude, suggesting a nonlinear viscoelastic behavior (Provenzano et al., 2001; Park and Ateshian, 2006; Duenwald et al., 2009). Though nonlinear viscoelasticity frameworks such as that of Schapery (1969) are used in biomechanics (Provenzano et al., 2002; Duenwald et al., 2010), they have not been adopted widely possibly because existing formulations remain complex. Nonlinear elasticity formulations broadly follow the elegant framework of Coleman and Noll (1963), where the stress response is derived from a free energy potential expressed as a function of the deformation gradient. However, that simplicity has not yet emerged in formulations of viscoelasticity.
Viscoelasticity is a macroscopic manifestation of the dissipation of energy in a loaded continuum. Microscopically, in long chain polymeric materials such as biological soft tissues, the mechanisms causing loss of free energy are typically related to breakage and reforming of weak molecular bonds under loading. Historically, formulations of viscoelasticity have relied on the introduction of internal variables to account for the relaxation mechanism characteristic of viscoelasticity, as first proposed by Green and Tobolsky (1946) for polymer solutions, and subsequently extended by Lubliner (1985) for isotropic solids and by Simo (1987) for anisotropic solids.
Internal state variables, also known as hidden variables, are non-observable by definition. Coleman and Gurtin (1967) provided a formalism for the thermodynamics of continua that employ internal state variables, which influence the free energy and are governed by differential equations involving the state of strain. Holzapfel and Simo (1996) and Holzapfel (1996) explicitly appealed to the formalism of Coleman and Gurtin (1967) in their modeling of solids with linear viscoelasticity.
Other authors, such as Fung (1981) and Puso and Weiss (1998), directly adopted the Boltzmann superposition principle for linear viscoelasticity with nonlinear elastic behavior. Fung (1981) described this type of material response as quasilinear viscoelasticity. These equivalent approaches have become the common standard for modeling viscoelastic tissues in the field of biomechanics.
An alternative approach to this traditional framework has been proposed by Wineman (2009), based on the concept of elastomer scission and cross-linking introduced by Tobolsky (1960), and using the framework of microstructural changes presented by Wineman and Rajagopal (1990) and Rajagopal and Wineman (1992).
The main objective of this study is to demonstrate that a complete framework for nonlinear viscoelasticity may be formulated using only observable state variables, where the stress is derived from a free energy potential using the traditional approach of Coleman and Noll (1963). This objective is achieved by reformulating Green and Tobolsky (1946)’s bond-breaking-and-reforming concept in the context of constrained reactive multigenerational solid mixtures (Ateshian, 2007; Ateshian and Ricken, 2010), where bonds are treated as mixture constituents whose breakage and reforming into new bonds is modeled as a reaction governed by the axiom of mass balance.
Permanent strong bonds are responsible for the elastic response and reacting weak molecular bonds that repeatedly break and reform are responsible for the viscous response. Consistent with concepts introduced by Green and Tobolsky (1946) and Tobolsky (1960), and reprised by Wineman (2009), this approach assumes that weak molecular bonds can only sustain their loaded configuration temporarily, eventually breaking and immediately reforming into a new unloaded configuration that coincides with the current configuration of the mixture. Multiple generations of breaking and reforming bonds may exist simultaneously, each with its own reference configuration.
2. Reactive Viscoelasticity
2.1. General Formulation
The detailed formulation of the reactive mixture viscoelasticity framework is presented in section S.1 of the Supplemental Materials. The key finding from this formulation is that the strain energy density Ψr of a viscoelastic solid is dependent on the free energy stored in strong bonds that are permanent (in the absence of damage), and in weak bonds that break and reform in response to the loading. Strong bonds provide the elastic response and weak bonds are responsible for the viscous response.
In the master reference configuration X of the viscoelastic solid, all bonds are unloaded and intact. Upon loading, weak loaded bonds progressively break over time; when they break, they immediately reform into unloaded weak bonds (section S.2). Newly formed weak bonds may break and reform again when subjected to further loading. Bonds formed at time t = u have a reference configuration Xu that coincides with the current configuration of the material at time u, thus Xu = χ(X, u), where χ(X, t) denotes the motion of the solid relative to the master configuration X, which also corresponds to the motion of the strong bonds. Weak bonds that (re)form at time u are described as u–generation bonds.
Different weak bond species may coexist in a viscoelastic solid, which may break and reform at different rates, or in response to different forms of loading. For example, some bonds may only break and reform in response to distortional strain, whereas others may respond to dilatational strain. These distinctions become important in the context of formulating a general viscoelasticity theory as addressed below. However, for simplicity, we start by assuming that there is only one species of weak bonds. All weak bonds can break and reform at any time t; let wu (X, t) represent the current mass fraction of total weak bonds from this species that were (re)formed at u. By definition, wu is bounded (0 ≤ wu ≤ 1) and its value is zero for t ≤ u. The bond mass fraction wu represents an observable (i.e., non-hidden) state variable in this formulation, whose temporal evolution is governed by the axiom of mass balance.
Let the free energy density of strong bonds be denoted by , where θ is the absolute temperature and F = ∂χ/∂X is the deformation gradient of the solid. Similarly, let the free energy density of weak bonds formed at u be denoted by , where is the free energy density of this weak bond species when all its bonds are intact (section S.3), and Fu = ∂χ/∂Xu is the deformation gradient relative to the reference configuration Xu. These two deformation gradients are related by
| (1) |
where F(X, u) = ∂Xu/∂X is time-invariant. Fu (X, t) is equivalent to Truesdell and Noll (1992)’s relative deformation gradient F(u) (X, t). When bond generations occur at discrete times u (i.e., if the strain changes stepwise at discrete time points), the net free energy density of the viscoelastic solid is given by
| (2) |
where wγ refers generically to all wu’s and the summation is taken over all discrete generations u; all state variables in this expression (i.e., θ, F or Fu, and wu) are evaluated at (X, t). In the treatment below, the following notational simplification is adopted: For state variables v, we may use the simplified notation v (t) ≡ v (X, t). For functions of state f, we may use the simplified notations f (v) ≡ f (v; X, t) and f [v (t)] ≡ f (v; X, t) when the time variable must be explicit.
For self-consistency in the summation of Eq.(2), the free energy density represents free energy per volume in the reference configuration X. The corresponding expression for the Cauchy stress T of the viscoelastic solid is derived from this expression using the standard hyperelasticity relation, as shown from the theory of constrained solid mixtures (Ateshian and Ricken, 2010),
| (3) |
Substituting Eq.(2) into Eq.(3), employing the relation of Eq.(1) and recognizes that wu’s are state variables independent of the deformation gradient produces
| (4) |
Here, Te (θ, F) is the Cauchy stress resulting from strong bonds,
| (5) |
where J = det F, and Tb (θ, Fu) is the Cauchy stress of fully intact weak bonds,
| (6) |
Details of the differentiation are presented in section S.4.
2.2. Bond Kinetics
The time evolution of the bond mass fraction wu is governed by the kinetics of bond breaking and reforming (section S.2), constrained by the axiom of mass balance for each bond generation,
| (7) |
where ŵu is the bond mass fraction supply to generation u from all other generations (section S.3). Since ŵu is a function of state, its functional form must be provided by a constitutive model that describes the rate of bond reforming and breaking in response to loading. In general, ŵu is a function of all the state variables (θ, F, wγ) in this framework. According to the axiom of mass balance for the mixture there can be no net change in total bond mass from this species,
| (8) |
Combining Eqs.(7)–(8), integrating the resulting expression and making use of the initial condition when there is only a single generation at rest produces a constraint on the mass fractions from all generations,
| (9) |
As shown in section S.5, step loading at time v > u from a prior state of rest shows that the solution wu (X, t) to Eq.(7) produces the reduced relaxation function for this reactive viscoelastic material, which may be denoted by g (θ, Fu (v); X, t − v) for t ≥ v. This notation emphasizes that the relaxation in response to a deformation Fu (v) may depend on the nature and magnitude of the strain at time v.
Using this functional representation of the solution to Eq.(7) for the first loaded generation, and assuming that all generations of a bond species relax according to the same functional response g, a recursive expression may be formulated for subsequent bond generations based on the constraint of Eq.(9). Thus, for u–generation bonds (re)forming in an unloaded state during the time interval u ≤ t < v, and subsequently breaking in response to loading at t = v, the bond mass fraction is given by
| (10) |
where
| (11) |
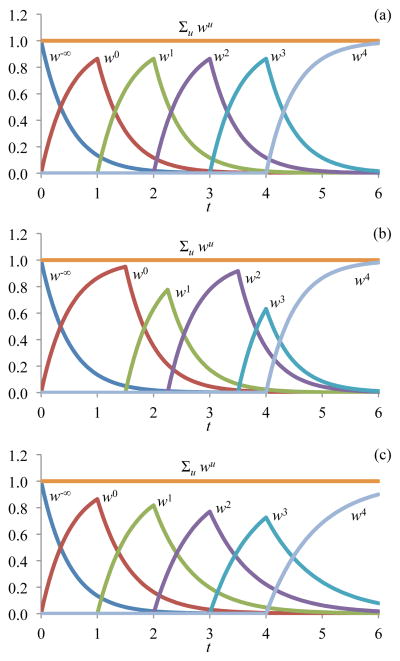
In this recursive expression, the earliest generation u = −∞, which is initially at rest, produces wu (t) = 1 for t < v and wu (t) = g (θ, Fu (v); X, t − v) for t ≥ v; this latter expression seeds the recursion for the subsequent generations. Therefore, providing a functional form for g suffices to produce the solution for all bond generations u (Figure 1). The evaluation of the strain energy density in Eq.(2) and stress in Eq.(4) may now be performed given the expression of Eq.(10).
Figure 1.
Examples of the temporal response of mass fractions wu for six generations of a bond species, evaluated from Eq.(10) with g = e−t/τ where (a) τ = 0.5 for all generations and time increments between consecutive changes in deformation are uniformly spaced; (b) τ= 0.5 for all generations and time increments between consecutive changes in deformation are non-uniformly spaced; and (c) τ varies with the state of deformation (from 0.5 at t = 0 to 0.9 at t = 4, by increments of 0.1) and time increments between consecutive changes in deformation are uniformly spaced.
For completeness, the expression for the mass fraction supply of each generation may be obtained by substituting Eq.(10) into Eq.(8),
| (12) |
where ġ is the time derivative of g. This result shows that ŵu is generally dependent upon the deformation as well as the bond mass fractions from all extant generations. For the earliest generation u = −∞, ŵu (t) = 0 for t < v and ŵu (t) = ġ (θ, Fu (v); X, t − v) for t ≥ v. We may refer to this constitutive model for bond breaking and reforming reaction as type I bond kinetics.
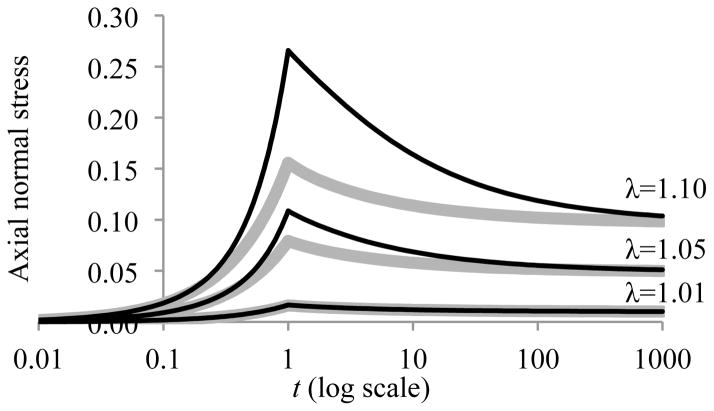
Type I bond kinetics may be used to model nonlinear viscoelastic responses where the reduced relaxation function g varies with a strain measure associated with Fu (v), as explained in section S.6 and illustrated in Figure 2.
Figure 2.
Representative stress-relaxation responses to a ramp-and-hold deformation in uniaxial tension, when g either varies with (black curves), or is independent of (gray curves) the deformation Fu (v). Three pairs of responses are shown, with increasing values of the stretch ratio λ at the end of the ramp. The functional form of g is given in Eqs.(S.28)–(S.29), with τ0 = 0.05, β = 0.5, α = 2, and τ1 = 100 (black curves) or τ1 = 0 (gray curves). The functional form of and is given in Eq. (S.42), with E = 1, ν = 0.3 and β = 0.5 for strong and weak bonds.
Consider the special case when the reduced relaxation function g is exponential and independent of the strain magnitude,
| (13) |
where τ(θ) is the relaxation constant (since θ is assumed constant in this isothermal framework). In this case, it may be shown that the recursion formula of Eq.(10) reduces to
| (14) |
and the mass fraction supply is given by ŵu =−wu/τ(θ) for the bond-breaking reaction (t ≥ v). This expression for ŵu is representative of first-order chemical kinetics for this reaction (Tinoco et al., 1995).
The pattern of wu (t) in Eq.(14) suggests that an alternative bond mass fraction solution may be proposed for any relaxation function g (t) which is independent of the strain magnitude,
| (15) |
This solution satisfies the mass balance for all bond generations, Eq.(9), and the corresponding form of ŵu is thus
| (16) |
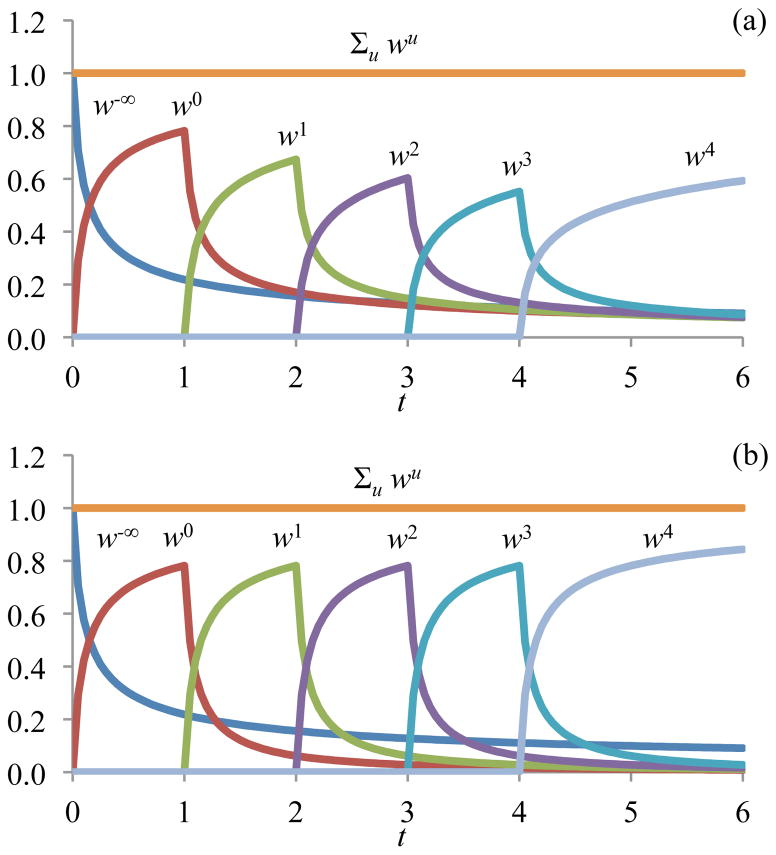
which satisfies Eq.(8). Except for the special case when g is exponential, the expressions of Eqs.(10) & (15) produce different solutions for wu as illustrated in Figure 3, emphasizing that there is no unique form for the constitutive relation of ŵu. We may refer to the constitutive relation of Eq.(16) as type II bond kinetics. Unlike Eq.(10), the form given in Eq.(15) cannot be used when g depends on strain since it is not possible to guarantee that wu (X, t) would remain positive for arbitrary strain histories. Therefore, nonlinear viscoelasticity requires type I bond kinetics.
Figure 3.
Comparison of the temporal responses of mass fractions wu for six generations of a bond species, when using (a) the solution of Eq.(10) for type I bond kinetics and (b) the solution of Eq.(15) for type II. In both cases, the reduced relaxation function is g = (1 + t/τ)−β, with τ= 0.05 and β = 0.5, and step changes in the deformation occur at uniformly distributed time increments.
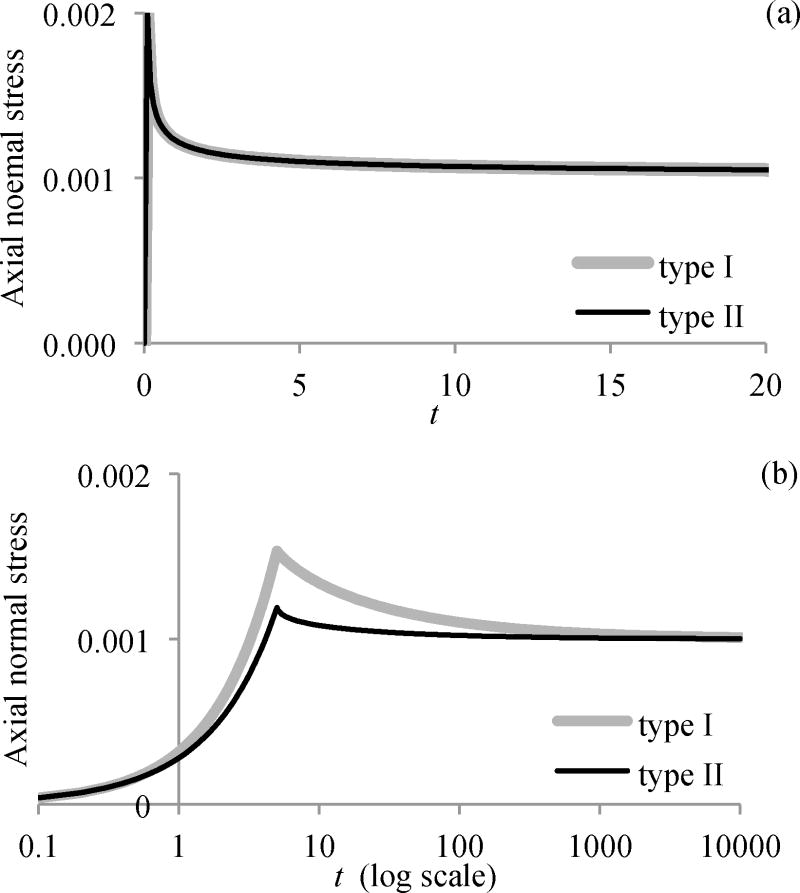
Using the form of g employed in Figure 3, an analysis of uniaxial tensile stress relaxation with type I and type II kinetics shows that the responses to a step deformation (single breaking bond generation) are identical for the two types, but differ substantially when the axial stretch is ramped at a finite rate (Figure 4). This behavior can be explained by the fact that type I bonds break at the same rate for all generations including the first one (Figure 3a), whereas type II bonds break significantly faster starting from the second generation (Figure 3b).
Figure 4.
Stress relaxation in response to (a) a step deformation and (b) a ramp-and-hold deformation, using type I and type II bond kinetics as described in Eqs.(10) and (15), respectively. The reduced relaxation function corresponds to that of Figure 3. The functional forms of and for evaluation of the stress from Eq.(4) correspond to a Hookean isotropic solid under infinitesimal strains, each with Young’s modulus = 1 and Poisson’s ratio = 0.3. The prescribed axial normal strain is 10−3.
2.3. Reactive Quasilinear Viscoelasticity
Now consider the case when the deformation varies continuously over time, such that new bond generations come into existence continuously. Letting v = u + du in the type II relation of Eq.(15), where du represents a differential increment in time, and recalling that g (0) = 1 produces wu (t) = −H (t − u) ġ (t − u) du for all generations subsequent to the initial one (u = −∞), and w−∞(t) = H (t) g (t) for the initial generation (assuming that loading starts at t = 0), where H (·) is the Heaviside unit step function. Therefore, the summations appearing in Eqs.(2) & (4) may be converted to integrals of the form
| (17) |
and
| (18) |
where Fu (t) = F(t) · F−1 (u) according to Eq.(1). Since the reduced relaxation function is independent of the strain magnitude, even though the dependence of the stress on the strain may be nonlinear, we may refer to this special case as reactive quasilinear viscoelasticity, understanding that reactive QLV generally employs type II bond kinetics.
2.4. Reactive Linear Viscoelasticity
For infinitesimal strains and infinitesimal rotations, the dependence of the functions of state on Fu (t) is equivalent to a dependence on ε(t) − ε(u), where ε is the infinitesimal strain tensor. In this case, Eqs.(17) & (18) reduce to
| (19) |
and
| (20) |
If the constitutive relation for the stress is linear, then Tb [ε(t) − ε(u)] = Tb [ε(t)] − Tb [ε(u)] and, recognizing that g (0) = 1, the expression for the stress reduces to
| (21) |
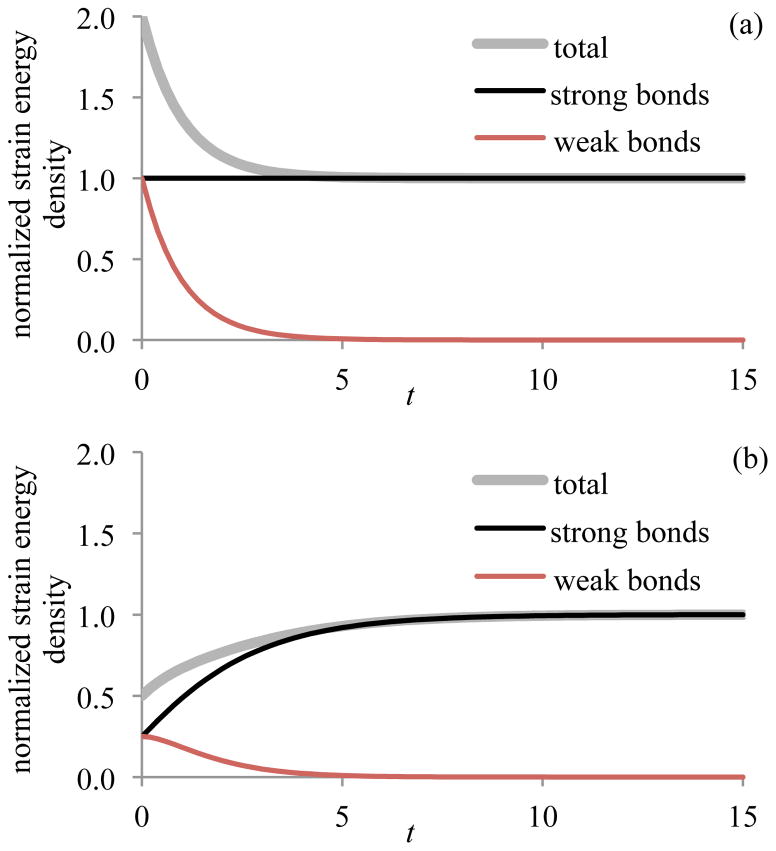
This equation represents the stress response for linear viscoelasticity with type II bond kinetics in this reactive viscoelasticity framework. As shown below, this expression for the stress is identical to the classical formulation for linear viscoelasticity. In section S.7, these expressions are used to derive the strain energy density and stress responses of a standard linear solid in creep and stress relaxation using the exponential relaxation of Eq.(13). Representative plots of the strain energy density response to these loading configurations are presented in Figure 5. These results demonstrate that the free energy density of weak bonds peaks immediately upon loading, then subsides to zero over time. In stress relaxation, the total free energy density decreases over time, whereas in creep it increases over time.
Figure 5.
Temporal response of the strain energy density for the standard linear solid in (a) stress relaxation and (b) creep, based on Eqs.(S.30) & (S.34), with β= 1 and τ= 1. The plotted strain energy density is normalized to in stress-relaxation and in creep. Also shown are the contributions from the strong bonds, , and from the weak bonds, .
2.5. Multiple Bond Species
When there are multiple weak bond species present in the material, such as species that relax at different rates or are triggered by different strain invariants, the additive framework presented above applies, under the assumption that there are no nonlinear interactions among the free energies of the various weak bond species, nor between those of weak and strong bond species. Thus, a generalization of Eq.(2) to multiple weak bond species presents as
| (22) |
where is made to depend on a reduced relaxation function gb as per Eq.(10), such that gb and may have different functional forms for different bond species. For example, it may be used to model anisotropic viscoelasticity, as illustrated in section S.8.
In the case of reactive quasilinear viscoelasticity, the integrals of Eqs.(17)–(18) may be generalized to the case of continuous relaxation spectra by assuming that has the same functional form for a continuous range of bond species that have distinct relaxation constants τb (θ), in which case the summation over b in the above relation would have to be converted to a suitable integral, as illustrated in section S.9.
3. Classical Quasilinear Viscoelasticity
Classical formulations of quasilinear viscoelasticity are generally presented in terms of the 2nd Piola-Kirchhoff stress S(θ, F) and the relaxation function G (t), with the form
| (23) |
where Se has the functional form of the elastic equilibrium stress and G (t → ∞) = 1 (Fung, 1981; Puso and Weiss, 1998). With no loss of generality, let G (0+) = 1 + β and recall that Se (t → −∞) = 0 in the resting configuration, so that the reduced relaxation function may be defined as g (t) = (G (t) − 1)/β and the above integral becomes
| (24) |
where Sb (θ, F) ≡ βSe (θ, F) for comparison with the reactive framework. Using integration by parts and assuming that loading starts at t = 0, this expression may be further rearranged as
| (25) |
The Cauchy stress is obtained from this expression using
| (26) |
Substituting Eq.(25) into Eq.(26) produces an expression that is generally different from the stress formulation for reactive quasilinear viscoelasticity as given in Eq.(18), except for the special case of stress relaxation in response to a prescribed step deformation as shown in section S.5. The responses to other loading configurations, including stress-relaxation following stretching at a constant rate, creep in response to a step normal stress, and simple shearing at a constant shear rate, demonstrate various degrees of differentiation based on the strain history, as illustrated in section S.10. These results demonstrate that, under large strains, the viscous (weak bond) stresses in the reactive framework dissipate faster than in the classical framework, when using an exponential reduced relaxation function.
In the range of infinitesimal strains and rotations however, the deformation gradient simplifies to F(t) ≈ I + ω (t) + ε(t) where ε is the infinitesimal strain tensor (symmetric part of the spatial displacement gradient) and I + ω is the infinitesimal rotation tensor (ω is the antisymmetric part of the spatial displacement gradient). In that case, S(θ, F) ≈ T(θ, ε) and the expression of Eq.(25) reduces exactly to Eq.(21), thus these two frameworks agree in the limit of linear viscoelasticity.
4. Conclusion
This study presents a framework for viscoelasticity where the free energy density depends on the stored energy of intact strong and weak bonds, Eq.(2), and where weak bonds break in response to loading. The resulting expression for the stress is evaluated by differentiating the free energy density with respect to the deformation gradient, Eqs.(4)–(6), similar to the conventional approach for hyperelasticity (Coleman and Noll, 1963). This approach becomes feasible because the breaking and reformation of weak bonds is treated as a reaction governed by the axiom of mass balance, where the constitutive relation for the mass supply governs the bond kinetics. As a result, the evolving mass contents of breaking and reforming weak bonds serve as observable state variables in this framework (Figure 1). Weak bonds are assumed to reform in an energy-free (and stress-free) state, therefore their reference configuration is given by the current configuration at the time of their reformation.
Two types of bond kinetics are presented in this treatment, with mass supplies summarized in Eqs.(12) and (16). Both of these constitutive relations employ a reduced relaxation function g whose form is also based on constitutive assumptions. When g is exponential, the two types of bond kinetics produce the same solution for the evolving weak bond mass content; for other forms of g the responses differ (Figure 3), resulting in different stress histories under general loading conditions (Figure 4). These examples illustrate the influence of constitutive assumptions for bond kinetics on the viscoelastic response.
A principal advantage of this reactive viscoelasticity formulation is the availability of a strain energy density function that depends only on observable state variables, also allowing for a separation of the contributions of strong and weak bonds (Figure 5). The Clausius-Duhem inequality is satisfied by requiring that the net free energy from all breaking bonds must be decreasing at all times (section S.3). In addition to providing insights about the evolving stored energy of a viscoelastic material, this formulation may be further extended in future investigations that examine breaking of strong bonds, as may occur in plasticity and damage mechanics.
Similarly, it is straightforward to extend this framework to viscoelastic fluids, by letting for compressible fluids, or for incompressible fluids (J = 1), and adding a viscous stress Tv (θ, F, D) which is a function of the rate of deformation D. In that case, the total stress would be T = −pI + Tv (θ, F, D) +Σu wuTb (θ, Fu), where p is the pressure ( in the compressible case). The constitutive relation for the viscous stress would need to satisfy Tv : D ≥ 0 according to the Clausius-Duhem inequality (Coleman and Noll, 1963).
This formulation of reactive viscoelasticity reproduces the framework of linear viscoelasticity exactly when g is exponential. This agreement is indicative of self-consistency between the classical approach and the reactive model. Note that the exponential form of g in Eq.(13) satisfies ġ = −g/τ, which represents the axiom of mass balance in the special case of a linear first-order ordinary differential equation with constant coefficients. This linear equation is a manifestation of first-order kinetics in the reaction of breaking and reforming bonds. Any other postulated form of g would necessarily be the solution of a nonlinear equation of mass balance, therefore only the exponential form in Eq.(13) strictly describes the framework of linear viscoelasticity.
For large strains, the classical quasilinear viscoelasticity framework has been constructed from the assumption that Boltzmann’s linear superposition principle may be extended to the case when the stress varies nonlinearly with the strain. In particular, the superposition principle has to be applied to the second Piola-Kirchhoff stress since it is insensitive to rigid body rotations, as needed to enforce objectivity of the time derivative appearing in Eq.(23). In contrast, the reactive viscoelasticity framework does not depend on Boltzmann’s principle and does not involve a time derivative of the stress. Instead, the Cauchy stress for weak bonds appearing in Eq.(4) is a function of the relative deformation gradient Fu (t), a concept also found in the framework of Wineman and Rajagopal (1990); Rajagopal and Wineman (1992); Wineman (2009). Therefore, for large strains, there is no exact equivalence between the reactive and classical quasilinear frameworks. Nevertheless, as illustrated in section S.10 with an implementation of reactive viscoelasticity in the FEBio finite element software (Maas et al., 2012), the responses may remain very similar for a broad range of loading conditions.
In conclusion, this study demonstrates that it is possible to formulate a viscoelasticity framework that depends only on observable state variables. This formulation complements existing tools for modeling the nonlinear viscoelastic response of biological soft tissues under large deformations. It also sets up a framework for accommodating more complex combinations of energy loss from viscoelasticity and various forms of damage and repair, which represents a significant concern in the modeling of pathological processes in biological tissues.
Supplementary Material
Acknowledgments
Research reported in this publication was supported by the National Institute of General Medical Sciences and the National Institute of Arthritis, Musculoskeletal and Skin Diseases of the National Institutes of Health under award numbers R01GM083925 and R01AR043628. The content is solely the responsibility of the author and does not necessarily represent the official views of the National Institutes of Health. The author would also like to thank Prof. Kristin Myers, Columbia University, for her insightful comments on the topic of this study.
Footnotes
Conflict of Interest
The author has no conflict of interest to report with regard to this study.
References
- Ateshian GA. On the theory of reactive mixtures for modeling biological growth. Biomech Model Mechanobiol. 2007;6 (6):423–445. doi: 10.1007/s10237-006-0070-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ateshian GA, Ricken T. Multigenerational interstitial growth of biological tissues. Biomech Model Mechanobiol. 2010;9 (6):689–702. doi: 10.1007/s10237-010-0205-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coleman BD, Gurtin ME. Thermodynamics with internal state variables. J Chem Phys. 1967;47 (2):597–613. [Google Scholar]
- Coleman BD, Noll W. The thermodynamics of elastic materials with heat conduction and viscosity. Arch Ration Mech An. 1963;13 (1):167–178. [Google Scholar]
- Criscione JC, Humphrey JD, Douglas AS, Hunter WC. An invariant basis for natural strain which yields orthogonal stress response terms in isotropic hyperelasticity. J Mech Phys Solids. 2000;48 (12):2445–2465. [Google Scholar]
- Duenwald SE, Vanderby R, Jr, Lakes RS. Viscoelastic relaxation and recovery of tendon. Ann Biomed Eng. 2009 Jun;37 (6):1131–40. doi: 10.1007/s10439-009-9687-0. [DOI] [PubMed] [Google Scholar]
- Duenwald SE, Vanderby R, Jr, Lakes RS. Stress relaxation and recovery in tendon and ligament: experiment and modeling. Biorheology. 2010;47 (1):1–14. doi: 10.3233/BIR-2010-0559. [DOI] [PubMed] [Google Scholar]
- Fung Y. Biomechanics. springer-verlag; New York: 1981. p. 445. [Google Scholar]
- Green M, Tobolsky A. A new approach to the theory of relaxing polymeric media. J Chem Phys. 1946;14 (2):80–92. [Google Scholar]
- Holmes MH, Mow VC. The nonlinear characteristics of soft gels and hydrated connective tissues in ultrafiltration. J Biomech. 1990;23 (11):1145–56. doi: 10.1016/0021-9290(90)90007-p. [DOI] [PubMed] [Google Scholar]
- Holzapfel GA. On large strain viscoelasticity: continuum formulation and finite element applications to elastomeric structures. Int J Numer Meth Eng. 1996;39 (22):3903–3926. [Google Scholar]
- Holzapfel GA, Simo JC. A new viscoelastic constitutive model for continuous media at finite thermomechanical changes. Int J Solids Struct. 1996;33 (20):3019–3034. [Google Scholar]
- Lubliner J. A model of rubber viscoelasticity. Mech Res Commun. 1985;12 (2):93–99. [Google Scholar]
- Maas SA, Ellis BJ, Ateshian GA, Weiss JA. Febio: finite elements for biomechanics. J Biomech Eng. 2012 Jan;134 (1):011005. doi: 10.1115/1.4005694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park S, Ateshian GA. Dynamic response of immature bovine articular cartilage in tension and compression, and nonlinear viscoelastic modeling of the tensile response. J Biomech Eng. 2006 Aug;128 (4):623–30. doi: 10.1115/1.2206201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Provenzano P, Lakes R, Keenan T, Vanderby R., Jr Nonlinear ligament viscoelasticity. Ann Biomed Eng. 2001 Oct;29 (10):908–14. doi: 10.1114/1.1408926. [DOI] [PubMed] [Google Scholar]
- Provenzano PP, Lakes RS, Corr DT, Vanderby R., Jr Application of nonlinear viscoelastic models to describe ligament behavior. Biomech Model Mechanobiol. 2002 Jun;1 (1):45–57. doi: 10.1007/s10237-002-0004-1. [DOI] [PubMed] [Google Scholar]
- Puso M, Weiss J. Finite element implementation of anisotropic quasi-linear viscoelasticity using a discrete spectrum approximation. J Biomech Eng. 1998;120 (1):62–70. doi: 10.1115/1.2834308. [DOI] [PubMed] [Google Scholar]
- Rajagopal KR, Wineman AS. A constitutive equation for nonlinear solids which undergo deformation induced microstructural changes. Int J Plasticity. 1992;8 (4):385–395. [Google Scholar]
- Schapery RA. On the characterization of nonlinear viscoelastic materials. Polym Eng Sci. 1969;9 (4):295–310. [Google Scholar]
- Simo J. On a fully three-dimensional finite-strain viscoelastic damage model: formulation and computational aspects. Comput Method Appl M. 1987;60 (2):153–173. [Google Scholar]
- Tinoco I, Sauer K, Wang JC. Physical chemistry: principles and applications in biological sciences. 3. Prentice Hall; Englewood Cliffs, N.J: 1995. [Google Scholar]
- Tobolsky AV. Properties and structure of polymers. New York and London: John Wiley & Sons. Inc; 1960. [Google Scholar]
- Truesdell C, Noll W. The non-linear field theories of mechanics. 2. Springer-Verlag; Berlin: 1992. [Google Scholar]
- Wineman A. On the mechanics of elastomers undergoing scission and cross-linking. Int J Adv Eng Sci Appl Math. 2009;1 (2–3):123–131. [Google Scholar]
- Wineman A, Rajagopal K. On a constitutive theory for materials undergoing microstructural changes. Arch Mech. 1990;42 (1):53–75. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.