Abstract
Synaptic transmission requires that vesicles filled with neurotransmitter molecules be docked to the plasma membrane by the SNARE protein complex. The SNARE complex applies attractive forces to overcome the long-range repulsion between the vesicle and membrane. To understand how the balance between the attractive and repulsive forces defines the equilibrium docked state we have developed a model that combines the mechanics of vesicle/membrane deformation with an apparently new coarse-grained model of the SNARE complex. The coarse-grained model of the SNARE complex is calibrated by comparison with all-atom molecular dynamics simulations as well as by force measurements in laser tweezer experiments. The model for vesicle/membrane interactions includes the forces produced by membrane deformation and hydration or electrostatic repulsion. Combining these two parts, the coarse-grained model of the SNARE complex with membrane mechanics, we study how the equilibrium docked state varies with the number of SNARE complexes. We find that a single SNARE complex is able to bring a typical synaptic vesicle to within a distance of ∼3 nm from the membrane. Further addition of SNARE complexes shortens this distance, but an overdocked state of >4–6 SNAREs actually increases the equilibrium distance.
Introduction
The soluble n-ethylmaleimide-sensitive-factor attachment protein receptor (SNARE) (1,2) complexes are the core protein machinery involved in synaptic vesicle docking and fusion. SNARE proteins form a link between vesicles and the plasma membrane, providing a mechanism for zippering the two together. The transmembrane vesicle-associated protein synaptobrevin (Syb or v-SNARE) forms a four-helix bundle with the proteins SNAP-25 and the transmembrane protein syntaxin (Syx), which are attached to the neuronal plasma membrane and termed the “t-SNARE”. SNAP-25 contributes two helices (SN1 and SN2) to the bundle, while both Syx and Syb contribute one helix each (3,4). During exocytosis the vesicles are first tethered or targeted toward the plasma membrane (>25 nm (5)), then they are docked at the plasma membrane with the help of the adhesive forces provided by SNAREs. After docking, priming occurs, which finally leads to vesicle-to-membrane fusion (1). The zippering of the SNARE bundle is thought to provide the necessary force to bring the vesicle in proximity to the plasma membrane by overcoming the hydration or electrostatic repulsion between the two.
The process of synaptic vesicle docking and fusion can be viewed as deformation of a mechanical system, in which a synaptic vesicle, a nearly spherical lipid bilayer shell, is brought in proximity to the plasma membrane, a nearly flat lipid bilayer, under the influence of the attractive forces exerted by the SNARE complex. Key structural characteristics of the SNARE bundle have been determined experimentally, including its x-ray crystal structure (6) and the location of the layers thought to be essential to SNARE’s function (7), which have been confirmed through single molecule force experiments (8). All-atom simulations have been performed to analyze the structural aspects of the SNARE bundle including detailed interactions between the different helices (9) as well as to investigate the effects of oxidation and reduction of the SNAP25 linker domain on the formation of the SNARE bundle (10). Some all-atom simulation work has been done on the unzippering of the SNARE bundle (11), but time constraints prevent simulations for large displacements and longer timescales. In an effort to overcome timescale limitations, some coarse-grained (CG) simulations have been performed (12,13). Force fields for CG simulations have been developed (14). However, to suit a wide range of applications, these force fields still need to be refined (15). Relatively little has been done on coupling the SNARE unzipping process to the vesicle-plasma membrane behavior to address questions including that of how docking depends on the number of SNAREs. This problem is difficult because it must capture large length-scale deformations and electrostatics in the vesicle-plasma membrane system as well as the amino-acid-level chemical specificity essential to the functioning of the SNARE bundle.
There is significant debate about how many SNARE complexes are required to make synaptic fusion happen. Earlier studies suggested that 5–8 SNARE complexes form the fusion pore (16). However, recent studies suggest a smaller number of SNARE complexes. Thus, it was suggested recently that a single SNARE complex can trigger fusion (17), while stating the fact that the fusion rate increases with the number of SNAREs. In Sinha et al. (18), it has been proposed that two Syb units are required for fusion, based on fluorescence response of tagged Syb. The work done in Mohrmann et al. (19) suggests that three SNARE units are needed to carry out the fusion, on the basis of fusion rate. At the same time, studies performed on model systems in vitro suggest numbers ranging between 5 and 11 (20).
To investigate how the number of SNARE complexes affects vesicle docking, we developed a continuum model of the lipid bilayers and combined it with a CG model for the SNARE that includes chemical specificity. Specifically, the proteins in the SNARE bundle are represented by an α-carbon-based CG model that includes both structural and chemical specificity by employing an elastic network model (ENM) (21,22) and Miyazawa and Jernigan (23–25) contact energies, respectively. The SNARE CG model is calibrated to match the peak unzipping force determined by Gao et al. (8), and is used to calculate a force displacement curve for the unzipping process, along with snapshots of corresponding structures that provide information about the unzipping pathway. The continuum model for bilayer deformation is based on lipid membrane theory developed in Jenkins et al. (26) and is an extension of work done in Long et al. (27). It computes the force required to counter the vesicle-membrane repulsion, bringing the vesicle to a given distance from the membrane while taking full account of the vesicle and membrane deformation. Balancing the SNARE-induced attraction against the vesicle-membrane hydration or electrostatic repulsion provides us with information on the equilibrium gap between the two membranes for a given number of SNAREs. Based on this information, we study the effect of the number of SNAREs from the point of view of the mechanics of the process.
Materials and Methods
All-atom simulations
We conducted all-atom molecular simulations of SNARE helices in order to obtain some of the parameters for the SNARE CG model. All-atom (AA) simulations of the four individual helices as well as the full SNARE bundle were performed using the GROMACS molecular simulation package (28) and the CHARM22 force field (29). The starting structures for the four individual helices and the full SNARE bundle were extracted from the final timestep of a 40-ns AA simulation with initial configuration given by the high-resolution x-ray structure PDB:1N7S (7,11). (See the Supporting Material for a discussion.) For each set of runs, the corresponding structure was solvated in a waterbox (70 × 150 × 70 Å), and potassium ions were added to neutralize the overall charge. Additional potassium and chloride ions were added so that there was a 150-mM concentration of KCl to mimic physiological conditions (30). All bonds were constrained. Dynamics were run at 300 K first using an NVT ensemble for 100 ps followed by NPT for 100 ps using the Parrinello-Rahman barostat. Five sets of 40-ns-long runs were conducted with a timestep of 2 fs for Syb, Syx, SN1, SN2, and the SNARE bundle. Computations were performed at the Texas Advanced Computing Center (Austin, TX) through Extreme Science and Engineering Discovery Environment (XSEDE) resources.
SNARE coarse-grained model
A principal result of this work is the development of a CG model for the SNARE complex. Our goal has been to make it as simple as possible while retaining the identity of individual residues. As shown in Fig. 1 A, in our SNARE model every residue is represented by a bead located at the α-carbon of that residue.
Figure 1.
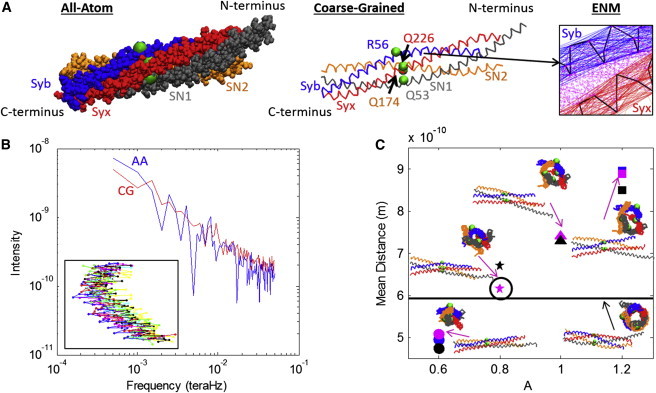
(A) The AA (left) and CG (middle) representations of the SNARE bundle are shown. Both models include helices Syb, Syx, SN1, and SN2 with each helix contributing one residue to the ionic layer (beads): R56, Q226, Q53, and Q174 respectively. The C-terminal ends of Syb and Syx play an integral role in the fusion process in that they attach to the vesicle (Syb) and plasma membrane (Syx). The ENM spring network (right) that maintains the individual helical structure is shown for Syb and Syx. (Thick lines) Cα backbones; (thin lines) ENM springs. The Miyazawa and Jernigan (23–25) contacts between Syb and Syx are also represented (dotted lines). (B) The spectra used to compare the fluctuations of the AA and CG models are shown for Syb. Values for ks of 0.0963 N/m and Rc of 20 Å were used for the CG model. (Inset) Ten snapshots of Syb during the corresponding AA simulation. (C) Mean distance for different values of parameter A along with snapshots of the SNARE bundle. (Black line) Original crystal. (Black circle) Version chosen for simulation. To see this figure in color, go online.
The size and mass of each bead are equivalent to the van der Waals radius and mass (31) of the bead’s corresponding residue. Two major types of interactions were accounted for in this CG model—those within individual helices, and those between them. An ENM (21,22) is used to represent the intrahelical bonds and interactions that maintain the individual helical structure as shown in Fig. 1 A. Pairs of beads within the cutoff distance, Rc, on the same helix are said to be in contact and are connected by a harmonic spring with the energy potential
| (1) |
where ks is the spring constant, r is the distance between the two beads, and r0 is the natural length of the spring. From the 40-ns-long individual helix AA simulations, it was observed that the natural state of each individual helix was a relatively straight conformation compared to the helices in the SNARE x-ray crystal structure. (The mean curvature of the helices in the SNARE bundle (3.11 × 107 l/m) is three times as large as that of the individual helices (1.03 × 107 l/m; see the Supporting Material.)) Because these straightened-out conformations represent the natural or relaxed state of the helices, they were used to construct the ENM. This is important because, as the helices unzip from the main bundle and break their helix-helix contacts, they revert to their natural straight conformation, releasing elastic energy.
The values of ks for the ENM were chosen by matching the spectrum of fluctuations of the AA simulations and the CG model for each helix independently. For the analysis of individual AA helix simulations, the positions of the α-carbons were extracted every 10 ps. For each α-carbon a time series of distance from its average location was calculated. The fast Fourier transform was then computed for each bead’s time series and averaged over all beads, yielding a single spectrum per helix. In order to make this comparison of the fluctuations, CG simulations were conducted for the four individual helices using Langevin dynamics at 300 K for a range of values of ks. (Details on numerical implementation of the CG simulation are provided in the Supporting Material.) The same fast Fourier transform analysis was conducted for individual helix CG simulations as the AA simulations. The time length of simulations required was determined by conducting a normal modes analysis on the CG model of the crystal structure, PDB:1N7S, for all helices individually using different values of ks. AA simulations were run for 2 ns, which is considerably longer than the characteristic time given as the inverse of the lowest natural frequency (see Table S1 in the Supporting Material). In order to best match the fluctuations, the root-mean-squared deviation between the AA and CG spectra was found for each run. An example of the comparison of both spectra is shown in Fig. 1 B for Syb with ks value of 0.0963 N/m. For all helices, ks was varied between 0.00009 N/m and 0.4816 N/m and the resulting root-mean-squared deviations for all values of ks are shown in the Supporting Material. Based on these data, a value of 0.0963 N/m was chosen for ks for all four helices.
The second main category of interaction in the CG model is the helix-helix interaction, which requires chemical specificity. These interactions are implemented by utilizing the contact energies from Miyazawa and Jernigan (23–25), which provide a scalable reference for residue-residue interactions (23–25). Any beads on separate helices interact if they are within the Miyazawa and Jernigan (23–25) cutoff distance, Rc_MJ. To avoid checking the distance between every bead during every timestep, a neighbor list is built every 1000 steps. Any beads on different helices that are within 1.5∗Rc_MJ of each other are added to the neighbor list. Contacts are determined from the pairs already chosen by the neighbor list.
Following Kim and Hummer (32), the interaction energy εij between residues i and j of the SNARE structure is scaled from the Miyazawa and Jernigan (23–25) contact energies eij (32):
| (2) |
Note that there is no self-interaction, i.e., Eq. 2 applies only for i ≠ j. Also, these interactions operate only between residues on different helices, intrahelical interactions being already represented by the ENM. There are two tunable parameters—a scaling parameter, λ, and a shifting parameter, e0. Throughout the tuning of parameters, e0 was set to 0. Although it was available as an extra parameter, it was not found necessary to match the SNARE structure and hence was not used in order to minimize the number of adjustable parameters.
Forces corresponding to the contact energies from Miyazawa and Jernigan (23–25) are implemented using a slightly modified 6-12 LJ potential. The format of this potential varies depending on whether there is attraction or repulsion between these residues as well as if the distance between beads is greater than or less than that the distance at which the potential minimum occurs, rij0. The sign of εij determines whether the interaction between the residues is attractive (negative) or repulsive (positive). The modified Lennard-Jones potentials (32) are as follows:
if εij < 0,
| (3) |
if εij > 0 and r < rij0,
| (4) |
and if εij > 0 and r ≥ rij0,
| (5) |
where r is the distance between the two beads and σij is the interaction radii. Eq. 4 contains a shift in the potential that ensures that repulsive pairs of beads will always repel each other.
The interaction radii is defined as the average of the van der Waals radii of residues i and j,
| (6) |
where is available as a tuning parameter and σi and σj are the van der Waals radii of residues i and j. In order to match both CG and AA behavior and structure, A was adjusted to match the SNARE bundle width, defined as the diameter of the tube-shaped space inside the bundle that can be seen if one looks along the center axis of SNARE. The reference bundle width was found by computing the mean distance of all of the nearest contacts of Miyazawa and Jernigan (23–25) from the SNARE crystal structure determined from PDB:1N7S. These 21 nearest contacts represent the distances between the inner residues of the bundle and therefore the bundle width. Fig. 1 C shows the mean distance for a few cases. The value of A is directly related to bundle width, and from Fig. 1 C we chose a value of A as 0.8 to produce a similar mean bundle width to the crystal structure. This value of A corresponds to interaction radii ranging from 3.6 Å for Gly-Gly and 5.44 Å for Trp-Trp (32).
The remaining parameter, λ, controls the strength of interhelical interactions and was determined by calibrating the results of simulated force-extension behavior of the SNARE complex by the recent experimental study by Gao et al. (8), which provided characteristic forces for the unzipping of the 4-helix SNARE bundle pulled apart in an optical tweezer experiment. The value of λ was calibrated to match the measured peak force of 14–19 pN (specifically, 17.2 pN). For our unzipping simulation, the C-terminal residues of Syx and Syb were each attached to a fixed bead by a spring with a spring constant kspb. Displacement control was used on the bead attached to the C-terminal Syb bead as opposed to the actual Syb C-terminal bead, to allow for rotation of the SNARE bundle.
To see how much the orientation of the pulling force on the SNARE matters, the simulations were performed in two ways: by applying a displacement to pulling beads attached to Syb89 and Syx256 through a spring (as shown in the article); and by directly applying displacements to Syb89 and Syx256. (The pulling beads allow for rotation of the SNARE bundle during the simulation and are hence less restrictive.) The results of these simulations were quite similar. To mimic the experimental setup in which the N-termini of Syx and Syb are connected, a FENE bond connecting the N-terminal residues of Syb and Syx was incorporated in the model to represent the additional residues, and the N-terminal disulfide bridge from the experiment of Gao et al. (8) is included. The potentials used to implement the FENE bond are as follows:
if r(t) < rc_FENE,
| (7) |
and if r(t) ≥ rc_FENE,
| (8) |
where r is the distance between two bonds at t; r0 is the maximum bond length; Δ is the resting bond length or, in this case, the original distance between the two beads (33); and rc_FENE is 0.9∗Δ. The value of r0 was determined by the number of residues that the spring represents, eight for Syb and five for Syx, times the maximum extension per residue, 3.65 Å (8). The FENE spring constant, kF, used was the same as ks for the ENM of 0.0963 N/m.
Before beginning the CG displacement control simulations, the SNARE structure was relaxed for 106 timesteps under quasi-static conditions, i.e., at 0 Kelvin. This relaxation was performed on the SNARE structure extracted from the final timestep of the 40 ns AA simulation in order to ensure that the initial structure was fully equilibrated. After this relaxation period, the C-termini beads were separated under displacement control using the two pulling beads that were discussed previously. The bead attached to the Syx C-terminus was held fixed, and all displacements were applied to the bead attached to the C-terminal Syb bead. For each displacement, this bead was moved 1 Å along the vector between the two pulling beads. After each displacement was applied, the structure was relaxed for 105 timesteps in order to allow it to equilibrate. At the end of the relaxation period, the forces on both pulling beads were nearly identical, and these forces were recorded as a function of displacement (see Fig. S4 in the Supporting Material).
Displacement control runs were conducted with 11 different values of λ between 0.16 and 0.72. This parameter directly adjusted the magnitude of the force, so it was used to match the peak unzipping force reported by Gao et al. (8) of between 14 and 19 pN. On this basis, a value of 0.3 was chosen to produce a peak force in the experimentally measured range of 17.2 pN.
Continuum model of the vesicle and plasma membrane
The vesicle and plasma membrane are subjected to forces from the SNARE complex drawing them together, and distributed distance-dependent electrostatic and hydration repulsion. During this process, the vesicle and plasma membrane both deform considerably and the task of the continuum model is to obtain a consistent solution of the deformed shape subject to these forces. The continuum calculations are based on the formulation of Jenkins et al. (26) and its extension to SNARE-mediated fusion by Long et al. (27). Our axisymmetric continuum model extends these formulations to include concentrated forces due to the SNARE molecules and the electrostatic forces due to the charges on the membranes or hydration repulsion.
The axisymmetric geometry is shown schematically in Fig. 2. We use a cylindrical coordinate system (r,θ,z), where θ is the angle of revolution about the z axis. Owing to the axisymmetric assumption, the forces exerted by the zipping of the SNARE complexes are represented by a circle of line force of magnitude F on a spherical vesicle of radius R (see Fig. 2 B) as well as on the plasma membrane. This line force counters the repulsive forces between the vesicle and the plasma membrane. As shown in Fig. 2 B, the line force acts along a latitude of the undeformed vesicle and is constrained to remain normal to the deformed surface. The location of the latitude is specified by the arc length S0 of a cross section in the reference configuration, which is taken to be a spherical vesicle. Because the plasma membrane is very large compared to the vesicle radius, its reference configuration is taken to be a flat circular membrane of radius L under pre-tension, T0. The SNARE forces act on a circle of radius S0 in the reference configuration, have the same magnitude F, and are always directed opposite to the force on the vesicle (Fig. 2, B and C).
Figure 2.
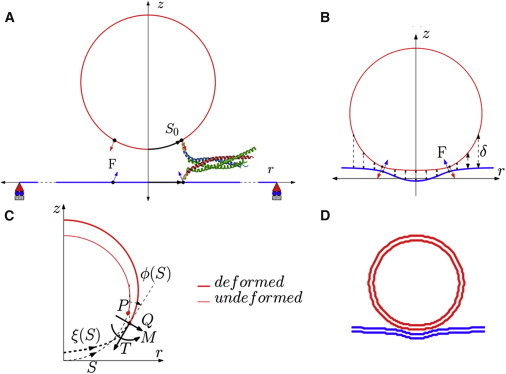
(A) A schematic of the axisymmetric model in the undeformed configuration showing the location of SNARE and direction of force applied. (B) The repulsive forces (shown by the dotted lines) act on the deformed configuration of the vesicle, as does the SNARE force, F. (C) The figure shows the convention for shear force (Q) in-plane tension (T) and moment (M) acting on the cross section of the membrane at location ξ(S), where ϕ(S) is the tangent angle in the undeformed configuration measured from the vertical. (D) Example of a deformed vesicle-plasma membrane complex for a 20-nm diameter vesicle docked by 15 SNAREs. To see this figure in color, go online.
In our model, the repulsive force depends only on the local separation δ, as shown schematically in Fig. 2. Following Bykhovskaia et al. (11), electrostatic and hydration repulsion between the vesicle and plasma membrane are calculated using Derjaguin’s approximation (34) in which interaction between curved surfaces is estimated assuming that the surfaces are locally flat. This approximation is valid if the length scale over which forces decay is much smaller than the radius of curvature of the vesicle. The applicable range of separations before vesicle to membrane fusion is 2–4 nm. In this range, the principal repulsive forces are due to electrostatics and hydration.
The functional form of both the electrostatic and hydration repulsion is approximately the same, an exponential decay. Electrostatics has the large decay length (typically 1 nm under physiological conditions) and smaller prefactor (34). The decay length for hydration repulsion is in the 1–4 Å range (34–37). Consequently, hydration dominates for small separation and electrostatics for larger separation. Much of the previous work suggests that the cross-over distance beyond which electrostatics dominates is ∼1.5 nm (34,36). However, recent work of Aeffner et al. (35) suggests that hydration repulsion exceeds electrostatic repulsion for distances up to ∼3 nm. Based on the work of Aeffner et al. (35), we have performed calculations taking hydration repulsion to be the dominant repulsive interaction. However, given some uncertainty regarding the relative importance of electrostatics and hydration, we have also computed results for the case where electrostatic repulsion is assumed to dominate. The hydration pressure takes on the form of an exponential decay,
| (9) |
where dw is the lipid bilayer separation, P0 is the hydration pressure amplitude, and λh is the decay length. According to Aeffner et al. (35), the prefactor, P0, ranges from 0.24 to 4.13 GPa and λh ranges from 2.3 to 3.7 Å. We chose to use a value of 0.43 GPa for P0 and a λh of 3.22 Å based on the parameters suggested for a synaptic vesicle corresponding to experiments performed in a physiologically relevant DOPC/Chol 70:30 mixture (35).
Local electrostatic interaction is determined by solving the Debye-Huckel equation for two infinite parallel planes separated by δ. We consider two limiting scenarios.
-
1.
The membranes have fixed charge density throughout the process of docking, which corresponds to the case when the lipid molecules are completely ionized and have a fixed charge.
-
2.
The membranes have fixed surface potential, which is achieved by adjusting the surface charge density of the ions in the Stern layer of the membrane or by varying the degree of ionization of the polarizable lipid molecules.
For the constant surface charge densities, the repulsive force along the z direction per unit area is given by
| (10) |
where σ1 andσ2 are the surface charge densities of the vesicle and neuron base, respectively; lD is the Debye length; ε is the relative permittivity of water; and ε0 is the permittivity of vacuum. The choice of surface charge σ1 is based on the force-displacement measurement by Marra (37) and the electrophoretic measurement by Ohsawa et al. (38). The reported value of surface charge is in the range 0.01–0.03 C/m2. Also, assuming the same surface charge density on the outer leaflet of the plasma membrane and based on the observation by Pekker and Shneider (39) that a charge density difference of only ∼0.0001 C/m2 between the inner and outer leaflet is necessary to maintain the resting potential difference of 70 mV for the neuron cell, we choose the value of σ1 = σ2 = −0.025 C/m2.
For the case of constant surface potential, the force per unit area is
| (11) |
When the two membrane structures are far away from each other, they have charge density given as σ1 = σ2 = −0.025 C/m2. The potentials on an isolated surface and charge density are related by
| (12) |
The value of surface potential for the bilayers, ϕ1 = ϕ2 = −25 mV, is evaluated using Eq. 12. As the vesicle approaches the membrane, the surface potential is held constant and Eq. 11 is used to obtain the force between the membranes. A similar approach was followed in Bykhovskaia et al. (11). However, in that work the mechanics of SNARE opening was not coupled to the electrostatic repulsion, and the SNARE-end opening was picked at 1 nm, whereas here the minimum separation of SNARE-ends is taken to be 2 nm. Primarily for this reason, the repulsive electrostatic forces in this work are in the range of tens of picoNewtons instead of the hundreds of picoNewtons quoted in Bykhovskaia et al. (11). Relevant parameters for modeling electrostatic forces are listed in Table S3.
Governing equations for the continuum membrane model and their solution
The vesicle-membrane system has been modeled under axisymmetry in an (r,θ,z) coordinate system. In the undeformed configuration, the vesicle is modeled as a sphere with radius R, whereas the undeformed plasma membrane is a circular disk of radius L >> R. As shown in Fig. 2, S refers to the undeformed arc length, whereas in the deformed configuration, the arc length is denoted by ξ. The tangent to the membrane makes an angle ϕ with the z axis and the mean curvature of the membrane surfaces is denoted by H.
The forces in the membranes are shear force, Q and the in-plane tension, T as shown in Fig. 2 C. The osmotic pressure inside the synaptic vesicle is represented by p0. As shown in Fig. 2 B, the repulsive electrostatic force per unit area, Fe in Eqs. 9 and 10, acts on both membranes, along the z direction. The force due to SNARE bundles is represented as line loads acting on the circles over the undeformed geometry of vesicle and plasma membrane (denoted by vectors F and −F, as shown in Fig. 2 B). On the vesicle, the radius of this circle, r0, is determined by the geometrical compatibility condition, which is based on the width of SNARE helix, d and number of SNARE bundles, as
| (13) |
The assumption here is that the packing of SNAREs is limited by steric hindrance between them and Eq. 13 represents the smallest radius that would accommodate the given number of bundles. The equivalent arc length value for load application is given by S0 = sin−1(r0/R). This arc length is same for both the vesicle and the membrane.
We assume that the strain energy density W of both membranes is given by (40)
| (14) |
and by variation of total energy, the governing equations for the vesicle-membrane system are obtained in Eq. S11 in the Supporting Material. These equations represent equilibrium in the normal (Eq. S11 a in the Supporting Material) and tangential (Eq. S11 f in the Supporting Material) directions at each point on the membranes. The geometrical constraints can be used to obtain Eqs. S11, b-e, in the Supporting Material. These governing equations form a nonlinear system of ordinary differential equations (ODEs). By specifying the input geometric parameters (R,L) and the force parameters (F, S0, Fe, and p0), this system of ODEs can be solved numerically to obtain an equilibrium configuration of the membrane system. We use the nonlinear boundary value problem solver BVP4C in the software MATLAB (The MathWorks, Natick, MA) to solve the ODEs.
Results and Discussion
Force-displacement response of the vesicle-membrane interaction
The equal and opposite forces on the Syx and Syb C-termini are transmitted to the plasma membrane and vesicle, respectively, as forces attracting them. Below separations of ∼2.5 nm, attractive forces are resisted primarily by hydration repulsion. A characteristic force-separation curve can be obtained for the vesicle-membrane system using the formulation described in Continuum Model of the Vesicle and Plasma Membrane. By specifying the number of SNARE bundles attached to the vesicle-membrane system, the location of the line load can be determined using Eq. 13. The effect of zipping of the SNARE bundle is simulated by varying the strength of the line load in small steps. For each increment in force, an equilibrium configuration of the membrane system is obtained, and hence we determine the separation between the two load points on vesicle and plasma membrane, respectively. This separation is the distance between residues Syb89 and Syx256. By varying the number of SNAREs, a series of force-separation curves can be obtained as shown in Fig. 3 A.
Figure 3.
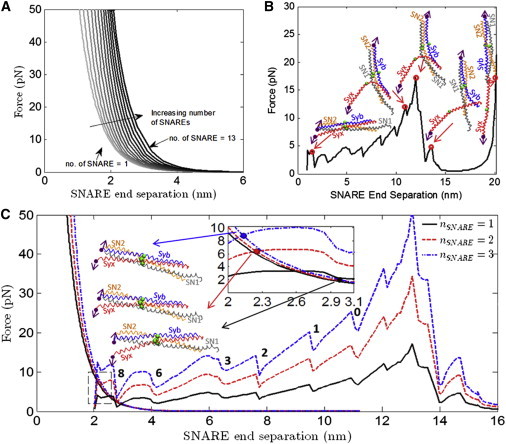
(A) Force versus SNARE end separation for the vesicle-membrane system for different numbers of SNAREs for the hydration repulsion case. (B) The force during separation of the ends of the SNARE bundle using λ of 0.30 for the CG model of SNARE along with snapshots of the SNARE bundle at the corresponding C-terminal end separation. The end separation is defined as the distance between the Syb and Syx C-terminal beads Syb89 and Syx256. Syb, Syx, the ionic layer residues (beads), and the C-terminal residues (beads with arrows) that are attached to pulling beads are shown in each SNARE snapshot. (Arrows) Direction along which the C-terminal beads are being pulled. (C) The force as a function of Syb-Syx C-terminal distance (between Syb89 and Syx256) is shown for the vesicle-membrane (the exponentially decreasing curves) and SNARE. One (solid line), two (dash line), and three (dash-dot line) SNAREs are shown in this plot. Intersections between the vesicle-membrane and SNARE force-displacement responses represent equilibrium states. There are a number of instabilities represented by load-drops. These correspond to separation of individual layers, and have been so-labeled. To see this figure in color, go online.
SNARE force-separation curve
Fig. 3 B shows the results of a simulation in which the SNARE bundle has been pulled apart for a total end-to-end separation of 20 nm between the C-terminal Syb and Syx end-beads.
Each drop in the force-displacement plot (Fig. 3 B) represents the system overcoming a barrier where there is a strong interaction between the SNARE bundles. Two examples are the snapshots at 10.9 and 11.9 nm in Fig. 3 B. With an increase of only 1.0 nm in displacement and little visible change in structure, there is a significant (5.1 pN) increase in force to a peak value of 17.2 pN, after which the force immediately drops to ∼2 pN. (Because a significant amount of the linker domain was not present in the crystal structure of SNARE that was used to build the CG model, the first force jump seen by Gao et al. (8) at 3 nm and 8–13 pN is not present in these results.) The CG model is able to capture the experimentally determined precipitous force-drop, after which the remaining interactions holding the SNARE bundle together are relatively weak and are therefore not measurable in a force-controlled experiment.
The subsequent increase in force is associated with stretching of the linkage between the N-termini of Syx and Syb, and presumably would not be present in a physiological setting. It is included here because this feature is also present in the experiments of Gao et al. (8). For simplicity, in the version of the elastic network model used here, we do not allow the helices to unravel, justified by the following facts. As the results of the next section show, the equilibrium separation for all the cases studied in this article is ∼3 nm or less. At these separations, the force on each SNARE is <5 pN. Based on the work of Gao et al. (8), the first unwinding event occurs at ∼10–12 pN. Thus our simplifying assumption (which will be relaxed in future work) that helices remain unfolded, is justifiable for the range of openings and displacements representative of the equilibrium docked state. We have checked the sensitivity of our results to this assumption by allowing small portions of the unzippered region to unfold, as shown in the Supporting Material.
Combined SNARE and vesicle-membrane results
In the previous two sections we have independently obtained force-separation results for the vesicle-membrane system (Fig. 3 A) and for the SNARE (Fig. 3 B). Before combining the two results, we first accounted for the fact that the distance between outer surfaces of the membranes is larger by ∼2 nm than the distance between Syb89 and Syx256, the SNARE residues that we move apart (see the Supporting Material). Specifically, we shifted the SNARE force-displacement curve to the right by 2 nm to obtain this consistency. Clearly, in the combined SNARE-vesicle-membrane system there is a single force and corresponding displacement. Applying this consistency condition between the two results determines equilibrium. Moreover, we can determine how equilibrium depends on the number of SNARES.
For systems with 1, 2, and 3 SNAREs, the information from Fig. 3, A and B, is combined to produce Fig. 3 C. Because it has been shown that SNAREs mediate vesicle to membrane fusion in a synchronous way, we assume that the force required to unzip two SNAREs would simply be twice the force required to unzip one SNARE, and so on (41,42). In all three cases, the curves intersect at an equilibrium SNARE end separation of between 2 and 3 nm, suggesting that even 1–3 SNAREs are sufficient to overcome hydration repulsion and allow the vesicle to dock at the plasma membrane. The corresponding structures for the intersection points for all three cases, shown in Fig. 3 C, also suggest there is no important conformational difference between the three structures other than a difference in the number of residues that have been unzippered.
It is instructive next to consider the energy landscape corresponding to the force-separation results shown in Fig. 3. For this purpose, the SNARE (positive) and vesicle-membrane (negative) force-separation results are integrated numerically. Fig. 4 B shows the results corresponding to the force-separation results shown in Fig. 3. Note that because the SNARE force-displacement response contains unstable jumps, the entire energy landscape is not represented in Fig. 4, B and C. Because of the nature of the displacement control simulations, there are several instabilities present in the original SNARE force-separation curve. An example of one of these instabilities is the drop at 7.5 nm, as shown in the SNARE curves in Fig. 3 C. Integrating across these instabilities makes the total energy of the system slightly more negative than it should be (see the Supporting Material). Fig. 4, B and C, shows contour plots of interaction energy as a function of the number of SNAREs and end-to-end separation. Fig. 4 B shows the results for a vesicle with radius of 20 nm, representing a synaptic vesicle. The gray circles represent the global energy minimum for each value of number of SNARES, corresponding to force equilibria in Fig. 3.
Figure 4.
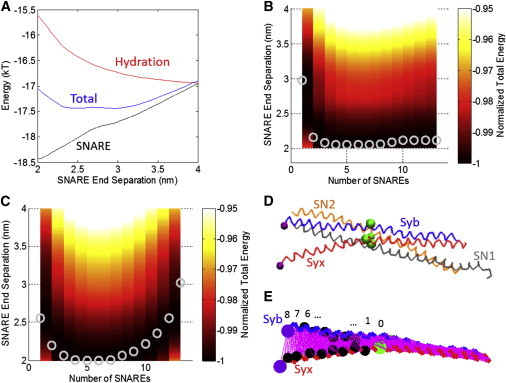
(A) Energy as a function of SNARE end separation when repulsion between the vesicle and plasma membrane is dominated by hydration repulsion. The energetic contributions from SNARE (attractive), hydration (repulsive), and the total (their sum) are shown. The hydration repulsion has been shifted vertically by −17 kT for clarity. (B) Contour plot of total energy as a function of SNARE end separation distance for different numbers of SNAREs under hydration repulsion. (Circles) Global energy minima representing the equilibrium SNARE end separation for a given number of SNAREs. Vesicle radius is 20 nm. (C) Contour plot of total energy as a function of SNARE end separation distance for different numbers of SNAREs under electrostatic repulsion for a fixed charge of −0.025 C/m2 on the vesicle and the membrane in the limit of high tension in the vesicle and plasma membrane. For this case, minimum lateral separation between the SNARE bundles has been increased from 3 to 4 nm. (D) The structure of SNARE corresponding to the case shown in (B), number of SNAREs = 1. Syb, Syx, SN1, and SN2 are shown with the ionic layer residues indicated as large beads. (E) The same structure as in (D) but showing only Syb and Syx for clarity. (Thin lines) All contacts for residues within 2σ of each other. To see this figure in color, go online.
An example of how these minima were determined is shown in Fig. 4 A. This was used to determine the global energy minimum for one SNARE for the hydration repulsion case. It is striking that a single SNARE produces a distinct energy minimum at ∼3 nm. As the number of SNAREs increases to four SNAREs, the equilibrium SNARE end-separation decreases. For 4–8 SNAREs, there is little difference in the equilibrium separation. For five SNAREs, the total energy per SNARE is ∼−17 kT, which is quite consistent with the 13–27 kT range reported by Zorman et al. (43). With increase in the number of SNAREs over 8, the equilibrium SNARE separation slowly increases; the minimum separation (∼2.1 nm) is achieved with four bundles. Thus, we may conclude that 4–8 SNAREs are sufficient to complete the zippering process and to bring the membrane and the vesicle at a distance of 2.1 nm. Importantly, a larger number of SNARE bundles does not bring the vesicle closer to the membrane, because steric hindrance pushes them out to a larger radius.
We next explored how electrostatics would affect the vesicle-to-plasma membrane repulsion. We recalculated the continuum model results using a fixed surface charge of −0.025 C/m2 on the vesicle and the membrane with electrostatic repulsion as shown in Fig. S9 B. For this case for one SNARE, the end separation is ∼2.4 nm, which is smaller than the 3 nm seen for the hydration repulsion case. However, when more than one SNARE is added to the system, the equilibrium SNARE end separation is constant at ∼2 nm for 2–13 SNAREs. In this case, the equilibrium configuration of the SNARE bundle would be a nearly completely zipped conformation. For this case with four SNARES the total energy per SNARE is ∼−14 kT, which again is within the range of 13–27 kT reported by Zorman et al. (43).
We next explored how the vesicle size would affect the number of SNAREs required to dock a vesicle to the membrane. Fig. S10, B and D, shows the results for the case of a vesicle that is 100 nm in radius, corresponding to vesicles in neurosecretory cells. For the hydration repulsion case, there is a considerable difference between the 20- and 100-nm vesicles. For the 100-nm case the minimum separation is also reached with four SNAREs, but that minimum separation is ∼2.5 nm as opposed to ∼2.1 nm for the 20-nm vesicle. For the case of electrostatic repulsion with a constant surface charge, the only difference between the two cases is for one and two SNAREs. For the 100-nm vesicle case, the equilibrium separation is ∼3.4 nm as opposed to ∼2.4 nm for the 20-nm vesicle. Additionally, for two SNAREs, there is also a larger separation for the 100-nm vesicle of 3 nm as opposed to 2 nm for the 20-nm vesicle. However for three or more SNAREs, there is little difference between the two vesicle sizes because both SNARE configurations are nearly completely zippered.
Fig. 4, B and C, represents results for an optimized set of parameters describing molecular details and electrostatic forces. To judge the robustness of the conclusions gleaned from these results, we explored several variations of parameters, including: 1) allowing a portion of Syb to melt with the surface charge held constant; 2) holding the surface potential constant instead of surface charge; 3) high osmotic pressure in the vesicle and low pre-tension in the plasma membrane; and 4) the limit of high tension in both the vesicle and plasma membranes. These variations in the modeling assumptions generally make little difference in the conclusions drawn from Fig. 4 (see the Supporting Material for details). The main conclusion that 4–8 SNAREs bring the vesicle to the minimum distance away from the membrane still holds. Because the equilibria of interest for the problem addressed in this work occur at relatively small separation and forces, in our model we have not allowed the helices to unravel. In order to see the potential effect of unraveling, the first two helical turns of Syb were melted and the force-displacement curve for SNARE was calculated from Fig. 3 B. The resulting energy surface for this case for a 20-nm vesicle with hydration repulsion is shown in Fig. S11 A. A quantity of 4–10 SNAREs brings the vesicle within a minimal distance of the plasma membrane. However, that minimal distance is ∼2.4 nm as opposed to the ∼2.1 nm for the case where Syb is not permitted to unravel.
In an effort to compare to the experimental prefusion structures of the vesicle and plasma membrane as shown by Malsam et al. (44) and Hernandez et al. (45), the continuum model was calculated using high osmotic pressure in the vesicle and low pre-tension in the plasma membrane. However, the resulting energy surface for this modification to the base cases shown in Fig. 4 has little effect on the results because the repulsive force is dominated by hydrostatic repulsion as shown in Fig. S14.
The limit of high tension in both the vesicle and plasma membrane was studied using an analytical model described in the Supporting Material. In order to test the sensitivity of the solution to the location of the SNAREs, calculated using Eq. 13, the diameter of the SNARE bundle was varied from 2 nm, Fig. S17 A, to 4 nm, whereas the base case used 3 nm. This variation seems to have the most significant effect on the solution. Decreasing the size of the SNARE bundle still yields similar results, in that for more than one SNARE, the bundle is nearly completely zipped shut. On the other hand, when the size of the SNARE bundle is increased, instead of having a nearly fully zippered bundle, there is a minimum separation that occurs at four SNAREs. With the addition of more than five SNAREs the equilibrium separation again begins to increase all the way up to ∼3 nm with 13 SNAREs.
Fig. 4, D and E, shows the equilibrium structures of SNARE at a 2.1-nm separation for the case shown in Fig. 4 B. SN1 and SN2 were removed from the structure for clarity in Fig. 4 E, and the residues of Syb and Syx that were in contact were determined. Because the forces from Miyazawa and Jernigan (23–25) greatly decrease after a separation of ∼2∗σ, that distance was used as the criteria for two residues being in contact. At the start of the displacement control simulation, Syb and Syx had 574 contacts between them. After a 2.1-nm separation, only 449 contacts remained. The removed contacts begin to create a cracklike defect separating the helices. After the 2.1-nm separation, residues 89 (Trp) of Syb and 256 (Lys) of Syx were still in contact. These residues are still far away from the ionic layer, showing that the SNARE bundle had not yet unzipped to that point.
Conclusions
The docking of vesicles onto the plasma membrane of a neuron involves interplay between the SNARE complexes that provide attractive forces, long-range repulsion between the vesicle and membrane, and deformation of all three components. Although each of these components has previously been investigated in detail, to understand the biophysics and mechanics of vesicle docking, it is imperative to combine them. To our knowledge, we report the first model to couple chemical specificity of the SNARE complex with hydration, electrostatic, and mechanical forces imposed on the vesicle and plasma membrane. Such a model can serve as a tool to investigate how mutations in the SNARE complex could affect the docking and fusion process.
We have developed separate coarse-grained models for the deformation of the SNARE complex and of the vesicle-membrane assembly. The vesicle-membrane model is based on a continuum description of membrane deformation subjected to either hydration or electrostatic repulsion and forces from the SNARE complexes. The fusion of lipid bilayers has been extensively modeled (46) to capture the intermediate states of fusion, including stalk formation, and to understand their energetics. Our goal in this study was to understand the forces produced by membrane bending and hydration or electrostatic repulsion that need to be overcome by the SNARE complexes to dock a vesicle to the membrane. The continuum membrane model was coupled with a coarse-grained model of the SNARE complex. The SNARE forces are represented in the continuum membrane model as an axisymmetric line force, an assumption that is increasingly accurate for increasing number of SNAREs. (A single SNARE at the axis of symmetry also presumably results in axisymmetric deformations of the vesicle/membrane.) For a given number of SNARES, the model holds fixed their anchor points in the vesicle and plasma membrane. This constraint potentially affects our results. However, we note that the position of the SNARE anchor points does vary as we change the number of SNAREs (Eq. 13). The number of SNAREs was varied from 1 to 13. Usually, for two or more SNAREs there is little difference in the equilibrium separation, suggesting that the model results probably will not vary much if we remove the constraint of holding the positions fixed.
The CG SNARE model is based on an elastic-network representation of each of the helices combined with potentials from Miyazawa and Jernigan (23–25) to capture interhelical interactions. It is a minimalistic model that still represents residue-specificity. Its few parameters are calibrated either by comparison with all-atom MD simulations of individual SNAREs, or by comparison to experimentally measured forces to separate a single SNARE complex (8) Specifically, we match the experimentally observed peak force of 17.2-pN force. Each of the two models separately yields a force-separation relationship. Enforcing consistency between the two yields equilibrium configurations for the SNARE-vesicle-membrane complex for a given number of SNAREs.
As the first application of our model, we explored here the effect of the number of SNARE complexes on the mechanics of vesicle docking and the prefusion state of the SNARE complex. It is still a matter of debate as to how many SNARE complexes need to assemble before the fusion process. High concentration of Syb on the vesicle (∼70 copies (47)), as well t-SNARE clusters at docking sites (48) suggest that in vivo fusion may be mediated by multiple SNARE complexes. At the same time, experiments and model systems suggest that one (49), two (18), or three (19,50,51) could be sufficient. Other studies, however, suggest a larger number of SNARE complexes per fusion, ranging between 5 and 11 (16,20,52). Finally, recent studies suggest that the number of assembled SNARE complexes may determine the release efficiency (53) and that it may vary (54). Thus, how vesicle docking might depend on the number of SNARE complexes remains an open question, previously not addressed from the biophysical and biomechanical point of view.
We find that one SNARE complex is sufficient to dock the vesicle onto the membrane. As few as 2–3 SNAREs are sufficient to bring the distance between the membrane and vesicle to the minimum and thus to complete the docking process. Interestingly, there is a point of diminishing returns such that a larger number of SNAREs (i.e., an overdocked state) does not further reduce the vesicle-membrane separation. The corresponding predicted SNARE end-to-end separation is in the range 2–3 nm (55,56), but one can expect significant fluctuation about the equilibrium state because the energy profile is relatively shallow (Fig. 4 A). This picture of a partially zippered docked state is consistent with the conclusions of an in vivo toxin cleavage assay in crayfish neuromuscular junctions. In this work, we only model docking, not fusion. That is, we calculate the equilibrium separation between the vesicle and plasma membrane during docking. The lower bound of ∼2-nm separation between the vesicle and plasma membrane is based on the steric hindrance of having to fit the SNARE bundles between the two surfaces. This distance is probably a bit too large for fusion to occur, which suggests that some additional mechanism other than SNARE zippering must act for fusion.
Several variations in the model including calculations under fixed charge, fixed surface potential, high vesicle pressure, high membrane tension, and varying vesicle radius, have all shown similar results.
Our results are consistent with the view that a prefusion state involves a partially assembled SNARE complex (57–59), which keeps the vesicle at a short distance from the plasma membrane in anticipation of Ca2+-induced fusion rather than the alternative view that SNARE zippering represents a final step of exocytosis and rapidly progresses once nucleated (60). Specifically, our model robustly predicts an equilibrium separation between the vesicle and the membrane to be of ∼2.0–3.0 nm corresponding to opening of, at most, layer 8.
Author Contributions
N.F. and A.J. developed the CG SNARE model; N.F. wrote the CG SNARE model code; and P.S. and C.-Y.H. developed the continuum model of the vesicle and plasma membrane. All authors analyzed and interpreted results.
Acknowledgments
The authors gratefully acknowledge several useful suggestions by Professor Jeetain Mittal.
This study is supported by grant No. R01 MH099557 from the National Institutes of Health. For molecular-dynamics computations, we acknowledge the support of XSEDE, which is supported by National Science Foundation grant No. OCI-1053575, and specifically the Texas Advanced Computing Center under grant No. TG-MCB100049 and the National Institute of Computational Science. VMD/NAMD software is developed with National Institutes of Health support by the Theoretical and Computational Biophysics group at the Beckman Institute, University of Illinois at Urbana-Champaign, Urbana, IL.
Supporting Material
Supporting Citations
References (61–68) appear in the Supporting Material.
References
- 1.Südhof T.C. The synaptic vesicle cycle: a cascade of protein-protein interactions. Nature. 1995;375:645–653. doi: 10.1038/375645a0. [DOI] [PubMed] [Google Scholar]
- 2.Hanson P.I., Heuser J.E., Jahn R. Neurotransmitter release—four years of SNARE complexes. Curr. Opin. Neurobiol. 1997;7:310–315. doi: 10.1016/s0959-4388(97)80057-8. [DOI] [PubMed] [Google Scholar]
- 3.Söllner T., Bennett M.K., Rothman J.E. A protein assembly-disassembly pathway in vitro that may correspond to sequential steps of synaptic vesicle docking, activation, and fusion. Cell. 1993;75:409–418. doi: 10.1016/0092-8674(93)90376-2. [DOI] [PubMed] [Google Scholar]
- 4.Rothman J.E. Mechanisms of intracellular protein transport. Nature. 1994;372:55–63. doi: 10.1038/372055a0. [DOI] [PubMed] [Google Scholar]
- 5.Gracheva E.O., Maryon E.B., Richmond J.E. Differential regulation of synaptic vesicle tethering and docking by UNC-18 and TOM-1. Front. Synaptic Neurosci. 2010;2:141. doi: 10.3389/fnsyn.2010.00141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Sutton R.B., Fasshauer D., Brunger A.T. Crystal structure of a SNARE complex involved in synaptic exocytosis at 2.4 Å resolution. Nature. 1998;395:347–353. doi: 10.1038/26412. [DOI] [PubMed] [Google Scholar]
- 7.Ernst J.A., Brunger A.T. High resolution structure, stability, and synaptotagmin binding of a truncated neuronal SNARE complex. J. Biol. Chem. 2003;278:8630–8636. doi: 10.1074/jbc.M211889200. [DOI] [PubMed] [Google Scholar]
- 8.Gao Y., Zorman S., Zhang Y. Single reconstituted neuronal SNARE complexes zipper in three distinct stages. Science. 2012;337:1340–1343. doi: 10.1126/science.1224492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Durrieu M.-P., Lavery R., Baaden M. Interactions between neuronal fusion proteins explored by molecular dynamics. Biophys. J. 2008;94:3436–3446. doi: 10.1529/biophysj.107.123117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Bock L.V., Hutchings B., Woodbury D.J. Chemomechanical regulation of SNARE proteins studied with molecular dynamics simulations. Biophys. J. 2010;99:1221–1230. doi: 10.1016/j.bpj.2010.06.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Bykhovskaia M., Jagota A., Littleton J.T. Interaction of the complexin accessory helix with the C-terminus of the SNARE complex: molecular-dynamics model of the fusion clamp. Biophys. J. 2013;105:679–690. doi: 10.1016/j.bpj.2013.06.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Durrieu M.P., Bond P.J., Baaden M. Coarse-grain simulations of the R-SNARE fusion protein in its membrane environment detect long-lived conformational sub-states. ChemPhysChem. 2009;10:1548–1552. doi: 10.1002/cphc.200900216. [DOI] [PubMed] [Google Scholar]
- 13.Lindau M., Hall B.A., Sansom M.S.P. Coarse-grain simulations reveal movement of the synaptobrevin C-terminus in response to picoNewton forces. Biophys. J. 2012;103:959–969. doi: 10.1016/j.bpj.2012.08.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Marrink S.J., Risselada H.J., de Vries A.H. The MARTINI force field: coarse-grained model for biomolecular simulations. J. Phys. Chem. B. 2007;111:7812–7824. doi: 10.1021/jp071097f. [DOI] [PubMed] [Google Scholar]
- 15.Lamberg A., Taniguchi T. Coarse-grained computational studies of supported bilayers: current problems and their root causes. J. Phys. Chem. B. 2014;118:10643–10652. doi: 10.1021/jp5053419. [DOI] [PubMed] [Google Scholar]
- 16.Han X., Wang C.-T., Jackson M.B. Transmembrane segments of syntaxin line the fusion pore of Ca2+-triggered exocytosis. Science. 2004;304:289–292. doi: 10.1126/science.1095801. [DOI] [PubMed] [Google Scholar]
- 17.van den Bogaart G., Jahn R. Counting the SNAREs needed for membrane fusion. J. Mol. Cell Biol. 2011;3:204–205. doi: 10.1093/jmcb/mjr004. [DOI] [PubMed] [Google Scholar]
- 18.Sinha R., Ahmed S., Klingauf J. Two synaptobrevin molecules are sufficient for vesicle fusion in central nervous system synapses. Proc. Natl. Acad. Sci. USA. 2011;108:14318–14323. doi: 10.1073/pnas.1101818108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Mohrmann R., de Wit H., Sorensen J.B. Fast vesicle fusion in living cells requires at least three SNARE complexes. Science. 2010;330:502–505. doi: 10.1126/science.1193134. [DOI] [PubMed] [Google Scholar]
- 20.Karatekin E., Di Giovanni J., Rothman J.E. A fast, single-vesicle fusion assay mimics physiological SNARE requirements. Proc. Natl. Acad. Sci. USA. 2010;107:3517–3521. doi: 10.1073/pnas.0914723107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Zhang Z., Pfaendtner J., Voth G.A. Defining coarse-grained representations of large biomolecules and biomolecular complexes from elastic network models. Biophys. J. 2009;97:2327–2337. doi: 10.1016/j.bpj.2009.08.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Chu J.W., Voth G.A. Coarse-grained modeling of the actin filament derived from atomistic-scale simulations. Biophys. J. 2006;90:1572–1582. doi: 10.1529/biophysj.105.073924. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Miyazawa S., Jernigan R.L. Estimation of effective interresidue contact energies from protein crystal structures: quasi-chemical approximation. Macromolecules. 1985;18:534–552. [Google Scholar]
- 24.Miyazawa S., Jernigan R.L. Residue-residue potentials with a favorable contact pair term and an unfavorable high packing density term, for simulation and threading. J. Mol. Biol. 1996;256:623–644. doi: 10.1006/jmbi.1996.0114. [DOI] [PubMed] [Google Scholar]
- 25.Miyazawa S., Jernigan R.L. Self-consistent estimation of inter-residue protein contact energies based on an equilibrium mixture approximation of residues. Proteins. 1999;34:49–68. doi: 10.1002/(sici)1097-0134(19990101)34:1<49::aid-prot5>3.0.co;2-l. [DOI] [PubMed] [Google Scholar]
- 26.Jenkins J.T. Static equilibrium configurations of a model red blood cell. J. Math. Biol. 1977;4:149–169. doi: 10.1007/BF00275981. [DOI] [PubMed] [Google Scholar]
- 27.Long R., Hui C.Y., Bykhovskaia M. Adhesion energy can regulate vesicle fusion and stabilize partially fused states. J. R. Soc. Interface. 2012;9:1555–1567. doi: 10.1098/rsif.2011.0827. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Hess B., Kutzner C., Lindahl E. GROMACS 4: algorithms for highly efficient, load-balanced, and scalable molecular simulation. J. Chem. Theory Comput. 2008;4:435–447. doi: 10.1021/ct700301q. [DOI] [PubMed] [Google Scholar]
- 29.Foloppe N., MacKerell A.D. All-atom empirical force field for nucleic acids: I. Parameter optimization based on small molecule and condensed phase macromolecular target data. J. Comput. Chem. 2000;21:86–104. [Google Scholar]
- 30.Alberts B., Johnson A., Walter P. 4th Ed. Garland Science; New York: 2002. Molecular Biology of the Cell. [Google Scholar]
- 31.Creighton T.E. 2nd Ed. W. H. Freeman; New York: 1993. Proteins: Structures and Molecular Properties. [Google Scholar]
- 32.Kim Y.C., Hummer G. Coarse-grained models for simulations of multiprotein complexes: application to ubiquitin binding. J. Mol. Biol. 2008;375:1416–1433. doi: 10.1016/j.jmb.2007.11.063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Argento C., Jagota A., Carter W.C. Surface formulation for molecular interactions of macroscopic bodies. J. Mech. Phys. Solids. 1997;45:1161–1183. [Google Scholar]
- 34.McIntosh T.J., Magid A.D., Simon S.A. Interactions between charged, uncharged, and zwitterionic bilayers containing phosphatidylglycerol. Biophys. J. 1990;57:1187–1197. doi: 10.1016/S0006-3495(90)82638-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Aeffner S., Reusch T., Salditt T. Energetics of stalk intermediates in membrane fusion are controlled by lipid composition. Proc. Natl. Acad. Sci. USA. 2012;109:E1609–E1618. doi: 10.1073/pnas.1119442109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.McIntosh T.J., Simon S.A. Hydration and steric pressures between phospholipid bilayers. Annu. Rev. Biophys. Biomol. Struct. 1994;23:27–51. doi: 10.1146/annurev.bb.23.060194.000331. [DOI] [PubMed] [Google Scholar]
- 37.Marra J. Direct measurement of the interaction between phosphatidylglycerol bilayers in aqueous electrolyte solutions. Biophys. J. 1986;50:815–825. doi: 10.1016/S0006-3495(86)83522-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Ohsawa K., Murata M., Ohshima H. Zeta potential and surface charge density of polystyrene-latex; comparison with synaptic vesicle and brush border membrane vesicle. Colloid Polym. Sci. 2005;264:1005–1009. [Google Scholar]
- 39.Pekker M., Shneider M.N. The surface charge of a cell lipid membrane. arXiv Prepr. arXiv. 2014:1401–1407. [Google Scholar]
- 40.Cooke I.R., Deserno M. Solvent-free model for self-assembling fluid bilayer membranes: stabilization of the fluid phase based on broad attractive tail potentials. J. Chem. Phys. 2005;123:224710. doi: 10.1063/1.2135785. [DOI] [PubMed] [Google Scholar]
- 41.Risselada H.J., Kutzner C., Grubmüller H. Caught in the act: visualization of SNARE-mediated fusion events in molecular detail. ChemBioChem. 2011;12:1049–1055. doi: 10.1002/cbic.201100020. [DOI] [PubMed] [Google Scholar]
- 42.Risselada H.J., Grubmüller H. How SNARE molecules mediate membrane fusion: recent insights from molecular simulations. Curr. Opin. Struct. Biol. 2012;22:187–196. doi: 10.1016/j.sbi.2012.01.007. [DOI] [PubMed] [Google Scholar]
- 43.Zorman S., Rebane A.A., Zhang Y. Common intermediates and kinetics, but different energetics, in the assembly of SNARE proteins. eLife. 2014;3:e03348. doi: 10.7554/eLife.03348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Malsam J., Parisotto D., Söllner T.H. Complexin arrests a pool of docked vesicles for fast Ca2+-dependent release. EMBO J. 2012;31:3270–3281. doi: 10.1038/emboj.2012.164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Hernandez J.M., Stein A., Jahn R. Membrane fusion intermediates via directional and full assembly of the SNARE complex. Science. 2012;336:1581–1584. doi: 10.1126/science.1221976. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Chernomordik L.V., Kozlov M.M. Mechanics of membrane fusion. Nat. Struct. Mol. Biol. 2008;15:675–683. doi: 10.1038/nsmb.1455. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Takamori S., Holt M., Jahn R. Molecular anatomy of a trafficking organelle. Cell. 2006;127:831–846. doi: 10.1016/j.cell.2006.10.030. [DOI] [PubMed] [Google Scholar]
- 48.Knowles M.K., Barg S., Almers W. Single secretory granules of live cells recruit syntaxin-1 and synaptosomal associated protein 25 (SNAP-25) in large copy numbers. Proc. Natl. Acad. Sci. USA. 2010;107:20810–20815. doi: 10.1073/pnas.1014840107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.van den Bogaart G., Holt M.G., Jahn R. One SNARE complex is sufficient for membrane fusion. Nat. Struct. Mol. Biol. 2010;17:358–364. doi: 10.1038/nsmb.1748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Hua Y., Scheller R.H. Three SNARE complexes cooperate to mediate membrane fusion. Proc. Natl. Acad. Sci. USA. 2001;98:8065–8070. doi: 10.1073/pnas.131214798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Shi L., Shen Q.-T., Pincet F. SNARE proteins: one to fuse and three to keep the nascent fusion pore open. Science. 2012;335:1355–1359. doi: 10.1126/science.1214984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Megighian A., Zordan M., Montecucco C. Evidence for a radial SNARE super-complex mediating neurotransmitter release at the Drosophila neuromuscular junction. J. Cell Sci. 2013;126:3134–3140. doi: 10.1242/jcs.123802. [DOI] [PubMed] [Google Scholar]
- 53.Acuna C., Guo Q., Südhof T.C. Microsecond dissection of neurotransmitter release: SNARE-complex assembly dictates speed and Ca2+ sensitivity. Neuron. 2014;82:1088–1100. doi: 10.1016/j.neuron.2014.04.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Hernandez J.M., Kreutzberger A.J.B., Jahn R. Variable cooperativity in SNARE-mediated membrane fusion. Proc. Natl. Acad. Sci. USA. 2014;111:12037–12042. doi: 10.1073/pnas.1407435111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Prashad R.C., Charlton M.P. SNARE zippering and synaptic strength. PLoS ONE. 2014;9:e95130. doi: 10.1371/journal.pone.0095130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Hua S.Y., Charlton M.P. Activity-dependent changes in partial VAMP complexes during neurotransmitter release. Nat. Neurosci. 1999;2:1078–1083. doi: 10.1038/16005. [DOI] [PubMed] [Google Scholar]
- 57.Sørensen J.B., Wiederhold K., Fasshauer D. Sequential N- to C-terminal SNARE complex assembly drives priming and fusion of secretory vesicles. EMBO J. 2006;25:955–966. doi: 10.1038/sj.emboj.7601003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Walter A.M., Wiederhold K., Sørensen J.B. Synaptobrevin N-terminally bound to syntaxin-SNAP-25 defines the primed vesicle state in regulated exocytosis. J. Cell Biol. 2010;188:401–413. doi: 10.1083/jcb.200907018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Li F., Kümmel D., Pincet F. A half-zippered SNARE complex represents a functional intermediate in membrane fusion. J. Am. Chem. Soc. 2014;136:3456–3464. doi: 10.1021/ja410690m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Jahn R., Fasshauer D. Molecular machines governing exocytosis of synaptic vesicles. Nature. 2012;490:201–207. doi: 10.1038/nature11320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Schlick T. Springer; New York: 2002. Molecular Modeling and Simulation: An Interdisciplinary Guide. [Google Scholar]
- 62.Kubo R. The fluctuation-dissipation theorem. Rep. Prog. Phys. 2002;29:255–284. [Google Scholar]
- 63.Ohsawa K., Ohshima H., Ohki S. Surface potential and surface charge density of the cerebral-cortex synaptic vesicle and stability of vesicle suspension. Biochim. Biophys. Acta. 1981;648:206–214. doi: 10.1016/0005-2736(81)90036-5. [DOI] [PubMed] [Google Scholar]
- 64.Deserno, M. 2007. Fluid Lipid Membranes—a Primer. http://www.cmu.edu/biolphys/deserno/pdf/membrane_theory.pdf.
- 65.Kweon D.H., Kim C.S., Shin Y.K. The membrane-dipped neuronal SNARE complex: a site-directed spin labeling electron paramagnetic resonance study. Biochemistry. 2002;41:9264–9268. doi: 10.1021/bi025934+. [DOI] [PubMed] [Google Scholar]
- 66.Kweon D.-H., Kim C.S., Shin Y.-K. Regulation of neuronal SNARE assembly by the membrane. Nat. Struct. Biol. 2003;10:440–447. doi: 10.1038/nsb928. [DOI] [PubMed] [Google Scholar]
- 67.Kim C.S., Kweon D.H., Shin Y.K. Membrane topologies of neuronal SNARE folding intermediates. Biochemistry. 2002;41:10928–10933. doi: 10.1021/bi026266v. [DOI] [PubMed] [Google Scholar]
- 68.Stein A., Weber G., Jahn R. Helical extension of the neuronal SNARE complex into the membrane. Nature. 2009;460:525–528. doi: 10.1038/nature08156. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


