Human Primary Immune Cells Exhibit Distinct Mechanical Properties that Are Modified by Inflammation

Abstract

T lymphocytes are key modulators of the immune response. Their activation requires cell-cell interaction with different myeloid cell populations of the immune system called antigen-presenting cells (APCs). Although T lymphocytes have recently been shown to respond to mechanical cues, in particular to the stiffness of their environment, little is known about the rigidity of APCs. In this study, single-cell microplate assays were performed to measure the viscoelastic moduli of different human myeloid primary APCs, i.e., monocytes (Ms, storage modulus of 520 +90/−80 Pa), dendritic cells (DCs, 440 +110/−90 Pa), and macrophages (MPHs, 900 +110/−100 Pa). Inflammatory conditions modulated these properties, with storage moduli ranging from 190 Pa to 1450 Pa. The effect of inflammation on the mechanical properties was independent of the induction of expression of commonly used APC maturation markers, making myeloid APC rigidity an additional feature of inflammation. In addition, the rigidity of human T lymphocytes was lower than that of all myeloid cells tested and among the lowest reported (Young’s modulus of 85 ± 5 Pa). Finally, the viscoelastic properties of myeloid cells were dependent on both their filamentous actin content and myosin IIA activity, although the relative contribution of these parameters varied within cell types. These results indicate that T lymphocytes face different cell rigidities when interacting with myeloid APCs in vivo and that this mechanical landscape changes under inflammation.

Introduction

T cells can initiate adaptive immunity shortly after a primary activation, which can be triggered by a wide variety of myeloid cells called antigen-presenting cells (APCs). T cell activation efficiency varies according to the nature of the APCs and their maturation states. This has mainly been interpreted in terms of the amount of T cell receptor (TCR) ligands present at the surface of the APC and expression of costimulatory molecules (1–3). Yet, hematopoietic cells, which include myeloid APCs, have different shapes, sizes, and mechanical properties (4–7) that might affect T cell activation.

Indeed, recent results demonstrated that T cell functions can be regulated by mechanical cues from their extracellular environment. In particular, T cells were shown to be sensitive to substrate stiffness (8,9) and to produce, after engagement of the TCR, pushing and pulling forces that adapt to rigidity (10). TCRs have been also reported to behave as mechanotransducers (10–12). Thus, T lymphocyte activation, a key event in the immunological response, is greatly affected by both nano- and microscale mechanics.

However, little is known about the mechanical landscape that human T lymphocytes encounter when interacting with primary myeloid APCs (6). In this work, we systematically measured the viscoelastic properties of these cells under resting and inflammatory conditions using a custom-made, single-cell rheometer (13,14). The viscoelastic properties were found to vary among different myeloid APCs and upon inflammatory treatments. These changes correlated with changes in the composition and activity of their actomyosin cytoskeleton.

Materials and Methods

Cell isolation and culture

Mononuclear cells were isolated from the peripheral blood of healthy donors on a Ficoll density gradient. Human CD14⁺ and CD4⁺ isolation kits (Miltenyi Biotech, Bergish Gladbach, Germany) were used for the purification of monocytes (Ms) and T cells, respectively. Dendritic cells (DCs) were generated as previously described (15) by culturing Ms in RPMI (Life Technologies, Carlsbad, CA)-10% fetal calf serum (FCS) supplemented with 100 ng/mL GM-CSF (Miltenyi Biotech) and 50 ng/mL IL-4 (Miltenyi Biotech) for 5 days. Macrophages (MPHs) were generated by culturing Ms in RPMI-10% FCS supplemented with 25 ng/mL M-CSF (ImmunoTools, Friesoythe, Germany) for 6 days. Maturation for DCs or MPHs was performed for 24 h with either 1 μg/mL human recombinant interferon-γ (IFNγ; Miltenyi Biotech), 10 ng/mL tumor necrosis factor-α (Miltenyi Biotech) plus 1 μg/mL prostaglandin E₂ (TNFα+PGE₂; Sigma Aldrich, St. Louis, MO), or 200 ng/mL lipopolysaccharide (LPS; Invivogen, San Diego, CA). Cells were tested for viability using the trypan blue exclusion assay (PAA Cell Culture, Cambridge, UK) and then harvested directly before experiments. For MPHs, a 40 min trypsin (PAA Cell Culture) treatment was performed to detach them from culture, followed by a 2.5 h culture under smooth agitation.

To check for maturation of APCs, the expression of specific cell-surface markers was assessed by flow cytometry (MACSQuant, Miltenyi Biotech) using fluorescent anti-human antibodies (anti-CD40-PE, anti-CD80-PE, anti-CD86-PE, anti-HLA-DR-PE, and anti-CD54 (ICAM-1)-APC) and the corresponding isotype IgG controls (BD Pharmingen, San Diego, CA).

T cell activation by myeloid antigen presenting cells

To test for T cell activation, DCs and MPHs were cultured with autologous CD4⁺ T cells in the presence of the superantigen TSST-1 (Toxin Technology, Sarasota, FL). Briefly, after APC maturation, cocultures were prepared for the differentially activated DCs and MPHs at a 1:4 APC/T cell ratio (cell numbers per well in a 96-well plate = 25,000:100,000, respectively) and with TSST-1 at concentrations ranging from 0 to 10 ng/mL. The cultures were left overnight in the incubator. IL-2 secretion in the culture medium was measured by ELISA (OptEIA; BD Biosciences, San Diego, CA). Values were normalized according to the median from each donor.

Single-cell viscoelastic measurements

For single-cell viscoelastic measurements, we used a previously described setup (13,16,17). Briefly, primary myeloid cells and Jurkat T cells were caught between two glass microplates: one rigid and one flexible with a calibrated bending stiffness (see Fig. 2). The position of the flexible plate was monitored by an optical sensor, which allowed us to measure the force applied to the cell and the resulting deformation. The plates were coated with 5 μg/mL of fibronectin (Sigma-Aldrich) for 30 min at 37°C. Oscillations were applied by a computer-controlled piezoelectric system and the resulting movement at the cell level was measured. Amplitude was kept in the limit of linear elasticity solicitations (10–15% of cell size), whereas the frequency range (0.02–6.4 Hz) allowed a three-decade sweep in a range where cells usually show a power-law behavior (18–20). The storage and loss moduli were as follows:

$$\{\begin{array}{l}{G}^{\prime }=\frac{k{L}_0}{S}\left(\frac{D_0}{d_0}\text{cos}\phi -1\right)\\ G^{″}=-\frac{k{L}_0}{S}\left(\frac{D_0}{d_0}\text{sin}\phi \right)\end{array},$$

where D₀ and d₀ are the amplitudes of the flexible plate base and tip signals, respectively; ϕ is the phase shift between these two signals; k is the bending modulus of the flexible plate; L₀ is the initial diameter of the cell; and S is the contact area between the cell and the plates. It is now widely accepted that G′ and G″ behave as power laws of frequency:

$$G^{\prime }\left(f\right)=G_0^{\prime }{f}^{\alpha };G^{″}\left(f\right)=G_0^{″}{f}^{\alpha }.$$

For each cell, the prefactors $G_0^{\prime }$ and $G_0^{″}$ are obtained by fitting the data as shown in Fig. S1 in the Supporting Material and used for comparison between cell types. It is then possible to derive the viscoelastic modulus $G_0^{\ast }$ from $G_0^{\prime }$ and $G_0^{″}$:

$$G_0^{\ast }=G_0^{\prime }+i{G}_0^{″}.$$

The Euclidean norm of $G_0^{\ast }$ also behaves as a power law of frequency:

$$\left|G_0^{\ast }\right|=\sqrt{G_0^{\prime 2}+G_0^{″2}}=G_0{f}^a,$$

where G₀ is a global modulus estimation that takes into account both $G_0^{\prime }$ and $G_0^{″}$, and α is linked to the ratio of $G_0^{\prime }$ and $G_0^{″}$ ($G_0^{″}/G_0^{\prime }=\tan \alpha \frac{\pi }{2}$). The data points of $\left|G_0^{\ast }\right|$ were fit by a power law, and G₀ and α were extracted for comparison between cells (Fig. S2).

Figure 2.

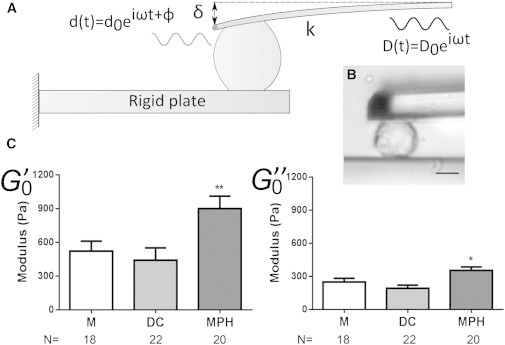
(A) Schematic view of the microplates experiment. Oscillations are applied at the base of the cantilever and the cell’s response at the tip is sampled via an optical sensor. The storage modulus ($G_0^{\prime }$) and loss modulus ($G_0^{″}$) are then derived from phase-shift and amplitude ratios between input and output signals. (B) Bright-field image of a MPH during an experiment; scale bar: 10 μm. (C) Storage ($G_0^{\prime }$) and loss ($G_0^{″}$) moduli for human Ms, DCs, and MPHs (^∗p < 0.05, ^∗∗p < 0.01, Mann-Whitney U test for each condition; N, number of cells tested, from at least three different donors). For values see Table 1.

T cell static modulus estimation

Briefly, primary CD4⁺ and Jurkat T cells were squeezed up to a 15–20% static deformation by applying a compression from the rigid plate (see Fig. 4). Deformation of the cell and deflection of the soft plate were simultaneously recorded. The system (microplates + cell) was supposed to behave as two springs in series, and the static apparent Young’s modulus of the cell was derived from the formula

$$E=k\delta /S_0\epsilon ,$$

where k is the bending stiffness of the soft plate, δ is the soft plate deflection measured optically, S₀ is the cell-plate contact area estimated from experiment images, and ε is the strain, i.e., the percentage compression of the cell ε = (L₀ − L)/L₀ (where L₀ and L are the lengths of the cell before and after compression, respectively).

Figure 4.

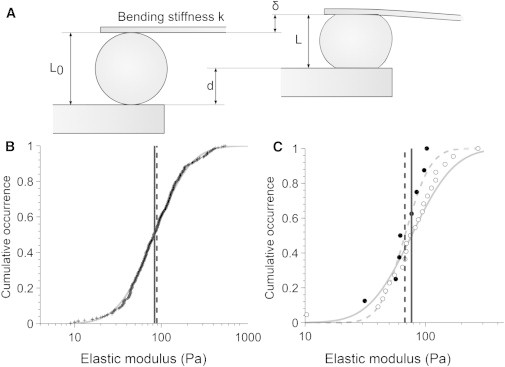
Measurement of the apparent Young’s modulus of primary CD4⁺ T cells and Jurkat T cells. (A) A cell was caught and squeezed between the plates by applying a displacement d on the rigid plate. The displacement of the flexible plate δ was optically measured and the length before and after compression was measured to derive the apparent static Young modulus E_app. (B) For primary CD4⁺ T cells, the data points (+) of the apparent Young’s modulus followed a log-normal distribution whose mean E_app (mean = 85 ± 5 Pa, solid line) matches the equivalent Young’s modulus E_eq (mean = 90 ± 10 Pa, dashed line) of Jurkat cells obtained through calculation. (C) Comparison of stepwise compression experiments (E_app data points in dark circles, mean = 70 +30/−20 Pa in dashed line) and dynamic mechanical analysis ($G_0^{\prime }$ data points in white circles, mean = 80 +70/−40 Pa in solid line) for Jurkat cells.

Derivation of equivalent Young’s modulus

Measurement of the primary T cell Young’s modulus does not allow for direct comparison with the dynamic mechanical measurements performed for the rest of the cells. Instead, one can estimate the static Young’s modulus of cells from the results of the dynamic mechanical measurements. Indeed, it is possible to predict the stress σ and the strain ε of a cell undergoing a constant rate-of-charge experiment (16) at a given time t:

$$\sigma \left(t\right)={\sigma }^{\ast }\frac{t}{{\tau }^{\ast }}\sum _{n=0}^{\infty }\frac{{\left[-\Gamma \left(1+\alpha \right){\sigma }^{\ast }A{t}^{\alpha }\right]}^n}{\Gamma \left(2+n\alpha \right)}$$

$$\epsilon \left(t\right)=\frac{t}{{\tau }^{\ast }}\left(1-\sum _{n=0}^{\infty }\frac{{\left[-\Gamma \left(1+\alpha \right){\sigma }^{\ast }A{t}^{\alpha }\right]}^n}{\Gamma \left(2+n\alpha \right)}\right).$$

In this expression, the creep function A is linked to the viscoelastic parameters G₀ and α by

$$A=\frac{{\left(2\pi \right)}^{\alpha }}{G_0\Gamma \left(1+\alpha \right)},$$

and Γ is defined as $\Gamma \left(1+\alpha \right)={\int }_0^{\infty }{e}^{-t}{t}^{\alpha }dt$. σ^∗ and τ^∗ refer to characteristic stresses and time, respectively, which are derived from the stepwise compression experiment. σ^∗ depends on the bending stiffness of the soft plate k, the initial length between the plates L₀, and the surface contact area between the cell and the plate S₀:

$${\sigma }^{\ast }=\frac{k{L}_0}{S_0}.$$

τ^∗ is linked to geometrical and experimental parameters by

$${\tau }^{\ast }=\frac{L_0{\tau }_0}{D_0},$$

where τ₀ is the time necessary to reach a displacement D₀ in a constant rate-of-charge experiment. Since we are applying a stepwise compression instead of a constant rate-of-charge, we measure the actual time needed to perform the typical step D₀ = 1 μm and derive τ₀ = 0.08 ± 0.01 s. This characteristic time is the main source of error in the estimation of cells equivalent Young’s modulus E_eq. As previously described (16), the first four terms (n ≤ 3) are sufficient to reach an accuracy of 1%, and these equations lead us to plot, for various time points t, the stress-strain curve for each cell type. The equivalent Young’s modulus E_eq is derived as the slope of the stress-strain curve under 15% of deformation, as shown for Jurkat cells on Fig. S3.

Fluorescent staining and microscopic analysis

Cells were analyzed for their content in total F-actin and myosin IIA heavy chain. DCs, MPHs, Ms, and T cells were harvested and then incubated for 20 min in room temperature on fibronectin (10 μg/mL; Sigma Aldrich)-coated glass coverslips. The cells were then fixed with 4% paraformaldehyde in PBS and made permeable with saponin (0.05% in PBS; Sigma Aldrich). Then they were stained with DAPI (Life Technologies) and phalloidin-Alexa-546 (Life Technologies), with rabbit-derived anti-human Myosin IIA heavy chain antibody (Covance, Princeton, NJ) as the primary antibody and anti-rabbit IgG-Alexa-488 antibody (Life Technologies) as the secondary antibody. The samples were then observed on an inverted spinning-disk confocal Nikon TiE microscope (Nikon, Tokyo, Japan) equipped with a piezo-stage NanoScanZ mounted on a Marzhauser XYZ motorized scanning stage. Three-dimensional stacks of images were acquired with a step of 0.2 μm using a 100× oil immersion objective and an EM-CCD iXon 897 Andor camera (Andor, Belfast, UK). Metamorph software (Molecular Devices, Sunnyvale, CA) was used for all acquisitions. Data analysis for the total amount of fluorescent staining was performed using ImageJ software. For each stack, cells were segmented using the auto-threshold function and total intensities were quantified using the 3D Objects Counter plugin. We normalized each experiment, i.e., each data set (fluorescence intensity obtained for a given donor in the different cell populations prepared from that donor), to the median value from all data (all cell types).

Western blotting

The amount of myosin regulatory light chain (myo-RLC) phosphorylated at Ser-19 was quantified by immunoblotting of the lysates of Ms, DCs, and MPHs (10⁶ cells per condition) using an anti-phospho-Ser-19 myo-RLC antibody (Rockland, Limerick, PA). A secondary antibody coupled to horseradish peroxidase (Jackson ImmunoResearch Laboratories, West Grove, PA) was used and antigen/antibody complexes were visualized by an electrochemiluminescence assay (Thermo Fisher Scientific, Waltham, MA). Band intensities were quantified using ImageJ software. Values were normalized according to the median from each donor.

Results and Discussion

Myeloid APCs have different efficiencies to activate T lymphocytes

Myeloid cells can present antigens to T lymphocytes and activate them as a result. Yet, their efficiency in doing so depends on their nature and maturation state. Therefore, we characterized these cells for their ability to activate autologous CD4⁺ T lymphocytes. DCs and MPHs were derived from Ms and left untreated or treated for 24 h with different maturation factors. We used three conditions: LPS (a bacterial product), a TNFα+PGE₂ cocktail (a potent maturation signal for DCs) (21,22), and IFNγ (which is known to regulate antigen presentation by myeloid cells) (23).

We analyzed the expression of maturation markers (Fig. 1 A), such as HLA-DR, which is directly involved in antigen presentation, and costimulatory molecules (CD80, CD86, ICAM1, and CD40), which bind activating receptors on the surface of T lymphocytes (24). Then, purified CD4⁺ T cells from the same donor were cultured with the untreated or treated myeloid cells in the presence of increasing amounts of the superantigen toxic shock syndrome toxin-1 (TSST-1). Production of IL-2 by T cells was measured 24 h later in the supernatants of cocultures (Fig. 1 B).

Figure 1.

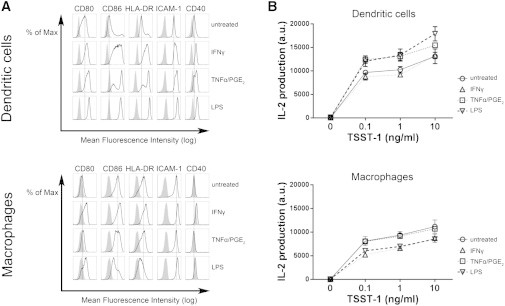
(A) Expression of surface markers by APCs (indicated above histograms) analyzed by flow cytometry for DCs and MPHs either untreated or treated with cytokines or LPS. Gray histograms: isotype control (nonspecific binding of fluorescent antibody); open histograms: binding of surface-marker-specific antibody; black line: mean fluorescence intensity for untreated cells. The shift of open histograms to the right side of the black line indicates increased expression of the surface marker. (B) Production of IL-2 from CD4⁺ T lymphocytes cultured overnight with autologous DCs or MPHs in the presence or absence of TSST-1 superantigen (0–10 ng/mL). Results were obtained from four different donors (values from each donor were normalized according to median).

The results led to three main observations. First, DCs were generally more sensitive than MPHs to maturation factors (Fig. 1 A) and induced more activation of T lymphocytes, as shown by IL-2 production (Fig. 1 B). Second, inflammation factors increased (with different efficiencies) the ability of DCs to induce IL-2 production by T cells. Third, the efficiency of T cell activation did not correlate with the expression of surface markers. For instance, although LPS was the most potent maturation factor, as reflected by the expression of maturation markers by DCs (Fig. 1 A), TNFα+PGE₂-treated and LPS-treated DCs were similarly efficient in inducing IL-2 production by T cells (Fig. 1 B). Also, whereas IFNγ treatment of both DCs and MPHs induced high expression of maturation markers, it did not increase the efficiency of MPHs to induce IL-2 production by T cells. Overall, these results suggest that increased expression of maturation markers is not the only inflammation-sensitive parameter that contributes to the modulation of T lymphocyte activation. Therefore, we investigated whether inflammation modulates other parameters, such as the mechanical properties of APCs.

Myeloid APCs have different mechanical properties

The mechanical response of any material (i.e., the way it deforms under stress) can be described in terms of two ideal behaviors: those of an elastic solid and those of a viscous liquid. Purely elastic solids, such as springs, deform instantaneously in proportion to the applied force and recover their shape when the force is canceled (energy storage and recovery). The ratio between stress σ and strain ε is constant and corresponds to the elastic modulus E = σ/ε, expressed in pascals (Pa). E quantifies the rigidity of the material. As is the case for the stiffness of springs, solids with high E are harder to deform.

Purely viscous fluids, such as water, will flow indefinitely when subjected to a constant force (energy loss). Thus, in contrast to elastic solids, stress here is proportional to the rate of strain, σ = η(dε/dt), where η is the viscosity of the liquid. For instance, honey displays a higher viscosity than water and thus is harder to flow. In dynamic tests, the oscillating deformation is delayed compared with the applied oscillating stress, and the phase shift between the two signals is constant and equal to 1/4 of the period T. Here, stress and strain amplitudes are related by a viscous modulus G = 2π fη = σ/ε, where f = 1 / T is the frequency of the oscillations and η is the viscosity of the material.

Most materials are viscoelastic and share characteristics of both elastic solids and viscous liquids. Depending on the timescale (or, equivalently, on the frequency), the elastic or viscous-like behavior may dominate the response of such a material. In a dynamic mechanical analysis, both the elastic and viscous-like parts of the response are measured as described by the storage ($G_0^{\prime }$) and loss ($G_0^{″}$) moduli, respectively.

We measured the viscoelastic properties of the aforementioned cells (Ms, DCs, and MPHs) by applying oscillations kept below 10% of deformation (Fig. 2). The storage and loss moduli ($G_0^{\prime }$ and $G_0^{″}$) behaved as power laws of the frequency (Fig. S1), as is usually observed for animal cells (18). Here, whereas Ms and DCs were found to have approximately the same modulus, MPHs showed an increase in both $G_0^{\prime }$ and $G_0^{″}$ (Fig. 2 C). Interestingly, the exponent α (related to the ratio between $G_0^{″}$ and $G_0^{\prime }$) was kept constant (Fig. S2 B), indicating that although the effective rigidity of the cell may be modified, the relative contributions of viscosity and elasticity are maintained throughout differentiation. The higher stiffness of the MPHs is consistent with previous results obtained from rat alveolar MPHs (25). Since MPHs are resident cells and DCs are more motile, their different rigidities may reflect adaptation to their functions (6).

Inflammation affects myeloid APC mechanical properties

Myeloid cells are highly sensitive to inflammatory environments, which induce strong phenotypic and morphologic modifications. These cells respond to pathogen-associated molecular patterns such as LPS, as well as cytokines produced during inflammatory processes. As shown in Fig. 1 B, inflammatory factors affect the ability of myeloid cells to activate T lymphocytes. Therefore, we sought to determine whether these factors could also modulate the viscoelastic properties of myeloid APCs.

We first assessed the influence of LPS on APC rigidity. DCs and MPHs were incubated for 24 h with LPS. This treatment led to an increase in $G_0^{\prime }$ and $G_0^{″}$ for DCs, but did not modify the viscoelastic properties of MPHs (Figs. 3 and S2 C). This differential effect of LPS on the mechanical properties correlates with the higher sensitivity of DCs to LPS, as shown by their higher expression of maturation markers (Fig. 1 A).

Figure 3.

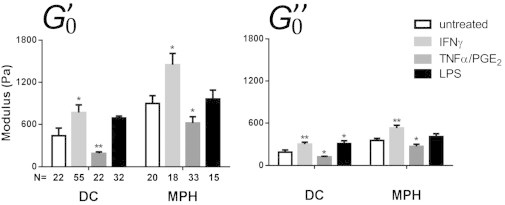
Storage ($G_0^{\prime }$) and loss ($G_0^{″}$) moduli of DCs and MPHs after treatment with different inflammation factors. Cells were incubated with IFNγ (light gray), TNFα/PGE₂ (dark gray), or LPS (black) for 24 h before testing (^∗p < 0.05, ^∗∗p < 0.01, according to Mann-Whitney U test compared with untreated cells; N, number of cells tested, from at least three different donors). For values, see Table 1.

We then tested the effect of TNFα+PGE₂.Treatment of DCs induced a 57% loss of elasticity and 37% loss of viscosity (Fig. 3), increasing the relative contribution of viscosity (increased α in Fig. S2 C). TNFα+PGE₂ treatment was also accompanied by an increase in the expression of maturation markers (Fig. 1 A). This decrease of elasticity and viscosity makes the cells easier to deform and flow, which may facilitate migration in a dense environment. Indeed, PGE₂ has been reported to promote DC migration (26). On MPHs, TNFα+PGE₂ also induced a 30% loss of elasticity and 25% loss of viscosity (Fig. 3), with a slight softening of the cells, without modifying the relative contributions of elastic and viscous-like behaviors (Fig. S2 C). Softening by TNFα+PGE₂ treatment and expression of maturation markers were less pronounced in MPHs than in DCs (Fig. 1 A), reflecting the difference in sensitivity of DCs and MPHs to these activators.

Regarding IFNγ, treatment of MPHs induced an increase in $G_0^{\prime }$ and $G_0^{″}$ of >60% and >50%, respectively, indicating stiffening without a significant change in the viscous/elastic ratio (Figs. 3 and S2 C). DC stiffness was also increased upon IFNγ stimulation, with a 75% increase of $G_0^{\prime }$ and a 60% increase of $G_0^{″}$ (Fig. 3). In both cell types, IFNγ led to an increased expression of maturation markers (Fig. 1 A).

These results reveal an original aspect of inflammation. Different inflammatory cytokines, which induce myeloid APC phenotypic maturation, can have opposite effects on the mechanical properties of myeloid APCs, i.e., softening for TNFα+PGE₂ and stiffening for IFNγ. They also reveal that the effects of inflammation on mechanical properties and on the expression of maturation markers are independent. Although T cells are mechanosensitive (10) and have been shown to be differentially activated by substrates with stiffnesses similar to the range of stiffnesses we report herein (27), no correlation was observed between T cell response and APC mechanical properties. However, these properties constitute additional information that could be integrated by the immune system in order to adapt its response to inflammatory conditions.

T lymphocytes are softer than myeloid cells

To gain insight into the relative rigidity of T lymphocytes as compared with APCs, we performed single-cell rheology measurements on the human leukemic Jurkat T cell line, which is commonly used as a T lymphocyte model (28). Dynamic mechanical analysis revealed that Jurkat cells were softer than myeloid cells ($G_0^{\prime }$ = 80 +70/−40 Pa), in agreement with previous measurements obtained by atomic force microscopy (29). We then decided to measure the rigidity of human primary CD4⁺ T lymphocytes. However, these cells were too small and did not adhere to the plates, so measurement of the viscoelastic properties through dynamic oscillations could not be performed as described above. Therefore, we applied a modified version of the protocol to assess the static Young’s modulus E. Briefly, a T cell was subjected to a stepwise compression between two parallel plates. The corresponding applied stress and deformation of the cell were measured and an apparent Young’s modulus E_app was derived (Fig. 4 A). The measured moduli distributed log-normally (Fig. 4 B) and the T lymphocyte Young’s modulus was E_app = 85 ± 5 Pa. No information on the viscous-like behavior of T lymphocytes could be estimated with this method.

The apparent Young’s modulus E_app represents a static estimation of the elastic behavior of the material and thus should match the $G_0^{\prime }$ values. Indeed, the value of the apparent Young’s modulus E_app of primary T lymphocytes was similar to the $G_0^{\prime }$ value of Jurkat cells. However, since these two parameters were not obtained in the same experimental conditions, we also applied the stepwise compression protocol to Jurkat cells. The apparent Young’s modulus of Jurkat cells was E_app = 70 (+30/−20) Pa, in agreement with the apparent Young’s modulus E_app of primary T cells (Fig. 4 C). Moreover, both protocols were applied on the same Jurkat cells (n = 8), and this equivalence between $G_0^{\prime }$ and the apparent Young’s modulus was confirmed (Fig. S4).

We also derived from the results of the dynamic mechanical analysis, through mathematical calculation (16), the equivalent Young’s modulus E_eq for all cell types studied (Table 1; Fig. 5 A; see also Materials and Methods and Fig. S3). The equivalent Young’s modulus E_eq of Jurkat cells was 90 ± 10 Pa, a value that matches the apparent Young’s modulus E_app of both primary and Jurkat T cells (Fig. 4). Therefore, Jurkat cells can also be used as a mechanical model of primary T lymphocytes.

Table 1.

Values for storage modulus $G_0^{\prime }$, loss modulus $G_0^{″}$, and equivalent Young’s modulus E_eq for the immune cells tested

	${G^{\prime }}_0$ (Pa)	${G^{″}}_0$ (Pa)	Eeq (Pa)
Monocytes
Untreated	520 +90/−80	250 ± 30	580 ± 30
Blebbistatin	50 ± 20	40 ± 20	98 ± 47
Dendritic cells
Untreated	440 +110/−90	190 ± 30	510 ± 20
TNFα+PGE2	190 ± 20	120 ± 10	240 ± 30
IFNγ	770 +110/−100	300 ± 30	830 ± 40
LPS	690 +130/−110	310 ± 40	760 ± 30
Blebbistatin	190 +30/−10	130 ± 10	250 ± 30
Macrophages
Untreated	900 +110/−100	350 ± 30	930 ± 40
TNFα+PGE2	620 +90/−80	270 ± 30	650 ± 30
IFNγ	1450 +160/−150	530 ± 40	1460 ± 80
LPS	960 +130/−110	410 ± 40	1000 ± 60
Blebbistatin	580 +140/−110	300 ± 60	630 ± 40
Primary CD4+ T cells	−/−	−/−	85 ± 5
Jurkat T cells	80 +70/−40	60 ± 10	90 ± 10

For primary CD4⁺ T cells, the value of the apparent Young’s modulus E_app is shown. Because viscoelastic moduli exhibited log-normal distributions, confidence intervals were not symmetric around the mean values. However, when the difference between the upper and lower limits was <10 Pa, the + and − errors were rounded up to the same value.

Figure 5.

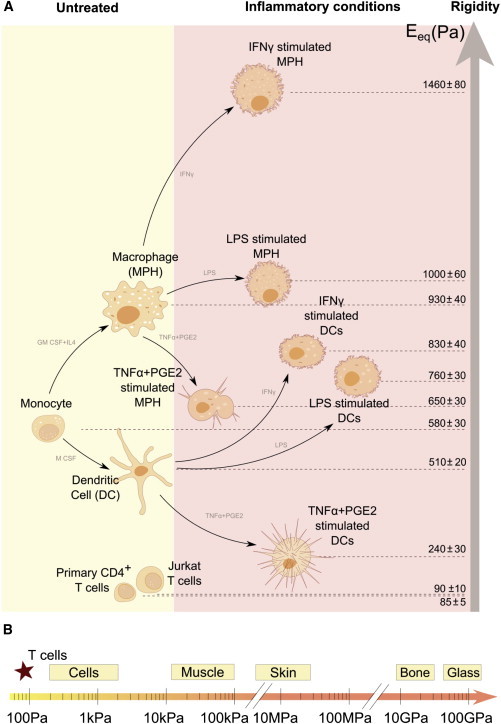
(A) Summary of elasticity values (equivalent Young’s modulus E_eq) for the immune cells tested. (B) Stiffness scale for cells and tissues. To see this figure in color, go online.

It is worth noting that the relative deformation of cells interacting with each other depends on their respective rigidity. When two cells form a surface contact, spreading will be facilitated for the cell presenting the lowest rigidity. Thus, T cells, which have a lower rigidity than myeloid APCs (E_T < E_APC), can spread on APCs, as indeed has been observed previously (30,31).

Our results reveal that T cells are among the softest cells described to date (Fig. 5 B). This property may account for the remarkable capacity of T lymphocytes to transmigrate and move inside dense tissues (32). This softness of peripheral T lymphocytes may be due to their differentiation in a soft tissue, the thymus, which may eventually influence T cell rigidity, as was previously shown for the effect of extracellular matrix stiffness on the mechanical and functional properties of mesenchymal stem cells (33).

The actomyosin cytoskeleton of myeloid APCs determines their cell rigidity

The mechanical properties of cells depend on their actomyosin cytoskeleton (34,35), as reflected by their sensitivity to inhibitors of filamentous actin (F-actin) formation and myosin IIA activity (36–38). To gain insight into the molecular mechanisms underlying the differences in cell rigidity of the myeloid APCs, we investigated the role of actin and myosin in these cells. Using confocal fluorescence microscopy (Fig. S5), we measured the total F-actin content in each cell type, either untreated or subjected to inflammatory conditions. The correlation between E_eq and F-actin content was more striking for MPHs in different conditions than for DCs (Fig. S6), suggesting that the mechanical properties of MPHs rely more on the F-actin content than do those of DCs. Altogether, the results showed a correlation between the F-actin content and the equivalent Young’s modulus E_eq (Pearson r_F-actin = 0.83; Fig. 6 A). This suggested that F-actin is the primary structural determinant of myeloid cell mechanical properties, as was previously shown for neutrophils (39).

Figure 6.

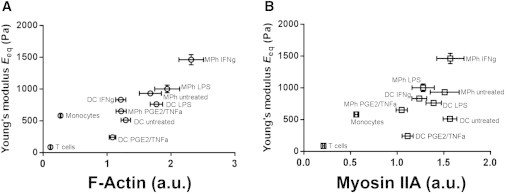
(A and B) Plots of the equivalent Young’s modulus E_eq versus (A) total F-actin and (B) total myosin IIA heavy chain contents measured in confocal microscopy images. Pearson correlation coefficients were calculated (r_actin = 0.83, r_myosin = 0.67).

We then investigated the role of myosin IIA in the mechanical properties of myeloid cells. First, we plotted the equivalent Young’s modulus E_eq versus the myosin IIA content (Fig. 6 B) measured by confocal microscopy (Fig. S5). Although a positive correlation was also observed, it was less important than that found for F-actin content (Pearson r_{myosin IIA} = 0.67). Moreover, plotting the [E/F-actin content] ratio as a function of the total myosin IIA heavy chain content in each cell type did not reveal any correlation, strongly suggesting that the Young’s modulus does not depend on the content of myosin IIA heavy chain (Fig. S7 A). In contrast, plotting the [E/myosin IIA content] ratio as a function of the total F-actin showed a positive correlation between the values (Fig. S7 B), which further confirmed that the mechanical properties of myeloid cells depend largely on their F-actin content.

Beyond myosin IIA heavy chain content, we further investigated the role of myosin IIA activity in the mechanical properties of myeloid cells. Cells were incubated with blebbistatin (5 μM for 15 min), a drug that blocks the myosin heads in a detached position (40), and then a dynamic mechanical analysis was performed. Inhibition of myosin IIA activity reduced the elasticity and viscosity ($G_0^{\prime }$ and $G_0^{″}$, respectively) and the equivalent Young’s modulus E_eq of myeloid cells (Fig. 7, A and B; Table 1), demonstrating that myosin IIA activity regulates myeloid cell mechanical properties. However, the different myeloid cell types responded differently to blebbistatin treatment, with Ms being the most sensitive (90% decrease in $G_0^{\prime }$) and MPHs being the least sensitive (36% decrease) (Fig. 7 B). These results suggested that the mechanical properties of Ms are particularly dependent on myosin IIA activity. This importance of myosin IIA activity in Ms correlated with a higher myosin IIA heavy chain/F-actin ratio in these cells (Fig. 7 C), as well as increased phosphorylation on Ser-19 of the myo-RLC (Fig. 7 D), which is known to increase the Mg²⁺-ATPase activity of myosin (41). This strong contribution of myosin IIA might explain why the E_eq of Ms does not correlate with F-actin content in the same way as does the E_eq of DCs and MPHs (Figs. 6 and S7).

Figure 7.

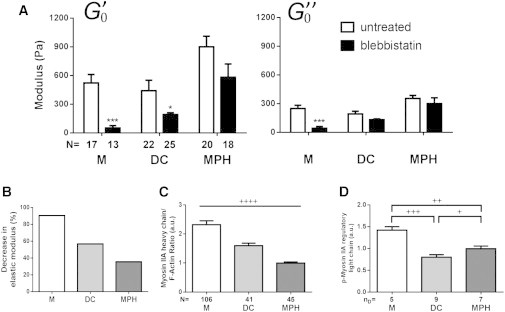
(A) Ms, DCs, and MPHs were subjected to 5 μM of blebbistatin for 15 min before dynamic mechanical testing was performed and the effect on storage ($G_0^{\prime }$) and loss ($G_0^{″}$) moduli (^∗∗p < 0.01, ^∗∗∗p < 0.001, according to Mann-Whitney U test compared with untreated; N, number of cells tested, from at least three different donors) was determined. (B) Blebbistatin-induced percentage decrease of the storage modulus $G_0^{\prime }$ as compared with that of untreated cells. (C) Comparison of the ratio of total myosin IIA heavy chain content and total F-actin content for Ms, MPHs, and DCs. (D) Quantification of western blot bands for the phosphorylated Ser-19 of the myo-RLC (⁺p < 0.05, ⁺⁺p < 0.01, ⁺⁺⁺p < 0.001, ⁺⁺⁺⁺p < 0.0001, unpaired t-test with Welch’s correction for each condition; N, number of cells tested, from four donors; n_D, number of donors).

Overall, these data show that the mechanical properties of myeloid cells depend on both their F-actin content and myosin IIA activity, with the relative contribution of each parameter varying among cell types. The differential effect of inflammation factors on the mechanical properties of myeloid cells (Figs. 3 and S2) may reflect their induction of different signaling cascades that in turn differentially modify the cytoskeleton of the treated cells. For example, PGE₂ increases cAMP cellular concentration, which in turn decreases myosin IIΑ activity (42); IFNγ activates Rac1, a small GTPase involved in actin remodeling (43); and LPS increases the activity of Rho kinase (ROCK), a known activator of myosin IIA (44).

A better understanding of the regulation of mechanical properties during immune responses will require an in-depth analysis of the regulation of myosin IIA activity and of actin-related proteins involved in polymerization and/or cross-linking of F-actin in immune cells. It will also be interesting to study how manipulating actomyosin activity in APCs can affect T cell activation by the APCs.

Conclusions

Altogether, our results show that human immune cells display a wide range of mechanical properties that are modified by inflammatory conditions and are remarkably conserved among donors. The values of the viscoelastic modulus of human myeloid cells are shown to depend on myosin IIA activity and to correlate with the F-actin content, which can be modified by cell differentiation and inflammatory conditions.

Inflammation also modifies the expression of myeloid cell maturation markers independently of the mechanical properties. This suggests that the viscoelasticity of myeloid cells is an additional parameter of inflammation that could be used by T cells along with biochemical factors to generate an integrated immune response. Indeed, our results show that neither maturation marker expression nor viscoelasticity correlates per se with T cell activation.

Finally, myeloid APCs are 10⁷- to 10⁸-fold softer than plastic or glass, both of which are typically used for in vitro culture of T lymphocytes (Fig. 5 B). This work presents a physiological range of rigidities that should be tested to investigate the mechanosensitivity of T lymphocytes.

Author Contributions

N.B. and M.S. designed research, performed research, analyzed data, and wrote the article. S.D., O.B., A.B., and A.R. performed research. M.M. analyzed data. C.H. and A.A. designed research, analyzed data, and wrote the article.