Linking morphodynamics and directional persistence of T lymphocyte migration

Abstract

T cells play a central role in the adaptive immune response, and their directed migration is essential for homing to sites of antigen presentation. Like neutrophils, T lymphocytes are rapidly moving cells that exhibit amoeboid movement, characterized by a definitive polarity with F-actin concentrated at the front and myosin II elsewhere. In this study, we used total internal reflection fluorescence (TIRF) microscopy to monitor the cells' areas of contact with a surface presenting adhesive ICAM-1 and the chemokine, CXCL12/SDF-1. Our analysis reveals that T-cell migration and reorientation are achieved by bifurcation and lateral separation of protrusions along the leading membrane edge, followed by cessation of one of the protrusions, which acts as a pivot for cell turning. We show that the distribution of bifurcation frequencies exhibits characteristics of a random, spontaneous process; yet, the waiting time between bifurcation events depends on whether or not the pivot point remains on the same side of the migration axis. Our analysis further suggests that switching of the dominant protrusion between the two sides of the migration axis is associated with persistent migration, whereas the opposite is true of cell turning. To help explain the bifurcation phenomenon and how distinct migration behaviours might arise, a spatio-temporal, stochastic model describing F-actin dynamics is offered.

1. Introduction

T lymphocytes are essential players in adaptive immune responses to infection, and the orchestrated, directed migration of these cells into targeted tissues and their recirculation are required for their functional responses [1]. Chemokines play a central role in directing T-cell trafficking by establishing tissue-specific ‘address codes’ that guide the lymphocytes to the proper sites [2]. Accordingly, chemokines synergize with adhesive ligands to promote migration of isolated, naive T cells [3]. The chemokine CXCL12 (or stromal cell-derived factor-1, SDF-1) is recognized by the G protein-coupled chemokine receptor, CXCR4, which mediates chemotactic responses of T cells and also naive B lymphocytes. Accordingly, CXCL12/CXCR4 signalling is critical for T-cell development in the thymus and T-cell trafficking into secondary lymphoid tissues (lymph nodes and spleen) [1]. Within those tissues, CXCL12 further guides lymphocyte movements and is especially important in the dynamics of germinal centres [4–6].

Lymphocyte function-associated antigen-1 (LFA-1) is a heterodimeric adhesion receptor of the integrin family that is abundantly expressed on the surface of T lymphocytes; it mediates lymphocyte adhesion to the extracellular matrix and to other cells [7–9]. LFA-1 engages intercellular adhesion molecule-1 (ICAM-1/CD54) molecules displayed by other cells, initiating cell–cell adhesion and immune synapse formation [3,9]. However, LFA-1 is maintained in a low-affinity state in the absence of chemokine stimulation. Inside-out signalling from active chemokine receptors to LFA-1 is required before integrin-mediated outside-in signalling can be activated [10,11]. Subsequent rearrangement of the cytoskeleton, including reorganization of the F-actin network at the cell's leading edge and myosin-dependent contraction at the rear, results in cell polarization and locomotion [12]. Studies have revealed a key role for myosin IIA in detachment of LFA-1 adhesions and tail retraction in T cells [13]. More recent evidence suggests further that myosin IIA and LFA-1 functions are integrated, manifest as distinct T-cell migration modes described as walking and sliding. Walking is characterized by fast migration and loose/sporadic adhesion to the surface, whereas sliding is characterized by slower migration and more extensive and continuous cell contact [14].

T-cell migration elicited by CXCL12 and other chemokines has been widely studied, yet most studies have focused on the result of migration rather than the mechanics of the process. Characterization of the cells' morphodynamics, i.e. how the shape of a cell changes during migration, lends direct insights into the statistics of cell centroid translocation and potentially about the coordination of F-actin polymerization and myosin contractility. In this study, we used total internal reflection fluorescence (TIRF) microscopy to illuminate the contact areas of primary T cells as they crawled on surfaces with immobilized CXCL12 and ICAM-1. We show that mouse T-cell migration is characterized by frequent bifurcation of the leading edge. Of the two protruding extensions generated by each bifurcation, one is a dominant extension that continuously protrudes forward, whereas the other ceases protrusion and acts as a pivot point for cell turning. Statistical analyses suggest that turning behaviour is not random, i.e. that T cells exhibit two distinct migration states: smooth turning, with less frequent bifurcations and protrusion dominating on the same side of the migration axis, and persistent migration, which is marked by more frequent bifurcation events and alternating/switching of the dominant protrusion between sides. To develop a hypothesis about the mechanism of leading-edge bifurcation, we formulated a computational model that combines stochastic F-actin dynamics and maintenance of fore/aft polarity. Model simulations reproduce the general bifurcation phenomena as well as features of the two migration states we observe.

2. Results

2.1. T lymphocyte migration is characterized by bifurcation of the lamellipodium at the cell's leading edge

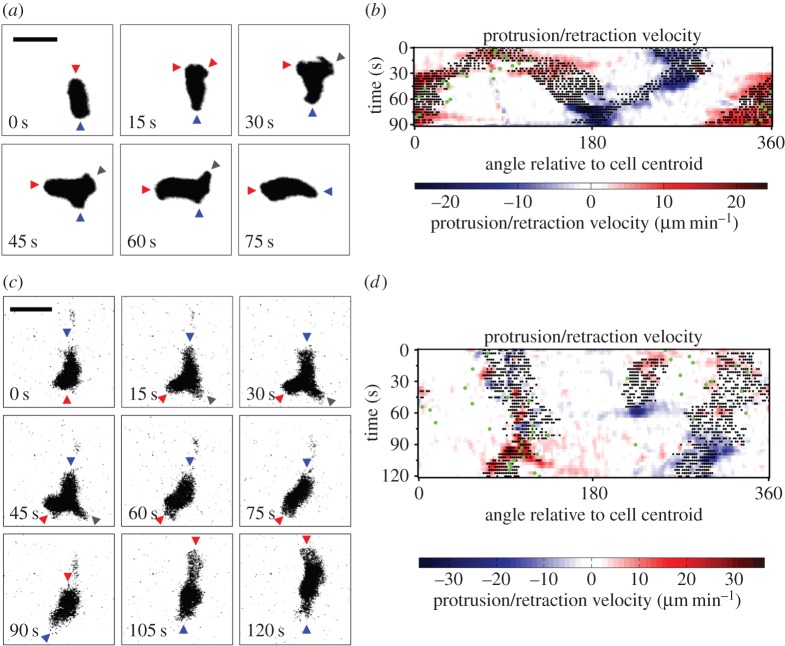
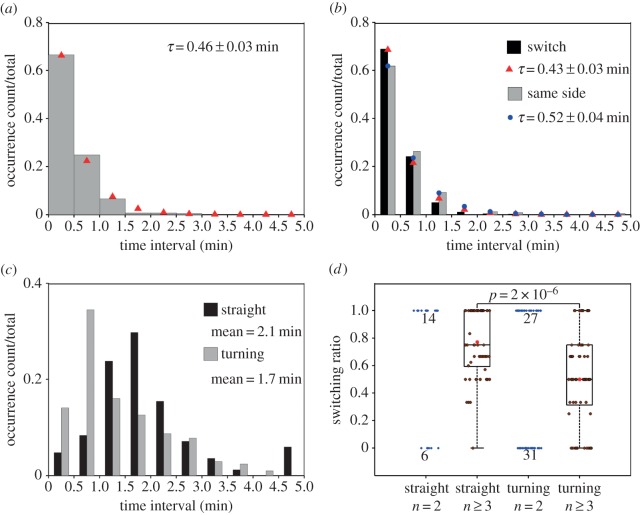
TIRF microscopy was used to monitor a cohort of 38 primary, murine (naive) T lymphocytes as they migrated randomly on surfaces with immobilized ICAM-1 and the chemokine, CXCL12/SDF-1. Analysis of these high-resolution data by morphodynamic mapping [15,16] elucidates changes in the shape of the contact area during T-cell crawling. The primary characteristic of these dynamics was found to be the bifurcation, or lateral branching, of the protruding leading edge into two distinct lobes. As shown for a representative sequence, the dominance of one branch over the other results in a change in the direction of overall cell migration (figure 1a). This phenomenon is depicted on the morphodynamic map (figure 1b) as follows. Pixels associated with the two protruding lobes are marked as structures that are morphologically extended from the cell body [15], as are the pixels associated with the uropod in the rear (black dots). These structures are distinguished by overlaying edge velocity data, with protrusion and retraction marked by red and blue hues, respectively. The map also shows changes in the direction of cell centroid translocation (green dots; figure 1b). Thus, the map shows the bifurcation and wave-like separation of the protruding lobes during the first 30 s of the sequence; thereafter, the dominant lobe accelerates its protrusion, whereas the other comes to rest, accompanied by a shift in translocation direction. Thus, the ‘abandoned’ protrusion serves as a pivot point for cell turning (figure 1b). During this sequence, the uropod maintains its direction of retraction, but the angular position of this movement relative to the centroid shifts with time (compare figure 1a,b).

Figure 1.

T lymphocyte migration is characterized by bifurcation of protrusions at the leading edge. (a) Representative TIRF montage of a murine T cell executing a turn by bifurcation of the leading edge. The arrowheads mark morphological extensions that are protruding (red), retracting (blue) or stationary (grey). Scale bar, 10 µm. (b) Morphodynamic map of the sequence depicted in (a). Pixels associated with structures that are morphologically extended from the cell body are marked as black dots overlaid with edge velocity data, with protrusion and retraction marked by red and blue hues, respectively. The map also shows changes in the direction of cell centroid translocation (green dots). (c) TIRF montage showing an uncommon instance of a T cell abruptly changing migration polarity. Extensions are labelled as in (a). Scale bar, 10 µm. (d) Morphodynamic map of the sequence depicted in (c), constructed as in (b).

In the sequence described above, the abandoned protrusion visibly merged with the trailing uropod, an occurrence observed for 41% of bifurcation events. More often (59% of bifurcation events), the abandoned protrusion fails to merge with the tail and is simply retracted, as shown in another representative sequence (figure 1c, 45 s). This particular cell also shows a rare behaviour (four instances total detected): reorganization, even reversal, of its front–rear polarity. In the representative sequence, this occurs between 60 and 90 s without gross changes in the size or shape of the contact area (figure 1c). In the morphodynamic map (figure 1d), the protruding and retracting regions pause and then swap positions, indicating a reversal of the migration polarity.

2.2. T lymphocyte migration directionality is determined by the fates of extensions formed by bifurcation of the leading edge

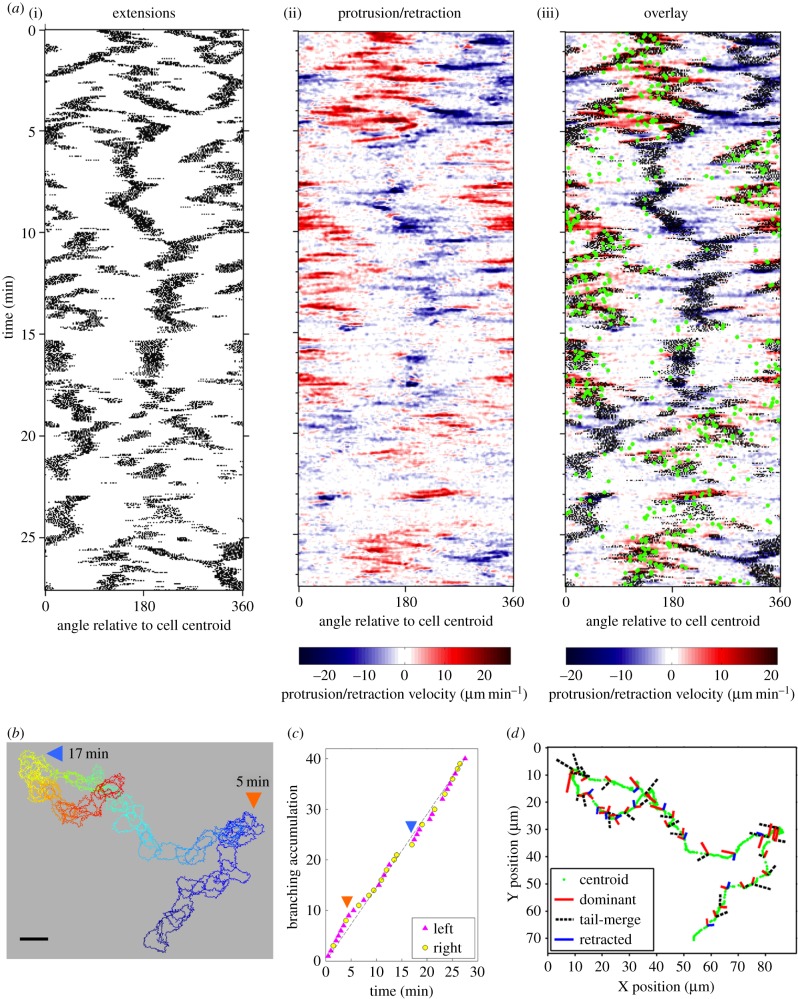
Having established the phenomenon of lamellipodial bifurcation in migrating T cells, we postulated that the fates of these protrusions govern turning behaviour and thus determine the cells' directional persistence. For extended periods of random migration, the spatio-temporal maps show frequent branching of extending protrusions at the leading edge and relatively smooth retraction of the cell rear (representative cell depicted in figure 2a). T cells migrated rapidly (average speed = 7.9 µm min⁻¹), with directionality shifting in alignment with the dominant protrusion. As a result, the cells typically exhibited frequent changes in direction, even while cell directionality exhibits persistence (i.e. remains correlated) over a somewhat longer timescale (figure 2a, green dots). The overlaid cell outlines exemplify how the cells actively changed shape and executed sharp turns during random migration (figure 2b). To relate turning behaviour to leading-edge branching, we documented the approximate time interval during which each branching event occurred (figure 2c) along with the fates of the two protrusions that were formed (figure 2d); with regard to the latter, we noted (i) whether the dominant protrusion extended to the left or to the right of the apparent migration axis and (ii) whether the abandoned extension persisted and merged with the uropod or was retracted. This information is depicted along with the path of the cell centroid as a graph (figure 2d), in which each branching event is marked by a pair of segments signifying the orientations of the nascent protrusions relative to the migration axis (left and right) and the fates of those protrusions (dominant, tail-merge and retracted); the relative length of each segment corresponds to the recorded lifetime of the extension. The graph for the representative cell illustrates that notable changes in directionality tend to be associated with the pivoting behaviour illustrated in figure 1a,b, i.e. when the abandoned extension merges with the tail. Strikingly, the cell achieved tight turns by executing a series of branches of this kind, oriented in the same direction (figure 2d, arrows).

Figure 2.

T lymphocyte migration directionality is determined by the fates of extensions formed by bifurcation of the leading edge. (a) Morphodynamic maps of a representative migrating cell. Left: pixels associated with structures that are morphologically extended from the cell body are marked as black dots. Centre: edge velocity data, with protrusion and retraction marked by red and blue hues, respectively. Right: overlay of the morphology and protrusion maps, also showing changes in the direction of cell centroid translocation (green dots). (b) Stacked outlines of the cell depicted in (a). Blue is the initial time point; red the end. Large-scale turning events are labelled with times as indicated. Scale bar, 10 µm. (c) Accumulation of bifurcation events for the cell shown in (a,b). Each event is labelled as indicated according to whether the dominant protrusion was on the left or right side of the migration axis. (d) For the same cell analysed in (a–c), bifurcation events marked on the cell centroid track (green) showing the fates and orientations (left and right) of each protrusion. The relative length of each segment corresponds to the recorded lifetime of the extension.

2.3. Lamellipodial bifurcation is rapid compared with cell movement and shows temporal characteristics of a spontaneous process

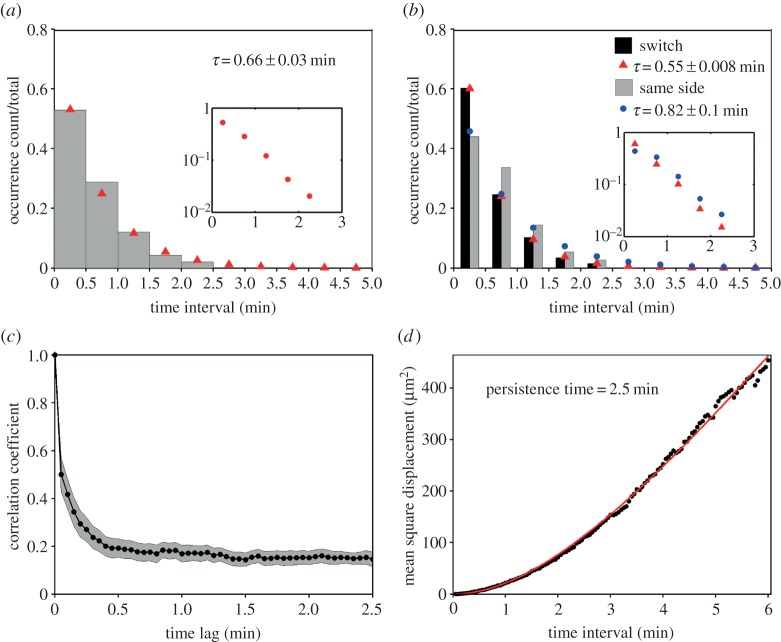
Having established the nature of the morphodynamics, we sought to characterize the process of protrusion bifurcation across the T-cell cohort in more quantitative terms. The waiting times between successive branching events were determined by inspection of the morphodynamic maps, within time intervals of 0.5 min (from experience, the limit of resolution for a manual estimate). The normalized waiting-time distribution (WTD) is presented as a histogram and compared with that of a spontaneous, memoryless process, i.e. an exponential distribution (figure 3a). The fit of the distribution is good, with a theoretical mean τ = 0.66 min. The experimental dataset showed a subtle but notable deviation from the fit for the 0.5–1 min bin, suggesting that a statistical model with more parameters might be needed to fully describe the data. Consistent with this view, we found a significant difference between the WTDs for successive bifurcation events that favoured the same side of the migration axis (τ = 0.82 min) versus those where the dominant protrusion switched sides (τ = 0.55 min; figure 3b); we also note that there is a modest bias towards switching (264/488 = 54%). These results suggest that the fates of bifurcated lamellipodia are not entirely random, and that there might be distinct modes of T-cell migration associated with the tendency to turn.

Figure 3.

Lamellipodial bifurcation is rapid compared with cell movement. (a) Normalized waiting-time distribution (WTD) for pairs of consecutive bifurcation events (n = 488). The red symbols are the corresponding best-fit values assuming an exponential distribution. The inset shows the semi-logarithmic plot of the same dataset. (b) WTDs for bifurcation pairs where the two dominant protrusions were on different sides of the migration axis (switch; n = 264) or on the same side (n = 224). The corresponding exponential fit values are indicated by red and blue symbols, respectively. The inset shows the semi-logarithmic plots of the switch (red) and same-side (blue) data. (c) The autocorrelation coefficient of the cell movement vector as a function of the time lag. The grey region indicates the 95% confidence interval. (d) Mean-squared displacement as a function of time interval. The red line is the best fit to a persistent random walk model.

To compare these temporal characteristics of lamellipodial bifurcation to those of the overall cell movement, we calculated the autocorrelation coefficient of the cell movement vector with varying time lag [17]. The analysis shows a rapid loss of correlated movement, within approximately 0.5 min, but also persistent positive correlation over longer periods of observation (figure 3c). Our interpretation is that the fast timescale is associated with leading-edge bifurcation and reflects the rapid shifts in cell centroid position seen in protrusion maps (e.g. figure 2a), whereas the slower timescale (more than 2 min) reflects the directional persistence of the overall translocation process. As a point of comparison, we fit the mean-squared cell centroid displacement as a function of time interval to a persistent random walk model [18] (figure 3d). The best-fit value of the persistence time is 2.5 min, comparable to the timescale of the slower decay of the autocorrelation coefficient.

2.4. Periods of T lymphocyte migration persistence/turning are associated with distinct leading-edge bifurcation tendencies

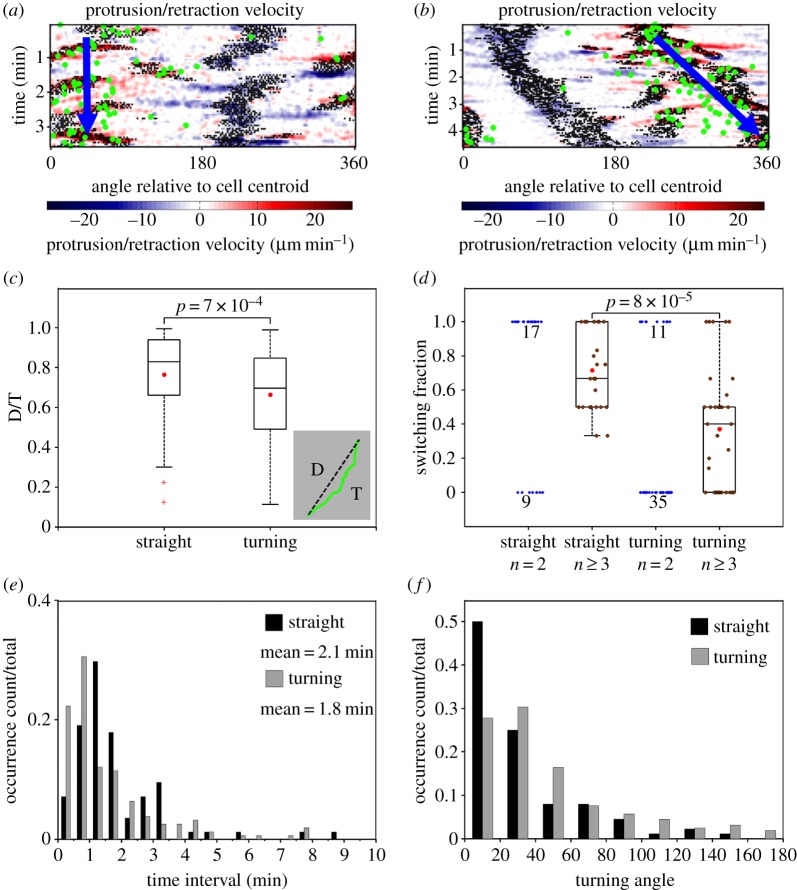
Taken together, the analysis presented thus far suggests that mouse T cells execute sharp turns when bifurcation of the leading edge favours clockwise/anticlockwise movement, i.e. with the dominant branch consistently on the right/left of the migration axis. The converse argument is that the cells must alternate the orientation of the dominant protrusion to maintain persistent motion. To verify this hypothesis, we first identified periods of straight migration (n = 84) and turning (n = 157) based on both the cell centroid tracks and the patterns visible in the cells' morphodynamic maps (figure 4a,b). Consistent with the WTD analysis described above, the temporal resolution was chosen as 0.5 min. Periods with notable curves in the centroid tracks were considered turning periods (otherwise, straight), and periods with low cell migration (path length < 3 µm) were excluded. For each period, the displacement-over-travelled distance (D/T) ratio of the centroid path was calculated as a measure of its directional persistence (figure 4c, inset), and the distributions of D/T values for straight and turning periods were compared (figure 4c). As expected, the analysis confirms that the D/T persistence values for the turning group are significantly lower. For straight and turning periods with at least two bifurcation events, we considered all pairs of consecutive bifurcation events and calculated the fraction of pairs that switched sides of the migration axis (left–right or right–left) for each period (figure 4d). Consistent with our hypothesis, the switching fraction of the straight group is significantly higher than that of the turning group, as shown for periods with at least three (two pairs of) bifurcations (figure 4d). In both groups, there are also many periods with only two branches, for which the switching fraction is either 1 or 0; among these, values of 1/0 are enriched in the straight/turning group (figure 4d, blue dots).

Figure 4.

Persistent and turning migration modes are associated with switching and same-side bifurcations. (a,b) Morphodynamic maps of representative straight (a) and turning (b) migration periods. Green dots indicate the cell centroid track. (c) Distributions of displacement-over-distance travelled (D/T) ratio for straight (n = 84) and turning (n = 157) periods. Each box and whiskers indicates the quartiles of the distribution; red dots: mean values. p-value: Student's t-test. (d) Distributions of bifurcation switching fraction for straight and turning periods. The switching fraction is defined as the fraction of consecutive bifurcation pairs that switch sides of the migration axis (left–right and right–left). Each box and whiskers indicates the quartiles of the distribution of periods with at least two bifurcation pairs (n ≥ 3). The blue dots are switching fractions for periods with only one bifurcation pair (n = 2); the numbers indicate the number of occurrences when the switching fraction was 0 or 1. Red dots: mean values. p-value: Student's t-test. (e) Normalized distributions of time duration for straight and turning periods. (f) Normalized distributions of absolute turning angle associated with the change in overall direction of migration between consecutive bifurcations, as observed during straight and turning periods with at least one bifurcation pair.

Straight and turning periods show other distinguishing characteristics. The durations of the straight and turning periods show non-exponential distributions, indicating a degree of memory (figure 4e). Consistent with that notion, the average durations of straight (2.1 min) and turning periods (1.8 min) are much longer than the estimated waiting time between bifurcation events and comparable to the estimated persistence time of 2.5 min. The distribution of the straight group is notably shifted in time relative to the distribution of the turning group (figure 4e), suggesting a subtle difference in the apparent memory effect. We note that there are substantial numbers of both straight and turning periods with durations less than 1 min (and with only one bifurcation event), explaining the broad distributions of D/T values for the two groups (figure 4c). The straight and turning groups also show distinct distributions of absolute turning angles (between directions of migration for bifurcation pairs contained within each period). Bifurcations during turning periods not only switch sides of the migration axis less often, but they also tend to yield larger changes in cell orientation (figure 4f).

2.5. A computational model based on plausible feedback mechanisms can explain lamellipodial bifurcation and T-cell migration behaviours

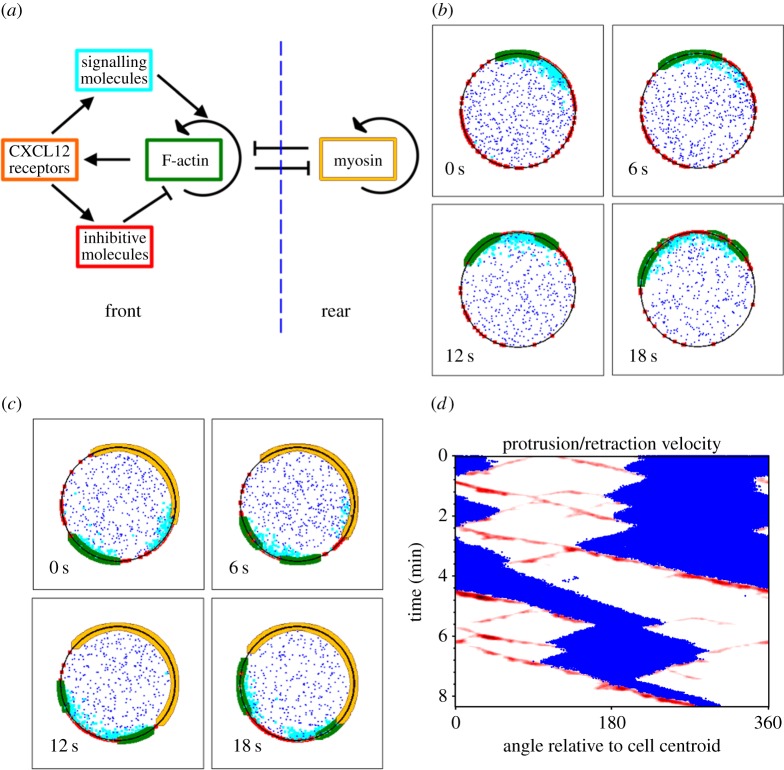
Certain hallmarks of amoeboid cell migration, such as spontaneous polarization and sensitivity to shallow chemoattractant gradients, suggest nonlinear dynamics at the level of signal transduction and/or the F-actin cytoskeleton [19,20]. Mathematical modelling provides a framework for testing the plausibility of mechanisms that might encode observed migration phenotypes [21–23]; considering that mechanistic/molecular details of T-cell migration are lacking, we sought to formulate a hypothetical model that explains observed phenomena on a qualitative level. To describe the dynamics of F-actin polymerization underlying the membrane protrusion phenomena exhibited by T cells, we formulated a spatio-temporal, stochastic model in which species of molecules or molecular assemblies are treated as Brownian particles, and transformations occur probabilistically (figure 5a) [24]. In the model, F-actin-barbed ends proliferate by branching in an autocatalytic fashion, facilitated by a hypothetical signalling pathway upstream of the Arp2/3 complex [25]. Protrusion of the leading edge in turn promotes activation of the signalling pathway, e.g. by promoting new interactions between chemokine receptors and integrins with their ligands immobilized on the surface. Positive feedback, with sufficiently high cooperativity, is commonly invoked in models of signalling polarization [26–28]. To balance the positive feedback, we included two processes. One is depletion of the inactive signalling molecule from the fast-diffusing, cytosolic pool; in effect, this process globally inhibits the signalling pathway, and under certain conditions it allows a stable polarity to be established [27]. To cause bifurcation of the leading edge, we reasoned that a second process must regulate or ‘poison’ the protrusion locally, as considered in other models [26,29,30]. In theory, such local inhibition/regulation may be important for the cell to track a non-stationary spatial cue [26]. A key feature is that the poison accumulates on a slow timescale relative to establishment of F-actin domains.

Figure 5.

A computational model can explain lamellipodial bifurcation and T-cell migration behaviours. (a) Schematic of the major interactions in the stochastic model. (b) Montage of a brief period of simulation during which an F-actin patch (green) bifurcates in the absence of a cell rear. Inactive and active signalling molecules (blue and cyan, respectively) and a membrane-localized inhibitor (red) are depicted. The receptor species is not shown. (c) Same as (b) but with an established cell rear module (beige). (d) Morphodynamic map of a simulated cell showing simulated F-actin waves as a proxy for protrusion (red) and the cell rear as a proxy for retraction (blue). See electronic supplementary material, movie S1 for an animation of the simulation.

Stochastic simulations of this model with a two-dimensional disc geometry confirm that the proposed circuit is capable of forming F-actin domains that readily bifurcate and move laterally away from each other (figure 5b). On the periodic boundary, however, the two domains most often coalesce on the other side, or in some instances, their waves become entrained, consistent with deterministic calculations for related models [30].

A key aspect of leucocyte migration that is missing from the model described above is the polarity of the cell. Hence, we added to the model a parallel wave-pinning model that defines the cell rear, in which F-actin domains are destroyed owing to myosin II-imposed contractility. Conversely, the model includes a mechanism acting over an intermediate spatial range by which F-actin domains inhibit the rear. The point of this feature of the model is not to impose the concept of opposing frontness and backness pathways per se; rather, the intention was to emulate the jostling of the front and rear by whatever mechanism(s), including mechanical tension [31]. With this modification, model simulations show bifurcating F-actin domains that are at any given time restricted to one side of the boundary (figure 5c).

We next addressed whether distinct motility behaviours of the types observed experimentally are recapitulated by the model, or if the simulated fates of the two domains produced by each bifurcation event are random. Although periods of more random behaviour were observed (as in the experiments as well), correlated behaviour was prominent in the simulations (figure 5d and electronic supplementary material, movie S1). In the context of the model, non-random outcomes depend on the balance between (i) pro-protrusion signalling feedback versus the negative influences of (ii) the poison and (iii) the cell rear. All three of these subprocesses contribute to ‘memory’ of the system, i.e. correlated behaviour that persists through multiple bifurcation events. When the dominant side of the cell front spawns a protrusion that moves to the other side, the new direction may be favoured if the poison has cleared there, and if the newly spawned F-actin domain is able to establish pro-protrusion signalling (with the parent domain weakened by the cell rear); thus, the dominant side alternates, consistent with persistent migration. On the other hand, when the dominant side of the cell front is able to maintain the lion's share of signalling to counteract the effects of the poison and cell rear, whereas the protrusion moving towards the other side cannot compete in that regard, the system tends to remain in a state consistent with active turning.

2.6. Statistics of simulated F-actin dynamics show qualitative trends that match those of leading-edge bifurcation in migrating T cells

Although the purpose of our stochastic model is to provide conceptual hypotheses, statistics of the simulated dynamics are nonetheless comparable to those extracted from experiments. This is achieved by analysis of simulated ‘protrusion/retraction’ maps, where F-actin density and the cell rear in the simulations are considered proxies for protrusion and retraction, respectively (as illustrated in figure 5d). Consistent with the analysis shown in figure 3a,b, the normalized WTD of simulated F-actin bifurcations was close to exponential, with estimated mean τ = 0.46 min (figure 6a), and there is a significant difference between the WTDs for successive bifurcation events where the dominant protrusion switched sides (τ = 0.43 min) versus those that favoured the same side of the migration axis (τ = 0.52 min; figure 6b). We note that the units of simulated time are arbitrary and could be rescaled to produce a better quantitative match with experiment. Qualitatively, the shorter mean waiting time for switching bifurcations in the simulations is explained as follows. In such instances, bifurcation is nearly coincident with the ‘collision’ of the F-actin domain with the cell rear boundary, whereas additional time is required to establish signalling that maintains a dominant protrusion on one side of the leading edge. To assess the properties of simulated F-actin bifurcations related to straight migration versus turning, we performed the same analysis as in figure 4. The durations of the straight (n = 84) and turning (n = 206) periods show non-exponential distributions with average durations of 2.1 and 1.7 min, respectively, similar to the experimental results (figure 6c). Consistent with experiment, the switching fraction of the straight group is significantly higher than that of the turning group (figure 6d). This analysis indicates that the computational model is not only capable of simulating the two types of bifurcation and turning behaviour, but it also adequately describes the timescales associated with shifting between the two.

Figure 6.

Comparison of simulated F-actin dynamics to experiment. (a) Normalized waiting-time distribution (WTD) for pairs of consecutive bifurcation events (n = 686) in simulations with the same set of parameters as used in figure 5. The red symbols are the corresponding best-fit values assuming an exponential distribution. (b) WTDs for switching (n = 450) or same-side (n = 236) bifurcation pairs. The corresponding exponential fit values are indicated by red and blue symbols, respectively. (c) Normalized distribution of time duration for straight (n = 84) and turning (n = 206) periods identified in the simulation results. (d) Distributions of bifurcation switching fraction for straight and turning periods of the simulated results, analysed as in figure 4f. Each box and whiskers indicates the quartiles of the distribution of periods with at least two bifurcation pairs (n ≥ 3). The blue dots are switching fractions for periods with only one bifurcation pair (n = 2); the numbers indicate the number of occurrences when the switching fraction was 0 or 1. Red dots: mean values. p-value: Student's t-test.

3. Discussion

The conceptualization of cell turning as a competition between the two sides of the leading edge is decades old [32] and has been refined by more recent experimental observations for different cell types [33,34]. This work characterizes the morphodynamics of murine T-cell migration in relation to turning behaviour that affects directional persistence. On a surface coated uniformly with CXCL12 and ICAM-1, T lymphocyte migration is marked by bifurcation of the cell front, with turning determined by the dominance of one of the protrusions thusly formed. Analysis of this process revealed that, although leading-edge bifurcation occurs with a characteristic frequency, the determination of the dominant protrusion is not random. Rather, the evidence suggests that control of leading-edge bifurcation manifests as two distinct migration phenomena: one that favours a persistent, straight migration path and the other that favours large-scale turns. The characteristics of these turning behaviours are unrelated to the walking and sliding modes of T-cell migration previously reported, which were distinguished based on cell speed and adhesion [14]. Our surfaces were coated with high ICAM-1 concentration, promoting stable cell adhesion. Therefore, the continuous T-cell contact areas we recorded and analysed match the description of sliding cells. A more complete conceptual model of T-cell locomotion should consider both the ‘translational’ and ‘rotational’ aspects of movement and how they vary as a function of the cell's microenvironment.

Given its amoeboid character, it is not surprising that T-cell migration behaviour shares certain similarities with that of the amoeba, Dictyostelium discoideum. Pseudopod splitting in D. discoideum is well established, as is the maintenance of directional persistence by alternating branch directions [35–37]. There are also marked differences between the two cell types. Morphologically, D. discoideum cells crawl by elongation of pseudopods from which new pseudopods split off at approximately a 60° angle [36], whereas leading-edge bifurcations in T cells occur more frequently (relative to cell speed) and form less pronounced extensions that separate from one another laterally. These features are not readily resolved using standard fluorescence microscopy; our analysis was enabled by TIRF microscopy. Further, periods of turning, during which T cells tend to pivot on the same side of the migration axis, have not been described in randomly migrating D. discoideum; in that context, turning has been attributed to de novo formation of pseudopods in random directions [36].

To develop provisional hypotheses that might help explain some of the qualitative aspects of T-lymphocyte morphodynamics, we formulated a computational model based on putative F-actin dynamics and cell polarization. Such feedback-based models have been successful in the prediction of D. discoideum random and directed migration, e.g. pseudopod splitting and cell turning behaviours [38,39]. Simulations produced F-actin polymerization waves at the leading edge, which have been observed in neutrophil-like cells [37], and bifurcations are readily produced through the activity of a negative regulator that accumulates in the virtual protrusion, i.e. this form of regulation is distinct from the antagonistic interactions that are thought to drive cell polarization. The recently discovered inhibitory protein, Arpin, might play such a role. Evidence implicates Arpin as the negative link in an incoherent feed-forward loop connecting the small GTPase Rac and the Arp2/3 complex [40]. We note, however, that accumulation of the ‘poison’ that causes leading-edge bifurcation in our model is a hypothetical process and could be represented instead by, e.g. depletion/sequestration of a slow-diffusing activator. The other important aspect of the model is competition between the protrusions, which gives rise to correlated outcomes; the dominant protrusion tends to either remain on the same side of the cell front or alternate between sides for some time. The concept that emerges from the simulations is that these correlations arise from short-term memory of the system, encoded by the lifetime of the local regulator, the strength of the positive feedback promoting F-actin polymerization, and the boundaries imposed by the cell rear. Clearly, this is a concept and hypothesis that will need to be refined or revised as new mechanistic/molecular details come to light. Nevertheless, the stochastic simulations of the model produced statistics that were in fine agreement with experiments, i.e. the collective short-term memory may be considered an emergent property of the system.

Although our experiments and modelling here are focused on random migration, there are implications for T-cell migration directed by chemokine gradients. CXCL12 secreted by stromal cells is important for both the recruitment of T cells from the circulation and their migration within lymphatic tissues. The chemotactic effects of CXCL12 on T cells is well established, yet whether active CXCL12 is soluble, immobilized or a combination thereof in vivo is unclear. The surface-bound CXCL12 distribution has been examined in vivo by antibody staining [6] or by imaging CXCL12-GFP knock-in mice [41]; however, information about soluble CXCL12 is currently inaccessible. Studies have suggested that the chemokine CCL21 is bound to extracellular matrix or to cell membranes through interactions with glycosaminoglycans (GAGs). CXCL12 also binds GAGs, and therefore it is plausible that CXCL12 is largely immobilized in vivo. A distinctive aspect of migration directed by an immobilized cue (haptotaxis) is that it is inherently an exploratory process that requires active protrusion to sense ligands; chemotactic sensing, on the other hand, requires only passive diffusion of ligands [42]. Thus, haptotactic sensing invokes a positive feedback loop of sorts, which is represented in the present model and previous ones dealing with adhesion-based signalling [43–45]: F-actin polymerization promotes protrusion, which in turn enhances receptor-mediated signalling to F-actin. This concept of haptotactic sensing warrants further study in our view.

4. Material and methods

4.1. Cell culture and preparation

T lymphocyte culture medium was RPMI1640 supplemented with 25 mM HEPES, 10% FBS and 1% sodium pyruvate. Mostly, naive T lymphocytes were isolated from C57BL/6 mouse spleens, kindly provided by the laboratory of Garnett Kelsoe (Duke University). Mouse spleens were cut in halves and ground with frost slides in culture medium. The cell mixture was filtered through a 130 µm mesh, and T cells were isolated following the standard protocol of the Dynabeads^® Untouched™ mouse T cells kit (Invitrogen). In brief, the cell mixture was re-suspended to 5 × 10⁷ cells ml⁻¹ and mixed with 125 µl pre-washed dynabeads for every 1 ml of the mixture. The cells and beads were incubated at room temperature with gentle tilting and rotation for 20 min prior to magnetic selection. The unbound T-cells in the supernatant were collected and re-suspended in T-cell culture medium at 2 × 10⁶ cells ml⁻¹. T cells were then transferred to 100 mm cell culture dish and kept in 37°C, 5% CO₂ cell culture incubator for the length of the tests without changing medium. The cells were collected for tests 24 and 48 h after isolation. All tissue culture reagents were purchased from Invitrogen unless otherwise indicated.

4.2. T-cell migration assay surface preparation

Glass-bottom dishes (MatTek) were coated first with 10 µg ml⁻¹ protein A (Invitrogen) and 5 µg ml⁻¹ chemokine CXCL12^−his at room temperature for 2 h. The surfaces were washed once with 1% mass per volume BSA (Sigma) in PBS. Then, 5 µg ml⁻¹ human or mouse ICAM-1/CD54 Fc chimera (R&D Systems) was added and incubated at room temperature for 2 h. The surfaces were washed once and blocked with 1% mass per volume BSA in PBS at 4°C overnight. The surfaces were washed with warm migration medium (phenol red-free RPMI1640, 1% mass per volume BSA) before adding cells. CXCL12^−his was kindly provided by the laboratory of William Reichert (Duke University). It was confirmed that the observed biological activity of CXCL12^−his was comparable to commercially available CXCL12.

4.3. Random migration assay

T cells were labelled with Vybrant® DiO (Invitrogen) following the manufacturer's protocol. In brief, T cells were re-suspended in warm migration medium at 10⁶ cells ml⁻¹ and mixed with DiO solution in the ratio of 5 µl DiO to 1 ml cell solution. The mixture was incubated at 37°C for 2 min and then washed with migration medium. The cells rested for 10 min prior to seeding. Approximately 2.5 × 10⁵ cells were added onto the migration surface and allowed to adhere for 5 min at 37°C. The cells were imaged by prism-based TIRF microscopy at 37°C in a humidified chamber. Images were acquired at a rate of 20 frames min⁻¹ with a 40×, 0.8 NA Achroplan water-dipping objective (Carl Zeiss), ORCA-ER cooled charge-coupled device (Hamamatsu Photonics) and MetaMorph software (Universal Imaging).

4.4. Computational image analysis

Image analysis was performed using MATLAB software (MathWorks). Codes for identification and spatio-temporal mapping of protruded/retracted areas and extended morphological structures were described previously [15]. Protrusion/retraction maps were constructed by binning the angular position (rounded to the nearest whole angle in degrees, relative to the vector pointed from the cell centroid in the negative x-direction) of each protruded/retracted pixel, when compared with the previous frame for each time interval of a time-lapse experiment. Protrusion or retraction velocity was calculated as the net change in number of protruded/retracted pixels along the indicated angle (multiplied by the pixel size), divided by the change in time. Extension maps were determined by summing the number of pixels within an extended structure (local cellular regions where the distance of perimeter pixels was greater than the local mean from the cell centroid), and they were plotted using the same structure as for protrusion/retraction maps.

4.5. Waiting-time distributions

The waiting time and lifetime of each phenotypic event were manually documented with a temporal resolution of 0.5 min. To compare the WTD with that of a random process, we assessed the quality of fit to an exponential distribution, i.e. the probability density function (PDF) as follows.

4.1

The probability that an event occurs between times t and t + Δt is found by integrating the PDF.

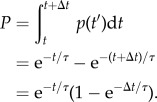4.2

Considering that the actual waiting time between events detected, for example, during successive detection periods varies between zero and 2Δt, the expected probability of detecting events during the nth interval is as follows

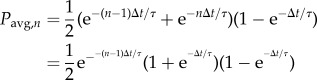4.3

We also consider the expected portion of the probability associated with missing those events that occur within the same period of observation as follows.

4.4

Thus, we confirm the validity of equation (4.2) as the correct probability, posed as follows for the nth interval, with Δt = 0.5 min.

4.5

All fits were obtained using the curve-fitting toolbox of MATLAB.

4.6. Persistent random walk model

The mean-square displacement, 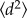, was calculated for varying time intervals Δt. The trend was fit to the common persistent random walk model [18] as follows.

4.6

The fit parameters are the speed S and persistence time P. The fit was obtained using the curve fitting toolbox of MATLAB.

4.7. Computational modelling

Spatial, stochastic models were implemented using Smoldyn, v. 2.31 (www.smoldyn.org) [24]. Details of the model are outlined in electronic supplementary material, text S1. The model code, Liu_etal_Tcell.txt, is also provided in the electronic supplementary material, Materials. In the analysis of the simulation results shown in figure 6, a conversion factor of 1 time unit = 2 s was applied, so that the time interval for analysis of bifurcations in the simulations matched the value used for analysis of the experimental data (0.5 min). This conversion factor was subsequently applied to the panels b–d of figure 5.

Data accessibility

The experimental data are available via ImmPort (http://immport.org), study number SDY367.

Funding statement

This work was supported under contract no. HHSN272201000053C from the National Institute of Allergy and Infectious Diseases. Computational work was supported by grant no. 1133476 from the National Science Foundation.

Authors' contributions

X.L. and J.M.H. designed the study. E.S.W. developed key image analysis codes. X.L. performed the experiments and computational analysis. J.M.H. developed the computational model. X.L. and J.M.H wrote the manuscript, and all authors contributed to the editing of the paper.

Conflict of interests

We have no competing interests.