Skip to main content
PMC home page
AIDS Research and Human Retroviruses logoLink to AIDS Research and Human Retroviruses
. 2015 May 1;31(5):531–542. doi: 10.1089/aid.2014.0211

Importance of Viral Sequence Length and Number of Variable and Informative Sites in Analysis of HIV Clustering

Vlad Novitsky 1, Sikhulile Moyo 2, Quanhong Lei 3, Victor DeGruttola 3, M Essex 1,,2,✉
PMCID: PMC4426322  PMID: 25560745

Abstract

To improve the methodology of HIV cluster analysis, we addressed how analysis of HIV clustering is associated with parameters that can affect the outcome of viral clustering. The extent of HIV clustering and tree certainty was compared between 401 HIV-1C near full-length genome sequences and subgenomic regions retrieved from the LANL HIV Database. Sliding window analysis was based on 99 windows of 1,000 bp and 45 windows of 2,000 bp. Potential associations between the extent of HIV clustering and sequence length and the number of variable and informative sites were evaluated. The near full-length genome HIV sequences showed the highest extent of HIV clustering and the highest tree certainty. At the bootstrap threshold of 0.80 in maximum likelihood (ML) analysis, 58.9% of near full-length HIV-1C sequences but only 15.5% of partial pol sequences (ViroSeq) were found in clusters. Among HIV-1 structural genes, pol showed the highest extent of clustering (38.9% at a bootstrap threshold of 0.80), although it was significantly lower than in the near full-length genome sequences. The extent of HIV clustering was significantly higher for sliding windows of 2,000 bp than 1,000 bp. We found a strong association between the sequence length and proportion of HIV sequences in clusters, and a moderate association between the number of variable and informative sites and the proportion of HIV sequences in clusters. In HIV cluster analysis, the extent of detectable HIV clustering is directly associated with the length of viral sequences used, as well as the number of variable and informative sites. Near full-length genome sequences could provide the most informative HIV cluster analysis. Selected subgenomic regions with a high extent of HIV clustering and high tree certainty could also be considered as a second choice.

Introduction

A major goal of public health in relation to HIV/AIDS is to prevent new transmissions in communities. Achievement of this goal could be facilitated by a better understanding of the structure and dynamics of HIV transmission networks and comprehensive HIV cluster analysis.1–20 The extent of viral clustering is one of the key factors in making inferences about epidemiologic processes inferred from viral phylogenies. However, it remains to be established how the selection of region across the HIV-1 genome and its length affects the extent of HIV clustering.

It seems likely that the size, complexity, and number of variable or informative sites in the multiple sequence alignment are important factors that impact the extent of HIV clustering. The nature of this effect could help inform the choice of design in studies employing HIV cluster analysis. It could also help in making choices regarding how subjects are sampled, requirements for laboratory facilities, duration of studies, and budget.

The contribution of different regions across the HIV-1 genome to the reconstruction of viral phylogeny has been addressed previously. Leitner et al. highlighted the importance of the choice of the HIV-1 gene fragment for reconstruction of true phylogeny, and showed that combining data on gag p17 and env V3 performed better than data on either p17 or V3 evaluated separately.21 The HIV-1 pol gene has been used for phylogenetic reconstruction of transmission events22 and for HIV cluster analysis over the past decade.3–7,9,11–13,15,19,20,23–32 Other HIV-1 genes have also been used for linkage analysis in discordant couples.33,34 A weaker clustering of subgenomic regions, as compared with the near full-length genome sequences, was demonstrated for HIV-1C from Ethiopia,35 although the set of viral sequences analyzed was relatively small.

The majority of studies cited above were performed in HIV-1 subtype B settings among men having sex with men (MSM). Most of the studies utilized partial HIV-1 pol sequences generated as a part of routine clinical care. However, little is known about clustering patterns of HIV-1 non-B subtypes in predominantly heterosexual epidemics, such as the HIV-1 subtype C epidemic in southern Africa.

In this study we address (1) the HIV clustering in structural viral genes, subgenomic regions, and near full-length genomes of HIV-1C; (2) the HIV clustering within sliding windows across the HIV-1C genome; and (3) potential associations between the extent of HIV clustering and sequence length. HIV clusters were identified by the bootstrapped maximum likelihood method at bootstrap thresholds from 0.7 to 1.0, as a statistical support for clustering.

Tree certainty, a novel measure for quantification of incongruence of phylogenetic signal, is defined as the sum of internode certainties.36 The internode certainty measures the level of support for a given internode by considering its frequency in a given set of trees jointly with the most prevalent conflicting bipartition in the same set of trees.36 Internode certainty values near zero indicate the presence of an almost equally supported bipartition that conflicts with the inferred internode, whereas values close to one indicate the absence of conflict.36,37

Materials and Methods

HIV-1C near full-length genome sequences

A set of 401 HIV-1C nonrecombinant near full-length genome sequences spanning the region that corresponds to HXB2 nt positions 790 (the first codon of gag) to 9,611 (−21 nt at the end of the R region in 3′-LTR) was retrieved from the LANL HIV Database (www.hiv.lanl.gov/). The entire 5′-LTR and parts of the R and U5 regions of the 3′-LTR were not included in the analysis because these regions were not available in the majority of 401 HIV-1C sequences retrieved from the LANL HIV Database. The criteria for sequence selection included nonrecombinant HIV-1 subtype C and single sequence per subject (if multiple sequences were available). The set of 401 HIV-1C near full-length nonrecombinant sequences included 279 from South Africa, 45 from Botswana, 16 from India, 14 from Tanzania, 10 from Zambia, 7 from Malawi, 6 from Brazil, 5 from Israel, 4 from China, 2 each from Ethiopia, Kenya, and Spain, and a single sequence each from Argentina, Djibouti, Georgia, Myanmar, Senegal, Somalia, the United States, Uruguay, and Yemen. A list of the 401 near full-length genome sequences used in this study and their accession numbers is presented in Supplementary Table S1 (Supplementary Data are available online at www.liebertpub.com/aid).

Analyzed subgenomic regions of the HIV-1C genome

The extent of HIV clustering using near full-length genome sequences was compared with the subgenomic regions spanning the three structural HIV-1C genes, gag, pol, and env, and several alternative subgenomic regions that have been used or proposed for HIV cluster analysis. These subgenomic regions included (1) a partial pol sequence spanning the region encoding HIV-1 protease and the first 335 amino acids of reverse transcriptase, which corresponds to the sequence produced by ViroSeq,38–41 nt positions 2,253–3,554; (2) partial env sequences spanning the region encoding the gp120 V1C5 region,42–44 nt positions 6,570–7,757; (3) “product 2” spanning the 3′-end of gag and almost the entire pol,45 nt positions 1,486–5,058; and (4) “product 4” spanning vpu, env, nef, and TATA-box in the U3 region of 3′-LTR,45 nt positions 5,967–9,517. In addition, combinations of the targeted subregions included gag+pol, gag+env, pol+env, gag+pol+env, and product 2+product 4. All but one of the multiple sequence alignments were trimmed from the LANL nt-based alignment. The V1C5 codon-based alignment was generated as described elsewhere42 using muscle46 in MEGA6.47

Sliding window analysis

Sliding window analysis is a commonly used method for studying the properties of molecular sequences.48 To estimate the extent of clustering across the HIV-1 genome, a sliding window analysis with windows advancing incrementally across the multiple sequence alignment (a window of a certain length slid along the sequence alignment) was employed. Two sizes of sliding window were used, 1,000 bp and 2,000 bp. Sliding steps were equal to 1/10 of the window size—100 bp for the 1,000-bp window, and 200 bp for the 2,000-bp window—and produced multiple sets of overlapping multiple sequence alignments. The sizes of the 1,000-bp and 2,000-bp sliding windows were chosen as a starting point to assess changes in HIV clustering patterns across the HIV-1 genome. Note that alternative sizes of sliding windows and/or sliding steps could also be used. A total of 99 alignment sets of 1,000 bp each, and 45 alignment sets of 2,000 bp each, were generated. The extent of HIV clustering was estimated for each window using the same phylogenetic inference (maximum likelihood) that was applied to the near full-length genome sequences and subgenomic regions.

Pairwise distances

Pairwise distances in multiple sequence alignments were computed using the Maximum Composite Likelihood model49 in MEGA6.47 To address the effects of gaps and missing data, two distance matrixes were generated: (1) with all positions containing gaps eliminated (complete deletion of gaps), and (2) with all ambiguous positions in each sequence pair removed (pairwise deletion of gaps).

Variable and informative sites

The numbers of variable and informative sites in each multiple sequence alignment were enumerated in MEGA6.47 Sites with missing/ambiguous data and gaps were included in the analysis. The estimated numbers were used for comparison across HIV-1 regions and in association analysis.

Character state changes

The number of character states in the identified informative sites was computed, according to Wortley and Scotland,50 as the minimum number of parsimony-informative character-state changes, Δmin. The Δmin parameter was calculated for each character across informative sites as one fewer than the number of states that are present in two or more taxa.50 The estimated numbers of character states were used for comparison across HIV-1 regions.

Phylogenetic inference

The maximum likelihood tree inference was implemented in RAxML51,52 under the GAMMA model of rate heterogeneity. The statistical support for each node was assessed by bootstrap analysis from 100 bootstrap replicates performed with the rapid bootstrap algorithm implemented in RAxML.51 The RAxML runs were performed using RAxML ver.7.7.5 at the high-performance computing cluster Odyssey (http://rc.fas.harvard.edu/kb/high-performance-computing/architectural-description-of-the-odyssey-cluster/) at the Faculty of Arts and Sciences, Harvard University (https://rc.fas.harvard.edu/).

Estimation of tree certainty

Tree certainty quantifies the degree of conflict or incongruence in a set of phylogenetic trees.36 The quantification of incongruence is based on Shannon's entropy.53 The internode certainty was measured by quantifying the degree of certainty for each individual internode by considering the two most prevalent conflicting bipartitions and calculating the log magnitude of their difference. An internode certainty close to 1 indicates high certainty of the targeted tree node and a lack of conflict in the data, while values of internode certainty close to 0 show a high degree of incongruence. For example, if the most prevalent bipartition is supported by 95% of the data and the next most prevalent conflicting bipartition is supported by the remaining 5%, then the value of the internode certainty is approximately 0.71, whereas if the two most prevalent conflicting bipartitions have the same frequency of support, then the internode certainty is zero.37 Tree certainty quantifies the degree of conflict for the whole tree, and is the sum of internode certainty over all internodes in a phylogeny.37 Tree certainty scores were calculated in RAxML ver. 8.0.052 as described by Salichos et al.37 Extended majority-rule consensus trees were computed using bootstrapped trees generated by RAxML for each set of HIV-1C sequences analyzed.

Statistical analysis

The HIV sequences in clusters were enumerated with PhyloPart v.254 using bootstrap thresholds 0.7, 0.8, 0.9, and 1.0. All confidence intervals (CI) of estimated proportions are asymptotic 95% binomial confidence intervals (95% CI) computed with the prop.test function in R version 3.0.1.55 Comparison between proportions of viral sequences in clusters was performed by McNemar's test in R, and p-values less than 1.0E-04 were considered statistically significant. The association between paired samples was tested by estimating Pearson's product-moment correlation coefficient using the cor.test function in R. For association analysis between sequence length and proportion of HIV sequences in clusters, we used loess regression with the default stat_smooth parameters to smooth the curve. We note that the assumption of independence of observations that underlies these tests is not strictly met. However, the correlation among observations is expected to be low.56 We validated this belief by comparing binomial and bootstrap confidence intervals in representative cases.

For association analysis between the number of variable and informative sites and the proportion of HIV sequences in clusters, we used linear regression without smoothing. The bootstrapped maximum likelihood analysis was performed using multiple sequence alignments of near full-length genome, gag, pol, and env sequences, and 100 replicates. Viral sequence replicates were generated by seqboot from the PHYLIP package ver. 3.695.57,58 We found confidence intervals to be nearly identical. Sliding windows across the HIV-1C genome were generated in R using spider.59 All plots were produced in R using ggplot2.60 All figures were finalized in Adobe Illustrator CS6.

Results

Definition of HIV cluster

We define the HIV cluster as a viral lineage that gives rise to a monophyletic subtree of the overall phylogeny with strong statistical support. We use the bootstrapped maximum likelihood method61–63 to determine the statistical support of clusters. Four levels of bootstrap threshold for identification of HIV clusters were estimated in this study: ≥0.7, ≥0.8, ≥0.9, and 1.0. A viral lineage (group, subtree) with at least two viral sequences and strong statistical support is considered to be an HIV cluster. Clusters were identified using a depth-first algorithm,54,64 a method for traversing or searching tree or graph data structures starting from the root. This approach allowed us to avoid double-counting of viral sequences and clusters in any cases in which clusters had internal structure with strong support.

Extent of HIV clustering across the HIV-1C genome

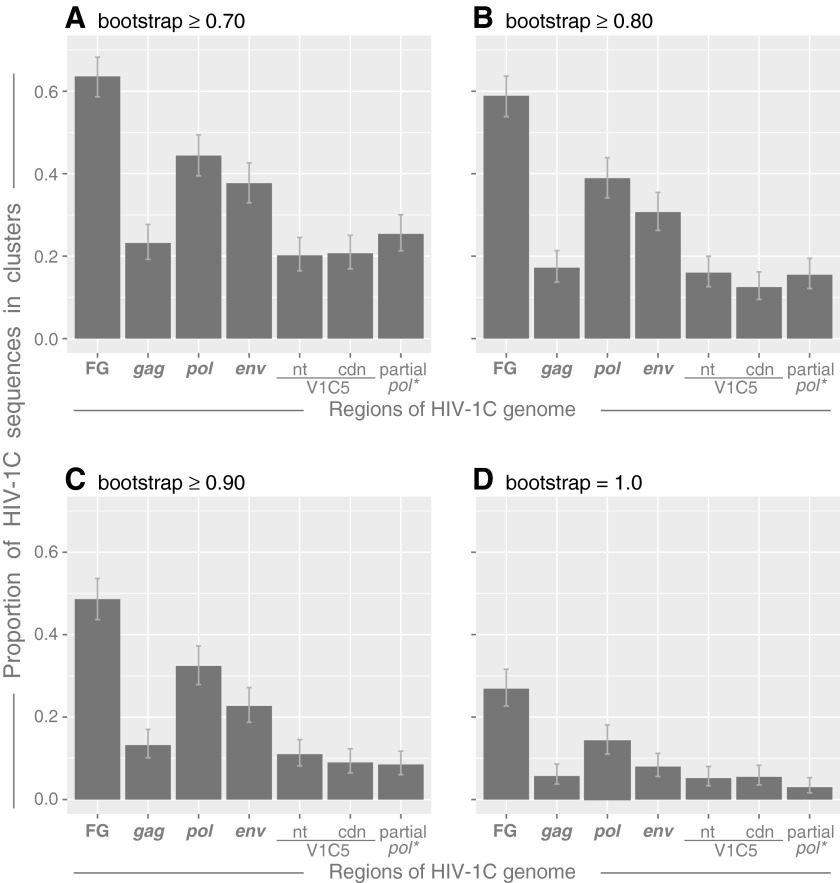
We addressed whether the extent of HIV clustering is associated with any particular HIV-1 gene or gene subregion. The proportion of clustered sequences was compared between near full-length genome HIV-1C sequences and subgenomic regions (Fig. 1). Three structural HIV-1C genes, gag, pol, and env, and two regions commonly used in HIV cluster analysis, gp120 V1C5 and partial pol spanning the region that encodes PR and the first 335 amino acids of RT (ViroSeq), were targeted. For the V1C5 region, two multiple sequence alignments, nt and codon based, were assessed. All sets of sequences included the same 401 HIV-1C sequences. The proportion of HIV sequences in clusters was estimated at the bootstrap thresholds for cluster definition from 0.7 to 1.0 under maximum likelihood inference.

FIG. 1.

FIG. 1.

Open in a new tab

The extent of HIV clustering. The proportion of HIV-1C sequences in clusters was estimated in the bootstrapped maximum likelihood (ML) analysis implemented in RAxML with 100 replicates. Axis y shows the proportion of HIV-1C sequences in clusters. Axis x shows targeted regions across the HIV-1C genome: near full-length genome sequences (FG), gag sequences, pol sequences, env sequences, nt-based alignment of the V1C5 region, codon-based alignment of the V1C5 region, and partial pol sequences corresponding to the region targeted by the ViroSeq system. (A–D) Graphs show the extent of HIV clustering at different bootstrap thresholds for cluster identification (at the top of each graph next to the figure letter): (A) ≥0.70, (B) ≥0.80, (C) ≥0.90, and (D) 1.0.

The highest proportion of HIV sequences in clusters was observed for near full-length genome HIV-1C sequences. The proportion ranged from 26.9% (95% CI 22.7% to 31.6%) at the most stringent bootstrap threshold of 1.0 (Fig. 1D) to 63.6% (95% CI 58.6% to 68.3%) at the most relaxed bootstrap threshold of 0.7 (Fig. 1A). Among the three structural HIV-1C genes, the highest proportion of HIV sequences in clusters was found in pol following by env and gag. For example, at the bootstrap threshold of 0.80 (Fig. 1B), 38.9% of pol sequences, 30.7% of env sequences, and 17.2% of gag sequences were found in clusters, while the proportion of viral sequences in clusters in the set of near full-length genome HIV-1C sequences was 58.9% (95% CI 53.8% to 63.7%). The difference in proportions of clustered sequences between the set of near full-length HIV-1C sequences and any of the three structural genes was statistically significant at all targeted bootstrap thresholds (all p-values from <0.0001, McNemar's test).

The extent of HIV clustering was statistically higher in HIV-1C pol sequences than in gag sequences at any bootstrap threshold used (all p-values<0.0001, McNemar's test). The proportion of HIV-1C pol sequences in clusters was larger than env sequences at a bootstrap threshold 0.9 (p-value <0.0001; McNemar's test), but did not reach significance of 1.0E-04 at other bootstrap thresholds (p=0.003 at 0.7, p=0.00018 at 0.8, and p=0.00012 at 1.0 bootstrap threshold). A larger proportion of the HIV-1C env sequences than gag sequences was found in clusters at bootstrap thresholds from 0.7 to 0.9 (p-values<0.0001 McNemar's test), but the difference was not statistically significant at the threshold of 1.0 (p-value 0.095).

The proportions of HIV V1C5 and partial pol sequences (ViroSeq) in clusters were at the level of gag sequences. The differences between gag and either V1C5 or partial pol sequences were nonsignificant for all comparisons based on McNemar's test and a significance threshold of 1.0E-04. Similarly, no difference in the proportions of HIV sequences in clusters was found between V1C5 and partial pol sequences, or between nt- and codon-based alignments of V1C5 sequences.

To assess the stability of HIV clusters we investigated clustering of near full-length genome sequences (FG) and genomic subregions—gag, pol, env, V1C5 region (nt and codon aligned), and ViroSeq—at four bootstrap thresholds, 0.7, 0.8, 0.9, and 1.0 (Supplementary Fig. S1). The analyzed subset included 236 of 401 near full-length HIV-1C sequences that were found in clusters in maximum likelihood analysis with a bootstrap threshold of ≥0.70. The comparison revealed substantial heterogeneity in HIV clustering based on (1) bootstrap threshold, (2) targeted region of the HIV-1 genome, and (3) sampling. While some sequences were found in clusters across all analyzed regions (filled blocks), other sequences cluster in few or no subgenomic regions (blank blocks). For example, sequences from India formed clusters in FG, pol, and env, and at low bootstrap thresholds in ViroSeq regions, but did not cluster in gag or V1C5. Interestingly, a comparison of clustering profiles between FG and ViroSeq illustrates that a substantial number of viral sequences clustered in FG would be found outside of clusters based on analysis of the ViroSeq, a region widely used in analysis of HIV clusters.

Hierarchy of tree certainty

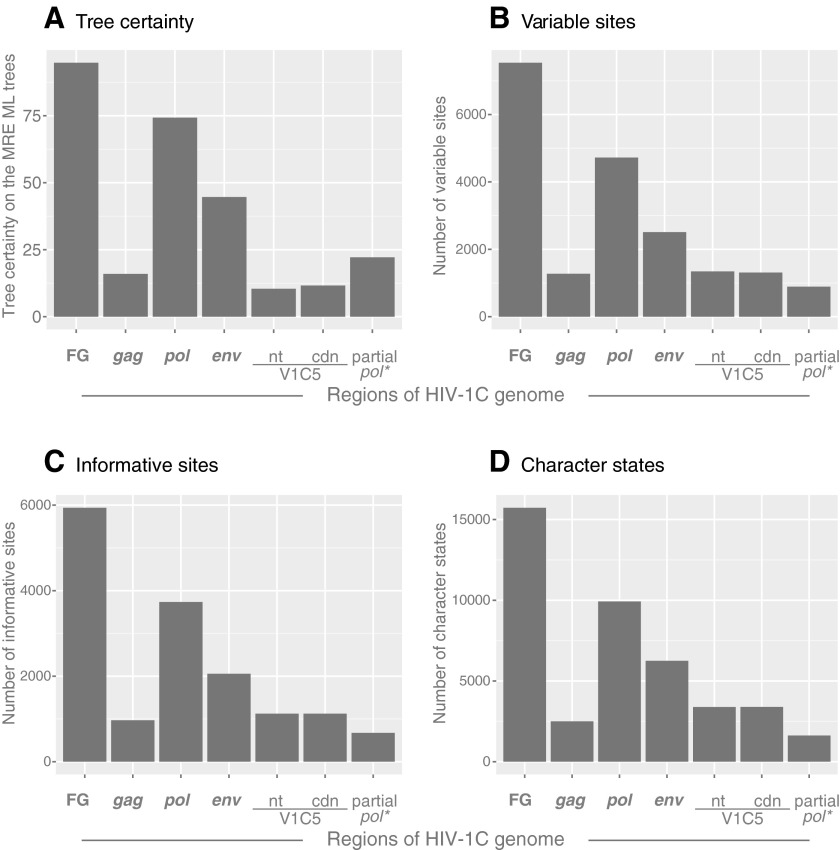
The degree of conflict or incongruence in the inferred trees was quantified by measuring tree certainty.36,37 The comparative tree certainty is presented in Fig. 2A. Overall, the profile of tree certainty data resembled the hierarchy of HIV clustering in Fig. 1. The tree based on near full-length genome sequences showed the highest tree certainty. The pol tree had the highest certainty among three structural HIV-1 genes, while the gag-based tree had the lowest certainty. The partial pol tree and V1C5-based trees showed relatively low tree certainty at the levels comparable with the gag tree certainty. The partial pol tree certainty was a little higher than the V1C5 trees certainty.

FIG. 2.

FIG. 2.

Open in a new tab

Tree certainty, variable and informative sites, and character states. Axis x shows targeted regions across the HIV-1C genome. (A) Relative tree certainty. Internode certainty was quantified by considering the two most prevalent conflicting bipartitions and calculating the log magnitude of their difference. Tree certainty was quantified as the sum of internode certainty over all internodes in a phylogeny.37 Tree certainty scores were calculated in RAxML ver. 8.0.0.52 Axis y shows the relative tree certainty estimated on the extended maximum rule consensus tree. (B) Variable sites. The number of variable sites was computed in MEGA6,47 and is shown on axis y. (C) Informative sites. The number of parsimony-informative sites was computed in MEGA6,47 and is shown on axis y. (D) Character states. The number of character states was computed as the minimum number of parsimony-informative character-state changes, Δmin, according to Wortley and Scotland,50 and is shown on axis y.

Variable and informative sites and character state changes

The profiles of variable sites (Fig. 2B), informative sites (Fig. 2C), and character states (Fig. 2D) across analyzed regions of HIV-1C resembled the proportions of viral sequences in clusters presented in Fig. 1 and the profile of tree certainty in Fig. 2A. The near full-length genome sequences showed the highest levels of variable and informative sites, and the highest number of character state changes.

Cluster size distribution

The sizes of identified clusters varied from 2 to 20 sequences per cluster. The majority of viral sequences were within small clusters. The number of clusters with 10+members was small, and decreased gradually with increasing stringency of the bootstrap threshold from 0.7 to 1.0. The cluster size distribution was similar between full-length genome HIV-1C sequences and analyzed subgenomic regions (Fig. 3). As was shown previously,7,19,42 the degree distribution inferred from cluster size data can be approximated by a power law.65 As shown in Fig. 3 (numbers in the upper right corner of each graph), the number of identified clusters and the number of viral sequences in clusters decreased gradually with tightening bootstrap support from 0.7 to 1.0.

FIG. 3.

FIG. 3.

Open in a new tab

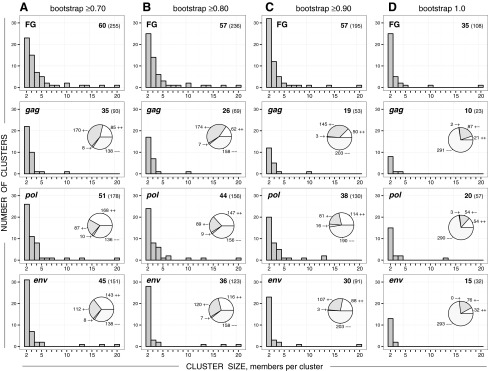
Cluster size distribution in the near full-length HIV-1C genome sequences (FG), gag, pol, and env. Histograms in each graph show the number of clusters (axis y) of specified cluster size (axis x). Numbers in the upper right corner of each graph indicate the number of identified clusters (shown in bold) and the number of viral sequences in clusters (shown in brackets). Pie charts within gag, pol, and env graphs show concordant (++ and −−) or discordant (+− and −+) clustering between near full-length genome (FG) clustering and the corresponding subgenomic region. Column (A): HIV clustering at bootstrap threshold ≥0.70. Column (B): HIV clustering at bootstrap threshold ≥0.80. Column (C): HIV clustering at bootstrap threshold ≥0.90. Column (D): HIV clustering at bootstrap threshold 1.0.

To investigate the stability of clusters, we compared whether sequences that clustered in the near full-length genome analysis also clustered in the subgenomic regions. The pie charts within the gag, pol, and env graphs in Fig. 3 show the number of viral sequences that (1) clustered in both the full-length genome and the subgenomic region (++ ), (2) clustered in the full-length genome but not in the subgenomic region (+−), (3) did not cluster in the full-length genome but did cluster in the subgenomic region (−+), and (4) clustered in neither the full-length genome nor the subgenomic region (−−). Concordant clustering (++ or −−) was more pronounced for pol and env, while discordant clustering (+− or −+) was more common for gag.

Sliding widow analysis

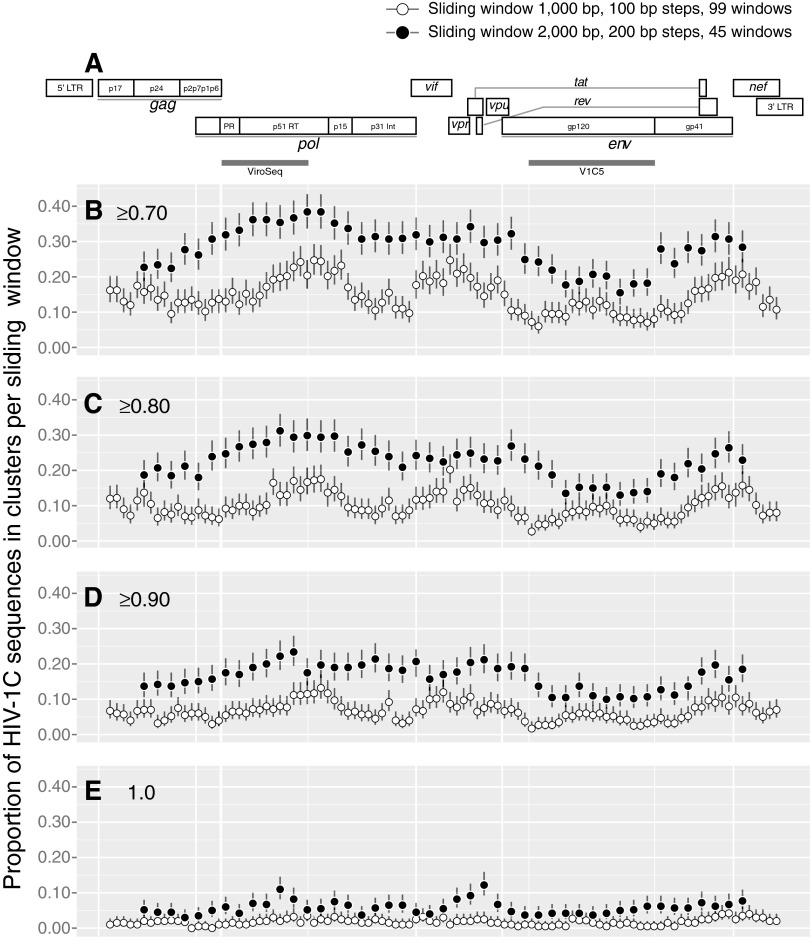
To assess the extent of HIV clustering across the HIV-1 genome, sliding window analysis was performed with window size of 1,000 bp and 2,000 bp, and sliding steps of 100 bp and 200 bp, respectively. This analysis allowed us to investigate how patterns of HIV clustering change across the HIV-1 genome.

The profile of HIV clustering across the HIV-1 genome was “wave shaped” (Fig. 4) suggesting a differential contribution of regions across the HIV genome to clustering. The highest extent of HIV clustering was associated with the region encoding the HIV-1 reverse transcriptase. Intermediate extents of HIV clustering were observed for regions encoding HIV-1 protease, integrase, vif/vpr/first exon of tat/first exon of rev/vpu, and gp41/nef. HIV-1C gag and gp120 showed the lowest extent of HIV clustering.

FIG. 4.

FIG. 4.

Open in a new tab

Sliding window analysis across the HIV-1C genome. (A) HIV-1 genome structure. The map is drawn according to the multiple sequence alignment of the near full-length genome sequences. gray bars spanning the protease and partial reverse transcriptase sequence in pol and the partial gp120 sequence represent the ViroSeq and V1C5 regions, respectively. (B–E) The extent of HIV-1C clustering for each sliding window at different bootstrap thresholds for cluster identification: (B) ≥0.70, (C) ≥0.80, (D) ≥0.90, and (E)=1.0. A total of 99 sliding windows with a length of 1,000-bp and 100-bp steps are shown as open circles. A total of 45 sliding windows with a length of 2,000-bp and 200-bp steps are presented as filled circles. Bars above and below the circles indicate 95% CI computed for each sliding window.

The size of the sliding window has a substantial effect on the extent of HIV clustering. Longer viral sequences with window size 2,000 bp were associated with higher extents of HIV clustering than sequences with window size 1,000 bp across the entire HIV genome (Fig. 4). The ups and downs in the profiles of HIV clustering were similar between longer and shorter HIV windows.

As expected, the bootstrap thresholds for cluster definition affected the extent of HIV clustering across the entire HIV genome, as shown in Fig. 4B (bootstrap threshold of ≥0.7) through 4E (bootstrap threshold of 1.0). The difference of HIV clustering between longer and shorter sequences gradually decreased with tightening of the bootstrap threshold.

To address the composition stability of HIV clusters, we analyzed the consistency of clustering across 1,000-bp (Supplementary Fig. S2) and 2,000-bp (Supplementary Fig. S3) sliding windows at a bootstrap threshold of ≥0.80. Only a subset of 236 HIV-1C sequences found in clusters in maximum likelihood analysis with bootstrap support of ≥0.70 were included in this analysis. A side-by-side comparison of Supplementary Figs S2 and S3 highlights the point that HIV clustering is more intense with the larger sliding window of 2,000 bp. A deeper look into sliding windows across the viral genome reveals substantial heterogeneity in HIV clustering based on the subgenomic region and sampling. For example, two sequences from Spain (located between ET/IL and CN sequences) clustered within all sliding windows across the entire viral genome. Note that these sequences were obtained from a 53-year-old man and a 62-year-old woman from Spain,66,67 and have 98.7% similarity between their pairwise distances in near full-length HIV-1C genome analysis.

In contrast, some other sequences were outside of clusters across all sliding windows. A subset of Indian sequences showed sporadic clustering across 1,000-bp windows, but demonstrated more consistent clustering in 2,000-bp windows over pol, vif, vpr, the first exon of tat, and the C1 region of gp120 followed by an abrupt stop of clustering across most of env. Analysis of potential reasons for such a differential clustering across the viral genome—such as searching for specific signatures associated with clustering—warrants dedicated future studies, and should be taken in the context of sampling.

Potential associations

The observed difference in the extent of HIV clustering between the two sliding windows, 1,000 bp and 2,000 bp, provided a rationale for taking a closer look at potential associations between the size of HIV sequences and the extent of HIV clustering. To assess these associations, we used viral sequences spanning subgenomic regions across HIV-1C genome, as described above in Materials and Methods, subsection “Analyzed subgenomic regions of HIV-1C genome”: gag, pol, env, partial pol (ViroSeq), V1C5, product 2 (3,573 bp; spans partial gag at the 3′-end and the entire pol; HXB2 nt positions 1,486–5,058),45 product 4 (3,558 bp; spans vpu, env, nef, and TATA-box in the U3 region of 3′-LTR; HXB2 nt positions 5,967–9,517),45 and combination of these subregions (a combination of products 2 and 4 spans about 80% of the unique full length HIV-1 genome sequence).

We found a strong positive association between the sequence length and the extent of HIV clustering (Fig. 5). Correlation coefficients above 0.9 for all tested bootstrap thresholds were accompanied by statistically significant p-values from 2.3E-07 to 9.6E-06. The estimated 95% CIs for correlation coefficients were relatively tight across all bootstrap thresholds used in this analysis. Similarly positive associations were found between the extent of HIV clustering and parameters related to the sequence length, such as the number of variable sites (correlation coefficients from 0.90 to 0.93) and the number of informative sites (correlation coefficients from 0.89 to 0.93).

FIG. 5.

FIG. 5.

Open in a new tab

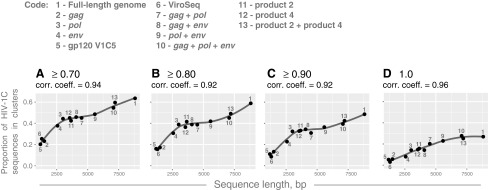
Sequence size and HIV clustering. Results of correlation analysis between the extent of HIV clustering and sequence length are shown. Axis y shows the proportion of HIV-1C sequences in clusters. Axis x shows the sequence length. (A–D) Graphs show the extent of HIV clustering at different bootstrap thresholds for cluster identification: (A) ≥0.70, (B) ≥0.80, (C) ≥0.90, and (D)=1.0. The code above the graphs indicates different sets of HIV-1C sequences including near full-length genome sequences (FG), structural genes, subregions, and their combinations.

We addressed whether parameters related to sequence length, such as the number of variable and informative sites, are associated with the proportion of HIV sequences in clusters. We computed the number of variable and informative sites in 99 alignments (401 HIV-1C sequences and 1,000 bp each alignment) that were generated in sliding window analysis. We found a moderate positive correlation between the number of variable (Fig. 6A–D) and informative (Fig. 6E–H) sites and the proportion of HIV sequences in clusters. Correlation coefficients between 0.40 and 0.43 for the number of variable sites, and between 0.27 and 0.39 for informative sites, were accompanied by statistically significant p-values below 0.01 for all analyzed bootstrap thresholds. However, 95% CIs for correlation coefficients were relatively broad, which was more evident at less stringent bootstrap thresholds.

FIG. 6.

FIG. 6.

Open in a new tab

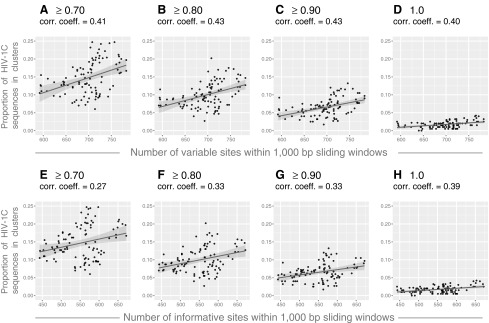
The number of variable and informative sites and HIV clustering. Results of correlation analysis between the extent of HIV clustering and the number of variable and informative sites are presented. Axis y shows the proportion of HIV-1C sequences in clusters. (A–D) Axis x shows the number of variable sites within 1,000-bp sliding windows across the HIV-1C genome. Graphs show the extent of HIV clustering at different bootstrap thresholds for cluster identification: (A) ≥0.70, (B) ≥0.80, (C) ≥0.90, and (D)=1.0. (E–H) Axis x shows the number of informative sites within 1,000-bp sliding windows across the HIV-1C genome. Graphs show the extent of HIV clustering at different bootstrap thresholds for cluster identification: (E) ≥0.70, (F) ≥0.80, (G) ≥0.90, and (H)=1.0.

The distribution of gaps in the multiple sequence alignment was not uniform. Therefore, to address whether gaps affect the observed extent of HIV clustering, we used two types of gaps deletion, pairwise and complete deletion. Under the pairwise deletion of gaps, distances were computed for each pair of sequences, ignoring only gaps that were involved in this comparison. Under the complete deletion of gaps, all sites with gaps were excluded from the multiple sequence alignment. We found no significant associations between the observed extent of HIV clustering and pairwise distances within the analyzed subgenomic regions across the HIV-1C genome (Supplementary Fig. S4). Results of analysis with pairwise deletion of gaps (Supplementary Fig. S4A–D) were similar to results of analysis with complete deletion of gaps (Supplementary Fig. S4E–H), suggesting that gaps have little to no effect on the association (or lack of association) between the observed extent of HIV clustering and pairwise distances.

Discussion

The dynamics of HIV transmission networks can be investigated through comprehensive HIV cluster analysis. HIV cluster analysis can provide insights into the dynamics of HIV spread, and the results of HIV cluster analysis can help inform public health prevention interventions, such as an optimal balance of Treatment-as-Prevention and Pre-Exposure Prophylaxis strategies. The higher the extent of HIV clustering, the more informative HIV cluster analysis could be.

In this study we investigated whether the extent of HIV clustering is associated with the size/length of targeted HIV sequences, or the number of variable and informative sites, or with a particular subgenomic region across the HIV-1 genome. The extent of HIV clustering was compared between the near full-length genome and subgenomic regions.

The near full-length genome HIV sequences were associated with the highest extent of HIV clustering. For example, 58.9% of near full-length HIV-1C sequences were found in clusters at the bootstrap threshold of 0.80 in maximum likelihood analysis. For comparison, only 15.5% of partial pol sequences (ViroSeq) were in clusters at the same running conditions. As expected, the bootstrap threshold affected the extent of HIV clustering. However, a higher extent of HIV clustering of near full-length genome sequences compared to subgenomic regions associated with HIV-1 structural genes was evident at any analyzed bootstrap threshold; the level of clustering dropped from 63.6% at a bootstrap threshold of 0.7 to 26.9% at a bootstrap threshold of 1.0. Among HIV-1 structural genes, pol showed the highest extent of clustering.

The estimated tree certainty, a novel metric for degree of conflict or incongruence, in the inferred phylogenetic tree was also the highest in the set of near full-length genome sequences, followed by pol. Combined with the extent of HIV clustering, the tree certainty estimates provide additional evidence that near full-length genome HIV sequences are the most informative choice for HIV cluster analysis.

The sequence size, or length, used in HIV cluster analysis appeared to have a dramatic effect on the extent of HIV clustering. This was evident from the comparison of HIV clustering between two sliding windows, 1,000 bp and 2,000 bp long, which were run across the entire HIV-1 genome with 100 bp and 200 bp steps, respectively. Despite fluctuations across the HIV-1 genome, the extent of HIV clustering was significantly higher for larger sliding windows spanning similar regions in the HIV-1 genome. The sliding window analysis allowed us to identify regions across the HIV-1 genome with higher propensities for HIV clustering.

To assess potential associations between the extent of HIV clustering and sequence length, we employed concatenated sets of HIV-1C genes and subgenomic regions, and included several previously described regions45 that can be used in HIV cluster analysis. We found strong associations between the sequence length and the proportion of HIV sequences in clusters, which was evident from high correlation coefficients between 0.92 and 0.96. The strong association pattern was replicated at different bootstrap thresholds for cluster definition, and with parameters related to sequence length, such as the number of variable sites, and the number of parsimony-informative sites in the multiple sequence alignment. Interestingly, the loess regression curve plateaued for the sequence length between about 3,000 bp and 6,000 bp for the bootstrap thresholds 0.7 to 0.9, but above 7,000 bp length for the 1.0 threshold (Fig. 5).

We also found a direct correlation between the number of variable and informative sites and the proportion of HIV sequences in clusters. This association was less pronounced than the association between sequence length and clustering, which was evident from correlation coefficients from 0.40 to 0.43 for variable sites and from 0.27 to 0.39 for informative sites (Fig. 6).

All 401 near full-length sequences used in this study were nonrecombinant HIV-1C, as this was the selection criterion from the LANL HIV Database. However, intrasubtype recombination in the analyzed sequences could not be ruled out without a special dedicated analysis, which warrants further studies. It has been suggested that intrasubtype recombination in HIV-1C could be extensive.68 While we reported frequent intrasubtype recombination in intrapatient viral quasispecies,69 reliable identification of recombination between patients infected with the same HIV-1 subtype is still challenging due to a lack of a straightforward and unambiguous methodology. Assuming that intrasubtype recombinants are identified with improved technology in future studies, the specifics and nature of intrasubtype recombination could either complicate or assist in the analysis of HIV clustering. For example, the analysis could be complicated due to overestimation of evolutionary rates and a skewed molecular clock.70–72 At the same time, if intrasubtype recombinants are involved in chains of viral transmission, the recombination footprints could be used as transmission signatures, and could help identify and trace the transmitting HIV lineages.

The results of the study are limited to the available set of 401 near full-length genome HIV-1C sequences retrieved from the LANL HIV Database. The sample size was relatively small; demographic and socioeconomic data, as well as stage of HIV infection at the time of sampling, were unavailable for most sequences, and representation of geographic areas was skewed toward one country, South Africa. Comparison with other HIV-1 subtypes is not currently feasible since, in the public domain, only HIV-1 subtypes B and C, and CRF01_AE, have decent representation of near full-length genomes, at least at the moment.

The current analysis is based on HIV-1C sequences collected from areas with a predominantly heterosexual mode of transmission. It is possible that patterns of HIV clustering might differ between modes of viral transmission and HIV-1 subtypes associated with particular modes of transmission. As we demonstrated recently,73 sampling density is another critical factor affecting the extent of HIV clustering.

In summary, the results of this study provide evidence that the extent of HIV clustering is directly associated with the length of viral sequences used in cluster analysis. Thus, near full-length genome sequences could be considered the top choice for the most informative HIV cluster analysis. An alternative approach to HIV cluster analysis could be based on selected subgenomic regions with an elevated extent of HIV clustering and high tree certainty.

Supplementary Material

Supplemental data
Supp_Table1.docx (162.7KB, docx)
Supplemental data
Supp_Fig1.pdf (431.4KB, pdf)
Supplemental data
Supp_Fig2.pdf (310.9KB, pdf)
Supplemental data
Supp_Fig3.pdf (400.4KB, pdf)
Supplemental data
Supp_Fig4.pdf (154.2KB, pdf)

Acknowledgments

We are grateful to the LANL HIV Database for the collection of near full-length genome HIV-1 sequences and multiple sequence alignment. V.D.G. was supported in part by AI R37-51164 from the NIH. We thank Lendsey Melton for excellent editorial assistance. We thank the editor of AIDS Research and Human Retroviruses, Dr. Brian Foley, for thoughtful comments and suggestions.

Author Disclosure Statement

No competing financial interests exist.

References

  • 1.Little SJ, Kosakovsky Pond SL, Anderson CM, et al. : Using HIV networks to inform real time prevention interventions. PLoS One 2014;9(6):e98443. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 2.Vrancken B, Rambaut A, Suchard MA, et al. : The genealogical population dynamics of HIV-1 in a large transmission chain: Bridging within and among host evolutionary rates. PLoS Comput Biol 2014;10(4):e1003505. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.Volz EM, Ionides E, Romero-Severson EO, et al. : HIV-1 transmission during early infection in men who have sex with men: A phylodynamic analysis. PLoS Med 2013;10(12):e1001568. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.Volz EM, Koelle K, and Bedford T: Viral phylodynamics. PLoS Comput Biol 2013;9(3):e1002947. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Volz EM, Koopman JS, Ward MJ, et al. : Simple epidemiological dynamics explain phylogenetic clustering of HIV from patients with recent infection. PLoS Comput Biol 2012;8(6):e1002552. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Volz EM, Kosakovsky Pond SL, Ward MJ, et al. : Phylodynamics of infectious disease epidemics. Genetics 2009;183(4):1421–1430 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Leigh Brown AJ, Lycett SJ, Weinert L, et al. : Transmission network parameters estimated from HIV sequences for a nationwide epidemic. J Infect Dis 2011;204(9):1463–1469 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Wertheim JO, Kosakovsky Pond SL, Little SJ, and De Gruttola V: Using HIV transmission networks to investigate community effects in HIV prevention trials. PLoS One 2011;6(11):e27775. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Wertheim JO, Leigh Brown AJ, Hepler NL, et al. : The global transmission network of HIV-1. J Infect Dis 2014;209(2):304–313 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Wertheim JO, Scheffler K, Choi JY, et al. : Phylogenetic relatedness of HIV-1 donor and recipient populations. J Infect Dis 2013;207(7):1181–1182 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Bezemer D, van Sighem A, Lukashov VV, et al. : Transmission networks of HIV-1 among men having sex with men in the Netherlands. AIDS 2010;24(2):271–282 [DOI] [PubMed] [Google Scholar]
  • 12.Bezemer D, Faria NR, Hassan AS, et al. : HIV-1 transmission networks amongst men having sex with men and heterosexuals in Kenya. AIDS Res Hum Retroviruses 2014;30(2):118–126 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Brenner BG, Roger M, Routy JP, et al. : High rates of forward transmission events after acute/early HIV-1 infection. J Infect Dis 2007;195(7):951–959 [DOI] [PubMed] [Google Scholar]
  • 14.Brenner BG, Roger M, Stephens D, et al. : Transmission clustering drives the onward spread of the HIV epidemic among men who have sex with men in Quebec. J Infect Dis 2011;204(7):1115–1119 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Brenner B, Wainberg MA, and Roger M: Phylogenetic inferences on HIV-1 transmission: Implications for the design of prevention and treatment interventions. AIDS 2013;27(7):1045–1057 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Kouyos RD, von Wyl V, Yerly S, et al. : Molecular epidemiology reveals long-term changes in HIV type 1 subtype B transmission in Switzerland. J Infect Dis 2010;201(10):1488–1497 [DOI] [PubMed] [Google Scholar]
  • 17.Leventhal GE, Gunthard HF, Bonhoeffer S, and Stadler T: Using an epidemiological model for phylogenetic inference reveals density dependence in HIV transmission. Mol Biol Evol 2014;31(1):6–17 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Stadler T. and Bonhoeffer S: Uncovering epidemiological dynamics in heterogeneous host populations using phylogenetic methods. Philos Trans R Soc Lond B Biol Sci 2013;368(1614):20120198. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Hughes GJ, Fearnhill E, Dunn D, et al. : Molecular phylodynamics of the heterosexual HIV epidemic in the United Kingdom. PLoS Pathog 2009;5(9):e1000590. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.Lewis F, Hughes GJ, Rambaut A, et al. : Episodic sexual transmission of HIV revealed by molecular phylodynamics. PLoS Med 2008;5(3):e50. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Leitner T, Escanilla D, Franzen C, et al. : Accurate reconstruction of a known HIV-1 transmission history by phylogenetic tree analysis. Proc Natl Acad Sci USA 1996;93(20):10864–10869 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Hue S, Clewley JP, Cane PA, and Pillay D: HIV-1 pol gene variation is sufficient for reconstruction of transmissions in the era of antiretroviral therapy. AIDS 2004;18(5):719–728 [DOI] [PubMed] [Google Scholar]
  • 23.Kaye M, Chibo D, and Birch C: Phylogenetic investigation of transmission pathways of drug-resistant HIV-1 utilizing pol sequences derived from resistance genotyping. J Acquir Immune Defic Syndr 2008;49(1):9–16 [DOI] [PubMed] [Google Scholar]
  • 24.Volz EM: Complex population dynamics and the coalescent under neutrality. Genetics 2012;190(1):187–201 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25.Brenner BG, Roger M, Moisi DD, et al. : Transmission networks of drug resistance acquired in primary/early stage HIV infection. AIDS 2008;22(18):2509–2515 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Dennis AM, Hué S, Hurt CB, et al. : Phylogenetic insight into HIV transmission networks in a southeastern US cohort. 6th IAS Conference on HIV Pathogenesis, Treatment and Prevention Rome, Italy, 2011. Abstract MOAC0205 [Google Scholar]
  • 27.Dennis AM, Hue S, Hurt CB, et al. : Phylogenetic insights into regional HIV transmission. AIDS 2012;26(14):1813–1822 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 28.Dennis AM, Murillo W, de Maria Hernandez F, et al. : Social network-based recruitment successfully reveals HIV-1 transmission networks among high-risk individuals in El Salvador. J Acquir Immune Defic Syndr 2013;63(1):135–141 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Stadler T, Kuhnert D, Bonhoeffer S, and Drummond AJ: Birth-death skyline plot reveals temporal changes of epidemic spread in HIV and hepatitis C virus (HCV). Proc Natl Acad Sci USA 2013;110(1):228–233 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 30.Bezemer D, Ratmann O, van Sighem A, et al. :. Ongoing HIV-1 Subtype B Transmission Networks in the Netherlands. CROI 2014; Boston, MA,2014 [Google Scholar]
  • 31.Hue S, Clewley JP, Cane PA, and Pillay D: Investigation of HIV-1 transmission events by phylogenetic methods: Requirement for scientific rigour. AIDS 2005;19(4):449–450 [DOI] [PubMed] [Google Scholar]
  • 32.Hue S, Pillay D, Clewley JP, and Pybus OG: Genetic analysis reveals the complex structure of HIV-1 transmission within defined risk groups. Proc Natl Acad Sci USA 2005;102(12):4425–4429 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 33.Campbell MS, Mullins JI, Hughes JP, et al. : Viral linkage in HIV-1 seroconverters and their partners in an HIV-1 prevention clinical trial. PLoS One 2011;6(3):e16986. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 34.Eshleman SH, Hudelson SE, Redd AD, et al. : Analysis of genetic linkage of HIV from couples enrolled in the HIV Prevention Trials Network 052 trial. J Infect Dis 2011;204(12):1918–1926 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 35.Harris ME, Maayan S, Kim B, et al. : A cluster of HIV type 1 subtype C sequences from Ethiopia, observed in full genome analysis, is not sustained in subgenomic regions. AIDS Res Hum Retroviruses 2003;19(12):1125–1133 [DOI] [PubMed] [Google Scholar]
  • 36.Salichos L. and Rokas A: Inferring ancient divergences requires genes with strong phylogenetic signals. Nature 2013;497(7449):327–331 [DOI] [PubMed] [Google Scholar]
  • 37.Salichos L, Stamatakis A, and Rokas A: Novel information theory-based measures for quantifying incongruence among phylogenetic trees. Mol Biol Evol 2014;31(5):1261–1271 [DOI] [PubMed] [Google Scholar]
  • 38.Sturmer M, Berger A, and Doerr HW: Modifications and substitutions of the RNA extraction module in the ViroSeq HIV-1 genotyping system version 2: Effects on sensitivity and complexity of the assay. J Med Virol 2003;71(4):475–479 [DOI] [PubMed] [Google Scholar]
  • 39.Eshleman SH, Jones D, Flys T, et al. : Analysis of HIV-1 variants by cloning DNA generated with the ViroSeq HIV-1 Genotyping System. Biotechniques 2003;35(3):614–618, 620, 622 [DOI] [PubMed] [Google Scholar]
  • 40.Mracna M, Becker-Pergola G, Dileanis J, et al. : Performance of Applied Biosystems ViroSeq HIV-1 Genotyping System for sequence-based analysis of non-subtype B human immunodeficiency virus type 1 from Uganda. J Clin Microbiol 2001;39(12):4323–4327 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 41.Cunningham S, Ank B, Lewis D, et al. : Performance of the Applied Biosystems ViroSeq human immunodeficiency virus type 1 (HIV-1) genotyping system for sequence-based analysis of HIV-1 in pediatric plasma samples. J Clin Microbiol 2001;39(4):1254–1257 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 42.Novitsky V, Bussmann H, Logan A, et al. : Phylogenetic relatedness of circulating HIV-1C variants in Mochudi, Botswana. PLoS One 2013;8(12):e80589. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 43.Novitsky V, Lagakos S, Herzig M, et al. : Evolution of proviral gp120 over the first year of HIV-1 subtype C infection. NIHMSID # 79286. Virology 2009;383(1):47–59 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 44.Novitsky V, Wang R, Rossenkhan R, et al. : Intra-host evolutionary rates in HIV-1C env and gag during primary infection. Infect Genet Evol 2013;19C:361–368 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 45.Gall A, Ferns B, Morris C, et al. : Universal amplification, next-generation sequencing, and assembly of HIV-1 genomes. J Clin Microbiol 2012;50(12):3838–3844 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 46.Edgar RC: MUSCLE: Multiple sequence alignment with high accuracy and high throughput. Nucleic Acids Res 2004;32(5):1792–1797 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 47.Tamura K, Stecher G, Peterson D, et al. : MEGA6: Molecular Evolutionary Genetics Analysis version 6.0. Mol Biol Evol 2013;30(12):2725–2729 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 48.Tajima F: Determination of window size for analyzing DNA sequences. J Mol Evol 1991;33(5):470–473 [DOI] [PubMed] [Google Scholar]
  • 49.Tamura K, Nei M, and Kumar S: Prospects for inferring very large phylogenies by using the neighbor-joining method. Proc Natl Acad Sci USA 2004;101(30):11030–11035 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 50.Wortley AH. and Scotland RW: Determining the potential utility of datasets for phylogeny reconstruction. Taxon 2006;55(2):431–442 [Google Scholar]
  • 51.Stamatakis A: RAxML-VI-HPC: Maximum likelihood-based phylogenetic analyses with thousands of taxa and mixed models. Bioinformatics 2006;22(21):2688–2690 [DOI] [PubMed] [Google Scholar]
  • 52.Stamatakis A: RAxML version 8: A tool for phylogenetic analysis and post-analysis of large phylogenies. Bioinformatics 2014;30(9):1312–1313 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 53.Shannon CE: A mathematical theory of communication. Bell Syst Tech J 1948;27:379–423, 623–656 [Google Scholar]
  • 54.Prosperi MC, Ciccozzi M, Fanti I, et al. : A novel methodology for large-scale phylogeny partition. Nat Commun 2011;2:321. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 55.R Core Team: R: A language and environment for statistical computing. www.R-project.org/ 2013
  • 56.Carnegie NB, Wang R, Novitsky V, and De Gruttola V: Linkage of viral sequences among HIV-infected village residents in Botswana: Estimation of linkage rates in the presence of missing data. PLoS Comput Biol 2014;10(1):e1003430. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 57.PHYLIP (Phylogeny Inference Package) version 3.6: Distributed by the author. [computer program]. Version. Department of Genome Sciences, University of Washington, Seattle, 2005 [Google Scholar]
  • 58.Felsenstein J: PHYLIP—Phylogeny Inference Package (Version 3.2). Cladistics 1989;5:164–166 [Google Scholar]
  • 59.Brown SD, Collins RA, Boyer S, et al. : Spider: An R package for the analysis of species identity and evolution, with particular reference to DNA barcoding. Mol Ecol Resour 2012;12(3):562–565 [DOI] [PubMed] [Google Scholar]
  • 60.Wickham H: ggplot2: Elegant Graphics for Data Analysis. Springer, New York, 2009 [Google Scholar]
  • 61.Felsenstein J: Confidence limits on phylogenies: An approach using a bootstrap. Evolution 1985;39:783–791 [DOI] [PubMed] [Google Scholar]
  • 62.Felsenstein J: Inferring Phylogenies. Sinauer Associates, Inc., Sunderland, MA, 2004 [Google Scholar]
  • 63.Nei M. and Kumar S: Molecular Evolution and Phylogenetics. Oxford University Press, New York, 2000 [Google Scholar]
  • 64.Even S: Graphic Algorithms, 2nd ed. Cambridge University Press, Cambridge, 2011 [Google Scholar]
  • 65.Clauset A, Shalizi CR, and Newman MEJ: Power-law distributions in empirical data. SIAM Rev 2009;51(4):661–703 [Google Scholar]
  • 66.Fernandez-Garcia A, Cuevas MT, Munoz-Nieto M, et al. : Development of a panel of well-characterized human immunodeficiency virus type 1 isolates from newly diagnosed patients including acute and recent infections. AIDS Res Hum Retroviruses 2009;25(1):93–102 [DOI] [PubMed] [Google Scholar]
  • 67.Cuevas MT, Fernandez-Garcia A, Pinilla M, et al. : Biological and genetic characterization of HIV type 1 subtype B and nonsubtype B transmitted viruses: Usefulness for vaccine candidate assessment. AIDS Res Hum Retroviruses 2010;26(9):1019–1025 [DOI] [PubMed] [Google Scholar]
  • 68.Rousseau CM, Learn GH, Bhattacharya T, et al. : Extensive intrasubtype recombination in South African human immunodeficiency virus type 1 subtype C infections. J Virol 2007;81(9):4492–4500 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 69.Kiwelu IE, Novitsky V, Margolin L, et al. : Frequent intra-subtype recombination among HIV-1 circulating in Tanzania. PLoS One 2013;8(8):e71131. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 70.Liu Y, Nickle DC, Shriner D, et al. : Molecular clock-like evolution of human immunodeficiency virus type 1. Virology 2004;329(1):101–108 [DOI] [PubMed] [Google Scholar]
  • 71.Schierup MH. and Hein J: Consequences of recombination on traditional phylogenetic analysis. Genetics 2000;156(2):879–891 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 72.Schierup MH. and Hein J: Recombination and the molecular clock. Mol Biol Evol 2000;17(10):1578–1579 [DOI] [PubMed] [Google Scholar]
  • 73.Novitsky V, Moyo S, Lei Q, et al. : Impact of sampling density on the extent of HIV clustering. AIDS Res Hum Retroviruses 2014;30(12):1226–1235 [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplemental data
Supp_Table1.docx (162.7KB, docx)
Supplemental data
Supp_Fig1.pdf (431.4KB, pdf)
Supplemental data
Supp_Fig2.pdf (310.9KB, pdf)
Supplemental data
Supp_Fig3.pdf (400.4KB, pdf)
Supplemental data
Supp_Fig4.pdf (154.2KB, pdf)

Articles from AIDS Research and Human Retroviruses are provided here courtesy of Mary Ann Liebert, Inc.

RESOURCES