Predicting traffic volumes and estimating the effects of shocks in massive transportation systems

Significance

We propose a new approach to analyzing massive transportation systems that leverages traffic information about individual travelers. The goals of the analysis are to quantify the effects of shocks in the system, such as line and station closures, and to predict traffic volumes. We conduct an in-depth statistical analysis of the Transport for London railway traffic system. The proposed methodology is unique in the way that past disruptions are used to predict unseen scenarios, by relying on simple physical assumptions of passenger flow and a system-wide model for origin–destination movement. The method is scalable, more accurate than blackbox approaches, and generalizable to other complex transportation systems. It therefore offers important insights to inform policies on urban transportation.

Abstract

Public transportation systems are an essential component of major cities. The widespread use of smart cards for automated fare collection in these systems offers a unique opportunity to understand passenger behavior at a massive scale. In this study, we use network-wide data obtained from smart cards in the London transport system to predict future traffic volumes, and to estimate the effects of disruptions due to unplanned closures of stations or lines. Disruptions, or shocks, force passengers to make different decisions concerning which stations to enter or exit. We describe how these changes in passenger behavior lead to possible overcrowding and model how stations will be affected by given disruptions. This information can then be used to mitigate the effects of these shocks because transport authorities may prepare in advance alternative solutions such as additional buses near the most affected stations. We describe statistical methods that leverage the large amount of smart-card data collected under the natural state of the system, where no shocks take place, as variables that are indicative of behavior under disruptions. We find that features extracted from the natural regime data can be successfully exploited to describe different disruption regimes, and that our framework can be used as a general tool for any similar complex transportation system.

Well-designed transportation systems are a key element in the economic welfare of major cities. Design and planning of these systems requires a quantitative understanding of traffic patterns and relies on the ability to predict the effects of disruptions to such patterns, both planned and unplanned (1).

There is a long history of analytic and modeling approaches to the study of traffic patterns (2), for example using simulated scenarios in simple transportation systems (3), and analysis of real traffic data in complex systems, either focusing on a small samples (4) or using more aggregate data (5, 6). Here we take this approach to the next level by making use of smart-card data and incident logs to (i) predict traffic patterns and (ii) estimate the effect of unplanned disruptions on these patterns. We analyzed 70 d of smart-card transactions from the London transportation network, composed of ∼10 million unique IDs and 6 million transactions per day on average, resulting in one of the largest statistical analyses of transportation systems to date.

A related literature deals with various aspects of dynamics in complex networks and complex systems in general (7–9), using a variety of data sources, from emails (10) to the circulation of bank notes (11) to online experiments on Amazon Turk (12). More recently, a number of analyses have leveraged mobile phone data as proxies for mobility (4, 13–15).

However, smart-card technology allows us to obtain large samples of passenger location and movements without requiring noisy and potentially unreliable proxies such as mobile Global Positioning System traces (16), while also leveraging a more structured environment that imposes hard constraints on patterns of urban mobility (17). In particular, these constraints of the system allow us to identify a global model of passenger behavior under local line and station closures.

Transport for London Data

The London transportation system is composed of several connected subsystems. We focus on the Underground, Overground, and Docklands Light Rail (DLR), all of which are train services aimed at fast commuting within the Greater London area only. A map of the system is provided in Fig. S1.

Transport for London (TfL) provided us with smart-card readings covering 70 d, from February 2011 to February 2012. Smart-card readings comprise more than 80% of the total number of journeys (18). Each reading consists of a time stamp, a location code, and an event code. The location code uniquely identifies each of the 374 stations of the system that were active during the months covered by our data. The two events of our interest are generated when a passenger touches the smart-card reader at the entrance (“tap-in” event) or at the exit (“tap-out” event) of a station. Passenger IDs are anonymized and ignored in our analysis. We discarded all tap-in readings that are not matched to a tap-out, and vice-versa. Time resolution of the recorded time stamps is 1 min. Each day is composed of 1,200 min, starting at 5:00 AM until 1:00 AM of the next calendar day. Our analysis covers weekdays only. Weekdays are assumed to be exchangeable (see Fig. S2).

Overview of Analysis

We show that we can reliably predict passenger origin–destination $\left(\text{OD}\right)$ traffic by combining around 140,000 nonparametric statistical models with hundreds of millions of smart-card data events. We also show that the same model provides features that explain behavior under a shock (or “disruption”) to the system, defined as an unanticipated period during which a station or a line is (partially) closed down. The resulting model allows us to predict the outcome of disruptions and to evaluate stations by how prone to overcrowding they are given disruptions at peak time.

Let $N_{ijt}$ be the number of tap-out events at station $S_j$ at time $t\in \left\{\mathrm{1,2},\dots ,1200\right\}$, caused by passengers who started their journey at station $S_i$ (at possibly different starting times). Station $S_i$ is the entering station, where a journey starts, and $S_j$ is the exit station. We call $N_{jt}$ the sum of $\left\{N_{ijt}\right\}$ over all possible entering stations, a quantity of interest for potential policies to deal with an excess number of passengers exiting through a particular destination.

Our approach can be divided into two steps. First, we develop a predictive model for $N_{ijt}$ for all $374\times 374\left(\approx \mathrm{140,000}\right)$ possible pairs of stations at any minute of the day. This model represents the natural regime, where no planned or unplanned disruptions take place. Second, we create a model for $N_{jt}$ under a disruption, knowing the type of disruption and the time period in which it occurs. Data on disruptions is provided by logs maintained by TfL, complementing the smart-card data. The model for the natural regime plays an important role here, because it is used to generate expected values of $N_{ijt}$ according to what would have happened if no disruption had taken place. Such estimates of counterfactual variables are used as covariates (inputs) for the model for the factual outcomes, along with other structural features derived from the topology of the transportation network, where stations are vertices and edges connect stations that are directly physically linked by train tracks. A linear model provides a simple description of the relationship between topological structures, the natural regime, and the regime under disruption.

Intuitively, our disruption model is motivated by the following postulated relationship between $N_{jt}^{\mathcal{S}}$, the number of exits from station $S_j$ at time t under a disruption, and $N_{jt}^0$, the number under the natural regime:

$$N_{jt}^{\mathcal{S}}=N_{jt}^0-{\text{In}}_{jt}+{\text{Out}}_{jt},$$ [1]

where ${\text{In}}_{jt}$ is the missing inflow, the number of passengers who cannot reach $S_j$ because of the disruption but would have exited through $S_j$ otherwise, and ${\text{Out}}_{jt}$ is missing outflow, the number of passengers who cannot progress in their journeys in the usual way and will exit early at station $S_j$. Under a disruption, the variables in the right-hand side are unobservable, but their expectations can be estimated and used as covariates in a model of $N_{jt}^{\mathcal{S}}$.

Modeling the Natural Regime: Results

We modeled $E\left[N_{ijt}|\mathsf{PAST}\right]$, the expected value of $N_{ijt}$ given all past tap-in and tap-out events up to the given time in that particular day. This model was designed to predict three unknowns: (i) entering (tap-in) counts, (ii) the rate at which passengers remain inside the transportation system given these counts, and (iii) the rate at which passengers exit (tap-out) given the number of passengers inside the system and the length of their stay, according to origin. For each of these we used nonparametric regression models to account for the nonstationarity of the process over time (Supporting Information). We call our method the tracking model, because it keeps track of the number of passengers inside the network.

To assess the adequacy of this model, we performed a cross-validation procedure for predicting the overall aggregations $\left\{N_{jt}\right\}$ for all stations $S_j$. With our model, this is obtained simply by summing over the predicted $N_{ijt}$ for each origin, for a fixed $S_j$. In Supporting Information and Figs. S3 and S4 we provide an illustration of predicting $N_{jt}$ for the Oxford Circus station and also report a sensitivity analysis on how predictions change under different aggregations of origins and destinations.

The tracking model consists of tens of thousands of components, so there is a danger of overfitting. One way of assessing its adequacy is by comparing our predictions against blackbox models fitted directly to the aggregated data. We assessed a blackbox spline model regressing $N_{jt}$ on the time index t. Notice that, for this model, $E\left[N_{jt}|\mathsf{PAST}\right]=E\left[N_{jt}\right]$. A second competing model is a standard linear autoregressive (AR) model, where each $N_{jt}$ depends on $N_{j\left(t-30\right)},N_{j\left(t-29\right)},\dots ,N_{j\left(t-1\right)}$ (Supporting Information).

The cross-validation procedure is fivefold, implying 14 d (70 d/5) of test data for each fold. For the tracking model, we calculated the root mean squared error (RMSE) averaged over all stations, time points, and test days. We obtained an RMSE of $6.76\pm 0.08$ tap-outs per minute for a 1-min-ahead forecast and $6.82\pm 0.09$ for a 30-min-ahead forecast.

To aid the interpretability of the comparisons, we define the RMSE difference per load as the average difference between the RMSE of our model and a competitor, first calculated at a station level and then aggregated by taking a weighted average across stations (weighted by the inverse of tap-out traffic volumes at that station). We discarded stations that have fewer than 10 tap-outs in the entire day.

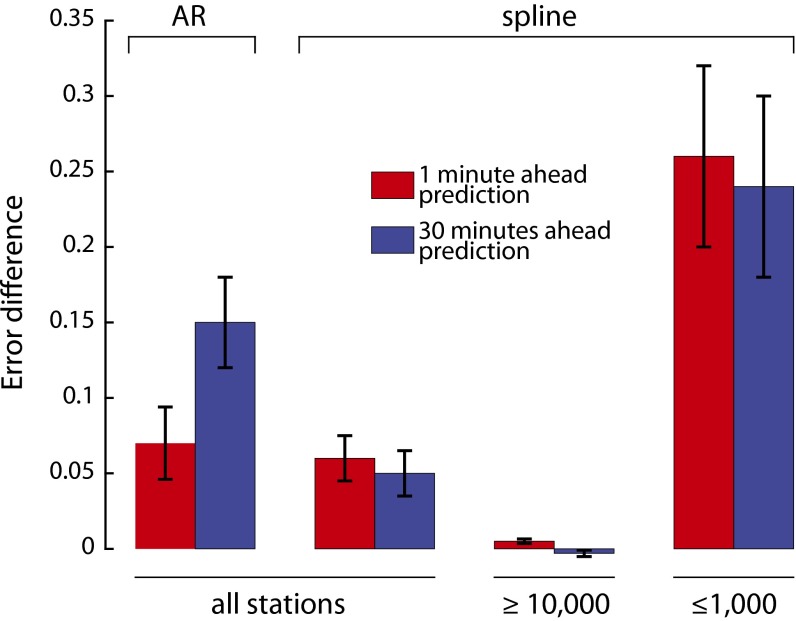
We summarize the results of the fivefold cross-validation in Fig. 1. For instance, the RMSE per load against the AR model using all stations for a 1-min-ahead forecast is 0.07. This means that the difference of RMSEs between the AR and tracking methods has a magnitude that is ∼7% of the total traffic on average. We also assessed how predictions change when looking at subsets of the population. After discarding all stations with fewer than 10,000 exits per test day, the difference between our method and the time-independent spline method is essentially zero. For smaller stations (≤1,000 exits per test day), the difference is substantial. Thus, our model does not suffer from overfitting when compared against a blackbox model that estimates the aggregated counts directly, and it also improves the performance for the smaller stations.

Fig. 1.

RMSE difference per load between (i) the AR model and the tracking model and (ii) spline model and the tracking model. Fivefold cross-validation averages for 1-min- and 30-min-ahead predictions. Higher numbers mean an improvement given by the tracking model. Error bars show a 95% confidence interval (3 SEs).

Modeling the Effect of Shocks

We modeled the behavior of passengers under two types of disruption: bidirectional line segment closures and station closures. A line segment is a sequence of adjacent stations in one of the lines of the system (e.g., Piccadilly Line, see Table S1). Lines in the London system typically allow trains to go in two directions, and closures in a single direction have a weaker effect compared with closures in both directions so are of less interest when modeling larger changes. Here, stations are assumed not to close during a line segment closure, but because of the lack of trains, disrupted stations without any connection outside of the affected line segment will typically display a dramatic reduction in the number of tap-outs. During station closures trains will not stop, so passengers who planned to exit through that station will not be able to do so. Line segments are not closed during these events.

Outcome Variable.

We assume that, for a given time interval $\left[t_1,t_F\right]=\left\{t_1,t_2,\dots ,t_F\right\}$ in which a disruption takes place, we have observed the behavior of the whole system up to time $t_1-1$. Our goal is to model the average expected tap-out count per minute, within the provided time interval, in each station of a given region of interest (ROI). A ROI is a subset of stations, selected independently of the data, in which a priori we expect to observe nontrivial changes in tap-out rate as a function of the topology of the network and type of disruption.

Although our model can predict the expected tap-out count at each minute individually, we modeled the average over $\left[t_1,t_F\right]$ because this quantity suffices to inform policy on station overcrowding and excess demand for alternative transportation. We assumed that the time interval is sufficiently short so that passenger behavior is not affected over time as a function of our covariates. As such, we define the outcome

$${\overline{N}}_{t_1:t_F}^{\mathcal{S}\left[j\right]}\equiv {\displaystyle \sum _{t=t_1}^{t=t_F}{N}_{jt}^{\mathcal{S}}/F},$$ [2]

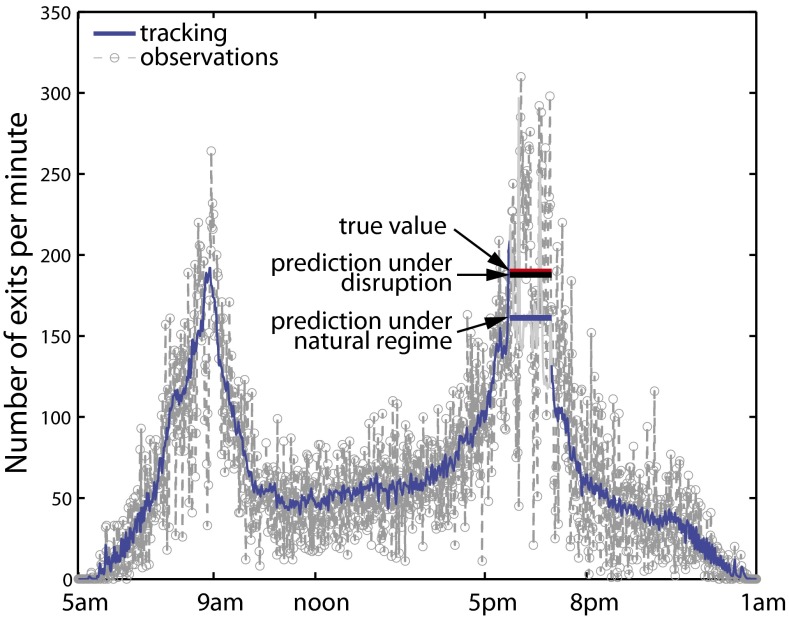
for each station $S_j$ in the chosen ROI. Here $N_{jt}^{\mathcal{S}}$ is the number of tap-outs from station $S_j$ at time t under disruption $\mathcal{S}$, excluding exits originated in $S_j$ itself. Modeling this type of exit is straightforward and therefore we did not include it in the study. Fig. 2 provides an example of the prediction given by our model at Victoria Underground station.

Fig. 2.

Average number of exits per minute at Victoria LU station on Tuesday, January 17, 2012. The blue curve represents the 1-min-ahead prediction under the natural regime using the tracking model. Given a disruption from 6:00 PM to 7:00 PM between Victoria station and Brixton station in the Victoria line, the blue horizontal line indicates the average expected exit rate given by the tracking model under the natural regime, the red line the averaged observed exit count, and the black line the prediction given by the disruption model (Eq. 5).

Covariates for Line Segment Disruption.

Consider the case where the disruption event $\mathcal{S}$ is the bidirectional disruption of line segment l along the sequence of stations ${\mathcal{K}}^l\equiv \left(S_{k\left(1\right)},\dots ,S_{k\left(M\right)}\right)$. Given this, we can define the set of covariates in the regression model for ${\overline{N}}_{t_1:t_F}^{\mathcal{S}\left[j\right]}$. To distinguish between the natural regime and the regime under disruption $\mathcal{S}$, let $N_{ijt}^0$ be the corresponding OD count at time t under the natural regime. Moreover, let ${\mu }_{ijt;t_1}^0$ be the expected value of $N_{ijt}^0$ conditioned on observing all events of the day up to time $t_1-1$. Our set of covariates are functions of ${\mu }_{ijt;t_1}^0$.

Ideally, for each station $S_{k\left(n\right)}\in {\mathcal{K}}^l$, the disruption will be related to the amount of traffic for each $\text{OD}$ pair $\left(S_O,S_D\right)$ that passes either through the links $S_{k\left(n\right)}\to S_{k\left(n+1\right)}$ or $S_{k\left(n\right)}\to S_{k\left(n-1\right)}$ in the natural regime. However, only a fraction of the flow $S_O\to \cdots S_{k\left(n\right)}\to S_{k\left(n-1\right)}\to S_D$ might exit early at $S_{k\left(n\right)}$ if there are routes from the origin that do not necessarily use $S_{k\left(n\right)}$ or that might continue from $S_{k\left(n\right)}$ in a different line.

Given the target station $S_{k\left(n\right)}$, the expected missing outflow ${\varphi }^{\text{OUT}}\left(n\right)$ for $S_{k\left(n\right)}$ at time t is defined as

$${\varphi }^{\text{OUT}}\left(n\right)\equiv {\displaystyle \sum _{t=t_1}^{t=t_F}{\varphi }_u^{\text{OUT}}\left(n,t\right)/F},$$ [3]

where

$${\varphi }^{\text{OUT}}\left(n,t\right)\equiv {\displaystyle \sum _{S_D\in {\mathcal{K}}_l\backslash S_{k\left(n\right)}}{\displaystyle \sum _{S_O\ne S_D}{\displaystyle \sum _{S_v\in {\mathcal{N}}_{{\mathcal{K}}_l}\left(n\right)}{\pi }_{k\left(n\right),v,l}^{\text{OD}}\times {\mu }_{\text{OD}t;t_1}^0}}}\mathrm{.}$$

In this equation, ${\mathcal{N}}_{{\mathcal{K}}_l}\left(n\right)$ are the neighboring stations to $S_{k\left(n\right)}$ in the set ${\mathcal{K}}_l$, and ${\pi }_{h,i,l}^{\text{OD}}$ is the probability (under the natural regime) of passing first through $S_h$ then $S_i$ at line l during a journey from $S_O$ to $S_D$ (regardless of time). We restrict $S_D$ to belong to ${\mathcal{K}}_l$, because these are the most difficult destinations to reach by an alternative route.

These probabilities are not directly identifiable from the smart-card data. The problem of estimating unobservable trajectories between two stations is a type of network tomography problem (19). However, TfL has survey data on passenger route choice, the Rolling Origin and Destination Survey (RODS) (20). Combined with prior information on likely routes using structural information of the network topology, we are able to produce Bayesian posterior expected values for ${\pi }_{h,i,l}^{\text{OD}}$ (Supporting Information). The use of RODS data minimizes the need for more sophisticated network tomography models (21–24), for which no software is readily available for the scale of the problem we are operating at (to the best of our knowledge).

A potential difficulty with using the missing outflow as a covariate for our regression model for ${\overline{N}}_{t_1:t_F}^{\mathcal{S}\left[k\left(n\right)\right]}$ is that, the more distant a destination is, the more likely a passenger will try a different route instead of tapping out early at $S_{k\left(n\right)}$. To control for this, we added as a second covariate ${\varphi }^{\text{DIST}}\left(n\right)$, the average physical distance (in kilometers) between $S_{k\left(n\right)}$ and each $S_{k\left(m\right)}\in {\mathcal{K}}^l$, $n\ne m$. This covariate is used in our model through a variety of nonlinear transformations (see Fig. S5 for an illustration).

A third covariate in this model is the missing inflow, the amount of traffic that would have exited through $S_{k\left(n\right)}$ but will not if the usual route would be through a vertex in the disrupted segment:

$${\varphi }^{\text{IN}}\left(n,t\right)\equiv {\displaystyle \sum _{S_O\ne S_{k\left(n\right)}}{\displaystyle \sum _{S_v\in {\mathcal{N}}_{{\mathcal{K}}_l}\left(n\right)}{\pi }_{v,k\left(n\right),l}^{O{k}_{\left(n\right)}}\times {\mu }_{O{k}_{\left(n\right)}t;t_1}^0}},$$

with ${\varphi }^{\text{IN}}\left(n\right)$ defined analogously.

The fourth covariate is just the expected outcome under the natural state,

$${\varphi }^{\text{NAT}}\left(n,t\right)\equiv {\displaystyle \sum _{S_O\ne S_{k\left(n\right)}}{\mu }_{O{k}_{\left(n\right)}t;t_1}^0}$$

and, again, ${\varphi }^{\text{NAT}}\left(n\right)$ is defined analogously.

Finally, a fifth covariate, ${\varphi }^{\text{DELAY}}$, is a binary indicator of whether there were delays elsewhere happening in the same line during the disruption event. We extracted this covariate from the textual description of the disruption events according to TfL logs (Supporting Information).

Covariates for Station Disruption.

Consider the disruption now being the closure of a single station $S_{\mathcal{K}}$, with no interruption of service except for the fact that no trains stop at $S_{\mathcal{K}}$. Our expectation is that, once $S_{\mathcal{K}}$ closes, passengers will have an increased probability of leaving at one of the stations $S_h$ adjacent to it. We estimated the expected number of exits at each $S_h$ with a regression model.

Define ${\pi }_h^{O\mathcal{K}}$ as the probability of passing through $S_h$ on a journey that starts at $S_O$ and ends at $S_{\mathcal{K}}$, regardless of which line is taken. We again used RODS data to estimate this quantity (Supporting Information). We define the expected missing outflow of $S_h$ into $S_{\mathcal{K}}$ as

$${\varphi }^{\text{OUT}}\left(h,t\right)\equiv {\displaystyle \sum _{S_O\ne S_{\mathcal{K}}}{\displaystyle \sum _{S_v\in {\mathcal{N}}_{{\mathcal{K}}_l}\left(S_{k\left(n\right)}\right)}{\pi }_h^{O\mathcal{K}}\times {\mu }_{O\mathcal{K}t;t_1}^0}}$$ [4]

with ${\varphi }^{\text{OUT}}\left(h\right)$ defined analogously.

This covariate is meant to capture the excess tap-outs in $S_h$ because of passengers leaving one station earlier than their intended destination $S_{\mathcal{K}}$. However, passengers might tap-out one station past $S_{\mathcal{K}}$, a role that can also be played by $S_h$ with respect to other origins $S_O$. For this we define ${\pi }_h^{O\mathcal{K}\prime }$ as the probability of $S_h$ being in the same line of the final leg of the journey between $S_O$ and $S_{\mathcal{K}}$, but coming after $S_{\mathcal{K}}$. Covariate ${\varphi }^{\text{OUT}\prime }\left(h\right)$ is defined as in Eq. 4, but using ${\pi }_h^{O\mathcal{K}\prime }$ instead.

We also define the covariate ${\varphi }^{\text{NAT}}\left(h\right)$, analogous to the case of line segment closure, and distance covariate ${\varphi }^{\text{DIST}}\left(h\right)$, the distance between $S_h$ and $S_{\mathcal{K}}$ in kilometers.

Results

For the period of 70 d, we obtained the corresponding two-way line segment disruption events with 768 data points, and the station closure events with 191 data points (see Fig. S6 for raw data plots). Each data point corresponds to the outcome of a particular station at a particular disruption. The least-squares method was used to fit all models.

Disruptions of Line Segments.

The ROIs for the line segment problems are stations within each affected segment $\mathcal{K}=\left\{S_{k\left(1\right)},\dots ,S_{k\left(M\right)}\right\}$ having other connections outside $\mathcal{K}$. Stations without other connections have very few tap-outs or none because no trains can reach them. Stations elsewhere in the system show weaker effects that we did not consider in this study.

We define the model for expected outcomes as

$$\begin{array}{l}{E}_x\left({\overline{N}}_{t_1:t_F}^{\mathcal{S}\left[k_{\left(n\right)}\right]}\right)\equiv E\left[{\overline{N}}_{t_1:t_F}^{\mathcal{S}\left[k_{\left(n\right)}\right]}|\mathsf{PAST},{\varphi }^{\text{DELAY}}=x\right]\\ \equiv {\beta }_{0x}+{\beta }_{1x}{\varphi }^{\text{NAT}}+{\beta }_{2x}{\varphi }^{\text{IN}}+f_x\left({\varphi }^{\text{DIST}}\right)\times {\varphi }^{\text{OUT}},\end{array}$$ [5]

where the second-order polynomial

$$f_x\left({\varphi }^{\text{DIST}}\right)\equiv {\beta }_{3x}+{\beta }_{4x}{\varphi }^{\text{DIST}}+{\beta }_{5x}{\varphi }^{{\text{DIST}}^2}$$

captures the impact of ${\varphi }^{\text{OUT}}$ regulated by the average distance between $S_{k\left(n\right)}$ and the remaining elements of the ROI; $x\in \left\{\mathrm{0,1}\right\}$, and we omit the indexing $\left(n\right)$ for clarity.

Before fitting the model in Eq. 5, we show models obtained without the distance covariate ${\varphi }^{\text{DIST}}$,

$$E_0\left({\overline{N}}_{t_1:t_F}^{\mathcal{S}\left[k_{\left(n\right)}\right]}\right)=1.15{\varphi }^{\text{NAT}}-1.28{\varphi }^{\text{IN}}+0.16{\varphi }^{\text{OUT}},$$ [6]

$$E_1\left({\overline{N}}_{t_1:t_F}^{\mathcal{S}\left[k_{\left(n\right)}\right]}\right)=1.24{\varphi }^{\text{NAT}}-1.23{\varphi }^{\text{IN}}+0.09{\varphi }^{\text{OUT}},$$ [7]

because they are easier to interpret than Eq. 5 [standard errors of coefficients: 0.02, 0.11, and 0.02 for the no-delay case and 0.02, 0.07, and 0.02 for the delay case, respectively (P < 10⁻⁷ each). Intercepts were removed (P > 0.75 each)]. This supports the postulated qualitative contributions of flows in Eq. 1, where the signs match the postulated contribution of the respective flows and the magnitude of the ${\varphi }^{\text{NAT}}$ component is not substantially different from unity. We conclude that, structurally, there is a significant contribution of missing inflows and outflows to the expected tap-out rate, which cannot be explained by a linear rescaling of the natural expected tap-out rate only. Most of the variability in the outcome can be explained by the natural regime and passenger flows $\left(R^2>0.9\right)$.

As a matter of fact, the counterfactual flow ${\varphi }^{\text{NAT}}$ was the covariate with the strongest contribution to the model: Fitting a model with this covariate only gives $E_0\left({\overline{N}}_{t_1:t_F}^{\mathcal{S}\left[k_{\left(n\right)}\right]}\right)=-0.29+1.10{\varphi }^{\text{NAT}}$ and $E_1\left({\overline{N}}_{t_1:t_F}^{\mathcal{S}\left[k_{\left(n\right)}\right]}\right)=-0.22+{\varphi }^{\text{NAT}}$ (with $R^2=0.9$ and 0.88, respectively). Interestingly, this model seems to hide the impact of closures in the ${\varphi }^{\text{DELAY}}=1$ case.

Table 1 presents the fitted models of Eq. 5. The entries of $f_x\left({\varphi }^{\text{DIST}}\right)\times {\varphi }^{\text{OUT}}$ can be interpreted as interaction terms in a linear model. The evidence suggests that the distance from affected stations to other affected stations matters in both cases. For the case with delays, discarding the nonsignificant quadratic term, the results agree with the intuition that as distance grows passengers may feel compelled to find alternative routes, and as such the missing outflow will be penalized. In the case without delays, the result seems contrary to intuition. We propose as an explanation that disruptions without delays are positively associated with line segments that offer fewer alternatives to reach their destinations. In fact, around $53\text{\%}$ of the no-delay disruption events we observed included the end of the line (a feature which, on its turn, is associated with longer distances among stations and lack of alternative routes). In contrast, only $38\text{\%}$ of the events with delays included the end of a line (Supporting Information).

Table 1.

Estimates of model for exit counts in affected line segments

Parameter	${\varphi }^{\mathrm{DELAY}}=0$ (N = 344, R2 = 0.93)		${\varphi }^{\mathrm{DELAY}}=1$ (N = 424, R2 = 0.92)
	Estimate ± SE	P value	Estimate ± SE	P value
Intercept	−0.05 ± 0.33	0.88	0.07 ± 0.38	0.85
${\varphi }^{\text{NAT}}$	1.16 ± 0.02	<10−15	1.25 ± 0.02	<10−15
${\varphi }^{\text{IN}}$	−1.21 ± 0.11	<10−15	−1.27 ± 0.07	<10−15
${\varphi }^{\text{OUT}}$	−0.05 ± 0.06	0.51	0.21 ± 0.06	<10−3
${\varphi }^{\text{OUT}}:{\varphi }^{\text{DIST}}$	0.10 ± 0.04	<0.01	−0.05 ± 0.02	0.05
${\varphi }^{\text{OUT}}:{\varphi }^{\text{DIST}2}$	−0.001 ± 0.004	<0.01	0.004 ± 0.002	0.11

We evaluated our framework by its predictive power using leave-one-out cross-validation (LOOCV). This consists of fitting a model with a training set containing all points but one, which is used for testing. For each fold, the error metric is the absolute difference between the predicted average number of tap-outs per minute against the true average in the test point.

We compare our performance against two baselines. The first is the model with ${\varphi }^{\text{NAT}}$ as the only covariate, and the second a model where flow probabilities ${\pi }_{k\left(n\right),v,l}^{\text{OD}}$ are defined to be constant (that is, they are removed from the definition in Eq. 3). We focused on fitting models that aggregate both delayed and nondelayed events. To better compare models, we report the difference in the test error averaged over a decreasing subset of test points. Because the amount of tap-outs per station has a skewed distribution, a large number of small-traffic stations will mask the benefits achieved at larger stations. Results are shown in Fig. 3A. We report the difference in error between each baseline and our model, for each subset of the test folds considered. As we assess stations of larger traffic, the difference among our method and the baselines becomes more evident. The absolute error of our disruption model for the line segment case varies from 3.0 (all stations) to 12.2 (stations with 85 tap-outs per minute or more) persons per minute. See Tables S2–S5 and Fig. S7 for the absolute error in each class of station, prediction and error scatterplots, and for sensitivity analyses assessing variations of the model in Eq. 5.

Fig. 3.

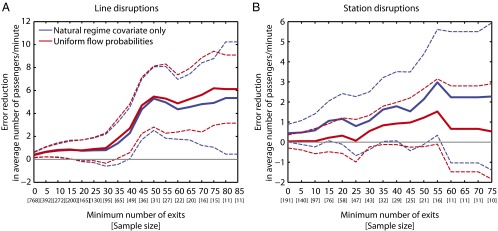
Reduction in error provided by the model in Eq. 5 compared with baselines (i) natural regime covariate only and (ii) uniform flow probabilities. Dashed lines show the pointwise 95% confidence intervals on the error reduction. Each point considers test cases with minimum number of tap-outs per minute indicated in the horizontal axis. The number in brackets indicates the number of test cases. (A) Relative errors for line segment events. The absolute error of tracking model for the line segment disruption varies from 3.0 (all stations) to 12.2 (stations with 85 tap-outs per minute or more) persons per minute. (B) Relative errors for station events. The absolute error varies from 3.5 (all stations) to 10.5 (stations with 75 tap-outs per minute or more) persons per minute.

Disruptions of Single Stations.

Our ROI for a station closure $S_{\mathcal{K}}$ consists of its neighbors $S_h$. The model for ${\overline{N}}_{t_1:t_F}^{\mathcal{S}\left[h\right]}$, the average tap-count at each $S_h$, is

$$\begin{array}{c}E\left[{\overline{N}}_{t_1:t_F}^{\mathcal{S}\left[h\right]}|\mathsf{PAST}\right]\equiv {\beta }_0+{\beta }_1{\varphi }^{\text{NAT}}+f\left({\varphi }^{\text{DIST}}\right)\times {\varphi }^{\text{OUT}}\\ +f\prime \left({\varphi }^{\text{DIST}}\right)\times {\varphi }^{\text{OUT}\prime },\end{array}$$ [8]

where $f\left({\varphi }^{\text{DIST}}\right)\equiv {\beta }_2+{\beta }_3{\varphi }^{\text{DIST}}+{\beta }_4{\varphi }^{{\text{DIST}}^2}$ and $f\prime \left({\varphi }^{\text{DIST}}\right)\equiv {\beta }_{2\prime }+{\beta }_{3\prime }{\varphi }^{\text{DIST}}+{\beta }_{4\prime }{\varphi }^{{\text{DIST}}^2}$. The fitted model is shown in Table 2.

Table 2.

Estimates of model for exit counts in affected neighboring stations

	Estimate ± SE (N = 191, R2 = 0.95)	P value
Intercept	−0.07 ± 0.59	0.90
${\varphi }^{\text{NAT}}$	1.07 ± 0.02	<10−15
${\varphi }^{\text{OUT}}$	0.59 ± 0.22	<0.01
${\varphi }^{\text{OUT}}:{\varphi }^{\text{DIST}}$	−0.32 ± 0.20	0.11
${\varphi }^{\text{OUT}}:{\varphi }^{\text{DIST}2}$	0.01 ± 0.02	0.32
${\varphi }^{\text{OUT}\prime }$	0.89 ± 0.23	<0.01
${\varphi }^{\text{OUT}\prime }:{\varphi }^{\text{DIST}}$	−0.86 ± 0.29	<0.01
${\varphi }^{\text{OUT}\prime }:{\varphi }^{{\text{DIST}}^2}$	0.17 ± 0.07	0.02

We performed a LOOCV comparison against two baseline models (Fig. 3B) analogous to the line disruption case. The absolute error varies from 3.5 (all stations) to 10.5 (stations with 75 tap-outs per minute or more) persons per minute (see Table S3 for further details). Although there is no strong evidence our model outperforms the uniform flow model statistically (Supporting Information), and the improvement over the natural regime baseline is very small, the model is competitive while also revealing insights on passenger behavior. In particular, it suggests that passengers who tap-out at a station $S_h$ immediately after $S_{\mathcal{K}}$ will do it less often as the distance between the two stations increases. This is a way of providing evidence of rational behavior of passengers, which can be used to validate whether announcements of station closures are being properly used by passengers—this might not be true if communication between staff and passengers is poor (i.e., if closures are announced only as the train passes through the closed station). This type of analysis can be applied to networks other than the London Underground as a validation of good communication between train drivers and passengers.

Station Sensitivity Index.

Besides solving prediction tasks, the models described here allow for a structural understanding of the London transportation system. We provide, as an illustration of information extraction from the fitted models, a categorization of stations by how sensitive they are to closures at line segments containing them, information that is crucial when analyzing the vulnerable points of a transportation network. In particular, for any given station S, consider all sequences of four stations $\left(S,S_1,S_2,S_3\right)$, all in the same line, which start at S and follow the physical adjacencies (if the line ends before four stations or if there is a bifurcation at a particular point, stop at the end or bifurcation instead). Consider the scaled expected change in exit numbers $\left(E\left[{\overline{N}}_{S,t_1:t_F}^{\mathcal{S}}\right]-{\varphi }^{\text{NAT}}\left(S\right)\right)/{\varphi }^{\text{NAT}}\left(S\right)$ as predicted by the model for endpoints without delays, where $t_1:t_F$ is the peak period from 8:30 AM to 9:30 AM. The station sensitivity index for each S is defined as the maximum over the corresponding normalized expected changes. Notice that the index can be negative, meaning that a station is expected to have fewer passengers tapping out compared with the natural regime. This is the case when missing inflows outnumber other factors, which cannot be captured by the simpler models with only ${\varphi }^{\text{NAT}}$ (Supporting Information).

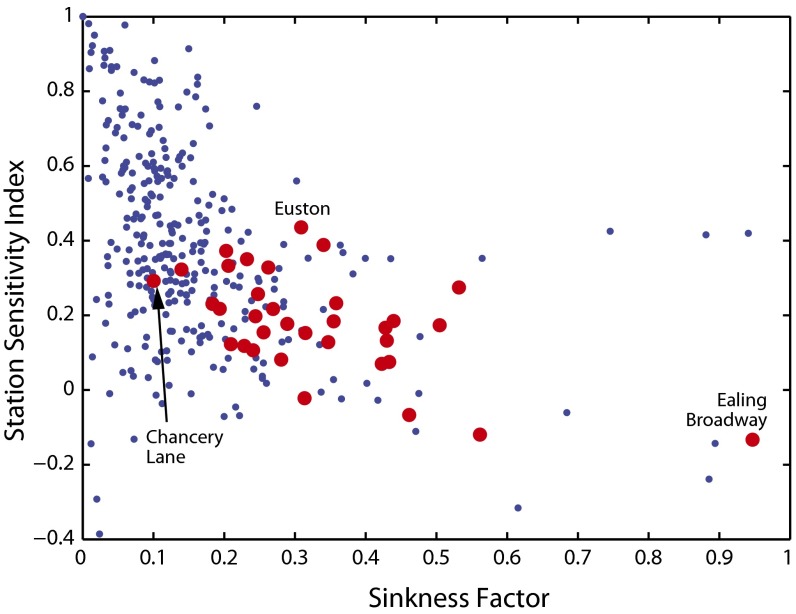
The station sensivity index is the implicit result of several factors, including the degree by which station S is the final destination of passengers who reach at least S in their journey—a “sinkness” factor. The sinkness factor of a station S is given by the ratio $N_S/M_S$, defined as follows: for each OD pair $\left(S_O,S_D\right)$ such that S lies in the shortest path between these two endpoints (as measured by the graph given by the union of all lines), add to $N_S$ the total number of $\left(S_O,S_D\right)$ journeys seen in our data, and add to $M_S$ the total number of journeys between $S_O$ and $S_{D\prime }$ where $S_{D\prime }$ lies between S and $S_D$ in the shortest path $S_O\cdots \to S\to \cdots \to S_{D\prime }\to \cdots S_D$. Notice that the ratio $N_S/M_S$ is large if S is the final destination point of a substantial fraction of journeys traversing it, and is equal to 1 if S is the end of a line. Fig. 4 shows a scatterplot between the station sensitivity index and the sinkness factor. The association is nonlinear and strong, summarized by a correlation coefficient of $-0.44$. In particular, the nonlinearity seems to be due to an interaction between station size with station sensitivity index and sinkness factor. We highlight the top 10% stations in Fig. 4, defined by their total volume of tap-outs in our data. In this case, the correlation coefficient is $-0.60$.

Fig. 4.

Station sensitivity index versus sinkness factor for all stations. Red points represent the top 10% of stations as measured by number of tap-outs. Stations with the trivial sinkness of 1 were removed for better visualization.

Discussion

We have shown that it is possible to predict traffic in a complex, real-world transportation network using a model consisting of tens of thousands of nonparametric statistical components. We have also shown how data from the London system provides overwhelming evidence for our hypothesis that traffic under disruption can be decomposed by contrasting it to a counterfactual output and flows that are split among over 100,000 OD pairs. This decomposition is validated by predictive performance under natural and disrupted regimes, and by structural insights that can be extracted from the model, of which we presented only a small sample of possibilities. The analysis presented, to the best of our knowledge, is the largest system-wide predictive study of a complex real urban railway network to date and integrates data from several sources, including smart-card data and passenger surveys.

In particular, our analysis introduces novel ideas on how to combine data from different regimes. Assumptions linking different regimes allow for estimating the effects of a particular shock using only observational data and natural experiments (25–27). Although our shocks are random and should not be strictly interpreted as nonrandom regime indicators, in the usual counterfactual sense (28), we believe that the work presented here provides an entirely novel way of modeling complex transportation networks. It explicitly makes use of modularity assumptions that allow structural claims from a relatively small set of unplanned shocks. Although we used the London transportation system as our case study, similar analyses can be undertaken in any transportation systems where smart-card data and disruption logs are available.