Shifted Hamming distance: a fast and accurate SIMD-friendly filter to accelerate alignment verification in read mapping

Abstract

Motivation: Calculating the edit-distance (i.e. minimum number of insertions, deletions and substitutions) between short DNA sequences is the primary task performed by seed-and-extend based mappers, which compare billions of sequences. In practice, only sequence pairs with a small edit-distance provide useful scientific data. However, the majority of sequence pairs analyzed by seed-and-extend based mappers differ by significantly more errors than what is typically allowed. Such error-abundant sequence pairs needlessly waste resources and severely hinder the performance of read mappers. Therefore, it is crucial to develop a fast and accurate filter that can rapidly and efficiently detect error-abundant string pairs and remove them from consideration before more computationally expensive methods are used.

Results: We present a simple and efficient algorithm, Shifted Hamming Distance (SHD), which accelerates the alignment verification procedure in read mapping, by quickly filtering out error-abundant sequence pairs using bit-parallel and SIMD-parallel operations. SHD only filters string pairs that contain more errors than a user-defined threshold, making it fully comprehensive. It also maintains high accuracy with moderate error threshold (up to 5% of the string length) while achieving a 3-fold speedup over the best previous algorithm (Gene Myers’s bit-vector algorithm). SHD is compatible with all mappers that perform sequence alignment for verification.

Availability and implementation: We provide an implementation of SHD in C with Intel SSE instructions at: https://github.com/CMU-SAFARI/SHD.

Contact: hxin@cmu.edu, calkan@cs.bilkent.edu.tr or onur@cmu.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

The emergence of massively parallel sequencing technologies, commonly called high-throughput sequencing platforms, during the past decade triggered a revolution in the field of genomics. These platforms enable scientists to sequence mammalian-sized genomes in a matter of days, which has created new opportunities for biological research. For example, it is now possible to investigate human genome diversity between populations 1000 Genomes Project Consortium (2010, 2012), find genomic variants likely to cause disease (Flannick et al., 2014; Ng et al., 2010, and study the genomes of ape species (Marques-Bonet et al., 2009; Prado-Martinez et al., 2013; Scally et al., 2012; Ventura et al., 2011) and ancient hominids (Green et al., 2010; Meyer et al., 2012; Reich et al., 2010) to better understand human evolution.

However, these new sequencing platforms drastically increase the computational burden of genome data analysis. In the first step of data analysis, billions of short DNA segments (called reads) are aligned to a long reference genome. Each read is mapped to one or more sites in the reference based on similarity with a process called read mapping.

Read mappers typically fall into one of two main categories: suffix-array and backtracking-based (Delcher et al., 1999; Langmead and Salzberg 2012; Li and Durbin 2010) or seed-and-extend-based (Ahmadi et al., 2011; Alkan et al., 2009; Li et al., 2009; Rumble et al., 2009; Weese et al., 2012). Suffix-array-based mappers use the Burrows-Wheeler transformation (Burrows et al., 1994) and are efficient at finding the best mappings of a read. Mappers in this category use aggressive algorithms to build their candidate pools, which may miss potentially correct mappings. Although mappers in this category can also be configured to achieve higher sensitivity by systematically inspecting all possible error scenarios of a read, such configuration increases their execution times superlinearly (Delcher et al., 1999; Langmead and Salzberg 2012; Li and Durbin 2010).

Alternatively, seed-and-extend-based mappers build comprehensive but overly large candidate pools and rely on filters and local alignment techniques to remove incorrect mappings (i.e. potential mappings with more errors than allowed) from consideration in the verification step. Mappers in this category are comprehensive (find all correct mappings of a read) and accurate (do not provide incorrect mappings), but waste computational resources identifying and rejecting incorrect mappings. As a result, they are slower than suffix-array-based mappers.

Fast and accurate filters, which detect and reject incorrect mappings using cheap heuristics can increase the speed of seed-and-extend mappers (by speeding up the verification procedure, Xin et al., 2013) while maintaining their high accuracy and comprehensiveness. An ideal filter should be able to quickly verify the correctness of a mapping, yet require much less computation than rigorous local alignment, which precisely calculates the number of errors between the read and reference using dynamic programming methods. More importantly, a filter should never falsely remove a correct mapping from consideration, as this would reduce the comprehensiveness of the mapper.

Recent work has shown the potential of using single instruction multiple data (SIMD) vector execution units including general-purpose GPUs and Intel SSE Intel (2012) to accelerate local alignment techniques (Farrar 2007; Manavski and Valle 2008; Szalkowski et al., 2008). However, these publications only apply SIMD units to existing scalar algorithms, which do not exploit the massive bit-parallelism provided by SIMD platforms.

In this article, we present shifted hamming distance (SHD), a fast and accurate SIMD-friendly bit-vector filter to accelerate the local alignment (verification) procedure in read mapping. The key idea of SHD is to avoid wasting computational resources on incorrect mappings by verifying them with a cheap, SIMD-friendly filter before invoking canonical complex local alignment methods. Our studies show that SHD quickly identifies the majority of the incorrect mappings, especially ones that contain far more errors than allowed, while permitting only a small fraction of incorrect mappings to pass SHD which are later filtered out by more sophisticated and accurate filters or by local alignment techniques.

This article makes the following contributions:

• We show that for seed-and-extend-based mappers, most potential mappings contain far more errors than what is typically allowed (Section 2).

• We introduce a fast and accurate SIMD-friendly bit-vector filter, SHD, which approximately verifies a potential mapping with a small set of SIMD-friendly operations (Section 3).

• We prove that SHD never removes correct mappings from consideration; hence, SHD never reduces the accuracy or the comprehensiveness of a mapper (Section 3).

• We provide an implementation of SHD with Intel SSE (Section 3) and compare it against three previously proposed filtering and local alignment implementations (Section 4), including an SSE implementation of the Smith–Waterman algorithm, swps3 (Szalkowski et al., 2008); an implementation of Gene Myers’s bit-vector algorithm, SeqAn (Döring et al., 2008) and an implementation of our Adjacency Filtering algorithm, FastHASH (Xin et al., 2013). Our results on a wide variety of real read sets show that SHD SSE is both fast and accurate. SHD SSE provides up to 3× speedup against the best previous state-of-the-art edit-distance implementation (Döring et al., 2008) with a maximum false-positive rate of 7% (the rate of incorrect mappings passing SHD).

2 Motivation

Read mappers identify locations within a reference genome where the read and the reference match within a user-defined error (i.e. insertions, deletions or substitutions) threshold, e. In practice, e is usually 5% of the read length, but most aligners can be configured to return only the best mapping (the mapping with the fewest errors). As seen in Figure 8 (in Supplementary Materials), most potential location mappings tested by seed-and-extend based mappers are incorrect (having more errors than allowed); in fact, when $e=5\%$ of the read length, more than 98% of mappings are incorrect. Since alignment is the primary computationally intensive task performed by seed-and-extend-based read mappers (Xin et al., 2013), it is crucial that incorrect mappings be rejected efficiently.

Many mechanisms have been proposed to efficiently calculate the edit-distance of strings and filter out incorrect mappings. These mechanisms can be divided into five main classes: (i) dynamic programming (DP) algorithms, (ii) SIMD implementations of DP algorithms, (iii) bit-vector implementations of DP algorithms, (iv) Hamming distance calculation and (v) locality-based filtering mechanisms. Notice that although mechanisms in both (ii) and (iii) are different implementations of (i), we separate them into two categories because they use different optimization strategies: while mechanisms in (ii) faithfully implement the DP algorithm in a SIMD fashion, mechanisms in (iii) use a modified bit-parallel algorithm to calculate a bit representation of the DP matrix (Myers 1999). Full descriptions of each strategy are provided in Supplementary Materials, Section S1.3.

In this article, we choose three representative implementations from (ii), (iii) and (v): swps3 (Szalkowski et al., 2008), SeqAn (Döring et al., 2008) and FastHASH (Xin et al., 2013) (for detailed analysis, see Supplementary Materials S1.3). These mechanisms were not designed as SIMD bit-parallel filters and are either fast or accurate (can filter out most incorrect mappings) but not both. Conversely, we designed SHD to leverage bit-parallelism and SIMD instructions to achieve high performance while preserving high accuracy.

3 Methods

Overview

Our filtering algorithm, SHD, uses simple bit-parallel operations (e.g. AND, XOR, etc.) which can be performed quickly and efficiently using the SIMD architectures of modern CPUs. SHD relies on two key observations:

1. If two strings differ by e errors, then all non-erroneous characters of the strings can be aligned in at most e shifts.

2. If two strings differ by e errors, then they share at most e + 1 identical sections (Pigeonhole Principle, Xin et al., 2013).

Based on the above observations, SHD filters potential mappings in two steps:

1. Identify basepairs (bps) in the read and the reference that can be aligned by incrementally shifting the read against the reference.

2. Remove short stretches of matches identified in step 1 (likely noise).

We call these two steps shifted Hamming mask-set (SHM) and speculative removal of short-matches (SRS), respectively. In the remainder of this section, we describe these two steps, then analyse SHD in terms of false negatives (defined as correct mappings that are falsely rejected by SHD) and false positives (defined as incorrect mappings that pass SHD).

3.1 Shifted Hamming Mask-Set (SHM)

SHM aligns basepairs in the read and the reference by horizontally shifting the read against the reference. SHM is based on the key observation that if there are no more than e errors between the read and the reference, then each non-erroneous basepair (bp) in the reference can be matched to a basepair in the read within $[-e,+e]$ shifts from its position. Thus, if there are more than e basepairs in the read that failed to find a match in the reference, then there must be more than e errors between the read and the reference, hence the potential mapping should be rejected.

Based on this observation, SHM verifies a potential mapping in two steps. First, SHM separately identifies all basepair matches by calculating a set of 2e + 1 Hamming masks while incrementally shifting the read against the reference (one Hamming mask per shift). Each Hamming mask is a bit-vector of ‘0’s and ‘1’s representing the comparison of the read and the reference, where a ‘0’ represents a bp match and a ‘1’ represents a bp mismatch (implementation details of computing Hamming masks using bit-parallel operations are provided in Supplementary Materials S1.1). Figure 1 illustrates the production of these Hamming masks for a correct mapping. Once found, SHM merges all basepair matches together through multiple bit-wise AND operations.

Fig. 1.

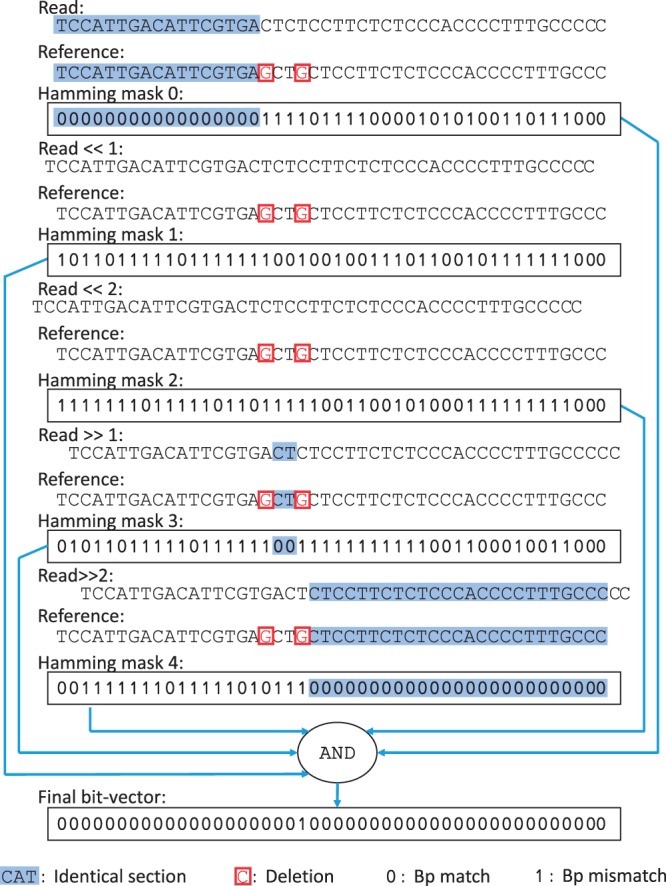
An example of applying SHM to a correct mapping, which contains two deletions. All matching basepairs are identified in the Hamming masks as 0s and are merged together using bit-wise AND operations

In SHM, to tolerate e errors, $2e+1$ Hamming masks must be produced where: e Hamming masks are calculated after incrementally shifting the read to the left by 1 to e bps; e Hamming masks are calculated by incrementally shifting the read to the right by 1 to e bps; one additional Hamming mask is calculated without any shifting. By incrementally shifting the read in SHM, all basepairs between the read and the reference of a correct mapping (except the errors) are brought into alignment with at least one matching bp of the read and identified in one or more of the $2e+1$ masks, as shown in Figure 1.

The Hamming masks are merged together in 2e bit-wise AND operations. When ANDing Hamming masks, a ‘0’ at any position will lead to a ‘0’ in the resulting bit-vector at the same position. When aligned with a match, a bp produces a ‘0’ in the Hamming mask, which masks out all ‘1’s in any other Hamming masks at the same position. Therefore, the final bit-vector produced after all bit-wise AND operations are complete is guaranteed to contain ‘0’s for all non-error basepairs; as a result, the number of ‘1’s that remain in the final bit-vector provides a lower bound on the edit-distance between the read and the reference. Since correct potential mappings must have e or fewer errors, SHM can safely filter mappings whose final bit-vector contains more than e ‘1’s, without any risk of removing correct read mappings.

3.2 Speculative Removal of Short-Matches (SRS)

SHM ensures all correct read mappings are preserved; however, many incorrect mappings may also pass the filter as false positives. For example, the read in Figure 2 is compared against a drastically different reference using SHM with an error threshold of two (e = 2). Despite the presence of substantially more than two errors, the final bit-vector produced by SHM does not contain any ‘1’s, as if there were no errors at all. In SHM, ‘0’s in the final bit-vector are considered to be matches and ‘1’s are considered to be errors. In this example, most basepairs in the reference find a match within two shifts of the read, so the read and the reference are considered similar enough to pass the filter.

Fig. 2.

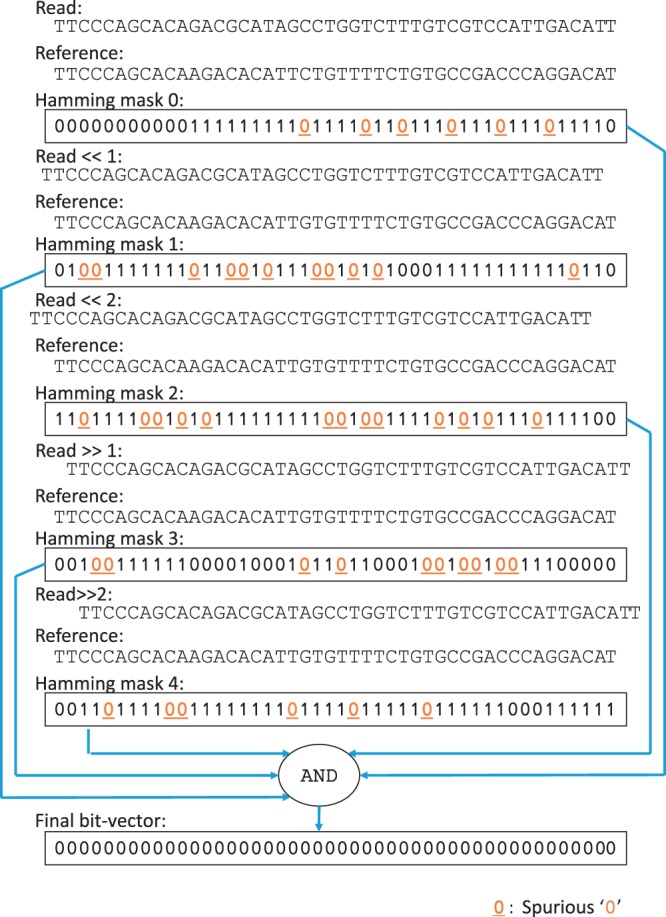
An example of an incorrect mapping that passes SHM. In this example, during the bit-wise AND operations, short streaks of ‘0’s at different locations in the Hamming masks overwrite (mask out) any ‘1’s in other Hamming mask that are at the same locations. As a result, the final bit-vector of SHM is full of ‘0’s. With SRS, streaks of ‘0’s that are shorter than three are marked as spurious and are subjected to removal later on

The false-positive rate of SHM increases superlinearly as e increases. Consider a random read and the reference pair, where each basepair in the read and reference are generated completely randomly (having 1/4 probability of being either A, C, G or T). The probability that a bp in the reference does not match any neighboring bp in the read during any of the $2e+1$ Hamming masks of SHM (hence rendering a ‘0’ at its position in the final bit-vector) is ${(3/4)}^{2e+1}$, which decreases exponentially as e increases. Therefore, when e is large, most basepairs in the reference find matches in the read during SHM, even if the read and the reference differ by more than e errors.

Some of the incorrect mappings that pass SHM can still be identified by checking if the read and the reference share large sections of identical substrings. According to our second observation, two strings that differ by e errors will share no more than e + 1 identical sections. These identical sections are simply the bp segments between errors. In fact, the goal of the entire local alignment (edit-distance) computation is to identify these identical sections and the errors between them. When basepairs of an identical section are aligned in SHM, all basepairs of this identical section in the read simultaneously match all basepairs in the reference, which produces a contiguous streak of ‘0’s in the Hamming mask (blue-highlighted region in Figure 1). Other ‘0’s in the Hamming masks (unhighlighted ‘0’s in the Hamming masks) that are not produced by an identical section represent only individual bp matches, which are not part of the correct alignment (the alignment produced by the local alignment computation) of the mapping. We call these ‘0’s spurious, as they conceal mismatch errors and give the false impression that the read and the reference have a small edit distance, even when they differ significantly.

We propose a heuristic, SRS, which aims to remove spurious ‘0’s. SRS uses one important observation: identical sections are typically long ($\ge 10$ bps) while streaks of spurious ‘0’s are typically short (<3 bps). This insight is confirmed empirically through experiments, but is also supported by theory. Given that for most mappers e is in general less than 5% of the read length L, the average length of an identical section is greater than 16 bps for, say, L = 80. ($l_{sec}\ge \frac{L}{0.05L+1}\approx 16$). The probability that a streak of n ‘0’s will be spurious (i.e. part of a random alignment between basepairs) is ${(1/4)}^n$. For streaks where n is greater than 3 bps, the probability of being spurious is below 1%.

Using this insight, we replace all streaks of ‘0’s in the Hamming masks that are shorter than three digits with ‘1’s. We call the ‘1’s that replace the ‘0’s (i.e. amended from ‘0’s) as amended ‘1’s. Amended ‘1’s do not affect the final bit-vector of the SHM as they are “transparent” during AND operations. The potential trade-offs and reasoning for choosing three as our threshold for SRS is discussed in Section 3.3. Note, the incorrect mapping which passed SHM in Figure 2 is identified and correctly rejected using SRS in Figure 3.

Fig. 3.

The incorrect mapping from Figure 2 is filtered correctly by SRS, since most of its short streaks of ‘0’s are turned into amended ‘1’s. Amended ‘1’s transparent during the AND operations

Since SRS amends all short streaks of ‘0’s, even the ones produced by correct alignments of basepairs, it could cause correct read mappings to be mistakenly filtered, as shown in Figure 4. To avoid this possibility, SRS counts the number of errors in the final bit-vector more conservatively than SHM. Each streak of ‘1’s in the final bit-vector could be the outcome of multiple streaks of amended ‘1’s. However, ‘0’s are changed only if they are two-or-fewer-bit ‘0’ streaks and are surrounded by ‘1’s. In the worst case, multiple back-to-back short identical sections that are separated by single errors can be mistakenly overwritten into a long streak of ‘1’s (e.g. 1001001 → 11111111). As a result, the number of errors covered by a streak of ‘1’s (e₁) of length l₁ after SRS is $e_1=1+[(l_1+1)/3]$. The streak of four ‘1’s in the final bit-vector of Figure 4 is now counted as only two errors rather than four and the correct mapping passes the filter. Using this counting scheme, we ensure all correct mappings will pass through the filter, while still identifying and removing read and reference pairs with errors up to 5% of the read length (results are provided in Section 4).

Fig. 4.

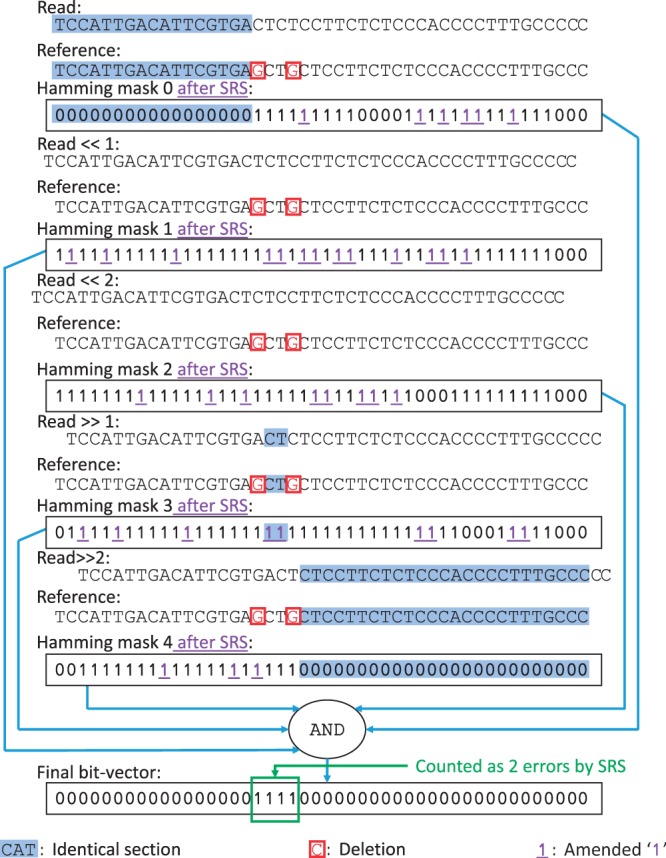
Correct short streaks of ‘0’s might also get overwritten by SRS. To avoid filtering out correct mappings, SRS counts the errors of a streak of ‘1’s in the final bit-vector conservatively, always assuming it was overwritten by a short streak of correct ‘0’s

SRS can be implemented using SIMD-friendly operations. As we explain in Supplementary Materials, the ability to implement SRS with SIMD instructions is crucial for the high performance of SHD, as it enables computing SRS in constant time with few instructions: both overwriting of short streaks of ‘0’s and counting the number of errors of streaks of ‘1’s can be computed in constant time using SIMD packed shuffle operations. See Section 1.3 in Supplementary Materials for details.

Combined with SHM, SRS and SHM form the two-step filtering algorithm SHD, which guarantees that correct read mappings are preserved, while quickly removing incorrect mappings with simple bit-parallel operations.

3.3 Analysis of SHD

3.3.1 Pseudocode

The pseudocode of SHD is shown in Algorithm 1. Overall, SHD computes $2e+1$ Hamming masks (ComputeHammingMask), with e of them computed with the read incrementally shifted to the left; e of them computed with the read incrementally shifted to the right, and one computed without any shifts. Each Hamming mask is then processed by SRS to amend short streaks of ‘0’s into ‘1’s (SRS_amend). Finally, all Hamming masks are merged together into a final bit-vector through bit-wise AND operations and a lower bound of errors is computed from the final bit-vector (SRS_count). Details of implementations of ComputeHammingMask, (SRS_amend) and SR S_count are discussed in Supplementary Materials.

3.3.2 False Negatives

SHD never filters out correct mappings; hence, it has a zero false-negative rate. As we discussed in Section 3.2, identical sections longer than 3 bps are recognized and preserved in the final bit-vector by SHD. Identical sections shorter than 3 bps are amended into ‘1’s; however, SHD counts ‘1’s in the final bit-vector conservatively, ensuring correct mappings are not filtered.

3.3.3 False Positives

SHD does allow a small portion of incorrect mappings to pass the filter as false positives. This is acceptable since SHD is only a filter. Incorrect mappings that pass SHD are discarded later by more rigorous edit-distance calculations. Below, we describe two major sources of false positives, both of which are related to the threshold of the SRS (the minimal length of a streak of ‘0’s that will not be amended by SRS).

First, long streaks of spurious ‘0’s are not identified by SRS. Although less likely, long streaks of ‘0’s can still be spurious (i.e. identical substrings between the read and the reference that do not belong to the correct alignment between the read and the reference). Long spurious streaks of ‘0’s in an incorrect mapping can mask out real errors (‘1’s in other Hamming masks) and produce a mostly ‘0’ final bit-vector even though the read and the reference differ by more errors. We can increase the SRS threshold beyond three bps, which amends longer streaks of ‘0’s, to reduce such false positives.

Second, SRS may underestimate the number of errors while examining the final bit-vector. SRS always assumes the worst case where any streak of ‘1’s in the final bit-vector is the result of amending short streaks of spurious ‘0’s, despite the possibility it could be a sequence full of real errors. When counting streaks of ‘1’s, SHD only assigns the minimal number of errors required to produce the pattern (e.g. 1001111 → 11111111 → 1001001 three errors counted when five errors are present). By always assuming the worst case, SHD may underestimate the number of errors in the final bit-vector and let incorrect mappings pass the filter. Although using a smaller SRS threshold would help filter out such false positives, it would also let long streaks of spurious ‘0’s pass the filter as we described in the previous paragraph. As a result, a carefully chosen SRS threshold should consider both factors: it should neither be too small to omit long spurious ‘0’s nor should it be too large to underestimate the number of errors. Figure 5a shows this dilemma, as the false-positive rate first drops and then slowly increases as SRS threshold increases. In this article, we chose three as our SRS threshold because: 1, the false-positive rate of SHD drops below 2% (with the configuration of e = 3) at three and remains steady afterwards and 2, with Intel SSE platform we are only able to provide an efficient implementation of SHD with an SRS threshold no-more-than three (further elaborated in Supplementary Materials).

Fig. 5.

A sweep of the false positive rate of SHD, against variant allowed error rate [(a), under a fixed SRS threshold of three bps] and variant SRS thresholds [(b), under a fixed allowed error rate of 3%], respectively. The sweep is produced with the first one billion potential mappings analyzed by mrFAST when it maps the read set ERR240728 from the 1000 Genomes Project (1000 Genomes Project Consortium 2012) under an error threshold of 3 bps

A sweep of the false-positive rate of SHD against variant allowed error rate (error threshold divide by read length) is shown in Figure 5b. While the false-positive rate of SHD increases with larger allowed error rate, at 5% error rate (which is the upper limit of most available mappers (Ahmadi et al., 2011; Alkan et al., 2009; Delcher et al., 1999; Langmead and Salzberg 2012; Li and Durbin 2010; Li et al., 2009; Rumble et al., 2009; Weese et al., 2012), the false-positive rate of SHD is only 7%, indicating a high accuracy ($>93\%$) of the filter.

4 Results

We implemented SHD in C, using Intel SSE. We compared SHD against three edit-distance calculation/filtering implementations, they are: SeqAn (Döring et al., 2008), an implementation of Gene Myers’s bit-vector algorithm (Myers 1999); swps3 (Szalkowski et al., 2008), a Smith-Waterman algorithm (Smith and Waterman 1981) implementation; and FastHASH (Xin et al., 2013), an Adjacency Filtering (AF) implementation. Both SeqAn and swps3 are also implemented with SSE and all implementations were configured to be single threaded.

We used a popular seed-and-extend mapper, mrFAST (Alkan et al., 2009), to retrieve all potential mappings (read-reference pairs) from 10 real datasets from the 1000 Genome Project Phase I (1000 Genomes Project Consortium 2012). Table 1 lists the read length and read size of each set. Each read set is processed using multiple error thresholds (i.e. e from 0 to 5 errors).

Table 1.

Benchmark data, obtained from the 1000 Genomes Project Phase I (1000 Genomes Project Consortium 2012)

	ERR240726_1	ERR240726_2	ERR240727_1	ERR240727_2	ERR240728_1
No. of Reads	4031354	4031354	4082203	4082203	3894290
Read Length	101	101	101	101	101
	ERR240728_2	ERR240729_1	ERR240729_2	ERR240730_1	ERR240730_2
No. of Reads	43894290	4013341	4013341	4082472	4082472
Read Length	101	101	101	101	101

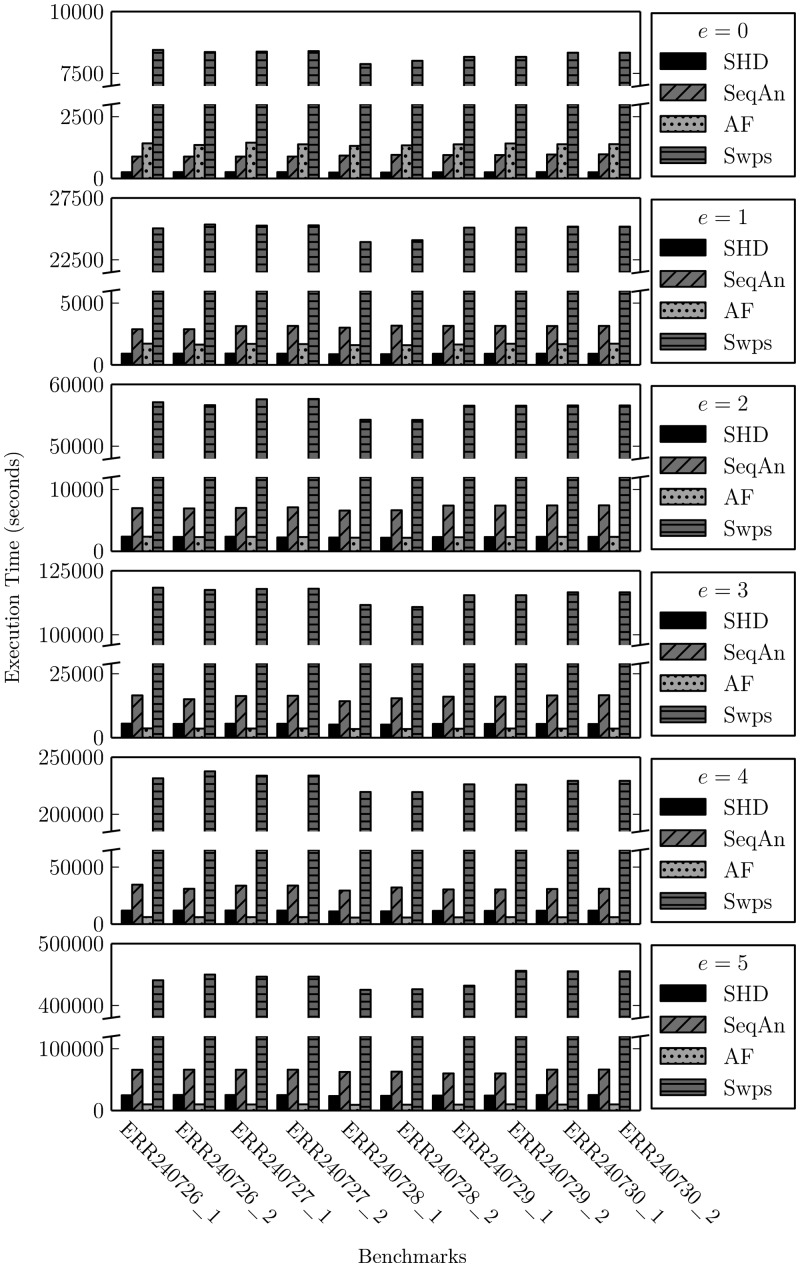
We benchmarked all four implementations using the same potential mappings (i.e. seed hits) produced by mrFAST for a fair comparison of the four techniques. Figure 6 shows the execution time of the four techniques with different error thresholds across multiple read sets. Notice that when the indel threshold is zero, SHD reduces to bit-parallel Hamming distance. A detailed comparison against bit-parallel Hamming distance implementation is provided in Supplementary Materials, Section S1.3.

Fig. 6.

The execution time of SHD, SeqAn, swps3 and FastHASH (AF) with different error thresholds (e) across multiple read sets

Among the four implementations, SHD is on average $3\times$ faster than SeqAn and $24\times$ faster than swps3. Although SHD is slightly slower than FastHASH (AF) when e is greater than two (e.g. $2.5\times$ slower when e = 5), SHD produces far fewer (on average, $0.25\times$) false positives than FastHASH (seen in Figure 7). Note, the speedup gained by SHD diminishes with greater e. This is expected since the number of bit-parallel/SIMD operations of SHD increases for larger e.

Fig. 7.

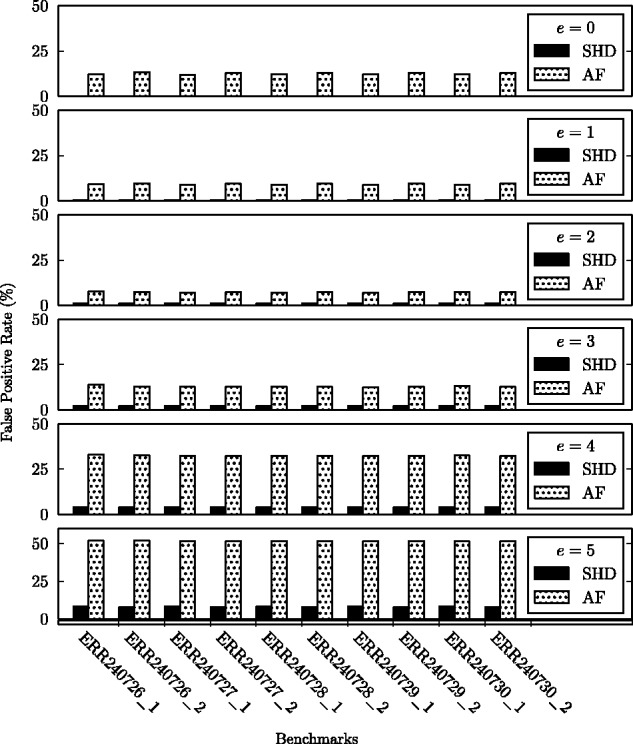
The false-positive rates of SHD and FastHASH (AF) with different error thresholds (e) across multiple read sets

Figure 7 illustrates the false-positive rates of SHD and FastHASH (AF). SeqAn and swps3 both have a 0% false-positive rate, compared with SHD which has a 3% false-positive rate on average. That being the case, SHD is only a heuristic to filter potential mappings while both SeqAn and swps3 must compute the exact edit distances of the potential mappings.

As we discussed in Section 3.3, the false-positive rate of SHD increases with larger e. Nonetheless, the false-positive rate of SHD at e = 5 is only 7%, much smaller than the false-positive rate (50%) of FastHASH (AF) as Figure 7 shows.

With these results, a mapper can selectively combine multiple implementations together to construct an efficient multi-layer filter/edit-distance calculator. For instance, a mapper can attach SHD with FastHASH, to obtain both the fast-speed of FastHASH and the high accuracy of SHD. A mapper can also combine SHD with SeqAn to obtain 100% accuracy without significantly sacrificing the speed of SHD. Of course, there are many possibilities to integrate SHD into a other mappers, but a comprehensive study of this topic is beyond the scope of this article and is part of our future work.

5 Conclusion

Most potential mappings that must be verified by seed-and-extend-based mappers are incorrect, containing far more errors than what is typically allowed. Our proposed filtering algorithm, SHD, can quickly identify most incorrect mappings (through our experiment, SHD can filter 86 billion potential mappings within 40 min on a single thread while obtaining a false-positive rate of 7% at maximum), while preserving all correct ones. Comparison against three other state-of-the-art edit-distance calculation/filtering implementations revealed that our Intel SSE implementation of SHD is $3\times$ faster than SeqAn (Döring et al., 2008), the previous best edit-distance calculation technique.

Funding

This study is supported by NIH Grants (HG006004 to O. Mutlu and C. Alkan, and HG007104 to C. Kingsford) and a Marie Curie Career Integration Grant (PCIG-2011-303772) to C. Alkan under the Seventh Framework Programme. C. Alkan also acknowledges support from The Science Academy of Turkey, under the BAGEP program.

Conflict of Interest: none declared.