Temporal contingency

Abstract

Contingency, and more particularly temporal contingency, has often figured in thinking about the nature of learning. However, it has never been formally defined in such a way as to make it a measure that can be applied to most animal learning protocols. We use elementary information theory to define contingency in such a way as to make it a measurable property of almost any conditioning protocol. We discuss how making it a measurable construct enables the exploration of the role of different contingencies in the acquisition and performance of classically and operantly conditioned behavior.

The concept of contingency has long been a shadowy presence in theoretically oriented discussions of classical (i.e., Pavlovian) and operant conditioning. In the operant-conditioning literature, many authors have observed that operant conditioning depends on the reward, or desired state of affairs being delivered contingent on a response of some particular kind (see Skinner, 1938; Thorndike, 1932). Similarly, in the Pavlovian-conditioning literature, many authors have observed that a classically conditioned response (CR) develops when the occurrence of the unconditioned stimulus (US; i.e., a reinforcer) is contingent on (conditioned on) the occurrence of the conditioned stimulus (CS; see Pavlov, 1927; Rescorla and Wagner, 1972). Its presence is, however, shadowy, because it has never been defined in such a way as to be generally useable; in consequence of which, it has never been a measurable aspect of most conditioning protocols and/or of the behavior-events relations that emerge when animals are exposed to conditioning protocols.

For the most part, contingency has been taken to be reducible to temporal pairing. Skinner (1948, p. 168) expressed a common conviction when he wrote: “To say that a reinforcement is contingent upon a response may mean nothing more than that it follows the response. It may follow because of some mechanical connection or because of the mediation of another organism; but conditioning takes place presumably because of the temporal relation only, expressed in terms of the order and proximity of response and reinforcement.” Rescorla (1967) gives a lengthy discussion of the issue of temporal pairing versus contingency from a theoretical and historical perspective.

The attraction of treating contingency as reducible to temporal pairing is that there should not be in principle a problem with operationalizing the concept of temporal pairing. Events are temporally paired if and only if they consistently occur together within some critical interval. Thus, we should be able to operationalize the concept of temporal pairing by determining empirically what the critical interval is and how consistently (i.e., with what probability) the times of occurrences of the two events have to fall within that interval in order for the brain (of some species) to treat them as temporally paired. In the event, however, a century of experimental work on simple associative learning has failed to determine the critical interval for any two events in any species in any classical- or operant-conditioning protocol (Rescorla, 1972; Gallistel and Gibbon, 2000). The concept of temporal pairing has eluded empirical definition. A fortiori, there has been no determination of what constitutes consistent temporal pairing.

The importance of distinguishing between contingency and temporal pairing was made clear by Rescorla’s experiments with a truly random control (Rescorla, 1968; see Fig. 1). In this experiment, Rescorla showed that contingency was not reducible to temporal pairing and that, when one tested whether it was temporal pairing or contingency that led to the emergence of conditioned responding in a Pavlovian conditioning protocol, it was contingency and not temporal pairing. This well known experiment did not, however, succeed in bringing the concept of contingency out of the theoretical shadows, because it continued to be a nebulous, undefined concept. If it was not temporal pairing, what was it? Could it be measured?

Fig. 1.

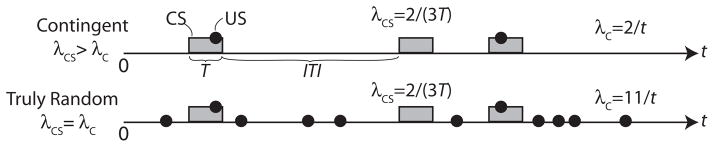
Schematic of Rescorl (1968) experiment distinguishing CS–US pairing from CS–US contingency. The temporal pairing of CS and US is the same in both conditions, but there is a CS–US contingency in the top protocol and none in the bottom protocol. Rats developed a conditioned response to the CS only when run in the top protocol.

What many researchers, including Rescorla, took away from Rescorla’s experiment was that contingency in Pavlovian conditioning was p(R|CS)/p(R), where R denotes reinforcement and CS the presence of a conditioned stimulus. In words, contingency is the probability of reinforcement given the conditioned stimulus divided by the unconditional probability of reinforcement. This notional definition is readily extended to the operant case by writing p(R|r)/p(R), where r denotes a response. The problem with this conclusion is that it takes no account of time; hence, both the unconditional and the conditional probabilities are undefined.

To see the problem, one need only ask what the unconditional probability of reinforcement was in Rescorla’s experiment, or, for that matter, what the conditional probability was. Although Rescorla’s experiment has generally been discussed in terms of the differential probability of reinforcement, what Rescorla in fact did was vary the rate parameter of a Poisson (random rate) process as a function of whether the conditioned stimulus was or was not present. Rate, unlike, probability, has a temporal dimension; it is number per unit time. Rates can be converted to probabilities only by integration—integration over some interval—and the result depends on the interval. Thus, the question, what is the probability of reinforcement given some random rate? is ill posed; it has no answer. One can ask what the probability is that reinforcement will occur within some interval, for example within one of the 2-min intervals during which the conditioned stimulus in Rescorla’s experiment was present. However, even this question is not well posed, because it does not specify what we understand by ‘the occurrence of reinforcement’: Does it matter how many reinforcers occur within the specified interval? Are two or even three shocks during one CS presentation to be regarded as no different from only one shock? The same indeterminancies arise when we attempt to apply the above intuitive definition of contingency to the operant case.

Intuitively, contingency is closely related to correlation. However, the conventional measures of correlation assume that co-occurrence, that is, the pairing of x and y observations has already been determined; the only question is whether variation in the x values predict variation in the y values with which they are paired.

Measures of contingency in the psychological literature are derived from 2 × 2 contingency table (Table 1). Several have been used, but only two have suitable mathematical properties, such as ranging from 0 to 1 and not depending on the number of observations (for a review, see Gibbon et al., 1974). Both of these are properties of the correlation coefficient, but that measure cannot be computed for dichotomous variables. For dichotomous variables, Pearson’s mean square coefficient of contingency

Table 1.

2 × 2 contingency table.

	#USs	#~USs	Row totals
#CSs:	a	b	a + b
#~CSs:	c	d	c + d
Col totals:	a + c	b + d

$$\varphi =\sqrt{{\chi }^2/N}=\sqrt{\frac{{(ad-bc)}^2}{(a+b)(c+d)(a+c)+(b+d)}}$$

is recommended by Gibbon et al. (1974) and others, while the difference in the conditional probabilities of the US,

$$\mathrm{\Delta }P=p(\text{US}\mid \text{CS})-p(\text{US}\mid ~\text{CS})=\frac{a}{a+b}\frac{c}{c+d}$$

has been used extensively in studies of human contingency and causality judgment (see, for example Allan et al., 2008).

There is, however, no unproblematic way to construct a contingency table in Pavlovian conditioning experiments, because they do not reliably have an empirically definable trial structure (Gallistel and Gibbon, 2000). The problem comes into strong relief when one considers how to construct the contingency table for Rescorla’s (1968) experiment schematized in Fig. 1. In that experiment, the CS lasted 2 min each time it occurred. The intervals between CS offsets and CS onsets varied around an average of 10 min. There is no doubt about how many CSs and USs there were, nor whether a given US occurred while the CS was present, so the first cell (a in Table 1) is no problem. All the other cells are problematic, because there is no objectively justifiable answer to the question, “How many not-USs and how many not-CSs were there and when did they occur?”

One approach to dealing with this problem is to suppose that the brain divides continuous time into a continual sequence of discrete “trials.” This is what Rescorla and Wagner (1972) assumed in their analysis of the experiment by Rescorla (1968) schematized in Fig. 1. They assumed that the protocol in Fig. 1 could be treated as consisting of a sequence of 2-min-long pseudo-trials, one immediately succeeding the other. During each pseudo-trial a US either occurred or it did not occur, and likewise for a CS. Thus, for example, if during one such fictitious trial, neither a US nor a CS occurred, then, for the purpose of constructing a contingency table, this would count as a “trial” on which one ~CS and one ~US occurred. They do not say how they scored pseudo-trials on which more than one US occurred.

The problem with this approach is obvious. It is impossible to say how often something does not occur. It is impossible to say, for example, how many not earthquakes London experienced in the year just passed. Without objectively defined trials, ~USs and ~CSs have no objectively definable relative frequency. This problem is even more acute in the case of operant conditioning, because in those protocols, there are often no trials of any kind, in the sense in which ‘trial’ is understood in the literature on classical conditioning. Thus, for example, it is impossible to say how many not-reinforcers occurred during an inter-reinforcement interval in an operant conditioning protocol.

A second problem with measures based on a contingency table, and with the correlation coefficient as well, is that they take no account of time. They do not do so, because they assume that the pairing of two events—which instances of one event are paired with which instances of the other—has already been determined. The contingencies of ordinary experience, however, are defined over time, and the temporal intervals between the events are centrally relevant to the psychological perception of contingency and causality. A psychologically useful measure of contingency must take into account the intervals between events.

The cross-correlation function does take time into account. It computes the correlation between two events as a function of the displacement in time of one event record relative to that of the other. Its computation, however, presupposes that time can be divided into discrete bins, because the two records are stepped relative to one another bin by bin, and the computation of the correlation coefficient at any given step treats the events in aligned bins as co-occurrences (i.e., x–y pairs). The results of a cross-correlation computation depend strongly on the choice of bin widths. To apply this to the analysis of contingency in conditioning paradigms, one would need to know the brain’s temporal bin widths. Knowing this is analogous to knowing what the brain regards as “close” in time; two events are “close” or “contiguous” or “concurrent” just in case they fall within the same time bin. As already noted, attempts to determine experimentally how wide such a bin might be have failed.

What is needed for contingency to emerge from the theoretical shadows is a definition that: (1) makes it measurable; (2) takes time into account; (3) can be applied to any kind of suggested contingency; and (4) does not depend fundamentally on an arbitrary discretization of continuous time (time bins). Information theory provides such a definition.

1. An information-theoretic definition of temporal contingency

Information (aka entropy) is a computable property of a probability distribution, just like its mean or its variance. A probability distribution associates probabilities or probability densities with the possible values for some variable. The possible values are called the support for the distribution. The entropy of the distribution, denoted H, is the probability of each possible value times the logarithm of its inverse:

$$H=\sum _i{p}_{i}log\left(\frac{1}{p_i}\right),$$

where i indexes the possible values of the support for the distribution.

When only one value is possible, the associated probability is 1, and the “distribution” has 0 entropy. In such a case, there is no information to be gained about the value of the support variable. The information available from that source is therefore 0. The more values a variable can assume and the more nearly equal their relative frequency, the greater the entropy of the probability distribution; hence, the more information there is to be gained from learning the current value of the support variable.

Events convey information about one another to the extent that knowledge of one event reduces our uncertainty about the other. This is Shannon’s (1948) definition of the amount of information that the signal events processed by a receiver convey about a source variable. The receiver’s average information gain from the signal events is measured by the difference in entropy between the receiver’s probability distribution on the source variable in the absence of the signal and its probability distribution in the presence of the signal. The entropy of the former measures the receiver’s uncertainty in the absence of a signal. This entropy is the upper limit on how much information the receiver can gain about that source. We will call this the basal entropy and denote it by H_b. We call the entropy of the receiver’s distribution given the signal the residual entropy and denote it by H_r. The proposed information-theoretic measure of contingency is:

$$C=\frac{(H_{\mathrm{b}}-H_{\mathrm{r}})}{H_{\mathrm{b}}}.$$

Consider, for example, pellets that are released into a feeding hopper by an approximation to a Poisson (random rate) process, with rate parameter, λ. The distribution of inter-pellet intervals is exponential with expectation μ = 1/λ. Its entropy is k log(1/λ) = k log(μ), where k is a scaling factor whose value is determined by the temporal resolution. This resolution-dependent scaling factor cancels out of the contingency measure, because it appears in both the numerator and the denominator, so we drop it from here on. The entropy of the inter-pellet interval (IPI) distribution is an example of a basal entropy. This entropy is commonly called the available information or the source information. It measures the uncertainty about when to expect the next pellet, in the absence of any other events that convey information about the timing of pellet release, including previous pellet releases.

Suppose, now, that there are such other events. Suppose, for example, that a brief tone precedes every pellet release by 1 s. The distribution of intervals from tone onset to pellet release has no entropy, because there is only one such interval. The objective contingency between tone onset and pellet release—the contingency for an observer with perfect timing—is 1, because for such an observer, the residual entropy is 0, so

$$C=\frac{(log(1/\mathrm{\lambda })-0)}{log(1/\mathrm{\lambda })}=1$$

For an animal observer, the residual entropy is not 0, because brains represent temporal intervals with scalar uncertainty (Gibbon, 1977; Killeen and Weiss, 1987). Thus, we may take the residual entropy to be the entropy of a normal distribution¹ whose standard deviation is proportional to the duration, d:

$$H_{\mathrm{r}}=H_{\mathrm{n}}(d,w)=.5log(2\pi \mathit{ewd}),$$

where w is the temporal Weber fraction and H_n(d, w) denotes the entropy of a normal distribution with mean d and coefficient of variation, w. Because the Weber fraction, w, is small (on the order of .16; Gallistel et al., 2004), the residual subjective entropy is small. For a fixed residual subjective entropy, the subjective contingency between CS and US depends on the expected interval between pellets; the larger the IPI, the stronger this subjective contingency is. Assuming w = 0.16 and an expected IPI of 10 s (and a tone-release interval of 1 s), the subjective tone-release contingency is 0.78. If we increase the expected IPI to 100 s, the tone-release contingency is 0.89. As the basal entropy, which appears in both the numerator and the denominator, becomes arbitrarily large, the contingency ratio becomes arbitrarily close to 1.

Suppose, now, that the experimental protocol schedules tones using a Poisson process with rate parameter λ, but on each tone “trial” it releases pellets with probability p(R|CS). In traditional parlance, we partially reinforce the tone. Doing so lengthens the expected IPI by 1/p(R|CS)—see Fig. 2. This increases by log(1/p(R|CS)) = −log(p(R|CS)) the basal uncertainty, H_b, about when the next pellet release will occur, which uncertainty is the denominator of the contingency ratio. Partial reinforcement increases the residual uncertainty, H_r, as well, which is the other term in the numerator of the contingency ratio. It does so because it introduces uncertainty about whether a pellet will be released at the conclusion of any given tone occurrence. The uncertainty about whether a pellet release will occur following a tone is independent of the uncertainty attendant on the application of the Weber fraction to the fixed delay between tone onset and pellet release. The entropies from independently distributed sources of uncertainty are additive. Therefore, the residual subjective entropy is the entropy of the normally distributed subjective uncertainty about when exactly pellet release will occur following tone onset, if it does occur on this presentation, plus the entropy of the distribution of trials-to-pellet release. This latter distribution is geometric with parameter p(R|CS)—see Fig. 3. The entropy of a geometric distribution is log(1/p(R|CS)). Thus, when we apply the information-theoretic measure of contingency, we have:

$$\begin{array}{l}{C}_{\text{US},\text{CS}}=\frac{H_{\mathrm{b}}+log(1/p(\mathrm{R}\mid \text{CS}))-(H_{\mathrm{n}}+log(1/p(\mathrm{R}\mid \text{CS})))}{H_{\mathrm{b}}+log(1/p)}\\ =\frac{H_{\mathrm{b}}-H_{\mathrm{n}}}{H_{\mathrm{b}}+log(1/p(\mathrm{R}\mid \text{CS}))}\end{array}$$ (1)

Fig. 2.

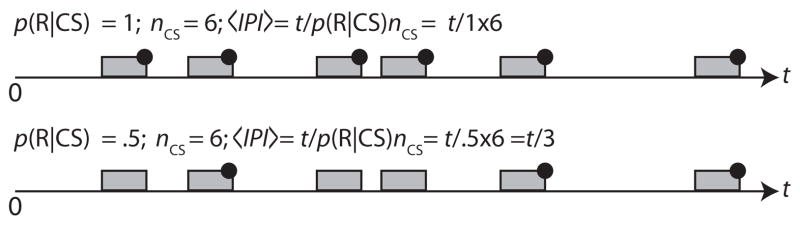
Partial reinforcement of a random fraction of the CS presentations lengthens the average interval between pellets, 〈IPI〉, by the reciprocal of the partial reinforcement fraction, that is, by 1/p(R|CS). This increases the basal entropy, the denominator of the contingency ratio, but it has no effect on the numerator of that ratio, which is the information about when to expect the US that the onset of the CS conveys. When to expect the US is altered only by whether the US will occur during this CS presentation. That source of uncertainty is independent of the uncertainty about when the US will occur if it occurs during this presentation, so the two entropies (the whether and when measures of uncertainty) combine additively (see Eq. (1)).

Fig. 3.

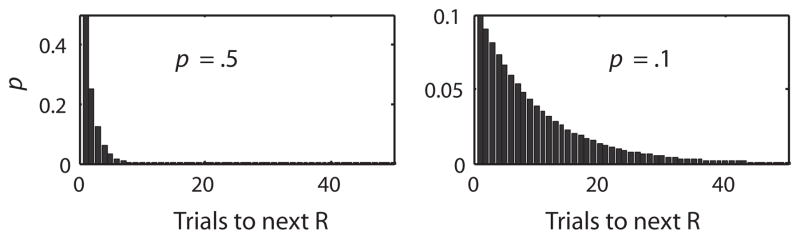
Geometric distributions for two different partial reinforcement schedules. A geometric distribution associates with successive future trials (e.g., future tones) the discrete probability that reinforcement will occur on that trial. The entropy of a geometric distribution is log(1/p(R)), where p(R) is the probability of a reinforcer on any given trial. Note that 1/p(R) is the expected number of trials to a reinforcer, just as 1/λ is the expected interval to the next reinforcer in a variable–interval protocol. The formula for the entropy of a geometric distribution is very similar to the formula for the entropy of an exponential distribution because the geometric distribution is the discrete approximation to the exponential distribution.

We see from Eq. (1) that partial reinforcement increases the denominator of the contingency ratio by log(1/p(R|CS)) while having no effect on the numerator. Therefore, partial reinforcement reduces the tone-pellet contingency, as one would expect.

The numerator in Eq. (1), which is unaffected by the partial reinforcement, is the information about US timing conveyed by the onset of a conditioned stimulus. Thus, partial reinforcement degrades the contingency between the conditioned stimulus and the unconditioned stimulus, but it does not diminish the information about US timing conveyed by the onset of a CS. Surprisingly, partial reinforcement has little or no effect on the number of reinforced presentations of the conditioned stimulus required for the appearance of a conditioned response (Williams, 1981; Gottlieb, 2004; Harris et al., 2011; Harris, 2011). Thus, it would appear that what matters for the acquisition of a conditioned response in a Pavlovian paradigm is not the CS–US contingency but rather how informative the onset of the CS is about how soon to expect the US (Balsam and Gallistel, 2009).

So far, we have considered only predictive contingency, but there are reasons to consider also retrospective contingency. We will want to do so most particularly when we come to consider the assignment of credit problem in operant conditioning (Staddon and Zhang, 1991). This is the problem of computing what one did that produced the reinforcer that has just been delivered. We introduce the concept of retrospective contingency here, because the predictive tone-pellet contingency is not the same as the retrospective pellet-tone contingency. When we consider the retrospective contingency, the basal entropy is the entropy of the intervals looking backward from one tone to the preceding tone (rather than forward from one pellet release to the next release). The distribution of these retrospective inter-tone-intervals (ITI’s) is the same as that of the IPI’s; it is exponential with parameter λ. Therefore, the basal entropy in the denominator of the retrospective contingency ratio is the same as in the denominator of the prospective contingency ratio already considered. The numerator, though, is another story. When we come to consider how well pellet releases retrodict tones, the distribution we consider in computing the residual entropy is the distribution of intervals looking backward from pellet releases to the first preceding tone. The distribution of these intervals has no entropy, regardless of the value of the partial reinforcement parameter, p(R|CS), because a tone invariably precedes every pellet release by 1 s.

By developing a measure of contingency, we have deepened and refined our understanding of what we might mean by it. To our knowledge, in discussing the contingency between events A and B (say, between CS and US events), no one previously has distinguished between the predictive contingency and the retrospective contingency. Because time was not present in previous conceptions of contingency, the distinction between prediction and retrodiction could not be made. This distinction becomes even more central when we turn to operant conditioning, as we now do.

Consider a pigeon pecking a key on a variable-interval (VI) schedule. On this schedule, the duration of the interval from one reinforcer to the next (denoted IRI) is approximately exponentially distributed. The inter-response intervals (iri’s) are much shorter than the IRI’s, so most responses (i.e., pecks) do not bring up the grain hopper. Every now and then, however, a peck does bring it up, with a very short fixed delay (.01 s). We pose the question, what is the response–reinforcement contingency in this protocol? We show that there are different ways to define it, depending on what one imagines is relevant to the observed behavior. The information-theoretic formula applies to each different way of defining it, giving us several different contingency measures. Thus, one can ask which measures, if any, predict the observed behavior. In this way, we address quantitatively the role of contingency in operant behavior.

The first contingency is the same as the one we first considered in discussing the prospective contingency between a CS (the tone) and a US (pellet release) in classical conditioning, only we replace CS onset times with response times. The basal entropy in the denominator of the contingency ratio is the entropy of the distribution of IRI’s (inter-reinforcer intervals). The residual entropy is the entropy of the distribution of r→R intervals (response-reinforcer intervals), where r denotes the time at which a response occurs and R the time at which the next reinforcer occurs.

For the r→R distribution, we go through the data peck by peck. We find for each peck the interval to the next reinforcer, ignoring any intervening pecks. We make a histogram of these intervals, normalize the counts to obtain an empirical discrete probability distribution, and apply Shannon’s formula bin by bin. To obtain a comparable empirical distribution for the basal entropy in the denominator, we take the record of reinforcement times, sprinkle on the time line as many random points as there were pecks, and find for each randomly chosen point in time the interval to the next reinforcer. From this tabulation we get an empirical probability distribution with the same bin widths as the empirical distribution of r→R intervals. We call these t→R distributions, where t denotes a randomly chosen moment in time.

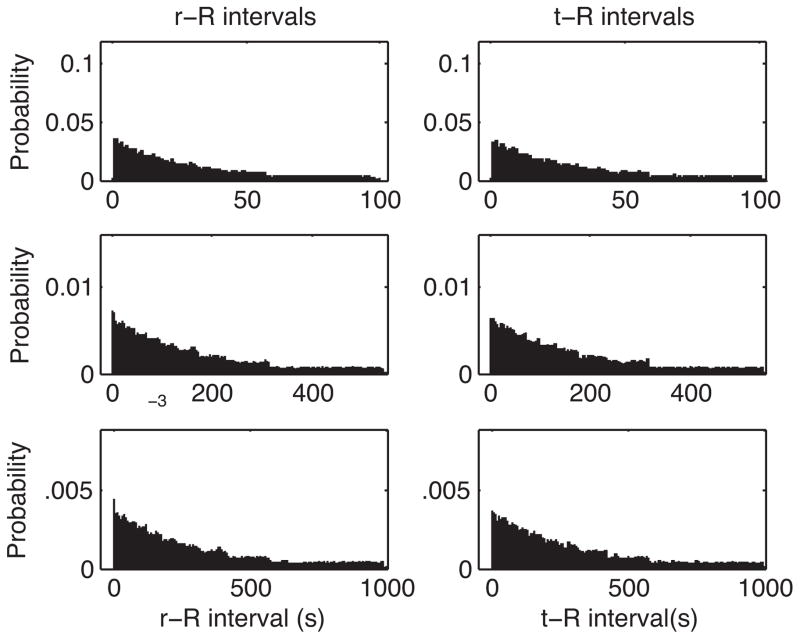
In the Shahan lab, we ran 8 pigeons on VI schedules with expected intervals of 30, 165, and 300 s, for 10 sessions at each expected interval. Representative r→R and t→R distributions from this experiment are shown in Fig. 4. Over an order of magnitude variation in VI, the r→R distribution is almost indistinguishable from the t→R distribution, which means that there is no prospective contingency between response and reinforcer delivery in a VI schedule of reinforcement. The residual entropies, which is to say the entropies of the r→R distributions, are the same as the basal entropies (the entropies of the t→R distributions). Thus, the numerators of the contingency ratios are 0, and the contingencies themselves are therefore 0.

Fig. 4.

Representative empirical distributions of r→R (peck time→reinforcer time) and t→R (random time→reinforcer time) intervals for one bird responding on VI schedules of reinforcement. Top row: VI 30 s. Middle row: 165 s. Bottom row: VI 300 s. The bin width in these histograms, for a given VI, is the same for both the r→R and the t→R distribution. It appears as a scale factor in both the numerator and the denominator of the contingency ratio. Therefore, it does not affect the contingency ratio (in the limit as the data sample gets large enough to put several counts in the bin with the fewest counts, as is the case in these normalized histograms).

The question arises: If there is no measurable prospective contingency between pecks and reinforcement—that is, if making a peck does not alter by any measurable amount the probability of reinforcement at any particular time in the future—then why do the birds peck? One possible answer is that there is a contingency between rate of pecking and rate of reinforcement. If pecking were very slow, so that the average inter-peck interval was much longer than the expectation of the VI schedule, then there certainly would be such a contingency, because almost every peck would produce a reinforcer; therefore, as the rate of pecking increased, so would the rate of reinforcement.

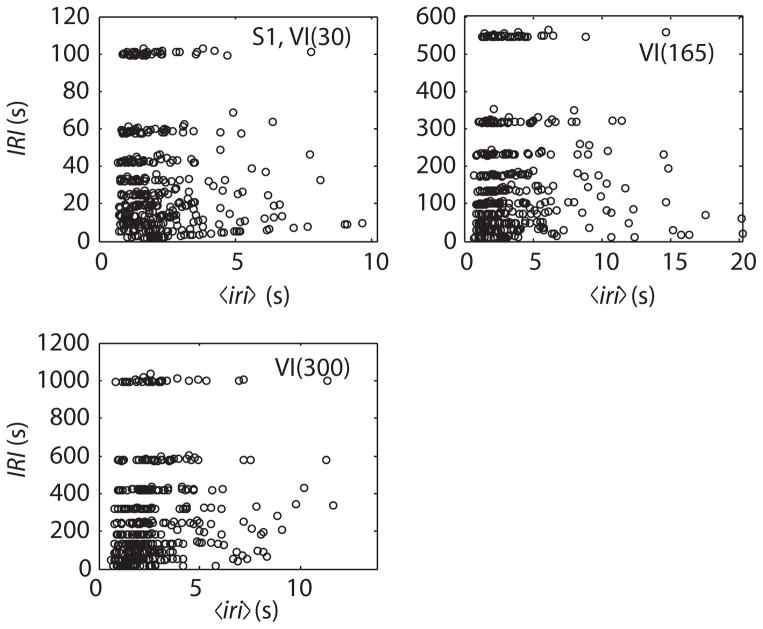
To estimate this contingency, we consider the joint distribution between the iri’s and the IRI’s. The support for a joint distribution is the set of all possible combinations of values for two variables. In this case, every IRI yields such a combination, because one can associate with every IRI a mean iri, namely the average interval between responses during the interval from the preceding reinforcer to the current reinforcer. We denote the average inter-response interval during an IRI by 〈iri〉 Empirically, for every reinforcer, we note the interval elapsed since the previous reinforcer, and we note the number of pecks, n_p, that occurred during that interval. The 〈iri〉 associated with that IRI is the IRI/n_p. This analysis of the record of peck and reinforcement times produces a (non-arbitrary) pairing of IRI’s and 〈iri〉’ s. The shorter the 〈iri〉, the faster the bird pecked during that IRI. Fig. 5 shows the three joint distributions for a representative bird when plotted against linear axes, while Fig. 6 shows them when plotted against log–log axes.

Fig. 5.

Representative joint distributions of Inter-Reinforcement Interval durations (IRI) and their associated mean inter-response intervals, 〈iri〉, from one bird responding for several sessions each on 3 different Variable Interval (VI) schedules, plotted against linear axes. The discrete character of the IRI’s arises from the way the VI schedules were implemented: The interval to the setting up of the next reinforcer was drawn from a uniform discrete probability distribution on a set of 10 intervals with equal logarithmic separations. The first peck after this interval elapsed delivered the reinforcer.

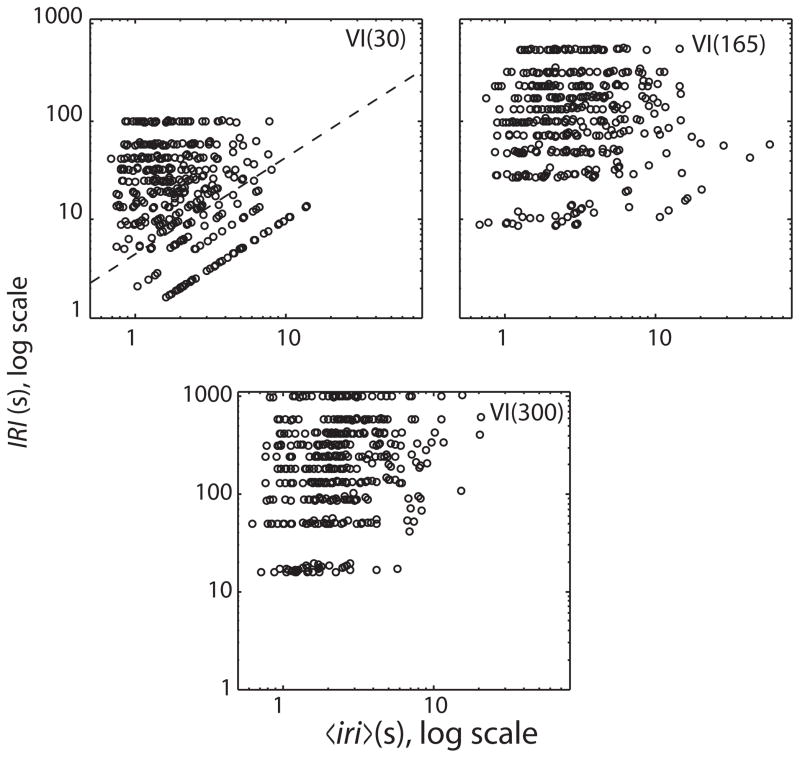
Fig. 6.

Same data as in Fig. 5, plotted against double logarithmic axes. The dashed diagonal line in the upper-left panel separates a portion that shows a strong prospective contingency between the mean iri and the IRI (below the line) from a portion that shows only weak contingency. This portion is largely missing from the upper right panel and missing altogether from the lower panel. Note that the locations of the IRI streaks move up as the VI-schedule parameter increases, whereas the location of the high density of mean iri’s remains roughly constant.

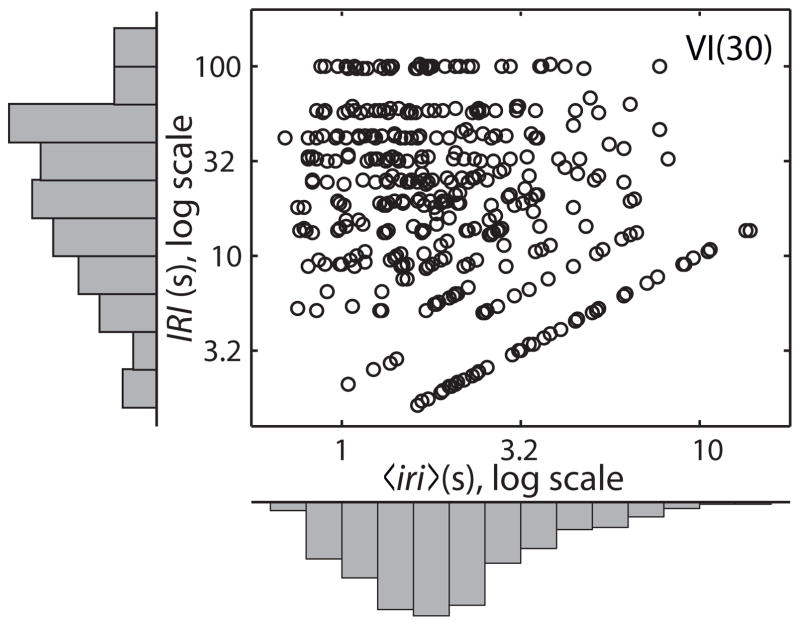
The information-theoretic measure of contingency tells us the extent to which the uncertainty in a conditional distribution differs from the uncertainty in an unconditional distribution. So far, the unconditional entropy has been the entropy of the distribution of intervals from randomly chosen points in time to the reinforcer (or response) first encountered as one looks forward (or backward) in time from that randomly chosen point. The conditional entropy has been that of the distribution of intervals looking forward or backward in time from either a response or a reinforcer. The points in time from which one looks forward or backward have no duration; that is, they are not themselves random variables. By contrast, both the intervals between reinforcers, the IRI’s, and the mean intervals between responses within an IRI, that is, the 〈iri〉’ s, are both random variables. When we ask to what extent the IRI is contingent on the 〈iri〉, we ask whether the distributions of IRI’s conditioned on the choice of smallish segments of the 〈iri〉 axis differ from the unconditioned distribution of IRI’s; that is, does p(IRI|〈iri〉_i) differ noticeably in shape or location from p(IRI|〈iri〉_j) for some choices of i and j? The unconditional distribution of IRI’s, p(IRI), is called the marginal distribution, because it is obtained by summing (or integrating) the joint distribution along the 〈iri〉 axis. This summing or integrating may be thought of as a kind of bulldozer that runs parallel to the 〈iri〉 axis and piles up probability against the margin of the plot (Fig. 7).

Fig. 7.

Data from the VI(30) condition showing both the scatter plot (the empirical joint distribution) and the two histograms (the empirical marginal distributions).

One can form an approximate estimate of the contingency between two associated random variables by inspecting their scatter plot, that is, their joint distribution (Figs. 5 and 6). The question is whether the extent to which the location or shape of the distribution of points differs as one considers different vertical or horizontal slices through the scatter plot. For example, does the vertical location of the region where the points are densest change noticeably from one vertical slice to another, and/or are the points notably more dispersed in one slice than in another? For all three plots in Fig. 5, the location of points and degree of dispersion within different vertical slices are much the same. Thus, we judge by inspection that the contingency between rate of responding (1/〈iri〉) and rate of reinforcement (1/IRI) is weak.

The picture changes somewhat when we plot the same data against log–log axes, as in Fig. 6. We see in the upper left plot a region (the region below the diagonal dashed line) in which there is a striking contingency between log(IRI) and log〈iri〉. In this region, log(IRI) increases as a linear function of log〈iri〉. This occurs because on a VI 30-s schedule, the three shortest reinforcer-arming intervals on the list from which the scheduling algorithm chose at random were as short or shorter than the basal average interval between responses. Whenever that happened, the actually experienced interval between reinforcers was dominated by the interval between two responses, each of which produced a reinforcer: Because reinforcers are in fact triggered by responses, the interval between the two reinforcers whose time of occurrences define an IRI can never be shorter than the average interval between responses associated with that IRI. Put another way, the 〈iri〉 associated with an IRI can never be longer than the IRI, whereas the reverse is not true; the 〈iri〉 can be—and generally is—much smaller than the IRI with which it is associated. This is what makes the feedback function for VI schedules complex (Baum, 1992).

It could be that the bird’s brain processed its experiences of its own 〈iri〉’ s and the IRI’s in such a way as to make the bird behaviorally sensitive to the contingency that is evident in a portion of the joint distribution of log(IRI)’s and their associated log(〈iri〉)’s. This contingency, however, disappeared when we lengthened the VI (see the upper-right and lower plots in Fig. 6). If this contingency were driving the pigeon’s responding, then we would expect this manipulation to change responding substantially. In fact, however, the manipulation of the VI has almost no effect: the marginal distributions of 〈iri〉’ s are very similar for all three plots, which means that the average rate of responding and the within-session variation in rate of responding were little affected by a manipulation that eliminated the low-end contingency between the 〈iri〉 and its associated IRI.

In principle, the entropy of a joint distribution, H_j, is computed in the same way as the entropy of a simple distribution; it is the probability of each possible combination times the log of the inverse of that probability:

$$H_{\mathrm{j}}=\sum _i\sum _j{p}_{i,j}log(1/p_{i,j})$$

The mutual information between the variables is:

$$H_{\text{xy}}=H_{\text{yx}}=H_{\mathrm{x}}+H_{\mathrm{y}}-H_{\mathrm{j}}$$

and the degree to which the y variable is contingent on the x variable is:

$$C_{\text{yx}}=\frac{H_{\text{xy}}}{H_{\mathrm{y}}}$$

In practice, the simple approach to estimating the entropy that works reasonably well for obtaining an estimate of the information-theoretic contingency from empirical distributions like those in Fig. 4 cannot be used with empirical distributions like those in Figs. 5–7. The distributions in Fig. 4 are histograms in which the number of observations, N, is much larger than the number of bins, m, in consequence of which, there are several counts in almost every bin. Therefore, the bin-by-bin empirical probabilities (n_i/N) are reasonable approximations to the true probabilities. Therefore, it is reasonable to apply Shannon’s entropy formula directly to these empirical probabilities. The resulting estimates of the entropies are inflated (biased) in a manner that depends on the N/m ratio; the larger this ratio is, the less biased the estimate of the entropy is, because the estimates of the true probabilities get better as this ratio gets larger. However, the bias is the same for both of the entropy estimates, H_b and H_r, that enter into the contingency ratio, so it cancels out.

When it comes to joint distributions, like those in Figs. 5–7, one needs a reasonable number of bins (at least 10) on each axis in order to get a reasonable discrete approximation to the true continuous distributions. Then, however, the total number of bins, m, is m_x × m_y (the numbers of bins on each axis), which is to say a much larger number of bins. If we used a minimum of 10 bins on each axis, the total number of bins for the joint distribution would be 100, and we only have N = 390 observations. Therefore, only a few of the 100 bins will have more than a few tallies, and many will have none. In that case, the empirical relative frequencies in these 100 bins are no longer reasonable estimates of the true joint probabilities. How to estimate the entropy under these circumstances has been studied intensely in recent years (Paninski, 2003; Nemenman et al., 2004; Paninski, 2004; Shwartz et al., 2005; Ho et al., 2010; Sricharan et al., 2011).

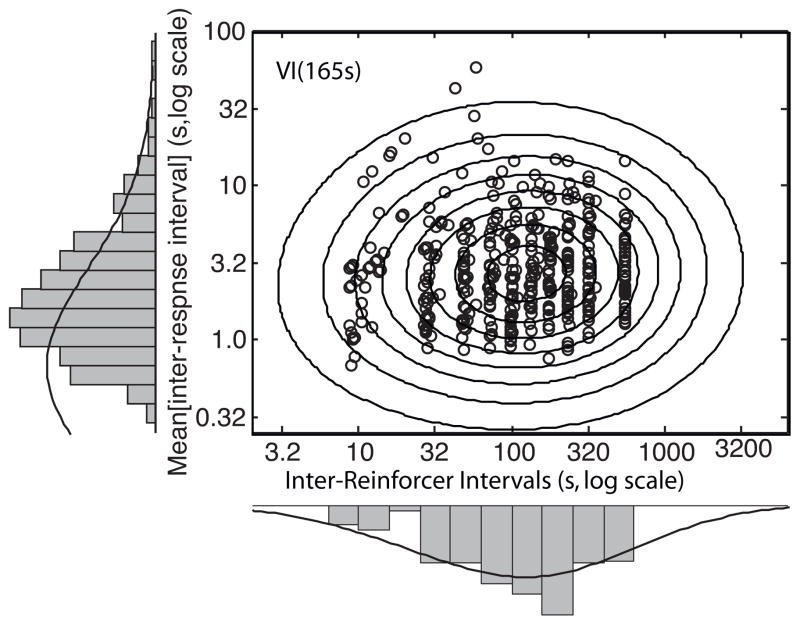
Fig. 8 makes clear what the problem is. As in Fig. 7, it shows the scatter plot for a joint distribution (from a bird responding on VI160 schedule) and the histograms for the two marginal distributions. In making this figure, we estimated the joint probability density distribution using a more or less standard 2-dimensional kernel smoothing operation. The resulting estimate is indicated by the contour lines (level curves of the estimated probability density function) that are superimposed on the scatter plot. The curves superimposed on the histograms are the estimates of the marginal distributions obtained by integrating along the orthogonal dimensions of the joint distribution. The unsatisfactoriness of the estimate of the joint probability density function is evident in the discrepancy between the histogram on the ordinate and the corresponding integral of the estimated joint probability density function, that is, between the observed marginal distribution (the histogram) and the estimated marginal distribution (the smooth curve). Reasonably precise estimates of contingencies in these cases depend on techniques for accurately estimating the joint distribution, because the three entropies must be computed from the smooth estimates of the three probability density distributions (the joint and the two marginals). However, none of this prevents one noting from simple inspection that this contingency is clearly weak.

Fig. 8.

Scatter plot of log 〈iri〉 versus log(IRI) with marginal histograms, for one bird responding on a VI160s schedule. An estimate of the 2-dimensional joint probability density function is shown by level curves (ovoid contour lines) superposed on the scatter plot. The smooth curves superposed on the marginal histograms are the suitably rescaled 1-dimensional integrals of this estimated joint probability density function.

We do not go into the issues surrounding techniques for estimating joint distributions here; they are highly technical and we do not pretend proficiency. Our proposed approach to measuring temporal contingency in conditioning protocols will achieve its full power only when the field settles on a demonstrably valid, generally applicable solution to the problem of estimating the entropies of sparse empirical distributions.

Purely empirical work can also help. The more data one has, the less problematic the estimation problem is, and operant methods lend themselves to the gathering of really large data sets. Also, VI schedules can now be implemented in ways that would remove the artificial discontinuities in the log(IRI) distribution evident in Figs. 5–8.

To summarize so far, when birds respond on VI schedules, there is a negligible prospective contingency between their responses and reinforcer deliveries, because the distribution of the r→R intervals, the intervals from a response to the next reinforcer, differs very little from the distribution of t→R intervals, where the t’s are randomly chosen points in time. Put most simply, having made a response changes hardly at all the expectations regarding the interval to the next reinforcer. By contrast with a fixed-ratio 1 (FR 1) schedule, where each response produces a reinforcer, there is a perfect prospective contingency between a response and a reinforcer delivery. This contingency gets gradually weaker as the parameter of the FR schedule increases. When birds respond on VI schedules, the contingency between their rate of responding and the rate of reinforcement is also negligible. By contrast, with a variable-ratio (VR) schedule, this contingency is strong, because the faster they respond, the sooner on average a reinforcer is delivered.

Another contingency that could be relevant to conditioned behavior with VI protocols is the retrospective contingency between reinforcers and immediately preceding responses, which we denote as the r→R contingency. The basal entropy for this contingency is the distribution of intervals from randomly chosen points in time backward to the immediately preceding response. This distribution is very similar to—hence, has approximately the same entropy as—the distribution of inter-response times. (NB: This is not the same as the distribution of 〈iri〉’ s, which are IRI/n_r, where n_r is the number of responses during the IRI.) The residual entropy for this contingency is the entropy of the distribution of intervals from reinforcers back to the immediately preceding response. The entropy of this distribution is 0, because every reinforcer is preceded by a response at an unvarying interval of 0.01 s. Thus, there is a perfect retrospective, r→R, contingency on a VI schedule. The same is true for all four elementary schedules of reinforcement [fixed interval (FI), VI, FR, and VR]. In every case, reinforcers are triggered by some one of the subject’s repeated responses. Whenever triggered, they occur at a fixed very short delay after the triggering response. Therefore, when one looks backward in time from reinforcer deliveries (R), one always finds a preceding response (r) at the same short unvarying remove.

Thus, the retrospective contingency between reinforcer and response may be an important variable in the emergence and sustenance of operantly conditioned behavior. We currently are investigating this idea by manipulating this retrospective distribution in various ways. Clearly, it is not the only important variable, because responding is, for example, much higher on a VR schedule than on a VI schedule when the two schedules produce equivalent rates of reinforcement (e.g., Lattal et al., 1989; Nevin et al., 2001). It does, however, seem plausible that the retrospective r < − R contingency is an important variable, perhaps even a sine qua non for the emergence of responding. If so, this will capture the intuition that operant conditioning differs in interesting ways from classical/Pavlovian conditioning. The latter appears to be driven primarily by the informativeness of the CS onset, that is, by the relative shortening of the expected interval to reinforcer delivery that occurs at CS onset (Balsam et al., 2006; Ward et al., 2012).

It has long been imagined that in operant conditioning, the reinforcer acts backward in time to stamp in a latent association between the stimulus situation in which a response was made and the response. Our analysis of contingency suggests that what may be correct about this idea is that the interval measured backward from the reinforcer to the response may be a key interval. In any event, we now have a powerful new tool for investigating the issues about temporal pairing versus contingency that Rescorla (1967) discussed almost half a century ago. We have finally brought time into the picture in a manner that does not rely on some indefensible artifice, such as the analytic imposition of pseudotrials, the assumed durations of which are without empirical justification. That is progress.