Ultrasonic-heating–encoded photoacoustic tomography with virtually augmented detection view

Abstract

Photoacoustic (PA) imaging of arbitrarily-shaped or oriented objects may miss important features because PA waves propagate normal to structure boundaries and may miss the acoustic detectors when the detection view has a limited angular range. To overcome this long-standing problem, we present an ultrasonic thermal encoding approach that is universally applicable. We exploit the temperature dependence of the Grueneisen parameter and encode a confined [[What does confined mean here?]] voxel using heat generated by a focused ultrasonic transducer. The PA amplitude from the encoded voxel is increased while those from the neighboring voxels are unchanged. Consequently, the amplitude-increased PA waves propagate in all directions due to the round cross-section of the encoded region and thus can be received at any viewing angle on the cross-sectional plane [[Please check throughout the manuscript for similar places.]]. We built a mathematical model for the thermally encoded PA tomography, performed a numerical simulation, and experimentally validated the ultrasonic thermal encoding efficiency. As a proof of concept, we demonstrate full-view in vivo vascular imaging and compare it to the original linear-array PA tomography system, showing dramatically enhanced imaging of arbitrarily oriented blood vessels. Since ultrasonic heating can be focused deeply, this method can be applied to deep tissue imaging and is promising for full-view imaging of other features of biomedical interest, such as tumor margins.

INTRODUCTION

The photoacoustic (PA) effect describes the generation of acoustic waves due to time-variant photon absorption and thermoelastic expansion. As optical absorbers are excited almost simultaneously, PA waves tend to propagate along directions normal to the boundaries of the absorbing structure [1–3]. To capture all the features of arbitrarily shaped objects, full-view ring or spherically shaped ultrasonic detection arrays have been used to cover all the PA propagation directions in two dimensions (2D) or three dimensions (3D). However, these transducers are usually custom-made, expensive, and have closed working spaces, limiting their applications to targets such as small animals, human fingers or breasts [4–6].

In order to image more anatomical sites, such as the liver, kidney, or brain of humans and large animals, ultrasonic transducers with one-sided accessibility, such as single-element focused transducers or linear transducer arrays, are often preferred [7–10]. However, these types of transducers suffer limited views, which must be addressed in order to avoid missing important features, such as vessels or tumor margins [11, 12]. A possible solution is to generate non-uniform PA emissions, so that the PA waves propagate in all directions. A novel approach based on optical speckle illumination has been utilized to induce such nonuniformity [13]. Because each optical speckle grain can be treated as a PA source, the PA emission angle is enlarged. A limitation in deep tissue is that the speckle grains may be small and densely distributed within the acoustic focus, which decreases the signal strength.

Here we present a different approach to virtually augment the PA detection view angle using ultrasonic thermal encoding, which is analogous to a method in microwave thermal imaging [14]. A focused ultrasonic transducer thermally encodes a voxel. Due to the temperature dependence of the Grueneisen parameter [15–19], the encoded voxel emits stronger PA waves than other voxels. The amplitude-increased PA waves propagate in all directions because of the round cross section of the heating spot. By scanning the thermally encoded spot, a full-view PA image can be formed despite the use of a limited-view PA detector.

PRINCIPLE

Under stress and thermal confinements, a short-pulsed laser beam illuminating an optically absorbing object generates an initial pressure rise p₀:

$$p_0(\overrightarrow{\rho })={\mathrm{\Gamma }}_0(\overrightarrow{\rho })\eta {\mu }_a(\overrightarrow{\rho })F(\overrightarrow{\rho }),$$ (1)

where ρ→ is a vector representing an arbitrary point, Γ₀ is the Grueneisen parameter at the baseline temperature, η is the percentage of the optical absorption that is converted into heat, μ_a is the optical absorption coefficient, and F is the local optical fluence. Here, we assume that the heat conversion efficiency η is spatially invariant.

The Grueneisen parameters for many materials, such as water, aqueous solutions, and many biological tissues, are temperature dependent. With a small temperature rise ΔT, the Grueneisen parameter Γ can be approximated using the first-order Taylor expansion as

$$\mathrm{\Gamma }(\overrightarrow{\rho },\mathrm{\Delta }T)={\mathrm{\Gamma }}_0(\overrightarrow{\rho })+{{\mathrm{\Gamma }}^{\prime }}_0(\overrightarrow{\rho })\mathrm{\Delta }T(\overrightarrow{\rho }),$$ (2)

where Γ′₀ is the temperature derivative of Γ at the baseline temperature.

With ultrasonic heating, the initial pressure rise $p_0^{th}(\overrightarrow{\rho })$ becomes

$$p_0^{th}(\overrightarrow{\rho })={\mathrm{\Gamma }}_0(\overrightarrow{\rho })\eta {\mu }_a(\overrightarrow{\rho })F(\overrightarrow{\rho })+{{\mathrm{\Gamma }}^{\prime }}_0(\overrightarrow{\rho })\mathrm{\Delta }T(\overrightarrow{\rho })\eta {\mu }_a(\overrightarrow{\rho })F(\overrightarrow{\rho }).$$ (3)

On the right hand side of Eq. (3), the first term represents the original initial pressure rise, and the second term is the initial pressure rise due to the temperature rise. The acoustic pressure p^th (ρ→, t) propagation in an inviscid medium can be described as [20]

$$\begin{array}{l}{p}^{th}(\overrightarrow{\rho },t)=\frac{{\mathrm{\Gamma }}_0(\overrightarrow{\rho })\eta F(\overrightarrow{\rho })}{4\pi v_s^2}\frac{\partial }{\partial t}\left[\frac{1}{v_{s}t}\int {\mu }_a({\overrightarrow{\rho }}^{\prime })\delta \left(t-\frac{|\overrightarrow{\rho }-{\overrightarrow{\rho }}^{\prime }|}{v_s}\right)d{\overrightarrow{\rho }}^{\prime }\right]\\ +\frac{{{\mathrm{\Gamma }}^{\prime }}_0(\overrightarrow{\rho })\eta F(\overrightarrow{\rho })}{4\pi v_s^2}\frac{\partial }{\partial t}\left[\frac{1}{v_{s}t}\int \mathrm{\Delta }T({\overrightarrow{\rho }}^{\prime }){\mu }_a({\overrightarrow{\rho }}^{\prime })\delta \left(t-\frac{|\overrightarrow{\rho }-{\overrightarrow{\rho }}^{\prime }|}{v_s}\right)d{\overrightarrow{\rho }}^{\prime }\right],\end{array}$$ (4)

where v_s is the speed of sound, and δ(·) is the Dirac delta function. The first term on the right hand side of Eq. (4) represents the original PA waves, whose propagation direction is determined by the absorber distribution μ_a(ρ→). The second term is generated from the augmented Grueneisen parameter, whose propagation direction is determined by product of the optical absorption distribution and the ultrasonic heating, i.e., ΔT(ρ→)μ_a(ρ→). Therefore, we can apply ultrasonic heating patterns ΔT(ρ→) to manipulate the propagation directions of the augmented PA waves, so that they can be received by the PA detector.

Let us consider a simplified example: a long cylindrical object uniformly illuminated by omni-directionally scattered light. Using the cylindrical coordinates z and r (i.e., r = (x² + y²)^1/2), the absorption coefficient can be written as

$${\mu }_a(r)={\mu }_{a0}U(R-r),$$ (5)

where R is the radius of the cylindrical object, and U is the Heaviside step function defined as

$$U(m)=\{\begin{array}{ccc}1& \mathit{for}& m\ge 0\\ 0& \mathit{for}& m<0\end{array}.$$ (6)

If the object is optically thin, i.e., μ_a0R ≪1, the optical energy will be uniformly deposited within the cylinder. In this case, by substituting Eq. (5) into Eq. (4), we can write the PA pressure as [21]

$$p_c(\tau )=\frac{{\mathrm{\Gamma }}_0\eta {\mu }_{a0}F}{\pi {(2r)}^{0.5}}{\int }_{-\chi }^0\frac{\xi +1}{{(\xi +\tau )}^{0.5}{\left[1-{(\xi +1)}^2\right]}^{0.5}}d\xi ,$$ (7)

where τ is the dimensionless retarded time from the edge of the cylinder, defined as $\tau =\left(\frac{v_s}{R}\right)\left[t-\frac{(r-R)}{v_s}\right]$, and χ is the lesser of 2 or τ. Here p_c(τ) represents a cylindrical PA wave, which propagates along only the radial direction, not the z-axis (not considering the ends of the cylinder). Hence, the limited-view problem appears when an ultrasonic transducer cannot receive the cylinder’s pressure wave in the radial direction.

After applying a spherical ultrasonic heating pattern with a radius R′ (let R′ ≤ R) to the long cylinder, we generate an additional spherical PA source due to the changed Grueneisen parameter. The new PA wave generated by the heated cylindrical object can be written as [21]

$$p(\tau ,{\tau }^{\prime })=p_c(\tau )+p_s({\tau }^{\prime })=p_c(\tau )+\frac{{\mathrm{\Gamma }}_0^{\prime }\mathrm{\Delta }T\eta {\mu }_{a0}F}{2\rho }(1-{\tau }^{\prime })\left[{\mathrm{\Theta }}_{0,1}({\tau }^{\prime })+{\mathrm{\Theta }}_{1,2}({\tau }^{\prime })\right],$$ (8)

where τ′ is the dimensionless retarded time from the edge of the sphere, defined as ${\tau }^{\prime }=\left(\frac{v_s}{R^{\prime }}\right)\left[t-\frac{(l-R^{\prime })}{v_s}\right],l=\sqrt{r^2+z^2}$ is the radial distance in a spherical coordinate, and Θ_i,j(·) is a square wave function defined as ${\mathrm{\Theta }}_{i,j}(m)=\{\begin{array}{ccc}1& \mathit{for}& i\le m\le j\\ 0& \mathit{else}& \end{array}$. Eq. (8) indicates that the ultrasonic heating generates an additional spherical PA wave that can be detected at any view angle.

Similarly, line-shaped ultrasonic heating patterns can also be used to manipulate the propagation direction of the PA waves. In this case, the normal direction of the heating line should be within the receiving angle of the ultrasonic transducer, and the distance between the lines should be greater than the ultrasonic resolution.

NUMERICAL SIMULATION

Numerical simulation was carried out to validate the full-view imaging capability offered by thermal encoding. We used the k-Wave toolbox [22, 23] for fast numerical simulation of PA wave propagation. Images were reconstructed with the time-reversal algorithm in the k-Wave toolbox. The simulation geometry is shown in Fig. 1 (a). A linear ultrasonic array was positioned orthogonally to a line-shaped numerical phantom. The linear transducer array has 200 elements, with a pitch of 0.1 mm and a 15 MHz bandwidth. The simulation was performed in a 2D plane with a field of view (FOV) of 20 × 20 mm² and a pixel size of 0.1 × 0.1 mm². To mimic the thermal encoding, we increased the initial pressure rise at the heated point. The simulation code can be found in supplemental materials.

Figure 1.

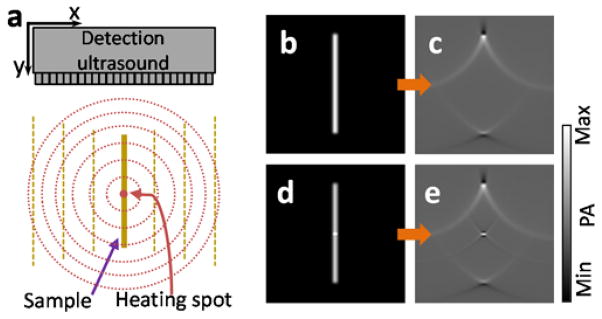
Numerical simulation of the virtually enabled full-view PA imaging using ultrasonic thermal encoding. (a), Schematic of the simulated imaging setup. The heating ultrasonic transducer is not shown. (b–e) Simulations of a vertical line object without and with point ultrasonic heating. (b) Initial pressure rise of the line object without ultrasonic heating. (c) Reconstructed PA image of the line object without ultrasonic heating. (d) Initial pressure rise of the line object with an ultrasonic heating spot. (e) Reconstructed PA image of the overlap between the ultrasonic heating spot and the line object.

Figures 1 (b–e) present the numerical simulation of a line object without and with point ultrasonic heating. Fig. 1 (b) shows the initial pressure rise without ultrasonic heating. Since the initial pressure rise on the line phantom was uniform, the PA waves propagated only along the two normal directions of the line (except at the two ends of the line object). Supplementary Video 1 shows the PA wave propagation process. Because the ultrasonic transducer array received PA signals only from the two ends, the reconstructed PA image in Fig. 1 (c) does not show the middle part of the line object. Using the k-Wave toolbox, we show the acoustic time-reversal process in Supplementary Video 2. When the simulated ultrasonic heating was on, the heated spot generated higher initial pressure rise, as shown in Fig. 1 (d). The PA wave propagation was simulated and is shown in Supplementary Video 3. While the baseline PA wave still propagated normal to the line object’s boundaries, the incremental PA wave from the heated spot propagated along all directions and was received by the linear transducer array. The reconstructed image in Fig. 1 (e) and a time-reversal animation shown in Supplementary Video 4 demonstrate that the heated spot in the line phantom could be detected by the limited view ultrasonic transducer array.

From the simulation results, we can find that the thermal encoding method successfully recovers the originally “invisible” point. Combined with raster scan, it can recover a full-view photoacoustic image.

EXPERIMENTAL SETUP

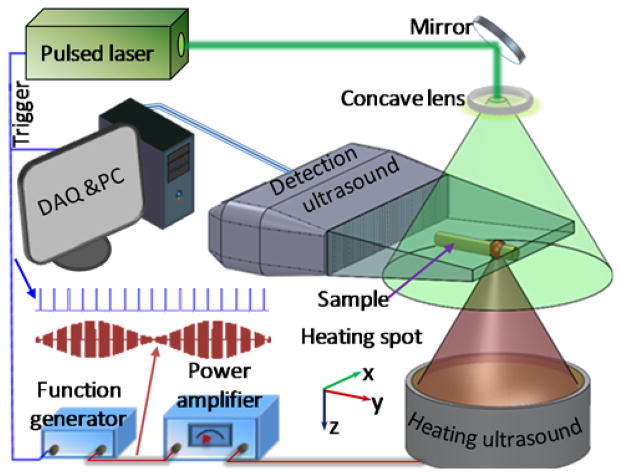
The experimental setup is illustrated in Fig. 2. A pulsed laser (Nd:YAG, Quantel; 532-nm wavelength; 10-ns pulse duration; 20-Hz pulse repetition rate) provided optical excitations. The output laser beam was expanded by a concave lens to illuminate the sample. A 256-element linear ultrasonic transducer array (MS200, Visualsonics Inc., Canada, 15-MHz central frequency, 9-MHz one-way bandwidth quantified as the full width at half maximum or FWHM) was used to detect the PA waves. The ultrasonic array was connected to a PA imaging system (Vevo LAZR, Visualsonics Inc., Canada), which could form a two-dimensional PA image using four laser pulses. The measured lateral (x-axis) resolution was 257 μm when the sample was positioned ~11 mm away from the transducer surface, and the measured axial (y-axis) resolution was 113 μm.

Figure 2.

Schematic of a full-view photoacoustic imaging system based on acoustic thermal tagging.

A custom-made ultrasonic heating transducer was employed for thermal encoding. The transducer had a resonant frequency of 7.5 MHz, an estimated FWHM focal diameter of 178 μm, and an estimated FWHM focal depth of 445 μm. The parameters of the heating transducer array were selected to generate a focal spot size smaller than the lateral resolution of the linear transducer array for isotropic detection. The heating beam was placed vertically and focused onto the PA imaging plane. A function generator synthesized a 7.5 MHz sinusoidal signal, whose amplitude was modulated by another sinusoidal wave at a frequency of 0.5 Hz. The modulated 7.5 MHz sinusoidal signal was amplified to drive the heating ultrasonic transducer. To avoid interference between the acoustic heating and PA detection, the heating ultrasound was turned off for one millisecond before and after each PA acquisition. At each heating spot, 50 consecutive 2D PA images were acquired at a speed of 5 images per second and reconstructed using the filtered backprojection algorithm [24]. The intensities of each pixel in the 50 2D images were transformed into the frequency domain, where the 0.5-Hz frequency component of every pixel was used to form an intermediate PA image. The focus of the heating ultrasonic transducer was raster scanned with a step size of 250 μm over the x-y plane. The step size was chosen to be close to the value of the lateral resolution to ensure the spatial fidelity while maximally reducing the scanning time. All the intermediate PA images were combined to synthesize a final PA image. Each pixel value of the synthesized PA image is determined from the maximum value from the corresponding pixels in all the intermediate PA images.

The thermal encoding effect was first tested by imaging bovine blood flowing in a silicone tube (0.5-mm inner diameter, and 1-mm outer diameter) placed along the x axis. The heating spot was placed at the center of the tube. To avoid possible heat accumulation, the blood was pumped to flow in the tube at a speed of ~5 mm/sec. The heating power was modulated at 0.5 Hz, with an average power of 1 W. The average power was calculated from the sinusoidal peak powers, which were read from the radio-frequency amplifier.

RESULTS AND DISCUSSION

Figure 3 (a) shows the measured PA signal amplitude varying at 0.5 Hz, following the heating power modulation. In another test, the average heating power was increased from 0 to 1 W. The PA modulation amplitudes were recorded at each power level, and are plotted in Figure 3 (b). The PA modulation amplitude is proportional to the average heating power, which again validates the linear assumption. There is a trade-off between the heating spot size and the heat loss rate due to thermal diffusion, which determines the choice of the heating ultrasonic transducer.

Figure 3.

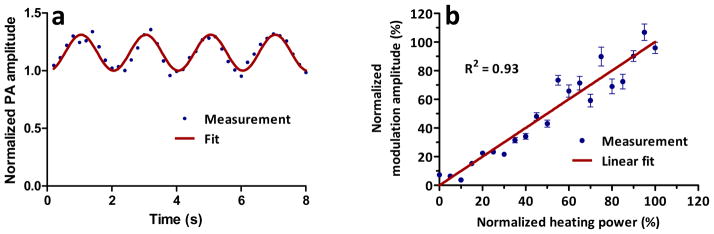
Fig. 3. Ultrasonic thermal encoding test. (a) PA amplitude change with 0.5-Hz modulated ultrasonic heating; (b) PA modulation amplitude versus ultrasonic heating power. Error bars represent standard errors. N = 8.

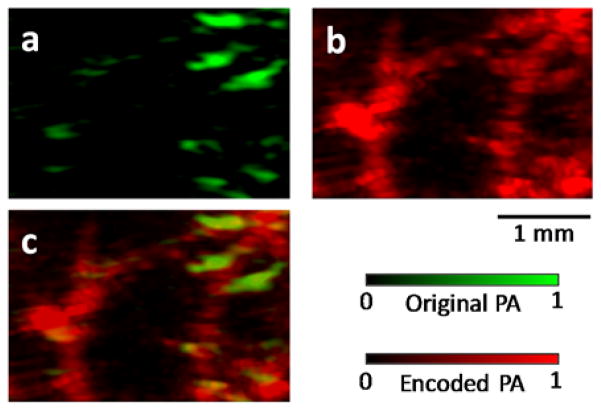
Next, a vertical (i.e., along the y axis) blood tube phantom was imaged to validate the augmented detection view. The experimental results are presented in the supplementary materials. Finally, as a validation of the concept, the vasculature in a mouse ear was imaged in vivo without and with ultrasonic thermal encoding. The mouse ear was mounted in the PA imaging plane. We first acquired a regular PA image without ultrasonic thermal encoding. As shown in Figure 4 (a), although the PA image has a decent SNR, it shows only horizontal or nearly horizontal blood vessels. Many vertical features are missing. Then we applied ultrasonic thermal encoding and acquired PA images of the same region. The synthesized PA image is shown in Figure 4 (b), where blood vessels along all directions are visible. Supplementary Video 5 shows the point-by-point ultrasonic thermal encoding process. To facilitate comparison, Figure 4 (c) presents an overlaid version of both images. This comparison shows the in vivo full-view imaging capability, even using a limited-view PA detector.

Figure 4.

(a) In vivo mouse vascular imaging without ultrasonic thermal encoding. Only horizontal or nearly horizontal blood vessel segments are visible. (b) In vivo vascular imaging with ultrasonic thermal encoding. More blood vessels are visible due to the enlarged view angle. (c) Overlay image showing co-registered original and thermally encoded PA images.

In the present experimental setup, the heating transducer and the PA detection transducer are deployed orthogonally. Rotating the sample by 45 degrees may allow accessing a large sample on one side. If the heating transducer has to be placed co-axially with the detection transducer, a high-NA heating transducer will be needed to make the heating voxel nearly spherical.

The images acquired with ultrasonic thermal encoding are sensitive not only to optical absorption, but also are affected by the acoustic absorption and the Grueneisen parameter’s first-order derivative with temperature.

To address the concern of tissue damage from ultrasonic heating, the maximum temperature rise was estimated from the PA amplitude increase. According to the results in Figure 3, the PA signal change was an appropriate indicator of temperature rise. In the phantom experiments, the maximum PA amplitude increase was 29±2%. Assuming that the Grueneisen parameter is proportional to temperature in degrees Celsius [25] and the baseline temperature is 20°C, the maximum temperature rise was estimated to be ~5.8°C. For the in vivo imaging, the baseline temperature was body temperature (37°C) and the maximum PA amplitude increase was ~12±3%. These values indicate a temperature rise of ~4.4°C. Considering that blood flow can dissipate heat efficiently, the moderate local ultrasonic heating does not likely cause thermal damage to biological tissue. Moreover, if we can improve the PA detection sensitivity, the temperature rise can be further reduced. Another limitation is that during thermal encoding heat may dissipate to neighboring tissues, which can lower the encoding efficiency. Shortening the thermal encoding time may mitigate this effect.

In this work, single-spot ultrasonic heating was raster scanned to generate a 2D image, which is time-consuming. For example, the in vivo mouse ear vascular image in Figure 4 (b) has a field of view of 5×5 mm² with 400 heating spots. At each heating spot, we acquired 50 frames of PA images at a speed of 5 frames per second (10 seconds per heating spot). Thus, it took 66 minutes to acquire the image. Because the main purpose of this paper is to demonstrate the principle, the imaging speed is not optimized here. In the future, faster PA imaging systems and shorter heating time can be used to improve the imaging speed. At each spot, the heating time should be long enough to allow heat exchange, which might limit the ultimate imaging speed. In addition, complex structured ultrasonic heating patterns, such as multiple spots, a single line, or even multiple lines, can be applied to simultaneously encode multiple features. These patterns can potentially be generated by either a cylindrically focused ultrasonic transducer or a 2D ultrasonic transducer array.

The thermal encoding in this work can potentially be implemented on a HIFU treatment system in the future to provide PA imaging capability during treatment. Since some HIFU setups have dynamic focusing capability in both depth and lateral direction, it becomes possible to achieve an electronic thermal encoding scan, instead of a mechanical scan [26].

CONCLUSIONS

We present a new approach using ultrasonic thermal encoding to solve the limited-view problem in many PA tomography variants. The ultrasonic thermal encoding was modeled and experimentally validated. Full-view PA imaging capability was demonstrated both in phantoms and in vivo, even using a limited-view PA detector. Since ultrasonic heating can be focused deeply, this method can be applied to deep tissue. The improved view angle dramatically enhanced the PA imaging of arbitrarily oriented blood vessels. The improved technique is promising for full view imaging of other features of biomedical interest, such as tumor margins.