Infrared identification of the Criegee intermediates syn- and anti-CH₃CHOO, and their distinct conformation-dependent reactivity

Abstract

The Criegee intermediates are carbonyl oxides that play critical roles in ozonolysis of alkenes in the atmosphere. So far, the mid-infrared spectrum of only the simplest Criegee intermediate CH₂OO has been reported. Methyl substitution of CH₂OO produces two conformers of CH₃CHOO and consequently complicates the infrared spectrum. Here we report the transient infrared spectrum of syn- and anti-CH₃CHOO, produced from CH₃CHI + O₂ in a flow reactor, using a step-scan Fourier-transform spectrometer. Guided and supported by high-level full-dimensional quantum calculations, rotational contours of the four observed bands are simulated successfully and provide definitive identification of both conformers. Furthermore, anti-CH₃CHOO shows a reactivity greater than syn-CH₃CHOO towards NO/NO₂; at the later period of reaction, the spectrum can be simulated with only syn-CH₃CHOO. Without NO/NO₂, anti-CH₃CHOO also decays much faster than syn-CH₃CHOO. The direct infrared detection of syn- and anti-CH₃CHOO should prove useful for field measurements and laboratory investigations of the Criegee mechanism.

Criegee intermediates—formed by the breakdown of alkanes in the atmosphere—are difficult to identify in the gas phase. Here, the authors report the infrared spectrum of the Criegee intermediate CH₃CHOO and identify both the syn- and anti-conformers.

Recent advances in the direct detection of the Criegee intermediates have stimulated active research on their structures, spectroscopy, reactions and implications for atmospheric chemistry1. The Criegee intermediates are carbonyl oxides that are produced during the reactions of ozone (O₃) with unsaturated hydrocarbons; they play a central role in controlling the atmospheric budget of OH, organic acids and secondary organic aerosols, especially under low-light conditions.

These Criegee intermediates have eluded detection in the gaseous phase until recently because of their great reactivity and small concentration. Previous understanding of the reactivity of Criegee intermediates, including reaction mechanisms and rate coefficients, was hence subject to large uncertainties, because only indirect experimental evidence was available. Welz et al.3 produced the simplest Criegee intermediate, formaldehyde oxide (CH₂OO), in a flow cell and confirmed its identification with tunable vacuum-ultraviolet photoionization mass spectrometry2. Following the reaction scheme of CH₂I+O₂→I+CH₂OO initially developed by Welz et al.3, CH₂OO has now been detected with ultraviolet depletion4, ultraviolet absorption5,6, infrared absorption7 and microwave spectroscopy8,9. The kinetics of reactions of CH₂OO with various atmospheric species have been directly investigated with some of these detection methods3,10,11,12,13,14,15.

In the atmosphere, O₃ reacts with larger alkenes and produces more complex Criegee intermediates RR′COO; the nature and location of the substituents R/R′ are predicted to affect their reactivity16. For example, the OH yield increases from ∼10% for O₃+C₂H₄ to ∼60% for O₃ + trans-2-butene17,18. The methyl-substituted Criegee intermediate, acetaldehyde oxide (CH₃CHOO), is an intermediate of reactions O₃ + 2-alkenes (such as trans-2-butene) and serves as a prototype to understand various fundamental issues in larger Criegee intermediates. CH₃CHOO exists in two conformers, syn-CH₃CHOO and anti-CH₃CHOO (Supplementary Fig. 1), with the former more stable than the latter by ∼15 kJ mol⁻¹ (refs 19, 20). Because of a large barrier ∼160 kJ mol⁻¹, the interconversion between syn-CH₃CHOO and anti-CH₃CHOO is unlikely. Taatjes et al.21 employed the reaction CH₃CHI + O₂ to produce CH₃CHOO and detected both conformers with photoionization. By employing photoionization at energies 9.37 and 10.5 eV to detect predominantly anti-CH₃CHOO and syn-CH₃CHOO, respectively, these authors reported that anti-CH₃CHOO is significantly more reactive towards H₂O and SO₂ than is syn-CH₃CHOO.

Although photoionization can distinguish these two conformers of CH₃CHOO via distinct ionization energies, a small contribution from the other conformer is unavoidable. The ultraviolet depletion22 and ultraviolet absorption experiments20 yielded a broad feature without structure and provided no information about the conformation of the CH₃CHOO carrier. Recently Sheps et al.23 separated the ultraviolet spectra of two possible conformers based on their distinct reactivity towards H₂O and SO₂, but the two spectra were broad and overlapping with each other. Although microwave spectroscopy was successful in providing structural information24, to employ it for monitoring these species in laboratory kinetic experiments is difficult. Liu et al.25 employed infrared activation of cold CH₃CHOO to produce OH, which was detected with laser-induced fluorescence, and assigned several absorption features in the region 5,600–6,100 cm⁻¹ to be the CH-overtone and combination bands of syn-CH₃CHOO; no bands of anti-CH₃CHOO were identified. It is thus desirable to develop an alternative spectral method that can be applied conveniently and can distinguish clearly these two conformers of CH₃CHOO.

We have demonstrated that coupling a step-scan Fourier-transform infrared (FTIR) spectrometer with a multipass absorption cell enables the recording of temporally resolved infrared absorption spectra of the simplest Criegee intermediate, CH₂OO (ref. 7); five distinct absorption bands of CH₂OO were clearly identified to provide a simple and direct detection method.

Here we report a further application of this technique to characterize the infrared absorption of methyl-substituted Criegee intermediate CH₃CHOO in two conformations and to demonstrate the conformation-dependent reactivity towards its self-reaction and reaction with NO/NO₂.

Results

Spectral analysis of CH₃CHOO

Even though only one H atom of CH₂OO was replaced with a methyl group to form CH₃CHOO, the infrared spectrum of the latter is expected to be much more complicated, because both syn- and anti-conformers contribute to the infrared absorption. In addition, the methyl group introduces low-energy vibrational modes such as the CH₃ torsion (internal rotation), which are populated with several vibrational quanta even at ambient temperatures; hot bands might consequently play important roles in the observed spectrum, as it was demonstrated in the spectrum of CH₂BrOO (ref. 26). Furthermore, the internal rotation of the methyl moiety may introduce torsional splitting in vibrational bands. Consequently, spectral identification and simulation of observed bands of CH₃CHOO are expected to be difficult. In this respect, sophisticated quantum-chemical calculations are essential to assist the spectral simulation and assignments.

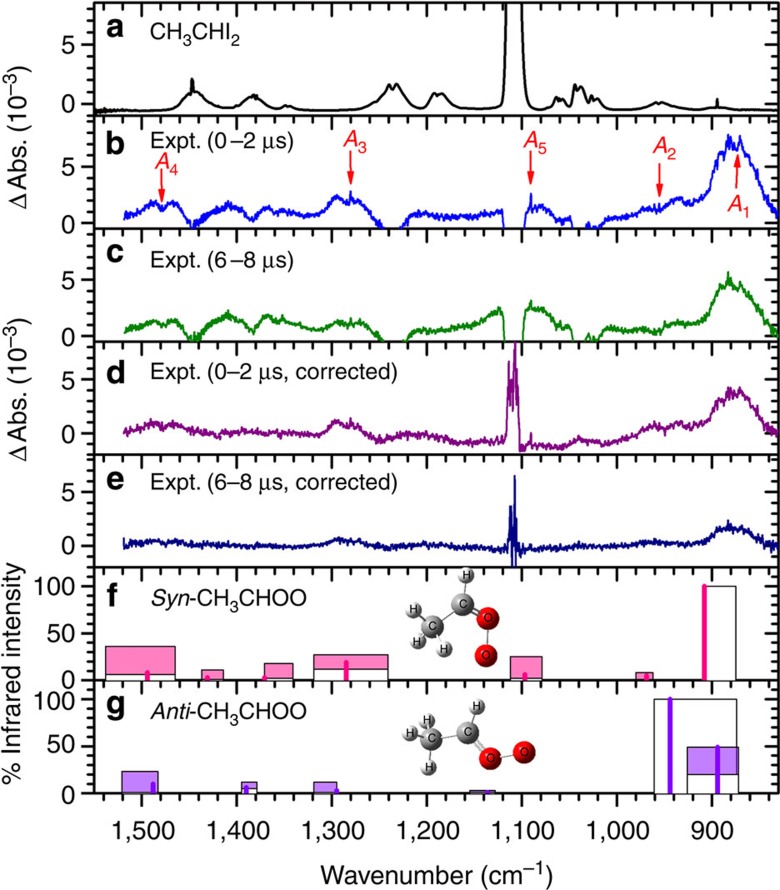
We employed a step-scan FTIR spectrometer coupled with a multi-reflection White cell to record time-resolved infrared spectra. The laser beam at 308 nm photodissociated a flowing mixture of 1,1-diiodoethane (CH₃CHI₂) and O₂ to produce CH₃CHI, which subsequently reacted with O₂ to form CH₃CHOO. The partial infrared absorption spectrum (830–1,550 cm⁻¹) of a flowing mixture of CH₃CHI₂/N₂/O₂ (1/13/288, 84 Torr) at 328 K exhibits an intense absorption line of CH₃CHI₂ near 1,108 cm⁻¹ and some much weaker ones near 894, 956, 1,024, 1,041, 1,061, 1,190, 1,236, 1,383 and 1,447 cm⁻¹ (Fig. 1a). On irradiation with light at 308 nm, the absorption of CH₃CHI₂ decreased because of photolysis, whereas new bands marked A₁–A₅ appeared in the difference spectrum recorded 0–2 μs after laser irradiation (Fig. 1b). The A₅ band was partially interfered with by the absorption of the precursor and the product acetaldehyde, but its sharp Q-branch is quite characteristic and can be readily recognized. These new lines decreased in intensity, as shown in Fig. 1c where 6–8 μs was recorded after ultraviolet irradiation and disappeared after ∼25 μs. To minimize interference from other products, we subtracted the spectrum recorded during 16.0–19.8 μs from these two spectra and stripped the contributions from the precursor and acetaldehyde, as shown in Fig. 1d,e.

Figure 1. Comparison of observed spectra with predicted stick spectra.

(a) Absorption spectrum of a flowing mixture of CH₃CHI₂/N₂/O₂ (1/13/288, 84 Torr) before photolysis. (b) Difference spectra recorded 0–2 μs and (c) 6–8 μs after irradiation of the sample at 308 nm. (d) Corrected spectra recorded 0–2 μs and (e) 6–8 μs after subtraction of the spectrum recorded at 16.0–19.8 μs and removal of the contributions of the precursor CH₃CHI₂ and stable product acetaldehyde. Resolution of all spectra is 0.5 cm⁻¹. New features are marked with arrows and labelled as A₁–A₅. (f) Possible ranges of anharmonic vibrational wavenumbers and infrared intensities of syn-CH₃CHOO and (g) anti-CH₃CHOO predicted with various methods (Supplementary Tables 1 and 2) shown as filled boxes; those predicted with the MULTIMODE method are shown with thick lines.

As photolysis of CH₃CHI₂ produces mainly CH₃CHI (ref. 27) and because this radical reacts readily with excessive O₂ in the system28, possible carriers of the observed new bands include conformers of CH₃CHOO and vinyl hydroperoxide (C₂H₃OOH), methyldioxirane and the stabilized adduct CH₃CHIOO. The structures of these species are shown in Supplementary Fig. 1. For all species except CH₃CHIOO, MP2, B3LYP and NEVPT2(8,8) methods were employed to predict their vibrational wavenumbers and infrared intensities. For CH₃CHIOO, the NEVPT2(1,1) method was used. Furthermore, the most sophisticated predictions were performed for syn- and anti-CH₃CHOO with high-level, full-dimensional quantum calculations, using the MULTIMODE method.29,30,31 The vibrational wavenumbers and infrared intensities of syn- and anti-CH₃CHOO calculated with these theoretical methods are given in Supplementary Tables 1 and 2. Those of methyl dioxirane, trans- and cis-vinyl hydroperoxide and syn- and anti-CH₃CHIOO are listed in Supplementary Tables 3–5, respectively. There is good consistency among these calculations, but there are significant variations in the calculated anharmonic vibrational wavenumbers and infrared intensities among these calculations. To indicate this, we show the ranges of values as filled rectangles, while the values predicted with the MULTIMODE method are depicted with thick lines in Fig. 1f,g, respectively, for syn- and anti-CH₃CHOO. Possible ranges of vibrational anharmonic wavenumbers and intensities of CH₃CHIOO, methyl dioxirane and vinyl hydroperoxide predicted with various methods are compared with the observed spectrum in Supplementary Fig. 2. A comparison of the observed new spectral features with those predicted theoretically excludes the possibility of assigning the observed spectral features A₁–A₅ to the carriers other than CH₃CHOO.

As shown in Fig. 1f and Supplementary Table 1, the more stable syn-CH₃CHOO conformer is predicted from the MULTIMODE calculations to have more intense absorptions near 908 (100), 969 (5), 1,097 (6), 1,285 (19) and 1,494 (8) cm⁻¹; the numbers in parentheses give relative infrared intensity of each vibration. The observed new features near 871 (100), 956, 1,091 (10), 1,281 (40) and 1,477 (30) cm⁻¹ agree satisfactorily with these predicted values. The predicted pattern of intense lines of anti-CH₃CHOO near 894 (49), 944 (100), 1,295 (3) and 1,488 (10) cm⁻¹ agrees less satisfactorily with the observed spectrum. We show below that the contribution from the anti-CH₃CHOO conformer, although less significant, is important for explaining the overall shape of the spectrum and is of primary importance for explaining some of the fine-structure spectral features of the spectrum.

Simulation of rotational contours

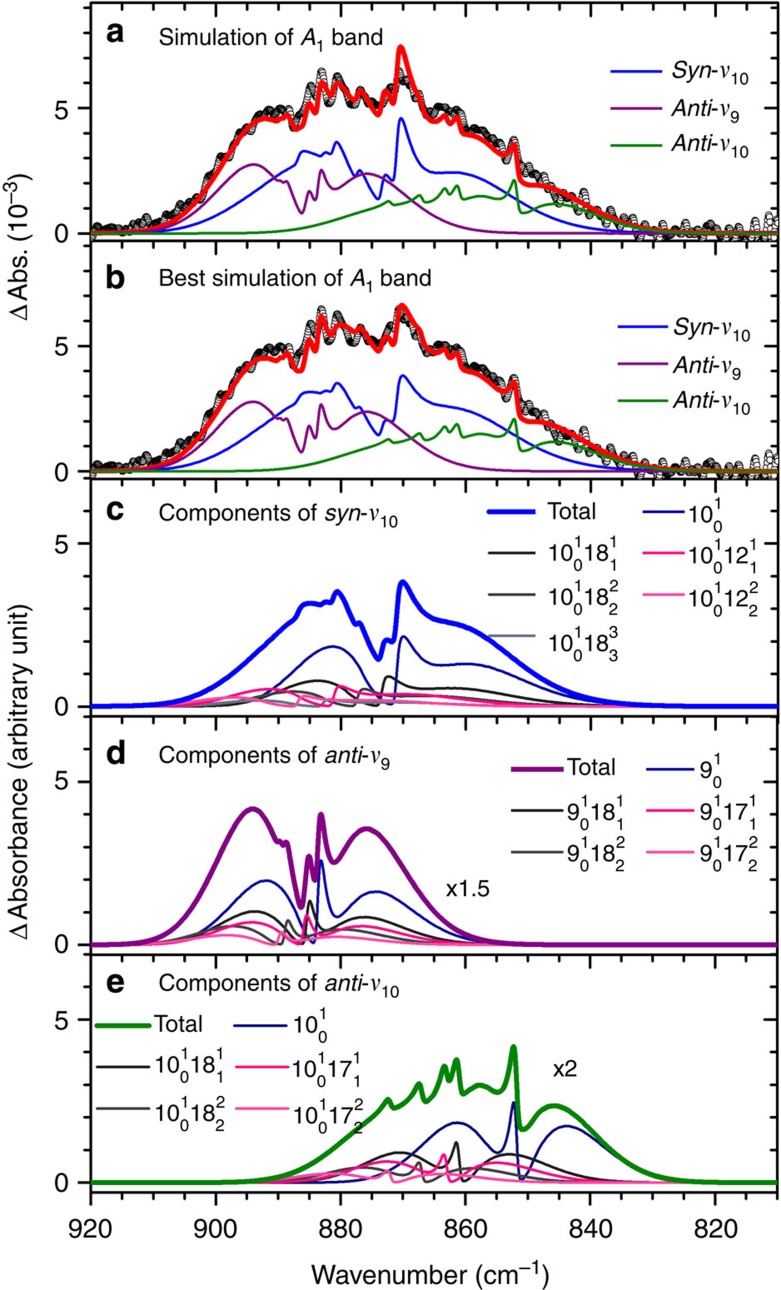
Further support for the presented assignment comes from analysis of the rotational contours of the observed bands. The rotational contour of the A₁ band near 871 cm⁻¹ recorded in the interval of 0–2 μs has several characteristic peaks; it cannot be simulated with a single band and was deconvoluted with guidance from calculations. The experimental data are presented with open circles and the resultant spectrum, simulated according to ratios of rotational constants of the excited and ground states predicted with the MULTIMODE method and the experimental rotational constants of the ground state, is shown as a thick solid line in Fig. 2a; the agreement is satisfactory. Figure 2b presents a comparison of experimental data with the spectrum simulated according to slightly modified ratios of rotational constants for an improved fit. For details of simulation using the PGopher programme32, see Supplementary Methods. This simulated feature consists of three bands: a dominant OO-stretching (ν₁₀) band of syn-CH₃CHOO at 871.2 cm⁻¹ and two smaller bands of OO-stretching (ν₉) and OO-stretching mixed with CH₂ wagging (ν₁₀) modes of anti-CH₃CHOO at 883.7 and 851.8 cm⁻¹, respectively, shown as thin lines in Fig. 2a,b; the fundamental Q-branches of these three modes correspond well with observed distinct peaks; hence, their vibrational wavenumbers can be determined accurately. It is found that several hot bands associated with the ν₁₈ (208 cm⁻¹) and ν₁₂ (314 cm⁻¹) low-energy vibrational modes of syn-CH₃CHOO and with the ν₁₈ (156 cm⁻¹) and ν₁₇ (255 cm⁻¹) low-energy vibrational modes of anti-CH₃CHOO contribute significantly to the observed spectral features. The individual contributions of fundamental and hot bands for these three vibrational modes are shown in Fig. 2c–e; the transitions of hot bands are expressed as 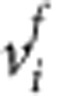in which v is the vibrational mode number, and i and f are vibrational quantum numbers of the lower and upper states, respectively. Detailed positions and relative intensities are listed in Supplementary Table 6. This simulation implies that (1) the hot bands are all blue shifted from the fundamental; the unusual but necessary blue shifts of about 2 and 10 cm⁻¹ for the hot bands involving ν₁₈ and ν₁₂ of syn-CH₃CHOO, respectively, agree qualitatively with the theoretical predictions (Supplementary Table 6). The calculations also indicate that torsional splitting is small for all vibrational modes so that it has no consequence on our spectral simulation. (2) At 328 K, assuming a Boltzmann distribution and that the infrared intensities of hot bands are the same as that of the fundamental band (in qualitative accord with calculations), observed relative intensities of these hot bands imply energies of the first excited states of ν₁₈ and ν₁₂ modes of syn-CH₃CHOO and those of ν₁₈ and ν₁₇ of anti-CH₃CHOO to be ∼193, 282, 149 and 239 cm⁻¹, respectively, which is consistent with theoretical predictions (Table 1 and Supplementary Tables 1 and 2). (3) The population fraction of anti-CH₃CHOO is 0.30 and 0.38 at 328 K, respectively, if infrared intensities predicted with the B3LYP and MULTIMODE methods are used. This fraction is consistent with a value of ∼0.30 derived from ultraviolet experiments23, but greater than values ∼0.20 from microwave experiments24 and ∼0.10 from photoionization experiments21.

Figure 2. Spectral simulation of band A₁.

(a) Comparison of experimental data (open circles, recorded 0–2 μs) with spectrum simulated according to theoretical predictions (thick red solid line) and (b) the best simulated spectrum (thick red solid line) with slightly modified parameters; contributions of ν₁₀ of syn-CH₃CHOO, and ν₉ and ν₁₀ of anti-CH₃CHOO are shown with thin lines. Resolution is 0.5 cm⁻¹. (c) Contributions of fundamental and hot bands of ν₁₀ of syn-CH₃CHOO, (d) ν₉ of anti-CH₃CHOO and (e) ν₁₀ of anti-CH₃CHOO. Detailed positions and relative intensities are listed in Supplementary Table 6. Spectral width of simulation is 0.64 cm⁻¹. The transitions of hot bands are expressed with 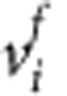in which v is the vibrational mode number, and i and f are vibrational quantum numbers of the lower and upper states, respectively.

Table 1. Comparison of experimentally observed wavenumbers (cm⁻¹) and intensities with the vibrational wavenumbers and infrared intensities of representative vibrational modes of CH₃CHOO predicted with the MULTIMODE method.

Symbol	Syn-CH3CHOO			Anti-CH3CHOO			Description*
	Mode	Experiment	Calculation	Mode	Experiment	Calculation
A'	ν4	1,476.8 (30)†	1,494 (8)†	ν4	1,479.0 (14)†	1,488 (10)†	CO str./HCO bend
A'	ν7	1,280.8 (40)	1,285 (19)	ν7	1,279.4 (17)	1,295 (3)	HCO bend/CO str.
A'	ν8	1,090.6 (10)	1,097 (6)	ν8		1,136 (1)	CH2 wag/CCH bend
A'	ν9	∼956.0 (−)	969 (5)	ν10	851.8 (73)	894 (49)	CCH bend/CH2 wag
A'	ν10	871.2 (100)	908 (100)	ν9	883.7 (100)	944 (100)	OO str.
A'	ν12		314 (3)‡	ν12		330 (7)	CCO/COO iph bend
A”	ν17		449 (0)	ν17		255 (0)§	op deformation
A”	ν18		208 (1)‡	ν18		156 (0)§	CH3 torsion

Ip, in-plane; iph, in-phase; op, out-of-plane; str., stretch.

^*Approximate mode description. For anti-CH₃CHOO, the HCO bending mode is replaced with CH ip bending mode for ν₇, ν₈ is mainly CCH bend, the CCH bend is replaced with OO stretch for ν₁₀, and the iph bend is replaced with oph bend for ν₁₂.

^†Relative infrared intensities normalized to the most intense line. The maximal intensities of syn- and anti-CH₃CHOO are predicted to be 44.4 and 43.6 km mol⁻¹, respectively, with the MULTIMODE method (18-mode coupling); values of 13-mode coupling for syn- and 14-mode coupling for anti-CH₃CHOO are 50.3 and 61.1 km mol⁻¹, respectively.

^‡Harmonic vibrational wavenumbers, as the anharmonic treatment of this mode is problematic using the methods employed here. Anharmonic vibrational wavenumbers are ν₁₂=290 cm⁻¹ and ν₁₈=221 cm⁻¹ predicted with the VCI/NEVPT2(8,8)/aug-cc-pVDZ method.

^§Harmonic vibrational wavenumbers, as the anharmonic treatment of this mode is problematic using the methods employed here. Anharmonic vibrational wavenumbers are ν₁₇=378 cm⁻¹ and ν₁₈=241 cm⁻¹ predicted with the VCI/NEVPT2(8,8)/aug-cc-pVDZ method.

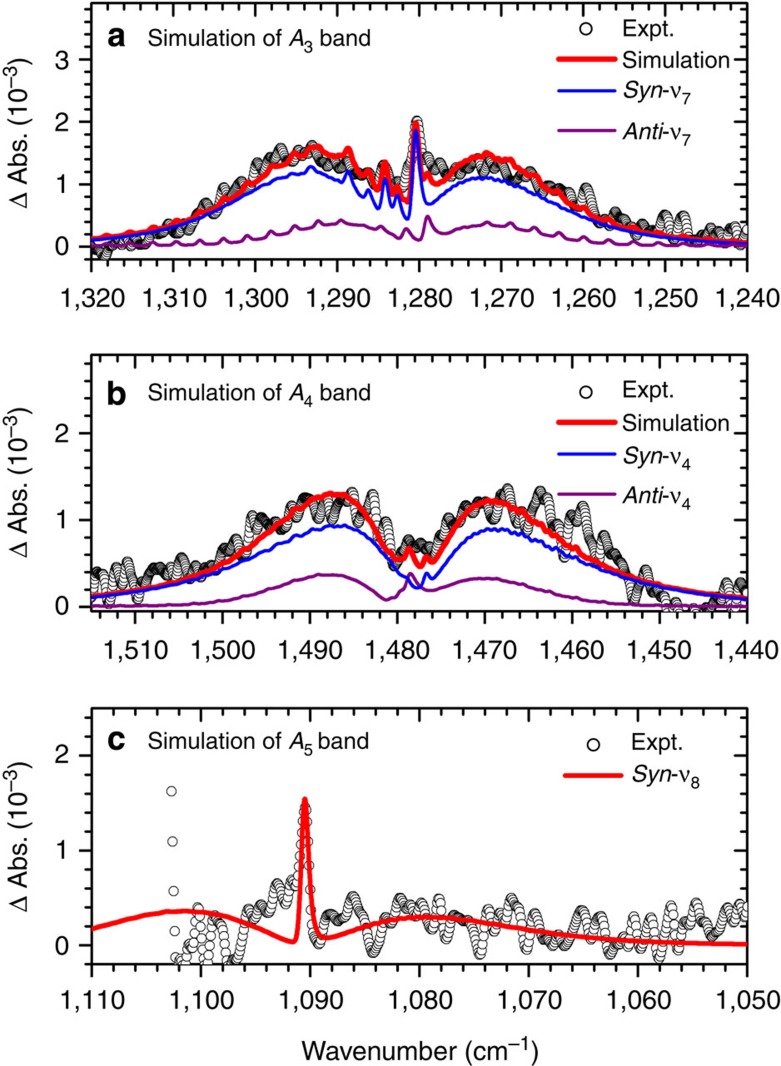
The weaker bands A₃ and A₄ can be simulated likewise with contributions of syn- and anti-CH₃CHOO, as presented in Fig. 3. Band A₃ has a prominent Q-branch at 1,280.8 cm⁻¹, which is assigned to the HCO bending coupled with the CO-stretching (ν₇) mode of syn-CH₃CHOO. A second feature with a weaker Q-branch at 1,279.4 cm⁻¹ is assigned to the corresponding ν₇ mode of anti-CH₃CHOO (Fig. 3a). Band A₄ has prominent P- and R-branches; this band is assigned to the CO-stretching mode coupled with the HCO bending (ν₄) mode of syn-CH₃CHOO. The observed weak Q-branch arises from a small contribution of the ν₄ mode of anti-CH₃CHOO. The contributions of fundamental and hot bands to these features are presented in Supplementary Figs 3 and 4. The a- and b-type spectra of related vibrational modes of syn- and anti-CH₃CHOO are presented in Supplementary Figs 5 and 6, respectively. As band A₂ is rather weak and subject to interference from absorption of C₂H₄, we could only estimate its position to be ∼956 cm⁻¹ from the Q-branch and assign it to the ν₉ mode of syn-CH₃CHOO. Band A₅ suffers from partial interference due to the precursor, but the prominent Q-branch indicates that this band is due to syn-CH₃CHOO and not anti-CH₃CHOO. The observed position at 1,090.6 cm⁻¹ is much closer to the predicted anharmonic vibrational wavenumber of 1,097 cm⁻¹ for syn-CH₃CHOO than the value 1,136 cm⁻¹ for anti-CH₃CHOO.

Figure 3. Spectral simulation of bands A₃ to A₅.

(a) Comparison of experimental data (open circles, recorded 0–4 μs) with simulated spectrum (thick red solid line) for band A₃; contributions of ν₇ bands of syn-CH₃CHOO and anti-CH₃CHOO are shown with thin lines. (b) Comparison for band A₄; contributions of ν₄ bands of syn-CH₃CHOO and anti-CH₃CHOO are shown with thin lines. (c) Comparison of band A₅ (recorded 0–2 μs); only the ν₈ band of syn-CH₃CHOO contributes. Spectral width of simulation is 0.64 cm⁻¹.

As shown in Table 1, the agreement between observed vibrational wavenumbers of syn- and anti-CH₃CHOO, and those calculated with the MULTIMODE method is quite satisfactory with differences <17 cm⁻¹, except for the OO-stretching mode, which has differences of 37 cm⁻¹ for syn-CH₃CHOO and 60 cm⁻¹ for anti-CH₃CHOO. A similar shift between experiment and MULTIMODE calculations was reported previously for CH₂OO for an analogous band33. Conceivably, the origin of the deviation is, as in CH₂OO, a slight deficiency in the level of electronic structure theory which is more sensitive to the OO-stretching mode.

Our observations also conform to an expectation that similar to CH₂OO, CH₃CHOO has a significant zwitterionic character with a strengthened C−O bond and a weakened O−O bond. The observed wavenumber of the OO-stretching mode of syn-CH₃CHOO near 871 cm⁻¹ is smaller than the corresponding value 908 cm⁻¹ of CH₂OO, consistent with theoretical predictions showing that the length of the O–O bond increases from 1.349 Å in CH₂OO to 1.380 Å in syn-CH₃CHOO.

Conformation-dependent reactivity

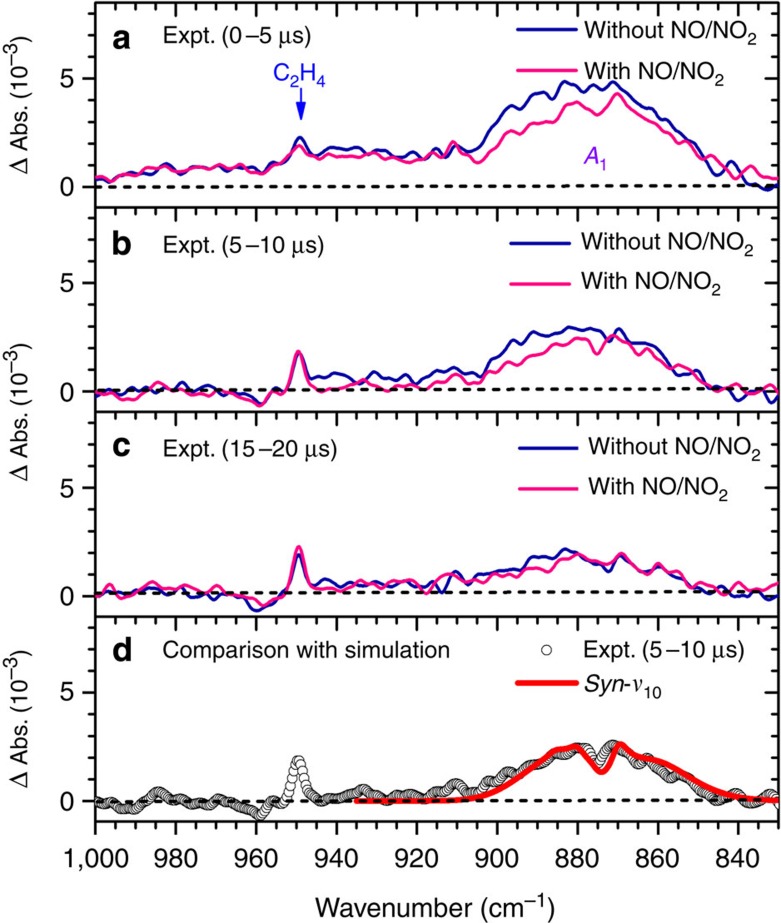
Further support for this assignment of the A₁ band comes from a comparison of low-resolution spectra recorded in experiments with and without NO/NO₂. Taatjes et al.21 reported that anti-CH₃CHOO is more reactive towards H₂O, SO₂ and NO₂ than syn-CH₃CHOO, with the effect much more significant for the former two. A direct test with H₂O in our system is difficult because of the intense infrared absorption of H₂O and the hygroscopic KBr windows we employed. A test with SO₂ is also infeasible, because the windows were contaminated by the products easily. Instead, we added NO/NO₂ to explore the differences. As shown in Fig. 4a, the difference between bands A₁ in the range 870–910 cm⁻¹ recorded in experiments with and without adding NO/NO₂ is significant during the interval 0–5 μs and the difference in the range 830–870 cm⁻¹ is smaller but non-negligible. The differences in these two regions are consistent with the contributions of ν₉ and ν₁₀ bands of anti-CH₃CHOO shown in Fig. 2a. This difference in spectra recorded in experiments with and without NO/NO₂ diminished at a later period and the spectrum recorded 5–10 μs after photolysis in the experiment with NO/NO₂ (Fig. 4b) agrees with that simulated for syn-CH₃CHOO only, as shown in Fig. 4d; this provides additional support that our simulation of these two conformers is reliable and most anti-CH₃CHOO was consumed within 10 μs.

Figure 4. Comparison of spectra recorded with and without added NO/NO₂.

(a) A flowing mixture of CH₃CHI₂/N₂/O₂ (1/21/129, 90 Torr) with and without added NO/NO₂ (∼3.0/0.18 Torr) recorded 0–5 μs, (b) 5–10 μs and (c) 15–20 μs after irradiation at 248 nm. (d) Comparison of experimental data (open circles) with simulated spectrum (thick red solid line) of ν₁₀ of syn-CH₃CHOO. Spectral width of simulation is 2.6 cm⁻¹.

Further indication of the greater reactivity of anti-CH₃CHOO than that of syn-CH₃CHOO comes from the observation of a more rapid decrease of peaks at 851.8 and 883.7 cm⁻¹ (assigned to anti-CH₃CHOO) relative to that at 871.2 cm⁻¹ (assigned to syn-CH₃CHOO) in the earlier stage of reaction. Without NO/NO₂, nearly all anti-CH₃CHOO diminished and only syn-CH₃CHOO survived after 10 μs; syn-CH₃CHOO became nearly diminished after 25 μs. The decay of syn-CH₃CHOO is likely to be mainly due to its self-reaction, similar to that observed for CH₂OO (refs 7, 14, 15). In Supplementary Fig. 7, we plotted the reciprocal absorbance (I⁻¹) integrated from 850 to 900 cm⁻¹ for band A₁ as a function of reaction period; the integrated absorbance I is proportional to concentration. The slope at the initial stage of reaction is twice that at a later stage of reaction. A qualitative analysis indicates that the overall removal of anti-CH₃CHOO could be up to 30 times faster than that of syn-CH₃CHOO; this probably reflects the difference in reactivity of these two conformers associated with some reactions with themselves or with other species. We are unable to derive absolute concentration of CH₃CHOO, because the infrared probe volume does not follow the photolysis volume in our experiments14; hence, accurate rate coefficient cannot be determined. In any case, it is clear that in the CH₃CHI + O₂ system the reactivity of anti-CH₃CHOO is much greater than that of syn-CH₃CHOO, so that most anti-CH₃CHOO was consumed within 10 μs under our experimental conditions. Future theoretical investigations on this distinct conformation-dependent reactivity will provide some insight on this important observation.

Discussion

We recorded the transient infrared spectrum of both syn- and anti-CH₃CHOO, produced from CH₃CHI + O₂ in a flow reactor, using a step-scan Fourier-transform spectrometer. The rotational contours, vibrational wavenumbers and relative infrared intensities of these observed bands provide definitive identification of both conformers; the rotational contours are critical in distinguishing these conformers. The assignments and spectral simulation are guided and supported by high-level full-dimensional quantum calculations. We found that anti-CH₃CHOO is more reactive towards NO/NO₂ than syn-CH₃CHOO. Without NO/NO₂, anti-CH₃CHOO also decays much more rapidly than syn-CH₃CHOO. This feature shall enable one to prepare nearly pure syn-CH₃CHOO either by adding NO/NO₂ or by waiting till a later reaction period. This distinct conformation-dependent reactivity is of fundamental interest and is also important in modelling reactions involving Criegee intermediates both in laboratory and in the atmosphere.

Our infrared identification provides an alternative way to probe CH₃CHOO directly in the atmosphere or in laboratory experiments. Although nearly all observed bands of anti-CH₃CHOO overlapped with syn-CH₃CHOO, the Q-branch of ν₈ near 1,090.6 cm⁻¹ is contributed solely by syn-CH₃CHOO, and that of ν₇ near 1,280.8 cm⁻¹ is also dominated by syn-CH₃CHOO; they can be unambiguously detected with a narrow-width infrared laser. This convenient detection scheme will be useful in providing information on the exact mechanism and detailed kinetics of reactions involving CH₃CHOO.

Methods

Experimental

The White cell of base path length 15 cm and effective absorbing path length 3.6 m was coupled with a step-scan FTIR spectrometer (Bruker, Vertex 80v) and served as a flow reactor. The flow reactor has volume ∼1,370 cm³ and accommodates two rectangular quartz windows (3 × 12 cm²) on opposite sides of the cell, to allow the photolysis beam to propagate through the cell. The photolysis light at 308 nm was generated from a XeCl excimer laser (Coherent, CompexPro 102F, 11 Hz, ∼170 mJ per pulse, beam size 2.9 × 1.2 cm²). In earlier experiments, light at 248 nm from a KrF excimer laser (Coherent, CompexPro 102F, 11 Hz, ∼200 mJ per pulse, beam size 1.5 × 1.0 cm²) was used. The photolysis beam passed the White cell and was reflected five times with two external mirrors, to enhance the photolysis. With appropriate optical filters to allow passage of light in a narrow spectral region, we performed undersampling to decrease the size of the interferogram, hence the duration of data acquisition. The infrared probing light was detected with a HgCdTe detector from which dc- and ac-coupled signals were recorded at each scan step on irradiation with the photolysis laser. These signals were sent either directly to the external 14-bit digitizer with resolution of 4 or 10 ns. For the ac signal, 5,000 data points at 4 (10) ns intervals were acquired to cover a period of 19.8 (48.0) μs after photolysis. These signals were typically averaged over 15 laser shots at each scan step. For spectra in the range 753–1,504 cm⁻¹ at resolution 0.5 cm⁻¹, 3,046 scan steps were completed in ∼1.5 h. For spectra in the range 1,089−1,633 cm⁻¹ at resolution 0.5 cm⁻¹, 2,206 scan steps were completed in ∼1 h. The spectral width (full width half maximum) at this resolution after apodization is 0.64 cm⁻¹. Fourteen spectra recorded under similar conditions were averaged to yield a spectrum with a satisfactory ratio of signal to noise. For experiments with added NO/NO₂, the resolution is 2.0 cm⁻¹ (full width half maximum 2.6 cm⁻¹) and one spectrum was recorded.

A small stream of O₂ from a main stream at flow rate of F_O2≅23 STP cm³ s⁻¹ (STP denotes standard temperature 273 K and pressure 1 atm) served to purge the windows. A small stream of N₂ (∼3.5 Torr in the reactor) was bubbled through liquid CH₃CHI₂ before entering the reactor. The total pressure was maintained in the range P_T=80–85 Torr, with a partial pressure of P_CH3CHI2≅0.28 Torr determined from its infrared absorption spectra. The average efficiency of photolysis of CH₃CHI₂ is estimated to be ∼8% according to an absorption cross-section of ∼3.1 × 10⁻¹⁸ cm² per molecule (ref. 27) and a laser fluence of ∼7 × 10¹⁶ photons per cm² at 308 nm. To obtain a desirable pressure of CH₃CHI₂, the samples and the flow reactor were heated to 328 K with heated water circulated from a thermostated bath through the jacket of the reactor. CH₃CHI₂ (96–98%), O₂ (99.99%) and N₂ (99.9995%) were used as received.

Computational

The harmonic and anharmonic vibrational wavenumbers have been computed using quadratic force field obtained with the MP2 (ref. 34) and the NEVPT2 methods35 implemented in MOLPRO quantum chemistry package36, using a complete active space defined by four highest occupied orbitals and four lowest unoccupied orbitals; no symmetry has been used in these calculations to avoid problems during numerical determination of force-field coefficients. The anharmonic wavenumbers37 have only an approximate character, as the effects of three- and four-mode couplings have been neglected due to great computational complexity.

For CH₃CHOO, we also employed the MULTIMODE method. See Supplementary Methods for more details. The MULTIMODE calculations employ full-dimensional potential energy surfaces (PESs) for syn-CH₃CHOO and anti-CH₃CHOO conformers. Most geometries are generated from classical dynamical trajectories with density functional theory (B3LYP). More points are chosen randomly around the equilibrium geometry and the torsion saddle point. To further increase the accuracy of the PESs, additional points are chosen along the grids of normal mode along the fully relaxed torsion path for both syn- and anti-CH₃CHOO. Finally, we get about 39,000 ab initio energies, which are computed with the CCSD(T)-F12b method38,39 and aug-cc-pVDZ basis for carbon and oxygen atoms, and cc-pVDZ basis for hydrogen atoms.

The PESs are fitted with permutationally invariant method, which has been described in detail somewhere else30,40. The Morse variable is applied in the PES function, in which y_ij=exp(–r_ij/α) and α is fixed at 2 bohr. The maximum polynomial order is 5 for both PES and the number of coefficients is 5,801. The fitting root mean squares of the PESs are 0.076 and 0.068 cm⁻¹ for syn- and anti-CH₃CHOO, respectively. The comparisons of energies and harmonic frequencies between the PES and CCSD(T)-F12b calculation for syn- and anti-conformer are given in Supplementary Tables 9 and 10. As seen, great agreement is achieved between the PES and direct ab initio calculation. In addition, the dipole moment surfaces, which are computed with MP2 methods, are fitted as well for the infrared intensity calculation.

The infrared intensities are calculated using the dipole transition matrix and each element is determined by integrating the ground and vibrationally excited-state wave functions and the dipole moment components. The calculated energies and intensities of fundamental states for syn- and anti-CH₃CHOO are listed in Supplementary Tables 1 and 2. Several fundamental states, especially the CH-stretching modes, are difficult to assign due to their strong coupling with other modes.

Rotation constants of the ground vibrational state and fundamental vibrational states are determined rigorously from calculated energy difference of J=1 and 0. The rotation constants of syn-CH₃CHOO ground vibrational state agree with those determined experimentally24. The computed rotation constants for syn- and anti-CH₃CHOO are shown in Supplementary Tables 7 and 8, respectively. These small energy differences are sensitive to the treatment of the torsion degree of freedom, and so several sets of calculations, including ones that eliminated that degree of freedom, were performed. The rotation constants that appear to be most consistent with the simulation of experimental bands are from the smaller set of calculation with 13 modes coupling for syn-CH₃CHOO (14 modes for anti) and these are given in the tables.

Author contributions

H.Y.L. and Y.H.H. performed the experiments and H.Y.L. analysed the data. X.W. performed the MULTIMODE calculations. Y.N. performed calculations with other methods. J.B. and H.A.W. conceived and designed the calculations, and contributed to writing sections of the paper. Y.P.L. conceived and designed the experiments and wrote a major part of the paper.

Additional information

How to cite this article: Lin, H.-Y. et al. Infrared identification of the Criegee intermediates syn- and anti-CH₃CHOO, and their distinct conformation-dependent reactivity. Nat. Commun. 6:7012 doi: 10.1038/ncomms8012 (2015).

Supplementary Material

Supplementary Information

Supplementary Figures 1-7, Supplementary Tables 1-10, Supplementary Methods and Supplementary References