Abstract
Resting-state functional magnetic resonance imaging allows one to study brain functional connectivity, partly motivated by evidence that patients with complex disorders, such as Alzheimer's disease, may have altered functional brain connectivity patterns as compared with healthy subjects. A functional connectivity network describes statistical associations of the neural activities among distinct and distant brain regions. Recently, there is a major interest in group-level functional network analysis; however, there is a relative lack of studies on statistical inference, such as significance testing for group comparisons. In particular, it is still debatable which statistic should be used to measure pairwise associations as the connectivity weights. Many functional connectivity studies have used either (full or marginal) correlations or partial correlations for pairwise associations. This article investigates the performance of using either correlations or partial correlations for testing group differences in brain connectivity, and how sparsity levels and topological structures of the connectivity would influence statistical power to detect group differences. Our results suggest that, in general, testing group differences in networks deviates from estimating networks. For example, high regularization in both covariance matrices and precision matrices may lead to higher statistical power; in particular, optimally selected regularization (e.g., by cross-validation or even at the true sparsity level) on the precision matrices with small estimation errors may have low power. Most importantly, and perhaps surprisingly, using either correlations or partial correlations may give very different testing results, depending on which of the covariance matrices and the precision matrices are sparse. Specifically, if the precision matrices are sparse, presumably and arguably a reasonable assumption, then using correlations often yields much higher powered and more stable testing results than using partial correlations; the conclusion is reversed if the covariance matrices, not the precision matrices, are sparse. These results may have useful implications to future studies on testing functional connectivity differences.
Key words: : brain networks, correlation, neuroimaging, partial correlation, rs-fMRI, statistical power
Introduction
Resting-state functional magnetic resonance imaging (rs-fMRI) has become a popular methodology for studying brain functional networks (Biswal, 2012). It holds promise for understanding brain functions and revealing disrupted brain connectivity underlying complex disorders, such as Alzheimer's disease (Huang et al., 2010; Wee et al., 2013). Recently, there has been great interest in group-level network analysis with the focus on estimation (Smith et al., 2012); however, in contrast to more established fMRI data analysis (Zhu et al., 2014), there is a relative lack of studies on drawing statistical inference, particularly for group comparisons in brain networks (Varoquaux and Craddock, 2013). For example, based on a study comparing functional networks between patients with Alzheimer's disease and a control group, even though estimated networks for the two groups may suggest some altered subnetworks, are the identified differences genuine? A rigorous statistical test can address this question before one possibly over-interprets the results based on the two point estimates. This is particularly important given often small sample sizes and high noise levels in rs-fMRI data.
A network is defined in graph theory as a set of nodes (or vertices) and the edges with weights between them. In the case of brain functional connectivity, nodes are spatial regions of interest (ROIs), for example, as obtained from brain atlases or from functional localizer tasks (Smith et al., 2011). A weight (either binary or continuous) is assigned to each edge to measure the association between the two nodes, for example, based on their BOLD time-course signals. Group comparison aims at testing whether the edge weights are different or not across groups. However, there is still a debate on what a continuous measure of pairwise association (or an edge-weight) should be used to characterize functional connectivity, which has important implications to not only estimation but also testing (Varoquaux and Craddock, 2013).
Many functional connectivity studies have used Pearson's (full or marginal) correlation between two nodes' BOLD time-course signals (Azari et al., 1992; Horwitz et al., 1987; Kim et al., 2014; Stam et al., 2007; Supekar et al., 2008), which is easy to calculate based on a sample covariance matrix. However, a drawback of using correlations is that it may not be able to distinguish whether the functional connection between two nodes is direct or not. Namely, a correlation captures the marginal association between two nodes, which may be caused by a third node. This distinction between marginal correlation and true, direct functional connection is very important if one aims at estimating the structure of a network (Huang et al., 2010). It is also relevant to testing because the numbers and magnitudes of nonzero associations may change with the specific measure being used, possibly influencing the final testing result. To overcome this limitation, a number of studies adopted partial correlations (Marrelec et al., 2006; Salvador et al., 2005). The partial correlation quantifies the association between two brain regions, conditioning on the other regions, where a zero partial correlation represents the absence of an edge in the estimated network, indicating conditional independence under the Gaussian assumption. Smith and colleagues (2011) concluded that network estimation using partial correlations outperformed that using correlations (when a suitable regularization was applied). A precision matrix, also called inverse covariance matrix, is useful for estimating partial correlations (Marrelec et al., 2006). Even with a small sample size (and/or high-dimensional data), we can estimate a precision matrix by applying regularization as implemented in the graphical lasso method (Banerjee et al., 2008; Friedman et al., 2008). In other words, the graphical lasso allows identifying not only the network structure (i.e., the zero and nonzero entries in the precision matrix) but also the edge weights for a large number of brain regions with even a small sample size.
However, even with some benefits from using partial correlations for network estimation, it is unknown whether using partial correlations as edge weights gives necessarily higher statistical power than using correlations to test group differences in brain connectivity. A key issue is that “partial correlations are intrinsically harder to estimate” (Varoquaux and Craddock, 2013). For example, with a small sample size, some regularization is necessary for estimating a precision matrix, but not for a covariance matrix, while suitable regularization is not trivial in practice. In addition, the power to test group differences may depend on some other factors, such as the sparsity levels of the networks to be tested. These issues have not been adequately addressed earlier; it is the goal of this article to investigate these issues.
We considered both correlations and partial correlations as edge weights at various sparsity levels of the estimated brain functional networks to test for differences between fetal alcohol spectrum disorder (FASD) patients and controls. Wozniak and colleagues (2013) used correlations to reveal significantly altered network connectivities in children with FASD based on the network measures of characteristic path and global efficiency. Kim and colleagues (2014) compared several statistical tests and concluded that two tests, network-based statistic (NBS) (Zalesky et al., 2012) and an adaptive sum of powered score (aSPU) test (Pan et al., 2014), were complementary to each other with at least one often showing great power in testing group differences in brain connectivity. NBS is a useful test developed in the neuroimaging community for detecting altered subnetworks while attaching a statistical significance. It takes advantage of the earlier assumption that altered edges would form connected subnetworks, and hence is believed to offer high power when the assumption holds. On the other hand, the aSPU test, built on a class of so-called sum of powered score (SPU) tests, does not impose such an assumption, and was found to be complementary to NBS with higher power under some situations when the goal is to assess overall network differences. Also, comparing some global network measures between two groups is a popular way to demonstrate brain connectivity differences (Wozniak et al., 2013). We adopted the aSPU and SPU tests, NBS, and several global network measures to compare brain connectivity between two groups. Our goal is not to directly compare these tests, but to investigate how they perform with the use of correlations and partial correlations to describe brain networks.
We used both the real FASD data and simulated data mimicking the FASD data. Our numerical study confirmed that suitable regularization on estimating covariance and precision matrices would have implications to the power of a test being applied to the estimated correlations or partial correlations. However, it was generally difficult to choose suitable regularization, especially for testing. For example, although cross-validation (CV) performed well in selecting suitable regularization parameters for network estimation, leading to nearly minimal estimation errors, a test using such estimated networks might be low powered. Most importantly, our study showed that the relative power of testing with either correlations or partial correlations depended on the sparsity levels of the true covariance and precision matrices. For example, if the true precision matrices for the two groups were sparse, using correlations as edge weights often gave higher power than using partial correlations in testing group differences. Note that a sparse precision matrix often induces a corresponding nonsparse covariance matrix; given that a precision matrix, but not a covariance matrix, can distinguish between direct and indirect connections in a network, assuming sparse precision matrices seems to be reasonable. On the other hand, the conclusion was the opposite if the true covariance matrices were indeed sparse. These results may have useful implications to future studies comparing functional connectivity.
This article is organized as follows. After introducing data and notation for brain connectivity, we review estimation methods for covariance and precision matrices for brain connectivity, followed by statistical methods for testing group differences in brain functional connectivity. In Application to the FASD Data section, we apply the described methods to the FASD data using either correlations or partial correlations with varying sparsity levels, to examine how the test results change for functional connectivity differences between a group of FASD patients and a control group. In Simulations section, we use simulated data mimicking the FASD data to investigate the effects of edge weights, true or estimated network sparsity levels, and other factors on testing results. We summarize the main conclusions and some related future work in Results section.
Materials and Methods
Data and notation
To test for between-group differences in brain connectivity, we consider a two-group scenario with a binary response/disease indicator and with possible covariates. For the disease status of subject 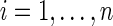 , we denote Yi=0 for controls, Yi=1 for cases. We denote
, we denote Yi=0 for controls, Yi=1 for cases. We denote 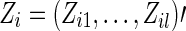 as the covariates for subject i.
as the covariates for subject i.
To compare brain functional connectivity between two groups, one must first estimate a connectivity (adjacency) matrix (or a network) for each subject. The connectivity matrix corresponds to a graph model (Bullmore and Sporns, 2009). Suppose we have N distinct brain ROIs that define the nodes of the networks or graphs, and suppose at each node brain activity is measured as fMRI BOLD time series at M time points. In a Gaussian graphical model, the BOLD signals from N regions across time points t, 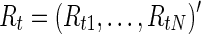 for
for 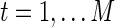 , are independent and identically distributed as a multivariate Gaussian N(μ, Σ), where
, are independent and identically distributed as a multivariate Gaussian N(μ, Σ), where 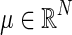 and ΣN×N is a positive definite covariance matrix. As a continuous measure of a pairwise association between two nodes, both (full) correlation and partial correlation are widely used. This measure is stored in a symmetric N×N connectivity matrix, where N is the total number of nodes. Each row/column of the connectivity matrix corresponds to a distinct node, such that position (p, q) uniquely stores the measured association between the pth and qth nodes' time series (i.e., Rtp and Rtq for
and ΣN×N is a positive definite covariance matrix. As a continuous measure of a pairwise association between two nodes, both (full) correlation and partial correlation are widely used. This measure is stored in a symmetric N×N connectivity matrix, where N is the total number of nodes. Each row/column of the connectivity matrix corresponds to a distinct node, such that position (p, q) uniquely stores the measured association between the pth and qth nodes' time series (i.e., Rtp and Rtq for 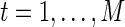 ).
).
The (full) correlation would measure the marginal association of the signals in two ROIs, which can be easily estimated from a sample covariance matrix,
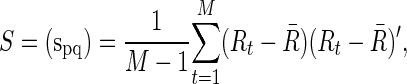 |
an unbiased estimator of Σ, where 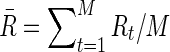 . For
. For 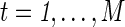 , the full correlation between nodes p and q, Corr(Rtp, Rtq) is estimated as
, the full correlation between nodes p and q, Corr(Rtp, Rtq) is estimated as 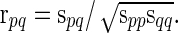
The partial correlations are obtained from the precision (i.e., inverse covariance) matrix Θpq=(θpq)=Σ. If we denote the partial correlation between nodes p and q by ρpq, it is defined as 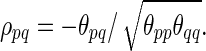 A partial correlation refers to the normalized correlation between two time series, conditioned on other time series from all other network nodes (Smith et al., 2011); ρpq =Corr(Rtp, Rtq|R–(p,q)) where
A partial correlation refers to the normalized correlation between two time series, conditioned on other time series from all other network nodes (Smith et al., 2011); ρpq =Corr(Rtp, Rtq|R–(p,q)) where 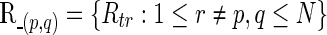 . Therefore, ρpq being nonzero is equivalent to Rtp and Rtq being conditionally dependent given all other variables
. Therefore, ρpq being nonzero is equivalent to Rtp and Rtq being conditionally dependent given all other variables  . Hence, partial correlations distinguish direct and indirect connections between two nodes, and for this reason, they are preferred compared with full correlations in the literature for network estimation (Huang et al., 2010; Marrelec et al., 2006; Smith et al., 2011). However, several problems can arise in estimating Θ. First, in a high-dimensional setting where the number of variables N is larger than the number of observations M, the sample covariance matrix S is singular and so cannot be inverted to yield an estimate of Θ. If N≈M, then even if S is not singular,
. Hence, partial correlations distinguish direct and indirect connections between two nodes, and for this reason, they are preferred compared with full correlations in the literature for network estimation (Huang et al., 2010; Marrelec et al., 2006; Smith et al., 2011). However, several problems can arise in estimating Θ. First, in a high-dimensional setting where the number of variables N is larger than the number of observations M, the sample covariance matrix S is singular and so cannot be inverted to yield an estimate of Θ. If N≈M, then even if S is not singular,  could be unstable with high variability. Hence, regularization is imposed to yield a better estimate
could be unstable with high variability. Hence, regularization is imposed to yield a better estimate  .
.
With either full correlations or partial correlations, once a symmetric N×N connectivity matrix is estimated for each subject, there are k=N×(N−1)/2 unique pairwise associations in it, since each node is potentially connected with every other node. Accordingly, each subject has k association measures for brain connectivity. Often the association measures (i.e., full correlations or partial correlations) are normalized by applying Fisher's z-transformation and we denote the k continuous association measures of subject i's brain connectivity as 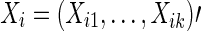 .
.
In matrix notation, we denote Yn×l as a vector for disease indicators, Xn×k as a matrix of pairwise associations between nodes (with each element as a z-transformed correlation or partial correlation), and Zn×l as a covariate matrix.
Estimating covariance and precision matrices via graphical lasso
Often one is interested in identifying pairs of ROIs that are unconnected in a network, which are conditionally independent; these correspond to zero entries in Θ with zero partial correlations between nodes. As discussed earlier, partial correlations can be estimated from the precision matrix, and a natural way to estimate the precision matrix Θ is to invert S. However, taking the inverse of S will, in general, yield a 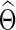 with no elements that are exactly equal to zero. More importantly, in high-dimensional and small sample size settings, due to the singularity problem, it is challenging to estimate Θ directly. More generally, some regularization can be imposed to obtain better estimates for a precision matrix.
with no elements that are exactly equal to zero. More importantly, in high-dimensional and small sample size settings, due to the singularity problem, it is challenging to estimate Θ directly. More generally, some regularization can be imposed to obtain better estimates for a precision matrix.
Banerjee and colleagues (2008) and Friedman and colleagues (2008) proposed a regularized estimator for a precision matrix Θ. The resulting estimate 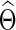 can be sparse or nonsparse, depending on the extent of regularization imposed. Specifically, for subject i, its estimate of precision matrix is obtained by maximizing the subject-specific penalized log likelihood,
can be sparse or nonsparse, depending on the extent of regularization imposed. Specifically, for subject i, its estimate of precision matrix is obtained by maximizing the subject-specific penalized log likelihood,
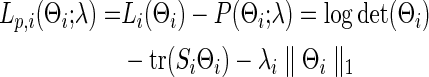 |
over the semi-positive definite Θi, where tr denotes the trace, Si is the sample covariance based on the subject i's BOLD time series, 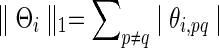 is the L1 norm for nondiagonal elements, and λi≥0 is a regularization parameter to be determined. Note that
is the L1 norm for nondiagonal elements, and λi≥0 is a regularization parameter to be determined. Note that 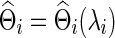 is a function of λi, and for simplicity we may suppress this dependency in notation. Consequently, imposing a high penalty (with a large λi) tends to increase the sparsity level of the estimated precision matrix. The optimal
is a function of λi, and for simplicity we may suppress this dependency in notation. Consequently, imposing a high penalty (with a large λi) tends to increase the sparsity level of the estimated precision matrix. The optimal 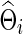 could be estimated from
could be estimated from 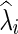 selected by a model selection criterion, often by maximizing a predictive loglikelihood based on CV. Thus, we obtain
selected by a model selection criterion, often by maximizing a predictive loglikelihood based on CV. Thus, we obtain
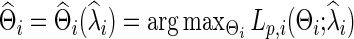 |
in which we also obtain a regularized estimate for the covariance matrix 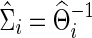 . These
. These 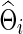 and
and 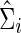 (with the same value of λi) are used to estimate the partial correlations and full correlations, respectively, to which we apply Fisher's z-transformation to generate brain connectivity data
(with the same value of λi) are used to estimate the partial correlations and full correlations, respectively, to which we apply Fisher's z-transformation to generate brain connectivity data 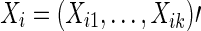 to be tested.
to be tested.
In our study, to test group differences in brain connectivity, we tried several ways to choose the regularization parameter λi. First, we tried to choose λi for each subject i separately. Second, we chose λi at the group-level; that is, we chose a common 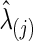 for all subjects in a group j. Since we assume a common covariance matrix within each group, the second way is more efficient; furthermore, the first way also gave results similar to the second way. Hence, we only describe the second way here. Denote the two groups as G(j), j=1, 2. Ten-fold CV was performed to estimate the optimal
for all subjects in a group j. Since we assume a common covariance matrix within each group, the second way is more efficient; furthermore, the first way also gave results similar to the second way. Hence, we only describe the second way here. Denote the two groups as G(j), j=1, 2. Ten-fold CV was performed to estimate the optimal 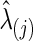 that maximizes the sum of group members' predictive log likelihood. Briefly, we split data into 10 almost equally sized subsets: 9 subsets form training data, while the other subset forms validation data. Given a candidate λ(j), the following two steps were performed repeatedly 10 times for each possible training-validation data partition for each group: Step 1. Apply the graphical lasso to the training data, obtaining a group level,
that maximizes the sum of group members' predictive log likelihood. Briefly, we split data into 10 almost equally sized subsets: 9 subsets form training data, while the other subset forms validation data. Given a candidate λ(j), the following two steps were performed repeatedly 10 times for each possible training-validation data partition for each group: Step 1. Apply the graphical lasso to the training data, obtaining a group level, 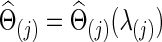 . Step 2. Based on
. Step 2. Based on 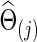 for j=1 and 2, evaluate the predictive log likelihood for the validation data. At the end, we sum over the predictive log likelihoods across the 10 partitions to obtain total predictive log likelihood. Using a grid search, we found
for j=1 and 2, evaluate the predictive log likelihood for the validation data. At the end, we sum over the predictive log likelihoods across the 10 partitions to obtain total predictive log likelihood. Using a grid search, we found 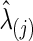 , which maximizes the total predictive log likelihood. Then, we apply the graphical lasso to all the data for each subject
, which maximizes the total predictive log likelihood. Then, we apply the graphical lasso to all the data for each subject 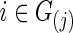 separately to obtain
separately to obtain 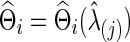 . The subject-level covariance matrix estimate
. The subject-level covariance matrix estimate 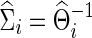 is also obtained. Note that the selected group-level regularization parameters
is also obtained. Note that the selected group-level regularization parameters 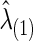 and
and 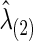 may be different, but in practice, they were very close as shown in our later example.
may be different, but in practice, they were very close as shown in our later example.
The graphical lasso can be also used to estimate brain connectivity with varying sparsity levels, which not only avoids the difficult issue of choosing a suitable 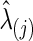 for each group but also offers an opportunity to investigate how testing results change with the varying network estimates. By using various values of the regularization parameter, we can estimate a precision matrix at a pre-defined sparsity level. To compare between-group differences in brain connectivity, a number of studies (Huang et al., 2010; Stam et al., 2007; Supekar et al., 2008) adopted a strategy to control the sparsity levels of the brain networks to be the same for all the groups, avoiding possible artifacts of any differences coming from topological or structural differences among the estimated networks. Suppose c is the target sparsity level, defined as connection density or the proportion of the nonzero elements in a precision matrix. In our study, we tried to find the group-level value
for each group but also offers an opportunity to investigate how testing results change with the varying network estimates. By using various values of the regularization parameter, we can estimate a precision matrix at a pre-defined sparsity level. To compare between-group differences in brain connectivity, a number of studies (Huang et al., 2010; Stam et al., 2007; Supekar et al., 2008) adopted a strategy to control the sparsity levels of the brain networks to be the same for all the groups, avoiding possible artifacts of any differences coming from topological or structural differences among the estimated networks. Suppose c is the target sparsity level, defined as connection density or the proportion of the nonzero elements in a precision matrix. In our study, we tried to find the group-level value 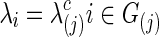 so that each subject's precision matrix has a connection density around c. Denote
so that each subject's precision matrix has a connection density around c. Denote 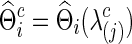 for each
for each 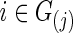 . Accordingly, we obtain
. Accordingly, we obtain 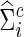 as the inverse of
as the inverse of 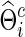 ; note that, in this way, the connection density c is for the precision matrix estimate, not for the covariance matrix estimate. As stated earlier, for any fixed c, we obtain marginal correlations and partial correlations for each subject, from which we test for group differences. At a lower estimated connection density, we test between-group differences with fewer but stronger individual brain connections, which, however, may ignore many weak connections and thus lead to loss of power. On the other hand, at higher estimated connection densities, many weak, including spurious, connections are introduced and thus may also yield low-powered testing. We also applied the same λi=λ for all subjects in both groups, and obtained similar results, as to be shown.
; note that, in this way, the connection density c is for the precision matrix estimate, not for the covariance matrix estimate. As stated earlier, for any fixed c, we obtain marginal correlations and partial correlations for each subject, from which we test for group differences. At a lower estimated connection density, we test between-group differences with fewer but stronger individual brain connections, which, however, may ignore many weak connections and thus lead to loss of power. On the other hand, at higher estimated connection densities, many weak, including spurious, connections are introduced and thus may also yield low-powered testing. We also applied the same λi=λ for all subjects in both groups, and obtained similar results, as to be shown.
Testing group differences in brain functional connectivity
We have discussed how to estimate subject-specific networks based on their covariance or precision matrices, from which subject-specific brain connectivity data 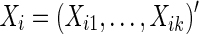 can be constructed using full correlations or partial correlations. Next, we review several representative statistical tests for group differences in brain connectivity.
can be constructed using full correlations or partial correlations. Next, we review several representative statistical tests for group differences in brain connectivity.
SPU and aSPU
The SPU test is a global test originally proposed for the association analysis of genomic data (Pan et al., 2014), but Kim and colleagues (2014) showed that it maintains great power for brain connectivity data. The SPU tests are a family of association tests such that at least one of them is powerful for a given situation. Each SPU test is based on the score vector from a general regression model. Consider a logistic regression model where k functional connections and l covariates are predictors:
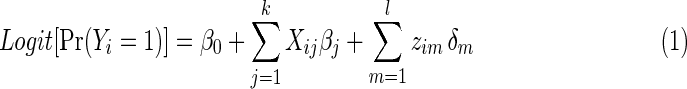 |
The null hypothesis to be tested is 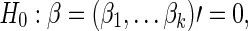 that is, no group differences in functional brain connectivity. Under the null hypothesis H0, the full model (1) is reduced to
that is, no group differences in functional brain connectivity. Under the null hypothesis H0, the full model (1) is reduced to
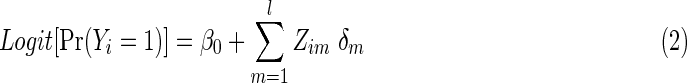 |
Denote the score vector for 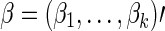 as
as 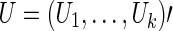 . Suppose
. Suppose 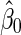 and
and 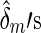 are maximum likelihood estimates under the null model (2) and
are maximum likelihood estimates under the null model (2) and 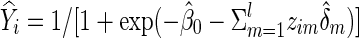 . Denote a residual
. Denote a residual 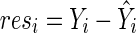 for
for 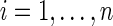 . Then, the SPU test is based on the score,
. Then, the SPU test is based on the score,
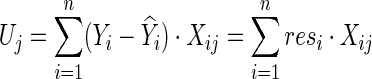 |
Note that, unless Xij=0 for all subjects i, the weights of the edge j across the subjects i contribute to the score vector. Given γ≥1, the test statistic of the SPU(γ) test is
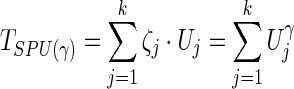 |
where 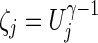 can be regarded as a weight for the jth component of U. With various values of integer γ≥1, one or more of the SPU(γ) tests may maintain high power across a wide range of unknown truth. As γ increases, the SPU(γ) test puts more weights on the larger components of U. Eventually, as γ→∞ , it only takes the maximum component of the score vector and the test statistic is defined as
can be regarded as a weight for the jth component of U. With various values of integer γ≥1, one or more of the SPU(γ) tests may maintain high power across a wide range of unknown truth. As γ increases, the SPU(γ) test puts more weights on the larger components of U. Eventually, as γ→∞ , it only takes the maximum component of the score vector and the test statistic is defined as 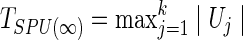 , which mimics mass-univariate testing.
, which mimics mass-univariate testing.
To draw statistical inference, Pan and colleagues (2014) proposed using permutations: First, we fit the null model to obtain 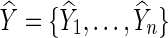 , and obtain residuals
, and obtain residuals 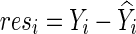 ; we permute the original set of residuals
; we permute the original set of residuals 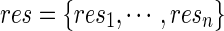 to create a new set of residual res(b), based on which we calculate the score vector U(b) and the null statistic
to create a new set of residual res(b), based on which we calculate the score vector U(b) and the null statistic 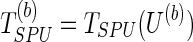 ; with
; with 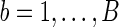 permutations, we compute the p-value as
permutations, we compute the p-value as 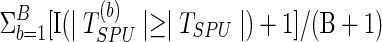 .
.
The power of the SPU(γ) test depends on the choice of γ. Pan and colleagues (2014) proposed an aSPU test that combines the p-values of multiple SPU tests with various values of γ, and its test statistic is defined as
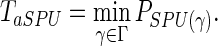 |
In this article, we considered 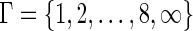 .
.
To obtain the p-value of aSPU test, we calculate a SPU test statistics TSPU(γ)(b) and corresponding p-value 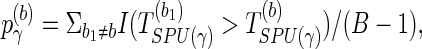 for
for 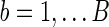 ; calculate the test statistics of aSPU,
; calculate the test statistics of aSPU, 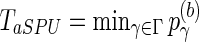 . The p-value of the aSPU test is obtained as follows:
. The p-value of the aSPU test is obtained as follows: 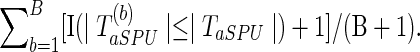
In this article, we focus on the use of SPU tests with γ=1, 2, and∞, since these three cases correspond to some known tests in the neuroimaging research community: SPU(1) test is similar to an fMRI network test proposed in Meskaldji and colleagues (2011); as pointed out in Kim and colleagues (2014), SPU(2) is closely related to multivariate distance matrix regression used by Shehzad and colleagues (2014), Reiss and colleagues (2010), and McArdle and Anderson (2001). SPU(∞) can be regarded as a mass-univariate testing (Nichols and Holmes, 2001). Weighted versions of the SPU and aSPU tests discussed in Kim and colleagues (2014) were also applied to numerical examples here; since they yielded similar results to those of SPU and aSPU tests, we skip their discussion.
R code for SPU and aSPU tests will be available at www.biostat.umn.edu/∼weip/prog.html.
Network-based statistic
NBS aims at detecting disrupted subnetworks across groups (Zalesky et al., 2010). It assumes and takes advantage of the proposition that the edges with altered weights cluster together and form some connected subnetworks; it uses the size of the largest altered subnetwork as its test statistic. In the presence of such clustering with disrupted subnetworks, NBS can potentially yield greater power than edge-based tests that ignore such clustering.
For each edge 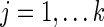 , a univariate edge-based test is separately applied to each connection. For the jth connection, we can consider a linear model,
, a univariate edge-based test is separately applied to each connection. For the jth connection, we can consider a linear model,
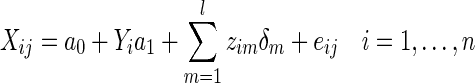 |
where the errors eij are assumed to be independent and identically distributed as N(0, σ2). We formulate a t contrast at each edge separately to test the null hypothesis H0 : a1=0. Denote 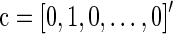 ,
, 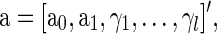 and D=[1 Y
Z]. The jth connection can be tested with the following t-statistic:
and D=[1 Y
Z]. The jth connection can be tested with the following t-statistic:
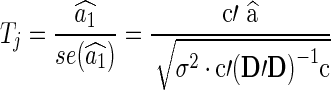 |
where 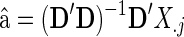 and
and 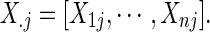
NBS discovers “supra-threshold edges” by selecting the edges that have test statistics Tj's exceeding a predetermined threshold, and it identifies the size of the largest such sub-network or cluster that is composed of the connected supra-threshold edges. Denote the size of the largest cluster as s. To draw inference, NBS employs permutations. In each permutation  , disease statuses of the subjects are randomly permuted and with each permuted sample, it measures the maximum size of the cluster, s(b), that is, maximum number of connected supra-threshold-edges. This yields an empirical null distribution of the maximal supra-threshold cluster size. Then, a p-value for the test of group network differences is calculated using this null distribution: p-value=
, disease statuses of the subjects are randomly permuted and with each permuted sample, it measures the maximum size of the cluster, s(b), that is, maximum number of connected supra-threshold-edges. This yields an empirical null distribution of the maximal supra-threshold cluster size. Then, a p-value for the test of group network differences is calculated using this null distribution: p-value=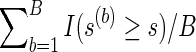 .
.
Such a supra-threshold-cluster test is believed to be more powerful than mass univariate edge-based testing. However, since mass univariate testing is low powered with small sample sizes, even in the presence of clustered edges with changed weights, they may not be detected. Hence, when either true or detected edges with changed weights are isolated from each other, forming no clusters, NBS will lose power (Zalesky et al., 2010). Furthermore, the power of NBS depends on the threshold being used, which is difficult to choose in practice (Kim et al., 2014). For ease of understanding, we follow the notation in Kim and colleagues (2014) where nbs(t) is defined as the NBS test with a predetermined threshold t, representing the tth percentile in absolute values of Tj's. We applied the NBS tests with multiple values of t, showing the power dependence on t; it is noted that, if we want to choose a single t giving the highest power, a multiple-testing adjustment is needed, though we do not pursue it here.
Software for the Network Based Statistic is available at https://sites.google.com/site/bctnet/comparison/nbs
Global network measures
Brain networks can be characterized by a few neurobiologically meaningful global network measures. Rubinov and Sporns (2010) discussed many global network measures that detect functional integration and segregation, quantify centrality of individual brain regions or pathways, characterize patterns of local anatomical circuitry, and test resilience of networks to insult. Each global network measure is computable with some positive normalized weights wij (i.e., 0≤wij≤1) for any edge connecting nodes i and j, or with a binary measure denoting the presence or absence of the connection.
Based on partial correlations and correlations, we consider four global network measures; characteristic path length (Charpath), global efficiency (Eglob), local efficiency (Elocal), and mean clustering coefficient (Eclust) to compare the FASD patient group with the controls.
For each subject, all pairwise associations (either correlations or partial correlations) are measured, and a weighted (not binary) network metric such as global efficiency is computed. We test group differences in each network measure based on logistic regression.
Open source Matlab toolbox BCT provides functions to calculate global network measures at www.brain-connectivity-toolbox.net.
Application to the FASD Data
MRI acquisition and processing
We used the FASD data of Wozniak and colleagues (2013). For the initial MRI data acquisition, a Siemens 3T TIM Trio MRI scanner with a 12-channel parallel array head coil was used. Scans included a structural T1-weighted scan, a resting-state fMRI scan (TR=2000 msec, TE=30 msec, 34 interleaved slices, no skip, voxel size=3.45×3.45×4.0 mm, FOV=220 mm, flip angle=77°, 180 measures), and a field map; Additional details are included in Wozniak and colleagues (2013). During the resting-state scan, participants were instructed to close their eyes and remain still.
The fMRI data were processed with modified “1000 Functional Connectome (TFC)” pre-processing scripts (www.nitrc.org/plugins/mwiki/index.php/fcon_1000). Tools from AFNI (Cox, 1996) and the FMRIB Software Library (FSL) version 4.1.6 (Smith et al., 2004; Woolrich et al., 2009) were used in the TFC processing. This included skull stripping, motion correction, geometric distortion correction using FSL's FUGUE (added to the TFC pipeline), spatial smoothing (FWHM of 6 mm), grand mean scaling, band-pass temporal filtering (0.005–0.1 Hz), and quadratic de-trending. The TFC processing of the T1 volume included skull stripping and FSL's FAST tissue segmentation to define whole brain, white matter, and ventricular cerebrospinal fluid (CSF) ROIs. The skull-stripped T1 and tissue segmentation ROIs were registered to the fMRI data using FSL's FLIRT. Timecourses from the three tissue segmentation ROIs, along with the six motion parameters, were used as voxel-wise nuisance regressors in the TFC processing of the fMRI data. Cortical parcellation of the T1 volume in 34 ROIs was done with FreeSurfer version 4.5 (surfer.nmr.mgh.harvard.edu) (Dale et al., 1999). Data were visually inspected, but hand-editing was not employed.
The 68 Freesurfer cortical parcellations (34 per hemisphere) were registered to the TFC-processed fMRI data using Freesurfer's bbregister (Greve and Fischl, 2009). The parcellations were dilated during registration. but none were allowed to overlap and voxels outside the TFC brain mask were excluded. ROIs that contained fewer than 10 fMRI voxels for any subject were excluded from the final analysis. This resulted in the exclusion of 6 ROIs (bilateral entorhinal, frontal pole, and temporal pole), leaving a total of 62 ROIs (31 per hemisphere). The mean fMRI time series of all voxels within each ROI were then extracted for each subject. In this paper, we added 12 subcortical ROIs to have a total of 74 ROIs.
Data analysis
Kim and colleagues (2014) applied various statistical tests to compare brain functional connectivity in 24 FASD patients, aged 10–17, with 31 matched controls using resting-state fMRI; more details of the original study can be found in Wozniak and colleagues (2013). The resting-state fMRI time-series signals for each region were measured at 180 time points. They considered N=74 cortical and sub-cortical ROIs and applied Fisher's z-transformation to the Pearson correlations between all pairs of N=74 ROIs for k=2701 edges to test the group differences.
In this paper, both partial correlations and correlations are used as the edge weights in subject-specific networks for testing between-group differences in brain connectivity. The regularization parameter λi was chosen in two ways. The first was to use a CV-selected group-level value: 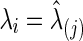 for all
for all 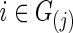 and j=1, 2. The second strategy was to control both groups to have a similar connection density (i.e., number of nonzero entries) in their estimated precision matrices as suggested by Huang and colleagues (2010); we set
and j=1, 2. The second strategy was to control both groups to have a similar connection density (i.e., number of nonzero entries) in their estimated precision matrices as suggested by Huang and colleagues (2010); we set 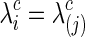 for all
for all 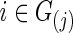 with various values of c. To create various sparsity levels of the estimated precision matrices, we gradually increased the regularization parameters
with various values of c. To create various sparsity levels of the estimated precision matrices, we gradually increased the regularization parameters 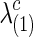 and
and 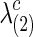 for both groups.
for both groups. 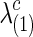 and
and 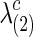 were calibrated so that the two groups had almost the same pre-defined connection density c. At the end, we applied the SPU, aSPU, NBS, and global network measures to test the group differences in brain functional connectivity.
were calibrated so that the two groups had almost the same pre-defined connection density c. At the end, we applied the SPU, aSPU, NBS, and global network measures to test the group differences in brain functional connectivity.
Using CV, we found the optimal 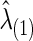 to estimate the best sparsity level of the precision matrix for each group. The control group had
to estimate the best sparsity level of the precision matrix for each group. The control group had 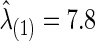 , at which the connection density (i.e., proportion of nonzero elements) of the estimated covariance matrix was 100% and that of the estimated precision matrix was 48%. For the FASD patient group, we had
, at which the connection density (i.e., proportion of nonzero elements) of the estimated covariance matrix was 100% and that of the estimated precision matrix was 48%. For the FASD patient group, we had 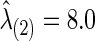 , giving 100% nonzero entries in the estimated covariance matrix and 50% in the estimated precision matrix, respectively. The p-values of the various tests with CV-selected
, giving 100% nonzero entries in the estimated covariance matrix and 50% in the estimated precision matrix, respectively. The p-values of the various tests with CV-selected 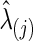 values are shown in Table 1. When using the correlations, we observed statistically significant group differences in brain connectivity. However, when using partial correlations, without multiple-testing adjustments, only some NBS tests detected significant differences between the two groups.
values are shown in Table 1. When using the correlations, we observed statistically significant group differences in brain connectivity. However, when using partial correlations, without multiple-testing adjustments, only some NBS tests detected significant differences between the two groups.
Table 1.
p-Values for Testing Group Differences in Brain Connectivity with the Cross-Validation-Selected 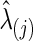 Values at the Group Level with the Fetal Alcohol Spectrum Disorder Data
Values at the Group Level with the Fetal Alcohol Spectrum Disorder Data
| Edge-weight |  |
 |
SPU(1) | SPU(2) | SPU(∞) | aSPU | nbs(0.1) | nbs(0.2) | nbs(0.5) | nbs(0.75) | nbs(0.9) | nbs(0.95) | Charpath | Eclust | Eglob | Eloc |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Corr | 7.8 | 8.0 | 0.012 | 0.320 | 0.675 | 0.038 | 0.005 | 0.005 | 0.030 | 0.050 | 0.103 | 0.096 | 0.477 | 0.162 | 0.216 | 0.126 |
| Part. corr | 7.8 | 8.0 | 0.613 | 0.357 | 0.703 | 0.732 | 0.012 | 0.030 | 0.052 | 0.022 | 0.390 | 0.612 | 0.423 | 0.134 | 0.556 | 0.174 |
aSPU, adaptive sum of powered score; SPU, sum of powered score.
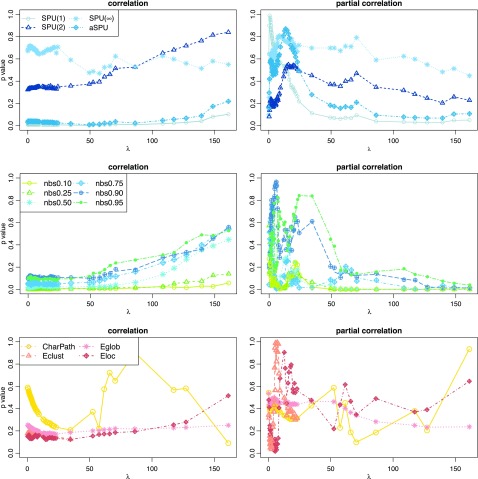
Figure 1 illustrates how the p-value of each test changes with the sparsity level of the estimated networks. We gradually increased both groups' regularization parameters λ(1) and λ(2) so that they shared a similar and decreasing connection density, then applied the group comparison tests. For simplicity, in Figure 1, we report a mean value of 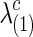 and
and 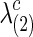 as λ, and they were very close. The results of p-values are color coded by statistical tests and sorted by plotting symbols for each category of the tests. Left panels show the p-values for testing group differences when using correlations, while right panels show those with partial correlations.
as λ, and they were very close. The results of p-values are color coded by statistical tests and sorted by plotting symbols for each category of the tests. Left panels show the p-values for testing group differences when using correlations, while right panels show those with partial correlations.
FIG. 1.
p-Values as a function of the regularization parameter for testing brain network differences with the fetal alcohol spectrum disorder data: left panel shows the p-values for testing group differences, using correlations sorted and color coded by statistical tests and each kind. Right panel shows the p-values with using partial correlations. Color images available online at www.liebertpub.com/brain
When using correlations, the p-value of a test tended to increase as λ increased (i.e., as higher regularization was applied to the precision matrix). When using partial correlations, the p-value did not show any consistent pattern: With no or little regularization, the p-values were unstable and fluctuated widely; with λ larger than 40, the p-values decreased and became stable.
Simulations
Using simulated data generated to mimic the FASD data, we compared whether using correlations would perform differently from using partial correlations, in terms of statistical power to detect network differences between two groups. Group differences in networks were generated in two ways: Unstructured differences were scattered across the networks, and structured differences with altered edges formed some clustered subnetworks in brain connectivity. Time-series data were generated from a multivariate Gaussian model, in which the mean vector was all zeros and a true group-level covariance matrix Σ(j) for j=1 or 2 was used. Our goal was to explore the effects of the sparsity levels of the true group-level precision matrices 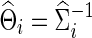 on testing power. Partial correlations were estimated from the subject-specific
on testing power. Partial correlations were estimated from the subject-specific 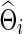 , which, in turn, could be estimated via CV or at various connection density levels with the graphical lasso; similarly, correlations were estimated from the corresponding
, which, in turn, could be estimated via CV or at various connection density levels with the graphical lasso; similarly, correlations were estimated from the corresponding 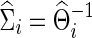 . For the main factors influencing power, the connection density of estimated precision matrices and that of the true precision matrices were considered. The number of time points of time-series of each subject was also explored for its possible effect on the power of testing group differences.
. For the main factors influencing power, the connection density of estimated precision matrices and that of the true precision matrices were considered. The number of time points of time-series of each subject was also explored for its possible effect on the power of testing group differences.
Simulation set-ups
Set-up 1: unstructured differences in brain networks
The differences between two group-level networks could come from isolated edges forming no topological structures. To create a realistic setting, the true nonsparse covariance matrix for 74 ROIs was estimated for each group of the FASD data as S(1) and S(2). From these group-level nonsparse covariance matrices, we generated different levels of sparse precision matrices by applying the graphical lasso. For example, if we tended to have connection density T=0.20 (i.e., having 20% of nonzero entries) for the true precision matrix, we applied different regularization parameters for each group via graphical lasso to create the sparse precision matrices, 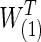 and
and 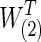 . In our simulations, we would control the group differences with a parameter
. In our simulations, we would control the group differences with a parameter 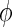 to have a wide range of power across the simulation scenarios, and used the true precision matrices as
to have a wide range of power across the simulation scenarios, and used the true precision matrices as
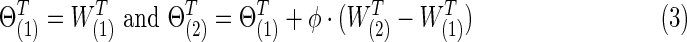 |
With 0≤φ≤1, each 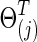 was positive definite. The corresponding true covariance matrices were obtained as
was positive definite. The corresponding true covariance matrices were obtained as 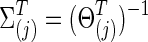 . Note that “T” represents the connection density of the true precision matrices, not of the covariance matrices. In our study, φ was set at 0 to generate simulated data with no group differences in brain connectivity, which were used for calculating type I error rates; or φ=0.15 for simulating data with group differences, which were used for power analysis.
. Note that “T” represents the connection density of the true precision matrices, not of the covariance matrices. In our study, φ was set at 0 to generate simulated data with no group differences in brain connectivity, which were used for calculating type I error rates; or φ=0.15 for simulating data with group differences, which were used for power analysis.
In previous studies, brain connections were found to be indeed sparse (Hilgetag, 2002; Oh et al., 2014): around 0.12 for the mouse brain structural network and around 0.27 for the cat cortex. Although we expected the human brain to have sparse functional connections, to be more general, we considered both sparse and nonsparse networks with T=0.20, 0.30, 0.60, and 0.80 as the connection density (i.e., proportions of nonzero entries) of the true precision matrices.
Set-up 2: structured differences in brain network
Now we consider that the differences between two group-level networks could come from edges comprising a connected subnetwork or cluster, reflecting perhaps a reasonable assumption on the brain's functional segregation. To have a realistic simulation set-up, we adopted the subnetworks detected by NBS for the FASD data as the truths. Specifically, suppose the two sample covariance (or precision) matrices for the two groups were 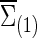 and
and 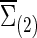 (or
(or 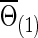 and
and 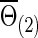 ) based on the FASD data. Applying the NBS to the FASD data and fixing the detected altered subnetwork at the connection density c=0.20, we obtained a binary indicator matrix Δr (or Δρ) as the altered covariance (or precision) matrix. Define
) based on the FASD data. Applying the NBS to the FASD data and fixing the detected altered subnetwork at the connection density c=0.20, we obtained a binary indicator matrix Δr (or Δρ) as the altered covariance (or precision) matrix. Define
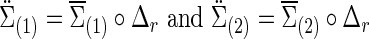 |
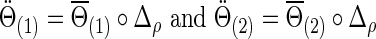 |
where 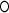 is the Hadamard (i.e., matrix element-wise) product. To ensure the positive definiteness, we added a small constant on the diagonal of each covariance or precision matrix. Finally, we used φ as a parameter to control the size of the group differences as used in [Eq. (3)]; then, the true
is the Hadamard (i.e., matrix element-wise) product. To ensure the positive definiteness, we added a small constant on the diagonal of each covariance or precision matrix. Finally, we used φ as a parameter to control the size of the group differences as used in [Eq. (3)]; then, the true 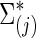 and
and 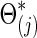 were defined by
were defined by
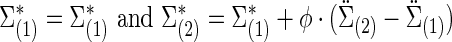 |
Similarly, 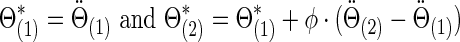 . We note that, to specify the sparsity levels of the true covariance and precision matrices separately, in this setting we had
. We note that, to specify the sparsity levels of the true covariance and precision matrices separately, in this setting we had 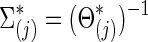 .
.
Generating simulated data
In set-up 1, the group-level true covariance matrices, 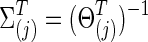 for j=1 and 2, were used to generate time-course BOLD signals from N regions at time point t as
for j=1 and 2, were used to generate time-course BOLD signals from N regions at time point t as
 |
for each subject in group j. We considered the simulation scenarios with M=180 as the default number of time points for each individual, and with n=50 subjects, including 25 controls and 25 cases. To investigate the effect of the number of time points M, we also considered M=90, 180, and 540. For set-up 2, similarly, we could use either the group-level precision matrices 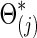 or covariance matrices
or covariance matrices 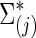 to generate subject-level BOLD time series.
to generate subject-level BOLD time series.
Estimating networks
With simulated time-series data, we would estimate each subject-specific covariance (or precision) matrix Σi (or Θi), from which we obtained the correlations (or partial correlations) of the brain regions for each subject before testing for their group differences.
As in the FASD data analysis, we chose the regularization parameter λi in two ways: With each simulated time-series data set, we found 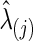 , for j=1, 2 that maximized the group-level predictive log likelihood and applied the graphical lasso to estimate
, for j=1, 2 that maximized the group-level predictive log likelihood and applied the graphical lasso to estimate 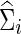 and
and 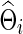 for
for 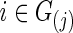 . In each simulation, we applied 10-fold CV to find the optimal
. In each simulation, we applied 10-fold CV to find the optimal 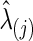 . Second, we also matched the sparsity levels of two groups' precision matrices. For the unknown true connection density (T) of the true precision matrix
. Second, we also matched the sparsity levels of two groups' precision matrices. For the unknown true connection density (T) of the true precision matrix 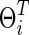 , we assumed that the estimated connection density (c) would not necessarily match with the truth as a result, since the true sparsity level is unlikely known in practice. For example, in our simulation, when the true sparsity was T=0.20, we considered that the estimated precision matrix could have connection density at
, we assumed that the estimated connection density (c) would not necessarily match with the truth as a result, since the true sparsity level is unlikely known in practice. For example, in our simulation, when the true sparsity was T=0.20, we considered that the estimated precision matrix could have connection density at 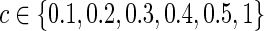 . Here, the connection density 1 represented the case of no regularization so that both precision and covariance matrices had 100% nonzero entries. The graphical lasso was employed to estimate each subject-specific precision matrix to have the pre-defined sparsity level. A grid search was performed to determine
. Here, the connection density 1 represented the case of no regularization so that both precision and covariance matrices had 100% nonzero entries. The graphical lasso was employed to estimate each subject-specific precision matrix to have the pre-defined sparsity level. A grid search was performed to determine 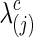 for each
for each 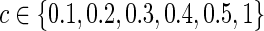 to yield
to yield 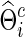 with a given connection density c. Then, the corresponding covariance matrix was estimated
with a given connection density c. Then, the corresponding covariance matrix was estimated 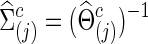 . Note that, for simplicity of notation, c was the connection density of the estimated precision matrix, not of the covariance estimate. Of course, a single
. Note that, for simplicity of notation, c was the connection density of the estimated precision matrix, not of the covariance estimate. Of course, a single 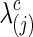 could not guarantee to yield the exact pre-defined sparsity level of the precision matrices for all subjects in all simulations, so the mean value of the estimated connection density is reported across simulations (Supplementary Tables S1 and S2; Supplementary Data are available online at www.liebertpub.com/brain).
could not guarantee to yield the exact pre-defined sparsity level of the precision matrices for all subjects in all simulations, so the mean value of the estimated connection density is reported across simulations (Supplementary Tables S1 and S2; Supplementary Data are available online at www.liebertpub.com/brain).
Type I error and power for testing
The correlations and partial correlations were obtained from 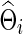 (or
(or 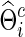 ) and
) and 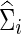 (or
(or 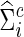 ), respectively, and the z-transformation was applied to both association measures. To test group differences in brain connectivity, we applied the SPU/aSPU tests, NBS, and univariate tests on some global network measures. Throughout the simulations, the test significance level was fixed at α=0.05. The results were based on 1000 independent replicates for each set-up to estimate empirical type I errors or empirical power as the proportion of rejecting the null hypothesis. The permutation number was 1000 for all tests.
), respectively, and the z-transformation was applied to both association measures. To test group differences in brain connectivity, we applied the SPU/aSPU tests, NBS, and univariate tests on some global network measures. Throughout the simulations, the test significance level was fixed at α=0.05. The results were based on 1000 independent replicates for each set-up to estimate empirical type I errors or empirical power as the proportion of rejecting the null hypothesis. The permutation number was 1000 for all tests.
Estimation errors in estimating networks
Denote 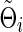 (or
(or 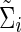 ) as an arbitrary estimate for Θi (or Σi). The adequacy of an estimate of a network (i.e.,
) as an arbitrary estimate for Θi (or Σi). The adequacy of an estimate of a network (i.e., 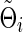 or
or 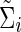 ) can be evaluated by an entropy loss (EL) or a quadratic loss (QL). The entropy loss, also known as the Kullback–Leibler divergence, is a well-accepted nonsymmetric measure of the discrepancy between an estimate and the truth (Pan and Fang, 2002). The two loss functions with respect to the true Σi can be defined as
) can be evaluated by an entropy loss (EL) or a quadratic loss (QL). The entropy loss, also known as the Kullback–Leibler divergence, is a well-accepted nonsymmetric measure of the discrepancy between an estimate and the truth (Pan and Fang, 2002). The two loss functions with respect to the true Σi can be defined as
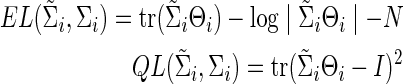 |
Similarly, for the true Θi and its arbitrary estimate 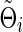 , we have
, we have
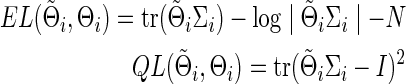 |
In each simulation, we obtained a loss from estimating individuals' networks (Σi or Θi) and averaged the loss based on 1000 replicates.
Results
Set-up 1: unstructured differences in brain networks
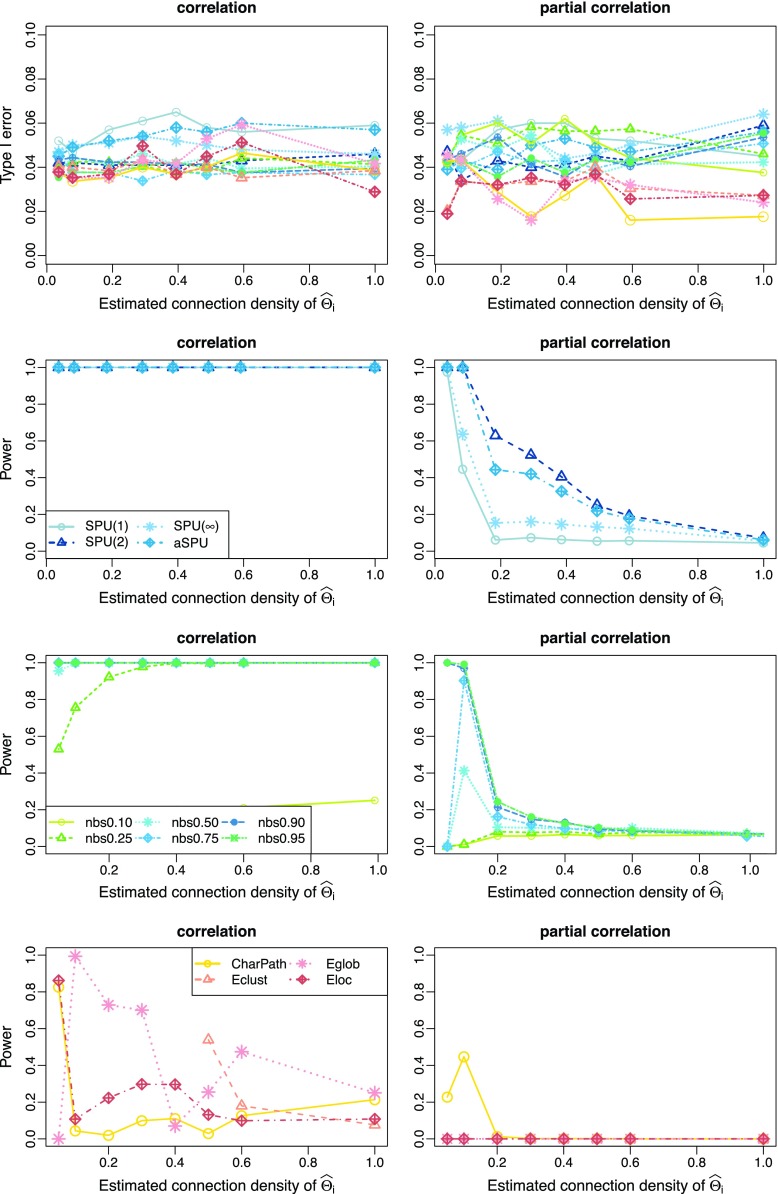
Varying connection density of networks
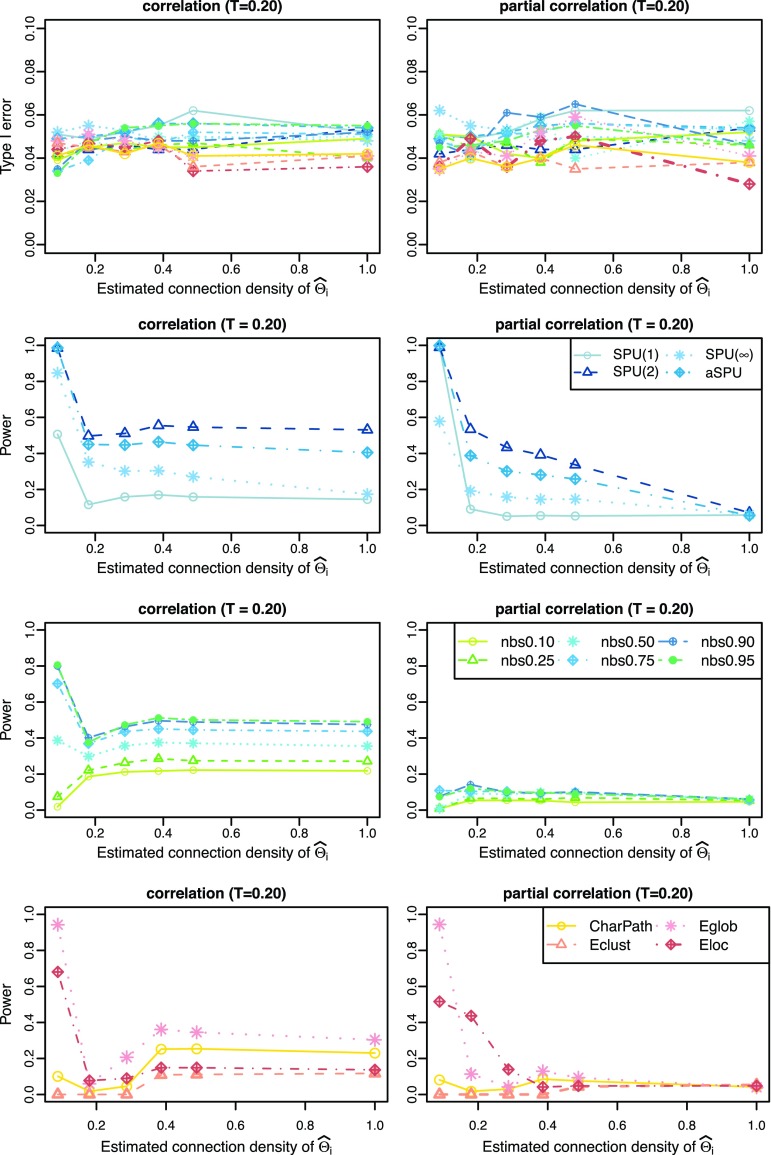
Figure 2 presents representative results with the connection density of the true precision matrix (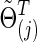 ) at T=0.20. We observe how power changed with the varying connection density (c) of the estimated precision matrices (
) at T=0.20. We observe how power changed with the varying connection density (c) of the estimated precision matrices (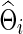 ). Group-level regularization value
). Group-level regularization value 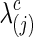 was imposed for each subject, and the test power was evaluated at different estimated connection density levels with
was imposed for each subject, and the test power was evaluated at different estimated connection density levels with 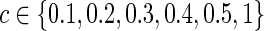 The left panels of Figure 2 show the type I error and power for testing group differences with correlations, while the right panels are with partial correlations. The top row presents the type I errors from all tests, which were close to the nominal level of 0.05. Figure 2 illustrates that using correlations gave higher power than using partial correlations for most tests. When high regularization was imposed (i.e., the estimated precision matrix had a very small connection density such as at c=0.1), both correlations and partial correlations yielded higher power. However, for NBS, even with high regularization, using partial correlations led to extremely low power.
The left panels of Figure 2 show the type I error and power for testing group differences with correlations, while the right panels are with partial correlations. The top row presents the type I errors from all tests, which were close to the nominal level of 0.05. Figure 2 illustrates that using correlations gave higher power than using partial correlations for most tests. When high regularization was imposed (i.e., the estimated precision matrix had a very small connection density such as at c=0.1), both correlations and partial correlations yielded higher power. However, for NBS, even with high regularization, using partial correlations led to extremely low power.
FIG. 2.
Type I error and power for testing unstructured network differences with varying connection density levels of the estimated precision matrices for true network connection density T=0.20; color coded by statistical tests (blue: SPU, green: NBS, red: global network measures). Color images available online at www.liebertpub.com/brain
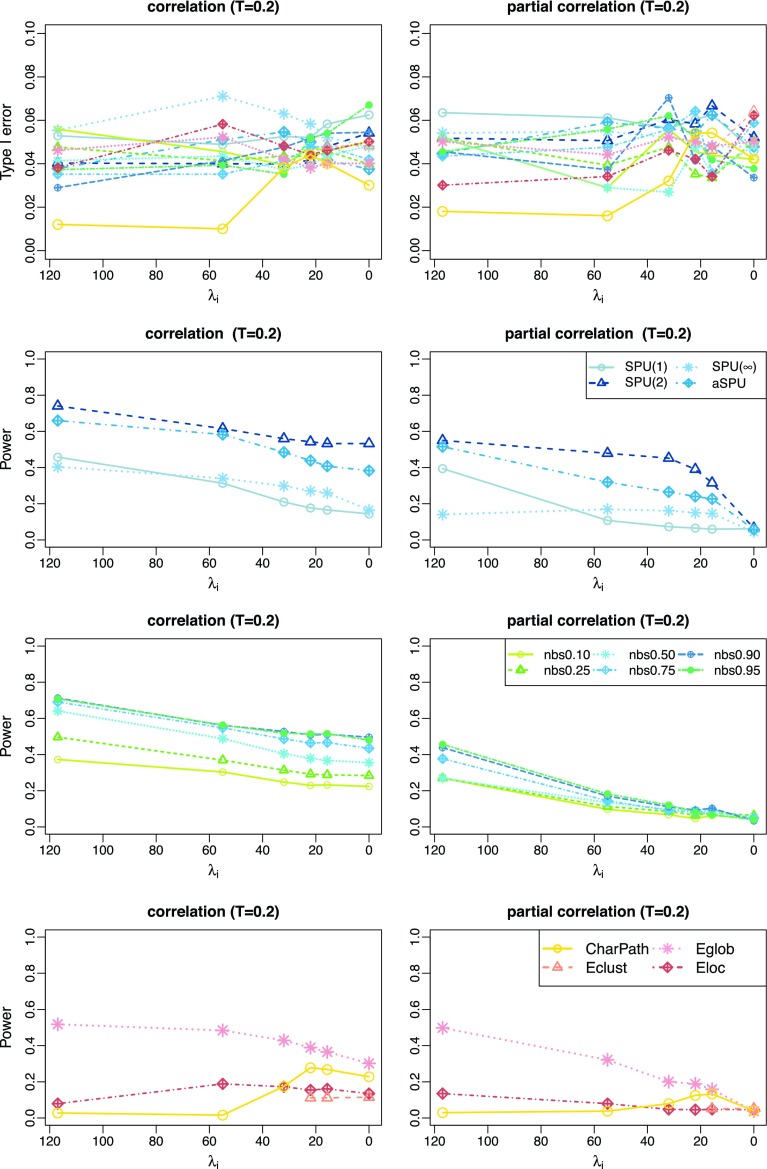
There might be a concern that setting different regularization parameters for the two groups could give rise to spurious between-group differences, though the controlled type I errors did not support this hypothesis. Nevertheless, we also applied the same value of λ to all the subjects in both groups, and obtained similar results as shown in Figure 3.
FIG. 3.
Type I error and power for testing unstructured network differences when the same regularization was imposed on all subjects: with varying connection density of the estimated precision matrix when the true network connection density is T=0.20. Note that the unit of x-axis is λi in reverse order; color coded by statistical tests (blue: SPU, green: NBS, red: global network measures). Color images available online at www.liebertpub.com/brain.
For the cases of higher true connection density levels at T=0.30, 0.60, and 0.80 with varying estimated connection density levels, the power analyses are provided in Supplementary Figures S1–S3; the general conclusions were the same. Detailed results for type I error rates are provided in Supplementary Tables S1 and S2.
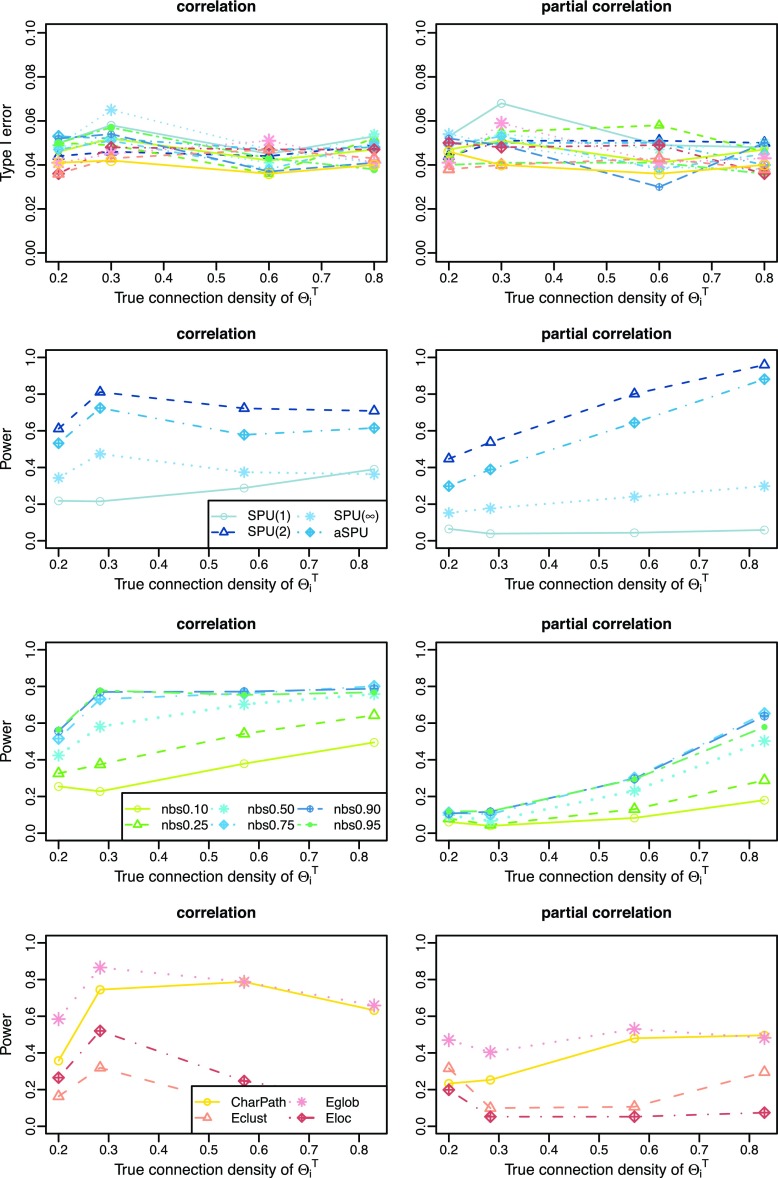
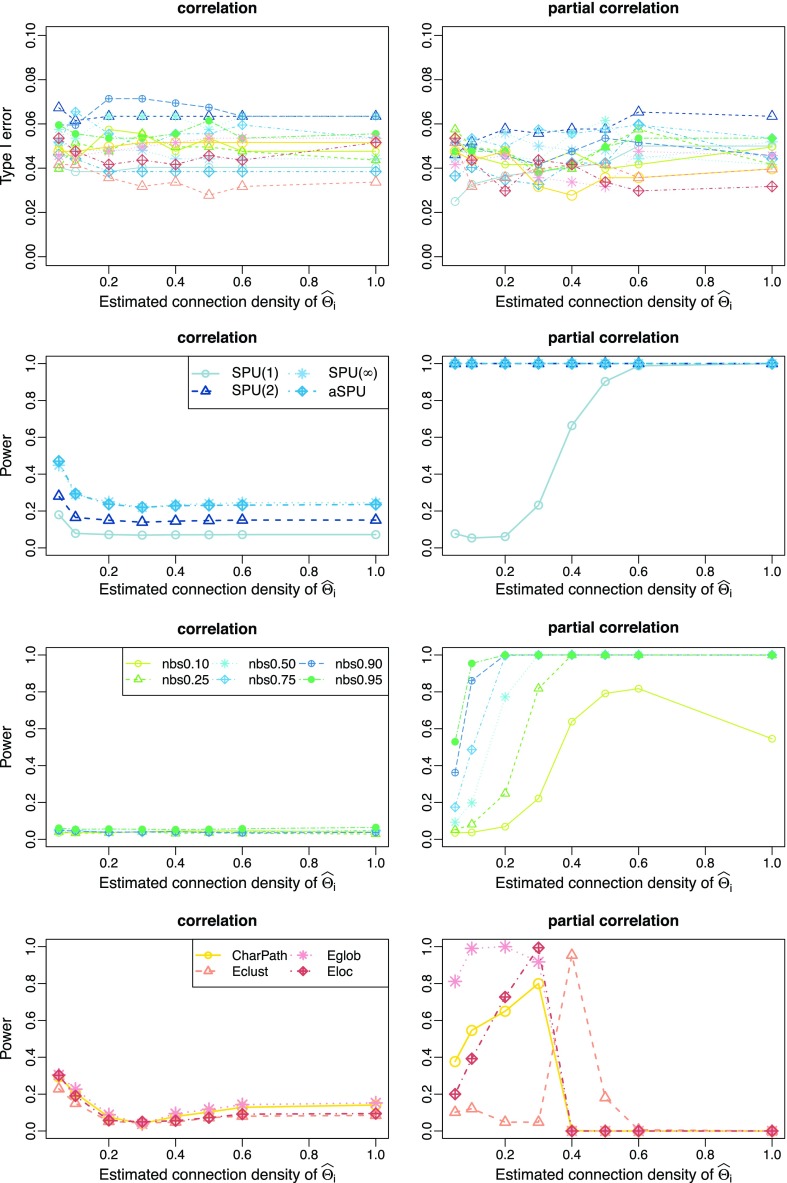
Cross-validation-selected connection density of estimated networks
Figure 4 illustrates the performance of the tests with CV-selected connection density at various connection density levels T of the true precision matrices 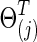 . T was set at 0.20, 0.30, 0.60, and 0.80, respectively. Each individual's network,
. T was set at 0.20, 0.30, 0.60, and 0.80, respectively. Each individual's network, 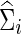 or
or 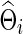 with
with 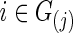 was estimated with a CV-selected group level
was estimated with a CV-selected group level 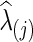 . Type I error was controlled in all tests applied. When the true connection density was low (T=0.20 or 0.30), using correlations gave higher power than using partial correlations. At a higher true connection density (T=0.80), testing with correlations gave higher power than using partial correlations with NBS and network metrics; but using partial correlations offered higher power with SPU(1) and aSPU tests. Using correlations seemed to yield more stable statistical power to detect network differences across various levels of true connection density. Among all tests applied, the SPU(2) test performed best, closely followed by aSPU; it is striking to see that the aSPU test was much more powerful than NBS and network measures when partial correlations were used.
. Type I error was controlled in all tests applied. When the true connection density was low (T=0.20 or 0.30), using correlations gave higher power than using partial correlations. At a higher true connection density (T=0.80), testing with correlations gave higher power than using partial correlations with NBS and network metrics; but using partial correlations offered higher power with SPU(1) and aSPU tests. Using correlations seemed to yield more stable statistical power to detect network differences across various levels of true connection density. Among all tests applied, the SPU(2) test performed best, closely followed by aSPU; it is striking to see that the aSPU test was much more powerful than NBS and network measures when partial correlations were used.
FIG. 4.
Cross-validation estimated networks: type I error and power for testing unstructured network differences at different connection density levels of the true precision matrices, T=0.20, 0.30, 0.60, and 0.80; color coded by statistical tests (blue: SPU, green: NBS, red: global network measures). Color images available online at www.liebertpub.com/brain
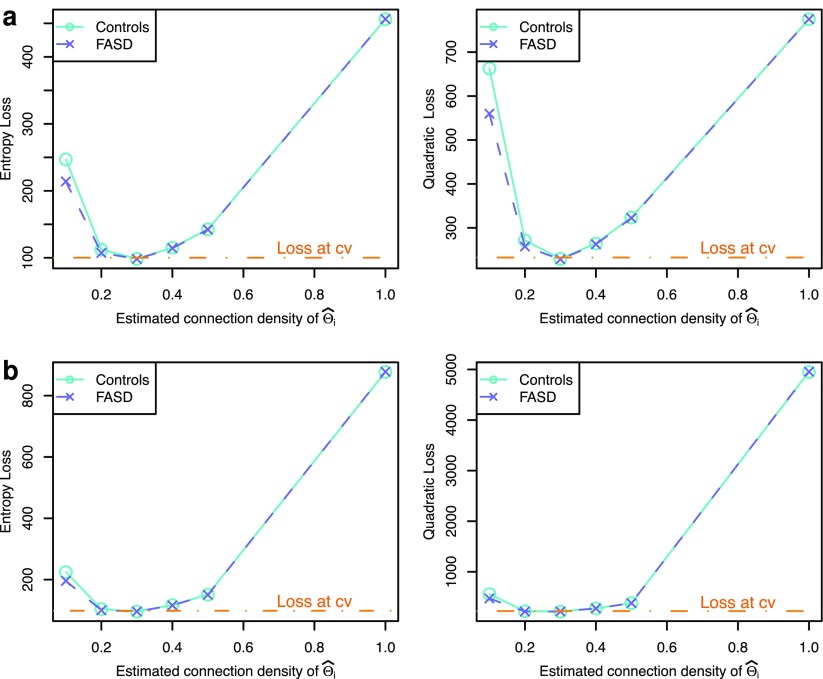
Performance in estimating networks
To explore whether our conclusions were unduly influenced by errors in estimating networks, we show Figure 5 to illustrate the performance in estimating networks (i.e., either 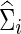 or
or 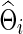 ) under the entropy and quadratic losses. We fixed the connection density of the precision matrix at T=0.20. In Figure 2, we varied the estimated connection density of the precision matrix
) under the entropy and quadratic losses. We fixed the connection density of the precision matrix at T=0.20. In Figure 2, we varied the estimated connection density of the precision matrix 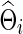 . Figure 5 depicts the discrepancy between true Σi and estimated
. Figure 5 depicts the discrepancy between true Σi and estimated 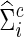 , and between true Θi and estimated
, and between true Θi and estimated 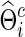 where
where 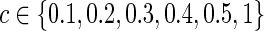 . We observed that the loss tended to be small when estimated connection density (c) was close to the truth T=0.20; in particular, CV seemed to give nearly optimal network estimates with minimal losses. However, compared with Figure 2, estimating covariance or precision matrices with a small loss did not directly translate into gaining statistical power in testing group differences. Consequently, CV was not satisfactory in choosing regularization parameters for testing group differences: It did not lead to power close to the highest one, though it was successful in estimating networks with nearly minimum losses. Both the entropy loss and quadratic loss showed similar patterns.
. We observed that the loss tended to be small when estimated connection density (c) was close to the truth T=0.20; in particular, CV seemed to give nearly optimal network estimates with minimal losses. However, compared with Figure 2, estimating covariance or precision matrices with a small loss did not directly translate into gaining statistical power in testing group differences. Consequently, CV was not satisfactory in choosing regularization parameters for testing group differences: It did not lead to power close to the highest one, though it was successful in estimating networks with nearly minimum losses. Both the entropy loss and quadratic loss showed similar patterns.
FIG. 5.
Performance of estimating networks with varying connection density levels of the estimated precision matrices for the true network connection density at T=0.20. (a) Performance of estimating covariance matrices Σi. (b) Performance of estimating precision matrices Θi. Color images available online at www.liebertpub.com/brain
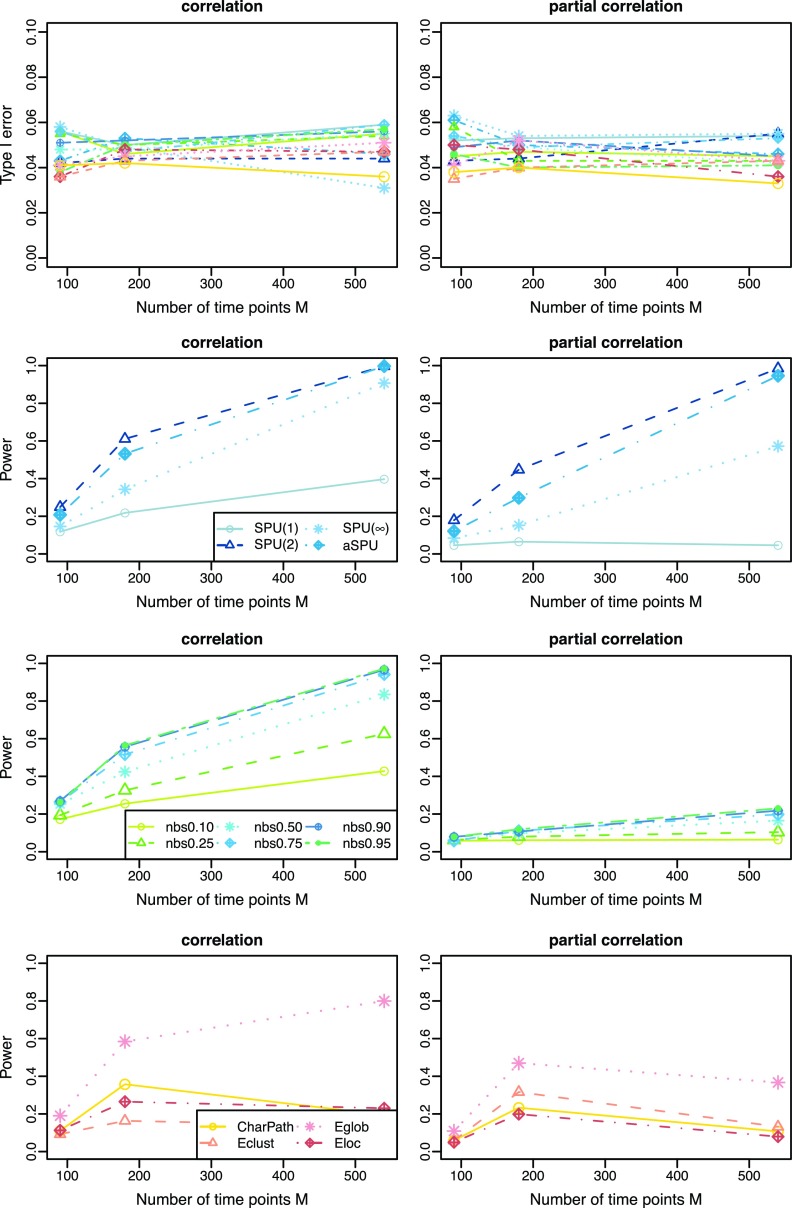
Number of time points
Figure 6 illustrates the effects of the number of time points M on statistical power. The true connection density was fixed at T=0.20, and we generated different numbers of BOLD signals for each subject at M=90, 180, or 540; we estimated Σi and Θi through 10-fold CV. In Figure 6, type I error rates were close to the nominal level of 0.05. As the number of time points (M) increased, as expected, the power went up with the use of both correlations and partial correlations in SPU and NBS, but not necessarily so in testing with summary network measures. Again, it is observed that using correlations seemed to yield higher power than using partial correlations across most tests. In addition, the power with partial correlations largely depended on the test being applied: Even with a large number of observations M=540, NBS gave low power no more than 0.2, which was much lower than those of SPU(2) and aSPU tests.
FIG. 6.
Cross-validation estimated networks: type I error and power for testing unstructured network differences with a varying number of time-courses M=90, 180, and 540 for the true network (precision matrix) connection density at T=0.20; color coded by statistical tests (blue: SPU, green: NBS, red: global network measures). Color images available online at www.liebertpub.com/brain
Set-up 2: structured differences in brain networks
Structured differences in sparse precision matrices
Figure 7 depicts empirical type I error rates and power for testing structured network differences in sparse true precision matrices. The patterns of the relative power between using correlations and partial correlations, and across estimated connection density levels, were similar to those observed in Figure 2 with unstructured network differences. In summary, using correlations consistently yielded higher power than using partial correlations; high regularization on estimating precision matrices often improved power; with the use of partial correlations, the SPU(2) and aSPU tests seemed to be more powerful than NBS, while testing with the summary network measures was low powered.
FIG. 7.
Type I error and power for testing structured network differences with sparse true precision matrices; color coded by statistical tests (blue: SPU, green: NBS, red: global network measures). Color images available online at www.liebertpub.com/brain
Structured differences in sparse covariance matrices
So far, we have almost exclusively considered cases with the true precision matrices with varying sparsity levels. The assumption of sparse precision matrices seems to be reasonable given that a precision matrix can distinguish direct and indirect connections in a network. Nevertheless, since little is known about the true architecture of human brain functional connectivity, we also explored a case with sparse true covariance matrices, not sparse precision matrices. Figure 8 presents the type I error and power for testing structured network differences present in sparse true group-level covariance matrices. Compared with Figure 7, the pattern of the relative power between using correlations and using partial correlations is reversed: Using partial correlations gave much higher power across almost all the tests at any estimated connection density level. Since the true covariance matrices were sparse, high regularization on covariance estimation yielded higher powered testing with correlations; on the other hand, the sparse true covariance matrices induced nonsparse precision matrices, implying that suitable regularization, not necessarily high regularization, on precision matrix estimation led to more powerful testing with partial correlations
FIG. 8.
Type I error and power for testing structured network differences with sparse true covariance matrices; color coded by statistical tests (blue: SPU, green: NBS, red: global network measures). Color images available online at www.liebertpub.com/brain
An explanation
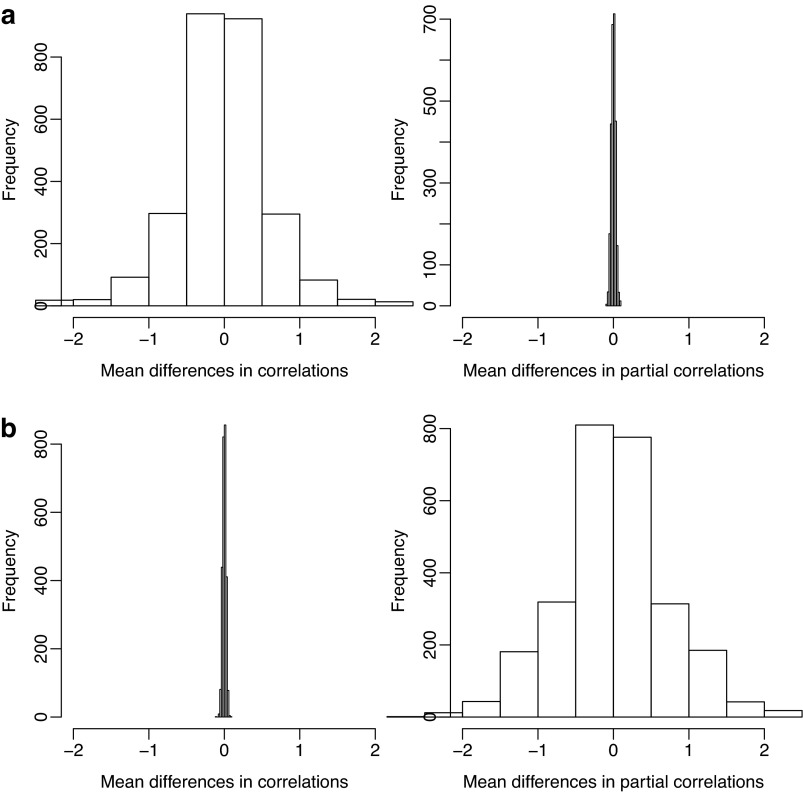
Figure 9a, b give the distributions of the network edge-wise mean differences between the two groups in terms of correlations or partial correlations; the univariate edge-wise t-statistics showed similar distributions (not shown). It is clear that, if the true precision matrices were sparse, there were much larger differences between the two groups in terms of edge-wise correlations than those in terms of partial correlations (Fig. 9a), suggesting higher power with the use of correlations. On the other hand, if the true covariance matrices were sparse, then an opposite conclusion can be drawn (Fig. 9b).
FIG. 9.
Distributions of edge-wise mean differences in z-transformed correlations or partial correlations. (a) Mean differences with sparse precision matrices: high power when using correlations. (b) Mean differences with sparse covariance matrices: high power when using partial correlations.
Discussion
Our numerical studies have revealed a number of interesting observations. First of all, if the true precision matrices are sparse across the groups, then using correlations often gives higher power and more stable results in testing group differences. On the other hand, if the true covariance matrices are sparse, then using partial correlations often yields more powerful tests. Since often it seems plausible to assume sparse precision matrices, we would recommend the use of marginal correlations; if this assumption is questionable as in practice, then to be safe one might want to try both marginal correlations and partial correlations. Second, optimal estimation of networks does not necessarily lead to high power for testing group differences in brain connectivity. As we observed, CV was successful in optimally estimating networks, giving a network estimate with a nearly minimal error, but did not necessarily yield high power for testing group differences in networks. Third, topological network structures, as group differences, do not seem to change our main conclusions.
For estimation of functional connectivity, partial correlation is known to be attractive in that it can distinguish direct connections from indirect ones. In addition, in the high-dimensional setting, estimating a sparse precision matrix (and using partial correlations) naturally identifies pairs of nodes that are unconnected in the graphical model. These features can provide a useful tool for visualizing the relationships among brain ROIs and for generating biological hypotheses. In our study, along with these attractive features, using partial correlations could maintain high power when high regularization was applied and an appropriate statistical test such as aSPU or NBS was chosen. In practice, however, it is not guaranteed to be able to choose an appropriate sparsity level in estimating the precision matrices to yield high power for any given data. In particular, our simulation results suggested that the conventional CV technique did not perform well in terms of statistical power, though it could estimate the networks accurately. Rather than choosing one single best regularization parameter value (or equivalently, sparsity level) for each estimated covariance or precision matrix, it would be interesting to develop an adaptive test that combines the testing results from using multiple values of the regularization parameter in estimating the covariance and precision matrices for testing group differences in brain functional connectivity. Furthermore, we have not discussed the use of other association measures (Varoquaux and Craddock, 2013); in particular, we have not considered the situation with dynamic functional (or directional) networks (Zhang et al., 2014), for which some new estimators of associations have just been proposed (Lindquist et al., 2014). These are interesting topics to be studied.
Supplementary Material
Acknowledgments
This research was supported by NIH grants R01GM113250, R01HL105397, R01HL116720, and R01GM081535, and by the Minnesota Supercomputing Institute.
Author Disclosure Statement
No competing financial interests exist.
References
- Azari NP, Rapoport SI, Grady CL, Schapiro MB, Salerno JA, Gonzales-Aviles A. 1992. Patterns of interregional correlations of cerebral glucose metabolic rates in patients with dementia of the Alzheimer type. Neurodegeneration 1:101–111 [Google Scholar]
- Banerjee O, Ghaoui LE, d'Aspremont A. 2008. Model selection through sparse maximum likelihood estimation for multivariate Gaussian or binary data. J Mach Learn Res 9:485–516 [Google Scholar]
- Biswal BB. 2012. Resting state fMRI: a personal history. Neuroimage 62:938–944 [DOI] [PubMed] [Google Scholar]
- Bullmore E, Sporns O. 2009. Complex brain networks: graph theoretical analysis of structural and functional systems. Nat Rev Neurosci 10:86–198 [DOI] [PubMed] [Google Scholar]
- Cox RW. 1996. AFNI: software for analysis and visualization of functional magnetic resonance neuroimages. Comput Biomed Res 29:162–173 [DOI] [PubMed] [Google Scholar]
- Dale AM, Fischl B, Sereno MI. 1999. Cortical surface-based analysis. I. Segmentation and surface reconstruction. Neuroimage 9:179–194 [DOI] [PubMed] [Google Scholar]
- Friedman J, Hastie T, Tibshirani R. 2008. Sparse inverse covariance estimation with the graphical lasso. Biostatistics 9:432–441 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greve DN, Fischl B. 2009. Accurate and robust brain image alignment using boundary based registration. Neuroimage 48:63–72 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hilgetag C, Kotter R, Stephan KE, Sporns O. 2002. Computational methods for the analysis of brain connectivity. In: Ascoli GA. (ed.), Computational Neuroanatomy. Totowa, NJ: Humana Press; p. 295 [Google Scholar]
- Horwitz B, Grady CL, Sclageter NL, Duara R, Rapoport SI. 1987. Intercorrelations of regional glucose metabolic rates in Alzheimer's disease. Brain Res 407:294–306 [DOI] [PubMed] [Google Scholar]
- Huang S, Li J, Sun L, Ye J, Fleisher A, Wu T, Chen K, Reiman E, Alzheimer's Disease NeuroImaging Initiative. 2010. Learning brain connectivity of Alzheimer's disease by sparse inverse covariance estimation. Neuroimage 50:935–949 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim J, Wozniak JR, Mueller BA, Shen X, Pan W. 2014. Comparison of statistical tests for group differences in brain functional networks. Neuroimage 101:681–694 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lindquist MA, Xu Y, Nebel MB, Caffo BS. 2014. Evaluating dynamic bivariate correlations in resting-state fMRI: a comparison study and a new approach. Neuroimage 101:531–546 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marrelec G, Krainik A, Duffau H, Pélégrini-Issac M, Lehéricy S, Doyon J, Benali H. 2006. Partial correlation for functional brain interactivity investigation in functional MRI. Neuroimage 32:228–237 [DOI] [PubMed] [Google Scholar]
- McArdle BH, Anderson MJ. 2001. Fitting multivariate models to community data: a comment on distance-based redundancy analysis. Ecology 82:290–297 [Google Scholar]
- Meskaldji DE, Ottet MC, Cammoun L, Hagmann P, Meuli R, Eliez S, Thiran JP, Morgenthaler S. 2011. Adaptive strategy for the statistical analysis of connectomes. PLoS One 6:e23009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nichols TE, Holmes AP. 2001. Nonparametric permutation tests for functional neuroimaging: a primer with examples. Hum Brain Mapp 15:1–25 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oh SW, Harris JA, Ng L, Winslow B, Cain N, Mihalas S, Wang Q, Lau C, Kuan L, Henry AM, Mortrud MT, Ouellette B, et al. . 2014. A mesoscale connectome of the mouse brain. Nature 508:207–214 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pan J, Fang K. 2002. Growth Curve Models and Statistical Diagnostics. New York: Springer-Verlag [Google Scholar]
- Pan W, Kim J, Zhang Y, Shen X, Wei P. 2014. A powerful and adaptive association test for rare variants. Genetics 197:1081–1095 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reiss PT, Stevens MHH, Shehzad Z, Petkova E, Milham MP. 2010. On distance-based permutation tests for between-group comparisons. Biometrics 66:636–643 [DOI] [PubMed] [Google Scholar]
- Rubinov M, Sporns O. 2010. Complex network measures of brain connectivity: uses and interpretations. Neuroimage 52:1059–1069 [DOI] [PubMed] [Google Scholar]
- Salvador R, Suckling J, Schwarzbauer C, Bullmore E. 2005. Undirected graphs of frequency dependent functional connectivity in whole brain networks. Philos Trans R Soc Lond B Biol Sci 360:937–946 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shehzad Z, Kelly C, Reiss PT, Craddock C, Emerson JW, McMahon K, Copland DA, Castellanos XC, Milham MP. 2014. A multivariate distance-based analytic framework for connectome-wide association studies. Neuroimage 93:74–94 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith SM, Beckmann CF, Andersson J, Auerbach EJ, Bijsterbosch J, Douaud G, Duff E, Feinberg DA, Griffanti L, Harms MP, Kelly M, Laumann T, Miller KL, Moeller S, Petersen S, Power J, Salimi-Khorshidi G, Snyder AZ, Vu AT, Woolrich MW, Xu J, Yacoub E, Uurbil K, Van Essen DC, Glasser MF, for the WU-Minn HCP Consortium. 2012. Resting-state fMRI in the Human Connectome Project. Neuroimage 80:144–168 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith SM, Jenkinson M, Woolrich MW, Beckmann CF, Behrens TE, Johansen-Berg H, et al. . 2004. Advances in functional and structural MR image analysis and implementation as FSL. Neuroimage 23(Suppl 1): S208–S219 [DOI] [PubMed] [Google Scholar]
- Smith SM, Miller KL, Salimi-Khorshidi G, Webster M, Beckmann CF, Nichols TE, Ramsey JD, Woolrich MW. 2011. Network modelling methods for FMRI. Neuroimage 54:875–891 [DOI] [PubMed] [Google Scholar]
- Stam CJ, Jones BF, Nolte G, Breakspear M, Scheltens P. 2007. Small-world networks and functional connectivity in Alzheimer's disease. Cereb Cortex 17:92–99 [DOI] [PubMed] [Google Scholar]
- Supekar K, Menon V, Rubin D, Musen M, Greicius MD. 2008. Network analysis of intrinsic functional brain connectivity in Alzheimer's disease. PLoS Comput Biol 4:1–11 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Varoquaux G, Craddock RC. 2013. Learning and comparing functional connectomes across subjects. Neuroimage 80:405–415 [DOI] [PubMed] [Google Scholar]
- Wee CY, Yang S, Yap PT, Shen D. 2013. Temporally dynamic resting-state functional connectivity networks for early MCI identification. In: Wu G. (ed.) Machine Learning in Medical Imaging. Nagoya, Japan: Springer; p. 139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woolrich MW, Jbabdi S, Patenaude B, Chappell M, Makni S, Behrens T, et al. . 2009. Bayesian analysis of neuroimaging data in FSL. Neuroimage 45(1 Suppl):S173–S186 [DOI] [PubMed] [Google Scholar]
- Wozniak JR, Mueller BA, Bell CJ, Muetzel RL, Hoecker HL, Boys CJ, Lim KO. 2013. Global functional connectivity abnormalities in children with fetal alcohol spectrum disorders. Alcohol Clin and Exp Res 37:748–756 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zalesky A, Cocchi L, Fornito A, Murray MM, Bullmore ED. 2012. Connectivity differences in brain networks. Neuroimage 60:1055–1062 [DOI] [PubMed] [Google Scholar]
- Zalesky A, Fornito A, Bullmore ET. 2010. Network based statistic: identifying differences in brain networks. Neuroimage 53:1197–1207 [DOI] [PubMed] [Google Scholar]
- Zhang T, Wu J, Li F, Caffo B, Boatman-Reich D. 2014. A dynamic directional model for effective brain connectivity using electrocorticographic (ECoG) time series. J Am Stat Assoc [Epub ahead of print]; DOI: 10.1080/01621459.2014.988213 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu HT, Fan JQ, Kong LL. 2014. Spatially varying coefficient models with applications in neuroimaging data with jumping discontinuity. J Am Stat Assoc 109:1084–1098 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.