Uncovering disease-disease relationships through the incomplete human interactome

Abstract

According to the disease module hypothesis the cellular components associated with a disease segregate in the same neighborhood of the human interactome, the map of biologically relevant molecular interactions. Yet, given the incompleteness of the interactome and the limited knowledge of disease-associated genes, it is not obvious if the available data has sufficient coverage to map out modules associated with each disease. Here we derive mathematical conditions for the identifiability of disease modules and show that the network-based location of each disease module determines its pathobiological relationship to other diseases. For example, diseases with overlapping network modules show significant co-expression patterns, symptom similarity, and comorbidity, while diseases residing in separated network neighborhoods are clinically distinct. These tools represent an interactome-based platform to predict molecular commonalities between clinically related diseases, even if they do not share disease genes.

Identifying sequence variations associated with specific phenotypes represents only the first step of a systematic program towards understanding human disease. Indeed, most phenotypes reflect the interplay of multiple molecular components that interact with each other (1–6), many of which do not carry diseases-associated variations. Hence, we must view disease-associated mutations in the context of the human interactome, a comprehensive map of all biologically relevant molecular interactions (6–12).

Yet, the predictive power of the current network-based approaches to human disease is limited by several conceptual and methodological issues. The first is the fact that high-throughput methods cover less than 20% of all potential pairwise protein interactions in the human cell (11–16), which means that we seek to discover disease mechanisms relying on interactome maps that are 80% incomplete. Second, the genetic roots of a disease are traditionally captured by the list of disease genes whose mutations have a causal effect on the respective phenotype. The disease proteins (the products of disease genes) are not scattered randomly in the interactome, but tend to interact with each other, forming one or several connected subgraphs that we call the disease module (Figure 1a). This agglomeration of disease proteins is supported by a range of biological and empirical evidence (7, 17, 18) and has fueled the development of numerous tools to identify new disease genes and prioritize pathways for disease relevance (8, 9, 19–28). However, despite its frequent use, the disease module hypothesis lacks a solid mathematical basis. Third, the relationships between distinct phenotypes are currently uncovered by identifying shared components like disease genes, SNPs, pathways, or differentially expressed genes involved in both diseases. This has resulted in the construction of ‘disease networks,’ unveiling the common genetic origins of many disease pairs (7, 29). Yet, shared genes offer only limited information about the relationship between two diseases. Indeed, mechanistic insights are often carried by the molecular networks through which the gene products associated with the two diseases interact with each other.

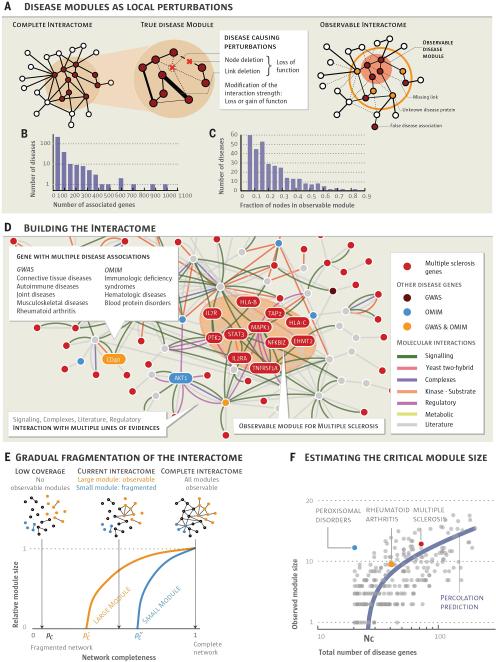
Fig. 1. From the Human Interactome to Disease Modules.

a, According to the disease module hypothesis, a disease represents a local perturbation of the underlying disease-associated subgraph. Such perturbations could represent the removal of a protein (e.g. by a nonsense mutation), the disruption of a protein-protein interaction, or modifications in the strength of an interaction. The complete disease module can be identified only in a full interactome map; the disease module observable to us captures a subset of this module, owing to data incompleteness. b, Distribution of the number of disease associated genes for 299 diseases. c, Distribution of the fraction of disease genes within the observable disease module. d, A small neighborhood of the interactome showing the biological nature of each physical interaction and the origin of the disease-gene associations used in our study (see also SM Sect. 1). Genes associated with multiple sclerosis are shown in red, the shaded area indicating their observable module, a connected subgraph consisting of eleven proteins. e, Schematic illustration of the predicted size of the observable disease modules (subgraphs) in function of network completeness. Large modules should be observable even for low network coverage; to discover smaller modules we need higher network completeness. f, Size of the observable module as a function of the total number of disease genes. The purple curve corresponds to the percolation based prediction (SM Sect. 6), indicating that diseases with N_d < N_c ≈ 25 genes do not have an observable disease module in the current interactome. Each gray point captures one of the 299 diseases.

The fragmentation of disease modules

We started by compiling 141,296 physical interactions between 13,460 proteins experimentally documented in human cells, including protein-protein and regulatory interactions, metabolic pathway and kinase-substrate interactions (Fig. 1, see also Figs. S1-S2 and SM Sect. 1 for a detailed discussion), representing a blueprint of the human interactome (Fig. 1d). We also compiled a corpus of all 299 diseases defined by the Medical Subject Headings (MeSH) ontology that have at least 20 associated genes in the current Online Mendelian Inheritance in Man (OMIM) and genome-wide association study (GWAS) databases (30, 31), involving 2,436 disease-associated proteins (Fig. 1b,c and SM Sect. 1).

Despite the best curation efforts, both the interactome and the disease gene list remain incomplete (6, 11–16) and biased towards much studied disease genes and disease mechanisms (32, 33). The consequences of this incompleteness are illustrated by multiple sclerosis: of the 69 genes associated with the disease, only 11 disease proteins form a connected subgraph (observable module, Fig. 1d); the remaining 58 proteins appear to be distributed randomly in the interactome. This pattern holds for all 299 diseases, their observable modules comprising on average only 20% of the respective disease genes (Fig. 1c). Several factors contribute to this fragmentation (Fig. 1a), the main being data incompleteness: missing links leave many disease proteins isolated from their disease module (Fig. 1a).

In percolation theory, if only a p fraction of links is available, a connected subgraph (disease module) of m nodes undergoes a phase transition under certain conditions (34, 35): if p is above $p_c^m$, some fraction of nodes continue to form an observable module; if, however, p is below $p_c^m$, the module becomes too fragmented to be observable (Fig. 1e, see also Fig. S14 and SM Sect. 6). To quantify this phenomenon, we calculated the minimum network coverage $p_c^m$ required to observe a disease module of original size m, finding that $p_c^m\sim 1∕m$, valid for an arbitrary degree distribution of the underlying interactome. Figure 1f illustrates a signature of this phenomenon in the interactome: the observable disease module size S_i versus the number of disease genes associated with each disease follows the predicted percolation transition (blue line). Hence, percolation theory predicts that for diseases with fewer than N_c ≈ 25 genes, the module is too fragmented to be observable in the current interactome; only diseases with N_d > N_c disease genes should have an observable disease module.

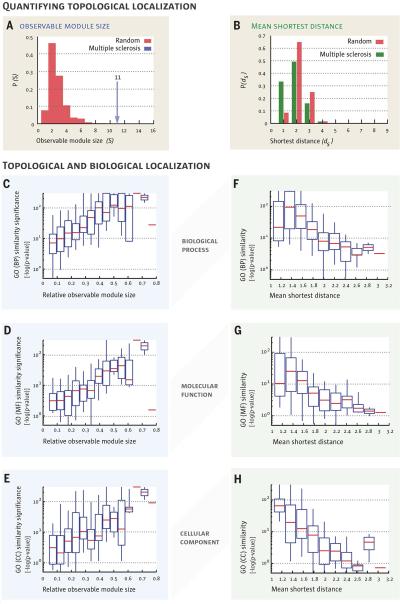
To see if the observed disease modules represent non-random disease gene aggregations, for each disease we compared the size S_i of its observable module with the expected $S_i^{\mathrm{rand}}$ if the same number of disease proteins were placed randomly on the interactome. For example, for multiple sclerosis the observed S_i = 11 is significantly larger than the random expectation $S_i^{\mathrm{rand}}$ (z−score = 5.8, p−value = 3.3×10⁻⁹, Figs. 1d and 2a), hence the observed multiple sclerosis module cannot be attributed to a random agglomeration of disease genes. We also determined for each disease protein the network-based distance d_s to the closest other protein associated with the same disease. Again, for multiple sclerosis P(d_s) is shifted towards smaller d_s compared to the random expectation P ^rand(d_s) (p−value = 2.6×10⁻⁶, Fig. 2b), indicating that the disconnected disease proteins agglomerate in the neighborhood of the observable module. Altogether, disease genes associated with 226 of the 299 diseases show a statistically significant tendency to form disease modules based on both S_i and P(d_s) (Fig. S4).

Fig. 2. Topological localization and biological similarity of disease genes.

a, The size of the largest connected component S of proteins associated with the same disease shown for multiple sclerosis. The observed module size, S = 11, is significantly larger than the random expectation S^rand = 2 ± 1. b, The distribution of the shortest distance of each disease protein to the next closest disease protein d_s. For multiple sclerosis, P (d_s) is significantly shifted compared to the random expectation, indicating that disease genes tend to agglomerate in each other's network neighborhood. c-h, The degree of the network-based localization of a disease, as measured by the relative size of its observable module s_i = S_i/N_d and the mean shortest distance 〈d_s〉, correlates strongly with the significance of the biological similarity of the respective disease genes. Using the gene ontology annotations, we determine for each disease how similar its associated genes are in terms of their biological processes (c,f), molecular function (d,g) and cellular component (e,h). Comparing the resulting values with random expectation we find that , the higher the the more localized a disease is topologically, i.e., the larger s_i or the shorter 〈d_s〉 significance in the similarity of the associated genes.

We also asked if there is a relationship between the tendency of disease proteins to agglomerate in the same interactome neighborhood and their biological similarity (7, 36, 37). We find that as the relative size s_i ≡ S_i/N_i of the observable module increases from 0.1 to 0.8, a sign of increasing agglomeration of the disease genes, the significance of the biological similarity in Gene Ontology (GO) annotations (biological processes, molecular function, and cellular component) increases ten- to one hundred-fold (Fig. 2c-e, Fig. S3a-c), an exceptionally strong effect (see SM Sect. 2 for statistical analysis). Similarly, as the mean shortest distance between disease proteins increases from 1 (agglomerated disease proteins) to 3 (scattered disease proteins), we observe a ten- to a one hundred-fold decrease in the significance of GO term similarity (Fig. 2f-h, Fig. S3d-f).

Taken together, we find that genes associated with the same disease tend to agglomerate in the same neighborhood of the interactome. Indeed, while ~80% of the disease proteins are disconnected from the observable module, these isolates tend to be localized in its network vicinity. This result offers quantitative support to the hypothesis that many local neighborhoods of the interactome represent the observable parts of the true, larger and denser disease modules.

Relationship between diseases

If two disease modules overlap, local perturbations leading to one disease will likely disrupt pathways involved in the other disease module as well, resulting in shared clinical characteristics. To test the validity of this hypothesis, we introduce the network-based separation of a disease pair, A and B, (Fig. 3a, see also Fig. S5-S7) using

$$s_{\mathrm{AB}}\equiv \langle d_{\mathrm{AB}}\rangle -\frac{\langle d_{\mathrm{AA}}\rangle +\langle d_{\mathrm{BB}}\rangle }{2}.$$ (1)

s_AB compares the shortest distances between proteins within each disease, 〈d_BB〉and 〈d_AA〉, to the shortest distances 〈d_AB〉 between A-B protein pairs. Proteins associated to both A and B have d_AB = 0. As discussed in Section 3.3 of the Supplementary Material, the generalization of s_AB to account for directed regulatory and signaling interactions does not alter our subsequent findings (Fig. S8).

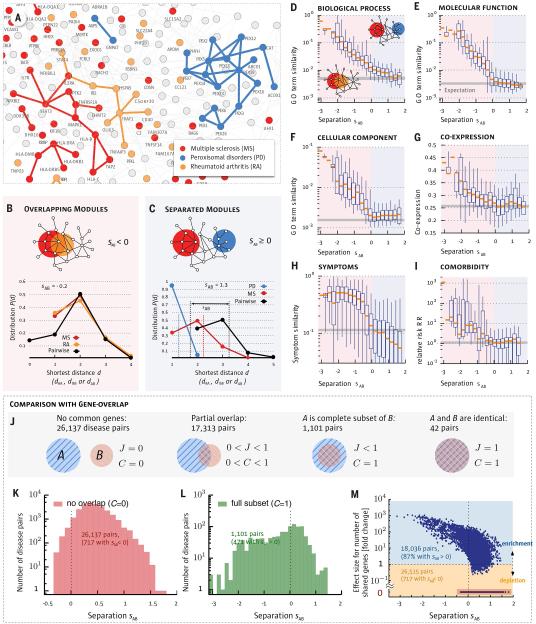
Fig. 3. Network Separation and Disease Similarity.

a, A subnetwork of the full interactome highlighting the network-based relationship between disease genes associated with three diseases identified in the legend. b,c, Distance distributions for disease pairs that have topologically overlapping modules (s_AB < 0, b) or topologically separated modules (s_AB > 0, c). The plots show P(d) for the disease pairs shown in (a). d-i, Topological separation vs. biomedical similarity. d,e,f, GO term similarity; g, gene co-expression; h, symptom similarity for all disease pairs in function of their topological separation s_AB. We highlight in red the region of overlapping disease pairs (s_AB < 0) and in blue the separated disease pairs (s_AB > 0). For symptom similarity we show the Cosine similarity (c_AB = 0 if there are no shared symptoms between diseases A and B and c_AB = 1 for diseases with identical symptoms). Comorbidity in (i) is measured by the relative risk RR (40). Bars in d-i indicate random expectation (SM Sect. 1): in d-g the expected value for a randomly chosen protein pair is shown. In h-i the mean value of all disease pairs is used. j-m, The interplay between gene-set overlap and the network- based relationships between disease pairs. j, The relationship between gene-sets A and B is captured by the overlap coefficient C =|A∩B|/min(|A|,|B|) and the Jaccard-index J=|A∩B|/|A∪ B|. More than half (59%) of the disease pairs do not share genes (J = C = 0), hence, their relation cannot be uncovered based on shared genes. k, Distribution of s_AB for disease pairs with no gene-overlap. We find that despite having disjoint gene sets, 717 diseases pairs have overlapping modules (s_AB < 0). l, Distribution of s_AB for disease pairs with complete gene-overlap (C = 1) shows a broad range of network-based relationships, including non-overlapping modules (s_AB > 0). m, Fold-change (fc) of the number of shared genes compared to random expectation vs. s_AB for all disease pairs. The 59% of all disease pairs without shared genes are highlighted with red back- ground. For 98% of all disease pairs that share at least one gene the gene-based overlap is larger than expected by chance. Despite this fact most (87%) of these disease pairs are separated in the network (s_AB > 0). Conversely, a considerable number of pairs (717) without shared genes exhibit detectable network overlap (s_AB < 0).

We find that only 7% of disease pairs have overlapping disease neighborhoods with negative s_AB (Fig. 3b); the remaining 93% have a positive s_AB, indicating that their disease modules are topologically separated (Fig. 3c). Since we lack unambiguous true positive and true negative disease relationships that could be used as reference, we use two complementary null models to evaluate the statistical significance of each disease pair compared to random expectation (see SM Sect. 2.2). At a global false discovery level of 5% we find that 75% of all disease pairs exhibit significant s_AB. To determine the degree to which this network-based separation of two diseases is predictive for pathobiological manifestations, we rely on four datasets:

(i) Biological similarity

We find that the closer two diseases are in the interactome, the higher the GO annotation-based similarity of the proteins associated with them (Fig. 3d-f). The effect is strong, resulting in a two-order-of-magnitude decrease in GO term similarity as we move from highly overlapping (s_AB ≈-−2) to well separated disease pairs (s_AB > 0).

(ii) Co-expression

We find that the co-expression-based correlation across 70 tissues (36) between genes associated with overlapping diseases is almost twice that of well separated diseases (Fig. 3g), falling to the random expectation for s_AB > 0.

(iii) Disease symptoms

We find that symptom similarity, as captured by large-scale medical bibliographic records (38), falls about an order of magnitude as we move from overlapping (s_AB < 0) to separated (s_AB > 0) diseases (Fig. 3h). Non-overlapping diseases share fewer symptoms than expected by chance.

(iv) Comorbidity

We used the disease history of 30 million individuals aged 65 and older (U.S. Medicare) to determine for each disease pair the relative risk RR of disease comorbidity (39) (Fig. 3i), finding that the relative risk drops from RR≥10 for s_AB < 0 to the random expectation of RR≈1 for s_AB > 0.

Thus, the network-based distance of two diseases indicates their pathobiological and clinical similarity. This result suggests a network model of human disease: each disease has a well-defined location and a diameter 〈d_AA〉 that captures its network-based size (Fig. 3a-c). If two disease modules are topologically separated (s_AB > 0), then the diseases are pathobiologically distinct. If the disease modules topologically overlap (s_AB < 0), the magnitude of the overlap is indicative of their biological relationship: the higher the overlap, the more significant are the pathobiological similarities between them. We therefore represent each disease by a sphere with diameter 〈d_AA〉 in a three-dimensional disease space, such that the physical distance r_AB between diseases A and B correlates with the observed network-based distance 〈d_AB〉 (Fig. 4a, see also Fig. S15 and SM Sect. 8). Disease modules that do not overlap in Fig. 4a are predicted to be pathobiologically distinct; for those that overlap, the degree of overlap captures their common pathobiology and clinical characteristics.

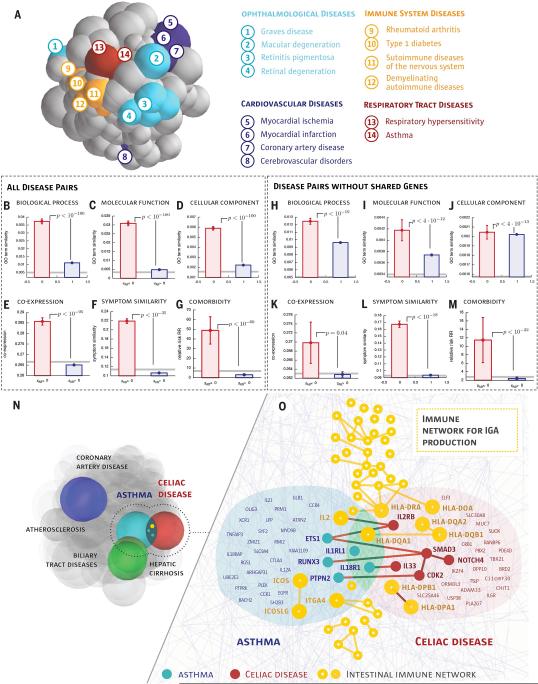
Fig. 4. Network-based Model of Disease-Disease Relationship.

a, To illustrate the uncovered network-based relationship between diseases, we place each disease in a 3D disease space, such that their physical distance to other diseases is proportional to 〈d_AB〉 predicted by the interactome-based analysis. Diseases whose modules (spheres) overlap are predicted to have common molecular underpinnings. The colors capture several broad disease classes, indicating that typically diseases of the same class are located close to each other. There are exceptions, such as cerebrovascular disease, which is separated from other cardiovascular diseases, suggesting distinct molecular roots. b-g, Biological similarity shown separately for the predicted overlapping and non-overlapping disease pairs (see Fig. 3d-i for interpretation). Error bars indicate the standard error of the mean. Gray lines show random expectation, either for random protein pairs (b-e,h-k) or for a random disease pair (f,g,l,m), p−values denote the significance of the difference of the means according to a Mann-Whitney U test. h-m, Biological similarity for disease pairs that do not share genes (control set). n, Three overlapping disease pairs in the disease space. Coronary artery diseases and atherosclerosis, as well as hepatic cirrhosis and biliary tract diseases, are diseases with common classification, hence their disease modules overlap. Our methodology also predicts several overlapping disease modules of apparently unrelated disease pairs (Table S1), illustrated through asthma and celiac disease. o, A network- level map of the overlapping asthma-celiac disease network-neighborhood, with yellow we also show the IgA production pathway that plays a biological role in both diseases. We show the names of genes that are either shared by the two diseases or by the pathway, or interact across the modules.

To test the predictive power of this model, we grouped the disease pairs with s_AB < 0 into the “overlapping” disease category, and those with s_AB > 0 into the “non-overlapping” disease category. As Fig. 4b-g indicates, all biological and clinical characteristics show statistically highly significant similarity for overlapping diseases, while the effects vanish for the non-overlapping disease pairs.

The disease separation allows us to identify unexpected overlapping disease pairs, i.e. those that lack overt pathobiological or clinical association (see Table S1 for twelve such examples). For example, we find that asthma, a respiratory disease, and celiac disease, an autoimmune disease of the small intestine, are localized in overlapping neighborhoods (s_AB < 0, Fig. 4n), suggesting shared molecular roots, despite their rather different pathobiologies. A closer inspection reveals evidence supporting this prediction: the two diseases share three genes identified via genome wide associations with genome-wide significance (HLA-DQA1, IL18R1, IL1RL1) and, recently, SNP rs1464510, previously associated with celiac disease, was also found to be associated with asthma (40). Although the two diseases have few common symptoms, they exhibit a remarkably high co-morbidity (RR = 6.18) and statistically significant co-expression between their genes (r = 0.32, p −value = 0.02). Furthermore, the top enriched pathway in the combined gene set of the two diseases is the immune network for IgA production (p−value = 5×10⁻¹⁵, Fig. 4o) with 48 genes, of which seven are associated with asthma and five with celiac disease. Measuring levels of IgA, an antibody against tissue transglutaminase, is widely used to screen for and diagnose celiac disease (41). At the same time, the IgA response to allergens in the respiratory tract of asthma patients plays a pathogenic role through eosinophil activation (42).

To see if we could have arrived to the same conclusion by identifying diseases with shared genes (7), we quantified the predictive power of gene overlap, finding that indeed disease pairs with large gene-overlap tend to be localized in the same network neighborhood (Fig. 3l,m). Yet, about 59% of disease pairs do not share genes, hence their relationship cannot be resolved based on the shared gene hypothesis (Fig. 3j, see also Figs. S9-S10). We therefore repeated the analysis of Fig. 4b-g for all disease pairs without common genes, finding that s_AB continues to accurately predict the biological similarity (or distinctness) of these disease pairs (Fig. 4h-m, SM Sect. 3). Overall we find 717 pairs with overlapping disease modules (s_AB < 0, Fig. 3k), relationships that cannot be predicted based on gene overlap. For example, lymphoma, a cancer, and myocardial infarction, a heart disease, do not share disease genes. Yet, they have strongly overlapping modules (s_AB = −0.24), indicating that they are located in the same neighborhood of the interactome. Indeed, we find that SMARCA4, a protein associated with myocardial infarction, interacts with ALK, MYC and NFKB2, which are lymphoma disease proteins. Cancer cells frequently depend on chromatin regulatory activities to maintain a malignant phenotype. It has been shown that leukemia cells require the SWI/SNF chromatin remodeling complex containing the SMARCA4 protein as the catalytic subunit for their survival and aberrant self-renewal potential (43). The relatedness of the two diseases is further supported by a high comorbidity (relative risk (RR) = 2.1) and the clinical finding that intravascular large cell lymphoma affect and obstruct the small vessels of the heart (44). Other disease pairs that lack shared genes but are found in the same neighborhood of the interactome include glioma and gout, glioma and myocardial infarction, and myeloproliferative disorders and proteinuria, each pair having high comorbidity (RR = 2.43, 6.3 and 2.0, respectively). A detailed discussion of these and other novel disease- disease relationships predicted by our approach is offered in Section 10 of the Supplementary Material.

Summary and Discussion

A complete and accurate map of the interactome could have tremendous impact on our ability to understand the molecular underpinnings of human disease. Yet, such a map is at least a decade away. Here we showed that despite its incompleteness, the available interactome has sufficient coverage to pursue a systematic network-based approach to human diseases. To be specific, we offered quantitative evidence for the identifiability of some disease modules, while showing that for other diseases the identifiability condition is not yet satisfied at the current incompleteness of the interactome. Most important, we demonstrated that the relative interactome-based position of two disease modules is a strong predictor of their biological and clinical similarity Throughout this paper we focused on the impact of network incompleteness, ignoring another limitation of the interactome: it is prone to significant investigative biases (12, 32, 33) (see also Fig. S13 and SM Sect. 5). We therefore repeated our analysis relying only on high-throughput data from yeast two-hybrid screens (12) (y2h, SM Sect. 4), finding that the diameter 〈d_AA〉 of the observable modules, the distance 〈d_AB〉 nd separation s_AB of all disease pairs measured in the full and the unbiased interactome show statistically highly significant correlations. Similarly, OMIM is also prone to selection and investigative biases, hence we repeated our measurements using only unbiased GWAS-associated disease genes. Comparing gene sets that include OMIM data and those that only contain GWAS associations, we again find highly significant correlations for 〈d_AA〉, 〈d_AB〉, and s_AB (Figs. S11-S12). Therefore, the disease modules and the overlap between them can be reproduced in the unbiased data as well, indicating that our key findings cannot be attributed to investigative biases. Our analysis further showed that while unbiased high-throughput data alone has not yet reached sufficient coverage to map out putative modules for many diseases, it can provide valuable insights on the properties of the complete interactome (SM Sect. 6). Indeed, as the current y2h data is expected to represent a uniform subset of the complete y2h network (12), we can use it to derive the minimum coverage ${\mathit{p}}_c^m$ of the latter. As the coverage of high-throughput maps improves, they will allow us to utilize the full power of unbiased approaches for disease module identification.

The true value of the developed interactome-based approach is its open-ended multi-purpose nature: it offers a platform that can address numerous fundamental and practical issues pertaining to our understanding of human disease. This platform can be used to improve the interpretation of GWAS data (see Fig. S16 and SM Sect. 10 for an application to type II diabetes), help us uncover new uses for existing drugs (repurposing) by identifying the disease modules located in the vicinity of each drug target (45–47) and the molecular underpinnings of undiagnosed diseases by exploiting the agglomeration of mutations and expression changes in network neighborhoods associated with well-characterized diseases. In the long run, network-based approaches, relying on an increasingly accurate interactome, are poised to become unavoidable in interpreting disease-associated genome variations.

Materials and Methods

Interactome Construction

We combine several sources of protein interactions: (i) Regulatory interactions derived from transcription factors binding to regulatory elements; (ii) binary interactions from several yeast two-hybrid high-throughput and literature curated datasets; (iii) literature curated interactions derived mostly from low throughput experiments; (iv) metabolic enzyme-coupled interactions; (v) protein complexes; (vi) kinase-substrate pairs; (vii) signaling interactions. The union of all interactions from (i)-(vii) yields a network of 13,460 proteins interconnected by 141,296 interactions. For more information on the individual datasets and general properties of the interactome see SM Sect. 1.

Disease-gene associations

We integrate disease-gene annotations from Online Mendelian Inheritance in Man (OMIM; http://www.ncbi.nlm.nih.gov/omim) (48) and UniProtKB/Swiss-Prot as compiled by (30) with GWAS data from the Phenotype-Genotype Integrator database (PheGenI; http://www.ncbi.nlm.nih.gov/gap/PheGenI) (31), using a genome-wide significance cutoff of p-value ≤ 5 × 10⁻⁸. To combine the different disease nomenclatures into a single standard vocabulary we use the Medical Subject Headings ontology (MeSH; http://www.nlm.nih.gov/mesh/) as described in SM Sect. 1. After filtering for diseases with at least 20 associated genes and genes for which we have interaction information we obtain 299 diseases and 3,173 genes associated with them.

Additional disease and gene annotation data

For the analysis of the similarity between genes and diseases we use (i) Gene Ontology (GO) annotations (49), (ii) tissue specific gene expression data (36), (iii) Symptom disease associations (38), (iv) comorbidity data (39) and (v) pathway annotations from the Molecular Signatures Database (MSigDB) (50). Full details on data sources, processing and analysis are provided in SM Sect. 1.

Network Localization

We use two complementary measures to quantify the degree to which disease proteins agglomerate in specific interactome neighborhoods: (i) Observable module size S, representing the size of the largest connected subgraph formed by disease proteins. (ii) Shortest Distance d_s. For each of the N_d disease proteins we determine the distance d_s to the next closest protein associated with the same disease. The average 〈d_s〉 can be interpreted as the diameter of a disease on the interactome. The network-based overlap between two diseases A and B is measured by comparing the diameters 〈d_AA〉 and 〈d_BB〉 of the respective diseases to the mean shortest distance 〈d_AB〉 between their proteins: s_AB = 〈d_AB〉-(〈d_AA〉+〈d_BB〉)/2. Positive s_AB indicates that the two disease modules are separated, negative values correspond to overlapping modules. Details on the analysis and the appropriate random controls are presented in SM Sect. 2.

Gene-based disease overlap

The overlap between two gene-sets A and B is measured by the overlap coefficient C = |A∩B|/min(|A|,|B|) and the Jaccard-index J = |A∩B|/|A∪B|. Both measures lie in the range [0,1] with J,C = 0 for no common genes. A Jaccard-index J=1 indicates two identical gene sets, whereas the overlap coefficient C=1 when one set is a complete subset of the other. For a statistical evaluation of the observed overlaps we use a basic hypergeometric model with the null hypothesis that disease associated genes are randomly drawn from the space of all N genes in the network, see SM Sect. 3 for full details.