Skip to main content
PMC home page
The ISME Journal logoLink to The ISME Journal
. 2015 Jan 30;9(6):1352–1364. doi: 10.1038/ismej.2014.220

A multitrophic model to quantify the effects of marine viruses on microbial food webs and ecosystem processes

Joshua S Weitz 1,2,*, Charles A Stock 3, Steven W Wilhelm 4, Lydia Bourouiba 5, Maureen L Coleman 6, Alison Buchan 4, Michael J Follows 7, Jed A Fuhrman 8, Luis F Jover 2, Jay T Lennon 9, Mathias Middelboe 10, Derek L Sonderegger 11, Curtis A Suttle 12, Bradford P Taylor 2, T Frede Thingstad 13, William H Wilson 14,16, K Eric Wommack 15
PMCID: PMC4438322  PMID: 25635642

Abstract

Viral lysis of microbial hosts releases organic matter that can then be assimilated by nontargeted microorganisms. Quantitative estimates of virus-mediated recycling of carbon in marine waters, first established in the late 1990s, were originally extrapolated from marine host and virus densities, host carbon content and inferred viral lysis rates. Yet, these estimates did not explicitly incorporate the cascade of complex feedbacks associated with virus-mediated lysis. To evaluate the role of viruses in shaping community structure and ecosystem functioning, we extend dynamic multitrophic ecosystem models to include a virus component, specifically parameterized for processes taking place in the ocean euphotic zone. Crucially, we are able to solve this model analytically, facilitating evaluation of model behavior under many alternative parameterizations. Analyses reveal that the addition of a virus component promotes the emergence of complex communities. In addition, biomass partitioning of the emergent multitrophic community is consistent with well-established empirical norms in the surface oceans. At steady state, ecosystem fluxes can be probed to characterize the effects that viruses have when compared with putative marine surface ecosystems without viruses. The model suggests that ecosystems with viruses will have (1) increased organic matter recycling, (2) reduced transfer to higher trophic levels and (3) increased net primary productivity. These model findings support hypotheses that viruses can have significant stimulatory effects across whole-ecosystem scales. We suggest that existing efforts to predict carbon and nutrient cycling without considering virus effects are likely to miss essential features of marine food webs that regulate global biogeochemical cycles.

Introduction

Viruses infect nearly all forms of cellular life, including the bacteria, archaea and microeukaryotes that are the base of the ocean food web. Empirical studies of viral infection in marine waters (Suttle, 1994; Fuhrman and Noble, 1995; Weinbauer et al., 2003; Wilhelm and Matteson, 2008) and sediments (Middelboe and Glud, 2006; Siem-Jorgensen et al., 2008; Corinaldesi et al., 2010; Umani et al., 2010) have demonstrated that the lysis of hosts by viruses releases cellular material (including carbon and nutrients) back into the microbial loop. Thus, lysis reduces the potential for consumption of microbes by larger organisms and subsequent trophic transfer up the food web (Bratbak et al., 1992; Wommack and Colwell, 2000; Weinbauer, 2004; Suttle, 2007; Danovaro et al., 2011). This virus-mediated recycling of organic matter has been termed ‘viral shunt' (Wilhelm and Suttle, 1999). Indeed, viruses are thought to turn over 20–50% of the marine bacterial community on a daily basis (Fuhrman, 1999). Such estimates were used ∼15 years ago to hypothesize that viruses may increase the flux of organic matter through ocean ecosystems when compared with idealized ecosystems without viruses (Fuhrman, 1999; Wilhelm and Suttle, 1999). This hypothesis is supported by manipulative experiments in which viral release of organic matter can have a stimulatory effect on the growth of nontargeted microbial populations (Middelboe et al., 1996; Gobler et al., 1997; Middelboe et al., 2003; Poorvin et al., 2004; Weinbauer et al., 2011; Shelford et al., 2012). However, even if one population is stimulated by the lysis of cells from another population in the short term, the same population may also be susceptible to lysis by other viruses in the community. Hence, the long-term consequences of viral lysis requires consideration of nonlinear feedbacks in a complex system.

Dynamic models of aquatic food webs provide one route to deepen our understanding of the effects and feedbacks of virus–host interactions over the long term. To this end, a limited number of food-web models that include a virus component have been proposed. These models suggest principles by which viruses, through selective lysis, can prevent competitive exclusion and stimulate diversity (Thingstad and Lignell, 1997; Thingstad, 2000) as well as stimulate secondary production (Thingstad, 2000; Miki et al., 2008). Yet, the processes by which viruses mediate carbon and nutrient cycling have still not been integrated into large-scale climate and Earth-system models (Follows et al., 2007; Stock et al., 2014). A key barrier to such integration is that previous models of aquatic food webs that incorporate viruses and nutrients have considered a single kind of limiting resource, for example, phosphate (Thingstad, 2000) or organic carbon (Miki et al., 2008). Here, we propose a step toward integration of viruses into global ecosystem models: a dynamic multitrophic model of a surface ocean microbial ecosystem. The model includes the interactions among organic and inorganic nutrients, phytoplankton (both cyanobacteria and eukaryotic autotrophs), heterotrophic bacteria, zooplankton and viruses—what we term a NPHZ-V model. Because of the in silico nature of the study, we are able to ask: ‘how do ecosystems differ with vs without viruses?' As we show, despite killing their hosts, virus-mediated recycling of nutrients is associated with stimulatory effects on ecosystem function that lay on a continuum between exclusive bottom-up or top-down control.

Materials and methods

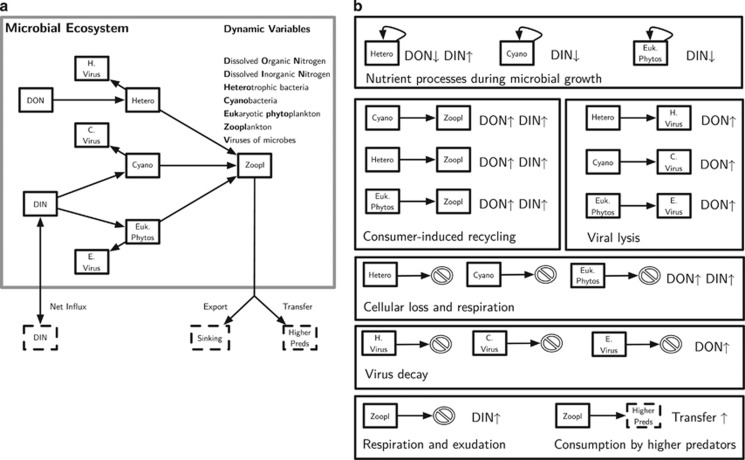
The NPHZ-V model considers the coupled dynamics of biological populations and nutrients in the euphotic zone of the surface ocean (see Figure 1). The biological populations represent functional groups, including three groups of microbes: heterotrophic bacteria (H), cyanobacteria (C) and eukaryotic autotrophs (E), three groups of viruses (that each exclusively infect only one of the three microbial groups, VH, VC and VE, respectively) and a general zooplankton group (Z, that can feed on all three types of microbes, analogous to a composite nano-/micro-zooplankton functional group). The nutrients considered are the concentration of bioavailable organic (xon) and inorganic matter (xin). The entire model utilizes nitrogen as a common currency, that is, organisms of each population have the same, fixed stoichiometry (see ‘Results and discussion' section for further treatment of this issue). We refer to densities of all biological populations in units of cells l−1 and nutrient concentrations in units of μmol l−1. The resulting coupled system of nonlinear, ordinary differential equations are presented in the Supplementary Appendix. We summarize the meaning of each process below.

Figure 1.

Figure 1

Open in a new tab

Schematic of the NPHZ-V model. (a) Interactions between populations and nutrients where arrows denote the flow of materials in the system. Note that decay processes are not depicted and the secondary effects on nutrients are depicted in (b). (b) Nutrient cycling in the system. Each of the different processes affect the levels of dissolved organic nitrogen (DON) and dissolved inorganic nitrogen (DIN), where the symbols ↑ or a ↓ denote whether a given process increases or decreases that particular pool, respectively.

Heterotrophic growth

Heterotrophic bacteria take up dissolved organic matter via a Michaelis–Menten saturating response. Organic matter is allocated to anabolic (growth) and catabolic (respiration) processes assuming a fixed growth efficiency.

Cyanobacterial and eukaryotic phytoplankton growth

Both groups of autotrophs take up inorganic nutrients via a Michaelis–Menten saturating response. This inorganic matter is fixed as biomass.

Cellular loss and respiration

Microbes undergo first-order decay terms because of release of organic cellular matter and respiration.

Viral lysis of microbes

For each virus group, successful infections with their target hosts occur at a rate proportional to the product of host and virus densities. Infections lead to the death of hosts and the release of a virus ‘burst'. Lysis includes the release of xon, assumed to be the difference between the nutrient content of hosts and the total nutrient content within the released viruses.

Viral decay

Viruses decay at a constant rate proportional to their densities. The nutrient content of decayed viruses is regenerated as organic matter.

Zooplankton grazing

Zooplankton consume each microbial population at a rate proportional to the product of the densities of zooplankton and each microbial population. Consumed biomass is subject to an ingestion efficiency that takes into account sloppy feeding (leading to release of organic matter) and growth efficiency (biomass allocated to growth vs respiration).

Zooplankton respiration

Total respiration consists of a basal component proportional to the biomass of zooplankton and an active component proportional to ingestion.

Zooplankton removal

Zooplankton biomass is ‘removed' from the system at a rate proportional to the squared density of zooplankton. This nonlinear removal rate implicitly models the effect of predation on zooplankton, assuming that the number of these unresolved predators scales with the number of the zooplankton prey (Stock et al., 2014). A fraction of the removed zooplankton biomass is exported from the system (for example, as pellets or other sinking material) and a fraction is considered to have been transferred to higher trophic levels.

Inorganic nutrient exchange

Exchange of water between the surface and subsurface leads to a change in inorganic matter concentration proportional to the difference between the surface concentration and subsurface concentration. Although the surface concentration of inorganic matter varies dynamically in the model, the subsurface concentration is held fixed.

Results and discussion

Virus–host interactions permit multitrophic coexistence

We derived the expected steady state including the coexistence of all biological populations. Such coexistence occurs for a wide range of parameters (see Supplementary Appendix for conditions), that is, coexistence does not require fine-tuning of parameters. Hence, we predict that the three functional types of viruses can persist and indeed (as we later show) promote coexistence in this multitrophic system. The key insight that enables the present derivation is that viruses, in this model, are assumed to exclusively lyse hosts. In the initial formulation, lysis of hosts is modeled as a type-I functional response, that is, proportional to the product of host and virus densities (Murray and Jackson, 1992). The burst size is equivalent to the total number of released viruses minus the virus necessary to initiate the infection. Virus population densities reach steady state when new viral production is balanced by virus particle decay. Both of these terms depend linearly on virus densities, implying that microbial host densities must be limited by viral lysis and not by a combination of resource availability and zooplankton grazing. This result is consistent with long-standing theory (Carpenter et al., 1985) and observations (Pace et al., 1999) on the potential of trophic cascades in multitrophic systems in which addition of a top predator switches control of consumer biomass from bottom-up to top-down. Similar observations have been made in models specifically developed for the study of virus–host interactions in the oceans (for example, the Kill-the-Winner model; Thingstad and Lignell, 1997; Thingstad, 2000). However, within food-web models, the nature of trophic cascade depends on the type of regulation and even the functional response of consumers to resources (Heath et al., 2014), suggesting that similar analysis of variations in the present model are warranted.

Coexistence in this model can occur either via a fixed point equilibrium or via an oscillatory steady state (see Supplementary Figure S1 for two examples). Such behavior suggests that there likely exists a Hopf bifurcation in the system, that is, a change in parameters destabilizes a fixed point equilibria so that the steady state becomes a limit cycle (Strogatz, 1994). We have not formally derived the criteria for the bifurcation given the complexity of the model. We note that prior analysis of models of virus–host interactions with implicit resources (but an explicit infected host class) (Beretta and Kuang, 2001) as well as models with explicit time delays between infection and lysis (Levin et al., 1977) also have yielded oscillatory dynamics at steady state. Hence, our multitrophic model further supports claims that oscillatory dynamics of complex marine ecosystems may be promoted because of endogenous feedbacks (here, including virus–host interactions and virus-mediated recycling), in addition to exogenous factors, for example, cyclical forcing associated with seasonality. The finding of stable coexistence raises the question: how do the population densities vary with respect to changes in parameters?

Steady-state densities predicted by model dynamics

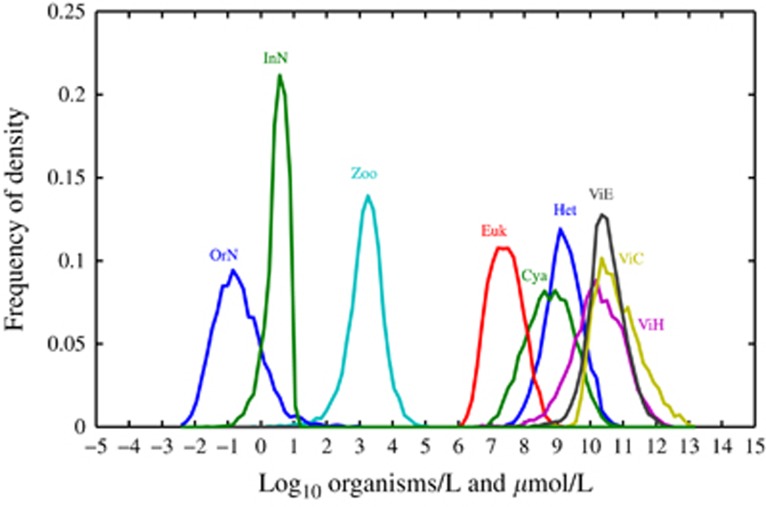
We systematically investigated the extent to which realistic features of microbial surface ocean communities could emerge within the model structure. First, we performed a global sensitivity analysis by varying all parameters independently. The parameter space was sampled with 106 model replicates using a Latin hybercube sampling scheme (McKay et al., 1979), using uniform distributions across logarithmically stratified uncertainty ranges (Thingstad, 2000; Miki et al., 2008; Williams and Follows, 2011) (see Supplementary Appendix for more details). We found that 4366 (≈0.45%) of the 106 model simulations led to coexistence among all types—we denote these parameter combinations as ‘feasible'. We consider the identification of ∼4.5 × 103 feasible model replicates to be substantial given the nonlinearity of the model and the high dimensionality of the underlying parameter space. The range of densities of populations and nutrients predicted in the Latin hybercube sampling coincide with biologically plausible population and nutrient levels (see Figure 2). We also classified the local stability of equilibrium points via a systematic examination of the eigenvalue spectra of all feasible coexistence points among 106 parameter combinations sampled via Latin hybercube sampling. We find that a majority (≈90%) of points correspond to locally stable fixed points, whereas a minority (≈10%) of points correspond to unstable spirals. Hence, stable coexistence in the model is both generic and compatible with observed densities of populations, organic and inorganic nutrients in the surface oceans. However, exceptions do occur, for example, some parameters lead to coexistence with seemingly unrealistic subsets of predicted densities and/or concentrations such as cyanobacteria at densities exceeding 1010 cells l−1. It is well known that parameters within model representations of complex multitrophic models often require further refinement to reach (realistic) steady states. Indeed, the present model includes 9 dynamic equations and 38 parameters for which manual optimization was considered infeasible.

Figure 2.

Figure 2

Open in a new tab

Variation in model output via a Latin hybercube resampling (LHS) of parameter space. Parameter space for LHS analysis is documented in the Supplementary Information.

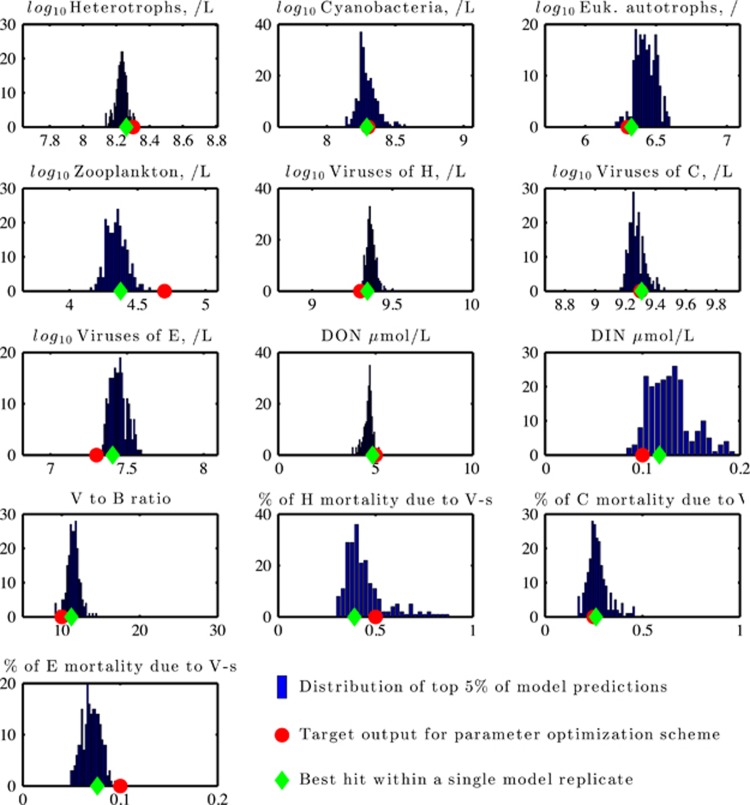
Instead, we developed an automated procedure to search through the 38-dimensional parameter space while minimizing the log-squared difference in predicted model densities relative to a ‘target'. Log-square differences weight the log ratio of deviations rather than absolute deviations. The use of log-square differences is appropriate when reconciling candidate and target predictions whose values differ across multiple orders of magnitude and in fundamental units. The target densities used in this procedure denote an idealized marine surface ecosystem (Table 1). In addition, the optimization procedure also included the following system features: total virus to bacterium ratio (10:1) and the fraction of mortality of H, C and E due to viruses (50%, 25% and 10%, respectively). Full details of the procedure are available in the Supplementary Appendix. The results of this optimization procedure are twofold: (1) a set of parameter combinations and (2) a set of predicted population densities. We then ranked each parameter combination according to the weighted deviation of model output to the target. The distribution of predicted population densities and ecosystem features associated with the top 5% of all ‘targeted' parameter combinations (218 distinct model replicates in total) can be seen in Figure 3. The features include relationships that have been empirically observed, including ratios of total viruses to bacteria on the order of 10:1 and the relative importance of viruses to cellular mortality ranging from marginal to dominant. For this target, 95% of the 218 top-performing model replicates were found to be locally stable (see Supplementary Figure S2). The parameter combinations associated with this optimization procedure can be seen in Supplementary Figure S3. These 218 parameter combinations that yield realistic microbial population densities and nutrient concentrations reflect an emergent feature of the model. Identification of replicates was enabled by our nonlinear optimization strategy to search a high-dimensional parameter space. As has been noted in the case of other models of nonlinear systems many of the parameters are relatively ‘sloppy', that is, changes in their values can be consistent with similar model outputs, whereas a few are stiff, that is, parameters must be narrowly constrained to yield similar model outputs (Gutenkunst et al., 2007). This notion applies here (see Supplementary Information and Supplementary Figures S6 and S7). For example, parameters associated with cyanobacterial interactions emerge as the stiffest, when using the top-performing parameter set as a reference. Moving forward, the relative stiffness of parameters presents one opportunity for testing putative mechanisms underlying model predictions. In summary, the NPHZ-V model, when suitably parameterized, is consistent with the emergence of multitrophic coexistence in which population densities, nutrient concentrations and ecosystem features are simultaneously compatible with biological variation in the marine surface environment.

Table 1. Target densities and concentrations used in the optimization procedure.

Pool Variable Target density Units
Heterotrophs H* 2 × 108 Cells l−1
Cyanobacteria C* 2 × 108 Cells l−1
Eukaryotic autotrophs E* 2 × 106 Cells l−1
Zooplankton Z* 5 × 104 Cells l−1
Viruses of H 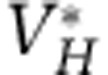Inline graphic 2 × 109 Particles l−1
Viruses of C 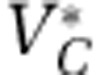Inline graphic 2 × 109 Particles l−1
Viruses of E 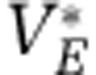Inline graphic 2 × 107 Particles l−1
Organic nitrogen 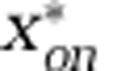Inline graphic 5 μmol l−1
Inorganic nitrogen 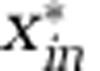Inline graphic 0.1 μmol l−1
Open in a new tab

Marine microbial densities based on variation reported for total cyanobacteria populations, exceeding 108 cells l−1 (Johnson et al., 2006), assuming similar concentrations of heterotrophic bacteria. Densities of eukaryotic autotrophs are in the range of 2 × 106 cells l−1 , during nonbloom conditions (Schartau et al., 2010), with the same study reporting total zooplankton exceeding 104 cells l−1 and, for some groups, exceeding 106 cells l−1 (Schartau et al., 2010). Total virus counts are centered in the range of 108–1011 particles l−1 (Danovaro et al., 2011; Breitbart, 2012) and are set here to be 10-fold higher than their corresponding microbial hosts (Suttle, 2007). Dissolved inorganic nitrogen is depleted in the ocean surface, with concentrations of <1 μmol l−1 typical in the subtropics (Williams and Follows, 2011), in contrast to dissolved organic nitrogen that is enriched in the ocean surface with concentrations in the range of 2 to 7 μmol l−1 (Letscher et al., 2013). Population densities and nutrient concentrations vary spatiotemporally, often deviating from the current set of target densities; other values could also be used in the targeted optimization procedure.

Figure 3.

Figure 3

Open in a new tab

Distributions of community properties obtained via nonlinear optimization. The distribution correspond to the top 5% of model feature output (blue histogram) as compared with target values (red circle), along with the properties associated with the best ranking model replicate (green diamond). The number of cases (out of 218 top-performing model replicates) are noted on the y axis.

Viral effects on community structure

Having established parameters within the NPHZ-V model that yielded biologically plausible coexistence, we evaluated the effects that viruses have on surface ocean ecosystems by comparing steady-state output and fluxes in systems with and without viruses while keeping all other parameters fixed. We performed this comparison with the entire suite of 4366 feasible parameter combinations and with the 218 targeted parameter combinations identified via a nonlinear optimization procedure. In comparing community structure to an ecosystem without viruses, we first solved the model while setting all virus densities to zero (see Supplementary Appendix). As we show in the Supplementary Appendix, the current model structure does not permit the fixed point coexistence of cyanobacteria and eukaryotic autotrophs unless viruses are present. This is a consequence of the fact that, in the present model without viruses, both the C and the E populations compete for the identical resources (xin) and are subject to the same predator (Z) that itself is subject to implicit predation. Hence, coexistence is not expected because of competitive exclusion (Armstrong and McGehee, 1980), unless C and E are subject to clade-specific parasites (for example, viruses). Coexistence would have been possible even without viruses, had we refined the model to include distinct nutrient sources, selective (or nonlinear) grazing or other forms of heterogeneity. Nonetheless, given the current model structure, this qualitative difference between steady states helps to strengthen support for the notion that viruses, even when strictly deleterious to host cells they infect, can have system-wide effects, including increasing biodiversity. The need to consider the role of parasites in food webs has only recently been highlighted (Lafferty et al., 2008), with some evidence (predominantly within aquatic food webs associated with coastal habitats) suggesting that parasites have the potential to increase diversity (Dunne et al., 2013).

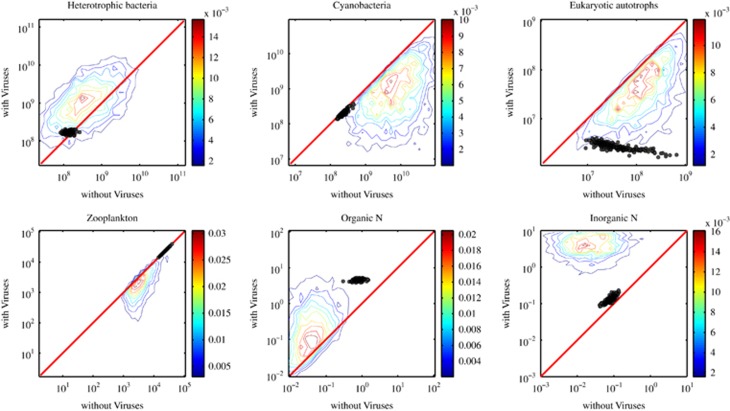
We can compare predictions of community structure with viruses with those without viruses by focusing on direct comparisons of H, C, Z, xon and xin within models where C*>0 but E*=0. The ‘*' denotes that the associated density or concentration is at steady state. Similarly, we utilize the results of models where E*>0 but C*=0 to compare with predicted densities of E with viruses. Note that our comparisons include results using the full range of parameter combinations (that is, the feasible replicates) and the optimized set (that is, the targeted replicates). In general, we find that viruses increase steady-state concentrations of inorganic nutrients in the system (see Figure 4). For example, models with viruses lead to steady-state concentrations of inorganic nitrogen between 0.1 and 10 μmol l−1 whereas without viruses, the steady states are characterized by inorganic nitrogen levels between 0.001 and 0.1 μmol l−1. We also find that viruses generally, but not inevitably, increase organic nutrients in the system. This increase in nutrients when a top predator is added is characteristic of the switch from a bottom-up system (that is, nutrient limited) to top-down system (that is, predator or parasite limited) (Hunter and Price, 1992). We also find that the effect sizes differ between the feasible and targeted replicates—this is expected, given that targeted replicates are consistent with a much narrower distribution of biomass, nutrients and ecosystem features than are the feasible replicates.

Figure 4.

Figure 4

Open in a new tab

Comparison of steady-state concentrations with and without viruses. The colored lines denote contours of equal probability among 4366 model replicates (obtained via Latin hybercube sampling (LHS)) that yielded a coexistence equilibrium (see main text; histograms conducted in logarithmic space as input for contour analysis). The circles denote comparisons for the 218 model replicates identified as part of the targeted nonlinear optimization procedure (see main text). The red line denotes the 1:1 line. Comparisons to results without viruses are restricted to model results where C*> 0 with the exception of the comparison of eukaryotic autotrophs. In each panel, viruses increase/decrease the pool of interest, as compared with ecosystems without viruses, when points (or contours) lie above/below the red line.

There are also emergent properties arising from the model that defy conventional intuition associated with a shift from bottom-up to top-down control. One might have expected that inclusion of viruses would inevitably decrease the density of heterotrophic bacteria. To the contrary, we find that heterotrophic bacteria densities typically increase by a factor of 5 in ecosystems with viruses vs those without (while holding all other parameters fixed). With viruses, heterotrophic density is top-down controlled and determined by the rates of virus decay relative to the product of virus–host contact rates and burst size. Without viruses, heterotrophic density is limited by a combination of zooplankton grazing and organic matter availability. Hence, the effect of including viruses in this surface microbial ecosystem model suggests that they can have a net stimulatory effect, via an indirect route, on the populations that they directly inhibit. As far as we are aware, this issue is underexplored in the study of host–viral interactions and, more generally, in the study of the role of parasites in ecosystem dynamics (Lafferty et al., 2008). Similarly, we found that although the total density of either the cyanobacteria or eukaryotic phytoplankton decreases in abundance when viruses are added (see Figure 4) their combined pool size increases in abundance when viruses are added. This observation raises the question of how viruses change the total amount of nitrogen in the distinct pools.

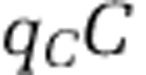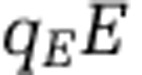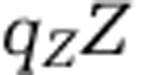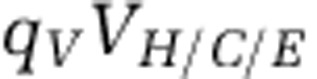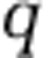We directly evaluated the change in the partitioning of biomass in the ecosystem by comparing the nitrogen content within the nutrient pools, xon and xin, and within each population: qHH, Inline graphic, Inline graphic, Inline graphic and Inline graphic, where Inline graphic denotes the nitrogen content per organism type (noted in the subscript). Figure 5 depicts the pool size corresponding to each population and nutrient type for the 218 targeted model replicates identified earlier. As is apparent, the total nitrogen concentration (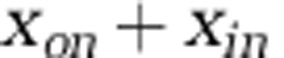Inline graphic) in the environment increases when viruses are included. A full examination of the response of the surface microbial ecosystem (and its total biomass) to the addition of viruses depends on the particular form of closure implicit in this model. Nonetheless, such stimulatory effects need not have occurred, given that all microbial groups were subject to viral lysis. It is the feedback between lysis and nutrient pools that enabled the system-wide stimulation to take place. However, as anticipated from the pairwise comparisons in Figure 4, we observed significant changes in the relative abundance of pool sizes in each population when discounting for the change in the total nutrients bound in the surface microbial ecosystem (P=10−10, Kolmogornov–Smirnov pairwise test). This result holds even for the case of zooplankton that do not change significantly in total biomass for the targeted parameter sets (see Figure 4). However, because of the overall increase in total biomass, the zooplankton decrease significantly in their relative abundance when viruses are included in the ecosystem (as is apparent in Figure 5). Moreover, as previously noted, the total pool size in the autotrophs increases when viruses are added (similar to the increase in heterotrophic biomass). Hence, viruses can alter both the total size of the microbial ecosystem and the relative partitioning within it.

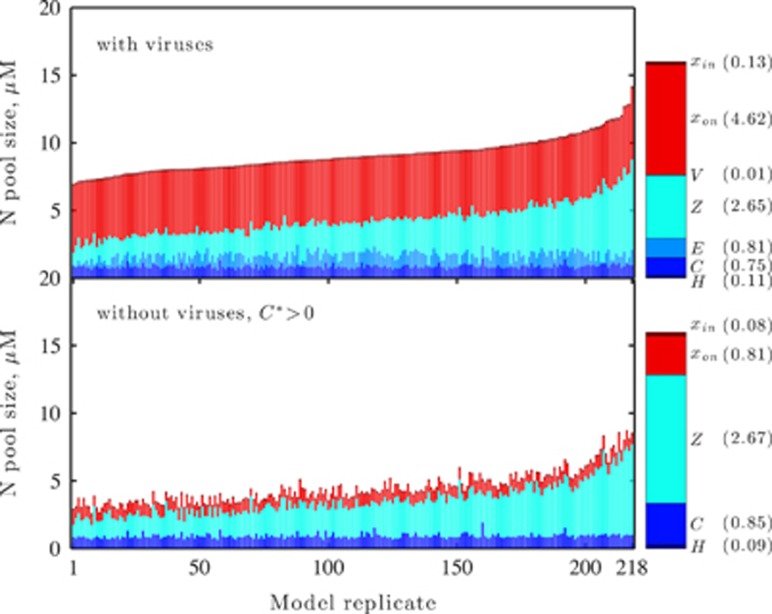
Figure 5.

Figure 5

Open in a new tab

Viral effects on community structure. The left panels (top and bottom) are stacked histograms of the concentration of nitrogen (N, in units of μM) partitioned in the different variables, H, C, E, Z, V (all types), xon and xin. The 218 stacked histograms correspond to each of the 218 parameter sets identified in the nonlinear optimization procedure described in the main text. The parameter sets were ordered based on the predicted total density of nitrogen (either organic or inorganic) at steady state within the specified variables. Hence, the top panel shows increasing total height. The 218 stacked histograms in the bottom-left panel show the expected average partitioning in ecosystems with the same parameters, although without viruses. The legend on the right includes information on both the color associated with each variable and the average concentration of N partitioned in that variable.

Viral effects on ecosystem functioning

We analyzed ecosystem-level effects of viruses, using the same sets of feasible and targeted parameters as explained in the previous section. We considered three classes of effects whose magnitude of flux might differ in ecosystems with viruses vs those without viruses: (1) organic matter regeneration, (2) transfer to higher trophic levels and (3) net primary productivity. We defined organic matter regeneration as the total flux of processes that return matter into the organic matter pool as a consequence of viral lysis of hosts and zooplankton grazing of microbes. We defined the transfer to higher trophic levels to be a fraction (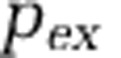Inline graphic) of the zooplankton biomass loss (that is, as consumed by higher trophic predators). We defined the net primary productivity to be the total rate of inorganic matter fixed by cyanobacteria and by eukaryotic phytoplankton. Each of these fluxes (in units of μmol lInline graphic daysInline graphic) is calculated at steady state in an ecosystem model with vs without viruses. We find that ecosystems with viruses exhibit (1) increased organic matter recycling, (2) reduced transfer to higher trophic levels and (3) increased net primary productivity (see Figure 6). Moreover, primary productivity in the targeted model replicates, in units of mg C m−2 days−1, have a mean of 1130 with s.d. of 270 (see Supplementary Figure S4). As a reference, note that empirical estimates of net primary productivity of 1140 (in the same units) have been derived for an Equatorial Pacific upwelling (Barber et al., 2001). The present model results are on the high end when compared with simulated net primary productivity for a multitrophic model without viruses, ranging from 200 to 1000 mg C m−2 days−1 (Stock et al., 2014). As we note below, the present model likely overestimates primary productivity because of the assumption of a highly efficient microbial loop.

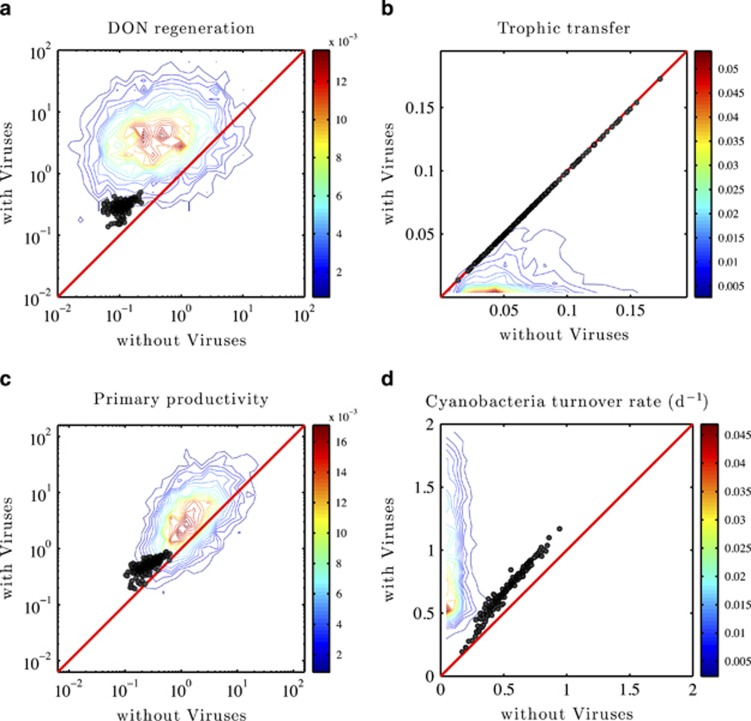
Figure 6.

Figure 6

Open in a new tab

Ecosystem functioning effects of viruses, including (a) DON regeneration; (b) trophic transfer; (c) primary productivity; (d) cyanobacteria turnover rate. The contour lines represent the probability distribution of pairwise comparisons for the 4366 model replicates identified by Latin hybercube sampling (LHS; see main text). The circle denote comparisons for the 218 model replicates identified as part of the targeted nonlinear optimization procedure (see main text). The red line denotes the 1:1 line and contours provide information on the relative density of observed point pairs (histograms conducted in logarithmic space for two left panels and in linear space for two right panels as input for contour analysis). All axes denoting ecosystem fluxes are in units of μmol(l days) −1, whereas the axes for cyanobacterial turnover are in units of days.

Viral-induced stimulation of the productivity of cyanobacteria was previously hypothesized to be a potential consequence of the viral shunt (Fuhrman, 1999; Wilhelm and Suttle, 1999). More generally, multiple groups have reported that viral lysis can stimulate the productivity of nontargeted populations in the short term (Middelboe et al., 1996; Gobler et al., 1997; Middelboe et al., 2003; Poorvin et al., 2004; Weinbauer et al., 2011; Shelford et al., 2012). Here, such effects are shown to be consistent with anticipated nonlinear feedbacks and nutrient dynamics of a multitrophic surface microbial ecosystem model over the long term, including both inorganic and organic nutrient pools. Note that although the targeted model replicates do exhibit reduced transfer to higher trophic levels, the reduction is minimal (see the near 1:1 correspondence in Figure 6 in the upper-right panel). This phenomenon is, in part, a consequence of the assumption of a highly efficient microbial food web. Note that the present model only considers the exchange of inorganic nitrogen across the nutricline (and therefore no loss of nutrients directly from the microbial pools). The only other loss term that can balance this exchange is associated with the consumption of zooplankton. Here, the consumption of zooplankton is implicit, that is, proportional to 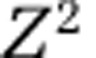Inline graphic, hence the steady state Inline graphic must be nearly identical to that in a virus-free model, so long as 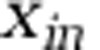Inline graphic is much smaller in the system than below the nutricline. In this limit, transfer to higher trophic levels and export will be nearly identical, with or without viruses. The extent to which the microbial loop generates export depends on its efficiency which is affected by microaggregation, direct sinking of particulate organic matter (some of which are generated by viral lysis of hosts) and downward mixing among other potential (Lomas and Moran, 2011; Williams and Follows, 2011; Stock et al., 2014). These mechanisms will likely prove relevant if Earth Systems models are to include virus–host interactions that would otherwise enhance the efficiency of the microbial loop.

Finally, recall the observation that steady-state densities of each group of primary producers are predicted to decrease when viruses are present. However, both the total combined biomass of autotrophs and net primary productivity are predicted to increase. This apparent paradox is resolved by observing that in systems with viruses, there is greater recycling of materials that increases the availability of inorganic nutrients (in part stimulated by remineralization by a larger heterotrophic pool), hence increasing primary productivity on a per-cell basis. We evaluated this hypothesis directly by estimating the turnover rate of cyanobacteria in ecosystems with and without viruses. As anticipated, the cyanobacteria turnover rate increases with viruses when compared with ecosystems without viruses (see Figure 6d). Importantly, the turnover rates of the targeted model replicates correspond to cyanobacterial residence times ranging from 0.7 to 3.3 days, with a median of 1.5 days. The relationship between residence times and steady-state densities for all biological populations and nutrient pools within the targeted model replicates can be seen in Supplementary Figure S5. In summary, viruses have the effect of stimulating the ecosystems by increasing DON regeneration, increasing primary productivity (and cyanobacterial turnover) and potentially decreasing transfer to higher trophic levels.

Conclusions

We have developed a dynamic model representing interactions within the microbial component of a surface ocean ecosystem. The NPHZ-V model developed here combines principles of NPZ models with a single limiting nutrient (Legovic and Cruzado, 1997; Klausmeier et al., 2004) with models of virus–host dynamics (Levin et al., 1977; Thingstad and Lignell, 1997; Thingstad, 2000), with explicit consideration of virus-mediated recycling (Menge and Weitz, 2009), but without explicit consideration of the infected state (Beretta et al., 2002). These simplifications enabled us to make specific predictions on the range of effects that viruses have on microbial ecosystems in marine surface waters. Given suitable parameterization, coexistence among each population occurs with steady-state densities in line with observed variation of populations and nutrients in the surface ocean. We further isolated the effect of viruses by comparing model dynamics with and without the inclusion of virus populations. In doing so, we found that ecosystems with viruses exhibit decreased abundance of zooplankton and increased abundance of organic and inorganic nutrients. These results would seem to be consistent with a shift from bottom-up (that is, nutrient limited) to top-down (that is, parasite limited) ecosystems. Yet, we also found that ecosystems with viruses could exhibit increased total biomass among heterotrophic bacteria and among autotrophs (combining the cyanobacteria and eukaryotic pools). We suggest this increase is a direct result of viral-induced recycling of nutrients. Indeed, we find that ecosytsem functioning is qualitatively changed when viruses are added. For example, ecosystems with viruses exhibit increased regeneration of nutrients, increased primary productivity (and corresponding cyanobacterial turnover rates) and decreased transfer of matter to higher trophic levels. These findings lend further quantitative support to prior hypotheses on the potential for viral-associated effects on global nutrient cycles (Fuhrman, 1999; Wilhelm and Suttle, 1999; Suttle, 2005; Brussaard et al., 2008; Weitz and Wilhelm, 2012).

The combination of analytical results and systematic analysis of variation in model output with respect to parameter variation provides significant support for the generality of our claims. Nonetheless, caution is warranted. Given the complexity of the model, one may ask: how does model output depend on the functional form of model interactions and even the diversity of biological populations, rather than exclusively on parameter variation given a fixed model? We cannot yet provide a complete answer to this question. Nonetheless, our choice of model structure reflects an intent to extend core models of marine microbial communities with minimal virus–host interactions. Hence, whereas explaining complex phytoplankton and nutrient dynamics in the absences of viruses may require consideration of these factors, it is not yet known how much of the unexplained variability in steady states, dynamics and responses could be attributed to virus–host interactions and virus-mediated recycling of nutrients. The in silico comparisons of ecosystem dynamics with and without viruses provide one step toward such a comparison. However, part of the difficulty in comparing models lies in the fact that even the relatively simple model structure examined here included 38 parameters. Hence, substantial variation in model output is possible given alternative parameterizations. Moreover, many parameter combinations led to estimates of densities and fluxes simultaneously in line with multiple observations from marine surface waters as well as novel predictions. Moving from testing predictions to testing parameters (and functional interactions) is an important challenge in reconciling complex models with data (Gutenkunst et al., 2007).

In moving forward, the current model provides a foundation for future explorations of the range of consequences associated with alternative fates of infected cells and virus particles in a systems context. In doing so, we highlight multiple priorities. First, it is essential to extend the current model to link increasingly strain-resolved information on microbial and viral diversity (Breitbart et al., 2002; Edwards and Rohwer, 2005; Allen et al., 2011) and interactions between viruses and their hosts (Flores et al., 2011; Deng et al., 2012; Weitz et al., 2013) the aggregated representation of virus–host interactions and nutrient feedbacks presented here (see the example of a calibrated model for dynamics including viruses of the algae Phaeocystis globosa; Ruardij et al., 2005). Strain-specific interactions also include the change in host physiology that occurs during infection, whether preceding lysis (Lindell et al., 2007; Ankrah et al., 2014) or during long-term associations with hosts, for example, lysogeny (McDaniel et al., 2008). Such extensions are analogous to the expanded representations of phytoplankton and zooplankton in terms of size-structured and/or functional type groups (Follows et al., 2007; Stock et al., 2014). Next, it is noteworthy that virus–host interactions unfold in a dynamic landscape of multiple nutrients, both organic and inorganic. A recent study suggested that virus lysis may be limited by phosphorus availability within hosts (Jover et al., 2014). Hence, viral lysis may transform (not just shunt) elements back into the microbial loop (Weitz and Wilhelm, 2012). Quantifying the effects of such elemental transformations requires integrating realistic ecological stoichiometry into the present model context (Sterner and Elser, 2003). In doing so, it will also be necessary to consider phytoplankton growth as limited by availability among multiple nutrients, rather than a single nutrient (Legovic and Cruzado, 1997; Klausmeier et al., 2004). The emergent ratios of organic elements have been shown to vary with latitude in the global oceans that may be driven by variation in the availability of inorganic nutrients (Martiny et al., 2013) Finally, there is a delay—the latent period—between infection and lysis, currently omitted from the model framework. Reported latent periods for marine viruses vary from less than an hour (Raytcheva et al., 2011) to dozens of hours (or more) (Suttle and Chan, 1993; Jacobsen et al., 1996; Lindell et al., 2007). Delays between infection and lysis can destabilize model predictions of population dynamics given a single virus–host pair (Levin et al., 1977; Smith and Thieme, 2012). Incorporating such delays into a multitrophic model requires resolving the likely heterogeneous distribution of latent periods in a given community (for example, see alternative representations of the delay in the models of Beretta and Kuang, 2001; Bonachela and Levin, 2014). In addition, inclusion of a pool of infected host cells also requires improved quantification of ocean processes, such as changes in nutrient uptake within infected cells (Bidle and Vardi, 2011; Ankrah et al., 2014) and grazing of infected cells by zooplankton.

We are aware of only one other attempt to integrate viruses into a NPZ framework, including both organic and inorganic nutrients, in the context of marine microbial communities (Keller and Hood, 2013). Viral dynamics in this model assumes that viral decay depends on virus density squared, rather than being proportional to virus density. A higher-order leading term for viral decay is not part of standard models of virus–host population dyanamics (Levin et al., 1977; Thingstad and Lignell, 1997; Thingstad, 2000; Beretta and Kuang, 2001; Beretta et al., 2002; Weitz et al., 2005; Menge and Weitz, 2009). Moreover, the number of infective viral particles in culture have been shown to decay exponentially, consistent with decay being a first-order process such that the population-level decay rate is proportional to virus density (De Paepe and Taddei, 2006). This difference may have unintended consequences on system dynamics. However, given the complexity of the remainder of the model in Keller and Hood (2013) (treating the microbial ecosystem with greater realism than considered here) steady-state derivations were not possible, limiting the ability to infer the effect of this choice on model dynamics without extensive numerical analysis. On the other hand, it is unlikely that purely exponential decay of viruses and type-I interactions with host populations (as we proposed) is to be expected. For example, marine viruses can be the target of grazing (Gonzalez and Suttle, 1993), adsorb to and aggregate on larger particles, such as marine snow (Weinbauer et al., 2009), and their life history traits, for example, replication rates (Lindell et al., 2007), burst sizes (Wilson et al., 1996) and latent periods (Baudoux et al., 2012), also depend on the physiological status of hosts. All of these factors would potentially give rise to higher-order loss terms or deviations from models with strict type-I functional responses (for example, see Weitz and Dushoff, 2008). Such higher-order losses have the potential to further shift the system away from top-down control by viruses.

In closing, the extension of NPHZ models to include a viral class and explicit nutrient dynamics highlights the potential effects that viruses have within multitrophic communities. Our choice in selecting a relatively low-complexity model representation enabled us to evaluate whether or not long-standing hypotheses regarding the stimulating nature of the viral shunt are consistent with dynamic nutrient feedbacks and their quantitative parameterization. We found that although viruses can have deleterious effects to the hosts they infect and lyse, they may nonetheless have a stimulatory effect at population and ecosystem scales. The dynamics emerging from the model also suggest that introduction of viruses that recycle nutrients can lead to ecosystem effects that are on a continuum between archetypal predictions of bottom-up and top-down control. It is our hope that the current model helps to identify the current state of uncertainty with respect to both the qualitative nature of virus–host interactions and the quantitative rates at which such interactions occur. In the process, we are also hopeful that the present NPHZ-V model provides a motivation for the critical need to collect quantitative data on virus–host interactions in marine surface waters so as to meaningfully integrate viral pools into predictive, global Earth system models.

Acknowledgments

This work was supported by participation in the Ocean Viral Dynamics working group at the National Institute for Mathematical and Biological Synthesis, an Institute sponsored by the National Science Foundation, the US Department of Homeland Security and the US Department of Agriculture through NSF Award EF-0832858, with additional support from The University of Tennessee, Knoxville. JSW acknowledges support from a Career Award at the Scientific Interface from the Burroughs Wellcome Fund and NSF OCE-1233760. We thank J Brum and M Sullivan for helpful comments on the manuscript.

The authors declare no conflict of interest.

Footnotes

Supplementary Information accompanies this paper on The ISME Journal website (http://www.nature.com/ismej)

Supplementary Material

Supplementary Information
Click here for additional data file. (628.4KB, pdf)

References

  1. Allen LZ, Ishoey T, Novotny MA, McLean JS, Lasken RS, Williamson SJ. Single virus genomics: a new tool for virus discovery. PLoS One. 2011;6:e17722. doi: 10.1371/journal.pone.0017722. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Ankrah NYD, May AL, Middleton JL, Jones DR, Hadden MK, Gooding JR, et al. Phage infection of an environmentally relevant marine bacterium alters host metabolism and lysate composition. ISME J. 2014;8:1089–1100. doi: 10.1038/ismej.2013.216. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Armstrong RA, McGehee R. Competitive exclusion. Am Nat. 1980;115:151–170. [Google Scholar]
  4. Barber RT, Marra J, Bidigare RC, Codispoti LA, Halpern D, Johnson Z, et al. Primary productivity and its regulation in the Arabian Sea during 1995. Deep Sea Res Part II: Top Stud Oceanogr. 2001;48:1127–1172. [Google Scholar]
  5. Baudoux A-C, Hendrix RW, Lander GC, Bailly X, Podell S, Paillard C, et al. Genomic and functional analysis of Vibrio phage SIO-2 reveals novel insights into ecology and evolution of marine siphoviruses. Environ Microbiol. 2012;14:2071–2086. doi: 10.1111/j.1462-2920.2011.02685.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Beretta E, Kuang Y. Modeling and analysis of a marine bacteriophage infection with latency period. Nonl Anal. 2001;2:35–74. doi: 10.1016/s0025-5564(97)10015-3. [DOI] [PubMed] [Google Scholar]
  7. Beretta E, Solimano F, Tang Y. Analysis of a chemostat model for bacteria and virulent bacteriophage. Discrete Continuous Dyn Syst. 2002;2:495–520. [Google Scholar]
  8. Bidle KD, Vardi A. A chemical arms race at sea mediates algal host-virus interactions. Curr Opin Microbiol. 2011;14:449–457. doi: 10.1016/j.mib.2011.07.013. [DOI] [PubMed] [Google Scholar]
  9. Bonachela JA, Levin SA. Evolutionary comparison between viral lysis rate and latent period. J Theor Biol. 2014;345:32–42. doi: 10.1016/j.jtbi.2013.12.006. [DOI] [PubMed] [Google Scholar]
  10. Bratbak G, Heldal M, Thingstad TF, Riemann B, Haslund OH. Incorporation of viruses into the budget of microbial C-transfer: a first approach. Mar Ecol Prog Ser. 1992;83:273–280. [Google Scholar]
  11. Breitbart M. Marine viruses: truth or dare. Annu Rev Mar Sci. 2012;4:425–448. doi: 10.1146/annurev-marine-120709-142805. [DOI] [PubMed] [Google Scholar]
  12. Breitbart M, Salamon P, Andresen B, Mahaffy JM, Segall AM, Mead D, et al. Genomic analysis of uncultured marine viral communities. Proc Natl Acad Sci USA. 2002;99:14250–14255. doi: 10.1073/pnas.202488399. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Brussaard CPD, Wilhelm SW, Thingstad F, Weinbauer MG, Bratbak G, Heldal M, et al. Global-scale processes with a nanoscale drive: the role of marine viruses. ISME J. 2008;2:575–578. doi: 10.1038/ismej.2008.31. [DOI] [PubMed] [Google Scholar]
  14. Carpenter SR, Kitchell JF, Hodgson JR. Cascading trophic interactions and lake productivity. BioSci. 1985;35:634–639. [Google Scholar]
  15. Corinaldesi C, Dell'Anno A, Magagnini M, Danovaro R. Viral decay and viral production rates in continental-shelf and deep-sea sediments of the Mediterranean Sea. FEMS Microbiol Ecol. 2010;72:208–218. doi: 10.1111/j.1574-6941.2010.00840.x. [DOI] [PubMed] [Google Scholar]
  16. Danovaro R, Corinaldesi C, Dell'Anno A, Fuhrman JA, Middelburg JJ, Noble RT, et al. Marine viruses and global climate change. FEMS Microbiol Rev. 2011;35:993–1034. doi: 10.1111/j.1574-6976.2010.00258.x. [DOI] [PubMed] [Google Scholar]
  17. De Paepe M, Taddei F. Viruses' life history: towards a mechanistic basis of a trade-off between survival and reproduction among phages. PLoS Biol. 2006;4:e193. doi: 10.1371/journal.pbio.0040193. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Deng L, Gregory A, Yilmaz S, Poulos BT, Hugenholtz P, Sullivan MB. Contrasting life strategies of viruses that infect photo- and heterotrophic bacteria, as revealed by viral tagging. mBio. 2012;3:e00373–12. doi: 10.1128/mBio.00373-12. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Dunne JA, Laferty KD, Dobson AP, Hechinger RF, Kuris AM, Martinez ND, et al. Parasites affect food web structure primarily through increased diversity and complexity. PLoS Biol. 2013;11:e1001579. doi: 10.1371/journal.pbio.1001579. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Edwards RA, Rohwer F. Viral metagenomics. Nat Rev Microb. 2005;3:504–510. doi: 10.1038/nrmicro1163. [DOI] [PubMed] [Google Scholar]
  21. Flores CO, Meyer JR, Valverde S, Farr L, Weitz JS. Statistical structure of host-phage interactions. Proc Natl Acad Sci USA. 2011;108:E288–E297. doi: 10.1073/pnas.1101595108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Follows MJ, Dutkiewicz S, Grant S, Chisholm SW. Emergent biogeography of microbial communities in a model ocean. Science. 2007;315:1843–1846. doi: 10.1126/science.1138544. [DOI] [PubMed] [Google Scholar]
  23. Fuhrman JA. Marine viruses and their biogeochemical and ecological effects. Nature. 1999;399:541–548. doi: 10.1038/21119. [DOI] [PubMed] [Google Scholar]
  24. Fuhrman JA, Noble RT. Viruses and protists cause similar bacterial mortality in coastal seawater. Limnol Oceanogr. 1995;40:1236–1242. [Google Scholar]
  25. Gobler CJ, Hutchins DA, Fisher NS, Cosper EM, Sañudo-Wilhelmy SA. Release and bioavailability of C, N, P, Se, and Fe following viral lysis of a marine chrysophyte. Limnol Oceanogr. 1997;42:1492–1504. [Google Scholar]
  26. Gonzalez JM, Suttle CA. Grazing by marine nanoflagellates on viruses and virus—sized particles: ingestion and digestion. Mar Ecol Prog Ser. 1993;94:1–10. [Google Scholar]
  27. Gutenkunst RN, Waterfall JJ, Casey FP, Brown KS, Myers CR, Sethna JP. Universally sloppy parameter sensitivities in systems biology models. PLoS Comput Biol. 2007;3:1871–1878. doi: 10.1371/journal.pcbi.0030189. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Heath MR, Speirs DC, Steele JH. Understanding patterns and processes in models of trophic cascades. Ecol Lett. 2014;17:101–114. doi: 10.1111/ele.12200. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Hunter MD, Price PW. Playing chutes and ladders: heterogeneity and the relative roles of bottom-up and top-down forces in natural communities. Ecology. 1992;73:724–732. [Google Scholar]
  30. Jacobsen A, Bratbak G, Heldal M. Isolation and characterization of a virus infecting Phaeocystis pouchetii (prymnesiophyceae) J Phycol. 1996;32:923–927. [Google Scholar]
  31. Johnson ZI, Zinser ER, Coe A, McNulty NP, Woodward EMS, Chisholm SW. Niche partitioning among Prochlorococcus ecotypes along ocean-scale environmental gradients. Science. 2006;311:1737–1740. doi: 10.1126/science.1118052. [DOI] [PubMed] [Google Scholar]
  32. Jover LF, Effler TC, Buchan A, Wilhelm SW, Weitz JS. The elemental composition of virus particles: implications for marine biogeochemical cycles. Nat Rev Microbiol. 2014;12:519–528. doi: 10.1038/nrmicro3289. [DOI] [PubMed] [Google Scholar]
  33. Keller DP, Hood RR. Comparative simulations of dissolved organic matter cycling in idealized oceanic, coastal, and estuarine surface waters. J Mar Syst. 2013;109-110:109–128. [Google Scholar]
  34. Klausmeier CA, Litchman E, Levin SA. Phytoplankton growth and stoichiometry under multiple nutrient limitation. Limnol Oceanogr. 2004;49:1463–1470. [Google Scholar]
  35. Laferty KD, Allesina S, Arim M, Briggs CJ, De Leo G, Dobson AP, et al. Parasites in food webs: the ultimate missing links. Ecol Lett. 2008;11:533–546. doi: 10.1111/j.1461-0248.2008.01174.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Legovic T, Cruzado A. A model of phytoplankton growth on multiple nutrients based on the Michaelis-Menten-Monod uptake, Droop's growth and Liebig's law. Ecol Model. 1997;99:19–31. [Google Scholar]
  37. Letscher RT, Hansell DA, Carlson CA, Lumpkin R, Knapp AN. Dissolved organic nitrogen in the global surface ocean: distribution and fate. Global Biogeochem Cycles. 2013;27:141–153. [Google Scholar]
  38. Levin BR, Stewart FM, Chao L. Resource-limited growth, competition, and predation: a model and experimental studies with bacteria and bacteriophage. Am Nat. 1977;111:3–24. [Google Scholar]
  39. Lindell D, Jaffe JD, Coleman ML, Futschik ME, Axmann IM, Rector T, et al. Genome-wide expression dynamics of a marine virus and host reveal features of co-evolution. Nature. 2007;449:83–86. doi: 10.1038/nature06130. [DOI] [PubMed] [Google Scholar]
  40. Lomas MW, Moran SB. Evidence for aggregation and export of cyanobacteria and nano-eukaryotes from the Sargasso Sea euphotic zone. Biogeosciences. 2011;8:203–216. [Google Scholar]
  41. Martiny AC, Pham CTA, Primeau FW, Vrugt JA, Moore JK, Levin SA, et al. Strong latitudinal patterns in the elemental ratios of marine plankton and organic matter. Nat Geosci. 2013;6:279–283. [Google Scholar]
  42. McDaniel L, Breitbart M, Mobberley J, Long A, Haynes M, Rohwer F, et al. Metagenomic analysis of lysogeny in Tampa Bay: implications for prophage gene expression. PLoS One. 2008;3:e3263. doi: 10.1371/journal.pone.0003263. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. McKay MD, Beckman RJ, Conover WJ. A comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics. 1979;21:239–245. [Google Scholar]
  44. Menge DNL, Weitz JS. Dangerous nutrients: evolution of phytoplankton resource uptake subject to virus attack. J Theor Biol. 2009;257:104–115. doi: 10.1016/j.jtbi.2008.10.032. [DOI] [PubMed] [Google Scholar]
  45. Middelboe M, Glud RN. Viral activity along a trophic gradient in continental margin sediments off central Chile. Mar Biol Res. 2006;2:41–51. [Google Scholar]
  46. Middelboe M, Jorgensen NOG, Kroer N. Effects of viruses on nutrient turnover and growth efficiency of noninfected marine bacterioplankton. Appl Environ Microbiol. 1996;62:1991–1997. doi: 10.1128/aem.62.6.1991-1997.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Middelboe M, Riemann L, Steward GF, Hansen V, Nybroe O. Virus-induced transfer of organic carbon between marine bacteria in a model community. Aquat Microbial Ecol. 2003;33:1–10. [Google Scholar]
  48. Miki T, Nakazawa T, Yokokawa T, Nagata T. Functional consequences of viral impacts on bacterial communities: a food-web model analysis. Freshwater Biol. 2008;53:1142–1153. [Google Scholar]
  49. Murray AG, Jackson GA. Viral dynamics: a model of the effects of size, shape, motion and abundance of single-celled planktonic organisms and other particles. Mar Ecol Prog Ser. 1992;89:103–116. [Google Scholar]
  50. Pace MG, Cole JF, Carpenter SR, Kitchell JJ. Trophic cascades revealed in diverse ecosystems. Trends Ecol Evol. 1999;14:483–488. doi: 10.1016/s0169-5347(99)01723-1. [DOI] [PubMed] [Google Scholar]
  51. Poorvin L, Rinta-Kanto JM, Hutchins DA, Wilhelm SW. Viral release of iron and its bioavailability to marine plankton. Limnol Oceanogr. 2004;49:1734–1741. [Google Scholar]
  52. Raytcheva DA, Haase-Pettingell C, Piret JM, King J. Intracellular assembly of cyanophage Syn5 proceeds through a scaffold-containing procapsid. J Virol. 2011;85:2406–2415. doi: 10.1128/JVI.01601-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Ruardij P, Veldhuis MJW, Brussaard CPD. Modeling the bloom dynamics of the polymorphic phytoplankter Phaeocystis globosa: impact of grazers and viruses. Harmful Algae. 2005;4:941–963. [Google Scholar]
  54. Schartau M, Landry MR, Armstrong RA. Density estimation of plankton size spectra: a reanalysis of IronEx II data. J Plankton Res. 2010;32:1167–1184. [Google Scholar]
  55. Shelford EJ, Middelboe MM, Møller EF, Suttle CAS. Virus-driven nitrogen cycling enhances phytoplankton growth. Aquat Microbial Ecol. 2012;66:41–46. [Google Scholar]
  56. Siem-Jorgensen M, Glud RN, Middelboe M. Viral dynamics in a coastal sediment: seasonal pattern, controlling factors and relations to the pelagic-benthic coupling. Mar Biol Res. 2008;4:165–U20. [Google Scholar]
  57. Smith HL, Thieme HR. Persistence of bacteria and phages in a chemostat. J Math Biol. 2012;64:951–979. doi: 10.1007/s00285-011-0434-4. [DOI] [PubMed] [Google Scholar]
  58. Sterner RW, Elser JJ. Ecological Stoichiometry: the Biology of Elements from Molecules to the Biosphere. Princeton University Press: Princeton, NJ; 2002. [Google Scholar]
  59. Stock CA, Dunne JP, John JG. Global-scale carbon and energy flows through the marine planktonic food web: an analysis with a coupled physical-biological model. Prog Oceanogr. 2014;120:1–28. [Google Scholar]
  60. Strogatz SH. Nonlinear Dynamics and Chaos. Addison Wesley: Reading, MA; 1994. [Google Scholar]
  61. Suttle CA. The significance of viruses to mortality in aquatic microbial communities. Microb Ecol. 1994;28:237–243. doi: 10.1007/BF00166813. [DOI] [PubMed] [Google Scholar]
  62. Suttle CA. Viruses in the sea. Nature. 2005;437:356–361. doi: 10.1038/nature04160. [DOI] [PubMed] [Google Scholar]
  63. Suttle CA. Marine viruses - major players in the global ecosystem. Nat Rev Microbiol. 2007;5:801–812. doi: 10.1038/nrmicro1750. [DOI] [PubMed] [Google Scholar]
  64. Suttle CA, Chan AM. Marine cyanophages infecting oceanic and coastal strains of Synechococcus: abundance, morphology, cross-infectivity and growth characteristics. Mar Ecol Prog Ser. 1993;92:99–109. [Google Scholar]
  65. Thingstad TF. Elements of a theory for the mechanisms controlling abundance, diversity, and biogeochemical role of lytic bacterial viruses in aquatic systems. Limnol Oceanogr. 2000;45:1320–1328. [Google Scholar]
  66. Thingstad TF, Lignell R. Theoretical models for the control of bacterial growth rate, abundance, diversity and carbon demand. Aquat Microb Ecol. 1997;13:19–27. [Google Scholar]
  67. Umani SF, Malisana E, Focaracci F, Magagnini M, Corinaldesi C, Danovaro R. Disentangling the effect of viruses and nanoflagellates on prokaryotes in bathypelagic waters of the Mediterranean Sea. Mar Ecol Prog Ser. 2010;418:73–85. [Google Scholar]
  68. Weinbauer MG, Brettar I, Hofle ML. Lysogeny and virus-induced mortality of bacterioplankton in surface, deep, and anoxic marine waters. Limnol Oceanogr. 2003;48:1457–1465. [Google Scholar]
  69. Weinbauer MG. Ecology of prokaryotic viruses. FEMS Microbiol Rev. 2004;28:127–181. doi: 10.1016/j.femsre.2003.08.001. [DOI] [PubMed] [Google Scholar]
  70. Weinbauer MG, Bettarel Y, Cattaneo R, Luef B, Maier C, Motegi C, et al. Viral ecology of organic and inorganic particles in aquatic systems: avenues for further research. Aquat Microb Ecol. 2009;57:321–341. doi: 10.3354/ame01363. [DOI] [PMC free article] [PubMed] [Google Scholar]
  71. Weinbauer MG, Chen F, Wilhelm SW.2011Virus-mediated redistribution and partitioning of carbon in the global oceansIn Jiao N, Azam F, Sanders S (eds)Microbial Carbon Pump in the Ocean Science/AAAS: Washington, DC; 54–56. [Google Scholar]
  72. Weitz JS, Dushoff J. Alternative stable states in host-phage dynamics. Theor Ecol. 2008;1:13–19. [Google Scholar]
  73. Weitz JS, Hartman H, Levin SA. Coevolutionary arms races between bacteria and bacteriophage. Proc Natl Acad Sci USA. 2005;102:9535–9540. doi: 10.1073/pnas.0504062102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  74. Weitz JS, Poisot T, Meyer JR, Flores CO, Valverde S, Sullivan MB, et al. Phage-bacteria infection networks. Trends Microbiol. 2013;21:82–91. doi: 10.1016/j.tim.2012.11.003. [DOI] [PubMed] [Google Scholar]
  75. Weitz JS, Wilhelm SW. Ocean viruses and their effects on microbial communities and biogeochemical cycles. F1000 Biol Rep. 2012;4:17. doi: 10.3410/B4-17. [DOI] [PMC free article] [PubMed] [Google Scholar]
  76. Wilhelm SW, Matteson AR. Freshwater and marine virioplankton: a brief overview of commonalities and differences. Freshw Biol. 2008;53:1076–1089. [Google Scholar]
  77. Wilhelm SW, Suttle CA. Viruses and nutrient cycles in the sea. BioScience. 1999;49:781–788. [Google Scholar]
  78. Williams RG, Follows MJ. Ocean Dynamics and the Carbon Cycle: Principles and Mechanisms. Cambridge University Press: Cambridge, UK; 2011. [Google Scholar]
  79. Wilson WH, Carr NG, Mann NH. The effect of phosphate status on the kinetics of cyanophage infection in the oceanic cyanobacterium Synechococcus sp. WH7803. J Phycol. 1996;32:506–516. [Google Scholar]
  80. Wommack KE, Colwell RR. Virioplankton: viruses in aquatic ecosystems. Microbiol Mol Biol Rev. 2000;64:69–114. doi: 10.1128/mmbr.64.1.69-114.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
Click here for additional data file. (628.4KB, pdf)

Articles from The ISME Journal are provided here courtesy of Oxford University Press

RESOURCES