Global typology of urban energy use and potentials for an urbanization mitigation wedge

Significance

Many case studies of specific cities have investigated factors that contribute to urban energy use and greenhouse-gas emissions. The analysis in this study is based on data from 274 cities and three global datasets and provides a typology of urban attributes of energy use. The results highlight that appropriate policies addressing urban climate change mitigation differ with type of city. A global urbanization wedge, corresponding in particular to energy-efficient urbanization in Asia, might reduce urban energy use by more than 25%, compared with a business-as-usual scenario.

Abstract

The aggregate potential for urban mitigation of global climate change is insufficiently understood. Our analysis, using a dataset of 274 cities representing all city sizes and regions worldwide, demonstrates that economic activity, transport costs, geographic factors, and urban form explain 37% of urban direct energy use and 88% of urban transport energy use. If current trends in urban expansion continue, urban energy use will increase more than threefold, from 240 EJ in 2005 to 730 EJ in 2050. Our model shows that urban planning and transport policies can limit the future increase in urban energy use to 540 EJ in 2050 and contribute to mitigating climate change. However, effective policies for reducing urban greenhouse gas emissions differ with city type. The results show that, for affluent and mature cities, higher gasoline prices combined with compact urban form can result in savings in both residential and transport energy use. In contrast, for developing-country cities with emerging or nascent infrastructures, compact urban form, and transport planning can encourage higher population densities and subsequently avoid lock-in of high carbon emission patterns for travel. The results underscore a significant potential urbanization wedge for reducing energy use in rapidly urbanizing Asia, Africa, and the Middle East.

Cities constitute the primary agglomerations of manufactured capital. Their infrastructures modulate energy flows in economic activities, buildings, and transport. Urban built environments, including transport infrastructure, shape energy consumption patterns for decades. Urban energy use significantly contributes to climate change. The most recent Intergovernmental Panel on Climate Change (IPCC) report shows that urban areas consume between 67% and 76% of global energy and generate about three quarters of global carbon emissions (1). This share of global greenhouse gas (GHG) emissions is likely to increase as global urban populations increase by two to three billion this century (2). Additionally, to accommodate growing urbanizing populations and economies, urban areas and their built environments are projected to more than triple between 2000 and 2030 (3). This ongoing urban transformation worldwide raises three key questions about future urbanization and climate change. How can cities contribute to climate change mitigation? What urban strategies are effective for different types of cities? What is the magnitude of the total mitigation potential of future urbanization?

Previous studies have identified significant factors that shape per capita urban GHG emission for individual cities (4), small sets of cities (5, 6), and for cities globally in a qualitative way (7). In these studies, factors that have been identified as correlating with urban GHG emissions include heating degree days, economic activity, population density, power generation, and technology (8). Other studies show that population density scales negatively with transport energy consumption and GHG emissions (9, 10), and also with GHG emissions from the residential sector (11). The recent IPCC report identifies urban form as a driver of urban emissions but does not provide guidance on its relative importance vis-à-vis other factors. In comparative studies, cities are often sampled from similar geographies (5, 12, 13) or population sizes (8). In these studies, causality is difficult to establish, and self-selection (14) as well as topological properties and specific urban form characteristics (15) partially explain the relationship between urban population density and transport energy consumption. Although these case studies have generated in-depth understanding for dozens of cities, there remain significant knowledge gaps. Missing from the literature is a comprehensive comparative analysis of what drives urban energy use and resulting GHG emissions globally that can help inform and identify effective mitigation strategies across different types of cities. Filling this knowledge gap would have two practical implications. First, it would allow a comparison of cities with approximately similar statistical drivers of urban GHG emissions. If cities can be clustered according to their energy end-use and GHG emission attributes, then more effective mitigation strategies could be developed, including peer-to-peer learning of climate action plans of comparable cities (16). Second, a comprehensive analysis of cities worldwide would help identify the aggregate potential of cities for mitigating climate change, something not possible with individual case studies.

To analyze urban attributes related to energy consumption, a comprehensive set of variables describing the multidimensional features of urban areas was required, including urban form, economic, and geographical characteristics. We used data from three established sources to proxy these variables, each collected using different methods: the World Bank (WB), the Global Energy Assessment (GEA), and the International Association of Public Transport (UITP) (Methods and Dataset S1). We used direct final energy use of cities, including electricity consumption and heating in building and energy use from urban transport from the GEA. We used information on final energy use in the urban transport sector provided by the UITP, and the WB data on GHG emissions in cities, comprising energy use, waste, and industrial processes but excluding marine and aviation emissions. We tested the robustness, stability, and statistical relationships across the datasets using advanced statistical and data-mining methods (Methods).

Although fuel composition often changes with urbanization (17), fuel composition and consumption-based emissions were not considered in this study. Limiting our scope to energy end-use within cities and direct emissions enabled this study to identify urbanization-relevant attributes that are not often included in technology-focused studies of climate stabilization. We did not analyze cross-boundary contributions to GHG emissions and consumption-based carbon footprints, studied elsewhere (6, 13). In total, our dataset (Dataset S1) includes 274 cities from 60 countries with a combined population of 775 million, or 21% of the global urban population (SI Appendix, Section 1; all data provided in Dataset S1). The cities in the study include all 21 megacities (cities with more than 10 million inhabitants) and are distributed across a range of population sizes, with the smallest city of 55,000.

We calculate the rank size of the entire sample cities to examine whether the 274 cities in the study are statistically representative of cities worldwide in terms of their size (18). The frequency of cities of different population sizes and their rank, where rank is determined by the frequency of occurrence, are connected through a power-law function P(i) ∼1/i^α with the exponent α close to unity, giving rise to the so-called Zipf Law (19). Sometimes called the rank-versus-frequency rule, it is a mathematical formulation of a long-observed phenomenon: the city with the largest population is about twice the size of the second largest and so on. Our results show that it scales log-log-linearly with population size (SI Appendix, Fig. S1). The slope between log city rank and log city size is −1.07, and the 95% confidence interval (CI) is between −1.21 and −0.93, including the value −1. This result confirms that the city sizes in this study are broadly representative of the global system of cities.

Results

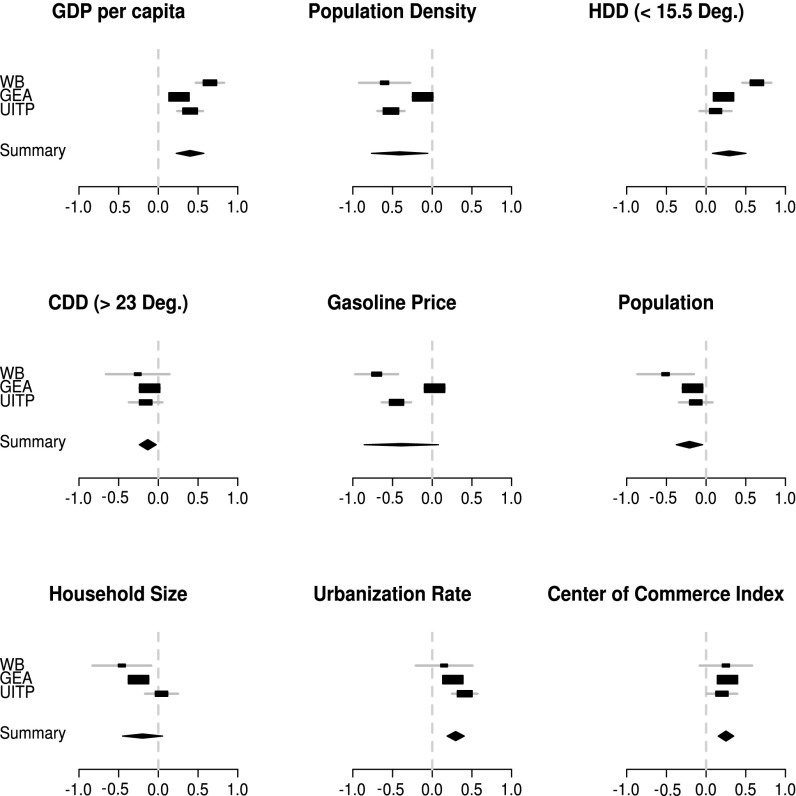
Our analysis (Fig. 1 and SI Appendix, Section 2) shows that gasoline price and population density correlate most strongly with transport energy use and GHG emissions, followed by economic activity. In contrast, the effect from economic activity dominates final energy consumption and is followed in importance by climatic variables [heating degree days (HDDs)], household size, and urbanization rate. The analysis shows that, across all datasets, economic activity, population density, and gasoline price are the most important factors in GHG emissions, but population size, household size, urbanization level, and an index of commercial centrality are also significant (SI Appendix, Table S1). However, out of the last four, only the commercial centrality index remains significant in the partial regression when we control for the other variables (SI Appendix, Table S1). Surprisingly, energy use decreases with an increase in cooling degree days (CDDs) (Fig. 1). This correlation is possibly an indirect effect of the concurrent reduction of HDD. A partial correlation, controlling inter alia for HDD, demonstrates a positive impact on energy use by increase in CDD (SI Appendix, Table S1). Coastal locations do not correlate significantly with either energy use or GHG emissions.

Fig. 1.

Confidence intervals (CIs) for Pearson's correlation coefficients with energy use of key variables in the three datasets and the combined correlation by metaanalysis; WB, GHG emissions; GEA, final energy consumption; UITP, transport energy consumption. The center squares of the CIs are proportional to weights used in metaanalysis. The summarizing measure with associated CI is given by the diamonds; associated CIs are given by the lateral tips of the diamonds. The gray, dashed vertical line represents the no effect.

The regression models (Methods) also show that four factors explain at least one-third of the variance in urban energy end-use and GHG emissions. According to the regression results, transport energy use is driven by fuel price, population density, and economic activity (Table 1). Together, economic (economic activity, gasoline prices), structural (population density), and geographical (HDD, but not CDD and coastal city location) variables explain an important fraction of the energy use variability of cities (adjusted R²: WB, 0.70; GEA, 0.35; UITP, 0.88) (Table 1). In general, economic factors (economic activity and gasoline prices) are more correlated with energy use and GHG emissions than structural variables (population density), whereas geographic variables (HDD) are highly significant but induce less marginal change in energy use (Table 1, substantiated by energy-driven top-down clustering; see SI Appendix, Sections 3 and 4). We also tested for nonlinear gross domestic product (GDP) terms, which were significant only for the UITP data (SI Appendix, Section 5 and Table S4, and discussion below).

Table 1.

Emission elasticities

Dataset	Dependent variable	No. of cities	GDP per capita	Pop. density	HDD	Fuel price	Adjusted R2
WB	GHGe per capita	26	0.18	−0.38**	0.13**	−0.76*	0.70
GEA	FE per capita	225	0.39***	−0.07***	0.07***	−0.37***	0.35
UITP	UT FE per capita	87	0.45***	−0.42***	0.02	−0.55***	0.88
Combined			0.39***	−0.28**	0.13*	−0.55***

FE, final energy; GHGe, greenhouse gas emissions; UT FE, urban transport final energy. Significance levels: ***P < 0.01; **P < 0.05; *P < 0.1.

Importantly, urban energy use is less elastic to changes in economic activity than observed in studies using national data (20). This observation may be a reflection of economies of scale in urban infrastructures and/or the relocation of energy-intensive urban production activities to rural areas. The elasticity of energy use with respect to fuel prices is significant, even in datasets of total direct urban energy use and emissions. This finding indicates that fuel prices influence energy use not only in transport, but possibly also in residential energy use. A plausible explanation for why fuel prices influence residential energy use is that, with higher transport prices, individuals will live closer to the city center and that the higher density reduces energy demand for heating (11) (SI Appendix, Section 3 and Table S2).

Urban Energy Use Typologies.

Beyond the aggregate statistics that are reported above, contextual factors such as development stage and historical development as well as the interaction between various attributes, might be equally important for explaining emission patterns across cities. To examine this hypothesis, we developed a typology of cities in the GEA dataset according to the combination of their emission attributes using endogenous threshold estimation and testing procedures in the regression context (GUIDE algorithm, see Methods; for cross-validation and confidence interval estimation, see SI Appendix, Sections 6–8).

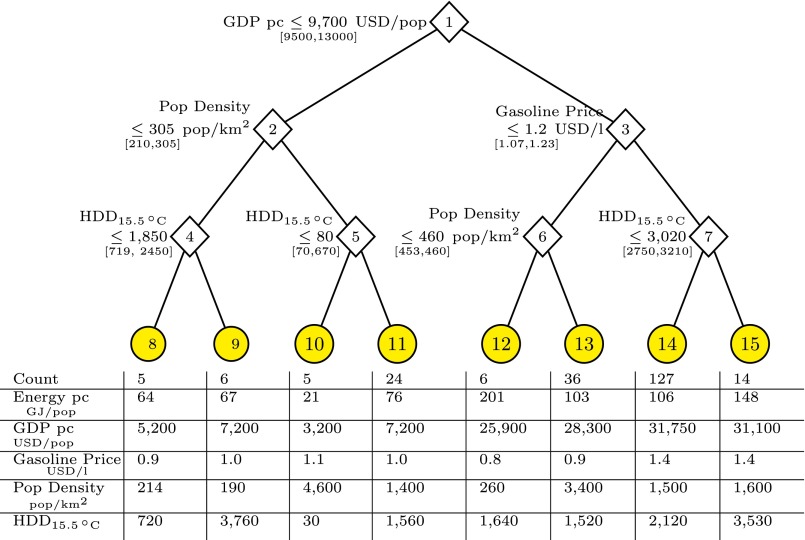
The analysis showed that the relationship between energy and its determinants varies across cities. Our analysis identified eight types of cities which are characterized by a combination of GDP per capita, population density, gasoline price, and HDD. Affluence is the most important thresholding variable at the top level (Fig. 2). Among affluent cities, those with high or medium gasoline prices and high population density have lowest emissions (Fig. 2). At the second level, threshold values in both population density and gasoline prices separate types of cities (Fig. 2). At the third, level heating degree days (HDDs) and population density further split cities into different types (Fig. 2).

Fig. 2.

Three-level threshold regression on GEA cities. Economic activity splits cities at the top level (node 1), population density and gasoline price at the second level (nodes 2 and 3), and HDD and population density at the third level (nodes 4–7). Eight typologies of cities emerge as a result (nodes 8–15); key statistics are given for each type in the table Below. See SI Appendix for regression models for each city type and the identity of cities belonging to each type.

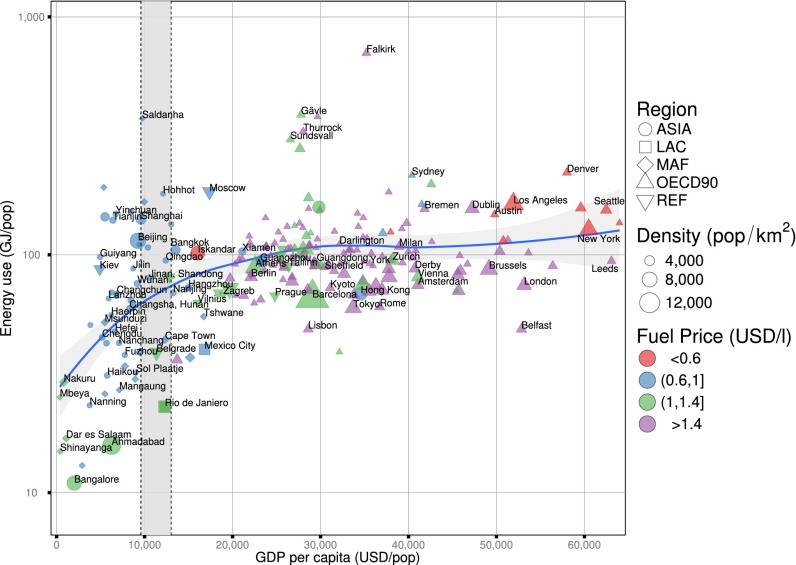
Cities with GDP less than 10,000 USD per capita (19% of all cities analyzed) show nearly three times lower energy use than those above this threshold (Figs. 2 and 3). Among less affluent cities (<10,000 USD per capita), the city type with the highest population densities (4,600 population per km²) and lowest HDD (30 in average) show the lowest energy use (∼20 GJ per capita) (Fig. 3). More affluent cities (>10,000 USD per capita), in contrast, are clustered by both gasoline prices and population density. Among these affluent cities, those with gasoline prices above 1.2 USD/L and less than 3,000 HDD have relatively low energy use (∼100 GJ per capita on average compared with ∼150 GJ per capita with HDD > 3000), but, if cities have a higher population density than 450 population per km², the relatively dense urban form can compensate for a lower gasoline price (∼100 GJ per capita compared with ∼200 GJ per capita for population density >450 population per km²) (Fig. 2).

Fig. 3.

Energy use increases with increasing economic activity, especially for GDP per capita <10,000 USD, but this increase slows down for GDP per capita above 30,000 USD (2005 US dollars in purchasing-power parity). The vertical gray-shaded area denotes the confidence interval for node 1 of threshold regression in Fig. 2. The lower gasoline price of very affluent, mostly North American cities is associated with another small increase in overall direct energy use.

The third-level thresholds in this clustering analysis show a surprising relevance of HDD. The linear regression model demonstrates a significant but weak influence of HDD. In contrast, the nonlinear threshold regression exhibits that HDD becomes a highly relevant variable, once affluence, transport prices, and urban form variables are controlled for. Among less affluent cities, energy consumption differs by a factor of three between cities in warmer (type 10) or cooler (type 11) climatic zones, and for more affluent cities by a factor of 1.5 (type 14 versus type 15) (Fig. 2). The less affluent types 8 and 9 display similar energy consumption at notably different HDD levels, but the lower level of HDD in type 8 is compensated by 10% lower gasoline costs (Fig. 2).

The relative importance of each individual factor (GDP per capita, population density, gasoline prices, HDD) changes with type of city (SI Appendix, Table S5).

Peak Urban Transport Energy Use.

Our analysis of the UITP dataset corroborates the analysis with the GEA data and shows that energy use saturates with increasing economic activity, specifically for urban transport (SI Appendix, Section 9 and Fig. S2). Energy consumption for urban transport increases with GDP at low GDP levels but decreases with GDP at high GDP levels (threshold regression, 29,300 USD; CI, 22,400–33,000 USD). Specifically, cities in developed countries with GDP per capita over 13,500 USD and with fewer than two million inhabitants show a slight decrease in transport energy use with increasing GDP (Pearson correlation coefficient r = −0.35, P = 0.06). All other cities show strong growth in transport energy use with GDP per capita (r = 0.65, P < 0.01). This finding is evidence that, at higher levels of income, urban transport decouples from GDP per capita, similar to what has been observed on the national level in OECD (Organisation for Economic Co-operation and Development) countries (21). Affluent cities with GDP per capita above 13,500 USD and population size below 2 million inhabitants, mostly European cities, have higher gasoline prices (P < 0.01) but lower population density than the other cities (P < 0.01). This result suggests that increases in economic activity increase the demand for urban land and thus reduce population density, but that an increase in gasoline taxes can mediate and even counterbalance this pattern.

An Urbanization Wedge.

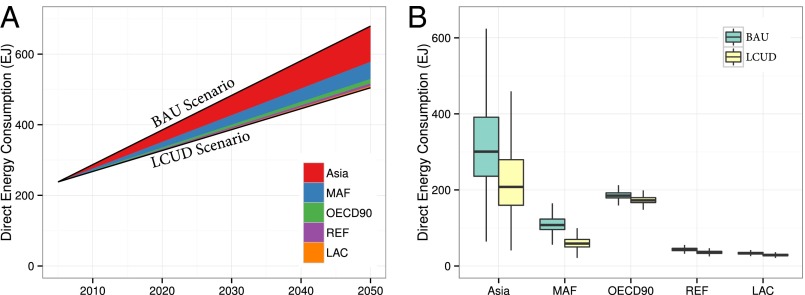
Our results point to the potential of urbanization to save energy and reduce associated GHG emissions. This raises the question of the potential magnitude of the global urbanization wedge between 2005 and 2050. In 2005, the global urban population of ∼3.2 billion consumed about 240 EJ of energy at end-use (SI Appendix, Section 10) (22). By 2050, the urban population is expected to double to around 6.4 billion (2). During this same period, the average GDP per capita could plausibly increase by 80% in OECD countries and 390% in Asia (23). Accounting for population growth and considering the economic activity elasticity in low and affluent types of cities, total energy consumption in cities worldwide could increase to around 730 EJ (Fig. 4A and SI Appendix, Section 10). This estimate omits potential interventions by urban planning or gasoline taxes, and assumes stable oil prices. If urban planning and fuel taxes are used, total urban energy consumption could increase to about 540 EJ (Fig. 4A), assuming a universal increase of gasoline prices to 1.6 USD/L (deflated to 2005 dollars; approximately reflecting the existing level of gasoline prices in European countries) (24) and assuming urban planning policies that support higher population densities, mixed-use development, and accessibility (Methods). More precisely, we model population density to increase half as fast as population growth. That is, when the total population of a world region increases by 10% between 2005 and 2050, then urban planning allows urban population density to increase by 5%. The mitigation potential is greatest in rapidly growing cities and in cities with low gasoline prices. The total urbanization wedge is about 180 EJ. More than half of this urbanization wedge is in Asia (57%), and nearly one-third (29%) is in Africa and the Middle East. In contrast, the OECD90 (OECD countries in 1990) possesses relatively low potential for reducing energy use in cities (6%), mainly because OECD90 cities are mature, built-up environments with established infrastructure and associated locked-in behavior and energy consumption patterns.

Fig. 4.

Potential of an urbanization wedge in energy use. (A) Urbanization wedge characterized by median business-as-usual (BAU) and low-carbon urban development (LCUD) scenarios. (B) Uncertainty in scenarios for the different world regions. The centerline is the median, the top and bottom of the boxes are the 25th and 75th percentiles, and lines present overall range. OECD90, OECD countries in 1990; LAM, Latin America and the Caribbean; MAF, Middle East and Africa; REF, reforming economies of Eastern Europe and the former Soviet Union.

The uncertainty underlying these scenarios is considerable. Structural uncertainty is based on uncertainties in economic growth, how urban energy use changes with economic growth, fuel prices, and population density changes. We rely on the spread of the SRES (Special Report on Emissions Scenarios) scenarios and confidence intervals obtained in the threshold regressions to estimate overall energy use in world regions in the business-as-usual and policy scenarios and report the uncertainty by a Monte Carlo simulation (Fig. 4B; for more details, see SI Appendix, Section 10). Despite the uncertainties, the scenarios illustrate the enormous potential for a mitigation wedge in urbanizing Asia, Africa, and the Middle East. The uncertainties change the magnitude of the potential, but the underlying reasons for the mitigation wedge remain. It is in those places where infrastructure is still nascent that there is the greatest mitigation potential.

Discussion

This study points to a considerable but differentiated potential for an urban mitigation wedge. Continued urban population growth and associated development of urban areas worldwide combined with projected increases in GDP per capita could lead to a tripling of urban energy use from 2005 to 2050. However, how the cities of tomorrow develop spatially, especially their urban form, will lock in patterns of energy consumption for decades to come. Recent forecasts suggest that the global urban footprint will triple between 2000 and 2030, an area of 1.2 million km², or equal to the size of South Africa (3). Thus, mitigation interventions related to urban form have the highest potential during early phases of urban development. This window of opportunity exists especially for low-emissions cities in Asia, the Middle East, and Africa where urbanization and associated rises in income could lead to high increases in urban energy use if current trends continue. However, demand-side policies, such as increased gasoline prices, encouraging compact and accessible urban forms, along with idiosyncratic urban design options, can also reduce urban energy use in developed cities (25, 26). Backed by increases in gasoline prices, urban form modifications could reduce global energy use in cities by 26% or 190 EJ, constituting a notable and possibly low-cost or negative-cost urbanization wedge for climate change mitigation.

To realize this urbanization wedge, different types of cities require different mitigation strategies. Currently thousands of cities worldwide are developing local climate action plans, but their aggregate impact on emissions is uncertain (1). This uncertainty is in part because of low accountability and lack of baseline data on urban emissions, but also because the strategies adopted may not be the most effective at lowering emissions for a particular type of city. Although many urban mitigation strategies have important local cobenefits, any measurable impact on emissions will require adopting strategies that target the main sources of emissions. If countries with fuel prices below 1.2 USD/L increased this price to 1.6 USD/L, they would enable a market-based transition toward more energy-efficient cities. Similarly, urban-planning policies, including mixed-used design and high connectivity and accessibility, which are themselves closely related to population density, could be supportive in establishing long-term energy savings. In addition, those city types with high HDD could reduce emissions by enforcing stricter building codes and retrofitting strategies. These results are not only highly policy-relevant. In addition, the results provide a promising base for integrated assessment models that investigate the interaction between urbanization and technological decarbonization options in global scenarios.

This study provides for the first time, to our knowledge, robust (taking into account cross-data heterogeneity), statistically meaningful observations on a globally representative set of cities. The large sample of 274 cities validates some previously observed effects while simultaneously providing more statistically meaningful results (Fig. 1 and SI Appendix, Figs. S1–S7 and Tables S1–S5) and statistically and quantitatively significant elasticities (Table 1). High-emissions cities display in aggregate high economic activity and low population density, low fuel prices, and high HDD whereas low-emissions cities have low economic activity, high population densities, and high fuel prices.

Fuel price as a potential driver of urban GHG emissions deserves particular attention for policy purposes. Although the importance of fuel prices as drivers of GHG emissions has been generally widely recognized (25), its specific importance for urban energy use and GHG emissions has not yet been systematically specified in the literature on cities and climate change. In the urban economics literature, gasoline prices and other transport costs have long been known to influence urban transport distances and modal choice, urban form, and population density (27, 28). Gasoline price is likely to influence GHG emissions directly and indirectly. Directly and in the short term, higher gasoline prices modify travel behavior and reduce transport distance traveled by cars inside and outside of cities alike (29). Indirectly and in the long run, higher gasoline prices could induce a shift in private vehicle ownership but also could change patterns of where people live and work (30), travel behavior, and electricity/heating demand via modified floor space (11).

Our analysis focuses on the direct energy use in cities, including also the energy use from economic production activities. A number of studies have emphasized the importance of production activities for the urban carbon footprint (6, 13, 31). As a crude proxy, the commerce index correlation indicates that economic commerce activity plays a role also in our global sample of cities. In fact, production activity is likely to explain a significant part of the variability left unexplained by our study. For example, some of the outlier cities in Fig. 3 displaying very high energy use are small cities with oil refining or an allied industry as a dominating business. This hypothesis is supported by an analysis of the United Kingdom demonstrating that territorial emissions, including production-based carbon footprints of human settlements, are highly variable (13). Our typology could therefore be extended by production-based material-flow data for cities worldwide. Overall, however, our results provide support for developing differentiated urban mitigation strategies that reflect the variation in the key drivers of urban emissions.

Methods

Correlation Analysis.

We performed the correlation analysis for each dataset using a distinct dependent variable: final direct energy consumption per capita for the GEA data, total transportation energy use per capita for the UITP data, and GHG emissions per capita for the WB data. Because dependent variables but also methods of data collection and year of data collection differed, datasets were not harmonized. We calculated the correlation (Pearson correlation coefficient; see SI Appendix) for 10 independent variables: GDP per capita, population density, heating degree days (HDDs; number of days with temperatures <15.5 °C), cooling degree days (CDDs; number of days with temperatures >23 °C), gasoline price, population size, household size, urbanization level, a center of commerce index (a comparative ranking of 75 of the world’s leading global cities and their instrumental role in driving the economy), and coastal location, a binary variable representing coastal city location. With the exception of coastal location, which did not show any significant correlation with energy use-related variables, results are presented in Fig. 1 and SI Appendix, Table S1. Even though recent studies have normalized GHG emissions of direct energy use with GDP (31, 32), we treat GDP as one of several attributes, which allows a distinction between different classes of cities based on complete bundles of attributes. Each dataset was analyzed independently. Correlation statistics (SI Appendix, Table S1) for each database were calculated individually. Heating degree days (HDDs), cooling degree days (CDDs), and household size were collected independently and were used for all datasets.

Statistical Analysis.

We used correlation coefficients as effect sizes to aggregate results across all datasets using the meta analysis random effect DerSimonian-Laird (DSL) approach (33). The random-effects analysis requires first an inverse variance weighting, and then a reverse unweighting by applying a random effects variance component, which is derived from the extent of variability of the underlying studies’ effect sizes. The random effect approach, as opposed to a fixed effect one, permits interference to extend beyond the datasets included in this study (34). It also allows for between-dataset heterogeneity as well as within-dataset variability. Individual studies taken separately tend to consistently underestimate heterogeneity (33).

Regression Analysis.

To estimate the relationship between energy consumption and determinants, we used a standard multiple regression approach with log-transformed variables as described in standard applied regression literature (35, 36). The estimated model has the following standard form,

$$\ln \left(E_i\right)={\alpha }_i+{\displaystyle \sum _{j=1}^k{\beta }_j{X}_{ij}+{\epsilon }_i}$$

with i = (1, …, N) representing cities. Here, E_i is a measure of city energy consumption, and X_j for j = (1,…, k), denotes the consumption determinants, with k the total number of regressors, and ε_i is the classical error term.

The variables included in the final regression were selected from a larger set of possible determinants: i.e., GDP per capita, population density, heating degree days, cooling degree days, gasoline prices, household size, urbanization rate, and commerce center index. The variables included were then reduced, applying the widely used backward elimination statistical procedure (35, 36). The model selection procedure is known as “general to specific approach.” The procedure starts with a large number of variables that are sequentially reduced by removing the least significant variable, one at the time, if its P value is above a chosen threshold, reestimating the model each time with the remaining variables. The initial selection criterion used was P > 0.2 to remove. The procedure stops, when all variables are significant at the 0.2 level. In the UITP dataset, in addition to the other variables reported in Table 1, household size was also significant at the P < 0.05 level. Coefficients from a regression model, where the dependent and independent variables of interest are in natural log form and linearly related to each other, can be conveniently interpreted as the average percentage change in the dependent variable corresponding to a percentage change in the independent variable (ref. 37, p. 55). The regression coefficients thus obtained are independent of the units used for measuring variables and are known as elasticities.

Threshold Regression.

Recursive data partitioning algorithms provide computationally efficient methods to produce the classification that requires processing multiple threshold variables as well as threshold values. In this paper, we used the recursive data-partitioning algorithm developed by Loh and Hansen et al. (38–40), known as GUIDE (generalized, unbiased, interaction detection and estimation) (see also SI Appendix, Section 7), which repeatedly splits the data into increasingly homogeneous groups. The resulting model can be conveniently presented as a binary tree graph. These models can be viewed as parsimonious strategies for a fully nonparametric estimation of a regression model. Regression-tree methods are known to be consistent in the sense that, under standard statistical assumptions, the predicted values converge to the unknown nonlinear regression function (see SI Appendix). GUIDE minimizes potential biases in variable selection and interaction detection and allows fitting a linear model at each node.