Limits to adaptation along environmental gradients

Significance

Why do species’ ranges often end when no obvious change in the environment suggests they should? Our theory explains that there is an inherent limit to adaptation arising in any (finite) natural population and identifies the key parameters that determine this limit to a species’ range. Two observable parameters describe the threshold when adaptation fails: (i) the loss of fitness due to dispersal to a different environment, and (ii) the efficacy of selection relative to stochastic effects in finite populations.

Abstract

Why do species not adapt to ever-wider ranges of conditions, gradually expanding their ecological niche and geographic range? Gene flow across environments has two conflicting effects: although it increases genetic variation, which is a prerequisite for adaptation, gene flow may swamp adaptation to local conditions. In 1956, Haldane proposed that, when the environment varies across space, “swamping” by gene flow creates a positive feedback between low population size and maladaptation, leading to a sharp range margin. However, current deterministic theory shows that, when variance can evolve, there is no such limit. Using simple analytical tools and simulations, we show that genetic drift can generate a sharp margin to a species’ range, by reducing genetic variance below the level needed for adaptation to spatially variable conditions. Aided by separation of ecological and evolutionary timescales, the identified effective dimensionless parameters reveal a simple threshold that predicts when adaptation at the range margin fails. Two observable parameters determine the threshold: (i) the effective environmental gradient, which can be measured by the loss of fitness due to dispersal to a different environment; and (ii) the efficacy of selection relative to genetic drift. The theory predicts sharp range margins even in the absence of abrupt changes in the environment. Furthermore, it implies that gradual worsening of conditions across a species’ habitat may lead to a sudden range fragmentation, when adaptation to a wide span of conditions within a single species becomes impossible.

Why a species’ range sometimes ends abruptly, even when the environment changes smoothly across space, has interested ecologists and evolutionary biologists for many decades (1–8). Haldane (2) proposed that, when the environment is spatially heterogeneous, a species may be unable to adapt and expand its range because gene flow from the center swamps the populations at the range margins, preventing their adaptation. Theory showed that, when genetic variance is fixed, adaptation indeed fails if the environment changes too steeply across space (9), and a sharp margin to the species’ range forms. The population remains well adapted only in the center of the range, and gene flow swamps variants adapted to the margins, preventing range expansion. This result also elucidates range margins in the presence of competitors: then, interspecific competition in effect steepens the environmental gradient (10). However, this limit to adaptation assumes that local genetic variation is fixed.

Current deterministic theory states that, when genetic variance can evolve, there is no sharp limit to a species’ range (11). The genetic mixing caused by gene flow inflates the genetic variance and facilitates further divergence. Gene flow across a phenotypic gradient maintained by the environment can generate much more variance than would be maintained by mutation alone (12, 13). This rise of genetic variance with environmental gradient can allow species to adapt to an indefinitely wide geographic range—and hence an indefinitely wide ecological niche. Adaptation only fails when the local load due to genetic variance becomes so large that the population is no longer sustainable because the mean Malthusian fitness (growth rate) declines below zero. On constant environmental gradients, this leads to extinction everywhere. On gradually steepening gradients, we would see a gradual decrease in density due to the rising genetic variance and the associated standing load.

The interface between ecology and evolution is critical for understanding the evolution of the species’ range. However, until now, no predictive theory has included the fundamental stochastic processes of genetic drift and demographic stochasticity. Genetic variation is often measurably lower in peripheral populations (4, 14) and experimental evidence suggests that low genetic variance coupled with high gene flow can prevent adaptation at the edge of a species’ range in nature (15–17). Thus, there is clear evidence that low genetic variation may limit adaptive range expansion. This may be because genetic drift reduces local variance (18, 19) and hence the potential of the population to adapt (20). Studies of range expansion with genetic drift are few, and limited to simulations (21–24). By manipulating dispersal and carrying capacity, these studies demonstrated that genetic drift may be important to theory of species’ range evolution. However, without establishing the key parameters, no quantitative predictions can be made that generalize beyond specific simulation models.

The goal of this study is to examine how finite population size, through its effect on genetic drift, and in combination with demographic stochasticity, affects the limits of a species’ range. We give the combination of parameters that describes the dynamics of evolution of a species’ range and especially, its limits, when genetic variance can evolve, the environment is heterogeneous, and populations are finite. We assume that, as the environment changes across space, there is a corresponding change in the optimal value of some phenotypic trait. Deviation from the optimum reduces fitness, and so range expansion requires adaptation to this environmental gradient. Demography and evolution are considered together, and both genetic variance and trait mean can freely evolve via change in allele frequencies. Crucially, we include both genetic and demographic stochasticity. The model is first outlined at a population level, in terms of coupled stochastic differential equations (Materials and Methods, Evolutionary and Ecological Dynamics). Using this formalization, we can identify the effective dimensionless parameters that describe the dynamics: these parameters are measurable and predict when adaptation to an environmental gradient fails. After separation of the timescales of ecology (fast) from evolution (slow), these reduce to just two key observable parameters—a major simplification for a model whose initial formulation requires seven parameters. Next, individual-based simulations determine the driving relationship between the key parameters and test its robustness [see SI: Individual-Based Model and Dataset S1 for Mathematica (Wolfram) simulation code].

Results

Deterministic Limit.

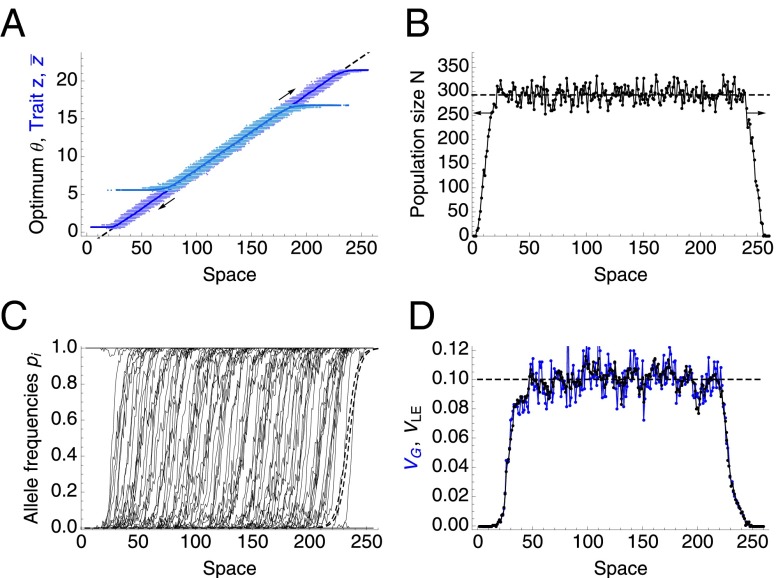
First, to both validate and illustrate the model, we show that the individual-based model matches the predictions at the deterministic limit (11), where the species’ range expands indefinitely. Fig. 1 illustrates the joint evolution of population size and trait mean and variance via change in allele frequencies, when genetic drift is weak—when $N\sigma \sqrt{s}\gg 1$ (25, 26), where population size within a dispersal distance σ is $N\sigma$, and s is the strength of selection per locus. N represents size of each deme, which corresponds to population density in continuous space. Genetic variance, $V_G$, evolves, and is generated primarily by gene flow due to mixing of genes from individuals with different phenotypes, well adapted to the diverse environments (Fig. 1D); the contribution from mutational variance is negligible.

Fig. 1.

Illustration of the individual-based model at the limit of weak genetic drift, when the species’ range keeps expanding as predicted by the deterministic model (11). (A) Trait mean $\overline{z}$ matches the optimum $\theta =bx$ (dashed line), shown for the starting population (light blue) and after 5,000 generations (dark blue). The spread of the trait values z for all individuals is shown with dots. (B) Local population size is close to the deterministic prediction (dashed line) $\widehat{N}=K{r}^{*}/r_m=K\left[1-\sigma b/\left(2\sqrt{V_s}{r}_m\right)\right]$, where K gives the carrying capacity for a well-adapted phenotype. (C) Clines for allele frequencies are shown by thin black lines; the predicted clines (dashed) have widths $w_s=4\sigma /\sqrt{2s}$ and are spaced $\alpha /b$ apart. (D) Total genetic variance is shown in blue, and the linkage equilibrium component is shown in black; the dashed line gives the prediction $V_G=V_{LE}=b\sigma \sqrt{V_s}$: each cline contributes genetic variance $V_{G,i}={\alpha }_i\sigma \sqrt{V_s}$, and per unit distance, there must be $b/\alpha$ clines if the trait mean matches into the optimum (11, p. 378). Parameters, defined in Table 1, are as follows: $b=0.1$, ${\sigma }^2=1/2$, $V_s=2$, $r_m=1.025$, $K=300$, $\alpha =1/\sqrt{20}$, $\mu ={10}^{-6}$, 5,000 generations.

Scaling and Separation of Timescales.

We now proceed by reducing the number of parameters (Table 1) in the model, including stochasticity (Materials and Methods, Rescaling). We seek a set of dimensionless parameters that fully defines the dynamics of a system, with a preference for those that are empirically measurable. Rescaling space, time, trait, and population density reveals that three dimensionless parameters fully describe the system, neglecting mutation and assuming linkage equilibrium between loci. The first parameter carries over from the phenotypic model of ref. 9: (i) the effective environmental gradient, $B=b\sigma /(r*\sqrt{2V_S})$, where b is the gradient in the optimum, $V_s$ is the width of stabilizing selection, and $r*$ gives the rate of return to equilibrium. Two additional dimensionless parameters come from including stochasticity: (ii) the efficacy of population regulation relative to demographic stochasticity, $N\sigma \sqrt{r*}$; and (iii) the efficacy of selection relative to the strength of genetic drift, $N\sigma \sqrt{s}$.

Table 1.

Definition of parameters

Parameter	Dimension†	Definition
B	$Z/D$	Gradient in the environmental optimum
$V_s$	$Z^{2}T$	Variance of stabilizing selection
σ	$D/\sqrt{T}$	Dispersal per generation
K	$T/D$	Carrying capacity for a well-adapted phenotype
$r_m$	$1/T$	Maximum exponential growth rate
α	Z	Allelic effect
μ‡	$1/T$	Mutation rate
s	$1/T$	Selection per locus: $s\equiv {\alpha }^2/\left(2V_s\right)$
$r*$	$1/T$	Rate of return to equilibrium population size: $r*\equiv {-N\hspace{0.17em}\partial \overline{r}/\partial N|}_{N\to \widehat{N}}=r_m-V_G/\left(2V_s\right)$
B	—	Effective environmental gradient,
		$B=b\sigma /\left(r*\sqrt{2V_s}\right)$
$N\sigma \sqrt{s}$	—	Efficacy of selection relative to strength of genetic drift
$N\sigma \sqrt{r*}$	—	Efficacy of population regulation relative to demographic stochasticity

Three scale-free parameters, B, $N\sigma \sqrt{s}$, and $N\sigma \sqrt{r*}$ (bottom), describe the system; the top section gives seven parameters of the model before rescaling and the middle section defines two important composite parameters.

^†Dimensions: T stands for time, D stands for distance, and Z stands for trait. Note that, with a Poisson number of offspring, the effective population size $N_e$ (which measures rate of genetic drift/coalescence) is identical to the N that regulates population growth due to crowding: hence, both carrying capacity K and population density N have units of $T/D$.

^‡Mutation rate μ is set to be small, with minimal contribution to the dynamics, and, hence, $\mu /r*$ is neglected in the rescaled parameterization.

The dynamics of evolution of species’ range simplifies further because selection per locus s is typically much smaller than the rate of return to equilibrium population density $r*$ (ref. 27 and ref. 28, appendix D) (Fig. S1 for values used here). This has two consequences. First, the ecological dynamics $\partial N/\partial t$ are faster than the evolutionary dynamics $\partial p/\partial t$ of the individual loci (where p denotes the allele frequency and t denotes time). Importantly, the genetic variance evolves slower than the mean: whereas the trait mean changes with the product of strength of selection and the genetic variance, the directional change in the variance is slower by the inverse of the number of locally polymorphic loci [precisely, the “effective number of loci” (29)]. Genetic drift only slowly degrades expected heterozygosity $\langle pq\rangle$ at each locus (Fig. S2), reducing the variance. Hence, over ecological timescales, genetic variance can be treated as constant. Second, the effect of fluctuations due to genetic drift, scaling in 1D habitat with $1/\left(N\sigma \sqrt{s}\right)$ (Fig. S2), is expected to dominate over the effect of demographic fluctuations, which rise with $1/\left(N\sigma \sqrt{r*}\right)$. Hence, we expect that the conditions determining whether adaptation to an environmental gradient is sustainable within a single species’ will be described by just two of the dimensionless parameters. These are the effective environmental gradient, B, and the efficacy of selection relative to the strength of genetic drift, $N\sigma \sqrt{s}$. We thus propose that the dynamics of species’ range evolution can be understood based on bulk parameters B and $N\sigma \sqrt{s}$, rather than by focusing on asymmetric gene flow near the range margins. Later, we show that the prediction holds even when B and $N\sigma \sqrt{s}$ change steadily across space.

Threshold for Collapse of Adaptation.

First, we simulated the basic model with a linear gradient, assuming equal phenotypic effects α of each allele and including both genetic and demographic stochasticity. Parameters were drawn at random from distributions consistent with our knowledge of the range of parameters expected in nature (ref. 28, discussion) and ensuring that, without genetic drift, all ranges would expand (Fig. S1). Then, we performed additional runs to test whether the threshold obtained from the linear gradient applies when parameters are changing gradually across space. Namely, we tested whether a stable range margin forms at the predicted value when the environmental gradient varies across space or when the carrying capacity is nonuniform. Last, we tested the model assuming that allelic effects ${\alpha }_i$ are exponentially distributed.

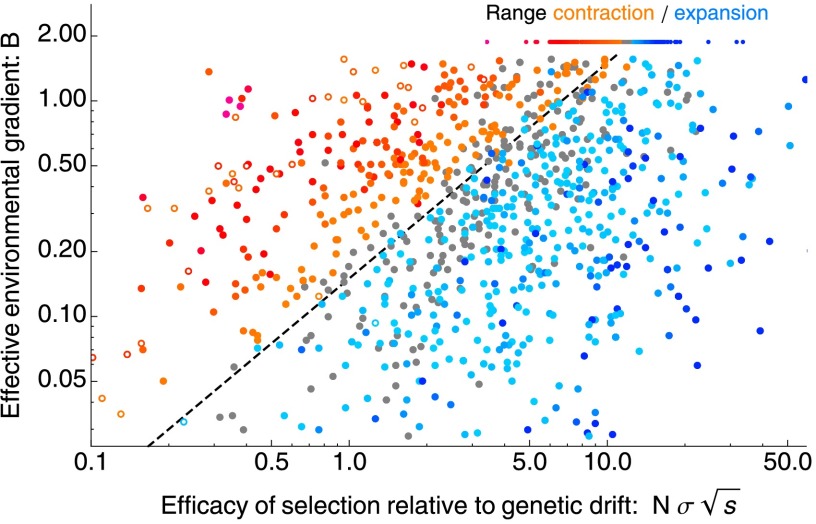
Fig. 2 shows our key result: the effective environmental gradient, B, and the efficacy of selection relative to the strength of genetic drift, $N\sigma \sqrt{s}$, determine the threshold for collapse of adaptation. This is because the genetic variance evolves primarily in response to $N\sigma \sqrt{s}$ and B, whereas the effect of demographic stochasticity, $N\sigma \sqrt{r*}$, is relatively weak. When $B\gtrsim 0.15N\sigma \sqrt{s}$, genetic drift strongly degrades adaptation to a steeply changing environmental optimum, and the species’ range contracts. The constant 0.15 is obtained as the best-fitting threshold for the data in Fig. 2. At the start of all simulations, the population is perfectly adapted in the central part of the available habitat. As both environmental gradient and carrying capacity are uniform across the habitat, populations either steadily expand or contract. Typically, populations contract from their margins and ultimately (over times much longer than 5,000 generations of the simulation runs) collapse to a state with no or very little clinal variation. However, when genetic drift is very strong, populations collapse abruptly or even fragment (Fig. S3): this second threshold, based on a “critical gradient” of a phenotypic model, is explained later. This model with an idealized linear gradient and uniform carrying capacity is used to identify the relationship between the driving parameters $N\sigma \sqrt{s}$ and B, which determine whether a population can adapt to an environmental gradient.

Fig. 2.

Species’ range starts to contract when the effective environmental gradient is steep compared with the efficacy of selection relative to genetic drift: $B\gtrsim 0.15N\sigma \sqrt{s}$, where $B=b\sigma /\left(r^{*}\sqrt{2V_s}\right)$. This threshold is shown by a dashed line. The rate of expansion increases from light to dark blue and rate of range contraction increases from orange to red. Gray dots denote populations for which neither expansion nor collapse is significant at $\alpha =2\text{\%}$. Open dots indicate fragmented species’ ranges (illustrated by Fig. S3). The ranges of the underlying (unscaled) parameters are in the following intervals: $b=\left[0.01,1.99\right]$, $\sigma =\left[0.5,4.8\right]$, $V_s=\left[0.006,8.4\right]$, $K=\left[\mathrm{4,185}\right]$, $r_m=\left[0.27,2\right]$ and $\alpha =\left[0.01,0.39\right]$, $\mu =\left[{10}^{-8},8\cdot {10}^{-5}\right]$; the number of genes is between 7 and 3,971. The selection coefficient per locus is hence in the interval of $s=\left[3\cdot {10}^{-4},0.66\right]$, with median of 0.007. Parameter distributions are shown in Fig. S1.

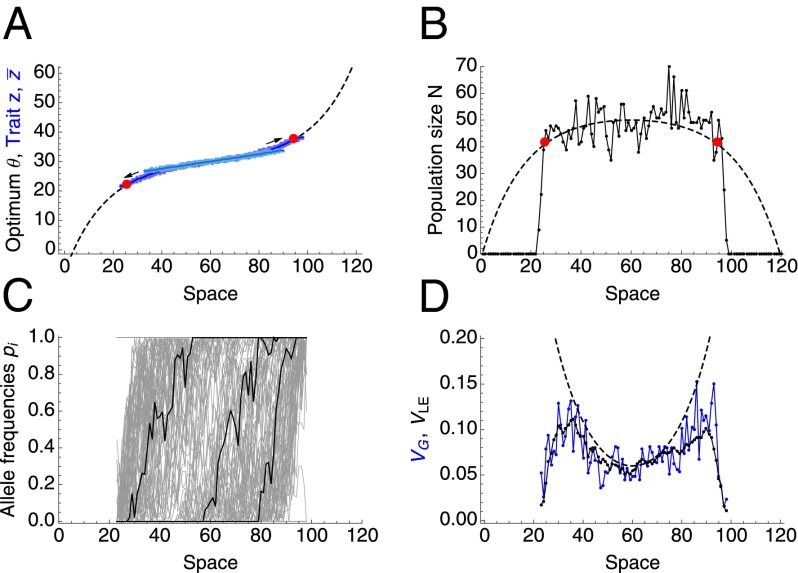
In reality, the environment does not vary precisely linearly, and the carrying capacity is not uniform. When the steepness of the environmental gradient varies steadily across space, this threshold, $B^{\ast }\approx 0.15N\sigma \sqrt{s}$, indicates where a stable range margin forms (Fig. 3). Without genetic drift, the genetic variance would steadily inflate with increasing environmental gradient, gradually reducing local population size due to an increasing number of maladapted individuals (dashed lines in Fig. 3D). With genetic drift, the variance is pushed below the level necessary to maintain adaptation, the trait mean abruptly fails to match the optimum, and so a sharp margin to the range forms. Similarly, a sharp range margin forms when $B\gtrsim 0.15N\sigma \sqrt{s}$, if carrying capacity declines across the habitat for extrinsic reasons (Fig. S4). Species’ range is more robust to spatial fluctuations in carrying capacity within the occupied habitat. Although range expansion stops at the predicted threshold, a (locally) large fall in density below the threshold is necessary for the range to fragment within a previously occupied habitat (Fig. S5).

Fig. 3.

With a steepening environmental gradient, a stable range margin forms when $B\gtrsim 0.15N\sigma \sqrt{s}$ (red dots). (A) The gradient in trait mean follows the environmental optimum (dashed line) until the gradients steepens so that $B\gtrsim 0.15N\sigma \sqrt{s}$, where expansion stops. (B) Population density drops off sharply when the predicted threshold (red dots) is reached. Dashed line gives the predicted population size assuming variation is not eroded by genetic drift. (C) Three representative clines are shown in black, and other clines form the gray background. (D) Adaptation fails when genetic variance fails to increase fast enough to match the steepening environmental gradient (total variance $V_G$ in black; linkage equilibrium component $V_{LE}$ in blue). For all subfigures, the dashed lines give deterministic predictions (Fig. 1 and ref. 11). Parameters are as follows: central gradient $b_0=0.12$, ${\sigma }^2=0.5$, $V_s=0.5$, $r_m=1.06$, $K=53$, $\mu =2\cdot {10}^{-7}$. Time = 100,000 generations; expansion stops after 40,000 generations; A also shows the initial stage in light blue.

A sharp range margin forms not only when all loci have equal allelic effects (i.e., the trait changes by a fixed value due to every substitution) but also when allelic effects are exponentially distributed. Then, range expansion slows down progressively around the threshold (Figs. S6 and S7), described by $B^{\ast }=0.15N\sigma \sqrt{\overline{s}}$, where the mean selection coefficient is $\overline{s}\equiv \overline{{\alpha }^2}/\left(2V_s\right)$. The mean selection coefficient gives an estimate for the expected range margin because clines at weakly selected loci are degraded by genetic drift (Fig. S2) (26), reducing the genetic variance. For the population to expand further beyond the threshold, positively selected alleles with increasingly large effect need to arise (Fig. S7) (30). In natural populations, these become ever rarer; and for any finite distribution of allelic effects (as in our model), are exhausted.

In the absence of genetic drift, low dispersal can enhance adaptation by reducing swamping by gene flow (11, 16). However, with genetic drift, this is no longer true. To a first approximation, both the efficacy of selection relative to genetic drift $N\sigma \sqrt{s}$ and the effective environmental gradient $B=b\sigma /\left(\sqrt{2V_s}r*\right)$ increase at the same rate with dispersal. Only a weak dependence on dispersal remains via $r*$ (because $\widehat{N}=Kr*/r_m$ and $r*$ decreases with increased genetic load due to mixing across the gradient), which favors low to intermediate dispersal (Fig. S8) (cf. ref. 23). The beneficial effect of intermediate dispersal can be stronger in one-locus models, because in the absence of recombination, dispersal only increases crowding in the new habitat (31) and flow of the advantageous mutants back to the old habitat (32) while bringing new targets for mutation and positively selected mutants. Increased dispersal can thus enhance fitness at the range edge even in the absence of inbreeding depression (cf. ref. 33).

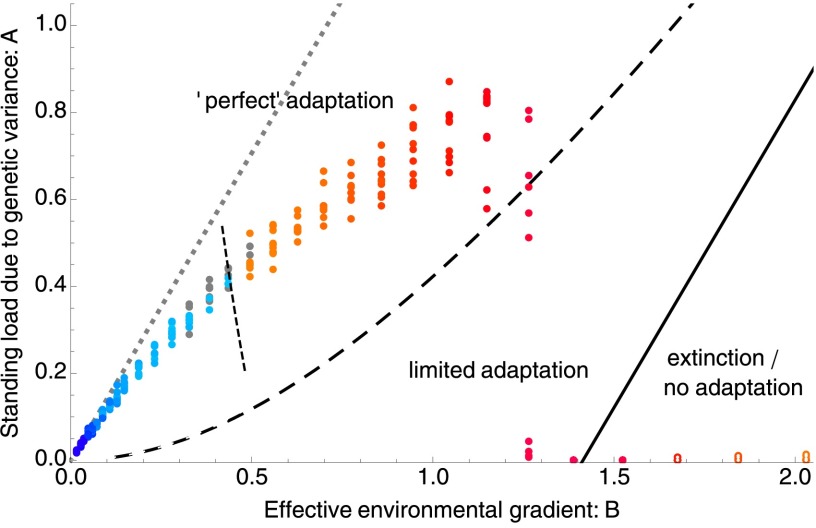
A second threshold, above which the population collapses abruptly, can be understood from a deterministic phenotypic model with fixed genetic variance (9). This theory showed that, when genetic variance $V_G$ is fixed, there is a critical environmental gradient, $B_c\sim \sqrt{2A}$ [where $A=V_G/\left(r*V_s\right)$], above which the trait mean fails to track the spatially changing optimum, and the population is well adapted only in the center of its range (ref. 9, p. 6, and ref. 28, figure 3). However, such a limit does not exist when genetic variance evolves due to gene flow across environments (11) in the absence of genetic drift. We show that genetic drift can reduce the variance such that the “critical gradient” $B_c$ is reached, despite the variance evolving: then, population abruptly loses most of its genetic variation and suffers a demographic collapse (Fig. 4). This demographic collapse may lead to either a rapid extinction from most of the species’ range or to range fragmentation, when a species cannot maintain adaptation throughout the whole range, yet multiple isolated populations persist (Fig. S3).

Fig. 4.

The phenotypic model predicts a second sharp transition in the dynamics ($B_c$, dashed curve). As the effective environmental gradient $B\equiv b\sigma /\left(r*\sqrt{2V_s}\right)$ increases, the scaled variance $A\equiv V_G/\left(r*V_s\right)$ increasingly deviates from the deterministic prediction with evolvable variance (11) (gray dotted line). The variance decreases due to the combined forces of genetic drift (Fig. S2A) and selection on small transient deviations of the trait mean from the optimum. Once $B_c\gtrsim \sqrt{2A}$ (dashed curve), the population collapses abruptly. Furthermore, no adaptation is maintained beyond the solid line $B_e=\left(2+A\right)/\sqrt{2}$, where the phenotypic model (9) predicts extinction. Open dots (Lower Right) denote fragmented species’ range (Fig. S3). The colors are as in Fig. 2; the threshold when range starts to contract, $B^{*}\approx 0.15N\sigma \sqrt{s}$, is illustrated by the short steep dashed line. Parameters are as follows: b increases from 0.025 to 1.25, ${\sigma }^2=1/2$, $V_s=1/2$, $K=50$, $\alpha =1/10$, $r_m=1.06$, 5,000 generations. Ten replicates are shown for each B.

Discussion

We are just becoming to be able to assess the genomics of local adaptation across a species’ range (34). Hence, there is a great need for a theory that integrates both genomic and demographic data. It would be exciting to see how our prediction improves experimental tests of the causes of range limits in 1D habitats such as along a deep valley or a river, such as ref. 16, that assumed fixed genetic variance (9). The predictive parameters can in principle be measured: transplanting individuals exactly 1 SD for the distribution of parent–offspring dispersal distances along the environmental gradient gives a loss of fitness $B^2/r*$. The parameter $r*$, which describes the rate of return of population to equilibrium can be estimated (e.g., following ref. 35). Neighborhood size in a 1D habitat, $\sqrt{\pi }N\sigma$, can be estimated from neutral markers (ref. 36, equation 2). The efficacy of selection relative to genetic drift, $N\sigma \sqrt{s_i}$, will vary across loci. The selection coefficients $s_i={\alpha }_i^2/\left(2V_s\right)$ can then be estimated either by mapping allelic effects ${\alpha }_i$ from the quantitative trait loci underlying an adaptive trait and measuring the strength of stabilizing selection $1/\left(2V_s\right)$, or by estimating the selection per locus directly from the steepness of the clines in allele frequencies across space. Steepness of clines gives the desired $s_i$ even under pleiotropy, whereas the first measure gives the stabilizing selection due to all pleiotropic effects. Given a fixed (finite) distribution of selection coefficients $s_i$, we can predict when adaptation is expected to fail: for example, when, given a reduction in population size, a species’ range would become prone to fragmentation.

Our main result, that adaptation fails when the effective environmental gradient is large relative to the efficacy of selection versus genetic drift, $B=b\sigma /\left(r*\sqrt{2V_s}\right)\gtrsim 0.15N\sigma \sqrt{s}$, can be rephrased to a form that is closely related to Haldane’s cost of selection (37). Haldane showed that, in a single population, each substitution requires a certain number of selective deaths (i.e., reduction in mean fitness relative to the maximum possible), which is nearly independent of the strength of selection per locus. In our model with a spatially varying environment, $b/\alpha$ substitutions are required per unit distance: as we assume hard selection, these substitutions need to also arise via selective deaths. If too many selected substitutions are needed relative to births in the population, such that $b/\alpha \gtrsim 0.15Nr*$, adaptation fails (Fig. S9). However, this failure is due to stochastic fluctuations and so depends on the effective number of deaths per generation, $Nr*$. Note that a sharp range margin cannot form when selection is soft—when K fittest phenotypes are always selected, a population spreads as long as its fitness is above zero.

This intrinsic limit to adaptation was found by analyzing 1D habitats: although initial simulations show that all driving parameters are preserved for a narrow 2D habitat, as habitats become wide ($\gtrsim 100\hspace{0.17em}\sigma$), the effect of genetic drift changes: stochastic fluctuations of allelic frequencies become only weakly dependent on selection (38). The range limits for broad 2D habitats will be the subject of a future paper.

Our theory shows that there is an inherent limit to adaptation arising in any (finite) natural population and identifies the key parameters that determine this limit to a species’ range. It explains that a sharp range margin forms when fitness cost, induced by a spatially varying environment, becomes too high relative to the efficacy of selection in the presence of genetic drift—even in the absence of fixed genetic constraints, such as insufficient genetic variance (9, 39) or rigid fitness trade-offs between traits (40, 41). Because the threshold depends only on the fitness cost of dispersal and the efficacy of selection per locus relative to genetic drift, it readily generalizes to many traits. It gives an upper limit: even in the absence of trade-offs (whether transient or rigid), adaptation fails at the estimated threshold. Throughout, we have assumed additivity between the allelic effects: that is consistent with the experimental evidence, suggesting that statistical epistasis is typically weak (42). The role of mutation rate is considered negligible (Fig. S10): standing genetic variation, essential for adaptation, is primarily maintained by gene flow in the heterogeneous environment, and eroded by genetic drift.

Within an already occupied habitat, small fluctuations in carrying capacity below the predicted threshold do not lead to range fragmentation. Nevertheless, the coherence of the species’ range is sensitive to habitat fragmentation: a local but large fall in carrying capacity facilitates extinction from its boundaries wherever the threshold has been crossed (Fig. S5). Swamping by gene flow at the existing margins, as emphasized by ref. 2, is important for the formation of a sharp range edge—even though the local bulk parameters B and $N\sigma \sqrt{s}$ predict where the range margin forms. Our theory is entirely consistent with the lack of evidence for an abundant center (43) and with only a small decrease in neutral diversity in peripheral populations (14): we show that even a small decrease in the attainable equilibrium density (carrying capacity) can lead to a sharp range margin.

The theory implies that gradual decrease in carrying capacity across the whole habitat can lead to a collapse of adaptation as genetic drift erodes the genetic variation, causing a sudden collapse or a fragmentation of a species’ range. When the effective environmental gradient B varies across space, steeper sections would act as barriers to a species’ spread—in contrast to the deterministic model (11). This is important for management of biological invasions when adaptation is required (44, 45) and for biological conservation (46): a species’ range may collapse due to genetic drift well before demographic factors (emphasized in ref. 47) become significant (46). Understanding species’ range limits in a constant environment is also essential before extending the model to account for temporally changing environments, such as when modeling joint adaptation and range expansion in species’ responding to climate change (48). Furthermore, the predicted emergence of inherent limits to species’ ranges across steadily varying environments offers extensions to the theory of ecological speciation and, eventually, may help us to elucidate macroecological patterns of biodiversity.

Materials and Methods

Evolutionary and Ecological Dynamics.

We model the joint evolution of (i) population size and (ii) trait mean and its variance via change in allele frequencies. The fitness of an individual declines quadratically with the deviation of the trait z from an optimum θ that changes linearly across space: $\theta =bx$, where b is the gradient in the environment and x is the distance in one dimension. The phenotypic trait z is determined by many additive diallelic loci, so that genetic variance can evolve. For simplicity, we use a haploid model: for additive allelic effects, the extension to a diploid model is straightforward.

The Malthusian fitness of a phenotype z is $r\left(z,N\right)=r_e\left(N\right)+r_g\left(z\right)$, where $r_e\left(N\right)$ is the growth rate of a perfectly adapted phenotype, and includes density dependence; $r_g\left(z\right)\le 0$ is the reduction in growth rate due to deviation from the optimum. N is the population density. The ecological component of growth rate $r_e$ can take various forms: we assume that regulation is logistic, so that fitness declines linearly with density N: $r_e=r_m\left(1-N/K\right)$, where $r_m$ is the maximum per capita growth rate in the limit of the local population density $N\to 0$. The carrying capacity K (for a perfectly adapted phenotype) is assumed uniform across space. Stabilizing selection on the optimum θ has strength $1/\left(2V_s\right)$. Hence, for any individual, the drop in fitness due to maladaptation is $r_g\left(z\right)=-{\left(z-\theta \right)}^2/\left(2V_s\right)$. The genetic component of the local mean fitness is then ${\overline{r}}_g\left(\overline{z}\right)=-{\left(\overline{z}-\theta \right)}^2/\left(2V_s\right)-V_P/\left(2V_s\right)$, where $V_P=V_G+V_E$ is the phenotypic variance. The loss of fitness due to environmental variance $V_E$ can be included in $r_m\ast =r_m-V_E/\left(2V_S\right)$; hence in this model, $V_E$ is a redundant parameter. We assume that selection is hard: the mean fitness—and hence attainable equilibrium density—decreases with increasing maladaptation: $\overline{r}\left(z,N\right)=r_e\left(N\right)+{\overline{r}}_g\left(z\right)$. In other words, we assume that resources become more difficult to acquire and process as maladaptation increases.

For any given additive genetic variance $V_G$ (assuming a Gaussian distribution of breeding values), the trait mean $\overline{z}$ satisfies the following:

$$\frac{\partial \overline{z}}{\partial t}=\frac{{\sigma }^2}{2}\frac{{\partial }^2\overline{z}}{\partial x^2}+{\sigma }^2\frac{\partial \ln \left(N\right)}{\partial x}\frac{\partial \overline{z}}{\partial x}+V_G\frac{\partial \overline{r}}{\partial \overline{z}}+\sqrt{\frac{V_{G,LE}}{N}}\hspace{0.17em}d{W}_{\overline{z}}.$$ [1]

The first term gives the change in the trait mean due to migration with mean displacement of σ, the second term describes the effect of the asymmetric flow from areas of higher density, and the third term gives the change due to selection (ref. 49, equation 2). The last term gives the fluctuations in the trait due to genetic drift over infinitesimally short time scales $dt$ (following ref. 25, and using that genetic variance at the linkage equilibrium is $V_{G,LE}={\displaystyle {\sum }_i{\alpha }_i^2{p}_i{q}_i}$). $d{W}_{*}$ represents white noise, uncorrelated in space and time, with expectation $\langle d{W}_{*}\rangle =0$ and $\langle d{W}_{*}\left(x,t\right)d{W}_{*}\left(x^{\prime },t^{\prime }\right)\rangle =\delta \left(x-x^{\prime }\right)\delta \left(t-t^{\prime }\right)dt\hspace{0.17em}dx$; δ is the Dirac delta (50).

Assuming additivity between loci, the trait mean is $\overline{z}={\displaystyle {\sum }_i{\alpha }_i{p}_i}$ for a haploid model, where $p_i$ is the ith allele frequency, $q_i=1-p_i$, and ${\alpha }_i$ is the effect of the allele on the trait—the change of the trait mean $\overline{z}$ as frequency of locus i changes from 0 to 1. [A diploid model would have $\overline{z}={\displaystyle {\sum }_i{\alpha }_i\left(p_i-q_i\right)}$.] The equation for the change of allele frequencies $p_i$ is the same for both haploid and diploid models:

$$\frac{\partial p_i}{\partial t}=\frac{{\sigma }^2}{2}\frac{{\partial }^2{p}_i}{\partial x^2}+{\sigma }^2\frac{\partial \log \left(N\right)}{\partial x}\frac{\partial p_i}{\partial x}+p_i{q}_i\frac{\partial \overline{r}}{\partial p_i}-\mu \left(p_i-q_i\right)+\sqrt{\frac{p_i{q}_i}{N}}\hspace{0.17em}d{W}_{p_i}.$$ [2]

The expected change of allele frequency due to a gradient in fitness and local heterozygosity is $p_i{q}_i\left(\partial \overline{r}/\partial p_i\right)=s_i{p}_i{q}_i\left(p_i-q_i-2{\mathrm{\Delta }}_i\right)$, where selection at locus i is $s_i\equiv {\alpha }_i^2/\left(2V_s\right)$ and ${\mathrm{\Delta }}_i=\left(\overline{z}-bx\right)/{\alpha }_i$ (ref. 11, two-allele model, appendix 3). The fourth term describes the change due to (symmetric) mutation at rate μ. The last term $\sqrt{p_i{q}_i/N}d{W}_{p_i}$ describes fluctuations in allele frequencies due to genetic drift (following ref. 25). Eq. 2 is only exact at linkage equilibrium (i.e., neglecting covariance between allele frequencies). This is a good approximation for unlinked loci: whereas migration across the habitat generates positive linkage disequilibrium between any pair of loci, stabilizing selection drives negative disequilibrium, and these cancel precisely unless selection per locus is strong. The derivation, which generalizes an ingenious but little known argument by Felsenstein (51), is given in SI: Linkage Equilibrium.

Population dynamics reflect diffusive migration, growth due to the mean Malthusian fitness $\overline{r}$, and stochastic fluctuations. The number of offspring follows a Poisson distribution with mean and variance of N. Fluctuations in population numbers are given by $\sqrt{N}d{W}_N$ (e.g., ref. 52), where $d{W}_N$ describes an independent white noise:

$$\frac{\partial N}{\partial t}=\frac{{\sigma }^2}{2}\frac{{\partial }^{2}N}{\partial x^2}+\overline{r}N+\sqrt{N}d{W}_N.$$ [3]

Rescaling.

The model can be further simplified by rescaling time t relative to the rate of return to equilibrium population size, $r*$ [which we consider equivalent to the strength of density-dependence (35)], distance x relative to dispersal σ, trait z relative to strength of stabilizing selection $1/\left(2V_s\right)$, and local population size N relative to equilibrium population size with perfect adaptation $\widehat{N}=Kr*/r_m$, as in refs. 9 and 11. The scaled dimensionless variables are $T=r*t$, $X=x\sqrt{2r*/{\sigma }^2}$, $Z=z/\sqrt{r*V_s}$, and $\tilde{N}=N/\widehat{N}$. The rescaled equations for evolution of allele frequencies and for demographic dynamics then are as follows:

$$\frac{\partial \tilde{N}}{\partial T}=\frac{{\partial }^2\tilde{N}}{\partial X^2}+\overline{R}\tilde{N}+\sqrt{\frac{\tilde{N}}{\widehat{N}\sigma \sqrt{r*}}}\hspace{0.17em}d{\tilde{W}}_{\tilde{N}},$$ [4]

$$\frac{\partial p_i}{\partial T}=\frac{{\partial }^2{p}_i}{\partial X^2}+2\frac{\partial \log \left(\tilde{N}\right)}{\partial X}\frac{\partial p_i}{\partial X}+\frac{s}{r*}\left(p_i{q}_i-2\frac{\overline{Z}-BX}{{\alpha }^{*}}\right)-\frac{\mu }{r*}\left(p_i-q_i\right)+\sqrt{\frac{p_i{q}_i}{\tilde{N}\widehat{N}\sigma \sqrt{s}}}\hspace{0.17em}d{\tilde{W}}_{p_i},$$ [5]

where $\overline{R}\equiv \overline{r}/r*=1-\tilde{N}-{\left(BX-Z\right)}^2/2$ and $d\tilde{W}*$ describes the independent Wiener processes in scaled time T and space X.

The rescaled Eqs. 4 and 5 show that four parameters fully describe the system. The first two are (i) the effective environmental gradient, $B\equiv b\sigma /\left(r*\sqrt{2V_s}\right)$, and (ii) the strength of genetic drift relative to selection, near the equilibrium $\tilde{N}=1$, $1/\left(\widehat{N}\sigma \sqrt{s}\right)$. As a third parameter, one can either take (iii) demographic stochasticity relative to strength of density dependence $1/\left(\widehat{N}\sigma \sqrt{r*}\right)$ or the ratio of $\widehat{N}\sigma \sqrt{s}$ to $\widehat{N}\sigma \sqrt{r*}$, which is the strength of selection relative to density dependence, $s/r*$. (The scaled effect of a single substitution, $\alpha *\equiv \alpha /\sqrt{r*V_s}=\sqrt{2s/r*}$.) The effect of this third parameter is small because $s\mathrm{⋘}r*$. The fourth parameter, $\mu /r*$, will typically be very small, and hence we will neglect it. Note that $\widehat{N}$ gives population density, where population is still well adapted: n = $\widehat{N}$ throughout most of the species’ range away from sink regions near the existing margins. Table 1 (bottom) summarizes the full set that describes the system.