Computational identification of MoRFs in protein sequences

Abstract

Motivation: Intrinsically disordered regions of proteins play an essential role in the regulation of various biological processes. Key to their regulatory function is the binding of molecular recognition features (MoRFs) to globular protein domains in a process known as a disorder-to-order transition. Predicting the location of MoRFs in protein sequences with high accuracy remains an important computational challenge.

Method: In this study, we introduce MoRF_CHiBi, a new computational approach for fast and accurate prediction of MoRFs in protein sequences. MoRF_CHiBi combines the outcomes of two support vector machine (SVM) models that take advantage of two different kernels with high noise tolerance. The first, SVM_S, is designed to extract maximal information from the general contrast in amino acid compositions between MoRFs, their surrounding regions (Flanks), and the remainders of the sequences. The second, SVM_T, is used to identify similarities between regions in a query sequence and MoRFs of the training set.

Results: We evaluated the performance of our predictor by comparing its results with those of two currently available MoRF predictors, MoRFpred and ANCHOR. Using three test sets that have previously been collected and used to evaluate MoRFpred and ANCHOR, we demonstrate that MoRF_CHiBi outperforms the other predictors with respect to different evaluation metrics. In addition, MoRF_CHiBi is downloadable and fast, which makes it useful as a component in other computational prediction tools.

Availability and implementation: http://www.chibi.ubc.ca/morf/.

Contact: gsponer@chibi.ubc.ca.

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

Intrinsically disordered protein regions (IDRs) are amino acid sequences that lack a unique 3D structure in solution. Proteins that are dominated by IDRs are called intrinsically disordered proteins. IDRs are enriched in binding sites that play significant roles in signaling and regulatory functions through binding to other proteins. Because of this functionality, their interactions need to be both specific and reversible (Babu et al., 2011; Mohan et al., 2006; Wong et al., 2013). The computational identification of candidate binding locations in IDRs is an important task in bioinformatics and an area of growing interest. Currently there are two main approaches to this problem being developed (Hsu et al., 2013). The first is based on the analyses of short linear sequence motifs (SLiMs). SLiMs are defined as conserved sequence stretches of 3–10 amino acids that are enriched in IDRs (Weatheritt and Gibson 2012) and promote interactions with specific domains. The second line of research is based on the theory that long interaction-prone segments in IDRs, called molecular recognition features or MoRFs, fold upon interacting with partners. These MoRFs vary in size and can be up to 70 residues long (Cumberworth et al., 2013; Mohan et al., 2006).

Various computational methods have been developed to identify SLiMs and MoRFs in protein sequences including MoRFpred (Disfani et al., 2012), MFSPSSMpred (Fang et al., 2013), PepBindPred (Khan et al., 2013); ANCHOR (Mészáros et al., 2009), SLiMpred (Mooney et al., 2012), SLiMDisc (Davey et al., 2006), SLiMFinder (Edwards et al., 2007) and Retro-MoRFs (Xue et al., 2010). Despite the fact that both MoRFs and SLiMs are interaction-prone elements in IDRs, the methods used to identify them have been very different. Because of their short length, the identification of SLiMs is very challenging and associated with the risk of high false positive rates (FPRs). Therefore, reliable identification of novel instances of known SLiMs or the de novo identification of SLiMs often relies on evolutionary information or the use of non-sequence information such as protein interaction data. Predictors of MoRFs take advantage of the fact that they are on average longer than SLiMs, which increases the signal to noise level for sequence features that distinguish MoRFs in IDRs from their surroundings. It is clear that there are overlaps between what can be defined as SLiM or MoRF. However, in this study we focus only on computationally identifying MoRFs as defined initially by Mohan et al. (2006) and Disfani et al. (2012).

All currently available MoRF prediction tools have been benchmarked by comparing their performances to those of two state-of-the art predictors that use very different approaches: ANCHOR (Mészáros et al., 2009) and MoRFpred (Disfani et al., 2012). ANCHOR is a downloadable predictor that is based on three properties of the residues in a polypeptide chain: binding residues must be in a long disordered region, residues are not able to fold with their neighbors and residues are able to interact with globular domains (Mészáros et al., 2009). A propensity value is generated by computationally predicting each of these three properties using the energy estimation approach of IUPred (Dosztanyi et al., 2005a, b), and finally, a weighted sum is used to join these three propensities into a single score. The weights of each of these three components and the neighborhood sizes of the first two (five values in total) are learned from a small training set. Unlike predictors that rely on traditional machine learning tools such as SVMs and Neural Networks, the chance of this training process to over-fit the training data is minimal. MoRFpred is a web based three-step predictor. First, an SVM with a linear kernel determines a MoRF propensity score based on nine sets of features: physiochemical properties of amino acids from the Amino Acid Index (Kawashima et al., 2008), conservation information in the form of Position Specific Scoring Matrices (PSSM) generated with PSI_BLAST (Altschul et al., 1997), relative solvent accessibility estimated by the Real-SPINE3 predictor (Faraggi et al., 2009), flexibility (B-factor) predicted by PROFbval (Schlessinger et al., 2006), and the results of five different intrinsic disorder predictors. Then, an alignment e-value is computed by aligning the input sequence to the training sequences using PSI-BLAST. Finally, the MoRF propensities of input sequence residues are adjusted by taking the alignment e-values into account. Performance evaluation using three different datasets provided area under the receiver operator characteristics (ROC) curve of ∼0.68 for MoRFpred and ∼0.61 for ANCHOR (Disfani et al., 2012). To the best of our knowledge, there is no predictor that has shown a significantly better performance than MoRFpred in a direct comparison. However, its software is not down-loadable, and therefore its use is limited to online submissions. It is significantly slower than ANCHOR; it can only process a maximum of five protein sequences at a time and it is limited to sequences with up to 1000 amino acids.

Here, we introduce a new approach for predicting MoRFs in protein sequences that we call MoRF_CHiBi. We developed MoRF_CHiBi by taking into consideration several properties of MoRFs that have been identified in previous studies: The amino acid composition of MoRFs is different from that of the general protein population (Disfani et al., 2012; Mészáros et al., 2009) and contrasts most with the sequences flanking them (Flanks). In addition, there are sequence similarities between MoRFs that can be exploited to improve MoRF predictions (Disfani et al., 2012). Finally, there is a very high level of noise in the data; the values of the top 5 features used by Disfani et al. (2012) to identify MoRFs show a very high variance. In order to integrate this knowledge, we use a three-step approach in which we generate sets of features from the physicochemical properties of the amino acids that represent different regions of proteins, train two SVM models, one to target direct similarities between MoRF sequences, and the other to focus on the general contrast of the amino acid composition of MoRFs, Flanks, and the general protein population, and finally compute a propensity for each residue to be a MoRF residue by joining the propensities (as probabilities) generated by the two SVM models using Bayes rule. The final predictor, MoRF_CHiBi, is down-loadable, fast, and has no upper limit on the size of protein sequences. Even though it is only uses the Amino Acid Index, MoRF_CHiBi is more accurate than ANCHOR and MoRFpred.

2 Methods

2.1 Datasets

In order to be able to reliably compare our predictor with MoRFpred, also a SVM-based approach, we decided to use the same training and test datasets as Disfani et al. (2012). They collected a large set of structures containing protein-peptide interactions from the Protein Data Bank PDB in 2008 and filtered them on a number of principles to identify a set of 840 protein sequences, which we refer to as TOTAL. Each of these sequences includes a peptide region with 5–25 residues presumed to be a MoRF. Disfani et al. (2012) divided TOTAL into a training set (TRAINING) and a test set (TEST). TRAINING consists of 421 sequences with a total of 245 984 residues including 5396 MoRF residues. TEST consists of 419 sequences with a total of 258 829 residues including 5153 MoRF residues. Disfani et al. (2012) also collected two other test sets that we refer to as NEW, and EXPER. NEW was collected using similar criteria as for TOTAL from more recent PDB entries deposited between January 1 and March 11, 2012; it consists of 45 sequences with a total of 37 533 residues including 626 MoRF residues. Finally, EXPER includes eight protein sequences with experimentally validated MoRF regions, two of which harbor MoRFs that are 31 and 71 residues long. Since MoRF_CHiBi is designed to predict MoRFs no longer than 25 residues (Section 2.7), we excluded these two sequences and refer to the resulting dataset as EXP6. To reduce the risk of overestimating performance due to sequence homology between training and test data, Disfani et al. (2012) filtered sequences in TRAINING and test sets such that no more than 30% identity exists between any sequence in TRAINING and the three test sets.

2.2 Data challenges

The datasets present two main challenges that need to be addressed:

2.2.1 Challenge one

When computing the propensity of a candidate region in a query sequence of being a MoRF, we need to target two types of information: sequence similarity between the candidate region and MoRF sequences in TRAINING, which we refer to as similarity information, and the contrast of the amino acid composition of the candidate region and its surroundings compared with the overall amino acid composition of all MoRFs and Flanks in TRAINING, which we refer to as composition contrast information.

To utilize these two types of information, we employed two SVM models. The first SVM targets composition contrast information and is trained on synthetic data (SYN4000) that includes only the compositions contrast information of TRAINING with no similarity information. Each of the 4000 synthetic sequences includes a MoRF region (sizes from 10 to 20 amino acids) in between two flanking regions (8 amino acids each), and a section that represents a general protein region (Other). Amino acid compositions for each region were derived from the amino acid compositions of its corresponding regions in TRAINING; i.e. each residue in each region R ∈ {MoRF, Flanks, Other} in SYN4000 is chosen by selecting at random (uniform) a residue from the collection of all R regions in TRAINING. Therefore, sequences in SYN4000 have no direct similarity to those in TRAINING and the three test datasets, but they do contain all the composition contrast information of TRAINING. The second SVM model is trained on TRAINING, and mainly target similarity information (Section 2.4.2).

2.2.2 Challenge two

In separating the sequences of TOTAL such that TRAINING and TEST share no more than 30% identity, we violated a basic principle in machine learning to prevent homologous from inflating the apparent true positive rate (TPR). This principle requires both the training and the test data to be extracted from the general population using the same distribution function. As a result, some information patterns in each set are under- or over-represented against the other. Since two-thirds of the sequences in TOTAL are homologous to one or more sequences in the dataset, this imbalance of information patterns is significant. Hence, we had to identify the appropriate number of features used in the model in order to avoid over-fitting TRAINING with respect to TEST. With the assumption that TOTAL represents the general MoRF population, we identified the appropriate number of features based on the following three principles:

• High performance on TEST (see below).

• Minimal number of selected features.

• Small difference between the performances on TEST and TRAINING.

The third principle is necessary otherwise the performance on TEST is likely to be uneven, with positive predictions coming mainly from sequences similar to those in TRAINING.

In general, when the training and test sets are extracted from the general population using the same distribution function, frequent information patterns are equally represented in both sets. In this case, differences between the training and test sets are mainly limited to noise. Therefore, the test set should not be used in identifying the appropriate model complexity. Otherwise, in selecting a set of features with high performance on the test set, one is most likely fitting some noise and contaminating the test set. However, here the effect of the imbalance of information patterns between TEST and TRAINING on the model performance overshadows that of random noise patterns. Consequently, noise patterns in TEST have no influence on the identification of the appropriate model complexity, and thus TEST is not contaminated. For more details see Supplementary Section 1.3.

2.3 Features generation

We used the physicochemical properties encoded by the standard 544 amino acid indexes. In addition, we used six new indexes that were generated by computing the percentage of each amino acid in each of the three regions (MoRFs, Flanks and Other) as described in table 1.

Table 1.

The six additional amino acid indexes 545–550

Index number	Index content
545	PMoRF–PFlanks
546	PMoRF–POther
547	PFlanks–POther
548	PMoRF/PFlanks
549	PMoRF/POther
550	PFlanks/POther

Note: Each residue type was counted and its percentage is computed in each region of the sequences in the training data (P_MoRF, P_Flanks and P_Other), then each residue percentage in each region is subtracted or divided by the residue percentage of one of the remaining two regions.

For training, balanced sampling was enabled by defining MoRFs and their Flanks in each sequence as the positive sample, and regions with the same length are selected at random as the negative sample (fake MoRFs and fake Flanks). Fake MoRFs and fake Flanks do not overlap with real MoRFs and their Flanks. For each MoRF (real or fake), features are generated from the Amino Acid Index such that each of the 550 indexes generates two features: one by averaging the index values over the amino acids of the supposed MoRF and one by averaging over the up to 16 (8 × 2) amino acids of its supposed Flanks (each Flank is 8 amino acids unless it is limited by a sequence edge). Each of the values in this SF is the initial set of 1100 features, is normalized to an average of zero and absolute value of one.

2.4 Model selection

As mentioned, we used two SVM models with high noise tolerance kernels (i.e. Sigmoid and Gaussian kernels) to evaluate compositions contrast and similarity information.

2.4.1 Model I: SVM_S

SVM_S is trained on SYN4000 to predict MoRF propensities based on composition contrast information. Because SYN4000 was generated from TRAINING using a single composition for each of the three structural regions, we used a Sigmoid kernel to enable the training process to weight input features appropriately. As this model is trained on synthetic data, the training data normalization parameters are inappropriate for query sequences, and thus query sequences are normalized independently.

2.4.2 Model II: SVM_T

SVM_T relies on the assumption that MoRF sequences can be clustered into groups based on their sequence similarity. Hence, we needed a non-linear classifier with high noise tolerance that is capable of scoring favorably a window in a query sequence when it shows similarities to any of the TRAINING MoRFs. We used a SVM classifier with an Radial Basis Function (RBF) Gaussian kernel. Similar sequences will have similar average amino acid indexes (features). To maintain the query features comparable to those of TRAINING, normalization of query features relies on the same normalization parameters from TRAINING.

Unlike SVM_S, which targets composition contrast information and is trained on synthetic data that only holds this information (Section 2.2.1), SVM_T is trained on TRAINING sequences that include composition contrast and similarity information. To direct the SVM_T training process toward similarity information and away from composition contrast information, we undertook the following three steps: homology clustering is ignored by the cross validation used on TRAINING (Sections 2.6 and 2.7), a large Gamma is used to enable the query features to be evaluated against the features of a large number of individual sequences, and a large enough number of features are used to identify sequence similarity among many sequences.

To evaluate the relative success in targeting similarity information of different sets of features, we use Bayes rule to combine the outcomes of each of these sets to the same composition contrast information result. The combined outcome is higher when more similarity information is used.

2.5 Scoring query sequences

We score query sequences using sliding windows for which features are calculated. Ideally, one would want to use sliding windows of the same size as the MoRF and the two flanking regions around it. However, MoRF sizes are not known in advance. Therefore, each query sequence is analyzed using 19 different sliding windows that range from 6 to 24 amino acids in size; we did not include sizes 5 and 25 to minimize the effect of noise. As a result, each residue in a query sequence except those near the sequence edges receives 285 scores (6 + 7 + ··· + 23 + 24). These scores are processed differently for each model. For SVM_S, each residue’s final MoRF propensity is set as the maximum of its 285 scores. However, using the maximum of these scores for SVM_T turned out to be unstable and yielded bad results. Therefore, the final MoRF propensity on SVM_T is the average of these scores.

For simplicity, we assumed that the MoRF propensity of each residue projected by each model is conditionally independent of that projected by the other model given the residue. Propensities (as probabilities) generated by both models are then joined using Bayes rule.

As our training data includes MoRF sizes up to 25 residues only, we explicitly limited the generation of MoRF features to a comparable set of MoRF window sizes. In having Flank features around these MoRF windows, the application scope of MoRF_CHiBi is limited to MoRFs with up to 25 residues. Even when two (or more) MoRFs happen to be adjacent, their total length should not exceed this limit.

2.6 Initial feature selection and parameter tuning

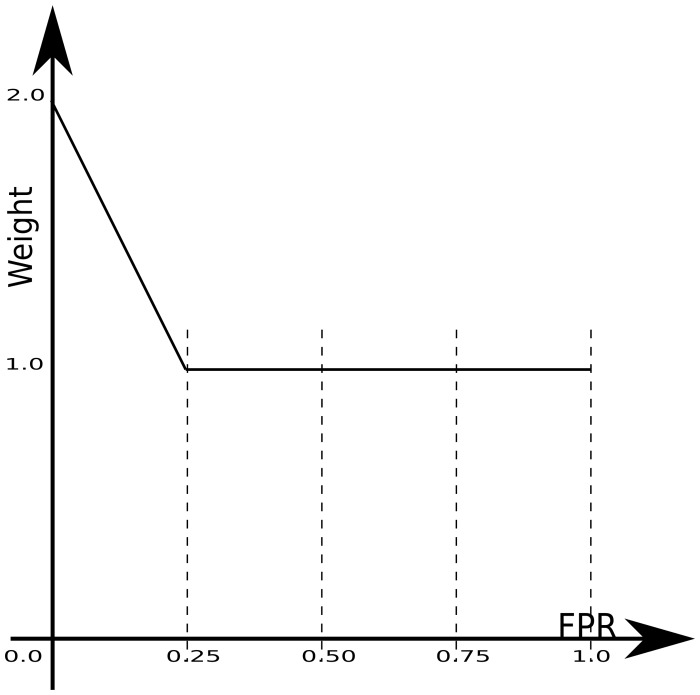
Features are selected according to two criteria: enabling a high AUC, and providing high prediction accuracy for top propensity residues. To achieve both goals, we used a weighted AUC, wAUC, as our feature selection objective function (Fig. 1). This wAUC allows features that produce receiver operator characteristics (ROC) curves with higher TPR near the lower left corner to be selected by generously rewarding these features.

Fig. 1.

wAUC weight distribution: The weight distribution of the wAUC used in feature selection

Feature selection together with parameter tuning is a ‘catch 22’ problem: in order to select features, we need to use some SVM parameters, and to run a ‘grid’ of values (Chang and Lin 2011) for parameter tuning, we need a set of features. Different features can lead to different parameters and different parameters will result in different sets of. We addressed this issue heuristically by using an initial feature selection algorithm (see Supplementary Section 1.1) with default parameters to select reasonably large numbers of features (39 features). Then we used these features to run a ‘grid’ of values for each model. Cells in each grid are divided into three groups based on their wAUC values. Finally, we selected a cell for each model that is approximately central to the high values group (Supplementary Fig. S3). SVM_S parameters were computed using SYN4000 with balanced sampling for training and TRAINING with balanced sampling for testing. This procedure resulted in C and Gamma values of 500 and 0.001, respectively. SVM_T parameters were obtained on TRAINING with balanced sampling and 5-fold cross-validation, which resulted in C and Gamma values of 500 and 1, respectively. We used the LIBSVM Library for Support Vector Machines (Chang and Lin, 2011) to develop the predictor.

2.7 Feature selection

Although feature selection is important for both models, it is especially crucial for the RBF SVM as the RBF kernels available weight all input features equally.

2.7.1 Efficiency

The main limitation in feature selection is its high computational cost. For instance, it takes up to 60 min to score the sequences in TRAINING on an SVM trained on SYN4000. Further, to select a single set of features, the feature selection algorithm (Supplementary Section 1.2) needs to score TRAINING tens of thousands of times. We adapted some techniques to reduce this computational cost, including substituting the residue scoring presented in Section 2.5 with two different feature selection residue scoring methods. F1 is a fast but not very accurate scoring used in earlier iterations of the feature selection process. Residues are scored with a single sliding window of the MoRF size. Thus each residue (except those near the edges) is scored between 5 and 25 times, and then its propensity is computed by averaging these scores. F2 is a more accurate scoring approach that is used in later iterations. Fourteen or more sliding windows are used for scoring, with sizes between 6 and W_max, where W_max is the maximum between 19 and the MoRF size. Thus, each residue (except those near the edges) is scored at least 175 times, and then its propensity is computed by averaging these score.

2.7.2 Algorithm

We used a stochastic feature selection algorithm that selects N features in five steps. Earlier steps are used to search the optimization space for some local maxima, while final steps tune in on that maxima. For more details see Supplementary Section 1.2.

Since our ISF is very large compared with the number of selected features N, the feature selection process fine tunes these N features around the model’s initial parameters, so we did not fine tune the initial rough parameters.

2.8 Performance evaluation

We used the same three evaluation metrics that were used by Disfani et al. (2012): AUC, success rate and accuracy, where AUC is the area under the ROC curve. Success rate is defined as the percentage of sequences with the average predicted propensity of native MoRF residues higher than that of non-MoRF residues (Disfani et al., 2012). Accuracy is computed as a function of the TPR where: accuracy = (TP + TN)/N, TPR = TP/N_MoRF, TP is the number of accurately predicted MoRF residues, TN is the number of accurately predicted non-MoRF residues, N is the total number of residues and N_MoRF is the number of MoRF residues.

3 Results

First, we identified an appropriate set of features for each of the two MoRF_CHiBi models. Then MoRF_CHiBi was evaluated on TEST, NEW and EXP6 and its results compared with MoRFpred and ANCHOR.

3.1 Feature selection and appropriate model complexity identification

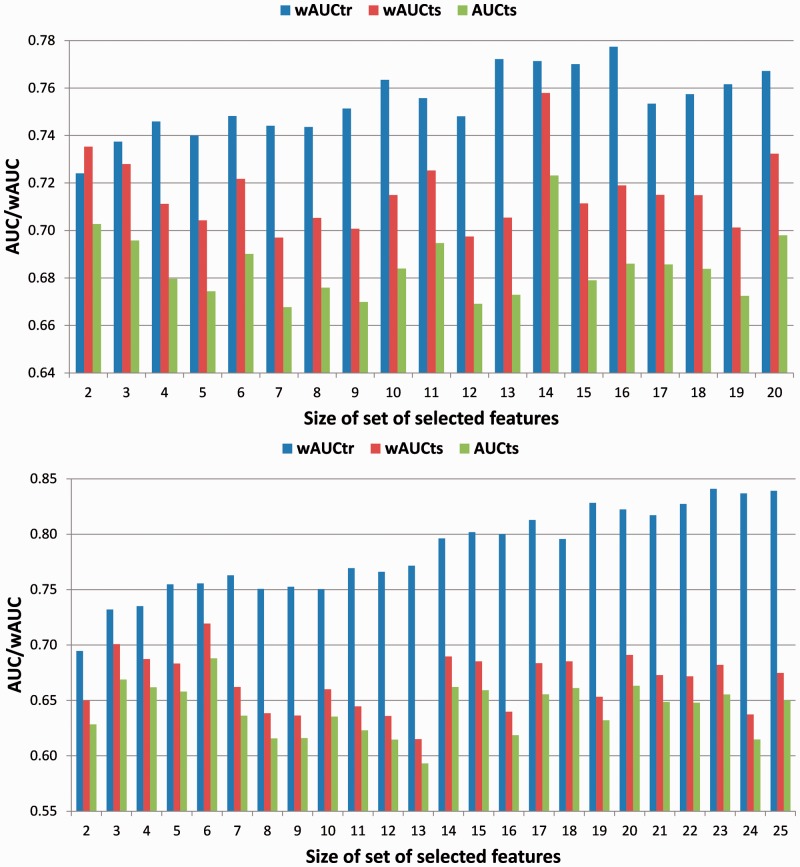
After the initial parameter tuning of both models, the appropriate set of features was identified by comparing each model’s performance on TRAINING and TEST (Fig. 2). For both models, wAUC of TRAINING steadily increases with larger sets of selected features, whereas wAUC of TEST drops, which is a strong indication of over-fitting. Following the three principles presented in Section 2.2.2, we chose the set with fourteen features (Fig. 2) for SVM_S. Its wAUC on TEST is the highest, with a small gap between the wAUC on TEST and TRAINING (for more please see Supplementary Section 2.1).

Fig. 2.

Model performance as a function of the number of features used for SVM_S (top), and SVM_T (bottom). wAUCtr and wAUCts are weighted AUCs for TRAINING and TEST respectively, AUCts is the AUC for TEST

In contrast to that of SVM_S, SVM_T’s wAUC on TEST as a function of the number of features shows three different zones (Fig. 2): high wAUC for sets with less or equal to 6 features, low wAUC for sets greater than 6 and less or equal to 13 and high wAUC for sets greater than 13 and less or equal to 25. In evaluating the relative success in targeting similarity information of different sets of features, as described in Section 2.4, we found that the high performance in the first zone is driven by a high level of composition contrast information. Therefore we excluded the first zone from the choices for model selection and focused on the next zone with high wAUC, i.e. zone 3. Following the three principles in Section 2.2.2, we chose the set with 14 features for SVM_T. This set of features has the smallest size, the highest wAUC on TEST and the smallest difference in wAUC between TRAINING and TEST in the third zone.

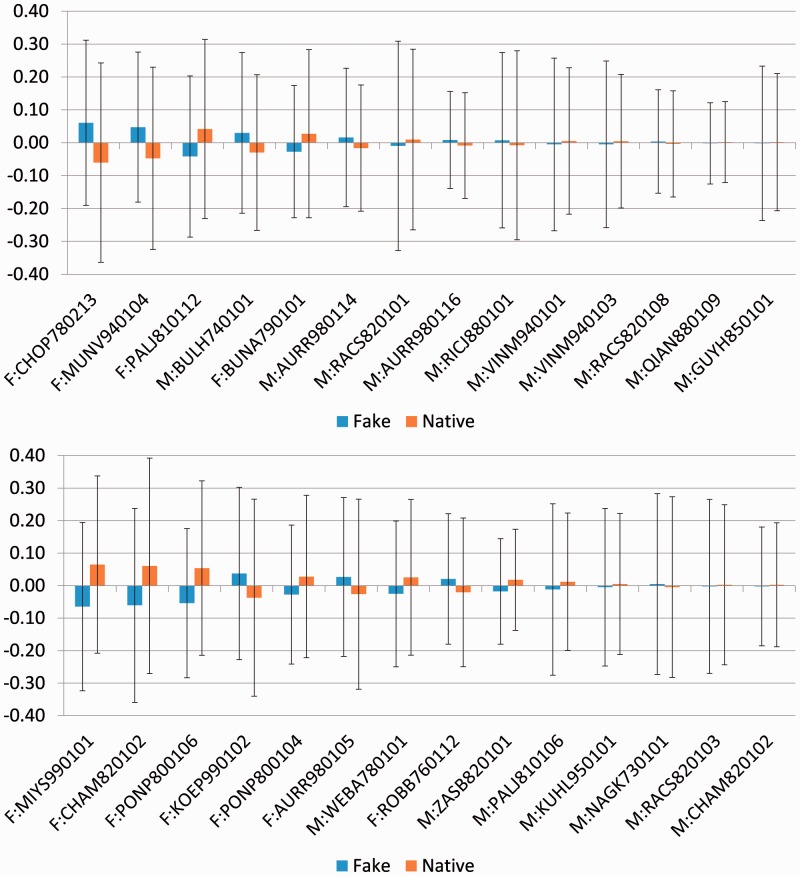
The average values and standard deviations for features selected for SVM_S and SVM_T are shown in Figure 3. While the features selected on SVM_S have a median of 23.84 for the ratio of standard deviation to average value, this ratio is 10.24 for those selected on SVM_T and 12.89 for the 1100 features in ISF. Consistent with known properties of MoRFs and features used by MoRFpred, many of the features selected by our approach relate to the hydrophobicity, secondary structure preference, solvation free energy and average flexibility (B-factors) of the residues in MoRFs and Flanks (see Supplementary Section 2.2 for full list). Nonetheless, rationalizing the selection of all features is quite impossible not least because many of the amino acid physiochemical properties are partially correlated.

Fig. 3.

The average values and standard deviation (as error bars) for the normalized features selected for SVM_S (top) and SVM_T (bottom). Features are sorted from left to right based on the absolute average value deferential between native and fake MoRFs. The feature names are the Amino Acid Index Accession numbers preceded by two characters ‘F:’ or ‘M:’, which indicate whether the feature was selected from Flanks or MoRFs

3.2 Comparison with existing predictors

Next, we evaluated MoRF_CHiBi by comparing its predictions with those obtained by MoRF_Pred and ANCHOR for the three test sets TEST, NEW and EXP6 [Disfani et al. (2012)]. Table 2 shows the AUC and success rate for the three predictors. MoRF_CHiBi outperforms MoRF_Pred and ANCHOR with respect to both parameters. It is important to note that a higher AUC and success rate of MoRF_CHiBi compared with the other two methods is consistently seen across all three test sets, which indicates that the improved performance is not the result of overfitting.

Table 2.

AUC and Success rate results

Data	AUC			Success rate
	MoRFCHiBi	MoRFPred	ANCHOR	MoRFCHiBi	MoRFPred	ANCHOR
TEST	0.746	0.673	0.600	0.759	0.718	0.611
NEW	0.770	0.697	0.638	0.778	0.756	0.578
EXP6	0.735	0.614	0.496	5/6	4/6	2/6

Note: AUC and success rate values of the three MoRF predictors using the three datasets; TEST, NEW and EXP6.

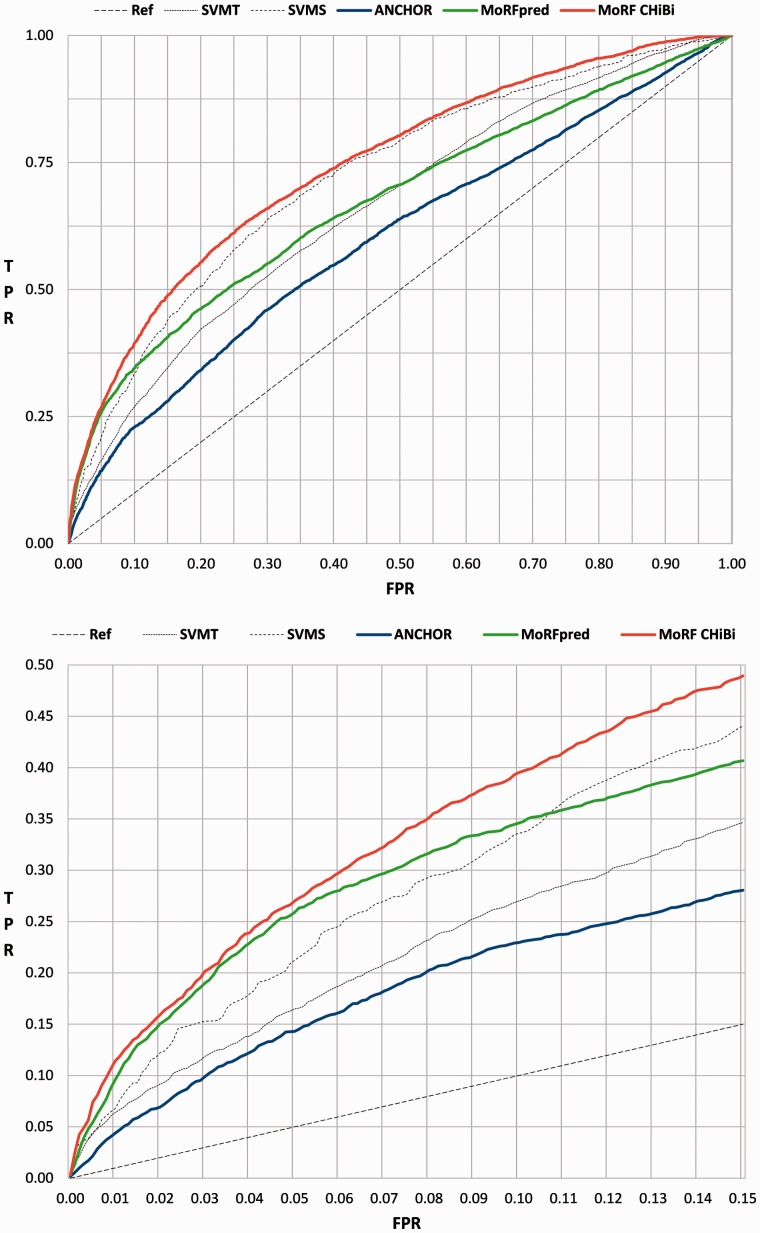
The superior performance of MoRF_CHiBi is also demonstrated by the evolution of the ROC curves generated for TEST and NEW (Fig. 4 and Supplementary Fig. S2). Even without relying on PSSM and the seven structural predictors used by MoRFpred, optimizing feature selection to maximize the weighted AUC enabled MoRF_CHiBi to achieve higher TPRs at low FPRs compared with MoRFpred and ANCHOR (Table 3).

Fig. 4.

ROC curves for the TEST dataset: (Top) The full ROC curve. (Bottom) The lower left corner of the curve. Vertical axis for true positive rate (TPR) and horizontal axis is false positive rate FPR. MoRF_CHiBi in red, MoRFpred in green and ANCHOR in blue. Two dotted lines showing the performance of each of the MoRF_CHiBi two component predictors

Table 3.

FPR and accuracy as a function of TPR

TPR	MoRFCHiBi		MoRFPred		ANCHOR
	FPR	ACC	FPR	ACC	FPR	ACC
0.222	0.035	0.951	0.037	0.948	0.092	0.894
0.254	0.045	0.942	0.049	0.937	0.125	0.863
0.389	0.098	0.893	0.137	0.854	0.253	0.740

Note: FPR and accuracy (ACC) as a function of TPR computed on the TEST set for MoRF_CHiBi, compared with published results (using the same TEST set) from MoRF_Pred, and ANCHOR. The same TPRs as in Disfani et al. (2012) were used, i.e. underlined numbers are obtained from Disfani et al. (2012).

As MoRF predictors are often used to screen large sets of proteins, we were also interested in their efficiencies. We tested prediction time of MoRFpred by submitting sequences to its corresponding web site, while MoRF_CHiBi and ANCHOR were tested on an Intel core i7, 3.44G desktop. ANCHOR is the fastest, processing 4 × 10⁶r/m (residues/minute), while MoRF_CHiBi came in second with 6 × 10³r/m MoRFpred was the slowest, with 48 r/m. This comparison is not entirely fair as processor speed used for the web-based MoRFpred is unknown. Nevertheless, the comparison of the computational costs clearly shows that MoRFpred, which comes closest in its prediction accuracy to MoRF_CHiBi, is significantly slower than the predictor introduced here.

4 Discussion

We present a new approach, MoRF_CHiBi, for predicting MoRFs within protein sequences. We compared its performance to that of ANCHOR and MoRFpred using three different test sets that have previously been assembled by Disfani et al. (2012). The results demonstrate that MoRF_CHiBi outperforms both predictors in AUC, accuracy and success rate, with high efficiency. Table 4 summarizes and compares the properties and the performances of the three predictors using the TEST dataset.

Table 4.

Overall comparison of MoRF_CHiBi, MoRFpred and ANCHOR

	MoRFCHiBi	MoRFpred	ANCHOR
Downloadable	Yes	No	Yes
Efficiency residues/minute	6 × 103	48	4 × 106
Max sequence size	Unlimited	1000 residues	Unlimited
AUC	0.746	0.673	0.600
FPR at 0.222 TPR	0.035	0.037	0.092
FPR at 0.389 TPR	0.098	0.137	0.253
Number of component predictors	0	8	0
MoRF size limitations	5–25 residues	No limits	No limits

Note: FPR as a function of TPR computed on the TEST set. MoRF_CHiBi outperformed its other two rivals in all categories except for its limitation on MoRF sizes.

The increased performance of MoRF_CHiBi is related to several points. First, two different types of information are targeted by MoRF_CHiBi: sequence similarity information and composition contrast information. The search for the former is justified by the fact that there exist sequence similarities between MoRFs. Indeed, MoRFs from different proteins that bind the same target can have a significant level of sequence identity (Oldfield et al., 2007). Hence, one can see SVM_T as the part of MoRF_CHiBi that targets new instances of ‘known’ MoRFs. Targeting purely composition contrast information with SVM_S can, in contrast, be seen as a de novo search for MoRFs. This objective was achieved by using a synthetic dataset with only composition contrast information for the training of SVM_S. Training on synthetic sequences may appear problematic. However, it is justified based on the premise that new MoRFs can be identified due to an inherent difference in amino acid composition between them and their surroundings. A second advantage of our approach is the use of a novel two step feature selection. In the first step, each SVM parameter is selected to best fit its target information, whereas in the second, a set of complementary features is selected to maximize the SVM performance. Finally, technical subtleties also contributed to the high performance of MoRF_CHiBi: a weighted AUC as an objective function in feature selection to improve TPR at low FPR and SVM models with noise tolerance kernels to overcome the high level of noise in the data.

While the outputs of both MoRF_Pred and ANCHOR include a numeric propensity value as well as a binary categorical prediction for each residue of being part of a MoRF, the MoRF_CHiBi output is limited to the numerical propensity values. We did not include a categorical prediction because different proteins are likely to have different levels of propensity scores and researchers are likely to require different cutoff values based on different applications. We believe that, although convenient, providing categorical predictions by assigning a static cutoff value can be a misleading oversimplification. However, if one needs such a cutoff, we suggest a value around 0.848. At this cutoff, MoRF_CHiBi has a (TPR, FPR) of (0.395, 0.100) and (0.412, 0.101) on TEST and NEW, respectively.

Overall, MoRF_CHiBi is light fast, and the most accurate MoRF predictor available today, which makes it useful in the analysis of small and large datasets. As it is down-loadable, MoRF_CHiBi can be used as an input component for other programs. We would like to stress again that there exist overlaps in the definition of MoRFs and SLiMs but that MoRF_CHiBi, just like MoRFpred, has been trained to predict MoRFs only. Other predictors are better suited to identify SLiMs in IDRs and structured domains (Davey et al., 2006; Edwards et al., 2007; Mooney et al., 2012).

Funding

NSERC, CIHR and Genome Canada.

Conflict of Interest: none declared.