Abstract
This study used the framework of the referent configuration hypothesis and slow changes in the external conditions during vertical oscillation of a hand-held object to infer the characteristics of hypothetical control variables. The study had two main objectives: (1) to show that hypothetical control variables, namely, referent coordinates and apparent stiffness of vertical hand position and grip force can be measured in an experiment; and (2) to establish relation(s) between these control variables that yield the classic grip-force-load-force coupling. Healthy subjects gripped a handle and performed vertical oscillations between visual targets at one of five metronome-prescribed frequencies. A Hapticmaster robot was used to induce slow changes in the vertical force applied to the handle, while the size of the handle was changed slowly leading to changes in the grip aperture. The subjects were instructed not to react to possible changes in the external forces. A linear, second-order model was used to reconstruct the referent coordinate and apparent stiffness values for each phase of the vertical oscillation cycle using across-cycle regressions. The reconstructed time profiles of the referent coordinates and apparent stiffness showed consistent trends across subjects and movement frequencies. To validate the method, these values were used to predict the vertical force and the grip force applied to the handle for movement cycles that were not utilized in the reconstruction process. Analysis of the coupling between the four variables, two referent coordinates and two apparent stiffness values, revealed a single strong constraint reflecting the coupling between the grip force and vertical force. We view these data as providing experimental support for the idea of controlling natural, multi-muscle actions with shifts in a low-dimensional set of referent coordinates.
Keywords: Referent configuration hypothesis, referent trajectories, endpoint stiffness, grip force, grip apparent stiffness, grip-force-load-force coupling
1. Introduction
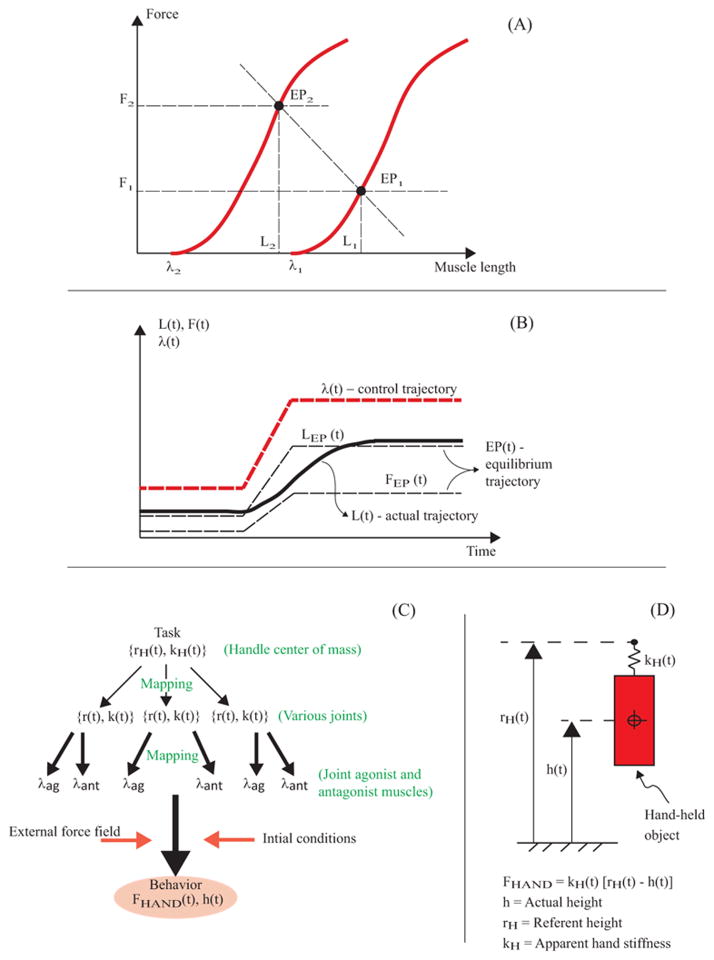
The equilibrium-point hypothesis (EP-hypothesis, Feldman, 1966, 1986) and its recent development in the form of the referent configuration hypothesis (RC-hypothesis, Feldman and Levin, 1995; Feldman, 2009) have been highly influential over the past 50 years. According to these hypotheses, the neural control of a motor action can be adequately described as time functions of spatial referent coordinates (referent trajectories) for salient variables. For single-muscle control, the EP-hypothesis considers threshold of the tonic stretch reflex (λ) as the salient referent coordinate, which is specified via sub-threshold depolarization of the corresponding alpha-motoneuronal pool. Changes in λ lead to movement, active force production, or both depending on external loading conditions. In Figure 1A, the dependence of active muscle force on muscle length (the bold curves) for two values of the threshold of the tonic stretch reflex (λi) are shown. For a given external load and λi, an equilibrium point (EPi) is characterized by a specific muscle length and a specific force exerted on the environment. A shift from λ1 to λ2 can lead to changes in both muscle length and force (a change from EP1 to EP2) depending on the external load characteristic. One such characteristic is illustrated in Figure 1A. By a simple extension, a centrally-specified time function λ(t) (dashed bold curve in Figure 1B) leads to changes in equilibrium values of muscle length and force (LEP(t) and FEP(t) in Figure 1B) and to actual muscle length changes L(t) (solid curve in Figure 1B) that would also depend on other factors, e.g., inertia.
Figure 1.
Panel (A) illustrates the dependence of active muscle force on muscle length (the bold curves) for two values of the threshold of the tonic stretch reflex (λi). For a given external load and given λi, an equilibrium point (EPi) is achieved and is characterized by a specific muscle length and a specific force. A shift from λ1 to λ2 can lead to changes in both muscle length and force (a change from EP1 to EP2) depending on the external load characteristic. One such characteristic is illustrated in Panel (A). Panel (B) depicts the time profile λ(t), which is a control trajectory (bold, dashed line). It leads to changes in the equilibrium values of muscle length and force, LEP(t) and FEP(t). Taken together, these time functions comprise the equilibrium trajectory. Actual trajectory of muscle length and force (only L(t) is illustrated) depends on many factors such as the inertia of the moving system. Panel (C) depicts a scheme in which hypothetical central control commands (i.e., referent variables) are transformed into tonic-stretch-reflex thresholds for all the muscles involved in the action via a series of few-to-many mappings. Behavior, such as measured mechanical variables, emerges as a consequence of the central commands and external conditions. The object in Panel (D) experiences a force from the subject’s hand. As a first approximation, the hand force is modeled as a linear relation between the difference in the current, h(t), and referent, rH(t), heights. The apparent hand stiffness, kH(t), is the proportionality constant.
Further extension of these ideas to multi-muscle movement is illustrated in Figures 1C and 1D. A hierarchical control scheme has been developed in which the central controller is presumed to specify a RC at the highest, i.e. task, level (Feldman and Levin 1995). While components of RC are spatial referent coordinates, their specification for an agonist-antagonist muscle pair controlling a joint results in two commands defined as the reciprocal command and co-activation command (Feldman 1980). The former defines the joint referent coordinate (see details in Discussion), while the latter is reflected in its apparent stiffness. This description can be generalized for a multi-joint system. For example, to execute vertical movement of a hand-held object (h(t) in Figure 1D), the centrally specified RC is reflected in the referent height rH(t) and the apparent stiffness (cf. Latash and Zatsiorsky, 1993) of the hand kH(t). The movement of the object h(t) emerges due to the specified input and external force field. Furthermore, one can view the task-level control input as being transformed by a sequence of few-to-many transformations that yield referent coordinates at lower hierarchical levels all the way down to λs for all involved muscles (for more detail see Latash, 2010).
One major obstacle in the development of the RC-hypothesis has been the lack of a method to measure RCs and their time changes during natural movements. The first attempt to develop such a method was made over 20 years ago and applied to reconstruction of referent trajectories during single-joint movements (Latash and Gottlieb, 1991, 1992; Latash, 1992).
To obtain the time course of the hypothetical control signals, Latash and Gottlieb developed a method based on comparing actual joint trajectories during repetitive movements in slightly varying external loading conditions. They assumed that the profiles of control variables were reproduced across trials. Regression analysis of the force-displacement data across trials at identical phases of the movement allowed the computation of referent joint coordinate and apparent stiffness values, which were later interpolated to approximate the assumed referent trajectories. This method was further developed for the analysis of two-joint action involving the elbow and wrist joints (Latash et al., 1999) using a modification that involved no explicit changes in external forces but relied instead on natural motor variability in one of the joint as the source of such changes for the other joint. Some of the results reported in the earlier studies, in particular the non-monotonic, N-shaped, referent joint trajectories were later criticized as possibly reflecting the simplified model of the joint motion assumed in the cited studies (Gribble et al., 1998).
The first major goal of this study was to generalize and apply this method to a natural movement involving multiple effectors for the first time. We selected vertical motion of a hand-held object as the action involving the entire arm and the hand. Another reason for choosing this task is that this action involves an explicit component (moving the object) and an implicit one (modulating the grip force). It is well known (Forssberg et al., 1991; Flanagan and Wing, 1993; Flanagan and Tresilian, 1994; Flanagan et al., 1993; Gao et al., 2005; Zatsiorsky et al., 2005) that motion of a vertically oriented hand-held object in the vertical direction is associated with feed-forward modulation of the grip force, which keeps the safety margin (the relative amount of grip force over the slippage threshold, Johansson and Westling, 1988; Johansson and Cole, 1993) relatively unchanged. The second major goal of our study was to explore causes for the reported grip-force-load-force coupling at the level of assumed and experimentally reconstructed control variables.
The grip-force-load-force coupling is interpreted within the RC-hypothesis framework as coupling between referent trajectories for the two task components (Latash et al., 2010). For example, during a cyclical object motion along the direction of gravity, referent height of the hand with the object (rH) is expected to move at the movement frequency; the time-varying difference between the referent and actual object heights (ΔRh = rH − h) leads to the force generated by the hand on the object (FHAND). The magnitude of FHAND also depends on the apparent stiffness of the hand, i.e., the coefficient of proportionality (kH) between the force and ΔRH: FHAND = kH×ΔRH. We assume a linear dependence as a first approximation of this relation.
Grip force production is a consequence of a difference between the hand’s actual aperture (the shortest distance between the opposing digits) and the referent aperture, which is smaller than the actual aperture (Pilon et al., 2007). The magnitude of the grip force (FGRIP) is expected to be proportional to the difference between the referent and actual apertures (ΔRG) with a coefficient of proportionality (kG), which is henceforth addressed as grip apparent stiffness: FGRIP = kG×ΔRG.
Note that the reported coupling between FHAND and FGRIP may be produced by various relations between the {kH; rH} and {kG; rG} pairs. We hypothesize that the FHAND−FGRIP coupling will be reflected as a constraint in the four-dimensional space of referent variables and the apparent stiffnesses.
The selected motion allowed introducing controlled, slow variations in the external conditions into an ongoing movement. These included variations in the external force as well as in the aperture size. This was achieved with two devices. The first is a HapticMaster robot used to modulate external forces acting on the handle moved by the subject. The second is the handle instrumented with a stepper motor allowing slow changes in the aperture size (Zatsiorsky et al., 2006; Ambike et al., 2014). While the handle motion was relatively fast (see Methods), changes in the aperture were slow. So, we could safely assume that problems with defining the damping (first-order) term in the second-order linear model were not applicable to our reconstruction of grip referent trajectory and apparent grip stiffness (cf. Gribble et al., 1998; Feldman et al., 1998). We also performed validation of the referent trajectories and apparent stiffness patterns by a forward simulation of the hand and grip force time profiles.
Note that while the experimental design may seem like a traditional system-identification setup, we did not use the more traditional analysis of the system’s response to controlled perturbations in the time domain; instead, we analyzed the system states at similar phases of the movement across multiple cycles (See Data Analysis). For more details, see Discussion.
To summarize, this paper has two main objectives: (1) to extend the method developed by Latash and Gottlieb to study vertical oscillation of a hand-held object and compute hypothetical, task-level control input as assumed within the referent-configuration hypothesis (namely, kH, rH, kG, rG), and (2) to establish relation(s) among the control variables for the explicit (oscillation) and implicit (grip-force modulation) components of the task that yield the grip-force-load-force coupling. These goals may be restated in the form of the following hypotheses: (1) the application of the experimental design and the computational scheme will lead to reproducible trajectories of task-level control variables, and (2) the FHAND−FGRIP force coupling will be seen as a constraint on the four-dimensional space of referent variables and apparent stiffness values.
2. Methods
2.1 Subjects
Four female and seven male healthy adults (age 28.8 ± 5.1 years, height 173.2 ± 9.5 cm, mass 72.2 ± 10.9 kg, hand length 18.65 ± 1.2 cm, hand width 8.79 ± 0.5 cm) voluntarily participated in the study. The subjects had no history of neuropathy or upper limb trauma. All the subjects were right-handed according to their hand usage during eating and writing. All subjects gave informed consent according to the procedures approved by the Office of Research Protections of The Pennsylvania State University.
2.2 Apparatus
The subject sat comfortably on a stool and grasped an instrumented handle with the fingertips of the right hand (See Figure 2A). The handle was oriented vertically. Five six-component (three force and three moment components) transducers (Nano 17, ATI Industrial Automation, Garner, NC) were mounted on the handle. The sensors were aligned in the XZ coordinate plane (See Figure 2B). An electric motor attached to a worm-and-screw arrangement was used to adjust the distance between the faces of the thumb and the finger sensors. This distance was defined as the grip aperture. Sandpaper (100-grit) was placed on the contact surface of each sensor to increase the friction between the digits and sensors. The digit pad–sandpaper static friction coefficient was about 1.4–1.5 (previously measured by Savescu et al, 2008). The handle was rigidly mounted on the HapticMaster robot (Moog, The Netherlands), an admittance-controlled robot with two main functional components: a control box and a three-degree-of-freedom robot arm. The subjects were free to translate the handle in the vertical and the anterior-posterior directions, and to rotate it about a vertical axis. With these degrees of freedom of the robot arm, the handle can occupy any position in the robot’s workspace. The robot accomplished two objectives. First, it compensated for the weight of the instrumented handle by generating a bias vertical force. Consequently, subjects experienced an inertial mass of 4 kg positioned at the end of the robot arm but no weight (to avoid fatigue). Second, the robot produced a smoothly varying force in the vertical direction (details in Section 2.4). The primary task was to oscillate the handle in the vertical direction. Subjects displayed a small translational component in the anterior-posterior direction: across all trials, the distance of the handle from the robot’s rotation axis varied between 55 and 85 cm, and the across-subject mean of the within-trial change in this distance was 6 cm, and the maximum change was 19 cm.
Figure 2.
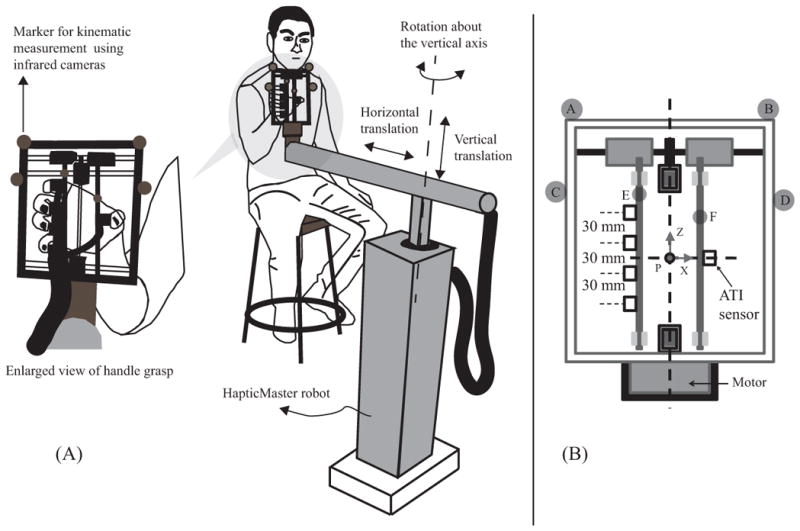
Experimental setup. Figure (A) shows the five-digit prismatic grip on the handle. It also shows the subject seated in front of the Haptic Master robot and its three degrees of freedom. Figure (B) shows the expanding handle with the force sensor and vision marker locations, and the stepper motor to adjust the grip aperture.
Three-dimensional kinematics of the handle were recorded at 100 Hz using the Qualisys Motion Capture System (Qualisys AB, Sweden) with five ProReflex MCU240 infrared light emitting cameras mounted on tripods positioned around the experimental space. The motion capture system was calibrated following the manufacturer’s instructions. Calibration was assumed to be successful if the standard deviation of the wand length, provided by the Qualisys Track Manager Software, was less than 1 mm. The 3D tracking maximum residual of the camera system was set at 5 mm.
Figure 2B shows the six markers attached to the handle. Markers A–D were placed on the rigid frame of the handle, and markers E and F were placed on the vertical posts that were moved horizontally by the handle’s motor to adjust the aperture. Markers A–D provided a handle-fixed reference frame as well as the height of the handle in the lab-fixed global reference frame, whereas, markers E and F provided a continuous measurement of the aperture.
Two-dimensional location of the robot’s endpoint corresponding to the height and the medio-lateral displacement was displayed on a computer screen placed in front of the subject. Note that the medio-lateral displacement of the handle was achieved by a simultaneous translation in the anterior-posterior direction and a rotation about the robot’s vertical axis. Two horizontal reference lines spaced 20 cm apart were also displayed on the screen. Thirty analog signals from the ATI force sensors (5 sensors × 6 components) were routed to an analog–digital converter (PCI-6031, National Instruments, Austin, TX). A customized LabVIEW program was used for data acquisition at 100 Hz with the 16-bit resolution.
2.3 Instructions and training
Subjects were instructed to grasp the handle with their right-hand fingertips and then perform smooth vertical oscillations of the handle between the two horizontal reference lines displayed on the computer screen. A metronome was used to specify the oscillation frequency in most cases (see Section 2.4 for details). Although the horizontal location of the handle was presented as feedback, the subjects were instructed to ignore this coordinate, and perform the oscillations roughly along a straight vertical line. The subjects were further instructed not to pay attention to either spatial or temporal accuracy of the performed oscillations. The subjects were instructed to ‘practice the movement until it became automatic’ and were given about 2–3 min of practice before the first perturbed trials (see section 2.4). They were given an additional 1 min of practice each time a new oscillation frequency was prescribed.
The general instruction was ‘not to intervene voluntarily’ or ‘do the same, no matter what change in external forces happens’. As additional explanation, subjects were told to not correct their behavior if they missed the horizontal reference lines (vertical handle position) or the metronome beat. Ensuring compliance with this instruction required an additional 1–2 min of practice.
2.4 Experimental protocol
The subject’s natural or preferred frequency of oscillation was measured first using three trials with no changes in the vertical bias force and aperture. The subjects were instructed to ‘perform smooth and consistent oscillations at the most comfortable frequency’. Each trial lasted 30 s. The frequency corresponding to the maximum power in the frequency spectrum of the handle oscillation along the vertical axis was averaged across the three repetitions to obtain the preferred (natural) oscillation frequency, fn. This frequency defined a set of five prescribed oscillation frequencies for that subject: FP = [fn − 0.2, fn − 0.1, fn, fn + 0.1, fn + 0.2] Hz. These will be referred to as Frequency 1 (slowest) to Frequency 5 (fastest). The subjects then performed the oscillations at metronome-specified frequencies. During these trials, the robot applied smoothly-varying vertical force (F̄robot) and the aperture was increased and then decreased to its initial value as described in the next section. Note that the characteristic times of external force changes were at least twice as long as the characteristic movement period. Three repetitions were performed at each prescribed oscillation frequency. The oscillation frequency was block randomized across subjects. Each trial lasted about 2.5 m, and the entire experiment lasted about 1.5 hours.
2.4.1 Changes in external conditions
Figure 3 shows the time courses of the aperture changes and the vertical force changes during a typical trial.
Figure 3.
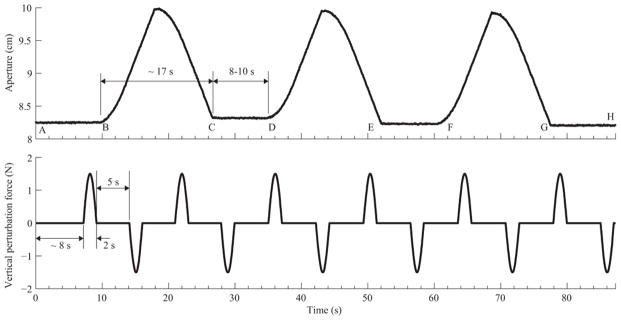
Time courses of typical perturbations in aperture and vertical force applied by the stepper motor and the robot, respectively.
Each trial began with a period of about 10 s during which the subject adjusted the oscillation frequency to match the metronome. No data were collected during this time. Data collection began when the experimenter was convinced that the subject had reached a stable oscillation pattern. The robot-induced force changes were introduced about 8 s after data collection began, followed by the aperture changes. This sequence was consistently maintained for all trials and subjects.
The robot vertical force trajectory consisted of alternating episodes of force increase (positive values in Fig. 3) and decrease (negative values in Fig. 3). Each episode was a half-sine-wave with the period of 0.5 Hz and peak value of 1.5 N. These parameters were defined based on pilot studies as leading to measurable modifications of the hand trajectory that were not accompanied by visible corrections by the subjects. The episodes were spaced by 5-s time intervals.
The aperture changes consisted of episodes of aperture increase (from 8.3 to 10 cm) over about 8.5 s and decrease back to the initial aperture value over the same time. These episodes were spaced by 8–10-s intervals as illustrated in Fig. 3.
We emphasize that the purpose of the described changes in external conditions (robot force and grip aperture changes) was not to use them as perturbations in a typical system identification meaning. Instead, we assumed that the subjects used the same central control signals across cycles and then analyzed the different movement consequences under different external conditions to infer the time profiles of the assumed control variables. This is described in more detail further.
2.5 Data analysis
All data (the motion analysis data and the finger forces from the ATI sensors) were low-pass filtered with a zero-lag, fourth-order Butterworth filter with cut-off frequency of 10 Hz. The data were then separated into steady states and variable-aperture portions according to the state of the motor on the handle. Therefore, the steady-state data consisted of the portions between time points A–B, C–D, E–F, and G–H in the top panel of Figure 3. Similarly, the variable-aperture data consisted of the portions between time points B–C, D–E, and F–G. Thus, there were twelve epochs (4 epochs × 3 repetitions) of steady-state data and nine epochs (3 epochs × 3 repetitions) of variable-aperture data for each subject and each frequency. The variable-aperture data were pooled across the epochs for each subject and frequency and further divided into individual vertical oscillation cycles by identifying the time instants at which the handle height was locally maximal. These divided data were pooled across the oscillations and time normalized using linear interpolation so that all the oscillations had the same number of data points. The steady-state data were subjected to the same process. The variable-aperture data were used to compute the referent parameters (see below). The steady-state data from the portion A–B were utilized to validate the developed model for vertical object oscillation, since this robot-force-free epoch is most easily located. All the steady-state data were used to validate the model constructed for grip-force production (see below).
2.5.1. Mechanics of vertical oscillation
We used a linear, second-order differential equation to model the vertical motion of the handle along the coordinate h:
| (1) |
where m is the mass of the handle, c1 is the damping coefficient, perhaps time varying, characterizing dissipative forces due to friction in the robot, air resistance and similar factors. The time derivative of a variable is denoted by the dot notation: . The external forces acting on the handle due to the subject’s hand and the robot, represented as vector quantities, are F̄HAND and F̄robot, respectively. The hand force F̄HAND is defined as the sum of the vertical forces exerted by the five digits.
The RC hypothesis provides a model for the hand force. Specifically, it assumes that the central controller specifies time courses of neural variables that produce the referent height rH(t) and apparent endpoint stiffness kH(t). These specifications are transformed into the thresholds of the tonic stretch reflexes for all the muscles involved in the action via a number of few-to-many mappings (Figure 1C). Muscle activations emerge in only those muscles whose current length exceeds their prescribed threshold value, leading to force generation in those muscles. Some of this force is consumed by friction and other dissipative factors within the body, partly due to the action of reflexes induced by velocity-sensitive receptor activity, and the remainder is measured at the fingertips as the net vertical force applied to the handle by the hand. Therefore, the hand force is modeled as
| (2) |
Here, we assume, as a first approximation, a linear relation between the discrepancy between the referent and actual height ΔRH = rH(t) − h(t) and the generated force at the hand. The constant of proportionality is the apparent stiffness kH(t). We lump the internal damping of the body and represent it as a single coefficient c2(t). The issue of damping is a contentious one. For example, in earlier studies, it was suggested that the damping term could be proportional to the difference between the effector velocity and referent trajectory velocity (Feldman and Levin 1995). We have decided to use the current form of Equation (2) to avoid adding more assumptions that currently remain untestable. As shown later, this difference remains theoretical since, in the final form of the model, the damping term is dropped altogether. From Equations (1) and (2) we obtain
| (3) |
where c(t) = c1(t) + c2(t).
This system is viewed as a mass (the handle) influenced by two forces: (1) the environment (including the robot force and external damping represented by c1), and (2) the hand. We assume that the external damping effects are small (c1 ~ 0). Furthermore, given the training trials, we assumed that subjects successfully ignored the small and slow changes in the external robot force. Therefore, we assume that the central commands rH(t) and kH(t) were reproduced across cycles independently of the external force changes. However, the handle kinematics h(t) were expected to change due to the changes in the environment (i.e., robot force), and consequently, the hand force was also expected to change according to Equation (2). (cf. Figure 1C).
2.5.2. Estimation of referent height and apparent hand stiffness trajectories
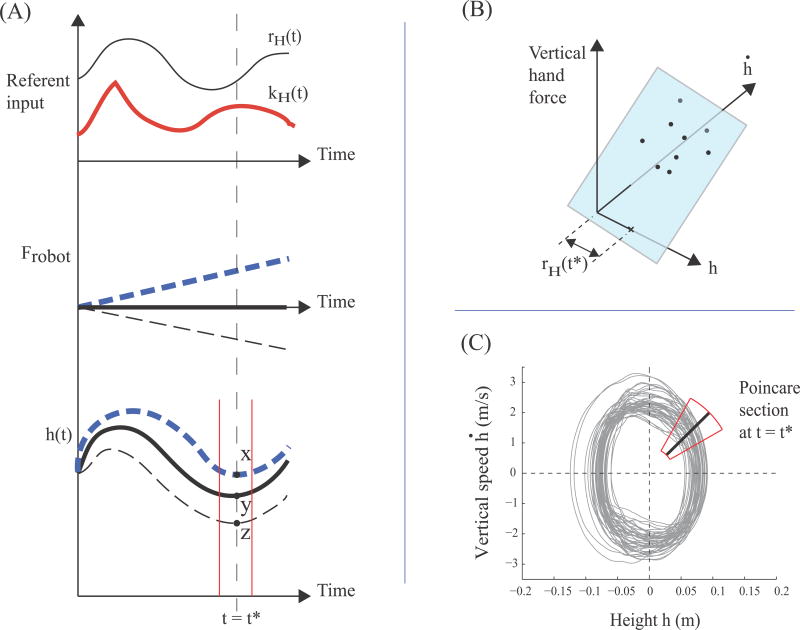
Under the above assumptions, we seek to compute the trajectories of the referent height (rH), the damping coefficient (c2) and the apparent stiffness (kH) over one oscillation of the handle. This is achieved by the method illustrated in Figure 4A and developed by Latash and Gottlieb (1991, 1992) and Latash (1992). The top panel in Figure 4 depicts the controller input rH(t) and kH(t) for one oscillation period; they are assumed to be cyclic over this period. The robot applies different disturbances during various cycles (middle panel of Figure 4A), and as a consequence, different trajectories of the hand are obtained (bottom panel in Figure 4A). A section at a given time instant t = t* is taken and the data at that phase of the motion obtained from multiple movement cycles (points x, y, and z in the bottom panel of Figure 4A) are used to run regression analyses. Figure 4B depicts the process of fitting a regression model to these data obtained for a single time instant. The model uses the vertical hand force as the response variable, and the hand vertical position and speed as the independent variables. If linear stiffness and damping are assumed, the regression provides the coefficients kH(t*) and c2(t*) from Equation (2). Additionally, when F̄HAND (t*) and ḣ(t*) are zero, Equation (2) yields rH(t*) = h(t*). Thus, the point of intersection of the regression plane with the h axis in Figure 4B yields the referent height at that time instant. Repeating this procedure for time sections over the entire oscillation period provides the time functions rH(t), kH(t) and c2(t).
Figure 4.
Schematic representation of the computational procedure. Figure (A) shows the referent variables, the robot-induced perturbations, and the resultant trajectory of the handle height for a single oscillation period. Three hypothetical cycles are depicted. The referent inputs remain the same for all cycles, but the robot forces and hence the output trajectories are different for each cycle. Taking a snapshot at time t = t* and averaging the data within a 20 ms window yields data points x, y and z for that phase. Figure (B) plots these data for the single time instant t* and applies a regression model represented here by the plane. This model potentially yields the referent coordinate, the apparent stiffness, and the damping coefficient. Figure (C) illustrates the Poincare section in the phase plane (h vs ḣ) at time t = t*. The intersection of the trajectory with the section over several oscillations yields a distribution of data points. The time window for averaging data for each oscillation is also depicted.
This procedure is akin to taking the Poincare section (Strogatz, 1994) of the hand trajectory in phase space composed by plotting the handle vertical speed against its vertical position. This is illustrated in Figure 4C. The repeated intersections of the hand trajectory with the Poincare section furnish the data depicted in Figure 4B. To construct the time functions rH(t), kH(t) and c2(t), the section is swept through the interval [0 2π].
The time sections (Poincare sections) were taken at the sampling frequency (100 Hz). The time-normalized data pooled across all three repetitions at the same frequency provided between 97 and 242 data points for each time section, depending on the oscillation frequency and the duration of the trial. The initial portion of the trial when the robot did not perturb the system (epoch A–B in Figure 3, top panel) was not included in this part of the analysis. For each time instant, the data in a 20-ms time window centered at t* were pooled across all available oscillation cycles. This data were sorted in an ascending order of handle height and then binned into eight equi-spaced bins along the handle-height axis. The mean of the data enclosed in each bin was utilized for regression analysis.
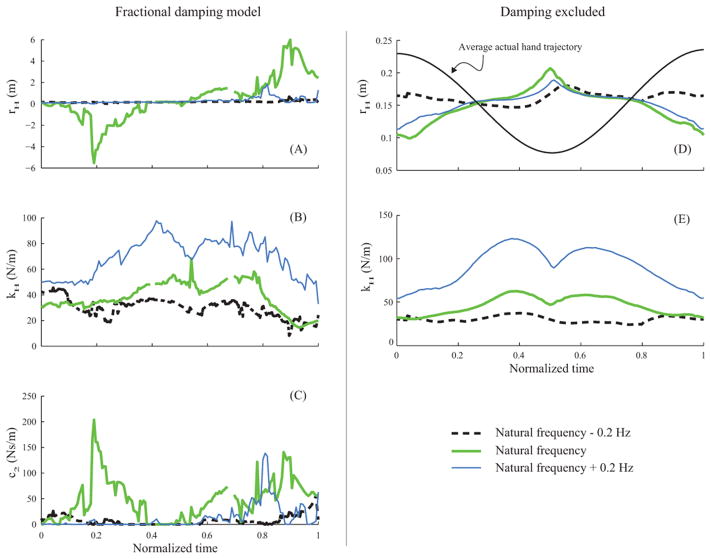
The original regression model, Equation (2), failed to provide smooth trajectories for any of the system parameters rH(t), kH(t), and c2(t). Therefore, we investigated a nonlinear dependence on the damping using a fractional-power-damping model of the form
| (4) |
based on the work of Gielen and Houk (1984). This model was motivated by the following considerations. Fast movements required high stiffness values, which were physiologically untenable. Another way to facilitate fast movement is to reduce the damping. However, this leads to an underdamped system with terminal oscillations. The solution is to have variable damping that is low when movement speed is high, and vice versa. This is achieved by the model in Equation (4). Note that for α = 1, Equation (4) is a reformulation of Equation (2) with A = −kH, B = −c2, and C = kHrH. The sign(ḣ) term ensures that the damping force always acts against the velocity vector for all possible values of α. This model assumes a linear stiffness coefficient A, and a damping contribution to the hand force that is proportional to some power α of velocity. The exponent α was determined as the value that maximizes the sum of the R2 values of the least-square fits to the data for all time points in the trial. Comparing Equations 2 and 4 yields the desired system parameters for the time instant t* as: kH = −A; c2 = −B; and rH = −C/A.
The fractional-damping regression model was also unable to provide smooth trajectories for any of the system parameters rH(t), kH(t), and c2(t). Furthermore, the exponent α varied across oscillation frequencies with no discernable pattern. Therefore, we dropped the damping term altogether in the equation and adopted a simpler regression model of the form:
| (5) |
With this model, the systems parameters are defined as kH = −A, and rH = −B/A. A comparison of the results with regression models with and without damping for one subject is shown in Figure 5. We stress that all the regression models used, Equations (2), (4) and (5), are assumed to be independently applicable at each single time instant.
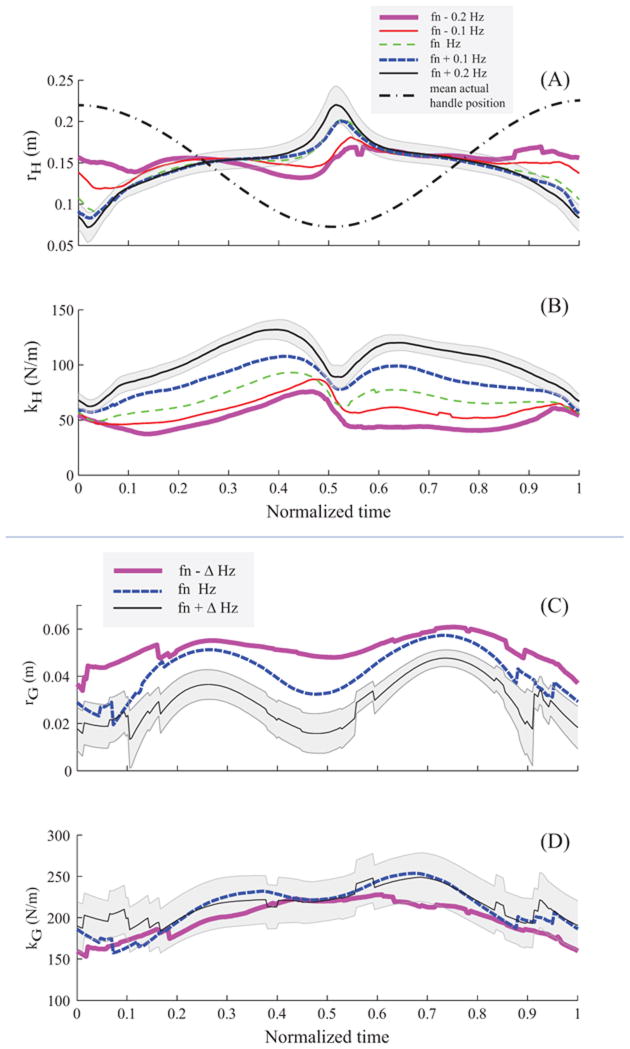
Figure 5.
Trajectories of the referent variables and damping computed for vertical handle oscillation for a representative subject. Figures (A), (B), and (C) show the referent height rH, apparent stiffness kH, and damping c2, respectively, for three oscillation frequencies computed using a fractional damping regression model. The exponent α for the damping term was 0.71, 0.04, and 0.16 for the movement frequencies fn − 0.2, fn, and fn + 0.2 Hz, respectively. Figures (D) and (E) show the referent height and the apparent stiffness for the same data computed using a damping-free regression model. Figure (D) also depicts the average (computed across all movement frequencies) trajectory of the actual hand movement. The natural-frequency curves in figures A, B, and C show missing data. At these locations, the regression was not significant, and hence these data were not included.
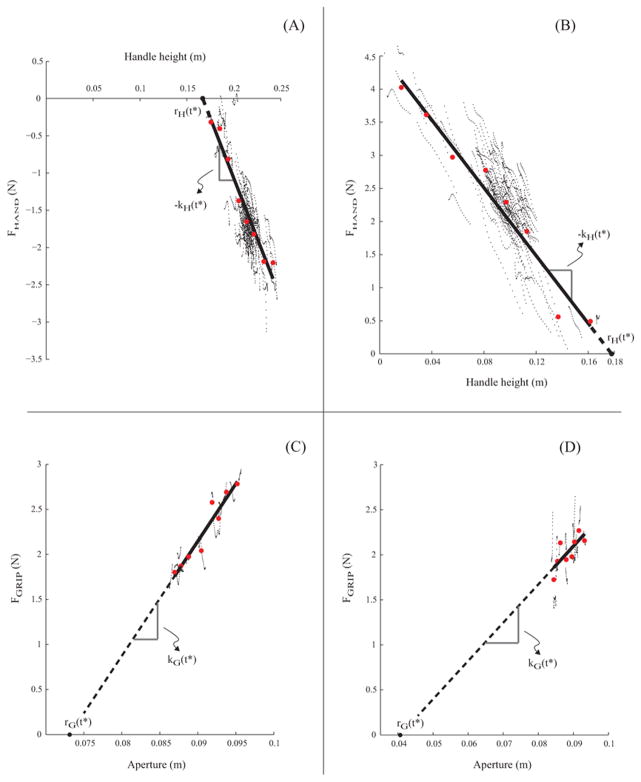
Figures 6A and 6B show the binning procedure for this model, the consequent linear regression model, and the computation of the referent height rH and the apparent stiffness kH for two distinct time sections. For each time section, the results of the regression model were accepted only if the regression R2 value was greater than 0.6. (Note that this corresponds to a p value of ~ 0.025 for the linear regression with eight data points.) Otherwise, the obtained data at that time slice were considered too noisy to estimate the referent variables. Therefore, the resulting referent trajectories sometimes had missing data.
Figure 6.
Figures A and B plot vertical hand force against the handle height at two distinct time sections or phases of the oscillatory movement. Data across all cycles of all repetitions of the task performed by one subject are plotted (black dots). The hand force is negative in figure A since the handle is being accelerated downward, and vice-versa for Figure B. These data are collapsed into 8 bins (red solid dots – see text), and a linear regression line is drawn through the binned data (solid line). The negative slope of this line is the apparent stiffness kH and the intersection of the line with the horizontal axis is the referent height rH at the respective time instants. Figures C and D plot grip force against the aperture length for two distinct time sections or phases of the oscillatory movement. Data across all cycles of all repetitions of the task performed by one subject are plotted (black dots). The data are collapsed into eight bins (red solid dots – see text) and a linear regression line (solid line) is drawn through the binned data. The slope of the regression line is the apparent grasp stiffness kG, and the intercept on the aperture axis is the referent aperture rG.
2.5.3 Grip mechanics
Grip force is the internal force exerted by the fingers and the thumb on the object, i.e., the force that does not cause object acceleration. Here, it is defined as min[|FZTH|, Σi(|FZi|)], i = {index, middle, ring, little}, where TH denotes the thumb, and the Z-direction of force application is normal to the digit-sensor contact interface. The grip force FGRIP is exerted along the horizontal direction, whereas, the arm movement causes vertical acceleration of the handle. When applied to grip force production, the RC hypothesis states that the central controller specifies a referent aperture rG as the desired position of the fingertips. Since the actual aperture (hG) is defined by the geometry of the gripped object, grip force emerges due to the difference between the actual and the referent apertures (ΔRG = hG − rG). The magnitude of the force, to the first approximation, is proportional to ΔRG. A method to measure the apparent stiffness kG relating ΔRG to the generated force is described in Zatsiorsky et al. (2006) and Ambike et al. (2014). There, the actual aperture was perturbed by an expanding handle, and the corresponding change in grip force was recorded. The slope of the force-aperture curve, which is well approximated by a straight line, is the kG, and the intercept of the linear fit on the aperture axis provides a measure of the referent aperture rG.
During vertical oscillation of a hand-held object, the grasp force is modulated in parallel with load during cyclical vertical movements (Flanagan and Wing, 1995). This grip force modulation is presumably achieved by varying rG and kG during the oscillation cycle. We aim to compute the time courses of these variables by combining the methods of Zatsiorsky et al. (2006) and Ambike et al. (2014) and those mentioned in the previous section. We assume that at each instant or phase of the vertical oscillation, the centrally specified values of rG and kG are identical across oscillation cycles and unaffected by the aperture variations imposed by the expanding and contracting handle. We also assume that the computational method developed for the static measurement of these quantities applies for each time slice during the vertical oscillation. We ignore the damping term in this computation, since the speed of the aperture variations was very low, on the order of 2 mm/s.
2.5.4 Estimation of referent aperture and apparent grasp stiffness trajectories
This analysis is similar to the one used to compute the referent variables for the vertical handle oscillation (described in section 2.5.2). For the present analysis, the portions of the data series when the stepper motor on the handle was engaged were utilized (epochs B–C, D–E, and F–G in Figure 3). They were time aligned with respect to the handle oscillation height, as described in Section 2.5, and a section was taken at time t = t*. Since the aperture variation was slower than the oscillation frequency (even for the slowest movements; see Figure 3), the grip force FGRIP and the aperture width hG trajectories crossed the Poincare section several times. The number of crossings varied between 52 and 136 depending on the oscillation frequency and the trial duration. The mean values of the grip force FGRIP and the aperture width hG over a 20 ms time window centered at t = t* were utilized as the values of those variables at that instant. These data were sorted in an ascending order of actual aperture hG and then binned into eight bins along the aperture axis. The linear regression model FGRIP = A×hG + B was used to fit the set of data points obtained by computing the mean of the data in each bin. The apparent grasp stiffness kG = A, and the referent aperture, rG, were obtained by extrapolation as the point on the regression line when the grip force is zero, i.e., rG = −B/A. (Note that the grip force never vanishes during the oscillations). Figures 6C and 6D show the binning procedure for this model, the consequent linear regression model, the computation of the referent aperture rG and the apparent grasp stiffness kG for two distinct time sections. At each time slice, the regression result was accepted only if the regression R2 value was greater than 0.6. (This corresponds to a p value of ~ 0.025 for linear regression with eight data points.) Otherwise, the obtained data at that time slice were considered too noisy to estimate the grip parameters {rG, kG}.
2.5.5 Relations between the handle oscillation and the grip force
It is well known that humans modulate grip force in relation to the inertial load experienced during the manipulation of a hand-held object (Flanagan and Wing, 1993; Flanagan et al., 1993; Smith and Soechting, 2005; Slota et al., 2011; Ambike et al., 2013). The trajectories of the grip force FGRIP and the vertical hand force FHAND were pooled across trials and oscillations and averaged for each subject and each oscillation frequency. The averaged force trajectories were then regressed against each other.
To determine if the grip-force-load-force coupling arises due to coupling between the referent variables for the two actions (gripping and vertical movement), similar analysis was performed for the computed trajectories of the referent variables. There is no clear distinction between regressor and regressed variables here. But since the vertical handle oscillation was the explicitly specified task, we assumed that the referent variables for the hand movement were the regressor variables and the grip-force referent variables were the regressed variables. Even with this assumption, the referent variables can be related in several ways. We explored this space of possibilities thoroughly up to quadratic polynomials. Quadratic relations did not yield significantly higher R2 values compared to those obtained from linear relations. The adjusted R2 values in some cases reduced with the addition of a quadratic term, indicating that the added complexity in the model was not statistically justifiable. For brevity, we present analyses only for two initial hypotheses regarding the relations between the variables and contrast their results with the strongest result that we obtained from another linear approach.
We initially hypothesized that the referent positions for the two actions were linearly related, and similarly, the apparent stiffness values were constrained by another linear relation. Therefore, the following linear relations were explored: (1) rG vs rH, and (2) kG vs kH. Finally, a single linear constraint relating all four referent variables was explored. The regression equations for these cases are:
| (6 i) |
| (6 ii) |
| (6 iii) |
These exploratory regression analyses were conducted separately for each subject and each frequency. Out of the 55 sets of trajectories, six sets were excluded since the trajectories for most of the oscillation cycle were missing in these cases (always those related to the grip-force variables). We selected a generalized linear model as the most unbiased method of linear analysis although other methods (such as MANCOVA) could also be used. Our method has the advantage of offering an explicit equation linking the four variables that could further be explored across subjects.
2.5.6 Validation of the apparent stiffness-based models for force generation
After computing the referent variable and the apparent stiffness for the vertical oscillation and the grip force, we used the regression models described earlier to predict the generated forces. For computing the vertical hand force, we used the initial portion of the trials during which the robot applied no force changes (portion A–B in top panel of Figure 3). Note that this portion of the trial was not used to compute the referent parameters kH(t) and rH(t). Similarly, for computing the grip force, we used the portions of the trial during which the motor on the handle was off, and these portions of the trials were not used in computing kG(t) and rG(t). The forces were computed using the equations
| (7 i) |
| (7 ii) |
where Ap is the actual aperture of the handle during the steady states (~ 8.25 cm). The input to these equations were actual aperture Ap, the computed trajectories of kH, kG, rH and rG, and the mean of the measured handle height h(t) during the unperturbed epoch A–B (Figure 3). The root mean squared (RMS) error between the predicted forces and the mean force trajectories during the corresponding unperturbed epochs (A–B for hand vertical force, and A–B, C–D, E–F, and G–H for the grip force) was computed and normalized by the maximum amplitude of the mean measured forces for each subject and oscillation frequency. Additionally, regression analysis was conducted to explore the FGRIP − FHAND coupling in the predicted forces.
2.6 Statistics
Most data in this paper are depicted as mean ± standard error (SE). The referent variables rH and rG and the apparent stiffness values kH and kG were sampled at four locations: [0%, 25%, 50%, 75%] of the oscillation cycle. The average of the variable over a 20% window of the oscillation cycle represents the variable value at the center of the corresponding interval (see Figure 6C for an example, also Figure 9). These values were subjected to two-way repeated-measures ANOVA with factors Frequency (5 levels) and Phase (4 levels). Data were pooled across subjects. Pair-wise contrasts were used wherever necessary with Bonferroni corrections. The purpose of this analysis was to determine whether the computed referent variables varied with the movement phase. Therefore, we assumed that the grip-force and hand-force production processes are independent, and subjected the referent variables associated with these two action components to independent ANOVAs. Subsequently, we explored possible correlations between the four referent variables using regression analyses.
Figure 9.
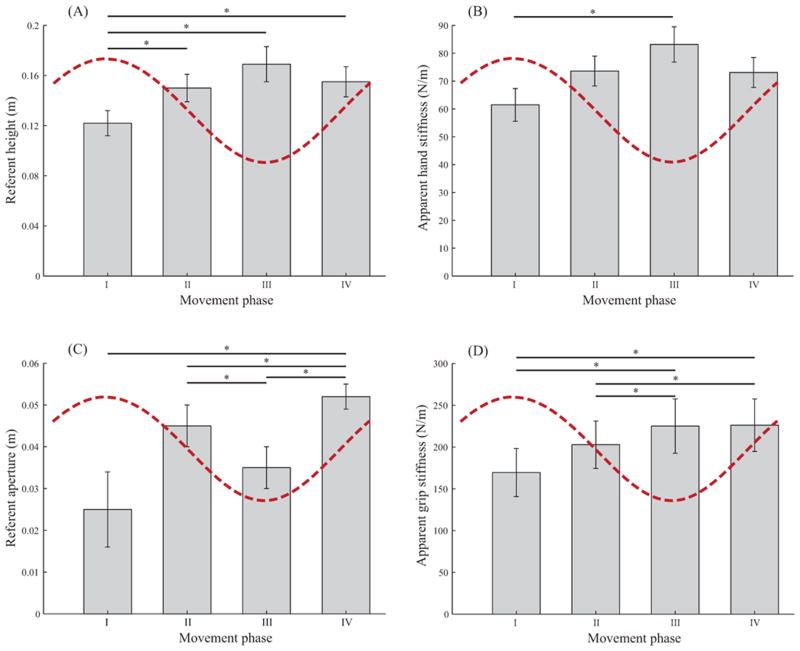
The mean ± SE of the referent variables rH, kH, rG and kG are plotted against the movement Phase in figures A, B, C, and D, respectively. The dotted curve in each panel depicts the actual handle height for one oscillation. Phases I and III coincide with the highest and lowest handle positions, and therefore, locations of highest acceleration magnitudes, respectively, and Phases II and III coincide with the middle of the oscillation cycle with roughly the minimum and maximum movement velocities, respectively. Note that the Phase representations on the x axes here are shifted relative to those in Figures 5, 7 and 8. Statistically significant pairs are indicated with an asterisk (*).
All statistics were performed using the SPSS statistical software using an α level of 0.05. Mauchly’s sphericity test was used to validate the use of repeated measures ANOVA; the Greenhouse-Geisser correction for the degrees of freedom was applied whenever a departure from sphericity was observed. Levene’s test was used to validate the use of one-way ANOVAs, and the Welch test for significance of mean differences was employed when Levele’s test was violated. Post hoc comparisons were performed using the Games-Howell tests in such cases.
3. Results
3.1 Typical subject behavior
Subjects were able to move the handle within the prescribed limits with reasonable accuracy (see Figure 7A for a representative subject’s behavior). The peak-to-peak amplitude of movement was consistent for all Frequencies (mean ± SE = 14.17 ± 0.5 cm). The peak-to-peak vertical hand force increased with the Frequency (Figure 7B). One-way ANOVA yields F(2.091,20.911) = 215.063, p < 0.01, and pair-wise contrasts revealed significant differences between all pairs. The grip force varied with Phase and Frequency (Figure 7C). Grip forces at the high acceleration points (i.e., top and bottom hand positions) were greater than those at the highest speed points (i.e., roughly in the middle of the oscillation when acceleration was zero). Additionally, the grip force at the bottom position was significantly higher than at all other positions. Mean grip force also increased with Frequency. A two-way ANOVA (Phase × Frequency) yields main effects for Phase (F(3,30) = 81.786, p < 0.01), Frequency (F(4,40) = 42.066, p < 0.01), and the interaction effect (F(12,120) = 31.000, p < 0.01). The across-frequency increase in the grip force was more pronounced during the high acceleration phases as compared to the high velocity phases.
Figure 7.
Typical subject response. Figure (A) plots the across-subject mean and standard deviation of the handle height against normalized time for all frequencies. Figure (B) plots the vertical hand force, and Figure (C) plots the grip force variation against normalized time. Figure (D) illustrates the across-subject mean of the grip force against the vertical hand force for all oscillation frequencies.
The measured grip force showed a quadratic dependence on the vertical hand force (Figure 7D). The curves in Figure 7D are averages across subjects. For each subject and frequency, a similar curve was computed using the data from the initial portion of the trial when the robot force was not imposed (see Figure 3, lower panel). Quadratic fits to these curves were significant (p < 0.01 for all cases) with high R2 values. The across-subject and -frequency median of the R2 values was 0.9 and the inter-quartile range was 0.07. (Also see Figure 10A).
Figure 10.
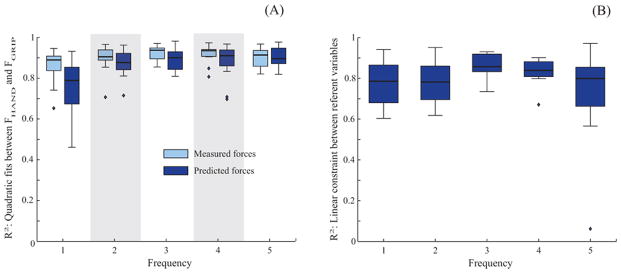
Box plots for R2 values. Each box shows the median (horizontal line within the box), the 25th and 75th quartiles (extent of the box), and median ± 1.5 × inter-quartile range, and the dots are the outliers. Figure (A) shows the R2 values of the quadratic fit between the hand and the grip forces, and Figure (B) shows the R2 values for the single linear constraint between the referent variables for hand oscillation and grip-force modulation.
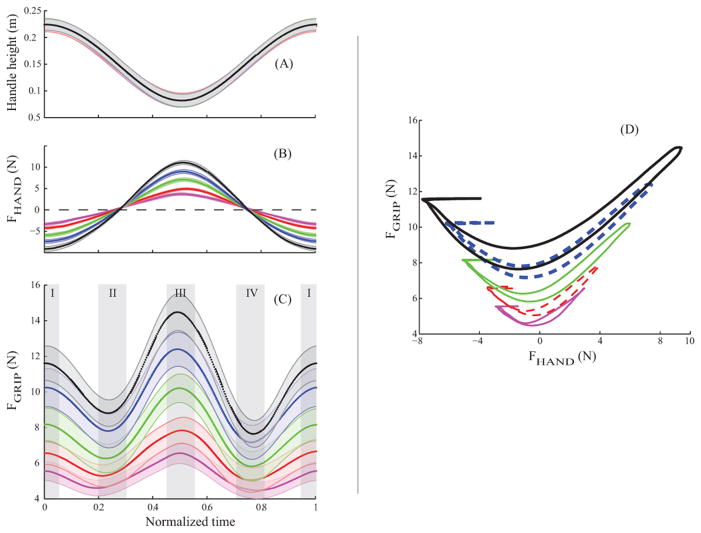
Figure 8 depicts the across-subject means of the referent variables for vertical handle oscillation (Figures 8A and 8B) and grip-force modulation (Figures 8C and 8D) plotted for one vertical oscillation cycle of the handle. For each subject and oscillation frequency, the vertical hand force and the handle height data from multiple oscillations were pooled for each phase in the handle movement cycle. A linear regression of the data yielded the apparent hand stiffness kH (slope) and the referent height rH (x-intercept; see Figures 6A and 6B). This process, repeated for all phases, yielded the time functions of kH and rH, which were then averaged across subjects. Similarly, the grip force and actual aperture data for each phase in the handle movement cycle were pooled across repetitions, and linear regression provided estimates of the apparent grip stiffness kG (slope) and the referent aperture rG (x-intercept; see Figures 6C and 6D). This process was repeated for all phases to obtain the time functions of kG and rG, which were then averaged across subjects (Figures 8C and 8D). The trajectories appear fairly smooth, except for the slowest frequency movement, which shows some step-like changes. These steps indicate that the regressions at these locations were rejected (R2 < 0.6) for some subjects, resulting in missing data, which, in turn, led to a sudden change in the mean (and SE) value(s). The estimation of the kG and rG trajectories was modestly successful, resulting in many missing points and noisy trajectories. To overcome this problem, the trajectories for the two lower frequencies and the two high oscillation frequencies were averaged; the results are depicted in Figures 8C and 8D.
Figure 8.
The across-subject means ± SE of the referent variables are plotted against normalized time or movement phase. The referent height (rH) and apparent hand stiffness (kH) are plotted in panels (A) and (B), respectively. The referent aperture (rG) and the apparent grip stiffness (kG) averaged across the two low, natural, and two high oscillation frequencies are plotted in panels (C) and (D), respectively. The standard error bands are shown only for the highest oscillation frequency data for clarity. The standard errors for other oscillation frequencies are of similar magnitude. The average handle height trajectory is depicted in Panel (A) as the dash-dot line.
The data were binned into four movement Phases (Figures 9A, 9B, 9C, and 9D). For the analysis of the referent variables that follows, the means of the variables over windows centered at [0% 25% 50% and 75%] of the oscillation cycle and 20% cycle width serve as estimates. Phases I and III (0% and 50% of oscillation cycle, respectively) correspond to the top and bottom limits of the oscillation (locations with maximal absolute vertical acceleration, and therefore, hand force), and phases II and IV (25% and 75% of oscillation cycle, respectively) correspond to the central part of the oscillation (locations with maximal absolute vertical velocity and low hand force).
3.2 Vertical handle motion
The absolute peak vertical hand force observed during Phases I and III increased with Frequency. This increase was associated with changes in both the referent height and apparent stiffness across the Frequencies. In contrast, the apparent stiffness in Phases II and IV increased with Frequency, but the referent height was Frequency invariant.
ANOVA demonstrated that the referent height rH varied with Phase (F(1.11,11.103) = 12.555, p < 0.01; Figure 9A) as well as Frequency (F(4,40) = 2.679, p < 0.05). It decreased with Frequency in Phase I (maximum downward acceleration); it increased with Frequency in Phase III (maximum upward acceleration), whereas, there was no change with Frequency in Phases II and IV (roughly smallest absolute vertical acceleration). This behavior was reflected in the significant Frequency × Phase interaction (F(12,120) = 13.351, p < 0.01). Pair-wise contrasts revealed significant differences between Phase pairs I–II, I–III and I–IV but not between any Frequency pair.
The hand apparent stiffness kH also varies with Phase (F(1.69,16.899) = 9.678; p < 0.01; Figure 9B) and it increases with Frequency (F(1.869,18.686) = 71.866; p < 0.01). It was significantly greater in Phase III (83.16 ± 6.4 N/m) than Phase I (61.47 ± 5.9 N/m), and no other pairs showed significant differences. In contrast, kH increased significantly with Frequency: Frequency 1 = 50.67 ± 3.9 N/m < Frequency 2 = 59.22 ± 4.9 N/m < Frequency 3 = 68.85 ± 5.4 N/m < Frequency 4 = 83.77 ± 5.6 N/m < Frequency 5 = 101.61 ± 7.6 N/m. All pairs showed significant differences. Furthermore, the rate of increase in kH with Frequency was highest in Phases II and IV, and smallest in Phase I. This was reflected in a significant interaction effect (F(12,120) = 8.800; p < 0.01).
3.3 Grip force modulation
The referent aperture rG and the apparent grip stiffness kG computations yielded noisy results. Therefore, the trajectories for the two slowest (Frequencies 1 and 2) and the two fastest (Frequencies 4 and 5) oscillation frequencies were combined, and the mean ± SE of three frequencies {fn − Δ, fn, fn + Δ} are depicted in Figures 8C and 8D. The symbol Δ indicates if the frequency of oscillation was more or less than the natural frequency. With these simplifications, reasonably smooth trajectories for the referent coordinates over the entire oscillation cycle were obtained for ten out of the eleven subjects. Therefore, the following statistical results utilize three levels for the Frequency factor and subject number = 10.
The grip force varied with Phase as well as Frequency (see Figure 6C, for example). The phase-dependent modulation was achieved by modulating both the referent aperture rG and the apparent stiffness kG. The frequency-dependent increase in grip force was primarily achieved by decreasing the referent aperture while the average apparent stiffness was maintained across the Frequencies (Figures 8C and 8D).
The referent aperture rG varied with Phase (F(1.232,11.086) = 9.762; p < 0.01; Figure 9C), and with Frequency (F(1.272,11.448) = 15.32; p < 0.01). There were no interaction effects. Pair-wise contrasts revealed significant differences between the Phase pairs I–IV, II–III, II–IV, and III–IV. The mean ± SE of rG were: fn − Δ = 0.05 ± 0.004 m, fn = 0.041 ± 0.006 m, and fn + Δ = 0.027 ± 0.007 m. Pair-wise contrasts revealed significant differences for all pairs.
The grip apparent stiffness kG varied with Phase (F(3,27) = 16.379; p < 0.01; Figure 9D), but not with Frequency (F(2,18) = 0.542; p = 0.591). There were no interaction effects. The mean ± SE of kG are: Phase I = 169.52 ± 28.8 N/m, Phase II = 202.79 ± 28.34 N/m, Phase III = 225.05 ± 32.5 N/m, Phase IV = 226.1 ± 31.4 N/m. Pair-wise contrasts revealed significant differences between the Phase pairs I–III, I–IV, II–III, and II–IV.
3.4 Relations between referent variables for vertical oscillation and grip force
The regression analyses revealed that combinations of {r; k} are strongly coupled between the two actions (hand oscillation and grip force production). While regressions between the referent positions alone and the apparent stiffness values alone yielded poor results, a strong linear constraint between all the four variables was observed.
Recall that only 49 out of the possible 55 data sets were used for the regression analyses, since the remaining ones had significant portions of missing data (See Section 2.5.5). The linear regressions between the grip and hand reference variables (See Equations 6i and 6ii) yielded poor results. For the rG vs rH analysis, the linear fits were not significant (p > 0.05) for 8 out of the 49 cases analyzed, and the across-subject and –frequency median and inter-quartile range of the R2 values were 0.17 and 0.25, respectively. Similarly for the kG vs kH analysis, the linear fits for 8 cases were not significant (p > 0.05), and the across-subject and –frequency median and inter-quartile range of the R2 values were 0.20 and 0.50, respectively.
In contrast, the linear regression representing a single constraint on all the referent variables (Equation 6iii) yielded significant regressions for all cases (p < 0.05) and displayed high R2 for all frequencies (Figure 10B). The median R2 values were 0.78, 0.78, 0.85, 0.83, and 0.79 for frequencies one through five, respectively, and the corresponding inter-quartile ranges were 0.18, 0.16, 0.08, 0.08, and 0.19. The mean and standard errors of the fit coefficients in Equation 6iii were: a = −2457.3 ± 399.2 m−1, b = 435.3 ± 114.8 m−1, c = 0.65 ± 0.1 and d = −33.3 ± 25 N/m.
3.5 Validation of the models for force generation
The Equations (7 i) and (7 ii) were used to predict the hand and grip forces. The input to these equations were the actual aperture Ap, the computed trajectories of kH, kG, rH and rG, and the mean of the measured handle height h(t) during the unperturbed epoch A–B (Figure 3). The root mean squared (RMS) error between the predicted forces and the mean force trajectories during the corresponding unperturbed epochs (A–B for hand vertical force, and A–B, C–D, E–F, and G–H for the grip force) was computed and normalized by the maximum amplitude of the mean measured forces for each subject and oscillation frequency.
The predicted hand forces matched well with the measured ones, while the agreement between the predicted and measured grip forces was modest. For the hand force, the mean ± SE of the normalized RMS errors were 4.42 ± 0.9%, 3.01 ± 0.4%, 2.64 ± 0.2%, 2.04 ± 0.2%, and 2.59 ± 0.4%, for Frequencies 1 through 5, respectively. Similarly, for the grip force, the values were 29.75 ± 5.6%, 21.6± 3.6%, 21.12 ± 3.8%, 19.78 ± 3.5%, and 16.21 ± 3.0%, for Frequencies 1 through 5, respectively. The performance of the model for the grip force shows a tendency to improve as the Frequency increases; however, the improvement was not statistically significant (one-way ANOVA yields F(4,50) = 1.401; p = 0.247).
The predicted grip and hand force trajectories were also regressed for each subject and frequency. Not surprisingly, the FGRIP − FHAND coupling that is evident in the measured forces was strongly reflected in the predicted forces, and similarly to the measured forces, the relation was quadratic. Figure 9A shows boxplots of the R2 values for the quadratic fits between the two force trajectories for both measured and predicted hand and grip forces. All the quadratic fits were significant (p < 0.01), and the R2 values for all frequencies (except the lowest) were comparable to those for the measured forces.
4. Discussion
The main result of this study is the demonstration that the time profiles of “hidden variables” within the referent configuration hypothesis (RC-hypothesis, reviewed in Feldman, 2009) can be reconstructed during a relatively natural action involving multiple effectors. Moreover, we reconstructed these variables, referent coordinates and apparent stiffness, for two components of the action, explicit (the instructed handle motion) and implicit (grip force modulation). The patterns of the referent coordinates and apparent stiffness showed consistent behavior across subjects as well as across changes in the action frequency compatible with earlier reports on the changes in grip-force during motion of hand-held objects (Forssberg et al., 1991; Flanagan and Wing, 1993; Flanagan et al., 1993; Gao et al., 2005; Zatsiorsky et al., 2005; Ambike et al., 2013). In particular grip force changed at twice the frequency of the handle motion, as seen from the quadratic relation between the measured force trajectories. An important step is the validation of the reconstructed patterns by using them as inputs into our model and performing forward simulation to predict mechanical variables during action cycles that were not used in the reconstruction process. Similar to the measured forces, these predicted force trajectories displayed a quadratic grip-force-load-force coupling. Furthermore, a strong linear relation between the four referent variables was discovered. Overall, we view these data as providing experimental support for the idea of controlling natural, multi-muscle actions with shifts in a low-dimensional set of referent coordinates (reviewed in Latash, 2010).
4.1 Two central commands and their peripheral consequences
The equilibrium-point hypothesis was originally introduced for the control of a single muscle (Feldman, 1966) and later generalized for the control of a joint spanned by two muscles, an agonist and an antagonist (Feldman, 1980). For a single muscle, threshold of the tonic stretch reflex (λ) was assumed to play the role of a referent coordinate. Hierarchically higher structures within the central nervous system were assumed to produce movements by shifting λ, while the actual muscle force, length, and activation level emerged depending on the external loading conditions. For example, in isotonic conditions, a shift in λ is expected to lead to a movement to a new value of muscle length, while in isometric conditions, the same λ shift leads to a change in the muscle force. For the control of a joint, two pairs of variables were considered, the two λs for the agonist-antagonist muscles {λag; λant}, and the reciprocal and co-activation command {r; c}. The r-command defines the location of a central point in an angular range within which both muscles show non-zero activation, and a shift in the r-command leads to a unidirectional shift of the two λs along the joint angle coordinate. The c-command defines the size of the angular range of co-activation of the two muscles. While both commands are spatial in nature, with respect to mechanical variables, r-command shifts the torque-angle joint characteristic along the angle axis while c-command rotates this characteristic. In other words, r-command defines a referent coordinate for the joint angle while c-command defines the joint’s apparent stiffness. The two variable pairs are equivalent for a joint spanned by only two muscles, while for more realistic joints spanned by a larger number of muscles, the transformation from the {r; c} pair to a set of λs is redundant.
This description can be generalized for any multi-muscle effector. Indeed, consider the endpoint of the human arm in a steady state against an external load. A change in the load leads to arm motion accompanied by changes in muscle activation levels via involuntary mechanisms representing superposition of all the tonic stretch reflex mechanisms of the involved muscles; these have been referred to as generalized displacement reflex (GDR, Latash, 1998). Voluntary movement to a new location may be described as a shift of the referent coordinate for the endpoint. In addition, one can also co-contract muscles without moving the endpoint; such an action may be viewed as a reflection of a change in a higher-level co-activation command. For brevity and consistency, we will refer to these two (potentially multi-dimensional) commands as R and C and address them collectively as the referent configuration at the hierarchically highest task level. Note that while voluntary movements are brought about by modulating the R and C commands, the actual movement patterns also depend on the external load and its possible changes. We used this dependence on external conditions to compute mechanical consequences of R and C changes, namely changes in the referent coordinate and apparent stiffness. (In the present experiment, one may view R := {rH; rG} and C := {kH; kG}).
There has been considerable confusion in using terms such as control trajectory, equilibrium trajectory, virtual trajectory, and actual trajectory in research within the EP- and RC-hypotheses (e.g., Latash and Gottlieb, 1991; Gomi and Kawato, 1996; Gottlieb, 1998; Feldman et al., 1998; Feldman and Latash, 2005). Figure 1 in the Introduction is used here to clarify these terms. Time profiles of λ for a single muscle (a similar description can be used for the {r; c} pair for a joint, and for the {R; C} pair for a multi-muscle effector) are under control (partial, see Feldman and Latash, 2005) of hierarchically higher structures within the CNS. Hence, these time profiles may be reasonably addressed as control trajectories (λ(t) in panel B of Figure 1). At any given time, a value of λ may correspond to different combinations of muscle force and length depending on external load; these combinations are represented in panel A of Figure 1 as bold curves. Such a combination is referred to as equilibrium point (EP) of the system, and its time profile may be addressed as equilibrium trajectory (compare EP1 and EP2 in panel A of Figure 1). While λ(t) is measured in length units, equilibrium trajectory has two components reflecting changes in muscle length and force corresponding to the shifting EP, LEP(t) and FEP(t). Note that a quick shift of λ leads to an equally quick shift of the EP (panel B of Figure 1). In contrast, the actual trajectory, measured in both spatial and force units, depends on a variety of factors, for example the inertial load, and its time profile may be quite different from that of the control and equilibrium trajectories (panel B of Figure 1).
The term virtual trajectory is the least clearly defined one. It has been used as a synonym of equilibrium trajectory reduced to a single spatial dimension, as a trajectory that the system would follow if the external load were zero (then it becomes equivalent to R), and as the trajectory that would be seen if the external load did not change as compared to some initial value (Latash, 1992; Won and Hogan, 1995; Bellomo and Inbar, 1997). Given the lack of clarity and consistency, it is better to avoid this term.
In general, the two components of referent configuration within a multi-muscle system, R and C, can change independently of each other. During natural movements, however, the two are coupled. For example, during single-joint cyclical movements, the R trajectory moves at the frequency of the action, while the C trajectory tends to show peaks within each half-cycle, i.e., it changes at twice the action frequency (Latash, 1992). We observed similar patterns (see panels D and E in Figure 5) of the hand referent coordinate rH (analogous to R) and apparent stiffness kH (which is expected to reflect primarily changes in C).
4.2 Force coupling during object manipulation
When people manipulate hand-held objects, they apply both resultant and internal forces (Mason and Salisbury, 1985; Kerr and Roth, 1986; Murray et al., 1994). Arguably, the most commonly studied internal force is the grip force, FGRIP, defined as the component of all the digit forces normal to the surface of the object that produces zero resultant. It is commonly assumed that the main function of grip force is to provide sufficient friction between the surfaces of the object and the digits to allow application of manipulation forces (FHAND) according to the task requirements. For example, when a person uses a prismatic grasp (similar to the one used in our experiment) to lift a vertically oriented object, grip force is modulated in a feed-forward fashion to ensure sufficient safety margin, i.e., a sufficient excess of the grip force above the minimum required for the application of vertical shear forces given a value of the friction coefficient (Johansson and Westling, 1988).
The most common explanation of the FGRIP−FHAND coupling has followed directly the observed phenomena and has been expressed in terms of forces (e.g., Forssberg et al., 1991; Flanagan and Wing, 1993; Jaric et al., 2006). This explanation assumes that the CNS predicts requisite forces for the planned action and then sends neural signals adequate to produce such forces (cf. Hinder and Miler, 2003). Since muscle forces show length and velocity dependence mediated by both peripheral properties of the tissues and length- and velocity-sensitive reflexes, sending a neural signal that would lead to requisite forces requires taking into account (predicting) the actual kinematics of muscle fibers. Note that, even in isometric conditions, the muscle fiber length changes. Such predictions have been assumed to happen in hypothetical neural structures addressed as internal models (reviewed in Wolpert et al., 1998; Kawato, 1999). Two types of models, direct and inverse, have been assumed to account for the complex mechanical and neural interactions within the body and the time delays typical of transmitting salient information along neural pathways.
There seem to be at least three major problems with this approach. First, as emphasized by Bernstein (1935), muscle forces and activations depend on time-varying external conditions and cannot be perfectly predicted. This fact places a major burden on the CNS that has to track the actual kinematics and introduce corrections at all times. Second, this approach views the very important adaptive properties of the neuromotor system, such as reflexes and length/velocity dependence of muscle force, as a nuisance, and a source of computational problems. Third, assuming computations within the CNS is equivalent to giving up any chances of discovering laws of nature that lead to the observable force patterns; it is equivalent to assuming computations performed by celestial objects to ensure their regular motion.
An alternative is offered by the EP (RC) hypothesis. According to this approach, digit forces emerge as consequences of the difference between the actual and referent coordinates. For example, grip force emerges as a peripheral consequence of the difference between the actual aperture between the opposing digits and the referent aperture defined by the CNS signals, which has to be smaller than the actual one to lead to non-zero grip force production (Pilon et al., 2007; Latash et al., 2010). In a simple linear approximation, FGRIP = kG × ΔRG, where ΔRG is the difference in the reference and actual aperture, and kG is apparent stiffness of the system. Typically, the actual grip aperture, defined by the rigid hand-held object, is constant, and the referent aperture and apparent stiffness are the only variables that define grip force. Note that in our experiment, we changed the actual grip aperture slowly in order to compute the time changes in referent aperture and apparent stiffness (see Methods). In our experiment, as well as in an earlier study (Ambike et al., 2014), slow, low-amplitude changes in the grip aperture led to consistent grip force changes, even under the instruction to the subject not to interfere with possible changes in external conditions. This observation by itself is sufficient to claim that the neural process was not defining grip force but some other variables that led to the observed dependence of grip force on grip aperture. We consider the pair {rG; kG} as such centrally defined variables.
Along similar lines, the actual trajectory of the handle (expressed in both spatial and force units) is a function of the difference between its actual and referent coordinates (ΔRH) and apparent stiffness: FHAND = kH×ΔRH. Within this framework, the coupling between the grip force and resultant vertical force has to be analyzed as coupling between the {k; r} pairs. In general, there are many ways to ensure coupling between FHAND and FGRIP at the level of two {k; r} pairs. We explored pair-wise relations between the r variables and between the k variables and obtained only weak-to-modest amounts of variance explained by these regressions. When all four variables were used in a single regression, however, strong correlations were observed (Figure 10B). Thus, we conclude that a single constraint was imposed in the four-dimensional space {rG; kG; rH; kH}.
This single constraint may be viewed as an example of control of a multi-dimensional system using the uncontrolled manifold principle (see UCM-hypothesis, Scholz and Schöner, 1999; reviewed in Latash et al., 2007). One may view the coupling between the two forces, FHAND and FGRIP, as a task-specific performance requirement. It defines a three-dimensional constraint manifold (a hyper-plane) embedded in the four-dimensional space of elemental variables {rH, kH, rG, kG} along which the variables vary during task performance. This translates into high variability (and, therefore, low stability) within the manifold as compared to low variability (and, therefore, high stability) in directions orthogonal to the manifold. This method of control does not require any pair-wise or three-way correlations. Note that we did explore pair-wise and three-way linear and quadratic regressions and none of them could account for consistently high amounts of variance that would be comparable to the results of the linear regression involving all four variables (as in Figure 10B).
4.3 Methodological aspects
We are the first to admit that the method we have used to reconstruct referent trajectories and apparent stiffness patterns is open to criticism. Unfortunately, we are unaware of a better alternative. First, the method is based on a linear, second-order model of the objects of study (handle motion and grip-force development). While such models have been used in many earlier studies (e.g., Lacquaniti et al., 1982; Flash, 1987; Bennett et al., 1992; Latash and Gottlieb, 1991, 1992; Won and Hogan, 1995; Gomi and Kawato, 1996), they ignore the well-documented, non-linear properties of muscles (reviewed in Zatsiorsky and Prilutsky, 2012). Furthermore, most studies had used computational procedures different from the one used in our study. For example, Lacquaniti et al. (1982), Bennett et al (1992) and Gomi and Kawato (1996) used brief perturbations and traditional system-identification techniques, whereas Flash (1987) analyzed steady states on the hand only. One can make a point, however, that, despite the non-linearity of motor and neural elements, intact muscles with reflexes behave in a more linear way as compared, for example, to deafferented muscles (Nichols and Houk, 1976). Furthermore, any non-linear dynamical system can be successfully approximated with a linear system whose coefficients are time-varying (Tomas-Rodriguez and Banks, 2010). This mathematical approximation can also be done independently on the control of the system. Thus, from a strictly mathematical point of view, we have not demonstrated that the time-varying parameters estimated here are relevant parameters reflecting the control of the system. It should be made clear, however, that we arrive at the nature of the control from neurophysiological considerations based on the RC framework, and not mathematical ones. Once the nature of control is presumed, we chose parsimonious linear models to explain our data.
Another simplification in the present model is the ignored damping component. This can be justified for the grip-force production component of the action because digit motion in the direction of grip force production was very slow. Ignoring damping for the vertical handle motion is less obvious. Available estimates of joint damping suggest that intact human joints are underdamped (Cannon and Zahalak, 1982; MacKay et al., 1986; Bennett, 1993; Lacquaniti et al., 1992; see, however, conditions for critical damping in Piovesan et al., 2013). On the other hand, all these estimates can be criticized as not accounting for reflex-mediated damping due to the velocity-sensitive signals from muscle spindles. Unfortunately, no reliable estimates of reflex-mediated damping are available. Note that assuming low damping results in more complex patterns of joint referent trajectories (so-called, N-shaped trajectories, Latash and Gottlieb, 1991, 1992), while assuming high damping leads to simpler, monotonic control trajectories (Feldman and Levin, 1995; Gribble et al., 1998).
We tried to explore different magnitudes of damping in our model, including fractional power damping (Gielen and Houk, 1984; Barto et al., 1999). However, adding any damping coefficient led to much less consistent results and frequently the regression model failed to account for the data. In contrast, setting damping to zero led to most consistent results and reasonably good fits by the reduced regression model. These findings confirm earlier studies with the reconstruction of equilibrium trajectories for one-joint and two-joint actions (Latash, 1992; Latash et al., 1999). In those studies, assuming non-zero damping was always detrimental with respect to the ability of the model to fit the data. We feel that the issue of damping remains unresolved, and hence, our current results have to be viewed with a grain of salt. On the other hand, our simulations presented in the Appendix show that the method of reconstructing referent trajectories based on a linear model is rather insensitive to variations of the damping coefficient within a wide range.
Another simplification of our model is ignoring the fact that several parallel loops with different time delays contribute to the muscle force-length (and handle force-coordinate) relations. Muscles develop force with stretch at close to zero time delay due to the peripheral tissue properties that scale with muscle activation level (reviewed in Zatsiorsky and Prilutsky, 2012; cf. the notion of preflexes, Loeb, 1999). In addition, reflex loops with variable time delays contribute to muscle force development to stretch, from the quickest monosynaptic reflexes to long-loop, polysynaptic responses.
Despite all the mentioned simplifications, our experiment led to consistent patterns of referent trajectories and apparent stiffness patterns across subjects and frequencies of motion. Moreover, using the reconstructed patterns as inputs into the model led to a reasonably accurate fit to the vertical hand-force data, while the fit to the grip-force data was somewhat less accurate. This could be due to the larger force modulation and larger effects of the slow imposed changes in external conditions for the handle motion as compared to the small and slow changes of the hand aperture. Overall, we are cautiously optimistic with respect to our method of reconstruction of referent trajectories and apparent stiffness time profiles during natural movements. The method has to be better validated across a broader range of tasks, and some of the mentioned simplifications have to be either lifted in future studies or better grounded in data that are currently unavailable.
4.4 The passive motion paradigm
A particular way of dealing with the problem of kinematic redundancy was suggested as the Passive Motion Paradigm (PMP, Mussa-Ivaldi et al., 1988). According to this idea, the CNS may solve the kinematic redundancy problem by choosing changes in joint configuration for voluntary movements that are equivalent to the changes in joint configuration that would occur naturally due to the mechanical properties of the multi-joint limb when an external force displaces the hand to the same location. There are intuitive similarities between the PMP and the approach advocated in our study, such as assuming that the movement is driven by a new desired position and that no unique solution to the problem of kinematic redundancy is computed. But there is also an important difference between the PMP hypothesis and the RC hypothesis. In the latter, the CNS uses spatial variables (RC displacements) and avoids computing forces necessary to produce a desired movement. Besides, implementation of PMP was assumed to depend on the tunable impedance of the motor elements due to changes in muscle activation levels. This mechanism refers to the α-model, in which the tonic stretch reflex does not play a role in defining the force-length muscle properties (Bizzi et al., 1982), while in the RC hypothesis afferent feedback is essential for active force generation (Feldman, 2009).
5. Conclusions
We have demonstrated the partial success of the method for extracting referent variables for the control of vertical oscillation of a hand-held object. The referent height and apparent stiffness were reliably reconstructed for five distinct handle oscillation frequencies. We were less successful in reconstructing the referent aperture and the apparent grasp stiffness – referent variables responsible for generating grip force – possibly due to the noise in our measurements and the relatively small changes in the external conditions induced by the small aperture variations.
We found a robust quadratic relation between grip force and the vertical load force on the handle. Note that, since the two forces in our model result from time varying changes in four control variables, the quadratic relations between the forces allows a range of relations within the four-dimensional space of the control variables. Remarkably, we found a linear constraint on the four referent variables reflecting the observed grip-force-load-force coupling.
We are cautiously optimistic of this theoretico-computational procedure to study human motor behavior. Much can be improved in the measurements and the computational aspects. We hope to have demonstrated that the approach can lead to novel insights on the neural control of natural movements.
Highlights.
Computed hypothetical neural control signals for cyclic motion of hand-held object
Computed control variables reproduced experimental data in a forward simulation
One linear constraint between four control variables yields grip-load force coupling
Data support control with referent configurations of natural multi-joint actions
Acknowledgments
This work was sponsored in part by NIH Grants NS-035032 and AR-048563.
Appendix
As further validation of the computational method used in this paper, we reconstruct the known control inputs to a mechanical mass-spring-damper system (Figure 1D). A forward simulation was used to generate the displacement h(t) of the center of gravity of the hand-held object given the control inputs rH(t) and kH(t). Gravity was ignored, and the mass was subjected to a time-varying external force Fr(t). The equation of motion for the mass is:
| (A1) |
The chosen system parameters were: m = 4 kg, and time functions rH(t) and kH(t) were obtained by concatenating the solutions for the fn +0.2 Hz frequency illustrated in Figures 8A and 8B. The oscillation frequency for these input signals was set at 1 Hz. The concatenated signal rH(t) is shown in Figure 11A. The external forcing function Fr(t) is shown in Figure 11C, and it was identical to the robot force as shown in Figure 3. We chose the function c(t) = 1 Nm/s (constant) arbitrarily, since we do not have a reliable estimate of this function. Sensitivity of the computational procedure to the constant c value was also explored. The initial conditions were: h(0) = rH(0), and ḣ(0) = 0. Thus the system starts from rest and with zero external force. The equation of motion was integrated forward in time for 60 s. A portion of the system response is depicted in Figure 11A. Figure 11B depicts the spring-damper force exerted on the handle.
Figure 11.
Simulation inputs and results. Panel A shows the input referent height for the oscillating mass (dotted trace). The solid trace is the response of the mass-spring-damper system. Panel B shows the spring-damper-induced force on the mass. Panel C depicts the robot force. Panel D shows the actual mass height averaged across cycles (dashed trace). The computed and input referent heights are also depicted. Panel E shows the input and the computed spring stiffness. Panel F shows the R2 values obtained from the regressions performed on discrete Poincare sections. The locations of the circles in panels D, E and F indicate the phases at which regressions were performed during the reconstruction process.
The spring-damper force at a time instant t = t* is:
| (A2) |
An across-cycle analysis, as described in the Methods section, was conducted on the simulated data. At each phase of the oscillation, the spring-damper force and the corresponding actual handle height compiled across cycles were regressed using the equation
| (A3) |
Remaining faithful to the computation in the paper, we ignored the damping component in the spring-damper force while trying to estimate the input parameters. Therefore, our regressions would be less than perfect even for this ideal system. Comparing coefficients in Equations (A2) and (A3) we obtained kH(t*) = −a1, and rH(t*) = −a2/a1.
Figure 11D shows the input referent height and the referent height computed as explained above. This panel of Figure 11 also shows the mean handle height for one oscillation. Figure 11E shows the input and the computed stiffness values, and Figure 11F shows the R2 values for the individual regressions.
Finally, we performed these computations for a set of constant damping coefficient values varying within two orders of magnitude: c = [0.1, 0.33, 3, 10] Ns/m. These changes resulted in small variations in the computed referent variables without much change in the general shape of the functions. The regressions were always reasonable. The median R2 values for the five c values were [0.99, 0.99, 0.97, 0.98], and the smallest R2 value we encountered was 0.84 for c = 10 Ns/m.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Ambike S, Paclet F, Latash ML, Zatsiorsky VM. Grip-force modulation in multi-finger prehension during wrist flexion and extension. Exp Brain Res. 2013;227:509–522. doi: 10.1007/s00221-013-3527-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ambike S, Paclet F, Zatsiorsky VM, Latash ML. Factors affecting grip force: anatomy, mechanics, and referent configurations. Exp Brain Res. 2014;232:1219–1231. doi: 10.1007/s00221-014-3838-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barto AG, Fagg AH, Sitkoff N, Houk JC. A cerebellar model of timing and prediction in the control of reaching. Neural Comput. 1999;11:565–594. doi: 10.1162/089976699300016575. [DOI] [PubMed] [Google Scholar]
- Bellomo A, Inbar G. Examination of the gamma equilibrium point hypothesis when applied to single degree of freedom movements performed with different inertial loads. Biol Cybern. 1997;76:63–72. doi: 10.1007/s004220050321. [DOI] [PubMed] [Google Scholar]
- Bennett DJ. Torques generated at the human elbow joint in response to constant position errors imposed during voluntary movements. Exp Brain Res. 1993;95:488–498. doi: 10.1007/BF00227142. [DOI] [PubMed] [Google Scholar]
- Bennett DJ, Hollerbach JM, Xu Y, Hunter IW. Time-varying stiffness of human elbow joint during cyclic voluntary movement. Exp Brain Res. 1992;88:433–442. doi: 10.1007/BF02259118. [DOI] [PubMed] [Google Scholar]
- Bernstein NA. The problem of interrelation between coordination and localization. Archives of Biological Science. 1935;38:1–35. (in Russian) [Google Scholar]
- Bizzi E, Accornero N, Chapple W, Hogan N. Arm trajectory formation in monkeys. Exp Brain Res. 1982;46:139–143. doi: 10.1007/BF00238107. [DOI] [PubMed] [Google Scholar]
- Cannon SC, Zahalak GI. The mechanical behavior of active human skeletal muscle in small oscillations. J Biomech. 1982;15:111–121. doi: 10.1016/0021-9290(82)90043-4. [DOI] [PubMed] [Google Scholar]
- Feldman AG. Functional tuning of the nervous system with control of movement or maintenance of a steady posture. II. Controllable parameters of the muscle. Biophysics. 1966;11:565–578. [Google Scholar]
- Feldman AG. Superposition of motor programs. I. Rhythmic forearm movements in man. Neurosci. 1980;5:81–90. doi: 10.1016/0306-4522(80)90073-1. [DOI] [PubMed] [Google Scholar]
- Feldman AG. Once more on the equilibrium-point hypothesis (λ-model) for motor control. J Mot Behav. 1986;18:17–54. doi: 10.1080/00222895.1986.10735369. [DOI] [PubMed] [Google Scholar]
- Feldman AG. Origin and advances of the equilibrium-point hypothesis. Adv Exp Med Biol. 2009;629:637–643. doi: 10.1007/978-0-387-77064-2_34. [DOI] [PubMed] [Google Scholar]
- Feldman AG, Latash ML. Testing hypotheses and the advancement of science: Recent attempts to falsify the equilibrium-point hypothesis. Exp Brain Res. 2005;161:91–103. doi: 10.1007/s00221-004-2049-0. [DOI] [PubMed] [Google Scholar]
- Feldman AG, Levin MF. Positional frames of reference in motor control: their origin and use. Behav Brain Sci. 1995;18:723–806. [Google Scholar]
- Feldman AG, Ostry DJ, Levin MF, Gribble PL, Mitnitski AB. Recent tests of the equilibrium-point hypothesis (λ model) Motor Control. 1998;2:189–205. doi: 10.1123/mcj.2.3.189. [DOI] [PubMed] [Google Scholar]
- Flanagan RJ, Tresilian JR. Grip-load force coupling: a general control strategy for transporting objects. J Exp Psych: Human Perception and Performance. 1994;20:944–957. doi: 10.1037//0096-1523.20.5.944. [DOI] [PubMed] [Google Scholar]
- Flanagan RJ, Tresilian JR, Wing AM. Coupling of grip force and load force during arm movements with grasped objects. Neurosci Lett. 1993;152:53–56. doi: 10.1016/0304-3940(93)90481-y. [DOI] [PubMed] [Google Scholar]
- Flanagan RJ, Wing AM. Modulation of grip force with load force during point-to-point reaching movement. Exp Brain Res. 1993;95:131–143. doi: 10.1007/BF00229662. [DOI] [PubMed] [Google Scholar]
- Flanagan RJ, Wing AM. The stability of precision grip forces during cyclic arm movements with a hand-held load. Exp Brain Res. 1995;105:455–464. doi: 10.1007/BF00233045. [DOI] [PubMed] [Google Scholar]
- Flash T. The control of hand equilibrium trajectories in multi-joint arm movements. Biol Cybern. 1987;57:257–274. doi: 10.1007/BF00338819. [DOI] [PubMed] [Google Scholar]
- Forssberg H, Eliasson AC, Kinoshita H, Johansson RS, Westling G. Development of human precision grip. I. Basic coordination of force. Exp Brain Res. 1991;85:451–457. doi: 10.1007/BF00229422. [DOI] [PubMed] [Google Scholar]
- Gao F, Latash ML, Zatsiorsky VM. Internal forces during object manipulation. Exp Brain Res. 2005;165:69–83. doi: 10.1007/s00221-005-2282-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gielen CCAM, Houk JC. Nonlinear viscosity for human wrist. J Neurophysiol. 1984;52:553–569. doi: 10.1152/jn.1984.52.3.553. [DOI] [PubMed] [Google Scholar]
- Gomi H, Kawato M. Equilibrium-point hypothesis examined by measured arm stiffness during multijoint movement. Science. 1996;272:117–120. doi: 10.1126/science.272.5258.117. [DOI] [PubMed] [Google Scholar]
- Gottlieb GL. Rejecting the equilibrium-point hypothesis. Motor Control. 1998;2:10–12. doi: 10.1123/mcj.2.1.10. [DOI] [PubMed] [Google Scholar]
- Gribble PL, Ostry DJ, Sanguineti V, Laboissiere R. Are complex control signals required for human arm movements? J Neurophysiol. 1998;79:1409–1424. doi: 10.1152/jn.1998.79.3.1409. [DOI] [PubMed] [Google Scholar]
- Hinder MR, Milner TE. The case for an internal dynamics model versus equilibrium point control in human movement. J Physiol. 2003;549:953–963. doi: 10.1113/jphysiol.2002.033845. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jaric S, Collins JJ, Marwaha R, Russell E. Interlimb and within limb force coordination in static bimanual manipulation task. Exp Brain Res. 2006;168:88–97. doi: 10.1007/s00221-005-0070-6. [DOI] [PubMed] [Google Scholar]
- Johansson RS, Cole KJ. Sensory-motor coordination during grasping and manipulative actions. Curr Opinion Neurobiol. 1993;2:815–823. doi: 10.1016/0959-4388(92)90139-c. [DOI] [PubMed] [Google Scholar]
- Johansson RS, Westling G. Programmed and triggered actions to rapid load changes during precision grip. Exp Brain Res. 1988;71:72–86. doi: 10.1007/BF00247523. [DOI] [PubMed] [Google Scholar]
- Kawato M. Internal models for motor control and trajectory planning. Current Opinions in Neurobiology. 1999;9:718–727. doi: 10.1016/s0959-4388(99)00028-8. [DOI] [PubMed] [Google Scholar]
- Kerr JR, Roth B. Analysis of multifingered hands. J Robotic Res. 1986;4:3–17. [Google Scholar]
- Lacquaniti F, Licata F, Soechting JF. The mechanical behavior of the human forearm in response to transient perturbations. Biol Cybern. 1982;44:67–77. doi: 10.1007/BF00353954. [DOI] [PubMed] [Google Scholar]
- Lacquaniti F, Borghese NA, Carrozzo M. Internal models of limb geometry in the control of hand compliance. J Neurosci. 1992;12:1750–1762. doi: 10.1523/JNEUROSCI.12-05-01750.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latash ML. Virtual trajectories, joint stiffness, and changes in the limb natural frequency during single-joint oscillatory movements. Neurosci. 1992;49:209–220. doi: 10.1016/0306-4522(92)90089-k. [DOI] [PubMed] [Google Scholar]
- Latash ML. Control of multi-joint reaching movement: The elastic membrane metaphor. In: Latash ML, editor. Progress in Motor Control: vol. 1: Bernstein’s Traditions in Movement Studies. Human Kinetics; Urbana, IL: 1998. pp. 315–328. [Google Scholar]
- Latash ML. Motor synergies and the equilibrium-point hypothesis. Motor Control. 2010;14:294–322. doi: 10.1123/mcj.14.3.294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latash ML, Aruin AS, Zatsiorsky VM. The basis of a simple synergy: Reconstruction of joint equilibrium trajectories during unrestrained arm movements. Human Movement Science. 1999;18:3–30. [Google Scholar]
- Latash ML, Gottlieb GL. Reconstruction of shifting elbow joint compliant characteristics during fast and slow movements. Neurosci. 1991;43:697–712. doi: 10.1016/0306-4522(91)90328-l. [DOI] [PubMed] [Google Scholar]
- Latash ML, Gottlieb GL. Virtual trajectories of single-joint movements performed under two basic strategies. Neurosci. 1992;47:357–365. doi: 10.1016/0306-4522(92)90252-w. [DOI] [PubMed] [Google Scholar]
- Latash ML, Zatsiorsky VM. Joint stiffness: Myth or reality? Human Movement Science. 1993;12:653–692. [Google Scholar]
- Latash ML, Scholz JP, Schöner G. Toward a new theory of motor synergies. Motor Control. 2007;11:276–308. doi: 10.1123/mcj.11.3.276. [DOI] [PubMed] [Google Scholar]
- Latash ML, Friedman J, Kim SW, Feldman AG, Zatsiorsky VM. Prehension synergies and control with referent hand configurations. Exp Brain Res. 2010;202:213–229. doi: 10.1007/s00221-009-2128-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loeb GE. What might the brain know about muscles, limbs and spinal circuits? Prog Brain Res. 1999;123:405–409. doi: 10.1016/s0079-6123(08)62875-7. [DOI] [PubMed] [Google Scholar]
- MacKay WA, Crammond DJ, Kwan HC, Murphy JT. Measurements of human forearm viscoelasticity. J Biomech. 1986;19:231–238. doi: 10.1016/0021-9290(86)90155-7. [DOI] [PubMed] [Google Scholar]
- Mason MT, Salisbury JK. Robot Hands and the Mechanics of Manipulation. Cambridge, MS: The MIT Press; 1985. [Google Scholar]
- Mussa-Ivaldi FA, Morasso P, Zaccaria R. Kinematic networks. A distributed model for representing and regularizing motor redundancy. Biol Cybern. 1988;60:1–16. doi: 10.1007/BF00205967. [DOI] [PubMed] [Google Scholar]
- Murray RM, Li Z, Sastry SS. A mathematical introduction to robotic manipulation. CRC Press; Boca Raton: 1994. [Google Scholar]
- Nichols TR, Houk JC. Improvement in linearity and regulation of stiffness that results from actions of stretch reflex. J Neurophysiol. 1976;39:119–142. doi: 10.1152/jn.1976.39.1.119. [DOI] [PubMed] [Google Scholar]
- Pilon J-F, De Serres SJ, Feldman AG. Threshold position control of arm movement with anticipatory increase in grip force. Exp Brain Res. 2007;181:49–67. doi: 10.1007/s00221-007-0901-8. [DOI] [PubMed] [Google Scholar]
- Piovesan D, Pierobon A, Mussa-Ivaldi FA. Critical damping conditions for third order muscle models: Implications for force control. J Biomech Eng. 2013;135(10):101010. doi: 10.1115/1.4025110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Savescu AV, Latash ML, Zatsiorsky VM. A technique to determine friction at the fingertips. J Applied Biomech. 2008;24:43–50. doi: 10.1123/jab.24.1.43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scholz JP, Schöner G. The uncontrolled manifold concept: Identifying control variables for a functional task. Exp Brain Res. 1999;126:289–306. doi: 10.1007/s002210050738. [DOI] [PubMed] [Google Scholar]
- Slota GP, Latash ML, Zatsiorsky VM. Grip forces during object manipulation: experiment, mathematical model, and validation. Exp Brain Res. 2011;213:125–139. doi: 10.1007/s00221-011-2784-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith AS, Soechting JF. Modulation of grasping forces during object transport. J Neurophysiol. 2005;93:137–145. doi: 10.1152/jn.00775.2004. [DOI] [PubMed] [Google Scholar]
- Strogatz SH. Nonlinear Dynamics and Chaos. Perseus Books Publishing; 1994. [Google Scholar]
- Tomas-Rodriguez M, Banks SP. Linear, Time-Varying Approximations to Nonlinear Dynamical Systems. Springer; 2010. [Google Scholar]
- Wolpert DM, Miall RC, Kawato M. Internal models in the cerebellum. Trends in Cognitive Science. 1998;2:338–347. doi: 10.1016/s1364-6613(98)01221-2. [DOI] [PubMed] [Google Scholar]
- Won J, Hogan N. Stability properties of human reaching movements. Exp Brain Res. 1995;107:125–136. doi: 10.1007/BF00228024. [DOI] [PubMed] [Google Scholar]
- Zatsiorsky VM, Gao F, Latash ML. Prehension stability: experiments with expanding and contracting handle. J Neurophysiol. 2006;95:2531–2529. doi: 10.1152/jn.00839.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zatsiorsky VM, Gao F, Latash ML. Motor control goes beyond physics: differential effects of gravity and inertia on finger forces during manipulation of hand-held objects. Exp Brain Res. 2005;162:300–308. doi: 10.1007/s00221-004-2152-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zatsiorsky VM, Prilutsky BI. Biomechanics of skeletal muscles. Human Kinetics; Urbana, IL: 2012. [Google Scholar]