Longitudinal Association Analysis of Quantitative Traits

Abstract

Longitudinal genetic studies provide a valuable resource for exploring key genetic and environmental factors that affect complex traits over time. Genetic analysis of longitudinal data that incorporate temporal variations is important for understanding genetic architecture and biological variations of common complex diseases. Although they are important, there is a paucity of statistical methods to analyze longitudinal human genetic data. In this article, longitudinal methods are developed for temporal association mapping to analyze population longitudinal data. Both parametric and nonparametric models are proposed. The models can be applied to multiple diallelic genetic markers such as single-nucleotide polymorphisms and multiallelic markers such as microsatellites. By analytical formulae, we show that the models take both the linkage disequilibrium and temporal trends into account simultaneously. Variance-covariance structure is constructed to model the single measurement variation and multiple measurement correlations of an individual based on the theory of stochastic processes. Novel penalized spline models are used to estimate the time-dependent mean functions and regression coefficients. The methods were applied to analyze Framingham Heart Study data of Genetic Analysis Workshop (GAW) 13 and GAW 16. The temporal trends and genetic effects of the systolic blood pressure are successfully detected by the proposed approaches. Simulation studies were performed to find out that the nonparametric penalized linear model is the best choice in fitting real data. The research sheds light on the important area of longitudinal genetic analysis, and it provides a basis for future methodological investigations and practical applications.

INTRODUCTION

In the classical theory of statistical genetics, the research is limited to analyze data in which phenotypes and related covariate measurements are observed only one time. For longitudinal human studies, multiple measurements of some quantitative or qualitative traits are taken for each individual over time, in addition to the genotype information and covariates such as gender, age, and familial income. For example, multiple measurements such as blood pressure, age, and body mass index (BMI) were recorded for individuals in Framingham Heart Study (FHS) data, which were available via Genetic Analysis Workshop (GAW) 13 and GAW 16 [Cupples et al., 2003; MacCluer et al., 2009]. Hence, multiple measurements are available for a subject, which depend on the subject’s age or time. However, there is very little research on statistical methods to analyze longitudinal genetic data. To our knowledge, there is no method for temporal linkage disequilibrium (LD) mapping or association analysis of longitudinal traits of population data and there is no handy software for the data analysis. Some studies propose to collapse the measurements to be a single value and then to run an analysis based on the classical theory of statistical genetics [Mukherjee et al., 2012]. Obviously, this method ignores the temporal nature of longitudinal data and it is not able to catch the temporal trend of the traits.

Due to the lack of statistical models and methods in analyzing longitudinal genetic data, investigators usually take a simple approach of averaging multiple response measurements of the same individual to analyze the longitudinal genetic traits. For instance, the sample averages of the blood pressure, age, and BMI were used in genome scan linkage studies for FHS data by Levy et al. [2000, 2009]. Although this approach makes it possible to apply the existing statistical methods and software to handle longitudinal traits, it is, essentially, not a longitudinal analysis of repeated genetic traits. The phenotype traits are usually varying with time, and so there are temporal variations [Fan et al., 2012; Mountz et al., 2001; Soler and Blangero, 2003]. After collapsing the multiple measurements to be a single value, no temporal variations can be detected in an analysis. This type of analysis may not always be able to get ideal results and to draw the best information from the data [Shi and Rao, 2008].

For certain traits of complex diseases, such as BMI and blood pressure, genetic determinants are important at some period of time of human development. At other time periods, environmental factors are more important, such as diet and family income. It is important to develop statistical models and methods which may better use the longitudinal data, and may reflect temporal trends [Lasky-Su et al., 2008]. For the phenotype traits which have an important genetic component, the power to localize the genetic location and to detect important genetic determinants of the traits can be high at the specific stage that genetic contribution is high. On the other hand, the power to localize the genetic location and to detect important genetic determinants can be low at the other stage that environmental factors are more important than genetic contribution. A better understanding of the temporal variations of the traits and the temporal genetic contribution to phenotype traits may provide more insights in mapping the temporal genetic traits and in determining the important genetic determinants. In addition, longitudinal genetics analysis may help with the detection of gene-environment interactions.

In GAW 13 and GAW 16, a wide range of methods and models was developed to analyze the FHS data and the similarly structured simulated data [Almasy et al., 2003a,b]. The research mainly focused on linkage analysis using family data in GAW 13. Variance component approach was extended to incorporate temporal trends for linkage analysis of longitudinal traits to detect quantitative trait loci (QTL) in de Andrade et al. [2002] and de Andrade and Olswold [2003]. The methods suffer from a large number of parameters when the number of measurements increases since each measurement corresponds to a set of variance-covariance parameters. In addition, parametric variance component models were developed for linkage analysis of longitudinal genetic data, which may not reflect the temporal trends well in Zhang and Zhong [2006]. Overall, the existing longitudinal statistical models are problematic in one or more aspects.

In this article, temporal association analysis methods are developed for the population longitudinal data. Both parametric and nonparametric models are proposed. By utilizing multiple genetic markers which can be either diallelic or multiallelic, we develop temporal association mapping models based on the motivation of population genetics model. By analytical formulae, we show that the models take both the LD and temporal trends into account. To reduce the number of parameters, variance-covariance structure is constructed to model the single measurement variation and multiple measurement correlations of an individual based on the theory of stochastic processes. This is a key different part between our methods and those proposed by de Andrade et al. [2002] and de Andrade and Olswold [2003] since our models contain very small number of parameters to facilitate data analysis for robust results. Novel penalized spline models are used to estimate the time-dependent mean functions and regression coefficients nonparametrically which makes our methods different from the parametric models of Zhang and Zhong [2006]. To describe the usefulness of the proposed approaches, the methods were applied to analyze FHS data of GAW 13 and GAW 16 to detect the temporal trends of systolic blood pressure (SBP). Simulation was performed to evaluate robustness, power, and parameter estimation accuracy of the proposed nonparametric and parametric models.

MATERIALS AND METHODS

Before discussing methods and models, we present in Figure 1 a time plot of SBP and total plasma cholesterol level against age in years. The plot is based on a sample from the GAW 13 data, Cohort 2 of Problem 1 of the FHS. The cohort includes 330 pedigrees. The sample consists of 330 individuals, one from a pedigree. From the time plot, it can be seen that both SBP and total plasma cholesterol increase as age increases. Thus, one needs to take this temporal trend into account in modeling the longitudinal genetic traits. In addition, there are large trait variations. For SBP, the variation seems homogeneous, while the variation of total plasma cholesterol level increases as age gets old.

Fig. 1.

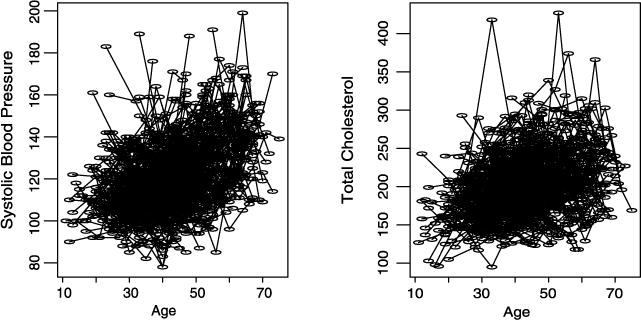
Time plot of systolic blood pressure and total plasma cholesterol level against age in years.

In the following, we are going to present a general temporal population quantitative genetics model. Then, we propose population temporal association models using typed genetic markers. The variance-covariance structure is constructed to describe the trait variation and to properly account for correlation between multiple measurements on the same subject. Penalized spline methods are used to approximate temporal mean function and regression coefficients.

A TEMPORAL POPULATION GENETICS MODEL

Consider a quantitative trait locus Q which has two alleles Q₁ and Q₂ with allele frequencies q₁ and q₂, respectively. To simplify the presentation, we first assume that QTL Q is the only major locus responsible for the trait value. In addition, neither covariates nor environmental nor polygenic effects are considered. For the trait value, let μ_ij(t) be the effect of genotype Q_i Q_j, i, j = 1, 2, μ₁₂(t) = μ₂₁(t), at the time t. Here the time t is usually age of an individual. Let the genic effect of allele Q_i be α_i(t), i = 1, 2. The genotypic effects at the time t can be expressed as

$$\begin{array}{l}{\mathrm{\mu }}_{11}(t)=\mathrm{\mu }(t)+2{\mathrm{\alpha }}_1(t)+d_1(t),\\ {\mathrm{\mu }}_{12}(t)=\mathrm{\mu }(t)+{\mathrm{\alpha }}_1(t)+{\mathrm{\alpha }}_2(t)+d_2(t),\\ {\mathrm{\mu }}_{22}(t)=\mathrm{\mu }(t)+2{\mathrm{\alpha }}_2(t)+d_3(t),\end{array}$$

where μ(t) is the overall population mean, and d_i(t) is the deviation of the related genotypic value from that of an additive effect model. Let us consider a fixed time t₀. Minimizing $F(\mathrm{\mu },{\mathrm{\alpha }}_1,{\mathrm{\alpha }}_2)={\displaystyle {\sum }_{i=1}^2{\displaystyle {\sum }_{j=1}^2{q}_i{q}_j{({\mathrm{\mu }}_{\mathit{ij}}(t_0)-\mathrm{\mu }(t_0)-{\mathrm{\alpha }}_i(t_0)-{\mathrm{\alpha }}_j(t_0))}^2}}$, classical theory of quantitative genetics provides the estimates of μ(t₀), α₁(t₀), α₂(t₀) as in other studies [Jacquard, 1974; Lange, 2002]

$$\begin{array}{l}\widehat{\mathrm{\mu }}(t_0)={\mathrm{\mu }}_{11}(t_0)q_1^2+2{\mathrm{\mu }}_{12}(t_0)q_1{q}_2+{\mathrm{\mu }}_{22}(t_0)q_2^2={\mathrm{\mu }}_0(t_0),\\ {\widehat{\mathrm{\alpha }}}_1(t_0)=q_1{\mathrm{\mu }}_{11}(t_0)+q_2{\mathrm{\mu }}_{12}(t_0)-\mathrm{\mu }(t_0),\\ {\widehat{\mathrm{\alpha }}}_2(t_0)=q_1{\mathrm{\mu }}_{21}(t_0)+q_2{\mathrm{\mu }}_{22}(t_0)-\mathrm{\mu }(t_0).\end{array}$$

Plugging these estimates into μ_ij(t₀), we can obtain the following expressions

$$\begin{array}{l}{\mathrm{\mu }}_{11}(t_0)={\mathrm{\mu }}_0(t_0)+2q_2{\mathrm{\alpha }}_Q(t_0)-q_2^2{\mathrm{\delta }}_Q(t_0),\\ {\mathrm{\mu }}_{12}(t_0)={\mathrm{\mu }}_0(t_0)+(q_2-q_1){\mathrm{\alpha }}_Q(t_0)+q_1{q}_2{\mathrm{\delta }}_Q(t_0),\\ {\mathrm{\mu }}_{22}(t_0)={\mathrm{\mu }}_0(t_0)-2q_1{\mathrm{\alpha }}_Q(t_0)-q_1^2{\mathrm{\delta }}_Q(t_0).\end{array}$$ (1)

Here, α_Q(t₀) = q₁μ₁₁(t₀) + (q₂ −q₁)μ₁₂(t₀) − q₂μ₂₂(t₀) is the average effect of gene substitution, and δ_Q(t₀)=2μ₁₂(t₀) − μ₁₁(t₀) − μ₂₂(t₀) is the dominance deviation. For an individual of a population, let the trait value be y(t) at the time t. Let G be the genotype of the individual at the QTL Q. Under an assumption of normality, the equation (1) imply that the trait can be expressed as

$$y(t_0)={\mathrm{\mu }}_0(t_0)+x_Q{\mathrm{\alpha }}_Q(t_0)+z_Q{\mathrm{\delta }}_Q(t_0)+\epsilon ,$$ (2)

where ε is a random error term, and x_Q and z_Q are dummy variables defined by

$$x_Q=\{\begin{array}{ll}2q_2\hfill & \text{if}G=Q_1{Q}_1\hfill \\ q_2-q_1\hfill & \text{if}G=Q_1{Q}_2\hfill \\ -2q_1\hfill & \text{if}G=Q_2{Q}_2\hfill \end{array},z_Q=\{\begin{array}{ll}-q_2^2\hfill & \text{if}G=Q_1{Q}_1\hfill \\ q_2{q}_1\hfill & \text{if}G=Q_1{Q}_2\hfill \\ -q_1^2\hfill & \text{if}G=Q_2{Q}_2.\hfill \end{array}$$ (3)

Assume that the trait locus Q is known, and the trait alleles Q₁ and Q₂ are correctly typed. Then the trait can be fully described by expression (2). In practice, information about trait locus Q is unknown, but the information of marker loci is available. This motivates us to develop appropriate models based on marker information to map QTL. In the following, we introduce population-based longitudinal LD mapping models.

LONGITUDINAL ASSOCIATION MAPPING MODELS USING DIALLELIC MARKERS

In our previous research, population-based regression association models of QTL are constructed in Fan and Xiong [2002] by using multiple diallelic markers in the analysis. The models are further extended to be variance component models for combined linkage and association mapping of QTL [Fan and Xiong, 2003; Jung et al., 2005]. The additive temporal models described as follows can be thought as longitudinal extension of the association mapping models in Fan and Xiong [2002]. In Supplementary Materials, we present models which model both additive and dominant effect.

Assume that I diallelic markers M_j, j = 1, 2,…, I are typed in a region of the trait locus Q. For marker M_j, the two alleles are denoted by M_j and m_j with frequencies $P_{M_j}$ and $P_{m_j}$, respectively (note here the notation M_j can be either marker or allele, whichever applies). Suppose that markers M_j are in Hardy-Weinberg equilibrium (HWE). However, they may be in LD. Denote the measure of LD between trait locus Q and marker M_j by $D_{M_{j}Q}=P(M_j{Q}_1)-q_1{P}_{M_j}$, and the measure of LD between marker M_j and marker M_k by $D_{M_j{M}_k}=P(M_j{M}_k)-P_{M_j}{P}_{M_k},j,k=1,2,\dots ,I$ [Hartl and Clark, 1989; Hedrick, 1987; Lewontin, 1988]. Here, P(M_j Q₁) and P(M_j M_k) are frequencies of haplotypes M_j Q₁ and M_j M_k, respectively.

Consider a population sample with N individuals. For the ith individual, let y_i be his/her quantitative trait value and let G_ij be his/her genotype at the marker M_j. An additive temporal LD regression mixed model extending (2) at the time t can be defined as

$$y_i(t)=\mathrm{\mu }(t)+w_i(t)\mathrm{\beta }(t)+{\displaystyle \sum _{j=1}^I{x}_{\mathit{ij}}{\mathrm{\alpha }}_j(t)}+U_i(t)+E_i+{\epsilon }_i.$$ (4)

The components of the above model are specified as follows. First, μ(t) is a nonrandom overall mean at time t and μ(t) is unspecified; w_i(t) is a row vector of covariates such as gender, BMI at the time t, and possibly their interaction terms; β(t) is a nonrandom column vector of regression parameters of the covariates w_i(t) with fixed effects. One may want to notice that the covariates can be time invariant like gender or can be time varying such as the BMI. In addition, x_ij are dummy variables defined by

$$x_{\mathit{ij}}=\{\begin{array}{ll}2\hfill & \text{if}{G}_{\mathit{ij}}=M_j{M}_j\hfill \\ 1\hfill & \text{if}{G}_{\mathit{ij}}=M_j{m}_j\hfill \\ 0\hfill & \text{if}{G}_{\mathit{ij}}=m_j{m}_j\hfill \end{array},$$

and α_j(t) are regression coefficients of the dummy variables x_ij at the time t. In model (4), U_i(t) is the correlation effect among repeated measurements due to both genetic and environmental factors of an individual, E_i is a random variation of subject i, and ε_i is a random measurement error term. Assume that U_i(t), E_i, and ε_i are independent. Moreover, assume that E_i is normal $N(0,{\mathrm{\sigma }}_E^2)$ and ε_i is normal $N(0,{\mathrm{\sigma }}_e^2)$

A similar character process model was developed by Pletcher and Geyer [1999] and Jafferzic and Pletcher [2000], which does not measure effects from specific genes and uses no marker information. The novel part of model (4) is that we include measured genotype components estimating association with genotyped markers, i.e., the terms involves x_ij [Fan and Jung, 2003; Fan et al., 2005; Fan and Xiong, 2002, 2003; Jung et al., 2005]. Let the variance-covariance matrices of the indicator variables x_ij be

$$V_A=2\left\{\begin{array}{llll}{P}_{M_1}{P}_{m_1}\hfill & D_{M_1{M}_2}\hfill & \dots \hfill & D_{M_1{M}_I}\hfill \\ D_{M_1{M}_2}\hfill & P_{M_2}{P}_{m_2}\hfill & \dots \hfill & D_{M_2{M}_I}\hfill \\ ⋮\hfill & ⋮\hfill & \dots \hfill & ⋮\hfill \\ D_{M_1{M}_I}\hfill & D_{M_2{M}_I}\hfill & \dots \hfill & P_{M_I}{P}_{m_I}\hfill \end{array}\right\}.$$

Such as equation (5) in Jung et al. [2005], the analytical formulas of parameter estimates of model (4) at the time t can be obtained as

$$\left\{\begin{array}{l}{\mathrm{\alpha }}_1(t)\\ ⋮\\ {\mathrm{\alpha }}_I(t)\end{array}\right\}=V_A^{-1}\left\{\begin{array}{l}2D_{M_{1}Q}\\ ⋮\\ 2D_{M_{I}Q}\end{array}\right\}{\mathrm{\alpha }}_Q(t).$$

Thus, it is clear that the parameters of LD (i.e., $D_{M_{j}Q}$ and $D_{M_j{M}_k}$) and gene effects at the time t (i.e., α_Q(t)) are contained in the mean coefficients. Model (4) simultaneously take care of the LD and the effects of the putative trait locus Q. Moreover, the interaction between the genetic effects and time or age is modeled.

In the model (4), the markers M_j, j = 1, 2,…, I, are assumed to be located in a region of a single trait locus Q. This assumption can be removed, i.e., the markers can be from different regions of one chromosome or even from different chromosomes. In one region, there can be one or more trait loci. Thus, the multiple trait loci jointly affect the phenotype. For most interest genetic traits, this is a realistic assumption. Similar arguments as above can be done to justify the models, but notations and formulations can be more complex and we do not provide the details in this article.

LONGITUDINAL ASSOCIATION MAPPING MODELS USING MULTIALLELIC MARKERS

In a region of the QTL Q, suppose that multiple multiallelic markers are typed, which may be microsatellite markers. For simplicity, we use two marker A and B in our analysis, but the models and methods can be easily generalized to use multiple markers. Suppose that the markers A and B are in HWE. Let us denote the alleles of marker A by A₁,…, A_a, where a is the number of alleles. Let the frequency of A_i be $P_{A_i}$, i=1, 2,…, a. There are J_A = a(a + 1)/2 possible genotypes, which can be listed as A₁ A₁, …, A_a A_a, A₁ A₂, …, A₁ A_a, …, A_a−1 A_a. The marker B has b alleles denoted by B₁,…, B_b. Let the frequency of allele B_k be $P_{B_k}$, k = 1, 2,…, b. There are J_B = b(b + 1)/2 possible genotypes, which can be listed as B₁B₁,…, B_b B_b, B₁B₂,…, B₁B_b,…, B_b−1B_b.

Again, consider a population sample with N individuals. For the ith individual, let y_i be his/her quantitative trait value with genotype G_Ai at marker A and genotype G_Bi at marker B. Following Fan et al. [2006], consider the following “additive effect model” under normality

$$\begin{array}{l}{y}_i(t)=\mathrm{\mu }(t)+w_i(t)\mathrm{\beta }(t)+{\displaystyle \sum _{j=1}^{a-1}{x}_{\mathit{Aij}}{\mathrm{\alpha }}_{\mathit{Aj}}(t)}\\ +{\displaystyle \sum _{j=1}^{b-1}{x}_{\mathit{Bij}}{\mathrm{\alpha }}_{Bj}(t)}+U_i(t)+E_i+e_i,\end{array}$$ (5)

where the dummy variables x_Aij and x_Bijl are defined by

$$\begin{array}{l}{x}_{\mathit{Aij}}=\{\begin{array}{ll}2\hfill & \text{if}{G}_{Ai}=A_j{A}_j\hfill \\ 1\hfill & \text{if}{G}_{Ai}=A_j{A}_l,l\ne j\hfill \\ 0\hfill & \text{else}\hfill \end{array},\\ x_{\mathit{Bij}}=\{\begin{array}{ll}2\hfill & \text{if}{G}_{Bi}=B_j{B}_j\hfill \\ 1\hfill & \text{if}{G}_{Bi}=B_j{B}_l,l\ne j\hfill \\ 0\hfill & \text{else}\hfill \end{array},\end{array}$$ (6)

and α_Aj(t), α_Bj(t) are regression coefficients of the dummy variables at the time t. The other terms of model (5) are similar as those of model (4).

In the Supporting Information, we extend additive effect model (5) to “genotype effect model” which takes both additive and dominance effects into account [Fan et al., 2006]. Moreover, we show that the parameters of LD and gene effects are contained in the regression coefficients. The models take care of both the LD and the effects of the trait locus Q. They are valid temporal models to fit association between genetic markers and the trait.

VARIANCE-COVARIANCE STRUCTURE

The variance-covariance structure of stochastic processes y_i(t) depends on the time or age, and can account for heterogeneity between subjects [Soler and Blangero, 2003]. Therefore, appropriate specification of the variance-covariance structure is a key step to successfully model the phenotype trait. For unrelated individuals in the sample, it is reasonable to assume that the quantitative traits are independent. For the same individual, however, the quantitative traits at different times/ages depend on each other. Hence, it is necessary to consider the variance-covariance structure carefully. Let ${\mathrm{\sigma }}_G^2(t)=\mathrm{Var}(U_i(t))$ be the variance of U_i(t) at the time t. For a pair of time points t and s, the covariance is given by

$${\mathrm{\sigma }}_G(t,s)=\mathrm{Cov}(U_i(t),U_i(s))={\mathrm{\sigma }}_G(t){\mathrm{\sigma }}_G(s){\mathrm{\rho }}_G\left(s,t\right),$$

where ρ_G(s, t) is correlation between U_i(t) and U_i(s). Let ${\mathrm{\sigma }}_{ga}^2(t)=2q_1{q}_2{[{\mathrm{\alpha }}_{\mathrm{Q}}(t)]}^2$ and ${\mathrm{\sigma }}_{gd}^2(t)={\left[q_1{q}_2{\mathrm{\delta }}_Q(t)\right]}^2$ be the major additive and dominant variances at the time t, respectively. The variance-covariance structure of stochastic process y_i(t) is characterized by

$$\begin{array}{l}\mathrm{Cov}(y_i(t),y_i(s))\\ =\{\begin{array}{ll}{\mathrm{\sigma }}_{ga}^2(t)+{\mathrm{\sigma }}_{gd}^2(t)+{\mathrm{\sigma }}_G^2(t)+{\mathrm{\sigma }}_E^2+{\mathrm{\sigma }}_e^2& \text{if}t=s\\ {\mathrm{\sigma }}_G(t,s)& \text{if}t\ne s\end{array}.\end{array}$$ (7)

In above formulation, the covariance Cov(y_i(t), y_i(s)) is assumed to be equal to the covariance of U_i(t) and U_i(s), t ≠ s. In practice, the correlation between y_i(t) and y_i(s) can be from the genetic and environmental factors or their combinations. For the population data, it is impossible to distinguish them. Hence, we simply put it as the correlation effect.

Suppose that the covariance function σ_G(t, s) (or correlation functions ρ_G(s, t)) is a function of t−s, i.e., they are functions of the time range. For instance, assume that the correlation effect is an Ornstein-Uhlenbeck Gaussian process $U_i(t)=\exp (-t/\mathrm{\rho })W_i(\frac{2}{\mathrm{\rho }}{e}^{2t/\mathrm{\rho }})$, ρ > 0, where W_i(t) is a standard Brownian motion. Then clearly, U_i(t) has zero mean at all times t. Moreover, the covariance function is ${\mathrm{\sigma }}_G(t,s)=\frac{2}{\mathrm{\rho }}\exp (-\left|t-s\right|/\mathrm{\rho })$ [Ross 1996, p. 400]. In this case, the correlation effect U_i(t) is a stationary Gaussian process. In our analysis, we are particularly interested in the Ornstein-Uhlenbeck Gaussian process U_i(t) for three reasons. First, it basically assume that the correlation of two measurements of an individual declines exponentially with the time range. This is a reasonable assumption in many situations. Second, we can fit the models conveniently in R using linear mixed model functions [Pinheiro and Bates, 2000]. Third, we fit models by assuming linear correlation in our data analysis, but they lead to higher Akaike information criterion (AIC) and Bayesian information criterion (BIC) values and so the models are not as good as the Ornstein-Uhlenbeck process modeling.

In certain cases, however, the covariance or correlation functions may not be functions of the time range. In this case, the correlation effect U_i(t) is a nonstationary process. For instance, assume that the correlation effect is a Wiener process U_i(t) = θ₁W_i(t), where W_i(t) is a standard Brownian motion. Then U_i(t) has zero mean at all times t. The covariance function is ${\mathrm{\sigma }}_G(t,s)={\mathrm{\theta }}_1^{2}min(t,s)$.

Another example of nonstationary Gaussian process is integrated Brownian motion, i.e., $U_i(t)={\mathrm{\theta }}_1{\displaystyle {\int }_0^{\tau }{W}_i(s)ds}$ where W_i(t) is a standard Brownian motion. Then U_i(t) has zero mean at all times t. The covariance function is ${\mathrm{\sigma }}_G(t,s)={\mathrm{\theta }}_1^2{s}^2(t/2-s/6)$, if s ≤ t [Ross 1996, pp. 369–370]. Other examples of Gaussian processes are $U_i(t)={\mathrm{\theta }}_1[W_i^2(t)-t]$ and $U_i(t)={\mathrm{\theta }}_1[\exp [{\mathrm{\theta }}_1{W}_i(t)-{\mathrm{\theta }}_1^{2}t/2]-1]$ [Ross 1996, pp. 381–382].

PENALIZED SPLINE ESTIMATIONS

To estimate the mean function μ(t) and genetic regression coefficients α_j(t), we may approximate them by linear combinations of penalized spline functions [Wang, 2011]. For instance, the q-order penalized spline model for μ(t) is

$$\mathrm{\mu }(t)={\mathrm{\mu }}_0+t{\mathrm{\mu }}_1+\dots +t^q{\mathrm{\mu }}_q+{\displaystyle \sum _{k=1}^K{u}_k{(t-{\mathrm{\kappa }}_k)}_{+}^q},$$ (8)

where μ_i, i = 0, 1,…, q, q ≥ 1, are fixed effects, and u_k, k=1, 2,…, K, are identically and independently normal distributed random variables, κ_k, k = 1, 2,…, K, is a preassigned sequence of knots, K is the number of knots, and q is the order of the spline. In addition,

$${(t-{\mathrm{\kappa }}_k)}_{+}^q=\{\begin{array}{ll}{(t-{\mathrm{\kappa }}_k)}^q& \text{if}t-{\mathrm{\kappa }}_k>0\\ 0& \text{else}\end{array}$$

Let u = (u₁,…, u_K)^τ. Assume that $\mathrm{Cov}(\mathbf{u})={\mathrm{\sigma }}_u^2{I}_K$, where I_K is the identity matrix of rank K. Similarly, the regression coefficients α_j(t) can be approximated by linear penalized spline models. For instance, the q-order penalized spline model for α₁(t) is

$${\mathrm{\alpha }}_1(t)={\mathrm{\alpha }}_{10}+t{\mathrm{\alpha }}_{11}+\cdots +t^q{\mathrm{\alpha }}_{1_q}+{\displaystyle \sum _{k=1}^K{v}_k{(t-{\mathrm{\kappa }}_k)}_{+}^q},$$ (9)

where α_1i, i = 0, 1,…, q, are fixed effects, and v_k, k 1, 2,…, K, are identically and independently normal distributed random variables. Let v (v₁,…, v_K)^τ. Assume that $\mathrm{Cov}(\mathbf{v})={\mathrm{\sigma }}_v^2{I}_K$

Putting all these together, the final model is a linear mixed model and it can be fitted in R. Usually, one may use the best linear unbiased prediction criteria to estimate the parameters μ_i, α_1i, ${\mathrm{\sigma }}_u^2$, ${\mathrm{\sigma }}_v^2$, ${\mathrm{\sigma }}_e^2$, etc. The details of the parameter procedure can be found in literature, and we omit them here. At the first glance, the model seems to be complicated, but in reality very convenient package is available for data analysis in R [Pinheiro and Bates, 2000].

RESULTS

EXAMPLE

We applied the proposed methods to analyze the FHS genetic data. The objective of the FHS was to identify the common factors that contribute to cardiovascular disease by following its development over a long period of time. The first cohort started in 1948 to recruit 5,209 subjects between the ages of 29 and 62 from the town of Framingham, Massachusetts. Since 1948, the subjects have continued to return to the study every 2 years. In 1971, the study enrolled a second-generation group to participate in similar examinations, i.e., Cohort 2. Between 2002 and 2005, the study enrolled the third generation of the FHS—4,095 offspring of the second generation [Splansky et al., 2007]. The first data we analyzed are from GAW 16, which contains phenotypes from the three cohorts and single-nucleotide polymorphism (SNP) genetic markers. The second data we analyzed are from GAW 13, which contains phenotypes of the first two cohorts of FHS and microsatellite markers. The detailed description of the GAW 13 and GAW 16 data can be found from these two workshops [Almasy et al., 2003b; Cupples et al., 2003; MacCluer et al., 2009].

In our analysis, we only use the information of unrelated individuals of GAW 13 or GAW 16 since our models are based on population data. For instance, the data of the two unrelated parents are used for a nuclear family but the data of the offspring are not. For GAW 16 data, a total of 4,156 individuals are eligible in our analysis with a total number of 11,136 measurements. For the GAW 13 data, the number of eligible individuals is 1,129 with a total number of 11,131 measurements. In the following, we present the results of GAW 16, while the results of GAW 13 are presented in the Supporting Information.

ANALYSIS OF FHS DATA FROM GAW 16

To analyze the GAW 16 data, we focused on three candidate regions reported by Levy et al. (2009) for the trait of SBP. Of the three regions, two are on chromosome 12, 88.4Mb–88.7Mb and 110.2Mb–110.5Mb, and the other on chromosome 11, 16.8Mb–16.9Mb.

We first fitted models without using any genetic information. When we fitted the mean function μ(t) by linear penalized spline $\mathrm{\mu }(t)={\mathrm{\mu }}_0+t{\mathrm{\mu }}_1+{\displaystyle {\sum }_{k=1}^K{u}_k{(t-{\mathrm{\kappa }}_k)}_{+}}$, the random term ${\displaystyle {\sum }_{k=1}^K{u}_k}{(t-{\mathrm{\kappa }}_k)}_{+}$ was significant (the details are presented below as results of nonparametric models). For quadratic or higher order spline $\mathrm{\mu }(t)={\mathrm{\mu }}_0+t{\mathrm{\mu }}_1+\cdots +t^q{\mathrm{\mu }}_q+{\displaystyle {\sum }_{k=1}^K{u}_k{(t-{\mathrm{\kappa }}_k)}_{+}^q}$ the random term ${\displaystyle {\sum }_{k=1}^K{u}_k}{(t-{\mathrm{\kappa }}_k)}_{+}^q$ was not significant, and the results of cubic approximation are presented as parametric models below.

Parametric Models

In the following, we present the results of parametric polynomial approximation of μ(t). We found that the following cubic linear mixed model can fit the data

$$\begin{array}{l}{y}_{\mathit{ij}}={\mathrm{\mu }}_0+t_{\mathit{ij}}{\mathrm{\mu }}_{\mathit{age}}+t_{\mathit{ij}}^2{\mathrm{\mu }}_{{\mathit{age}}^2}+t_{\mathit{ij}}^3{\mathrm{\mu }}_{{\mathit{age}}^3}+{\mathit{sex}}_i{\mathrm{\beta }}_{\mathit{sex}}+bm{i}_{\mathit{ij}}{\mathrm{\beta }}_{\mathit{bmi}}\\ +U_i(t_{\mathit{ij}})+E_i+e_{\mathit{ij}},\end{array}$$ (10)

where sex_i indicates the gender of the subject i (sex_i = 1 for male, sex_i = 2 for female), t_ij = age of subject i at visit j—mean of age, bmi_ij is the BMI for the subject i at visit j, U_i(t_ij) is the random correlation effect, E_i is the random variation of SBP for the subject i, and e_ij is the error term. The variances of E and e_ij are ${\mathrm{\sigma }}_E^2$ and ${\mathrm{\sigma }}_e^2$ respectively. In addition, we assumed that y_ij and y_ik are correlated to each other with an exponential correlation exp (−|t_ij − t_ik|/ρ), i.e., U_i(t_ij) are Ornstein-Uhlenbck Gaussian processes.

In the model (10), we used the difference between age and its mean as time variable t. This was for the convenience of computational consideration, and we took the difference as time t in a hope to avoid big number multiplications and to achieve numeric stability. We also fitted linear correlation for the trait values, but it led to higher AIC and BIC values. Hence, we preferred the exponential correlation [Pinheiro and Bates, 2000]. By fitting linear mixed effect model in R, it was possible to distinguish $\mathrm{Var}(e_{\mathit{ij}})={\mathrm{\sigma }}_e^2$ and Var(U_i(t_ij)) = 2/ρ. The outputs included the estimations of sum variance $\mathrm{Var}(U_i(t_{\mathit{ij}}))+\mathrm{Var}(e_{\mathit{ij}})=2/\mathrm{\rho }+{\mathrm{\sigma }}_e^2={\mathrm{\sigma }}_s^2$, subject variance ${\mathrm{\sigma }}_E^2$, and correlation range ρ. The variance estimations of model (10) were ${\widehat{\mathrm{\sigma }}}_E^2={8.48}^2$ and ${\widehat{\mathrm{\sigma }}}_S^2={12.54}^2$, and correlation range estimation $\widehat{\mathrm{\rho }}=4.56$. Thus, the estimation of ${\mathrm{\sigma }}_e^2$ is ${\widehat{\mathrm{\sigma }}}_e^2={12.54}^2-2/4.56=156.813$ The regression results of model (10) are presented in Table I.

TABLE I.

Parametric association results of blood systolic pressure and SNPs M₁ = rs17249754, M₂ = rs11024074, M₃ = rs3184504 for FHS data, GAW 16

Model	Coefficient	Estimates	Std error	t-value	P-value
Model (10)	μ0	99.92110	1.116201	89.52	<0.0001
	μage	0.33315	0.019624	16.98	<0.0001
	${\mathrm{\mu }}_{{\mathit{age}}^2}$	0.00521	0.000669	7.79	<0.0001
	${\mathrm{\mu }}_{{\mathit{age}}^3}$	−0.00013	0.000036	−3.43	0.0006
	βsex	−3.22158	0.409038	−7.88	<0.0001
	βbmi	616.1159	26.939680	22.87	<0.0001
Model (11) based on M1 = rs17249754	μ0	100.2625	1.121348	89.41	<0.0001
	μage	0.33286	0.019618	16.97	<0.0001
	${\mathrm{\mu }}_{{\mathit{age}}^2}$	0.00519	0.000669	7.76	<0.0001
	${\mathrm{\mu }}_{{\mathit{age}}^3}$	−0.00012	0.000036	−3.41	0.0006
	βsex	−3.21477	0.408619	−7.87	<0.0001
	βbmi	617.6547	26.924825	22.94	<0.0001
	α10	−1.08444	0.373864	−2.90	0.0037
Model (11) based on M2 = rs3184504	μ0	100.7971	1.150034	87.65	<0.0001
	μage	0.33362	0.019624	17.00	<0.0001
	${\mathrm{\mu }}_{{\mathit{age}}^2}$	0.00523	0.000669	7.82	<0.0001
	${\mathrm{\mu }}_{{\mathit{age}}^3}$	−0.00015	0.000036	−3.41	0.0006
	βsex	−3.19846	0.408522	−7.83	<0.0001
	βbmi	615.9503	26.913737	22.89	<0.0001
	α20	−0.86881	0.281312	−3.09	0.002
Model (11) based on M3 = rs11024074	μ0	99.41874	1.132271	87.81	<0.0001
	μage	0.33312	0.019622	16.98	<0.0001
	μage2	0.00520	0.000669	7.77	<0.0001
	μage3	−0.00014	0.000036	−3.41	0.0007
	βsex	−3.23002	0.408668	−7.90	<0.0001
	βbmi	616.9971	26.924911	22.92	<0.0001
	α30	0.80590	0.309139	2.61	0.0092
Model (12) based on M1 = rs17249754, M2 = rs3184504, M3 = rs11024074	μ0	100.66600	1.171086	85.96	<0.0001
	μage	0.35035	0.021427	16.35	<0.0001
	${\mathrm{\mu }}_{{\mathit{age}}^2}$	0.00522	0.000668	7.79	<0.0001
	${\mathrm{\mu }}_{{\mathit{age}}^3}$	−0.00013	0.000036	−3.47	<0.0001
	βsex	−3.20479	0.407887	−7.86	<0.0001
	βbmi	618.3573	26.885682	23.00	<0.0001
	α10	−1.13894	0.373911	−3.05	0.0023
	α1,age	−0.04428	0.022312	−1.99	0.0472
	α20	−0.86859	0.280898	−3.09	0.0020
	α30	0.78825	0.308546	2.55	0.0107

The overall likelihood ratio test of model (12) vs. model (10) to test H₀: α₁₀ = α_1,age = α₂₀ = α₃₀ = 0 is 28.63, df = 4, P-value < 0.0001.

Next, we performed analysis by using one SNP a time to fit additive model (4). In the region 88.4Mb–88.7Mb of chromosome 12, three SNPs, rs17249754, rs10858904, and rs17465266, were found to have association signal with the SBP at a significance level of 0.05. However, rs17249754 was the only SNP which showed significant association when we added one of rs10858904 or rs17465266 or both to the model in addition to rs17249754. This must be due to the strong LD among the three SNPs. In the region 110.2Mb–110.5Mb of chromosome 12, two SNPs, rs3184504 and rs2301658, were found to have association signal with the SBP at a significance level of 0.05. However, rs3184504 was the only SNP which showed significant association when we added rs2301658 to the model in addition to rs3184504. In the region 16.8Mb–16.9Mb of chromosome 11, three SNPs, rs414219, rs11024074, and rs2041236, were found to have association signal with the SBP at a significance level of 0.05. However, rs11024074 was the only SNP which showed significant association.

In Table I, we present the results of the linear mixed additive models with each of rs17249754, rs3184504, and rs11024074 as a diallelic marker, and the models were

$$\begin{array}{c}{y}_{\mathit{ij}}={\mathrm{\mu }}_0+t_{\mathit{ij}}{\mathrm{\mu }}_{\mathit{age}}+t_{\mathit{ij}}^2{\mathrm{\mu }}_{{\mathit{age}}^2}+t_{\mathit{ij}}^2{\mathrm{\mu }}_{{\mathit{age}}^3}+{\mathit{sex}}_i{\mathrm{\beta }}_{\mathit{sex}}\\ +bm{i}_{\mathit{ij}}{\mathrm{\beta }}_{\mathit{bmi}}+x_{\mathit{ik}}{\mathrm{\alpha }}_{k0}+U_i(t_{\mathit{ij}})+E_i+e_{\mathit{ij}},\end{array}$$ (11)

where

$$x_{i1}=\{\begin{array}{c}2\text{if}{G}_i=A/A\\ 1\text{if}{G}_i=A/G\\ 0\text{if}{G}_i=G/G\end{array}$$

is the number of allele A in the genotype G_i of subject i at SNP rs17249754,

$$x_{i2}=\{\begin{array}{c}2\text{if}{G}_i=C/C\\ 1\text{if}{G}_i=C/T\\ 0\text{if}{G}_i=T/T\end{array}$$

is the number of allele C at SNP rs3184504, and similarly

$$x_{i3}=\{\begin{array}{c}2\text{if}{G}_i=C/C\\ 1\text{if}{G}_i=C/T\\ 0\text{if}{G}_i=T/T\end{array}$$

is the number of allele C at SNP rs11024074.

Finally, we used all three SNPs, rs17249754, rs3184504, and rs11024074, in the analysis, and we found the final model is

$$\begin{array}{l}{y}_{\mathit{ij}}={\mathrm{\mu }}_0+t_{\mathit{ij}}{\mathrm{\mu }}_{\mathit{age}}+t_{\mathit{ij}}^2{\mathrm{\mu }}_{{\mathit{age}}^2}+t_{\mathit{ij}}^3{\mathrm{\mu }}_{{\mathit{age}}^3}+{\mathit{sex}}_i{\mathrm{\beta }}_{\mathit{sex}}\\ +bm{i}_{\mathit{ij}}{\mathrm{\beta }}_{\mathit{bmi}}+x_{i1}{\mathrm{\alpha }}_{10}+x_{i1}{t}_{\mathit{ij}}{\mathrm{\alpha }}_{1,\mathit{age}}+x_{i2}{\mathrm{\alpha }}_{20}+x_{i3}{\mathrm{\alpha }}_{30}\\ +U_i(t_{\mathit{ij}})+E_i+e_{\mathit{ij}}.\end{array}$$ (12)

The results of model (12) are presented in Table I. We actually fitted α_i(t) by linear spline model (9) and found that the random term ${\displaystyle {\sum }_{k=1}^K{v}_k{(t-{\mathrm{\kappa }}_k)}_{+}}$ had little effect on the model. As the final model (12) shows, α₁(t) = α₁₀ + tα_1,age can be fitted as a linear relation, and α₂(t) and α₃(t) do not depend on the time t. Each of α₁₀, α_1,age, α₂₀, α₃₀ in model (12) was significant at 95% significance level (Table I). The overall likelihood ratio test of model (12) vs. model (10) to test H₀: α₁₀ = α_1,age = α₂₀ = α₃₀ = 0 was 28.63, df = 4, P-value < 0.0001.

Therefore, the three SNPs, rs17249754, rs3184504, and rs11024074, are independently associated with the SBP in addition to the effects of age, sex, and BMI. The impact of allele A of SNP rs17249754 on the SBP decreases as the time t or age increases; the allele C of the SNP rs3184504 has negative impact on SBP and the allele C of the SNP rs11024074 has positive impact, but both have no significant time- or age-dependent impact.

Nonparametric Models

In model (10), the population mean μ(t) was fitted by cubic regression without random spline term ${\displaystyle {\sum }_{k=1}^K{u}_k{(t_{\mathit{ij}}-{\mathrm{\kappa }}_k)}_{+}^3}$. The reason was that the random term was not significant since ${\mathrm{\sigma }}_u^2$ was not significantly larger than 0 at a significance level 0.05, and the same story happened for the quadratic case (data not shown). For linear case, however, the random term ${\displaystyle {\sum }_{k=1}^K{u}_k{(t_{\mathit{ij}}-{\mathrm{\kappa }}_k)}_{+}}$was significant (the likelihood ratio test is 62.64 with a P-value < 0.0001 to test the null $H_0:{\mathrm{\sigma }}_u^2=0$). Therefore, we started with the linear spline model as follows

$$\begin{array}{l}{y}_{\mathit{ij}}={\mathrm{\mu }}_0+t_{\mathit{ij}}{\mathrm{\mu }}_{\mathit{age}}+{\displaystyle \sum _{k=1}^K{u}_k{(t_{\mathit{ij}}-{\mathrm{\kappa }}_k)}_{+}+{\mathit{sex}}_i{\mathrm{\beta }}_{\mathit{sex}}+bm{i}_{\mathit{ij}}}{\mathrm{\beta }}_{\mathit{bmi}}\\ +U_i(t_{\mathit{ij}})+E_i+e_{\mathit{ij}},\end{array}$$ (13)

where the number of knots K = 20, and the knots κ_k were uniformly chosen on the interval. By adding each of the three SNPs, rs17249754, rs3184504, and rs11024074, in the analysis, we found significant result for the model below

$$\begin{array}{l}{y}_{\mathit{ij}}={\mathrm{\mu }}_0+t_{\mathit{ij}}{\mathrm{\mu }}_{\mathit{age}}+{\displaystyle \sum _{k=1}^K{u}_k{(t_{\mathit{ij}}-{\mathrm{\kappa }}_k)}_{+}+{\mathit{sex}}_i{\mathrm{\beta }}_{\mathit{sex}}+bm{i}_{\mathit{ij}}}{\mathrm{\beta }}_{\mathit{bmi}}\\ +x_{\mathit{ik}}{\mathrm{\alpha }}_{k0}+U_i(t_{\mathit{ij}})+E_i+e_{\mathit{ij}},\end{array}$$ (14)

where x_ik are defined above using SNPs, rs17249754, rs3184504, and rs11024074, and k = 1, 2, 3. The results are presented in Table II. By adding all the three SNPs in the analysis, the final model is

$$\begin{array}{l}{y}_{\mathit{ij}}={\mathrm{\mu }}_0+t_{\mathit{ij}}{\mathrm{\mu }}_{\mathit{age}}+{\displaystyle \sum _{k=1}^K{u}_k{(t_{\mathit{ij}}-{\mathrm{\kappa }}_k)}_{+}+{\mathit{sex}}_i{\mathrm{\beta }}_{\mathit{sex}}+bm{i}_{\mathit{ij}}}{\mathrm{\beta }}_{\mathit{bmi}}\\ +x_{i1}{\mathrm{\alpha }}_{10}+x_{i1}{t}_{\mathit{ij}}{\mathrm{\alpha }}_{1,\mathit{age}}+x_{i2}{\mathrm{\alpha }}_{20}+x_{i3}{\mathrm{\alpha }}_{30}+U_i(t_{\mathit{ij}})\\ +E_i+e_{\mathit{ij}},\end{array}$$ (15)

and the results are presented in Table II. As we did for model (12), we fitted α_i(t) by linear spline model (9) and found that the random term had little effect on the model (15).

TABLE II.

Nonparametric association results of blood systolic pressure and SNPs M₁ = rs17249754, M₂ = rs11024074, M₃ = rs3184504 for FHS data, GAW 16

Model	Coefficient	Estimates	Std error	t-value	P-value
Model (13)	μ0	98.6284	6.867915	14.36	<0.0001
	μage	0.0605	0.209519	0.29	0.77
	βsex	−3.2366	0.408893	−7.92	<0.0001
	βbmi	614.1032	26.929997	22.80	<0.0001
Model (14) based on M1 = rs17249754	μ0	99.0071	6.845307	14.46	<0.0001
	μage	0.0629	0.208835	0.30	0.76
	βsex	−3.2297	0.408470	−7.91	<0.0001
	βbmi	615.6503	26.914968	22.87	<0.0001
	α10	−1.0865	0.373734	−2.91	0.0037
Model (14) based on M2 = rs3184504	μ0	99.4904	6.864736	14.49	<0.0001
	μage	0.0606	0.209273	0.29	0.77
	βsex	−3.2135	0.408378	−7.87	<0.0001
	βbmi	613.9346	26.904021	22.82	<0.0001
	α20	−0.8690	0.281214	−3.09	0.0020
Model (14) based on M3 = rs11024074	μ0	98.1551	6.836669	14.36	<0.0001
	μage	0.0624	0.208559	0.30	0.76
	βsex	−3.2449	0.408523	−7.94	<0.0001
	βbmi	614.9878	26.915266	22.85	<0.0001
	α30	0.8034	0.309029	2.60	0.0094
Model (15) based on M1 = rs17249754, M2 = rs3184504,M3 = rs11024074	μ0	99.3246	6.846793	14.51	<0.0001
	μage	0.0750	0.208707	0.36	0.72
	βsex	−3.2196	0.407736	−7.90	<0.0001
	βbmi	616.3468	26.875826	22.93	<0.0001
	α10	−1.1405	0.373783	−3.05	0.0023
	α1,age	−0.0436	0.022303	−1.96	0.05
	α20	−0.8688	0.280794	−3.09	0.0020
	α30	0.7860	0.308430	2.55	0.0109

The overall likelihood ratio test of model (15) vs. model (13) to test H₀: α₁₀ = α_1,age = α₂₀ = α₃₀ = 0 is 28.52, df = 4, P-value < 0.0001.

Like parametric model (12), each of α₁₀, α_1,age, α₂₀, α₃₀ in model (15) was significant at 95% significance level (Table II). The overall likelihood ratio test of model (15) vs. model (13) to test H₀: α₁₀ = α_1,age = α₂₀ = α₃₀ = 0 was 28.52, df = 4, P-value < 0.0001, which is similar to that of the parametric model (12).

Comparison of Parametric and Nonparametric Models

In Figures 2 and 3, we plotted the predicted SBP vs. age by parametric model (12) and nonparametric model (15). The plots captured the temporal trends of SBP. Before age 40, the SBP was relatively stable and after age 40, it increased. The predicted SBP of female was about 3.2 lower than that of male. Before age 30, the genetic effects were relatively small. After that, the genetic effects gradually got larger. Interestingly, Figures 2 and 3 showed that the temporal trends of the predicted SBP vs. age by parametric model (12) and nonparametric model (15) are very similar, although the parametric predictions shown in Figure 2 are more smooth that those of nonparametric predictions shown in Figure 3.

Fig. 2.

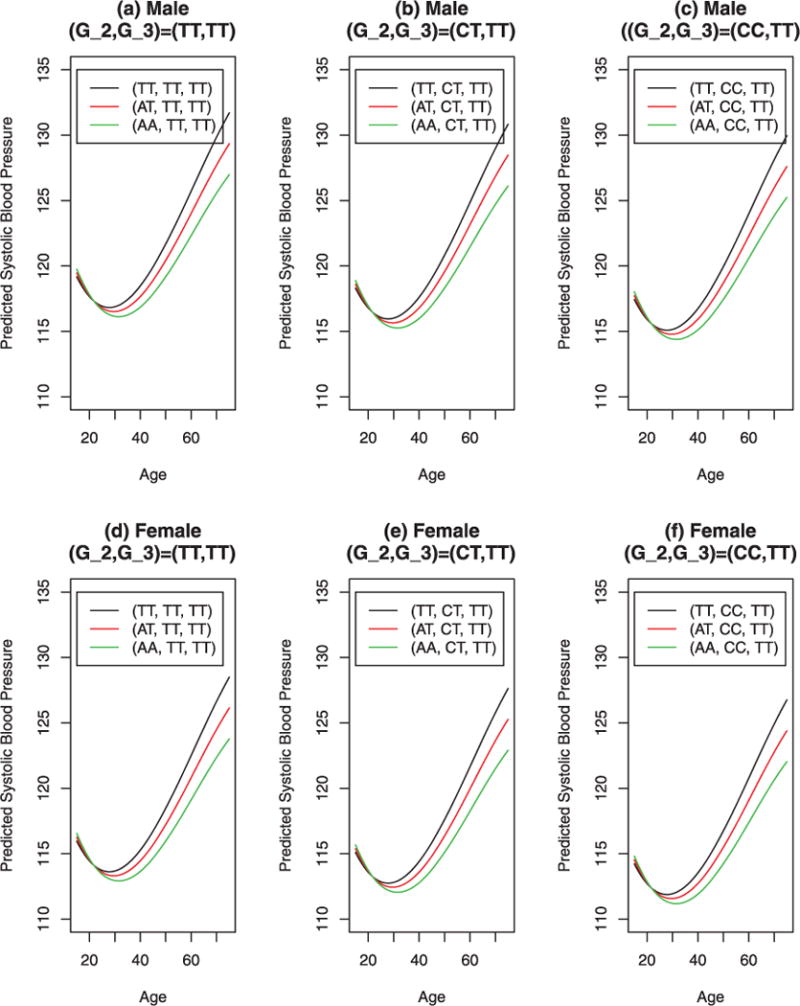
Predicted systolic blood pressure against age in years for male and female by SNPs M₁ = rs17249754, M₂ = rs11024074, M₃ = rs3184504, and sex, based on parametric model (12). In the graphs, the legends give the genotypes of the three SNPs; for instance, (AT, CT, TT) means G₁ = AT, G₂ = CT, and G₃ = TT. G_i is the genotype of M_i, i = 1, 2, 3.

Fig. 3.

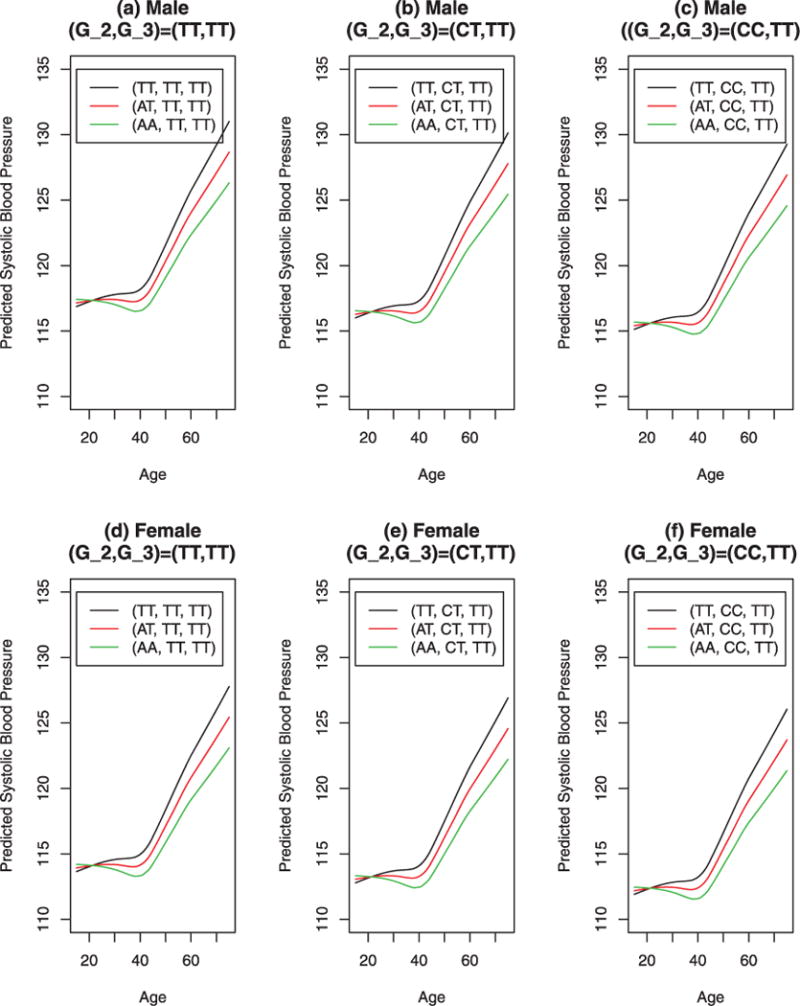
Predicted systolic blood pressure against age in years for male and female by SNPs M₁ = rs17249754, M₂ = rs11024074, M₃ = rs3184504, and sex, based on nonparametric model (15). In the graphs, the legends give the genotypes of the three SNPs; for instance, (AT,CT, TT) means G₁ = AT,G₂ = CT, and G₃ = TT. G_i is the genotype of M_i, i = 1, 2, 3.

For nonparametric penalized linear models (13), (14), and (15), the random term ${{\displaystyle {\sum }_{k=1}^K{u}_k(t_{\mathit{ij}}-{\mathrm{\kappa }}_k)}}_{+}$ is significant since the null hypothesis $H_0:{\mathrm{\sigma }}_u^2=0$ is rejected with extremely small P-values. However the regression coefficient of age is not significant, i.e., the null hypothesis H₀: μ_age=0 is not rejected due to big P-values (Table II). This is somehow expected. Taking model (13) as an example, the coefficient μ_age is the coefficient for the time trend between smallest age and the first knot. The coefficient for the time trend between the first knot and the second knot is μ_age+u₁, and the coefficient between the second and the third+ knot is μ_age + u₁ + u₂, and so on. Since the SBP does not change with time at early ages (between smallest age and the first knot), so we do not expect μ_age to be significant. For cubic parametric linear mixed models (10), (11), and (12), the significant results for ${\mathrm{\sigma }}_u^2$ disappear but the regression coefficients of age, age², age³ are significant. Hence, the relation between SBP and age is nonlinear.

In short, the nonlinear trends in nonparametric linear penalized spline models were absorbed into the random component ${{\displaystyle {\sum }_{k=1}^K{u}_k(t_{\mathit{ij}}-{\mathrm{\kappa }}_k)}}_{+}$. In cubic parametric linear mixed models, the nonlinearity is reflected by the significant results of regression coefficients of age, age², age³.

SIMULATION STUDY

To evaluate the performance of the proposed models, simulation studies were carried out to calculate empirical type I error rates, power, and bias of parameter estimation. The results are presented in Table III. We simulated 200 individuals with an age range from 20 to 65 years. For each individual, the number of observations ranged from 3 to 6 and each individual was examined every 2 or 4 years. Due to the random nature of each simulation, the number of total observations were slightly different from each other in the simulation settings, which ranged from 889 to 926 (column 4 of Table III). In the simulation, we assumed that the phenotype was affected by gender that male people’s trait was bigger than that of females by 5. One SNP marker was simulated with additive effect and a minor allele frequency of 0.25. For the mean function, we used one logarithm function μ(t) = −34.2 + 81.7 log(0.3(t + 21.7)) and an exponential function μ(t) = 110 exp(0.0002(t − 25)²). The curves of the two functions are plotted in Figure 4. The logarithm function μ(t) = −34.2 + 81.7 log(0.3(t + 21.7)) was taken from Daw et al. [2003] and Wang et al. [2012] whose estimates were from the FHS cholesterol data, and the exponential function μ(t) = 110 exp(0.0002(t − 25)²) was used to mimic the SBP data of FHS. For the variance components, the subject variance ${\mathrm{\sigma }}_E^2$ was 25 and the error variance ${\mathrm{\sigma }}_e^2$ was 10.

TABLE III.

Simulation results at 95% significance level of testing additive genetic effect H0: α₁ = 0 in model y_i(t) = μ(t) + sex_iβ_sex + x_i1α₁ + U_i(t) + E_i + ε_i by nonparametric linear penalized spline model, a correctly specified nonlinear function, and misspecified parametric functions of μ(t)

μ(t): Mean function	Type I error or power (bias)	α1	No. of obsc	Empirical results: type I error or power (bias ${\mathrm{\alpha }}_1-{\widehat{\mathrm{\alpha }}}_1$)
				Nonparametric modeld	Correctly specifiede	Misspecified: Linearf	Misspecified: Cubicg
Logarithma	Type I error (bias)	0	926	0.0535 (0.011)	0.0555 (0.005)	0.0615 (0.0161)	0.0540 (0.009)
		0.5	896	0.1620 (−0.068)	0.1595 (−0.054)	0.2430 (−0.254)	0.1605 (0.509)
	Power (bias)	1	926	0.4010 (0.005)	0.4055 (0.003)	0.5695 (−0.291)	0.4015 (1.009)
		2	889	0.9465 (−0.008)	0.9470 (−0.001)	0.9000 (0.137)	0.9475 (2.009)
		3	902	0.9980 (−0.007)	0.9980 (0.001)	0.9970 (0.124)	0.9980 (3.010)
Exponentialb	Type I error (bias)	0	916	0.0525 (−0.015)	0.0525 (−0.018)	0.009 (−0.242)	0.0525 (−0.032)
		0.5	908	0.1215 (0.003)	0.1240 (0.003)	0.0785 (−0.343)	0.1205 (0.467)
	Power (bias)	1	900	0.3540 (−0.002)	0.3505 (0.001)	0.3120 (−0.522)	0.3430 (0.967)
		2	906	0.8545 (−0.005)	0.8535 (−0.008)	0.7175 (−0.358)	0.8430 (1.966)
		3	916	0.9990 (−0.015)	0.9990 (−0.018)	0.9910 (−0.242)	0.9990 (2.968)

^aTrue μ(t) = −34.2 + 81.7log(0.3(t + 21.7)).

^bTrue μ(t) = 110exp(0.0002×(t − 25)²).

^cThe total number of observations.

^dμ(t) is estimated by nonparametric linear penalized spline model.

^eμ(t) is correctly specified.

^fμ(t) is misspecified as μ(t) = μ₀ +μ₁t.

^gμ(t) is misspecified as μ(t) = μ₀ + μ₁t + μ₂t² + μ₃t³.

Fig. 4.

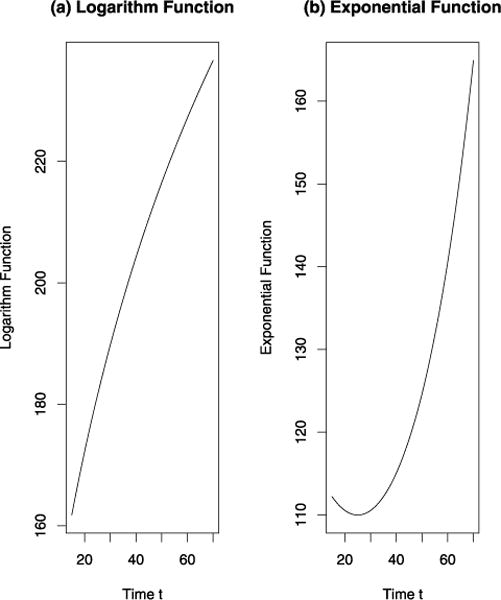
The curves of (a) logarithm function μ(t) = −34.2 + 81.7 log(0.3(t + 21.7)) and an (b) exponential function μ(t) = 110 exp(0.0002 × (t − 25)²)).

We are mainly concerned about the performance of detecting the genetic effect in the model y_i(t) = μ(t) + sex_iβ_sex + x_i1α₁ + U_i(t) + E_i + ε_i. In Table III, the empirical results of type I error rates and power at 95% significance level were reported to test additive genetic effect H₀: α₁ = 0 by nonparametric linear penalized spline model, a correctly specified nonlinear function, and misspecified parametric functions of μ(t). Each empirical type I error rate in Table III was calculated based on 2,000 simulations. That is, we simulated 2,000 random samples. To calculate the type I error rates, we assumed that α₁=0 in our simulation, i.e., the trait was independent of genetic factor. We calculated an empirical test value of likelihood ratio test for each sample. The empirical type I error rates at nominal level α = 0.05 are reported in Table III and represented the proportions of the test values calculated for the 2,000 samples, that exceeded the 95th percentiles of the ${\chi }_1^2$-distribution. The empirical power was calculated similarly by assuming α₁ = 0.5, 1, 2, 3 based on 2,000 simulations.

Encouragingly, the empirical type I error rates were all around the nominal level 0.05 except for the linear misspecified case. The empirical power was very close for each of the three cases: the nonparametric linear penalized spline model, the correctly specified nonlinear function, and the cubic misspecified case. In the linear misspecified case, the empirical type I error rate of 0.009 was unbelievably low for the exponential function and it was 0.0615 which is relatively high for the logarithm case. Thus, the linear misspecified case can give unstable results. The power of linear misspecified case was different from the other cases. Most likely, this was because linear function was far away from the true logarithm and exponential functions, which can be seen from Figure 4. Relatively, the cubic function performs better than the linear function.

To get an understanding about the parameter estimation, we calculated the average of the 2,000 estimates of the coefficient α₁ and then took difference with the true value of α₁ as the bias. From the results in Table III, the nonparametric linear penalized spline model and the correctly specified nonlinear function gave very small bias values. However, both linear and cubic misspecified cases generated big biases. In practice, it is almost impossible to correctly specify the true mean function. Thus, the nonparametric linear penalized spline model is the best choice to analyze data. In addition, high-order parametric methods such as cubic polynomial function can give reasonable results for power and type I errors, but they can generate large biases in parameter estimations.

DISCUSSION

Longitudinal genetic studies provide a very valuable resource for exploring key genetic and environmental factors that affect complex traits over time. Genetic analysis of longitudinal phenotypic data that incorporate temporal variations is important for understanding genetic architecture and biological variations of common complex diseases. It may provide a powerful tool to identify genetic determinants of complex diseases, and to understand at which stage of human development that the genetic determinants are important [Friedlander et al., 1997; Lasky-Su et al., 2008]. Moreover, important environmental factors that are associated with the complex diseases, such as diet, familial income, and smoking status, can be identified. Thereafter, the interactions of genetic determinants and environmental factors, i.e., gene-gene and gene-environment interactions, can be investigated in the presence of temporal trends of phenotypic traits. Although they are important, there is a paucity of statistical methods to analyze longitudinal human genetic data.

In this article, we develop association models to analyze longitudinal data of human genetic studies. Population-based association mapping models are proposed on the basis of temporal population genetic models. The models can be applied to multiple diallelic genetic markers such as SNPs and multiallelic markers such as microsatellites. Theoretical arguments are provided to justify the approaches. The variance-covariance structure is constructed to analyze multiple measurements per individual based on the theory of stochastic processes. To estimate time-dependent mean functions and genetic regression coefficients, we propose approximations by nonparametric penalized spline models. Similar approximations are used in association mapping of nuclear family data and pedigree linkage analysis of longitudinal traits in which only one marker is used in the analysis [Wang 2012; Wang and Huang, 2012]. Another way is to use parametric models in the analysis.

The proposed approaches were applied to analyze GAW 13 and GAW 16 SBP data from FHS. We focused on three candidate regions detected by Levy et al. [2009] for GAW 16 data and an important marker GATA25A04 (D17S1299) for GAW 13 data detected by Levy et al. [2000]. One may want to notice that no temporal trends were studied for the SBP in Levy et al. [2000, 2009] since sample average of each individual’s measurements was used in the analysis. Both parametric and nonparametric models were fitted to identify the important SNPs for GAW 16 data and important allele for GAW 13 at marker locus GATA25A04. We tried to obtain the temporal relations and genetic effect on SBP for these data. When markers are in high LD, collinearity may affect model fitting and selection. In our analysis, collinearity does not cause problem in our analysis of GAW 16 data. However, this does not mean it is not a problem for the other data analysis. In practice, one can calculate the variance inflation factor to make sure that collinearity does not appear to be a potential problem. For markers in strong LD, one may want to use the most significant SNP in the analysis to report the results.

To evaluate the robustness of the nonparametric penalized spline models and parametric models, simulation studies were carried out to calculate and to compare empirical type I error rates and power. In order to understand the accuracy of the parameter estimation, we calculated the biases for parameter to model the genetic effect. The nonparametric penalized spline models are found to perform well in terms of reasonable type I error rates, power, and parameter estimation accuracy.

One merit of the proposed models is that the number of parameters does not depend on the number of multiple measurements. The number of parameters is fixed after carefully specifying regression models and variance-covariance structure. This is different from the method proposed in de Andrade et al. [2002] and de Andrade and Olswold [2003], in which the number of variance-covariance terms to be estimated depends on the number of multiple measurements and grows rapidly when the number of measurements increases. In our proposed models, the parameters are specified through two components based on the theory of stochastic processes: (i) temporal regression models (4) and (5); (ii) temporal variance-covariance functions given by equation (7). If spline functions are used, some parameters can be specified by spline models. In theory, more measurements will lead to more accurate estimation of the parameters. On the one hand, the number of parameters in the proposed models can be significantly smaller than that of de Andrade et al. [2002]. On the other hand, the structure of variance and covariance matrix and mean coefficients of the proposed models is very flexible. These features can be crucial in successful modeling.

In the literature, the phenotypes of longitudinal data can be characterized as function-valued traits [Jaffrezic and Pletcher, 2000; Pletcher and Geyer, 1999]. Specifically, a function-valued trait is a function y(t), where t is a continuous variable, such as age or time. These traits are also called infinite-dimensional traits since the traits can take values at an infinite number of ages [Kirpatrick and Heckman, 1989]. In practice, trait values are observed at a finite set of times t₁,…, t_m for an individual, i.e., longitudinal data. Based on the observed data, different methods are proposed to analyze the function-valued traits. In animal breeding, random regression models have been used for the longitudinal data [Diggle et al., 1994; Jamrozik et al., 1997]. An approximation of covariance matrices by orthogonal polynomials has been also proposed [Kirpatrick and Heckman, 1989]. Based on the theory of stochastic processes, the character process model was proposed by Pletcher and Geyer [1999]. These methods were summarized and evaluated in Jafferzic and Pletcher [2000], and used in analyzing empirical data of Drosophila reproduction and mortality and growth in beef cattle. However, the methods do not use any genetic marker data. Functional mapping methods were developed to estimate the dynamic changes of QTL effects during a course of ontogenetic growth [Ma et al., 2002; Wu et al., 2003]. The general concepts and theory of functional data analysis can be found in Ramsay and Silverman [1996]. In our analysis, we adopted some ideas of the character process to build variance-covariance structure, and we use polynomials to approximate the temporal mean function and regression coefficients.

The proposed approaches can only analyze population data. It will be very interesting and important to extend the methods to analyze family data or combinations of population and family data. For genetics community, there is no handy software and statistical models for longitudinal phenotypic traits. For instance, there is no combined linkage and association analysis of the FHS data. The reason is that there are no longitudinal statistical models, methods, and software for a joint linkage and association study of temporal quantitative traits of complex diseases. The proposed methods, in theory, can be extended to analyze the family data or combinations of population and family data. To achieve the goals, temporal variance component models can be built as follows.

The temporal regression models (4) and (5) can be used to model the trait means, which take care of the association information. The temporal variance-covariance functions given by equation (7) can be used for one individual’s measurements. For family members, the temporal variance-covariance functions can be constructed in the same way as variance component models presented [Lange, 2002]. The linkage information then is incorporated into the variance-covariance matrix function of pedigree data. If the number of measurements or the size of the pedigrees is large, the dimension of the variance-covariance matrix is large but it should be manageable. If a moderate number of measurements is taken for each individual, it will be interesting to compare the results of our models with those of de Andrade et al. [2002]. For instance, for GAW 13 Cohort 2 of Problem 1 of the FHS, each individual’s phenotypes and covariates are measured five times. This provides an opportunity to compare the results by using the real data.

In this article, we propose temporal association mapping models for longitudinal quantitative traits. The models are basically linear mixed effect models. It is interesting in developing temporal models to analyze qualitative genetic traits. To deal with the discrete longitudinal traits, one may use generalized linear mixed models. As the first step, one may start with population data, and then extend to family data or combinations of family data and population data.

We do not deal with various issues such as missing data, population stratification, and heterogeneity in the current study. Surely, these are important topics. For instance, it is unclear how the models performs in the presence of missing data, population stratification, and heterogeneity. All these issues deserve more investigation for future studies.

In summary, the research in this article sheds light on the important area of longitudinal genetic analysis, and it provides a basis for future methodological investigations and practical applications. Many important issues need more insight investigations in the future studies. In our analysis, we use R for our data analysis and simulations. In a long run, user-friendly software and algorithms are needed for genetic public to facilitate data analysis.