A Bayesian Two-Part Latent Class Model for Longitudinal Medical Expenditure Data: Assessing the Impact of Mental Health and Substance Abuse Parity

Summary

In 2001, the U.S. Office of Personnel Management required all health plans participating in the Federal Employees Health Benefits Program to offer mental health and substance abuse benefits on par with general medical benefits. The initial evaluation found that, on average, parity did not result in either large spending increases or increased service use over the four-year observational period. However, some groups of enrollees may have benefited from parity more than others. To address this question, we propose a Bayesian two-part latent class model to characterize the effect of parity on mental health use and expenditures. Within each class, we fit a two-part random effects model to separately model the probability of mental health or substance abuse use and mean spending trajectories among those having used services. The regression coefficients and random effect covariances vary across classes, thus permitting class-varying correlation structures between the two components of the model. Our analysis identified three classes of subjects: a group of low spenders that tended to be male, had relatively rare use of services, and decreased their spending pattern over time; a group of moderate spenders, primarily female, that had an increase in both use and mean spending after the introduction of parity; and a group of high spenders that tended to have chronic service use and constant spending patterns. By examining the joint 95% highest probability density regions of expected changes in use and spending for each class, we confirmed that parity had an impact only on the moderate spender class.

1. Introduction

The Federal Employees Health Benefits (FEHB) Program sponsors health insurance benefits for more than 8.5 million federal employees and retirees, plus their spouses and dependents. Over 250 health plans currently participate in the FEHB program. At the beginning of 2001, the U.S. Office of Personnel Management implemented a parity policy that required all health plans participating in the FEHB Program to offer mental health and substance abuse benefits on par with general medical benefits (U.S. OPM, 2000). An early evaluation of the policy examined changes in total mental health expenditures, including out-of-pocket and plan spending, from 1999 to 2002, and found that, on average, parity did not result in either the large increases in spending predicted by opponents of parity or the increased service use anticipated by mental health advocates (Goldman et al., 2006). Because most of the literature on the impact of parity has focused on the average effect of the policy on costs and access to mental health and substance abuse care, little is known about its impact on specific enrollee subpopulations—for example, the sickest patients or those carrying the greatest financial burden of illness.

To answer this question, there are three key features of longitudinal medical expenditure data that must be addressed. The data are semi-continuous, assuming non-negative values with a spike at zero for those who use no services, followed by a continuous, right-skewed distribution for those who have used services. Table 1 provides a description of the total spending data for a sample of 1581 FEHB enrollees from one state, each with four years of data, yielding a total of 6324 observations. Over 80% of enrollees had no annual mental health expenditures, while a small fraction had large expenditures. The percentage of spenders increased steadily over time, while median spending increased immediately following introduction of the parity directive and then returned to baseline levels by 2002.

Table 1.

Descriptive statistics for FEHB study.

Year	n	% Nonspenders	Median Mental Health Spending* (IQR)
1999	1581	84.69	362.30 (61.97, 1150.28)
2000	1581	83.36	367.95 (75.09, 845.41)
2001†	1581	82.16	403.16 (118.96, 941.13)
2002	1581	19.48	80.52 (69.14, 864.95)

^*Among subjects with nonzero expenditures.

^†Parity mandate introduced.

Another important feature of the data concerns repeated measurements. In the FEHB data, each enrollee contributes an observation for each of the four study years, introducing within-subject correlation. Moreover, in each year, there are two outcomes per enrollee: use of mental health/substance abuse services, and if use, the level of use as measured by expenditures. Further, it may be reasonable to assume that the probability of some use is correlated with the expected level of spending. An appropriate statistical model should address these multiple sources of correlation.

One modeling strategy is to apply a longitudinal two-part model (Olsen and Schafer, 2001; Tooze, Grunwald, and Jones, 2002; Ghosh and Albert, 2009). Two-part models are mixtures of a point mass at zero followed by a right-skewed distribution (e.g., lognormal) for the nonzero values. The two mixture components are modeled in stages. First, the probability of service use is modeled via mixed effects probit or logistic regression. Next, conditional on some usage, the expected spending level is modeled through (most commonly) a lognormal mixed effects model. The random effects for the two components are typically assumed to be correlated; ignoring this potential correlation can yield biased inferences (Su, Tom, and Farewell, 2009).

Finally, because enrollees tend to share characteristics related to spending, it is reasonable to assume that FEHB enrollees’ trajectories fall into a small number of classes. One natural mechanism to handle this feature is to use latent class models, in particular latent class “heterogeneity” or “growth mixture” models (Verbeke and Lesaffre, 1996; Muthén and Shedden, 1999; Muthén et al., 2002). Growth mixture models (GMMs) assume that subjects first fall into one of a finite number of latent classes characterized by a class-specific mean trajectory; then, about these class means, subjects have their own unique longitudinal trajectories defined by a set of random effects with class-specific variance parameters. As such, GMMs can be viewed as finite mixtures of random effects models.

Growth mixtures have become increasingly popular as a way of decomposing complex heterogeneity in longitudinal models. Lin et al. (2000) developed a GMM to estimate class-specific PSA trajectories among men at risk for prostate cancer. Proust-Lima, Letenneur, and Jacqmin-Gadda (2007) proposed a GMM to jointly model a set of correlated longitudinal biomarkers and a binary event. Lin et al. (2002) and Proust-Lima et al. (2009) developed related models to analyze longitudinal biomarkers and a time to event. Beunckens et al. (2008) proposed a GMM for incomplete longitudinal data. In the Bayesian setting, Lenk and DeSarbo (2000) describe computational strategies for fitting GMMs; Elliott et al. (2005) developed a Bayesian GMM to jointly analyze daily affect and negative event occurrences during a 35-day study period; and recently, Leiby et al. (2009) fitted a Bayesian latent class factor-analytic model to analyze multiple outcomes from a clinical trial evaluating a new treatment for interstitial cytitis.

We build on this previous work to develop a Bayesian two-part growth mixture model for characterizing the effect of parity on mental health use and expenditures. The advantages of Bayesian inference are well-known and include elicitation of prior beliefs, avoidance of asymptotic approximations, and, as we demonstrate below, practical estimation of parameter contrasts and multidimensional credible regions. Within each class, we fit a probit-lognormal model with class-specific regression coefficients and random effects. An attractive feature of the model is that it permits the random effect covariance to vary across the classes. For example, one class might comprise enrollees with frequent high expenditures (positive correlation between the probability of spending and the actual amount spent), whereas another class might comprise enrollees with frequent but modest expenditure (negative correlation between probability of spending and amount spent).

The remainder of this paper is organized as follows: Section 2 outlines the proposed model; Section 3 describes prior elicitation, posterior computation, model comparison, and evaluation of model fit; Section 4 describes a small simulation study; Section 5 applies the method to the FEHB study; and the final section provides a discussion and directions for future work.

2. The Two-Part Growth Mixture Model

The two-part model for semi-continuous data is a mixture of a degenerate distribution at zero and a positive continuous distribution, such as a lognormal (LN), for the nonzero values. The probability distribution is expressed as

$$f(y_i)={(1-\varphi )}^{1-d_i}{[\varphi \times \mathrm{LN}(y_i;\mu ,{\tau }^2)]}^{d_i},i=1,\dots ,n;0\le p\le 1,$$

where y_i is the observed response of the random variable Y_i; d_i is an indicator that y_i > 0; ϕ = Pr(Y_i > 0); and LN(y_i; μ, τ²) denotes the lognormal density evaluated at y_i, with μ and τ² representing the mean and variance of log(Y_i∣Y_i > 0). When ϕ = 0, the distribution is degenerate at 0, and when ϕ = 1, there are no zeros and the distribution reduces to a lognormal density.

The model can be extended to allow for repeated measures and latent classes by introducing a latent categorical variable C_i that takes the value k (k = 1, …, K) if subject i belongs to class k. In its most general form, the model is given by

$$\begin{array}{lll}\hfill f(y_{\mathit{ij}}\mid C_i=k,{\mathbf{b}}_i)& =& {(1-{\varphi }_{\mathit{ijk}})}^{1-d_{\mathit{ij}}}{[{\varphi }_{\mathit{ijk}}\times \mathrm{LN}(y_{\mathit{ij}};{\mu }_{\mathit{ijk}},{\tau }_k^2)]}^{d_{\mathit{ij}}}\\ \hfill g({\varphi }_{\mathit{ijk}})& =& {\mathit{x}}_{1\mathit{ij}}^{\prime }{\mathit{\alpha }}_k+{\mathit{z}}_{1\mathit{ij}}^{\prime }{\mathbf{b}}_{1i}(\mathrm{binomial\; component})\\ \hfill \log ({\mu }_{\mathit{ijk}})& =& {\mathit{x}}_{2\mathit{ij}}^{\prime }{\mathit{\beta }}_k+{\mathit{z}}_{2\mathit{ij}}^{\prime }{\mathbf{b}}_{2i}(\mathrm{lognormal\; component}),\end{array}$$ (1)

where y_ij is the j-th observed response for subject i (j = 1, …, n_i); g denotes a link function, such as the probit or logit link; x_lij and z_lij are p_l × 1 and q_l × 1 vectors of fixed and random effect covariates for component l (l = 1, 2), including appropriate time-related variables (e.g., polynomials of time or binary indicators representing measurement occasions); α_k and β_k are fixed effect coefficients specific to class k; and ${\mathbf{b}}_i\mid C_i={({\mathbf{b}}_{1i}^{\prime },{\mathbf{b}}_{2i}^{\prime })}^{\prime }\mid C_i~{\mathrm{N}}_{q_1+q_2}(\mathbf{0},{\mathbf{\sum }}_k)$ is a stacked vector of random effects for subject i, with class-specific covariance Σ_k. When q₁ = q₂ = 1, the model reduces to the widely used random-intercept two-part model. For the standard random-slope model, q₁ = q₂ = 2 and Σ_k is a 4 × 4 matrix that includes cross-covariances between the random intercepts and slopes of the two components. While this model captures additional heterogeneity over time, restrictions on Σ_k may be needed to aid identifiability.

To complete the model, we assume that the class indicator C_i has a “categorical distribution” taking the value k with probability π_ik, where π_ik is linked to a r-dimensional covariate vector, w_i, via a generalized logit model; that is,

$$\begin{array}{lll}\hfill C_i& ~& \mathrm{Cat}({\pi }_{i1},\dots ,{\pi }_{\mathit{iK}}),\\ \hfill {\pi }_{\mathit{ik}}& =& \frac{e^{{\mathit{w}}_i^{\prime }{\gamma }_k}}{{\sum }_{h=1}^K{e}^{{\mathit{w}}_i^{\prime }{\gamma }_h}},\mathrm{with}{\gamma }_1=0\mathrm{for\; identifiability}.\end{array}$$ (2)

(We use the term “categorical distribution” in lieu of “multinomial distribution” since C_k is an integer-valued variable ranging from 1 to K.) And finally, throughout the paper, we assume that the number of classes, K, is known. In Section 3.3, we discuss Bayesian model-selection strategies for determining the optimal value of K, and in the Discussion section, we note alternatives to fixing K.

The latent class two-part model is quite general in that it allows the fixed effects and random effect covariances to differ across classes. For the special case when K = 1, the model reduces to a Bayesian version of the standard two-part model for semi-continuous data (c.f., Tooze et al., 2002). For K > 2 classes, the model introduces two levels of between-subject heterogeneity: one induced by the latent classes, and a second represented by the within-class covariances Σ_k. Our model can therefore be viewed as a two-part growth mixture model. Note that Σ_k may vary across classes. For example, for some classes, b_1i and b_2i may be positively correlated, while for others they may be negatively correlated or even uncorrelated. In fact, the structure of Σ_k can itself vary across classes. For instance, in one class, there may be no particular structure (unstructured covariance), while in another, an exchangeable or an AR1 structure may be more suitable.

3. Priors Specification, Posterior Computation and Model Selection

3.1 Prior Specification

Under a fully Bayesian approach, prior distributions are assumed for all model parameters. To ensure a well-identified model with proper posteriors determined almost entirely by the data, we assign weakly informative proper distributions to all class-specific parameters {α_k, β_k, ${\tau }_k^2$, Σ_k, γ_k}. For the fixed effects, we assume exchangeable normal priors: α_k ~ N_p1 (μ_α, Σ_α) and β_k ~ N_p2 (μ_β, Σ_β). We assume that the prior hyperparameters are identical across classes, but this is not necessary. Each Σ_k is assumed to have a conjugate inverse-Wishart IW(ν₀, D₀) (ν₀ ≥ k) distribution. Our experience suggests that the conjugate IW prior performs well in zero-inflated models with low-dimensional random effect covariance matrices (c.f., Neelon, O’Malley, and Normand, 2010).

For, the lognormal precisions, ${\tau }_k^{-2}$, we assume conjugate Ga(λ, δ) priors. Following Garrett and Zeger (2000) and Elliott et al. (2005), we recommend γ_k ~ N_r[0, (9/4)I_r], which induces a prior for π_ik centered at 1/K and bounded away from 0 and 1. If there are no class-membership covariates (i.e., r = 1), a conjugate Dirichlet(e₁, …, e_K) prior can be placed directly on the class-membership probabilities π = (π₁, …, π_K)′, which can lead to convenient closed-form full conditionals. Frühwirth-Schnatter (2006) recommends choosing e_k > 1 to bound π_k away from zero.

3.2 Posterior Computation

Let ${\mathit{\theta }}_k={({\mathit{\alpha }}_k^{\prime },{\mathit{\beta }}_k^{\prime },{\tau }_k^2)}^{\prime }$. Assuming prior independence, the corresponding joint posterior is given by

$$\begin{array}{l}\pi ({\mathit{\theta }}_1,\dots ,{\mathit{\theta }}_K;\mathit{C};\mathbf{b};{\mathbf{\sum }}_1,\dots ,{\mathbf{\sum }}_K;{\mathit{\gamma }}_2,\dots ,{\mathit{\gamma }}_K\mid y)\propto \\ \prod _{k=1}^K\left\{\prod _{i=1}^n{\left[\prod _{j=1}^{n_i}f(y_{\mathit{ij}}\mid {\mathit{\theta }}_k,{\mathbf{b}}_i){\pi }_{\mathit{ik}}f({\mathbf{b}}_i\mid {\mathbf{\sum }}_k)\right]}^{{\mathrm{I}}_{(C_i=k)}}\pi ({\mathit{\alpha }}_k)\pi ({\mathit{\beta }}_k)\pi ({\tau }_k^2)\pi ({\mathbf{\sum }}_k)\right\}\prod _{h=2}^K\pi ({\mathit{\gamma }}_h),\end{array}$$

where f(y_ij∣θ_k, b_i) is given in equation (1) and $\mathbf{b}={({\mathbf{b}}_1^{\prime },\dots ,{\mathbf{b}}_n^{\prime })}^{\prime }$.

For posterior computation, we propose an MCMC algorithm that combines draws from full conditionals and Metropolis steps. After assigning initial values to the model parameters, the algorithm iterates between the following steps:

1. For k = 2, …, K, update the vector γ_k using a random-walk Metropolis step;

2. Sample the class indicators C_i (i = 1, …, n) from a categorical distribution with posterior probability vector p_i = (p_i1, …, p_iK);

3. For k = 1, …, K, sample α_k, β_k, ${\tau }_k^{-2}$, and Σ_k from their full conditionals;

4. Update b_i using a random-walk Metropolis step.

Details of the algorithm are provided in the Web Appendix. Convergence is monitored by running multiple chains from dispersed initial values and then applying standard Bayesian diagnostics, such as trace plots; autocorrelation statistics; Geweke’s (1992) Z-diagnostic, which evaluates the mean and variance of parameters at various points in the chain; and the Brooks-Gelman-Rubin scale-reduction statistic R̂, which compares the within-chain variation to the between-chain variation (Gelman et al., 2004). As a practical rule of thumb, a 0.975 quantile for R̂ ≤ 1.2 is indicative of convergence. In the application below, convergence diagnostics were performed using the R package boa (Smith, 2007).

A well-known computational issue for Bayesian finite mixture models is “label switching” in which draws of class-specific parameters may be associated with different class labels during the course of the MCMC run. Consequently, class-specific posterior summaries that average across the draws will be invalid. In some cases, label switching can be avoided by placing constraints on the class probabilities (Lenk and DeSarbo, 2000) or on the model parameters themselves (Congdon, 2005). However, as Frühwirth-Schnatter (2006) notes, these constraints must be carefully chosen to ensure a unique labeling. She describes several exploratory procedures useful for identifying appropriate constraints. As an alternative, Stephens (2000) proposed a post-hoc relabeling algorithm that minimizes the Kullback-Leibler distance between the posterior probability p_ij that individual i is assigned to class j under the current labeling, and the posterior probability under the “true” labeling, estimated as the posterior mean of p_ij. We apply Stephens’ approach in the case study below.

3.3 Determining the Number of Classes

To determine the number of latent classes, we adopt a model selection approach and use the deviance information criterion (DIC) proposed by Spiegelhalter et al. (2002) to compare models under various fixed values of K(K = 1, …, K_max). This approach has been applied in several previous studies involving latent class models (Elliott et al., 2005; White et al., 2008; Leiby et al., 2009).

Like Akaike’s information criterion (AIC), the DIC provides an assessment of model fit as well as a penalty for model complexity. The DIC is defined as D̄(θ) + p_D, where D̄(θ) = E [D(θ)∣y] is the posterior mean of the deviance, D(θ), and p_D = D̄(θ) − D̂(θ) = E[D(θ)∣y] − D(E[θ∣y]) is the difference in the posterior mean of the deviance and the deviance evaluated at the posterior mean of the parameters. The deviance, typically taken as negative twice the log-likelihood, is a measure of the model’s relative fit, whereas p_D is a penalty for the model’s complexity. For fixed effect models, the complexity—as measured by the number of model parameters—is easily determined. For random effect models, the dimension of the parameter space is less clear and depends on the degree of heterogeneity between subjects (more heterogeneity implies more “effective” parameters). DIC was proposed to estimate the number of effective parameters in a Bayesian hierarchical model.

As a rule of thumb, if two models differ in DIC by more than three, the one with the smaller DIC is considered the best fitting (Spiegelhalter et al., 2002). For finite mixture models, Celeux et al. (2006) recommend a modified DIC, termed DIC₃, which estimates D̂(θ) using the posterior mean of the marginal likelihood averaged across the classes, a measure invariant to label switching. Specifically,

$${\mathrm{DIC}}_3=2\overline{D}(\mathit{\theta })+2\log \left[\prod _{i=1}^n\widehat{f}({\mathit{y}}_i)\right],$$

where f̂(y_i) is the posterior mean of the marginal likelihood contribution for subject i averaged across the classes. As Celeux et al. (2006) point out, DIC₃ is closely related to the measure proposed by Richardson (2002) to avoid overfitting the number of components. In the application below, we use a hybrid DIC that combines DIC₃ with the original DIC measure: for the fixed effects, we average across classes, as in DIC₃; for the within-class random effects, we condition on the posterior draws, as in the original DIC. This approach preserves the conditional nature of the model, and provides a penalty for the effective number of random effect parameters. The approach can also be viewed as a natural extension of the one-class DIC measure provided in standard Bayesian software, such as WinBUGS (Spiegelhalter et al., 2003).

3.4 Assessment of the Final Model Fit

To assess the adequacy of the selected model, we use posterior predictive checking (Gelman, Meng, and Stern, 1996), whereby the observed data are compared to data replicated from the posterior predictive distribution. If the model fits well, the replicated data, y^rep, should resemble the observed data, y. To quantify the similarity, we can choose a discrepancy measure, T = T(y, θ), that takes an extreme value if the model is in conflict with the observed data. Popular choices for T include sample moments and quantiles, and residual-based measures.

The Bayesian predictive p-value (P_B) denotes the probability that the discrepancy measure based on the predictive sample, T^rep = T(y^rep, θ), is more extreme than the observed measure T. A Monte Carlo estimate of P_B can be computed by evaluating the proportion of draws in which T* > T. A p-value close to 0.50 represents adequate model fit, while p-values near 0 or 1 indicate lack of fit. The cut-off for determining lack of fit is subjective, although by analogy to the classical p-value, a Bayesian p-value between 0.05 and 0.95 suggests adequate fit. In some cases, a stricter range, such as (0.20, 0.80), might be more appropriate.

For the latent class two-part model, we recommend two test statistics to assess the fit of both the binomial and lognormal components. For the binomial component, we recommend T₁ = the proportion of observations greater than zero. For the nonzero observations, we suggest a modification of the omnibus chi-square measure proposed by Gelman et al. (2004)

$$T_2=\frac{1}{M}{\sum _k\sum _{i,j:y_{\mathit{ij}}>0}\left[\frac{[\log (y_{\mathit{ij}})-{\mu }_{\mathit{ijk}}]}{{\tau }_k}\right]}^2\times {\mathrm{I}}_{(C_i=k)},$$

where, for the random intercept model, ${\mu }_{\mathit{ijk}}={\mathit{x}}_{\mathit{ij}}^{\prime }({\mathit{\beta }}_k)+b_{2i}$ and M denotes the number of nonzero observations. To generate replicate data, we first draw replicate class indicators $C_i^{\mathit{rep}}\left(i=1,\dots ,n\right)$ using expression (2); then, conditional on $C_i^{\mathit{rep}}$, we generate ${\mathbf{b}}_i^{\mathit{rep}}$ from N₂(0, Σ_k); finally, we draw $y_{\mathit{ij}}^{\mathit{rep}}$ from (1). An alternative approach is to use the actual posterior draws of C_i and b_i; however, this approach does not mimic the data-generating process as accurately as the former approach. That said, for the analysis presented in Section 5, the two approaches yield similar results.

4. Simulation Study

To examine the properties of the proposed model, we conducted a small simulation study. First, we simulated 100 datasets from a three-class model according to equation (1). The datasets contained 500 subjects, each with five observations, for a total of 2,500 observations per dataset. The binomial and lognormal components contained class-specific fixed-effects intercepts, fixed-effect linear time trend, and random intercepts. That is, α = (α_k1, α_k2)′, β = (β_k1, β_k2)′ and given C_i = k, b_i = (b_1i, b_2i)′ ~ N₂(0, Σ_k), with

$${\mathbf{\sum }}_k=\left(\begin{array}{cc}{\sigma }_{k1}^2& {\rho }_k{\sigma }_{k1}{\sigma }_{k2}\\ {\rho }_k{\sigma }_{k1}{\sigma }_{k2}& {\sigma }_{k2}^2\end{array}\right),k=1,2,3.$$

We also allowed the class membership probabilities to include an intercept and a single covariate w_i; hence, γ₂ = (g₂₁, g₂₂)′, γ₃ = (g₃₁, g₃₂)′, and γ₁ = (0, 0) for identifiability.

Next, we fitted one to four class models to each of the 100 datasets and compiled the results. Web Table 1 presents the DIC statistics for each of the four fitted models. As expected, the average DIC across the 100 simulations was lowest for the three-class fitted model (i.e., the true model). Moreover, the three-class model had the lowest DIC values for each of the 100 datasets, followed in general by the two-class model, which had the second-lowest DIC in 97 of the 100 simulations. For the most part, the four-class model had the highest DIC score, alleviating concerns that the hybrid DIC measure proposed in Section 3.3 overestimates the number of classes.

Web Table 3 provides summary statistics for the three-class model parameters. Column 1 presents the estimated class precentages, averaged across the 100 simulations. These were identical (up to two decimal places) to the true class percentages of 31%, 26%, and 43% for classes 1, 2, and 3, respectively. Column 5 presents the average posterior estimates across the 100 simulations. The bias was extremely low for all parameters, including the random effect variance components. The coverage rates ranged from 0.91 to 0.99, but for the most part, were close to the nominal value of 0.95. Variability in coverage rates was likely due to the size of the simulation.

5. Assessing the Impact of Mental Health and Substance Abuse Parity

To analyze the FEHB data described in the introduction, we fitted a series of two-part growth mixture models, allowing the number of classes, K, to range from one to four. For each class, we fit a fixed effects model, a model with uncorrelated random intercepts, a model with correlated random intercepts, and a model with random intercepts for each component and a random slope for the lognormal component. We also fitted a model with an additional random slope for the binomial component (i.e., four random effects), but the model was poorly identified and failed to converge according to standard MCMC diagnostics. We consider identifiability issues related to this model further in the Discussion section.

Within each class, we assumed a probit-lognormal two-part model as in equations (1) and (2). For both components, the fixed-effect covariate vector x_ij comprised an intercept term and three dummy indicators representing years 2000–2002. Because our study included only four measurement occasions, we chose to model time categorically to allow for maximum flexibility in capturing the time trend. Alternative parameterizations of the time trend—such as polynomials or splines—may be appealing in other settings, particularly if there are a large number of time points. For K > 2 classes, we allowed gender and employee status to serve as class-membership covariates; specifically, w_i in equation (2) represented a 3 × 1 vector consisting of an intercept and indicator variables for female gender and employee vs. dependant status. To investigate the impact of between-subject heterogeneity, we compared fixed effects models to models with correlated and uncorrelated random intercepts.

The models were fitted in R version 2.8 (R Development Core Team, 2008) using a MCMC code developed by the authors. For each model, we ran three, initially dispersed MCMC chains for 200,000 iterations each, discarding the first 50,000 as a burn-in to ensure that a steady-state distribution had been reached. We retained every 50th draw to reduce autocorrelation. Run times ranged from six to 12 hours depending on the number of classes. MCMC diagnostics, such as trace plots, Geweke Z-statistics (Geweke, 1992), and Brooks-Gelman-Rubin scale reduction statistics (Gelman et al., 2004), were used to assess convergence of the chains. There was little evidence of label switching within individual chains, and Stephens’ (2000) relabeling algorithm tended to converge rapidly. In some cases, the class labels required reordering across chains, but the proper order was easily identified in each case.

For model comparison, we used the hybrid DIC measure proposed in Section 3.3. The results are presented in Table 2. For each class, the correlated random intercept model had the lowest DIC value. Overall, the three-class model with correlated random intercepts was preferred, followed by the two- and four-class correlated models.

Table 2.

Model comparison statistics for FEHB study.

Number of Classes	Model Description	DIC
1	Fixed Effects	22397
	Uncorrelated Random Intercepts*	19891
	Correlated Random Intercepts	18819
	Correlated Random Intercepts and Slope†	19588
2	Fixed Effects	20687
	Uncorrelated Random Intercepts	19241
	Correlated Random Intercepts	18755
	Correlated Random Intercepts and Slope	19315
3	Fixed Effects	20341
	Uncorrelated Random Intercepts	19230
	Correlated Random Intercepts	18736
	Correlated Random Intercepts and Slope	19441
4	Fixed Effects	20414
	Uncorrelated Random Intercepts	19480
	Correlated Random Intercepts	18772
	Correlated Random Intercepts and Slope	20270

^*Random intercepts for both components.

^†Random intercepts with a random slope for the lognormal component.

Web Figure 1 presents post-burn-in trace plots for four representative parameters from the 3-class random intercepts model: α₂₂ (change in log odds use at year 2 compared to year 1, class 2); β₂₂ (increase in log-spending at year 2 for class 2); γ₂₂ (log odds of class-two membership, female vs. male); and ρ₂ (class-2 random effect correlation). For clarity of presentation, we have graphed only two of the three MCMC chains. The overlapping trajectory lines suggest convergence and efficient mixing of the chains. The Geweke Z-diagostic p-values ranged from 0.35 (β₂₂) to 0.64 (α₂₂), indicating no significant difference in posterior means across regions of the chains; the 0.975 quantiles of the Brooks-Gelman-Rubin statistic were each less than 1.04, again indicating convergence of the chains. However, we did observe modest autocorrelation in the chains: the lag-10 autocorrelations ranged from 0.01 for α₂₂ to 0.16 for ρ₂.

Table 3 presents the posterior means and 95% posterior intervals for the three-class model.

Table 3.

Posterior means and 95% credible intervals (CrIs) for the three-class correlated model.

Class (%)	Model Component	Parameter (Variable)	Posterior Mean (95% CrI)
1 (67%)	Binomial	α11 (Intercept)	−2.64 (−3.78, −2.06)
		α12 (Year2)	−0.13 (−0.61, 0.17)
		α13 (Year3)	−0.50 (−1.35, −0.01)
		α14 (Year4)	−0.29 (−1.38, 0.26)
	Lognormal	β11 (Intercept)	4.22 (2.98, 5.30)
		β12 (Year2)	−0.36 (−0.78, 0.06)
		β13 (Year3)	−0.32 (−0.82, 0.14)
		β14 (Year4)	−1.02 (−1.92, −0.38)
	Variance Components	${\tau }_1^2$ (Lognormal Variance)	1.11 (0.98, 1.27)
		${\sigma }_{11}^2$ (Var[b1i])	3.65 (2.03, 8.22)
		${\sigma }_{12}^2$ (Var[b2i])	2.64 (1.74, 3.98)
		ρ1 (corr[b1i, b2i])	0.35 (−0.05, 0.69)
2 (23%)	Binomial	α21 (Intercept)	−2.02 (−3.27, −0.90)
		α22 (Year2)	0.41 (0.01, 0.84)
		α23 (Year3)	1.25 (0.77, 1.80)
		α24 (Year4)	1.38 (0.84, 1.98)
	Lognormal	β21 (Intercept)	2.02 (0.89, 3.03)
		β22 (Year2)	0.99 (0.30, 1.75)
		β23 (Year3)	2.26 (1.50, 3.09)
		β24 (Year4)	2.54 (1.70, 3.38)
	Variance Components	${\tau }_2^2$ (Lognormal Variance)	1.14 (0.97, 1.30)
		${\sigma }_{21}^2$ (Var[b1i])	2.07 (0.83, 4.22)
		${\sigma }_{22}^2$ (Var[b2i])	2.26 (1.04, 3.96)
		ρ2 (corr[b1i, b2i])	0.85 (0.65, 0.96)
3 (10%)	Binomial	α31 (Intercept)	0.86 (−4.23, 2.66)
		α32 (Year2)	1.73 (0.04, 6.50)
		α33 (Year3)	1.06 (−0.55, 5.13)
		α34 (Year4)	0.17 (−0.67, 1.39)
	Lognormal	β31 (Intercept)	6.55 (5.13, 6.95)
		β32 (Year2)	0.04 (−0.09, 0.16)
		β33 (Year3)	0.13 (−0.01, 0.24)
		β34 (Year4)	−0.01 (−0.14, 0.13)
	Variance Components	${\tau }_3^2$ (Lognormal Variance)	0.37 (0.32, 0.42)
		${\sigma }_{31}^2$ (Var[b1i])	6.80 (0.15, 30.74)
		${\sigma }_{32}^2$ (Var[b2i])	0.87 (0.55, 1.81)
		ρ3 (corr[b1i, b2i])	0.17 (−0.51, 0.82)
	Class Parameters	γ21 (Class 2 Intercept)	−1.55 (−2.92, −0.22)
		γ22 (Class 2 Female)	0.91 (0.22, 1.71)
		γ23 (Class 2 Employee)	−0.18 (−0.88, 0.44)
		γ31 (Class 3 Intercept)	−2.70 (−3.70, −0.78)
		γ32 (Class 3 Female)	1.05 (0.35, 1.68)
		γ33 (Class 3 Employee)	−0.003 (−0.56, 0.52)

A few general trends are worth noting:

1. Class 1 comprised an estimated two-thirds of the population and was characterized by low initial probability of spending (α₁₁) as well as low baseline median spending (β₁₁). These subjects, termed the “low spenders,” were relatively rare users of mental health services who exhibited a decreasing spending pattern over time;

2. Class 2, comprising an estimated 23% of subjects, included “moderate spenders” who had an increasing spending pattern over time. For these individuals, spending and use were closely linked, as demonstrated by the large increases in use and spending in 2001 and 2002, after enactment of the parity mandate. It appears that parity had the most impact on these individuals. We provide more formal assessment of the parity effect below;

3. Class 3 comprised the fewest subjects (10%) and was characterized by a high probability of spending and high median spending. Individuals in this “high spending” group tended to be chronic service users whose trends remained relatively stable over time.

The variance component estimates also reveal interesting trends. Classes 1 and 2 showed moderate to high positive correlation among the random intercepts (ρ₁ = 0.35 and ρ₂ = 0.85), suggesting a strong association between the probability of spending and the amount spent. Class 3, on the other hand, exhibited low correlation (ρ₃ = 0.17), with a credible interval well-overlapping zero. Thus, there was little evidence of an association between the probability of spending and the amount spent in this class. Note that these are conditional correlations (i.e., assuming class membership is known); they represent the additional correlation between the model components beyond that captured by class membership. In particular, for class 3, the marginal correlation (prior to knowing class membership) is quite high, since the probability of spending and amount spent both take on large values on their respective scales. However, once class 3 membership is known, there is little residual correlation between the components, as evidenced by the low ρ₃ value. Thus, given class 3 membership, knowing how likely one is to spend provides little additional information about the actual amount spent.

The class membership probabilities (γ’s) indicate that females were much more likely than males to be in higher spending classes. There was minimal impact for employee status. Table 4 presents these results on the probability scale. For example, an estimated 18% of male dependants were in class 2, compared to 31% of female dependants.

Table 4.

Predicted class-membership probabilities by covariate profile.

Gender	Employee Status	Class-Membership Probabilities
		Class 1	Class 2	Class 3
Male	Non-Employee	0.75	0.18	0.07
Male	Employee	0.77	0.16	0.07
Female	Non-Employee	0.57	0.31	0.12
Female	Employee	0.60	0.28	0.12

Figure 1 presents the posterior mean spending patterns for the three classes. (Web Figure 2 provides an enlarged view of classes 1 and 2.)

Figure 1.

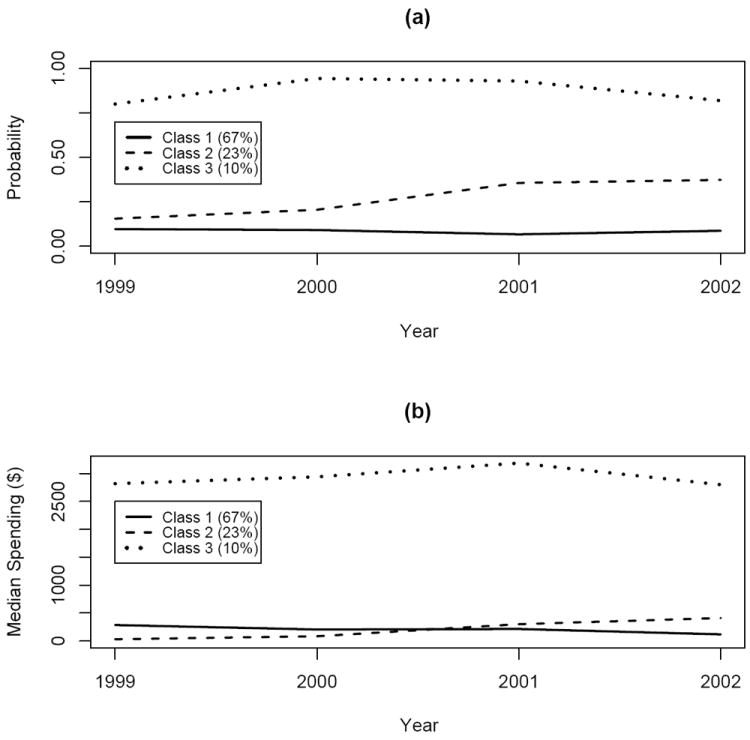
Posterior class trajectories for (a) probability of spending > $0 and (b) median spending (given some spending). See Web Figure 2 for an enlarged view of classes 1 and 2.

Again, three distinct groups emerge: “low spenders,” whose spending decreased over time; “moderate spenders,” who showed a substantial increase in spending, particular in 2001 when the parity directive went into effect; and “high spenders,” who spent large amounts on mental health services throughout the study period. Thus, it appears that parity had the largest impact on the moderate spenders. This policy may have encouraged class 2 individuals to use services more, thereby increasing their median annual spending. The findings also illustrate the relevance of uniquely modeling the probability of use and median spending given use: doing so revealed the direct impact of increased use on increased spending for subjects in class 2.

To formally assess the impact of the parity policy, we constructed parameter contrasts to compare the effect of parity on both the log-odds of spending and mean log-spending. In particular, for each class, we formed two contrasts:

$$\begin{array}{lll}\hfill \mathrm{change\; in\; log}­\mathrm{odds}(\mathrm{any\; spending})& =& ({\alpha }_{k3}+{\alpha }_{k4}-{\alpha }_{k2})/2,\mathrm{and}\\ \hfill \mathrm{change\; in\; mean\; log}­\mathrm{spending}& =& ({\beta }_{k3}+{\beta }_{k4}-{\beta }_{k2})/2.\end{array}$$

Positive contrasts estimates indicate an increase in the likelihood of spending and amount spent following parity. Because these contrasts are correlated, we plotted their joint posterior 95% highest probability density (HPD) regions, and examined whether these regions included the origin. As shown in Figure 2, the HPD regions for classes 1 and 3 contain the origin, indicating no significant parity effect for these classes. The circular plot for class 3 suggests low correlation between the contrasts, which is consistent with the small random effect correlation (ρ₃) estimate observed in Table 3. On the other hand, the HPD region for class 2 is situated away from the origin in the upper-right quadrant, suggesting a significant increase in both the probability of spending and amount spent following enactment of parity. This supports the earlier observation that parity has the greatest impact on class 2 subjects.

Figure 2.

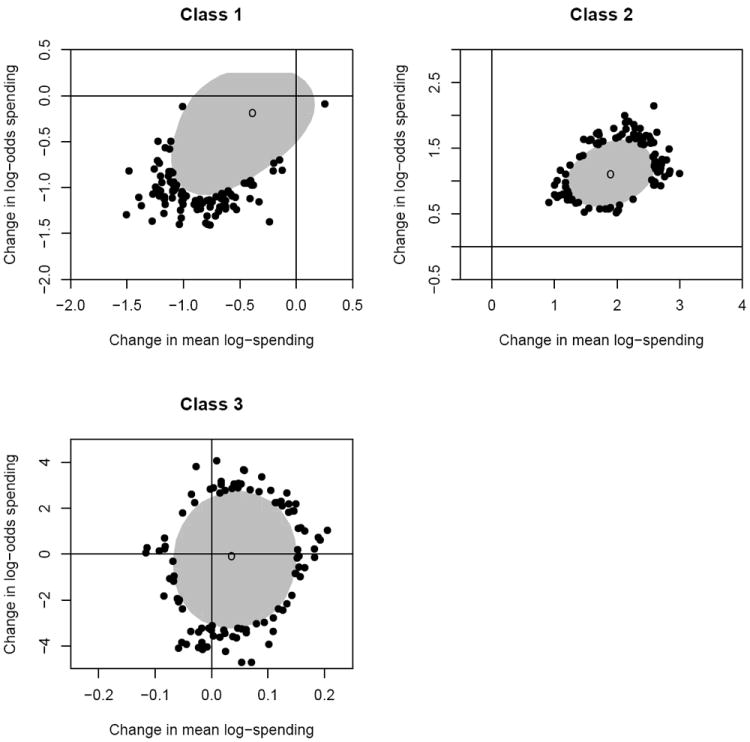
Posterior 95% highest probability density (HPD) regions for contrasts assessing the effect of the parity law. Y-axes represent the change in log-odds of any spending before and after introduction of parity; x-axes represent the change in the average amount spent (on the log scale) before and after parity. Shaded regions correspond to the bivariate 95% HPD regions, open circles denote posterior modes, and dots denote observations outside the 95% contours. For classes 1 and 3, the 95% HPD regions intersect the origin, suggesting no significant change due to parity. Conversely, class 2 showed a significant increase in both the log odds of any spending and the mean amount spent following parity.

As a final assessment of model fit, we conducted posterior predictive checks using the two discrepancy measures described in Section 3.4: the sample proportion of subjects with nonzero spending (T₁), and the omnibus chi-square statistic applied to subjects with nonzero spending (T₂). Web Figure 3(a) shows the posterior predictive distribution of T₁; the shaded region corresponds to the Bayesian predictive p-value of 0.29. For T₂, the observed and posterior predicted values vary across MCMC samples (both being functions of the posterior parameter draws). Therefore, Figure 3(b) provides a two-dimensional scatterplot of the posterior predicted values based on y^rep versus the observed values based on y. The Bayesian predictive p-value of 0.37, corresponding to the proportion of samples above the diagonal, again indicates adequate fit of the three-class, correlated random effects model.

6. Discussion

We have described a Bayesian approach to fitting a two-part growth mixture model for longitudinal medical expenditure data. The model includes correlated random effects with class-specific covariance structures, thus permitting the variance and correlation between the two model components to vary across classes. Advantages of the approach include distinct modeling of zero and nonzero values; flexible modeling of time trends, class membership probabilities, and between-subject heterogeneity (both within and across classes); full posterior inference, including estimation of complex parameter contrasts and their corresponding HPD regions; incorporation of prior information; and, in our experience, improved computation over non-MCMC estimation techniques.

In our application, we were able to identify three distinct types of individuals: a group of low spenders, who generally made little use of mental health services, thereby minimizing their spending; a group of chronic spenders who, perhaps due to medical conditions, tended to use mental health services often and in more costly ways; and a group of moderate users, primarily female dependants, who after introduction of the parity mandate, tended to use services more often, subsequently increasing their expenditures. Future parity efforts might target these moderate spenders who are most likely to benefit from increased mental health coverage.

We have focused primarily on the probit-lognormal two-part model commonly used to analyze medical expenditures. This model has the particular advantage of yielding closed-form full conditionals for many of the model parameters, resulting in efficient MCMC computation. Although the model can be fit in standard Bayesian software, such as WinBUGS, sampling “traps” can occur for complex models with many classes. To overcome this problem, we implemented the MCMC algorithm in R using the full-conditionals described in the Web Appendix.

The model can be easily adapted to allow for a logit link for the binomial component, as well as multivariate random effects (e.g., random slopes as well as random intercepts). The standard random-slope model implies a 4 × 4 covariance matrix that induces cross-correlations between the intercepts and slopes for the two components. In some cases, particularly when the ratio of observation to parameters is low, it may be necessary to impose a structure to this matrix to ensure the model is well identified. Note that adding a single random slope to the model yields n additional parameters, along with several class-specific variance components. It is therefore not surprising that in our application the full random effects model with random intercepts and slopes for both components failed to converge to a stationary distribution. With only four observations per subject, attempting to include random slopes for both components yielded more parameters than observations, thereby impeding identifiability. As a result, we focused our analysis on models with at most three random effects (two random intercepts and a random slope for the lognormal component).

The model can also be extended to accommodate multiple outcomes by assuming, for example, conditional independence between outcomes given class membership and subject-specific random effects. Alternatively, the factor-analytic approach recently proposed by Leiby et al. (2009) can be used to avoid the conditional independence assumption. Future work might also allow the covariance structures themselves to vary across classes, permitting, say, an AR1 structure in one class and a compound symmetric structure in another.

The two-part semi-continuous model is closely related to zero-inflated models for count data, such as the Poisson hurdle model and the zero-inflated Poisson (ZIP) model. In fact, hurdle models for count data are structurally very similar to two-part semi-continuous models, leading to many analogous interpretations of model parameters. See Neelon, O’Malley, and Normand (2010) for a discussion of Bayesian approaches to fitting zero-inflated count models.

To estimate the number of latent classes, we adopted a commonly used model-comparison approach based on DIC. A limitation of this approach is that the analysis must be conducted several times in order to compare models with varying numbers of classes. This approach also fails to incorporate the uncertainty associated with the unknown number of classes K. One way to accommodate random K is to employ reversible jump MCMC (Green, 1995), which shifts between models of different dimensions K ∈ 1, …, K_max. The drawback here is potentially slow mixing of the MCMC chain. An alternative strategy is to specify an infinitely large mixture via a Dirichlet process (DP) prior on the number of mixture components (Ferguson, 1973).

The models proposed here have wide applicability to a variety of settings, including health economics, health services research, psychometrics, substance-abuse research—essentially, any of a number of fields in which semi-continuous data, typified by a large spike at zero, arise.