Enhancing the mathematical properties of new haplotype homozygosity statistics for the detection of selective sweeps

Abstract

Soft selective sweeps represent an important form of adaptation in which multiple haplotypes bearing adaptive alleles rise to high frequency. Most statistical methods for detecting selective sweeps from genetic polymorphism data, however, have focused on identifying hard selective sweeps in which a favored allele appears on a single haplotypic background; these methods might be underpowered to detect soft sweeps. Among exceptions is the set of haplotype homozygosity statistics introduced for the detection of soft sweeps by Garud et al. (2015). These statistics, examining frequencies of multiple haplotypes in relation to each other, include H₁₂, a statistic designed to identify both hard and soft selective sweeps, and H₂/H₁, a statistic that conditional on high H₁₂ values seeks to distinguish between hard and soft sweeps. A challenge in the use of H₂/H₁ is that its range depends on the associated value of H₁₂, so that equal H₂/H₁ values might provide different levels of support for a soft sweep model at different values of H₁₂. Here, we enhance the H₁₂ and H₂/H₁ haplotype homozygosity statistics for selective sweep detection by deriving the upper bound on H₂/H₁ as a function of H₁₂, thereby generating a statistic that normalizes H₂/H₁ to lie between 0 and 1. Through a reanalysis of resequencing data from inbred lines of Drosophila, we show that the enhanced statistic both strengthens interpretations obtained with the unnormalized statistic and leads to empirical insights that are less readily apparent without the normalization.

Introduction

A selective sweep, the process whereby beneficial mutations at a locus that contribute to the fitness of an organism rise in frequency to become prevalent in a population, can occur through two main mechanisms that leave distinct genomic signatures (Pritchard et al., 2010; Cutter and Payseur, 2013; Messer and Petrov, 2013). A relatively new adaptive allele can proliferate so that the single haplotype on which it has occurred reaches a high frequency, resulting in a signature of a “hard” selective sweep (Maynard Smith and Haigh, 1974; Kaplan et al., 1989; Kim and Stephan, 2002). Alternatively, a mutation that arises de novo multiple times or exists as standing genetic variation on several haplotype backgrounds before the onset of positive selection can increase in frequency; in these cases, multiple favored haplotypes have relatively high frequencies, generating a signature of a “soft” selective sweep (Hermisson and Pennings, 2005; Przeworski et al., 2005; Pennings and Hermisson, 2006a). Soft sweeps can provide an effective mechanism for natural selection and might explain a sizeable fraction of selective events in many systems (Orr and Betancourt, 2001; Innan and Kim, 2004; Pritchard et al., 2010; Messer and Petrov, 2013).

Most statistical methods that have been designed to detect selective sweeps from patterns of genetic polymorphism search for patterns expected under a hard-sweep model, such as the presence of a single common haplotype (Hudson et al., 1994), high haplotype homozygosity (Depaulis and Veuille, 1998; Sabeti et al., 2002; Voight et al., 2006), high-frequency derived variants and related features of site-frequency spectra (Tajima, 1989; Braverman et al., 1995; Fay and Wu, 2000; Nielsen et al., 2005), or local loss of variation near a putative selected site (Maynard Smith and Haigh, 1974; Begun and Aquadro, 1992; Kim and Stephan, 2002). Many methods that search for patterns expected with hard sweeps, however, can be less well suited to the problem of identifying soft sweeps (Pennings and Hermisson, 2006b; Teshima et al., 2006; Cutter and Payseur, 2013). Therefore, current genomic scans for selective sweeps might be limited in their ability to uncover an important class of adaptive events.

Recently, it has been shown that statistics based on haplotype homozygosity can identify both hard and soft sweeps from population-genomic data (Ferrer-Admetlla et al., 2014; Garud et al., 2015). Garud et al. (2015) developed a haplotype homozygosity statistic, H₁₂, relying on the principle that in a soft sweep, the most frequent haplotype might not predominate in frequency, and instead, multiple frequent haplotypes might be present. In terms of frequencies p_i ≥ 0 for i = 1, 2, 3, . . . with ${\sum }_{i=1}^{\infty }{p}_i=1$ and p₁ ≥ p₂ ≥ p₃ ≥ . . ., Garud et al. (2015) defined H₁₂ as

$$H_{12}={(p_1+p_2)}^2+\sum _{i=3}^{\infty }{p}_i^2.$$ (1)

This statistic calculates homozygosity by combining the two largest haplotype frequencies into a single value and then computing a haplotype homozygosity. Garud et al. (2015) determined that H₁₂ has reasonable power to detect both hard and soft sweeps, applying the statistic to Drosophila population-genomic data and identifying abundant signatures of natural selection.

To determine whether the genomic regions with the highest values of H₁₂ were compatible with either a hard-sweep or soft-sweep pattern, Garud et al. (2015) examined a second statistic, H₂/H₁, a ratio of a haplotype homozygosity H₂ that excludes the most frequent haplotype and a haplotype homozygosity H₁ that includes this haplotype:

$$H_1=p_1^2+p_2^2+\sum _{i=3}^{\infty }{p}_i^2$$ (2)

$$H_2=p_2^2+\sum _{i=3}^{\infty }{p}_i^2.$$ (3)

For high values of H₁₂, hard sweeps are expected to produce relatively low values of H₂/H₁ because they produce a single high-frequency haplotype (very high p₁, low p₂). Soft sweeps, on the other hand, produce multiple high-frequency haplotypes (high p₁, p₂, and perhaps others), and are expected to produce higher values of H₂/H₁.

Garud et al. (2015) found that this two-step process—identification of regions with high H₁₂ followed by examination of H₂/H₁—could both detect selective sweeps in general and distinguish hard and soft sweeps. As we will show, however, a complication in the approach is that the permissible range of H₂/H₁ varies with the value of H₁₂. Thus, the magnitude of H₂/H₁ that might be regarded as indicative of a soft or hard sweep can depend on the associated values of H₁₂. This potential difference in interpretations for values of H₂/H₁ as a function of H₁₂ can present a particular challenge when comparing H₂/H₁ at multiple loci with a wide range of H₁₂ values.

In a line of work separate from the use by Garud et al. (2015) of homozygosity-based soft sweep statistics, Rosenberg and Jakobsson (2008) and Reddy and Rosenberg (2012) analyzed the properties of homozygosity statistics in relation to the frequency of the most frequent allele, identifying upper and lower bounds on homozygosity given the frequency of the most frequent allele. This work, along with related work on other statistics (Long and Kittles, 2003; Hedrick, 2005; Jost, 2008; Vanliere and Rosenberg, 2008; Maruki et al., 2012; Jakobsson et al., 2013), seeks to understand mathematical bounds on population-genetic statistics, so that their application and interpretation can be suitably informed by the mathematical constraints on their numerical values.

Here, to facilitate the interpretation of the statistics of Garud et al. (2015) and to enhance comparisons among values of these statistics at loci with different haplotype homozygosities, we use a result from Rosenberg and Jakobsson (2008) to determine the upper and lower bounds on H₂/H₁ as a function of H₁₂. The upper bound provides a basis for normalization of H₂/H₁ to produce a statistic with the same range, from 0 to 1, irrespective of the value of H₁₂. Using the upper bound and the new normalized statistic, we reexamine Drosophila data analyzed by Garud et al. (2015), demonstrating that the upper bound, (H₂/H₁)_max, and the normalized statistic, (H₂/H₁)′, enable improved insights regarding soft selective sweeps on the basis of genetic polymorphism data.

Theory

Our goal is to determine the maximum of H₂/H₁ given the value of H₁₂, for 0 < H₁₂ ≤ 1. For convenience, we denote Z = H₂/H₁. We denote the desired upper bound by Z_max.

For generality in our description, we consider “alleles” at a locus. These distinct “alleles” can be viewed as representing distinct haplotypes at a specific location in the genome; the assumption is that a set of distinct genetic types is considered, representing perhaps distinct haplotypes or distinct alleles in the traditional sense, and the sum of the frequencies of the types is 1.

We sort alleles in descending order of frequency, so that p₁ > 0 and p₁ ≥ p₂ ≥ p₃ ≥ ... ≥ 0. The number of alleles is left unspecified, and it can be arbitrarily large; thus, ${\sum }_{i=1}^{\infty }{p}_i=1$. For our mathematical analysis, we consider parametric allele frequencies; that is, the p_i are treated as known frequencies in a population rather than values estimated from samples. The mathematical setting follows Rosenberg and Jakobsson (2008).

We let M = p₁ + p₂. Because p₁ > 0, M, H₁₂, and H₁ are all strictly positive. By analogy with H₁ and H₂, denote $H_3={\sum }_{i=3}^{\infty }{p}_i^2$. Thus, by eq. 1,

$$H_{12}=M^2+H_3.$$ (4)

The upper bound on H₂/H₁ given H₁₂

We proceed in two main steps. First, for fixed H₁₂ and fixed M, we determine the maximum of Z as a function of p₁. Next, we identify the value of M that maximizes Z. This pair of steps constructs the set of allele frequencies ${\left\{p_i\right\}}_{i=1}^{\infty }$ that generates the maximal Z at fixed H₁₂. A graphical overview of the argument appears in Figure 1.

Figure 1.

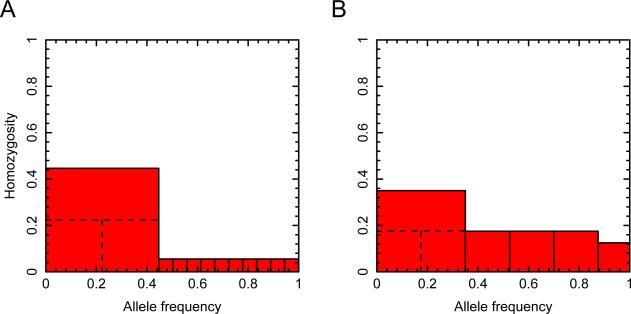
A geometric illustration of the argument for finding the upper bound on H₂/H₁ as a function of H₁₂. In both panels, the unit interval (x-axis) is partitioned into components representing allele frequencies. H₁₂ is represented by the sum of the areas of the red shaded regions, each indicating a squared frequency; the largest red square indicates (p₁ + p₂)² or M². (A) Step 1: for fixed H₁₂ and fixed M, H₂/H₁ is maximal when p₂ = p₁. The maximal H₂/H₁ requires p₁ to be as small as possible, but p₁ ≥ p₂ by definition; at the maximal H₂/H₁, p₁ and p₂ are equal. (B) Step 2: allowing M to vary while keeping H₁₂ fixed, H₂/H₁ is maximal when M is as small as possible. At the maximum for H₂/H₁, M is reduced to the point where p₁ and as many subsequent alleles as possible have identical frequency, and at most one remaining allele of smaller frequency completes the unit interval. In both panels, H₁₂=0.23. Part A uses $(10+3\sqrt{170})∕110\approx 0.4465$ for M and $(100-3\sqrt{170})∕1100\approx 0.0553$ for each of 10 additional alleles. The dashed lines illustrate the choice of p₂ = p₁ = M/2. Part B achieves the maximum of H₂/H₁ = 221/270 ≈ 0.8185 (eq. 12), with M = 0.35.

Maximizing Z for fixed H₁₂ and fixed M

Because $H_2=p_2^2+H_3$ and p₂ = M – p₁, H₂ can be rewritten

$$H_2={(M-p_1)}^2+H_3.$$ (5)

Note that by eq. 4, for fixed H₁₂ and fixed M, H₃ is constant. Because M = p₁ + p₂, p₁ ≥ p₂, and p₁ > 0, it follows that M/2 ≤ p₁ ≤ M. Treated as a function of p₁, on the interval [M/2, M], (M – p₁)² + H₃ is decreasing.

Using eq. 5, Z = H₂/H₁ can be written

$$\begin{array}{cc}\hfill Z=& \frac{{(M-p_1)}^2+H_3}{p_1^2+{(M-p_1)}^2+H_3}\hfill \\ \hfill =& \frac{1}{p_1^2∕[{(M-p_1)}^2+H_3]+1}.\hfill \end{array}$$ (6)

In eq. 6, for fixed H₁₂ and fixed M, $p_1^2$ is increasing in p₁ and (M – p₁)² + H₃ is decreasing. The ratio $p_1^2∕[{(M-p_1)}^2+H_3]$ is therefore increasing in p₁, so that the entire expression for Z decreases with p₁. It is therefore maximized when p₁ is minimized—in other words, when p₁ = p₂ = M/2. The maximal Z for fixed H₁₂ and fixed M is

$$Z=\frac{4H_{12}-3M^2}{4H_{12}-2M^2}.$$ (7)

It remains to maximize Z by finding the value of M that maximizes eq. 7 for fixed H₁₂. By rewriting eq. 7 as Z = 1 – M²/(4H₁₂ – 2M²), it can be seen that for fixed H₁₂, as M increases, M² increases, 4H₁₂ – 2M² decreases, and Z decreases. Thus, for fixed H₁₂, the maximal Z, treated as a function of M, occurs when M isas small as possible.

The minimal value of M given H₁₂

We have shown that maximizing Z for fixed H₁₂ and M requires p₁ = p₂ = M/2, and hence, using the descending order of the allele frequencies, p₃ ≤ M/2. We have also shown that maximizing Z for fixed H₁₂ over all possible M requires us to find the minimal M permissible for fixed H₁₂. This problem can be solved with a known result. We first ignore the trivial case of H₁₂ = 1, for which the maximal Z has M = 1, p₁ = p₂ = 1/2, H₁ = 1/2, H₂ = 1/4, and Z_max = 1/2.

By eq. 4, minimizing M for fixed H₁₂ amounts to maximizing H₃. Lemma 3 of Rosenberg and Jakobsson (2008) obtains the maximal sum of squares for a set of nonnegative numbers in a non-increasing sequence, each of which lies below the same specified constant, and whose sum is specified. In our case, the sequence is ${\left\{p_i\right\}}_{i=3}^{\infty }$, the entries are bounded above by M/2, and their sum is 1 – p₁ – p₂ = 1 – M.

Applying the lemma, we obtain

$$H_3\le K(K-1){\left(\frac{M}{2}\right)}^2-2(1-M)(K-1)\frac{M}{2}+{(1-M)}^2,$$ (8)

where K = ⌈(1 – M)/(M/2)⌉ = ⌈2/M⌉ – 2 and ⌈x⌉ denotes the smallest integer greater than or equal to x; in the application of the lemma, K gives the number of nonzero numbers in the sequence ${\left\{p_i\right\}}_{i=3}^{\infty }$ that achieves the maximum. Equality is achieved if and only if ⌈2/M⌉ – 3 alleles (in addition to alleles 1 and 2) have frequency M/2, and one allele has frequency (1 – M) – (⌈2/M⌉ – 3)(M/2) = 1 – (⌈2/M⌉ – 1)(M/2).

The minimal M is obtained by substituting the upper bound from eq. 8 for H₃ in eq. 4 and solving for M. The equation that must be solved is

$$H_{12}=\frac{K^2+3K+4}{4}{M}^2-(K+1)M+1.$$ (9)

Note that K is currently considered a function of M, equaling ⌈2/M⌉ – 2. However, we can instead determine the value of K as a function of H₁₂, so that eq. 9 becomes a simple quadratic equation in M. To solve eq. 9 for M at a given H₁₂, we must find the value of K—the number of alleles of nonzero frequency (not including alleles 1 and 2)—that applies for the given value of H₁₂.

We break the unit interval (0, 1) into disjoint intervals [2/I, 2/(I – 1)) for integers I ≥ 3. On the interval [2/I, 2/(I – 1)) for M, K = I – 2. Inserting K = I – 2 into eq. 9, for M in this interval, the minimal M in terms of H₁₂ is obtained by solving

$$H_{12}=\frac{I^2-I+2}{4}{M}^2-(I-1)M+1$$ (10)

for M. Thus, identifying the value of K in terms of H₁₂ for use in eq. 9 amounts to finding the value of I in terms of H₁₂ for use in eq. 10.

The right-hand side of eq. 10 is monotonically increasing on the interval [2/I, 2/(I – 1)), as it is a concave-up parabola in M with minimum at M = 2(I – 1)/(I² – I + 2) = 2/[I + 2/(I – 1)] < 2/I. The vertex of the parabola lies to the left of the left endpoint of the interval, M = 2/I, so that on [2/I, 2/(I – 1)), the parabola is increasing.

At the left endpoint M = 2/I, H₁₂ = (I + 2)/I², and at the right endpoint M = 2/(I – 1), H₁₂ = (I + 1)/(I – 1)². Consequently, because H₁₂ increases as a function of M on the interval [2/I, 2/(I – 1)), for this interval, H₁₂ lies in [(I + 2)/I², (I + 1)/(I – 1)²).

As a strictly monotonic continuous function from [2/I, 2/(I – 1)) to [(I + 2)/I², (I + 1)/(I – 1)²), H₁₂ is invertible as a function of M. Treated as a function of M in (0, 1), I satisfies 2/I ≤ M < 2/(I – 1); similarly, as a function of H₁₂ in (0, 1), I satisfies (I + 2)/I² ≤ H₁₂ < (I + 1)/(I – 1)². In other words, given H₁₂, I must be equal to the smallest integer for which (I + 2)/I² ≤ H₁₂.

Solving this inequality, either $I\ge (1+\sqrt{8H_{12}+1})∕\left(2H_{12}\right)$ or $I\le (1-\sqrt{8H_{12}+1})∕\left(2H_{12}\right)$. The latter root is negative and can be discarded as I ≥ 3. The smallest integer that satisfies the former inequality is

$$I=\lceil \frac{1+\sqrt{8H_{12}+1}}{2H_{12}}\rceil .$$ (11)

We can now complete the solution for the minimal M as a function of H₁₂: this minimum is a solution to eq. 10 when eq. 11 is used for I. The equation has two roots; the smaller root is smaller than 2/I, and therefore lies outside the interval [2/I, 2/(I – 1)) in which M must fall when H₁₂ satisfies eq. 11. The minimal M therefore equals the larger root.

The formula for Z_max

Compiling the steps we have completed, we have that as a function of H₁₂,

$$Z_{\max }\left(H_{12}\right)=\frac{4H_{12}-3M^2}{4H_{12}-2M^2},$$ (12)

where M is the larger root of eq. 10,

$$M=\frac{2(I-1)+2\sqrt{(I^2-I+2)H_{12}-(I+1)}}{I^2-I+2},$$ (13)

and I satisfies eq. 11. The formula for Z_max holds for all H₁₂ in (0, 1]; in the H₁₂ = 1 case that we initially discarded, eq. 12 gives the correct value Z_max = 1/2. Z_max is reached when I – 1 alleles each have frequency M/2 and one allele has frequency 1 – (⌈2/M⌉ – 1)(M/2).

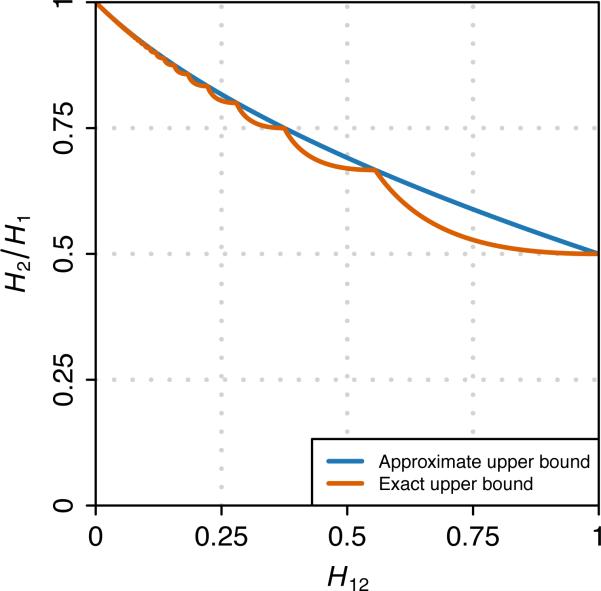
Figure 2 plots eq. 12 as a function of H₁₂ over the unit interval. A piecewise structure of the upper bound Z_max is visible, reflecting the fact that at points H₁₂ = (I + 2)/I² for integers I ≥ 3, the value of I as a function of H₁₂ changes, and Z_max is not differentiable. Z_max approaches a limiting value of 1 as H₁₂ approaches 0, and it declines monotonically to a value of 1/2 at H₁₂ = 1.

Figure 2.

The upper bound on H₂/H₁ as a function of H₁₂. The exact upper bound is given by eq. 12, and the approximate upper bound is given by eq. 15.

An approximation to Z_max

It is convenient to consider a simple approximation to Z_max by examining the points H₁₂ = (I + 2)/I² for integers I ≥ 3. At these points, applying eqs. 11-13,

$$I=\frac{1+\sqrt{8H_{12}+1}}{2H_{12}},$$ (14)

M = 2/I, and Z_max = (I – 1)/I. Eqs. 11-13 simplify because Z_max is achieved when I alleles each have frequency 1/I, unlike for other H₁₂ < 1, where one nonzero frequency differs from the others.

We can approximate Z_max by finding a function Y_max that satisfies

$$Y_{\max }\left(\frac{I+2}{I^2}\right)=\frac{I-1}{I}$$

at the points specified by integers I ≥ 3 and using this function to interpolate across all values of H₁₂. When H₁₂ = (I + 2)/I² for integers I ≥ 3, I satisfies eq. 14, and

$$\frac{I-1}{I}=\frac{1+\sqrt{8H_{12}+1}-2H_{12}}{1+\sqrt{8H_{12}+1}}.$$

Multiplying the numerator and denominator of this equation by $1-\sqrt{8H_{12}+1}$, we have

$$Y_{\max }\left(H_{12}\right)=\frac{5-\sqrt{8H_{12}+1}}{4}.$$ (15)

This approximate bound agrees with the strict bound Z_max at points H₁₂ = (I + 2)/I² for integers I ≥ 3, and it matches Z_max at the endpoints of the unit interval. In Figure 2, it can be seen that Y_max provides a reasonable approximation to Z_max over the entire interval.

Not only is Y_max an approximation to the strict upper bound Z_max, Y_max ≥ Z_max for H₁₂ in (0, 1], so that Y_max is itself an upper bound. To prove this result, using eqs. 15 and 12, we have

$$Y_{\max }\left(H_{12}\right)-Z_{\max }\left(H_{12}\right)=\frac{(2H_{12}+M^2)-(2H_{12}-M^2)\sqrt{8H_{12}+1}}{4(2H_{12}-M^2)}.$$

The denominator is positive, as 2H₁₂ – M² = M² + 2H₃ > 0. It remains to show that

$$2H_{12}+M^2\ge (2H_{12}-M^2)\sqrt{8H_{12}+1}.$$

Squaring both sides, Y_max(H₁₂) – Z_max(H₁₂) ≥ 0 if

$$-8H_{12}[4H_{12}^2-4M^2{H}_{12}+(M^4-M^2)]\ge 0.$$

As H₁₂ is positive, Y_max(H₁₂) – Z_max(H₁₂) ≥ 0 if H₁₂ lies in the closed interval bounded by the roots of the quadratic term in brackets, or (M² – M)/2 and (M² + M)/2. Because 0 < M ≤ 1, the smaller root is at most 0, and H₁₂ ≥ (M² – M)/2 always holds. It thus suffices to prove H₁₂ ≤ (M² + M)/2.

Recalling eq. 4, we must show that H₃ ≤ (M – M²)/2. Eq. 8 provides a maximum on H₃ in terms of M; substituting this maximum for H₃, we have H₃ ≤ (M – M²)/2 if

$$\frac{1}{4}(KM+M-2)(KM+2M-2)\le 0.$$

This last inequality is true by definition of K = ⌈2/M⌉ – 2, as 2/M – 2 ≤ K < 2/M – 1 implies KM + M – 2 < 0 and KM + 2M – 2 ≥ 0. We can therefore conclude that H₃ ≤ (M – M²)/2, and hence H₁₂ ≤ (M² + M)/2, and Y_max(H₁₂) – Z_max(H₁₂) ≥ 0 for H₁₂ in (0, 1].

The lower bound on H₂/H₁ given H₁₂

It is straightforward to show that for any H₁₂ in (0, 1], H₂/H₁ can get arbitrarily close to 0. For H₁₂ = 1, we set p₁ = 1 – ε and p₂ = ε for a small ε > 0. Then H₂/H₁ = ε²/[(1 – ε)² + ε²], which approaches 0 as ε → 0. Otherwise, we construct a scenario with one frequent allele and K rare alleles, and demonstrate that H₂/H₁ → 0 as K → ∞.

Suppose $p_1=\sqrt{K{H}_{12}-1}∕\sqrt{K-1}$ and $p_2=p_3=\dots =p_{K+1}=(1-\sqrt{K{H}_{12}-1}∕\sqrt{K-1})∕K$ for large K. Frequency p₁ is large and the remaining frequencies are small. In this case,

$$\begin{array}{cc}\hfill \frac{H_2}{H_1}=& \frac{K{p}_2^2}{p_1^2+K{p}_2^2}\hfill \\ \hfill =& \frac{{(1-\frac{\sqrt{K{H}_{12}-1}}{\sqrt{K-1}})}^2∕K}{\frac{K{H}_{12}-1}{K-1}+{(1-\frac{\sqrt{K{H}_{12}-1}}{\sqrt{K-1}})}^2∕K}\hfill \\ \hfill =& \frac{{(\sqrt{K-1}-\sqrt{K{H}_{12}-1})}^2}{K(K{H}_{12}-1)+{(\sqrt{K-1}-\sqrt{K{H}_{12}-1})}^2}.\hfill \end{array}$$

The denominator has higher degree in K than the numerator, so that lim_{K → ∞}(H₂/H₁) = 0.

The mean range of H₂/H₁ given H₁₂

Determining the mean of the range of Z, treated as a function of H₁₂ over the unit interval, can provide a sense of the magnitude of the constraint placed by H₁₂ on Z. For a statistic with a larger mean range, a greater proportion of the unit interval can be achieved, and the statistic is less constrained than is one with a smaller mean range.

Because Y_max(H₁₂) ≥ Z_max(H₁₂), the simpler Y_max can assist in evaluating the mean size of the range of Z. As the minimum Z approaches 0 for all H₁₂ in (0, 1], the size of the range for Z is simply Z_max. On the unit interval, Y_max has mean

$${\int }_0^1{Y}_{\max }\left(H_{12}\right)d{H}_{12}=\frac{17}{24}\approx 0.708,$$ (16)

and therefore, the mean Z_max is smaller than 17/24. This mean exceeds 1/2, as the minimal Z_max for H₁₂ in (0, 1], at H₁₂ = 1, is 1/2. Numerical integration of eq. 12 to obtain the mean Z_max gives

$$\sum _{I=3}^{\infty }{\int }_{(I+2)∕I^2}^{(I+1)∕{(I-1)}^2}{Z}_{\max }\left(H_{12}\right)d{H}_{12}\approx 0.684.$$ (17)

This result illustrates that the mean across the unit interval for H₁₂ of the error in the approximation of Z_max by Y_max is small, approximately 0.708 – 0.684 = 0.024. Further, although the range of Z is constrained, the mean range over all values of H₁₂ in (0, 1] is larger than corresponding mean constraints in other contexts involving homozygosity, F_st, the r² statistic for linkage disequilibrium, and the frequency of the most frequent allele (Rosenberg et al., 2003; Rosenberg and Jakobsson, 2008; Vanliere and Rosenberg, 2008; Reddy and Rosenberg, 2012; Jakobsson et al., 2013; Edge and Rosenberg, 2014).

Normalized statistics

Because H₂/H₁ can approach 0 for any H₁₂, a normalization of H₂/H₁ to lie in [0, 1] need only be concerned with the upper bound on H₂/H₁. We can therefore define exact and approximate normalizations of Z at given values of H₁₂ as follows:

$$Z^{\prime }=\frac{Z}{Z_{\max }\left(H_{12}\right)}$$ (18)

$$Z^{″}=\frac{Z}{Y_{\max }\left(H_{12}\right)},$$ (19)

The denominators of these equations are computed using eqs. 12 and 15, respectively.

Application to data

We illustrate the bounds on H₂/H₁ as functions of H₁₂ by reexamining two Drosophila melanogaster data sets studied by Garud et al. (2015), each containing fully sequenced genomes of inbred lines generated from samples taken in North Carolina. First, we consider the Drosophila Genetic Reference Panel (DGRP) data set consisting of sequences of 145 inbred lines (Mackay et al., 2012). Next, we examine the Drosophila Population Genomic Panel (DPGP) consisting of 40 strains. We consider these two data sets generated with different samples both to show an example use of the upper bounds and to demonstrate how inferences from samples with differing numerical patterns in H₁₂ and H₂/H₁ can be viewed as comparable.

DGRP data

We first consider the DGRP data set studied by Garud et al. (2015). As a consequence of inbreeding, the DGRP genomes are largely homozygous. On each of the four autosomal arms, Garud et al. (2015) examined haplotypes within analysis windows of 400 single-nucleotide polymorphisms (SNPs, ~10kb). Because low recombination rates can result in high haplotype homozygosities, Garud et al. (2015) excluded analysis windows overlapping 100 kb tracts measured by Comeron et al. (2012) to have recombination rates lower than 5 × 10^–7 centimorgans per base pair (cM/bp). To classify haplotypes within windows, Garud et al. (2015) assigned the 400-SNP haplotypes into groups according to exact sequence identity. If a haplotype with missing data matched multiple haplotypes at all genotyped sites in the analysis window, then the haplotype was randomly assigned to one of these classes. In the DGRP data set, all heterozygous sites in a strain were treated as missing data. Examining all 4,013,703 segregating sites across the 145 strains, 0.7% heterozygous sites per base pair per strain and 4.2% missing data per base pair per strain were observed. If a haplotype could not be conclusively assigned based on the information at non-missing data sites, then the haplotype was randomly assigned to a haplotype class that matched at all other sites; across all analysis windows and strains, 18% of assignments to haplotype classes used this method of random assignment. Windows were incremented by 50 SNPs, so that consecutive windows overlapped by 350 SNPs.

Each window has a haplotype frequency distribution across the 145 lines, enabling computations of H₁₂, H₁, and H₂. To avoid inflating the number of selective events inferred in a genomic region, Garud et al. (2015) grouped together consecutive windows as belonging to the same “peak” if the H₁₂ values in all of the grouped windows were above a critical H₁₂ value calculated under a neutral demographic model. They assigned H₁₂ and H₂/H₁ values to individual peaks by using the values calculated in the analysis window with the largest H₁₂ within a peak. Garud et al. (2015) focused on the 50 peaks with the largest H₁₂ values, none of which possessed two or more windows sharing the same highest H₁₂ value. The top three peaks coincided with the loci Ace, Cyp6g1, and CHKov1, prominent cases of adaptation previously discovered by detailed focused analyses (Daborn et al., 2001; Catania et al., 2004; Menozzi et al., 2004; Aminetzach et al., 2005; Karasov et al., 2010; Schmidt et al., 2010; Magwire et al., 2011).

Effect of normalization in the DGRP data

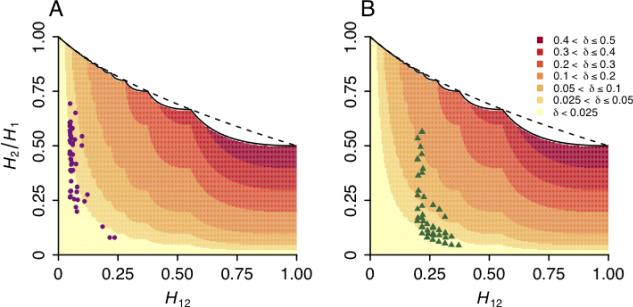
We assessed the effect of the application of Z′ to H₁₂ and H₂/H₁ values calculated for the top 50 peaks in the DGRP data set. To do so across the full range of possible values for (H₁₂, H₂/H₁), we first calculated the change δ = Z′ – Z in H₂/H₁ produced by the normalization. For any value of H₁₂, as H₂/H₁ increases, δ also increases, reflecting the monotonicity of the upper bound on H₂/H₁ with increasing H₁₂ (Figure 3A). The maximal δ of 1/2 is achieved when H₁₂ = 1 and H₂/H₁ = 1/2.

Figure 3.

The effect of the application of Z′ on H₂/H₁ values in data from Drosophila. The shaded regions show the change δ in H₂/H₁ values after applying the normalization, where δ = Z′ – Z. Overlaid are points representing the top 50 windows for H₁₂ in Drosophila melanogaster genome scans. (A) Drosophila Genetic Reference Panel (DGRP) data. (B) Drosophila Population Genomic Panel (DPGP) data. The solid line shows the exact upper bound on H₂/H₁ (eq. 12), and the dashed line shows the approximate upper bound (eq. 15).

Overlaid in Figure 3A are the H₁₂ and H₂/H₁ values from the 50 top peaks in the DGRP data set. The values of H₁₂ generally lie below 0.25, with most values occurring near 0.1. The values of H₂/H₁ span a wide range, with most (H₁₂, H₂/H₁) combinations lying in a region of the space where δ is between 0.025 and 0.05.

DPGP data

Our second example considers the DPGP data set that was also studied by Garud et al. (2015). The DPGP data set (Mackay et al., 2012) consists of 40 of the original 145 inbred lines in the DGRP data set, sequenced and assembled separately from the DGRP data (www.dpgp.org).

In the DPGP data set, considering all 2,337,358 segregating sites across the 40 lines, there were 1.2% heterozygous sites per base pair per strain, and the missing data rate was 7.5%. With this reduced sample size compared to the DGRP data—and hence, with both shorter distances over which haplotypes become unique and faster computation times—Garud et al. (2015) measured H₁₂ values in shorter overlapping analysis windows of 100 SNPs incremented by 1 SNP. The treatment of haplotypes and missing data proceeded in the same manner as in the DGRP analysis. In this scan, averaging across lines, haplotypes with missing data were clustered with other haplotypes matching at all other positions at a lower rate of 2.7%.

As in the DGRP analysis, Garud et al. (2015) identified the 50 peaks with the highest H₁₂. This analysis produced a distinct but overlapping set of high-H₁₂ windows as the DGRP top 50 peaks, again recovering known cases of adaptation at Ace, Cyp6g1, and CHKov1.

Effect of normalization in the DPGP data

As in our analysis of the DPGP data, we assessed the effect of the application of Z′ to high-H₁₂ peaks in the DPGP data set. Figure 3B plots the (H₂/H₁, H₁₂) values for the top 50 peaks in the DPGP data. In comparison to those seen in the DGRP data set, the H₁₂ values in the DPGP data are generally greater, and the H₂/H₁ values lower. As a consequence, the points in the DPGP data lie in a region of the space in which normalization has a greater effect, often with δ > 0.05.

Comparison of DGRP and DPGP

Garud et al. (2015) compared the positions of the top 50 peaks in the DPGP data set according to H₁₂ with the positions of the top 50 peaks in the DGRP data set to determine if the same selective events were identified in the two data sets. To do so, Garud et al. (2015) overlapped the edge coordinates of the peaks in the two data sets, where the edge coordinates of each peak correspond to the positions of the first SNP of the first analysis window and the last SNP of the last analysis window within a peak. An overlap was defined as a non-empty intersection of the two genomic regions defining the boundaries of the two peaks, one from one data set and one from the other. Garud et al. (2015) found that 16 DPGP peaks overlapped 13 DGRP peaks, 10 of which were among the top 15 peaks in the DGRP scan. In three cases, two DPGP peaks overlapped one DGRP peak because multiple non-overlapping peaks in the DPGP data were in the same region as a DGRP peak. These multiple proximate peaks in the DPGP data set might have been part of the same selective events.

Jointly considering the DGRP and DPGP data sets, different sample depths and analysis window sizes can result in different distributions of H₁₂ and H₂/H₁ values, and thus, in different inferences about selection. As a consequence, although several H₁₂ peaks overlap in the DGRP and DPGP scans, the H₁₂ and H₂/H₁ values for the top peaks differ between the two data sets. This result complicates the comparison of the selection signals obtained between the two data sets. Application of our normalization, however, can facilitate a meaningful comparison of the H₁₂ and H₂/H₁ values measured in different data sets that potentially uncover the same selective events.

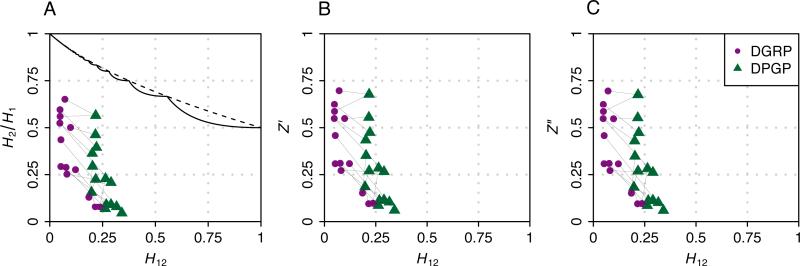
We applied the Z′ and Z″ normalizations to overlapping peaks in the two data sets. Figure 4A shows that prior to normalization, the H₂/H₁ values for DGRP exceed those of DPGP, as was seen previously in the plots of all 50 windows in Figure 3. However, after normalization, the distributions of H₂/H₁ values for the two scans are comparable despite the differences in H₁₂. We quantified this change with a paired two-tailed Wilcoxon signed-rank test, testing the null hypothesis that the distributions of H₂/H₁ values in the DGRP and DPGP data are the same before and after application of Z′ and Z″. Because 16 peaks in the DPGP data set overlap 13 peaks in the DGRP set, where three pairs of DPGP peaks each overlap unique peaks in the DGRP data, we removed one of the overlapping peaks from each pair in order to perform a paired test. We applied this procedure eight times to account for every possible combination of discarded peaks, finding that in all cases, before application of Z′ or Z″, H₂/H₁ was greater in the DGRP data than in the DPGP data (P = 0.0473, averaged across the eight choices). After application of Z′ and Z″, however, the comparison of DGRP and DPGP did not produce a significant difference (P = 0.1946 and P = 0.1781 for Z′ and Z″, respectively, averaged across the eight choices). Thus, because normalization reduces the difference in H₂/H₁ values between corresponding peaks in the DGRP and DPGP data, the normalization suggests that differences in H₂/H₁ for corresponding peaks are attributable largely to the different values of H₁₂ in the two data sets rather than to genuine differences in the biological signals that the two data sets provide.

Figure 4.

H₁₂ and H₂/H₁ values calculated in overlapping peaks in the DGRP and DPGP data sets before normalization and after the application of Z′ and Z″. Corresponding points for the DGRP and DPGP data sets are connected by lines. Note that because the 16 DPGP peaks overlap 13 DGRP peaks, three DGRP points are each connected to a pair of DPGP points. Also, two pairs of DPGP points with different chromosomal locations have the same (H₁₂, H₂/H₁) coordinates. (A) Unnormalized H₂/H₁ values. Overlaid are the exact upper bound (solid) and the approximate upper bound (dashed) as given by eq. 12 and eq. 15. (B) Values of Z′ (eq. 18). (C) Values of Z″ (eq. 19).

Note that normalization can in principle change the rank order of peaks for a given data set, as a lower H₂/H₁ at a higher H₁₂ can be shifted after normalization above a higher H₂/H₁ at a lower H₁₂. In our examples with the DGRP and DPGP data sets, however, relatively few reorderings of peaks took place upon normalization. We calculated a Spearman rank correlation coefficient to quantify the difference in rank order of Z and Z′ values and Z and Z″ values for the overlapping peaks in the DGRP and DPGP data sets, and in all four calculations (DGRP Z to Z′, DGRP Z to Z″, DPGP Z to Z′, DPGP Z to Z″), the correlation coefficient exceeded 0.999.

Discussion

Statistical methods for detecting selective sweeps from genomic data have enabled the identification of cases of adaptation in multiple organisms. Many statistics have been developed to identify hard selective sweeps, and recent attention has now also focused on detecting soft sweeps (Messer and Neher, 2012; Peter et al., 2012; Fu and Akey, 2013; Messer and Petrov, 2013; Vitti et al., 2013; Ferrer-Admetlla et al., 2014; Jensen, 2014; Wilson et al., 2014). Garud et al. (2015) recently proposed the haplotype homozygosity statistics H₁₂ and H₂/H₁ to discover both hard and soft selective sweeps and to differentiate whether top candidates for selection have signatures of hard or of soft sweeps. They applied their method to two Drosophila population-genomic data sets, DGRP and DPGP, recovering known cases of adaptation as well as finding new candidates.

In this paper, we have shown that the permissible range of H₂/H₁ values is dependent on their associated H₁₂ values, and that therefore, the interpretation of H₂/H₁ in distinguishing hard and soft sweeps can be challenging when comparing H₂/H₁ values across loci with a broad distribution of H₁₂ values. To facilitate interpretation of H₂/H₁ values measured in scans with a wide range of H₁₂ values, we developed approximate and exact normalizations Z′ and Z″ that can be applied to H₂/H₁. The application of the statistics Z′ and Z″ to data has the greatest impact for H₂/H₁ values with high associated H₁₂ values (>0.5).

We illustrated the use of the new bounds and normalizations using data from Drosophila. Garud et al. (2015) compared the H₁₂ peaks in the DGRP and DPGP data sets, finding that 13 DGRP peaks overlapped 16 DPGP peaks. However, the overlapping H₁₂ peaks in the two data sets had significantly different H₂/H₁ values despite presumably reflecting the same selective events. In applying Z′ and Z″ to the H₂/H₁ values observed at the highest, overlapping H₁₂ peaks in the two data sets, we found that the comparison of distributions of H₂/H₁ values observed in the two scans did not produce a significant difference after normalization. Thus, the differences in distributions of H₁₂ and H₂/H₁ across data sets might be attributable to differences in sample sizes and analysis window sizes in the two scans rather than to differences in biological signal. Indeed, the two data sets differed in a number of ways that could have generated higher H₁₂ values on average for DPGP compared to DGRP. DPGP had a smaller sample size; in evaluating H₁₂ from a finite sample of size n ≥ 2, eq. 1 has a minimum of (n + 2)/n², which is greater for smaller n. H₁₂ was also applied to DPGP in smaller analysis windows; decreasing the window size increases the probability of haplotype identity, thus increasing measures of homozygosity.

Our work on the relationship between H₁₂ and H₂/H₁ parallels other studies (Long and Kittles, 2003; Rosenberg et al., 2003; Hedrick, 2005; Rosenberg and Jakobsson, 2008; VanLiere and Rosenberg, 2008; Maruki et al., 2012; Reddy and Rosenberg, 2012; Jakobsson et al., 2013; Edge and Rosenberg, 2014) in obtaining bounds on population-genetic statistics. A shared feature common to these studies is that in each study, unexpected or counterintuitive bounds are identified that are informative for sensible interpretation. As in some of these studies, however, our calculations consider an unspecified number of haplotypes K. If we instead required that K be specified as a finite constant, it would not be possible to reach the lower bound of 0 on H₂/H₁ because the lower bound is obtained from a limiting scenario with large numbers of low-frequency alleles. The difference in bounds between arbitrary-K and finite-K cases can for some statistics be nontrivial, especially for small K (Reddy and Rosenberg, 2012); for future work, it will be of interest to determine the magnitude of the effect on the H₂/H₁ bounds of fixing the value of K.

The proposed normalizations, Z′ and Z″, offer an improvement in the interpretation of the H₁₂ and H₂/H₁ statistics proposed by Garud et al. (2015). Further simulation-based investigation of the influence on H₁₂ and H₂/H₁ of such variables as haplotype window sizes and sample sizes will be important for continuing to clarify the behavior of the statistics in models of selective sweeps. Nevertheless, as shown in our Drosophila example, the normalization of H₂/H₁ in data sets of varying sample sizes and SNP densities can help with the interpretation of selection scans, especially as data for testing population-genomic hypotheses become increasingly available in a variety of organisms.