Analysis of composition of microbiomes: a novel method for studying microbial composition

Abstract

Background

Understanding the factors regulating our microbiota is important but requires appropriate statistical methodology. When comparing two or more populations most existing approaches either discount the underlying compositional structure in the microbiome data or use probability models such as the multinomial and Dirichlet-multinomial distributions, which may impose a correlation structure not suitable for microbiome data.

Objective

To develop a methodology that accounts for compositional constraints to reduce false discoveries in detecting differentially abundant taxa at an ecosystem level, while maintaining high statistical power.

Methods

We introduced a novel statistical framework called analysis of composition of microbiomes (ANCOM). ANCOM accounts for the underlying structure in the data and can be used for comparing the composition of microbiomes in two or more populations. ANCOM makes no distributional assumptions and can be implemented in a linear model framework to adjust for covariates as well as model longitudinal data. ANCOM also scales well to compare samples involving thousands of taxa.

Results

We compared the performance of ANCOM to the standard t-test and a recently published methodology called Zero Inflated Gaussian (ZIG) methodology (1) for drawing inferences on the mean taxa abundance in two or more populations. ANCOM controlled the false discovery rate (FDR) at the desired nominal level while also improving power, whereas the t-test and ZIG had inflated FDRs, in some instances as high as 68% for the t-test and 60% for ZIG. We illustrate the performance of ANCOM using two publicly available microbial datasets in the human gut, demonstrating its general applicability to testing hypotheses about compositional differences in microbial communities.

Conclusion

Accounting for compositionality using log-ratio analysis results in significantly improved inference in microbiota survey data.

Our knowledge of the role of microbiota in human health and disease has expanded substantially over the past few years (2). It is now well known that health outcomes in later life can be affected by early-life microbial compositions (3–6), demonstrating the need to better understand microbiota composition. The composition of human microbial ecosystems is diverse, containing hundreds to thousands of species-level phylotypes, and analysis of such complex data requires special statistical methods (7).

Current technologies for studying the microbiota at a community-wide level are based on operational taxonomic units (OTUs), which are microbial genomic sequences clustered by sequence similarity. OTUs are then typically mapped to a taxonomic reference database (e.g. Greengenes [8]). High-throughput sequencing provides an estimate of the abundance of each OTU in the specimen (e.g. a fecal sample); crucially, they are not to be interpreted as the true parametric abundance of the corresponding taxon in the microbial ecosystem (e.g. the human gut) from which the specimen was derived. It is critical to understand what the observed data represent and what statistical parameters are being tested. The current literature on the analysis of microbiome data is not very precise and may potentially lead to misinterpretation of the biology. To help researchers understand the distinctions among various statistical parameters, we provide a detailed description in the online supplementary files.

Comparison of microbial composition between two or more populations on the basis of OTUs in the specimen is not equivalent to comparing the abundance of the taxa in the microbial ecosystems from which the specimen is obtained. Consider the following example: Suppose that, in two random samples of 100 animals each captured from two different forests, there are 20 and 30 bears, respectively. It is then reasonable to estimate that 20 and 30% of the animals in the two forests, respectively, are bears. But we may not conclude that there are more bears in the second forest than in the first. For example, if the first forest has 10,000 animals and the second 500 animals, then based on the above observed proportions of bears, there are an estimated 2,000 bears in the first forest but only 150 in the second. It is thus inappropriate to draw inferences regarding the total abundance in the ecosystem from the abundance of OTUs in the specimen. However, it is more reasonable to draw inferences regarding the relative abundance of a taxon in the ecosystem using its relative abundance in the specimen. In this paper we exploit this feature of the data.

Microbial relative abundances within a specimen sum to one and thus result in compositional data residing in a simplex (9) rather than the Euclidean space. As a consequence, standard statistical methods such as the Pearson correlation coefficient, t-test, ANOVA, linear regression analysis, and so on are not directly applicable for analyzing microbiome relative abundance data. Ignoring the fact that the data are in a simplex may result in incorrect or misleading results (10). For example, because the sum of the relative abundances is unity, it is a mathematical requirement that the Pearson correlation coefficient be negative for at least one pair of taxa. It is therefore impossible to distinguish between true negative correlations and those induced by the compositional structure, which could potentially lead to misinterpretations of association between taxa pairs. Recently, Friedman and Alm (11) introduced the method of sparse compositional correlation (SparCC) to analyze correlation networks among OTUs in 16S rRNA amplicon studies. SparCC uses the variance of log-ratios of pairwise components (fraction of OTUs) instead of the Pearson product moment correlation to appropriately describe networks between OTUs. Although determination of pairwise correlations among taxa is useful for understanding associations among taxa, they cannot be used for comparing two or more populations in terms of the abundance of taxa, a common problem of interest.

Recent publications (12, 13) have advocated modeling OTU counts using variants of the multinomial distribution, including the Dirichlet-multinomial distribution. This family of probability models may not be appropriate for microbiome data because, intrinsically, such models impose a negative correlation among every pair of OTUs (see Equation 16 on page 68 of Ref. [14]). The microbiome data, however, display both positive and negative correlations. To illustrate this point, we obtained Pearson correlation coefficients among all pairs of OTUs in the global gut data (15). The resulting histogram of the correlation coefficients (Fig. 1) suggests that there is a high frequency of both positive and negative correlations, which indicates against the use of distributions such as the multinomial and Dirichlet-multinomial distribution for microbiome data.

Fig. 1.

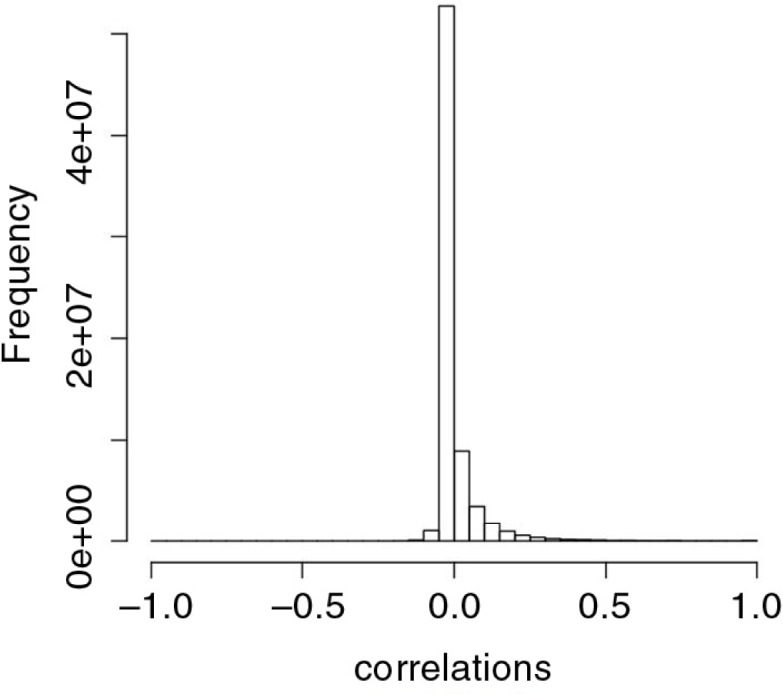
Histogram of pairwise Pearson correlation between operational taxonomic units in the global gut data set.

In view of the above observations, motivated by (9), we propose a novel methodology based on compositional log-ratios, called ANCOM (analysis of composition of microbiomes), for detecting differences in microbial mean taxa abundance. The proposed methodology is computationally straightforward and can process thousands of taxa. Our extensive simulation studies show that ANCOM outperforms Zero Inflated Gaussian (ZIG) methodology (1) by substantially reducing the FDR and increasing power. Detailed descriptions of the methodology and simulations are provided in the online supplementary files. Using two publicly available datasets of human gut microbiota (15, 16), we illustrate how ANCOM detects differences in microbial compositions.

Results

Comparison of ANCOM, t-test, and ZIG

We compared the performance of ANCOM with that of the t-test and ZIG using a variety of configurations of parameters, such as the number of microbial taxa (500 or 1,000) and proportion of differentially abundant taxa π (ranging from 0.05 to 0.25). To mimic a real data scenario, we chose model parameters such that 10% of the taxa had high abundance, 30% medium abundance, and 60% low abundance. The number of subjects in the two study groups was 20 and 30, respectively. A complete description of the parameters and the probability model is provided in the online supplementary files. We used the R program provided in (1) to implement ZIG. The FDR and power were estimated using 100 simulation runs. Because many researchers (17–19) use the t-test on the relative abundance data to test hypotheses regarding the population abundance, presumably because of its familiarity rather than its applicability to microbiome data, we also evaluated the performance of the t-test.

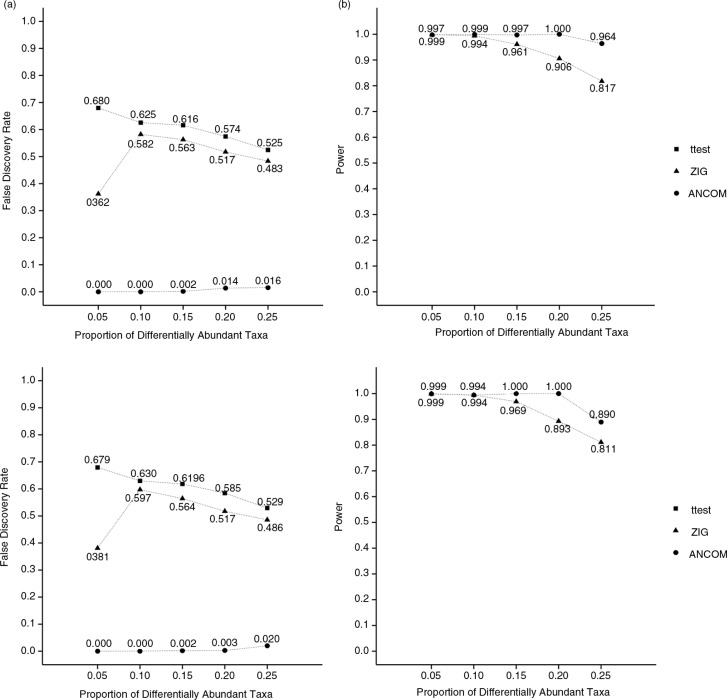
Figure 2 summarizes the simulation results. Using the observed OTUs at the specimen level, in all our simulations we estimated the FDR and power for hypotheses regarding the mean abundance of taxa in the ecosystem, which is the parameter of interest to a biologist, rather than the mean abundance of taxa at the specimen level. Thus, for a given taxon, in our simulation study, under the null hypothesis both groups have the same mean abundance (at the ecosystem level). The top panels correspond to 500 taxa, the bottom panels to 1,000 taxa. In each panel, results of FDR comparisons for different patterns of π are provided on the left and power on the right. The overall results vary little with the number of taxa. In every case, we note that the t-test and ZIG have inflated FDRs, whereas ANCOM almost always has a very small FDR. The FDR of the t-test and ZIG can be very high, for example 68% for t-test and nearly 60% for ZIG, meaning that far more than half of the discoveries made by these two procedures could potentially be wrong. Interestingly, ANCOM not only controls the FDR but increases power. In the supplementary file, we provide results from a simulated example where the OTU abundances are much smaller than abundances in the ecosystem. In that case, we observed that the FDR of ZIG could be as high as 60% (68% for t-test), whereas that for ANCOM never exceeded 5%. Our simulation studies clearly illustrate that, using the relative abundance at the specimen level, our methodology can successfully draw inferences regarding taxon abundance at the ecosystem level.

Fig. 2.

Comparison of (a) false discovery rate and (b) statistical power to detect differentially abundant microbial taxa by t-test, ZIG, and analysis of composition of microbiomes, based on 100 simulated data sets consisting of 500 (top panels) and 1,000 (bottom panels) taxa. Value of π ranges from 0.05 to 0.25. Power for the t-test is unity over the entire range of π and is not shown on the plots.

Application of ANCOM to real data

To demonstrate that the above concerns are not simply theoretical and that improved power to detect differences can alter biological conclusions, we reanalyzed data from a recent paper (16). This exciting study examined temporal changes in the composition of the microbiome in preterm babies, focusing primarily on three classes of bacteria: Bacilli, Clostridia, and Gammaproteobacteria. Using standard t-tests/ANOVA within linear mixed models, they concluded that temporal changes in the relative abundance of Bacilli, Clostridia, and Gammaproteobacteria in premature babies were minimally influenced by the mode of delivery, antibiotic use, or breast milk. These results were surprising, because a substantial body of literature has found these variables to have systematic effects (20). However, because the denominator in calculating the proportion of any one taxon is the sum of the abundance of all taxa, the relative abundance of any given taxon is confounded by the abundance of others. Consequently, even if the absolute abundances of most taxa remain unchanged, the relative abundance of all taxa may change because of changes in the abundance of one taxon.

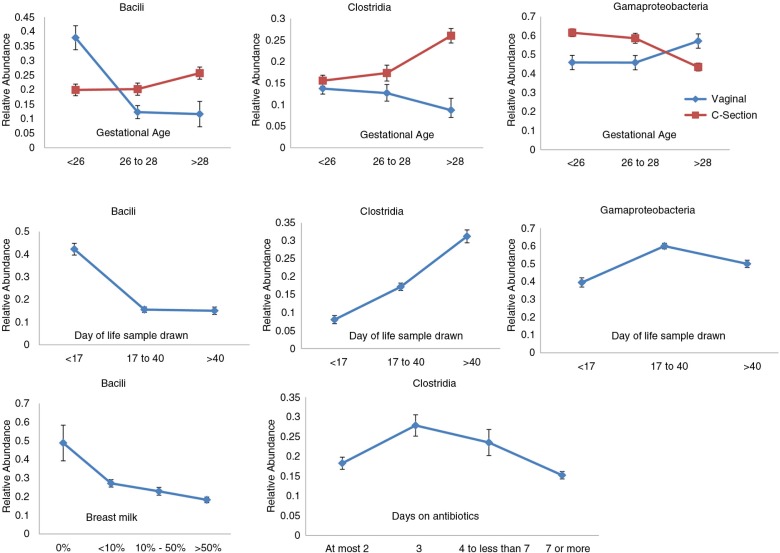
A reanalysis of the data in (16) using ANCOM suggests that, when analyzed using an improved statistical model, the findings are more consistent with what has been previously observed in the literature. Specifically, using ANCOM, we find that the abundance of Bacilli, Clostridia, and Gammaproteobacteria in premature babies is influenced by factors including delivery mode, antibiotic use, and breast milk (Fig. 3), in accordance with previous literature. The difference in abundance of each of the three bacterial classes between babies delivered by C-section and those delivered normally also changed significantly with gestational age. All three classes of bacteria showed a significant interaction between gestational age and the effect of C-section. Although all statistical inferences are based on the log-ratios (see the supplementary file for more details), in Fig. 3, we illustrate the relationship graphically using the raw data, namely the unadjusted OTU relative abundances for the three bacterial classes against variables with significant effects. For plotting purposes, we discretized days on antibiotics into four categories.

Fig. 3.

Unadjusted raw average OTU relative abundance and standard errors of Bacilli, Clostridia, and Gammaproteobacteria against the variables detected as having significant effects by application of ANCOM on the microbial dataset provided in LaRosa et al. (16). The mean OTU relative abundances for the two modes of birth at different gestational age categories are provided in the first row. The second row provides the mean OTU relative abundances at different ‘Day of life’ categories. The third row provides the mean OTU relative abundance for Bacilli against categories of breast milk variable and for Clostridia against categories of ‘Days on antibiotics’. Although, as in LaRosa et al. (16), ‘Day of life’ and ‘Days on antibiotics’ were analyzed as continuous variables, for simplicity of plotting in this figure they were discretized.

In many studies where finer taxonomic resolution is of interest, both in host-associated microbial communities and in environmental samples, populations can be compared on the basis of thousands of OTUs. ANCOM is designed to accommodate such larger data sets. For example, we applied ANCOM to the cross-cultural human gut microbiota comparison mentioned above (15), consisting of 11,905 OTUs. Subjects were classified into five age groups: 0–2 years (Group 1), 2–10 (Group 2), 10–20 (Group 3), 20–50 (Group 4), and greater than 50 years (Group 5), from three countries (USA, Malawi, and Venezuela). We first tested for temporal patterns from early to later life at the phylum level. Our analysis revealed that Firmicutes (p-value<0.001), Euryarchaeota (p-value<0.0001), and Lentisphaerae (p-value<0.001) differed between Groups 1 and 2. Comparing subjects in Groups 2 and 3, we noted that the rare Fusobacteria (p-value<0.01), Spirochaetes (p-value<0.0001), Cyanobacteria (p-value<0.0001), and Elusimicrobia (p-value<0.0001) were significantly different; little is known about the role of these phyla in the human gut. Cyanobacteria (p-value<0.01) was the only phylum detected to be significantly different between Groups 3 and 4. No phyla were detected to differ at later stages of life. This further supports the idea that major changes in the human gut microbiome occur early in life and stabilize later (as described in the original paper) but suggests that follow-up work on low-abundance taxa may be especially important in understanding the basis for these changes.

To investigate differences in microbial composition by geographical location among infants aged 0–2 (Group 1), we analyzed the 11,905 OTUs from global gut data (15). As typically done (13), to avoid sparsely observed OTUs, which tend to introduce noise, we investigated only those OTUs that were prevalent in at least 25% of the sample. The results of ANCOM are summarized in Table 1.

Table 1.

Differentially abundant OTUs identified by ANCOM when comparing samples from infants (younger than 2 years) obtained from Malawi, Venezuela, and USA. The number of OTUs considered for each comparison was determined using a prevalence cutoff of 25% on the entire set of 11,905 OTUs. Detected differentially abundant OTUs are grouped into phyla level based on corresponding taxonomy classification.

USA vs. Malawi		Malawi vs. Venezuela		Venezuela vs. USA
Number of OTUs considered=1408		Number of OTUs considered=1597		Number of OTUs considered=1760
Phyla	Significantly different OTUs	Phyla	Significantly different OTUs	Phyla	Significantly different OTUs
Firmicutes	128	Firmicutes	5	Firmicutes	126
Bacteroidetes	48	Proteobacteria	1	Bacteroidetes	43
Proteobacteria	16	Cyanobacteria	1	Proteobacteria	11
Actinobacteria	3			Tenericutes	9
Tenericutes	3			Actinobacteria	3
Cyanobacteria	2			Cyanobacteria	3
Spirochaetes	1			Elusimicrobia	1
Fusobacteria	1
Total	203	Total	7	Total	196

We observed significant differences in the composition between samples from the United States and Malawi or Venezuela, with the majority of detected OTUs belonging to Firmicutes, Bacteroidetes, and Proteobacteria, among the dominant taxa in the gut. These differences could be caused by contrasting diet, feeding practices, and hygiene during early life. On the other hand, only seven OTUs were detected as significantly different between Malawi and Venezuela, indicating the close similarity in composition between these two populations, despite being geographically far apart.

All computations were carried out in the publicly available software R (version 3.0). ANCOM took 17, 23, and 25 min to process the three examples shown in Table 1, consisting of approximately 12,000 OTUs total (a typically sized data set), on a Macbook Pro (Intel Core i7, 2.4 GHz, 16 GB RAM). This example illustrates that ANCOM is applicable for analysis of a typical OTU count data set.

Discussion

True taxon abundances in the ecosystem of interest are typically unobservable, but data are available only for the specimen obtained from the ecosystem. Differences in the abundance of OTUs at the specimen level cannot be extrapolated to differences in abundance at the ecosystem level. However, assuming that specimens are random observations from the ecosystem of interest, it is reasonable to assume that the expected relative abundance of a taxon in a specimen is the same as it is in the ecosystem. Thus, comparison of the expected relative abundances at the specimen level is approximately equivalent to making comparisons at the ecosystem level. However, because the relative abundance of taxa sum to 1, it is not appropriate to use standard statistical methods such as the t-test, ANOVA, and so on directly on the relative abundances, because the standard methods implicitly assume that there are no such restrictions on the data (9). Similarly, it is not appropriate to use methods based on the multinomial or Dirichlet-multinomial distributions, because such distributions require all pairs of OTUs to be negatively correlated. However, as demonstrated in this paper, this requirement may not be valid for microbiome data, since some pairs of OTUs may be positively correlated. Lastly, our simulation studies indicate that the ZIG methodology (1) can produce unacceptably high FDRs and hence may not be suitable for comparing the mean taxa abundance at the ecosystem level between two or more populations. Furthermore, according to the statistical model given in the middle of page 2 of the online supplementary files of (1), the ZIG methodology appears to implicitly require that the sum of all observed OTUs be a constant, and not a random variable. However, it is not clear how (or whether) this information is used in the distributional assumptions made in (1).

As noted in the online supplementary files, it is not feasible to estimate taxa abundance at the ecosystem level. However, by assuming that either (a) out of p taxa, at most p-2 are differentially abundant (in log scale) or (b) if all taxa are differentially abundant then the mean abundance (in log scale) of every taxon does not change by the same amount between two (or more) populations, ANCOM can be used for drawing inferences regarding taxa abundance at the ecosystem level using the specimen level relative abundance data. To restate the second assumption more precisely, suppose $(E[log({\gamma }_1^{\text{group1}})],E[log({\gamma }_2^{\text{group1}})],\mathrm{...},E[log({\gamma }_p^{\text{group1}})])\text{'}$ and $(E[log({\gamma }_1^{\text{group2}})],E[log({\gamma }_2^{\text{group2}})],\mathrm{...},E[log({\gamma }_p^{\text{group2}})])\text{'}$ denote the expected abundance (in log scale) of p taxa in a random ecosystem (e.g. the gut of a randomly chosen baby) from two groups (e.g. vaginally delivered babies and C-section babies, respectively). Then ANCOM assumes that $E[log({\gamma }_i^{group1})$ and $E[log({\gamma }_i^{group2})$ do not differ by the same constant for all taxa i. In practice, these are very reasonable assumptions to make. However, if these are not valid, then ANCOM can still be used for comparing the relative abundances of taxa at the ecosystem level by taking log-ratios relative to a predefined taxon. Further, as commonly done in classical data analysis involving log transformations (e.g. Box–Cox transformations), to deal with zeros in the data, ANCOM adds a small positive constant before performing log transformations. The choice of the positive constant is not based on a rigorous statistical theory, but is arbitrary. The effect of the choice of the constant on the FDR and power of the methodology requires careful investigation. As demonstrated in this article, ANCOM dramatically controls the FDR while maintaining high power. In large genomic surveys, where each taxon is represented by several thousands of OTUs, ANCOM provides a computationally simple methodology. Thus, apart from ANCOM, none of the methods described in this paper appear to be appropriate for comparing populations on the basis of taxa abundance at the ecosystem level; at best, some of them may be useful for comparing abundance at the specimen level. A concise description of the relevant assumptions and parameters of interest is provided in Table S2 of the online supplementary file.

Finally, similar to the usual linear regression analysis for Euclidean space data, ANCOM can be used for longitudinal analysis of microbial composition. It can be easily adapted to include covariates and assess their effects in the model. Although ANCOM draws its motivation from microbiome data, it is a general methodology that can be applied to similar data types in other functional categories, such as genes, transcripts, or metabolites. The mathematical formulation would be equivalent in these cases, and it is enough to obtain data on the relative proportions of these categories, without accurately observing the actual abundances. In our opinion, this strength significantly broadens the impact of ANCOM among researchers in the biological community.

Conflict of interest and funding

Research done by SM and ME was supported by the Norwegian Research Council [214324]; research done by SDP was supported, in part, by the Intramural Research Program of the NIH, National Institute of Environmental Health Sciences [Z01 ES101744-04]. The funders had no role in study design, data collection, or analysis.