Fishing amplifies forage fish population collapses

Significance

Forage fish provide substantial benefits to both humans and ocean food webs, but these benefits may be in conflict unless there are effective policies governing human activities, such as fishing. Collapses of forage fish induce widespread ecological effects on dependent predators, but attributing collapses to fishing has been difficult because of natural fluctuations of these stocks. We implicate fishing in forage fish stock collapses by showing that high fishing rates are maintained when stock productivity is in rapid decline. As a consequence, the magnitude and frequency but not duration of stock collapses are far greater than expected from natural fluctuations. Risk-based management policies would provide substantial ecological benefits with little effect on fishery catches.

Abstract

Forage fish support the largest fisheries in the world but also play key roles in marine food webs by transferring energy from plankton to upper trophic-level predators, such as large fish, seabirds, and marine mammals. Fishing can, thereby, have far reaching consequences on marine food webs unless safeguards are in place to avoid depleting forage fish to dangerously low levels, where dependent predators are most vulnerable. However, disentangling the contributions of fishing vs. natural processes on population dynamics has been difficult because of the sensitivity of these stocks to environmental conditions. Here, we overcome this difficulty by collating population time series for forage fish populations that account for nearly two-thirds of global catch of forage fish to identify the fingerprint of fisheries on their population dynamics. Forage fish population collapses shared a set of common and unique characteristics: high fishing pressure for several years before collapse, a sharp drop in natural population productivity, and a lagged response to reduce fishing pressure. Lagged response to natural productivity declines can sharply amplify the magnitude of naturally occurring population fluctuations. Finally, we show that the magnitude and frequency of collapses are greater than expected from natural productivity characteristics and therefore, likely attributed to fishing. The durations of collapses, however, were not different from those expected based on natural productivity shifts. A risk-based management scheme that reduces fishing when populations become scarce would protect forage fish and their predators from collapse with little effect on long-term average catches.

Forage fish are small pelagic fish, such as herrings, anchovies, and sardines, that provide multiple benefits to people and marine food webs. These species support the largest fisheries in the world, accounting for 30% of global fisheries landings by weight and benefiting aquaculture and livestock industries through the production of fish meal and fish oil (1). At the same time, these species are important for marine food webs, because they provide a key linkage from lower trophic-level planktonic species to upper trophic-level predators, such as large fish, seabirds, and marine mammals (2–4). These predators also have economic value through fisheries (2), tourism (5), or nonmarket existence values (6). Collapses of forage fish populations, which have been frequent (7, 8), can, therefore, generate widespread ecological effects (9–11). Because of these concerns, there is a growing movement to develop and apply robust management approaches to forage fisheries to avoid the risk of fisheries-induced stock collapses and attendant ecological consequences (11, 12).

One of the principal challenges in assessing the ecological consequences of forage fish fisheries is that these stocks undergo large cyclical fluctuations in abundance (13, 14) (Fig. 1). Fishing can potentially exacerbate naturally caused collapses, because shifts in populations’ spatial distributions coupled with fish schooling behavior allow fisheries to be economically viable, even when abundance is low (7, 15). Because of these fluctuations, standard static reference points used to judge stock status [e.g., unfished biomass (biomass that maximizes long-term sustainable yield)] have little meaning for the management of forage fish stocks. Most reference points are based on a presumed relation between population production and population biomass, but such a relationship rarely exists among these populations (Fig. S1). Moreover, these fluctuations greatly reduce our ability to ascertain effects of fishing on stock dynamics (16), and by extension, effects of fishing on dependent predators. Some have concluded that fishing acts primarily to accelerate population collapses that were destined to occur because of natural processes (7). To date, it has not been possible to determine whether fishing also makes collapses more frequent, more severe, or more prolonged.

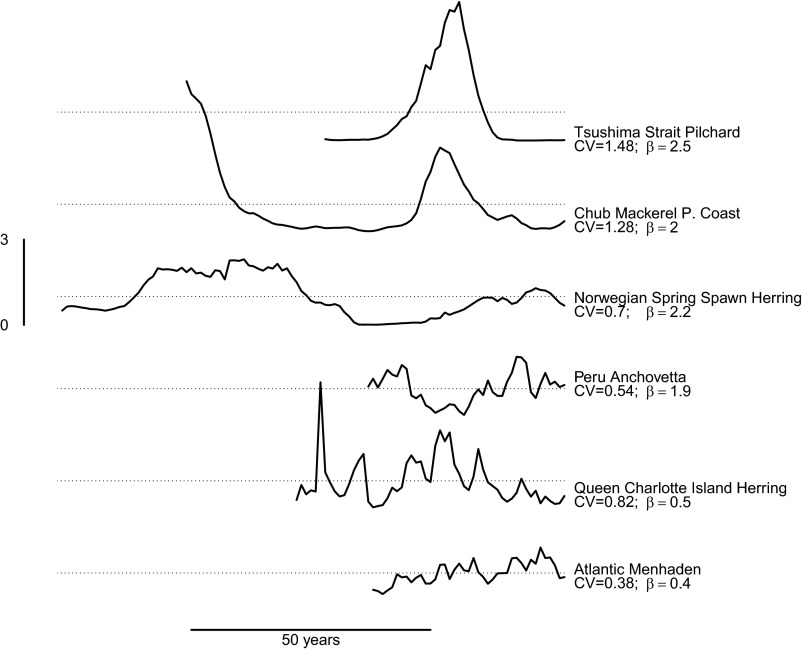
Fig. 1.

Examples of forage fish biomass trends showing magnitudes and characteristics of population fluctuations. Dotted lines denote the long-term mean biomass for each stock, and horizontal and vertical bars show time and biomass scale (expressed as a ratio of annual biomass to mean biomass), respectively. Time series are not aligned according to actual start and end date; β is the Fourier spectral scaling exponent, where variance scales with frequency as f ^−β. Five stocks show the range of population fluctuations from extreme long- (Tsushima Strait Pilchard) to short-term (Atlantic Menhaden) variability. Across all 40 stocks for which there were sufficiently long biomass time series to estimate β, the average coefficient of variation (CV) and β were 0.5 and 1.9, respectively. For comparison, a common decadal scale environmental index, the Pacific Decadal Oscillation (33), has β near 1.0.

Here, we contribute to understanding ecological consequences of forage fish fisheries to ask how fishing has affected population characteristics that are most relevant for dependent predators. Predators are most sensitive to changes in forage fish abundance when forage abundance is low (9), and therefore, we focus on the effects of fishing with respect to the magnitude (scale of fluctuation), frequency (proportion of stocks at low abundance), and duration (number of years until recovery) of stock collapse. We compiled time series of population biomass and fisheries catches on stocks around the globe from stock assessments, restricting our analysis to 55 stocks with a time series that spanned at least 25 y (Table S1). Forage fish stocks used in this analysis included anchovies, capelin, herrings, mackerels, menhaden, sand eels, and sardines, which since 2000, supported average annual catches of 17 million tons y⁻¹ and comprised 65% of global forage fish catches (17).

Results and Discussion

Nearly one-half (n = 27) of the small pelagic fish populations collapsed at a threshold of 25% of average population biomass, whereas nearly one-third (n = 16) collapsed at a lower threshold of 15% of average biomass. There was no discernable trend in probability of collapse by decade (from the 1950s to the 2000s; P = 0.47), and there was no difference in the probability of a stock collapse among five main regions (North Atlantic, South Atlantic, North Pacific, South Pacific, and Mediterranean Sea; P = 0.79) or finer oceanic regions (SI Methods). We conducted multiple sensitivity analyses to determine whether results were robust to our operational definition of stock collapse. Although specific results varied by alternative method, none revealed systematic trends through time or among regions in collapse frequency (Methods and SI Methods). Collectively, these results indicate that severe collapses of forage fish populations have been relatively common and that no particular time period or region is unambiguously more prone to collapses than others.

We examined stock collapses in more detail to identify common patterns of fishing rate (fraction of fish biomass caught) and natural stock productivity (new biomass produced), finding that a combination of sustained high fishing rate, rapid decline in natural productivity, and delayed response of the fishery to low productivity contributed to population collapses. For this analysis, we only used populations for which we could estimate fishing rate and natural population productivity, which was a subset (n = 15) of 27 populations that collapsed. For these collapsed populations, periods preceding collapses were associated with exceptionally high fishing rates (50–200% higher than average annual fishing rates), with one-third of the populations experiencing fishing rates that exceeded 0.75 y⁻¹ (Fig. 2). High fishing rates continued until after stock collapse, when fishing was eventually reduced to lower levels. We compared fishing rates with natural stock productivity, which is the rate of change that the population would have experienced in the absence of fishing, and therefore, it provides a signal for the integrated effects of environmental conditions and population biomass (the latter of which is minimal) (Fig. S1). Average population productivity declined sharply beginning 2–3 y before collapse, plummeting to −0.02 y⁻¹ (expressed as the fraction of average population biomass) immediately before collapse and rebounding shortly thereafter. For stocks that did not collapse (defined as minimum biomass > 0.3 to clearly separate collapsed and noncollapsed stocks; n = 19), we observed different patterns of fishing and natural productivity preceding the year of minimum population biomass. There was little trend in fishing mortality rate among these populations, and overall fishing rates were lower than those documented in collapsed stocks (Fig. 2). As was the case for collapsed stocks, natural population productivity declined before the year of minimum biomass (Fig. 2).

Fig. 2.

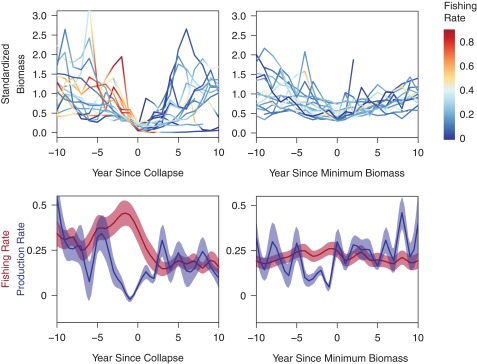
(Upper) Time trends of population biomass and fishing rate (Left) before and after population collapse and (Right) before and after minimum biomass for populations that did not collapse. High fishing rates (>60% of population biomass removed by fishing annually) were not uncommon in collapsed populations before stock collapse but were less common among noncollapsed populations. For collapsed stocks, fishing rates were commonly reduced after collapse. (Lower) Mean (± SE) fishing rate and natural population production rate (Left; surplus production standardized by each population’s average biomass) before and after population collapses and (Right) before and after minimum biomass for populations that did not collapse. On average, collapsed stocks experienced high fishing rates for several years before collapse, and stock productivity consistently declined sharply 1–2 y before stock collapse. Extreme fishing rates and extreme drops in natural population productivity were less common among stocks that did not collapse. To stabilize variance in productivity, we took the average and SE after omitting the smallest and largest values for each year.

We conducted two additional analyses of the populations where we had time series of population productivity and fishing rates to quantify the role of fishing in stock collapses. First, we asked whether mean fishing rates and mean natural population productivity differed between collapsed and noncollapsed populations. We used the mean fishing and productivity rates during 2 y before collapse or minimum biomass, because this time interval seemed to be a key period when fishing was sharply greater than natural productivity and could, thereby, contribute to collapses (Fig. 2). The mean fishing rate during these periods was significantly different (P = 0.014) between collapsed and noncollapsed populations, with mean rates of 0.44 and 0.26 y⁻¹ in collapsed and noncollapsed populations, respectively. The differences in mean natural productivities, 0.022 and 0.15 y⁻¹ for collapsed and noncollapsed populations, respectively, were not significantly different (P = 0.12), largely because of high variance across stocks. Second, we used time series of natural population productivity of collapsed stocks to quantify the likely minimum biomass and collapse frequency had there been no fishing for 2 y before collapse using standard population modeling techniques. Models predict that only 4 of these 15 populations would have collapsed from natural productivity declines alone and that the average minimum biomass levels would have been six times greater if fishing had not occurred during the years immediately leading up to collapse.

The above analysis provided evidence implicating high fishing rates as a factor promoting population collapse, but that analysis was restricted to a subset of collapsed populations for which we could reconstruct natural productivity and fishing rate trends. We sought to reveal the fingerprint of fishing on all population dynamics to evaluate whether stock collapses were more extreme, occurred more frequently, or persisted longer than expected if stocks were fluctuating randomly without trend but with comparable variance and spectral scaling of natural population growth rates. To this end, we applied a randomization test analogous to a Population Viability Analysis (18), in which we estimated the annual natural population growth rates for each stock in each year, characterized the variance and spectral scaling of growth rate, and then, simulated time series from these characteristics (SI Methods and Fig. S2). This procedure revealed that the minimum forage fish biomass levels were significantly lower than those expected based on natural productivity characteristics (Fig. 3), with the median minimum biomass 44% lower than expected from the randomization test. This result was robust to alternative assumptions regarding the extent that biomass dictates population productivity (SI Methods and Fig. S3). Moreover, the proportion of stocks collapsed (7 of 51) in 2006 (the year with the most collapsed stocks) was marginally greater than the maximum level expected (P = 0.10). At a lower collapse threshold (20%; 4 of 52 collapsed), the maximum annual collapse frequency was significantly greater than expected (P = 0.025). In contrast, the average duration of stock collapse (mean = 8.7 y; defined as the number of years to recover from collapse to average biomass) was not different from expected if stocks were fluctuating randomly.

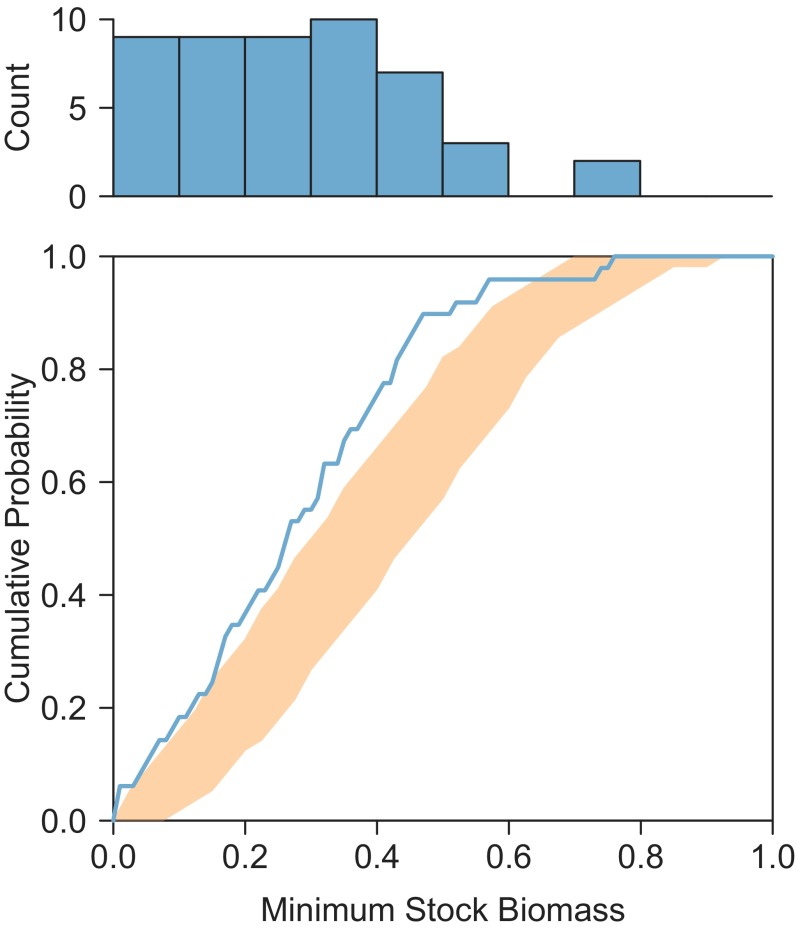
Fig. 3.

Comparison of minimum stock biomass levels (shown as a histogram in Upper and a cumulative frequency distribution line in blue in Lower), with expected 95% range of cumulative frequency distribution (orange) from randomization test. The randomization test simulated populations with similar characteristics (time series lengths, variability, and spectral scaling of population growth rate) but without any long-term trend in abundance. The observed frequencies of very low minimum biomass levels are greater than expected if populations were fluctuating randomly.

There are essentially two management tools to protect dependent forage fish predators by avoiding or dampening stock collapses. The first tool is to develop early warning indicators of changing stock productivity and incorporate that knowledge into management systems so that fishing rates can be adjusted (8, 19). The performance of this approach has been mixed, with a few successes when processes were well-known and management systems were adaptive to indicators (8) but many more failures when environmental proxies did not give accurate predictions (20). The second tool admits these limitations and thereby, relies on a risk-based approach (21), where fishing is restricted during high-risk periods to account for this uncertainty. We weighed the ecological benefits and foregone catch under a hypothetical risk-based harvest policy that protects forage fish from fishing when they are susceptible to collapse and when predators are most sensitive to forage fish abundance (9). We simulated consequences of this hypothetical harvest rule, wherein fishing was suspended if biomass was less than one-half of the mean, and fishing occurred at observed levels otherwise, assuming that population productivity was independent of stock biomass (whereas a sensitivity analysis indicated that results were robust to this assumption) (SI Methods and Fig. S1). The application of this rule to time series of stock biomass and fishing catches led to a nearly 80% increase in minimum biomass levels and a 64% reduction in the number of collapsed stocks. In contrast, average catches were reduced very little (1.7%), because fishing closures allowed stocks to recover to higher abundance more quickly and catches were already low during these periods. The application of this on–off rule is intended here only to compare possible benefits and costs, but in practice, harvest policies need to be tailored to the socioeconomic and ecological context of each fishery (e.g., allowing a low level of catch to maintain job security). Regardless of whether no fishing or very limited fishing is allowed, restricting fishing opportunities when forage fish are moderately scarce would have little effect on fishery catches while providing substantial ecological benefits.

The ecological consequences of stock collapses will depend on the compensatory capacity of ecosystems and adaptive capability of predators. For example, anchovy and sardine populations are thought to oscillate out of phase (22), but long-term records and models do not suggest that this is always consistent through time (8, 14); typically, one species reaches higher peak abundances than the other. Some predators, particularly piscivorous fishes, are generalist consumers that can adapt to changing prey abundances by shifting foraging strategies (23). Finally, not all forage fish are critically important for food webs (24, 25), and therefore, some stock collapses may not have widespread ecological effects. These considerations are important, but it is equally important to identify ways that our assessment might underestimate ecological consequences. Population biomass is a crude measure of population status, because it does not consider important components of population structure (e.g., spatial, temporal, and size). Fishing can erode stock structure of forage fish populations (26), which in turn, can magnify variance in the delivery of ecosystem services to natural predators and fisheries (27). The spatial range of stocks often changes with abundance (15), which can amplify or dampen vulnerability of central place predators (e.g., seabirds and pinnipeds) to reductions in forage stock abundance depending on whether critical foraging sites are at the edges or within the core of stock ranges. These predators can also be sensitive to localized depletion, especially during critical breeding and nesting periods (28). Because stock collapses have been made more frequent by fishing and are caused by overly high fishing rates when abundance and productivity are low, simple measures that protect stocks when they are most susceptible to collapse would provide a positive step toward an ecosystem-based management strategy that can reduce the frequency and magnitude of collapses, protecting forage fish and the food webs and fisheries that depend on them.

Methods

Time series of catch, exploitation rate, and population biomass were available from the RAM Legacy Stock Assessment database (29). When total biomass and spawning stock biomass were both provided, we preferentially used total biomass. We only considered time series that spanned at least 25 y, which was the minimum number of years that we deemed adequate to reliably estimate minimum biomass levels and other population attributes given the dominance of low-frequency variation. The longest time series was 106 y, and the mean was 41.7 y. All biomass time series were standardized by their mean to permit comparisons across stocks. Note that biomass time series are stock assessment outputs generated by fitting data to population models. As such, each time series has a different estimation uncertainty, and assumptions of the population models could induce biases in autocorrelation (spectral scaling) in abundance and population productivity. Because we used a large number of populations assessed with a wide range of methods, there is no basis to believe that our main conclusions are biased.

To test for changes in the proportion of populations collapsing among decades, we enumerated for each decade the number of populations that had their first collapse year in that decade and the number of stocks for which there were at least 5 y of population estimates. For reported analyses, we defined a collapse as any population level below 0.25 of the mean. Only one stock collapsed more than one time (Barents Sea Capelin), and therefore, for simplicity, we only used the first instance of collapse, because visual analysis of fishing and productivity trends revealed nearly identical dynamics leading up to the second collapse. We tested for differences across decades by fitting a binomial generalized linear model, where the number of collapsed stocks and the number of stocks with estimates by decade comprised a bivariate response variable and decade was a categorical variable. To confirm that the results were not driven by our biomass threshold, we repeated the analysis for collapse thresholds equal to 0.5 and 0.15. For the former, we found no evidence of changes in collapse frequency, whereas for the latter, we found evidence for higher collapse frequency in the 1960s and 1980s, with similar collapse frequency in the other decades. We used the same framework to test for differences in collapse frequency among five main ocean regions: North Pacific, North Atlantic, South Pacific, South Atlantic, and Mediterranean Sea (SI Methods). We performed secondary sensitivity analyses that used different measures of collapse and finer regional classifications, finding similar results (SI Methods).

To characterize fishing trends for collapsed stocks, we used the ratio of catch to total biomass as our estimate of fishing rate (exceptions are discussed in SI Methods). Natural population productivity was calculated as the annual change in total biomass plus fishery catches (i.e., surplus production). This calculation gives the natural population surplus productivity or the rate of change in the population that would have occurred in the absence of fishing based on the following standard population dynamic model:

$$\frac{\mathrm{\Delta }{B}_t}{\mathrm{\Delta }t}\mathrm{=}S{P}_t\mathrm{-}{F}_t{B}_t,$$ [1]

where B_t is population biomass in year t, SP_t is the surplus productivity in year t, and F_t is the ratio of catch to biomass in year t (details on the estimation of natural productivity are given in SI Methods). We standardized surplus productivity in the same way that we standardized population biomass by dividing by the average population biomass. This analysis could only be conducted for populations that had estimates of total biomass and fishery catches (i.e., spawning biomass series cannot be used). We compared mean fishing rates and surplus productivity rates before collapse using two-sided t tests, assuming unequal variances.

We tested whether observed minimum stock biomass levels would be expected from chance by generating random biomass time series that had equivalent productivity characteristics as the actual biomass time series and comparing simulated with observed minimum biomass levels. Details of the analysis are presented in SI Methods, but we provide an overview of the process here. From the biomass time series, we estimated the log of the population growth rates [ln(B_t+1/B_t + F_t), where B_t is the population biomass in year t, and F_t is the fishing rate in year t] for each stock. From these, we estimated the variance and spectral scaling of population growth rate of each stock and used these to fit a bivariate kernel density function from which random draws of variance and spectral scaling could be drawn. Spectral scaling (30) of population productivity was calculated by using the method of multiple segments (31), which estimates how log(spectral density) scales with frequency. We generated time series of 200 y by drawing variance and spectral scaling from the kernel density function using spectral synthesis to generate a time series of log(growth rate) based on those characteristics (32) and then, generating a time series of population biomass based on the time series of growth rates. We then truncated the time series so that simulated time series had the same length as the true time series. We performed several checks to confirm that the simulated biomass time series were adequately capturing properties of the actual biomass time series (SI Methods). We conducted 1,000 iterations of the randomization test, calculating the cumulative density of minimum biomass over the simulated stocks for each iteration. A sensitivity analysis that relaxed the assumption that population productivity was related to biomass revealed stronger support that the minimum biomass levels were lower than expected by chance (SI Methods).

We simulated consequences of a hypothetical fishery rule, wherein fishing was suspended if biomass was below one-half of the mean, and fishing equaled observed levels otherwise. In this analysis, we applied the following model to any stock with standardized minimum biomass that was less than 0.5 (e.g., one-half below the mean):

$$B_{t\mathrm{+}1}\mathrm{=}\{\begin{array}{ll}{B}_t\mathrm{+}S{P}_t\mathrm{-}{F}_t{B}_t,\hfill & \text{if}\hspace{0.17em}{\mathit{B}}_{\mathit{t}}\mathrm{>}0.5\hfill \\ B_t\mathrm{+}S{P}_t,\hfill & \text{otherwise}\hfill \end{array},$$ [2]

where B_t is stock biomass, SP_t is the surplus production, and F_t is the fishing mortality rate in year t. SP_t was calculated from the time series of biomass and catches. We projected population biomass forward 10 y starting with the first year that B < 0.5. We compared the projected with actual minimum biomass for each population as the ratio min(B_projected)/min(B) and reported the average of this ratio across stocks. We also conducted a second analysis as a sensitivity analysis, in which population productivity was a linear function of population biomass. This alternative model predicted even larger ecological benefits and a net benefit to fisheries (SI Methods).

All computer code (R code) and data are available at https://github.com/tessington/PNASForageFish.