Polyphasic feedback enables tunable cellular timers

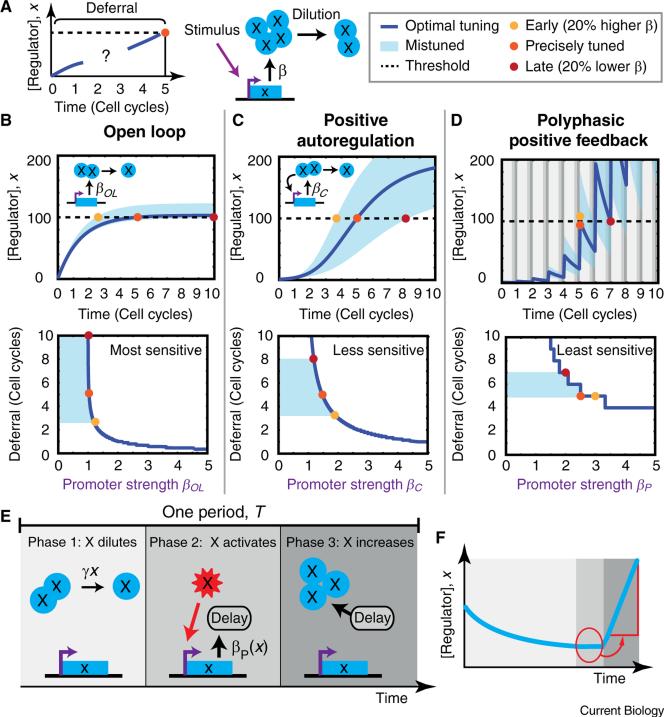
Cellular ‘timers’ provide an important function in living cells [1]. Timers help cells defer their responses to stimuli, often for time intervals extending over multiple cell cycles (Figure 1A, left). For example, mammalian oligodendrocyte precursors typically proliferate for ~7 divisions before differentiating during neural development [2]. The bacterium Bacillus subtilis can respond to sudden nutrient limitation by transforming into a dormant spore after ~5 cell cycles [3]. Timers can balance proliferation with differentiation to control the sizes of various cell populations. Some timers appear to operate in a largely cell-autonomous fashion, but the underlying genetic circuit mechanisms that enable this remain poorly understood. Protein dilution poses stringent challenges to timer circuits by continually diluting out timer components in proliferating cells (Figure 1A, right). Recent work suggests that pulsatile or oscillatory dynamics can facilitate timer functions [3,4]. Here, we show how polyphasic positive feedback — a pulsed architecture that breaks a feedback signal into temporally distinct phases — counteracts protein dilution to facilitate timer behavior.

Figure 1. Count-up timers.

(A) Cellular timers defer differentiation for multiple cell cycles. In a count-up timer in proliferating cells, a master regulator (blue x) is produced by a circuit and constantly diluted away due to cell growth. The timer circuit enables x to accumulate slowly over multiple cell cycles, despite dilution, until it reaches a critical threshold for differentiation (dashed line). (B–F) Count-up timer circuit architectures show distinct tuning properties. (B) Open loop count-up timers relax to steady state in ~1–2 cell cycles (top). Only a narrow range of promoter strengths, β_OL, permit x to cross the threshold after a specific number of cell cycles (bottom). Mistuning β_OL by ±20% (blue shaded region) causes the regulator to accumulate either too quickly, resulting in early differentiation (yellow dot) or too slowly, resulting in late differentiation (dark red dot). (C) Continuous positive feedback timers balance dilution with positive feedback to extend deferral times (top). This sensitive balance requirement means only a limited range of β_C values support multiple cell cycle deferrals (bottom). (D) Polyphasic positive feedback timers separate feedback regulation into three non-overlapping phases, which cycle repeatedly (top). Polyphasic timers are significantly less sensitive to feedback strength variations and thus easier to tune (bottom). Circuit dynamics (E) and time trace (F) of a single polyphasic period are shown for illustration. In the model, phase 2 is assumed to be very brief compared to the other phases, but is enlarged here for clarity. In tuning curves (B–D, bottom), the promoter strength of each circuit is normalized by the minimal value necessary to cross threshold. (C) and (D) use saturating feedback. See Supplemental Information for simulation details.

What genetic circuits can generate a timer in individual cells? One possibility is a count-down mechanism which dilutes or depletes a repressor of differentiation during cell proliferation, as in the Xenopus mid-blastula transition [5]. Alternatively, cells could ‘count up’, gradually increasing levels of a master regulator until it exceeds a threshold for differentiation (Figure 1A). Count-up timers have been observed in Bacillus subtilis sporulation [3] and Dictyostelium social aggregation [4], where the concentration and activity of master regulators increase in pulses until reaching a critical threshold [6,7].

In proliferating cells, count-up timers face a fundamental challenge: cell growth and division prevent proteins from accumulating over timescales longer than the cell cycle. To see this, consider ‘open-loop’ production of a regulatory protein x(t), whose concentration does not affect its production rate. If x(t) is produced at a constant rate β_OL and diluted at rate γx(t), where γ is inversely proportional to the cell cycle duration, then

$$\frac{dx\left(t\right)}{dt}=-\gamma x\left(t\right)+{\beta }_{OL}$$ (1)

Starting from x(t = 0) = 0, the solution is

$$x\left(t\right)=\frac{{\beta }_{OL}}{\gamma }(1-e^{-\gamma t})$$ (2)

Here, x(t) equilibrates in ~1–2 cell cycles, regardless of the production rate, β_OL (Figure 1B, top). For most values of β_OL, x(t) crosses the threshold either almost immediately or not at all (Figure 1B, bottom). This ‘now or never’ β_OL dependence makes the simple open loop circuit a very poor multi-cell cycle timer.

Positive feedback circuits, where the regulator activates its own production, can improve the tuning sensitivity of count-up timers by counteracting dilution (Figure 1C). The feedback can cancel out dilution across a range of regulator concentrations. We consider a simple linear model of positive feedback far from saturation, with production rate constant β_C:

$$\frac{dx\left(t\right)}{dt}=-\gamma x\left(t\right)+{\beta }_{C}x\left(t\right)$$ (3)

Starting from a non-zero initial condition x(t = 0) = x₀,

$$x\left(t\right)=x_0{e}^{({\beta }_C-\gamma )t}$$ (4)

Here, x(t) accumulates with an exponential rate constant that depends linearly on β_C. To make x(t) accumulate slowly over multiple cell cycles, a cell must tune β_C to be only slightly greater than the dilution rate γ. Even in more realistic models with saturating feedback (Figure 1C), multi-cell-cycle deferral only occurs for a narrow range of production rates, making this system relatively impractical as a timer.

This tuning problem can be tamed by using a ‘polyphasic’ positive feedback, which breaks the feedback function into temporally non-overlapping phases (Figure 1D–F). Consider a polyphasic circuit that cycles repeatedly through 3 phases of total duration T (Figure 1E,F). In the first phase, there is no feedback — the regulator x(t) is inactive and dilutes out due to cell growth. In the second phase, which is assumed to be relatively short, the regulator is transiently activated (e.g., phosphorylated), initiating transcription from its target promoter at a rate proportional to its concentration. Critically, new x(t) is not produced immediately in phase 2, but is delayed until phase 3 due to indirect regulation or delays in transcription and translation. In phase 3, the regulator deactivates, while new x(t) is finally produced.

Consider a simple model of polyphasic feedback with period T. We assume phase 2 is instantaneous and phase 3 has duration Δt. For the nth period (starting at n = 1), phase 1 occurs in the time interval t ∈ [(n–1)T, nT – Δt), phase 2 occurs at t = nT – Δt, and phase 3 occurs in the interval t ∈ (nT – Δt, nT). The production of new x(t) in phase 3 of the nth cycle depends on the amount of x(t) in phase 2 of that same cycle, x(nT – Δt), and on feedback strength β_P:

$$\frac{dx\left(t\right)}{dt}=-\gamma x\left(t\right)+\frac{{\beta }_P}{\Delta t}x(nT-\Delta t)$$ (5)

Δt normalizes the feedback strength to allow comparison of different phase 3 durations. Because it is only active in phase 2, x(t) produced during phase 3 does not cause any further production of new x(t) during the same period. In this linear feedback approximation, assuming short pulses, the solution at the end of the nth period, with initial condition x(t = 0) = x₀, is:

$$x\left(nT\right)=x_0{e}^{n\log (1+{\beta }_P)}{e}^{-\gamma nT}$$ (6)

Here, the exponential growth rate of x(t) depends logarithmically, rather than linearly, on β_P, indicating that polyphasic feedback reduces the sensitivity of deferral time to promoter strength. More realistic models in which the feedback saturates similarly generate a less sensitive tuning curve compared to continuous positive feedback (Figure 1D). The model is less sensitive not because of the pulses alone, but rather because these pulses prevent the entire feedback loop from being simultaneously engaged, thereby reducing the rate at which errors compound. In the limit where pulse frequency increases and pulse strength decreases, polyphasic feedback becomes equivalent to continuous feedback (see Supplemental Information, published with this article online).

In Bacillus subtilis sporulation, repeated pulsatile phosphorylation of the master regulator Spo0A could combine with a hypothesized time delay in positive feedback to generate such a polyphasic feedback loop [3].

Compound interest, a financial positive feedback, provides an analogy for polyphasic feedback. We establish a relation (Supplemental Information) between polyphasic positive feedback and infrequently compounding interest, showing they have similar tolerance to changes in feedback strength and interest rate, respectively.

We can compare the polyphasic circuit to previously studied timers. The Xenopus oocyte mid-blastula transition uses a count-down molecular depletion mechanism [5]. Mechanisms like slow phosphorylation kinetics (cyanobacterial circadian clock [8]) and multi-step transcriptional cascades remain sensitive to dilution (Supplemental Information). Speculative mechanisms like slow chromatin spreading may be insensitive to dilution.

The functions of pulsing, including pulse timing and phasing, remain relatively unexplored in genetic circuits. For timers, a pulsed polyphasic design can overcome the fundamental circuit challenges posed by protein dilution. Thus, a pulsed, ‘discretized’ system can outperform corresponding continuous systems [9,10]. As more pulsatile systems are discovered, it will be interesting to better understand the interplay between fast regulatory dynamics, such as pulsing, and the behavior of cells over longer timescales.