Abstract
Purpose
Continuously Moving Table (CMT) MRI is a high throughput technique that has multiple applications in whole-body imaging. In this work, CMT MRI based on a Golden Angle (GA, 111.246° azimuthal step) radial sampling is developed at 3 Tesla, with the goal of increased flexibility in image reconstruction using arbitrary profile groupings.
Methods
CMT MRI with GA and Linear Angle (LA) schemes were developed for whole-body imaging at 3 Tesla with a table speed of 20 mm/sec. Imaging was performed in phantoms and a human volunteer with extended z field of views of up to 1.8 meters. Four separate LA and a single GA scan were performed to enable slice reconstructions at four different thicknesses.
Results
GA CMT MRI produced high image quality in phantoms and humans and allowed complete flexibility for reconstruction of slices with arbitrary slice thickness and position from a single data set. LA CMT MRI was constrained by predetermined parameters, required multiple scans and suffered from stair step artifacts that were not present in GA images.
Conclusion
GA sampling provides a robust flexible approach to CMT MRI for whole-body examination with the ability to reconstruct slices at arbitrary positions and thicknesses from a single scan.
Keywords: Continuously moving table MRI, linear angle, golden angle, radial
INTRODUCTION
Many clinical studies such as whole-body water/fat quantification (1), peripheral vascular angiography (2–4), whole-body diffusion weighted imaging (5–7), detection of tumor metastases (8, 9,10), and multi-contrast anatomical imaging (11,12) demand either whole-body coverage or field of views larger than the uniform z extent of the scanner bore. One approach of performing, such studies is multi-station scanning, which is time consuming and prone to data consistency errors. Continuously Moving Table (CMT) MRI is a high throughput imaging technique, which offers a powerful alternative for rapid whole-body MR examination. In CMT MRI, data are acquired with concurrent uniform velocity z direction motion of the patient table, which allows scanning of different locations of the body in a single table sweep. CMT MRI has been successfully demonstrated in several applications including multi-contrast anatomical imaging (13–15), oncology (16–19), water/fat quantification (20,21), MR angiography (22–28) and diffusion weighted imaging (29).
Existing CMT MRI implementations include a variety of 2D and 3D cartesian methods (13,14,22,25,30–33) including integration with parallel imaging with multiple static or moving coil elements (34,35). Several non-Cartesian approaches have also been explored for CMT MRI (36–38), including continuous single slice radial acquisitions with linear angle (LA) azimuthal profile increments (39). A specific benefit of this technique is that the data are acquired in the most homogeneous region of the magnet, which minimizes field in homogeneity artifacts often encountered in multislice and 3D acquisitions that employ wider field of views. In this paper, we investigate CMT MRI based on single slice Golden Angle (GA, 111.246° azimuthal step) radial sampling, with the goal of exploiting its optimal azimuthal sampling property for slice reconstructions with flexible position and thicknesses.
THEORY
One of the drawbacks of LA radial CMT MRI is that angular segments of k-space within a single-slice are acquired from different anatomical areas, which can give rise to coherent image artifacts. Another disadvantage is that once the data are acquired, images can be retrospectively reconstructed without significant artifacts only to the fully sampled nominal z resolution (or reconstructed slice thickness, Δz), which is defined as
| (1) |
where v is the table velocity, TR is the repetition time and N is the number of projections in a full 180° sampling. Slices reconstructed to a thickness less than Δz with fewer than N profiles will result in undersampling artifacts. Slices reconstructed with thicknesses that are non-integer multiples of Δz, also result in coherent artifacts. The nominal pitch (P) of the measurement is defined as
| (2) |
where Nsl is the number of profiles included in each reconstructed slice (which may be different from N in Eqn. 1) and Tex is the excitation slice thickness. The numerator represents the table travel per reconstructed slice, which can be different from the excited slice thickness.
In dynamic radial acquisitions, a GA sampling pattern can potentially provide benefits over linear sampling with regard to retrospective profile binning flexibility for arbitrary slice thickness reconstruction with mitigated data under-sampling artifacts, as has been demonstrated in the context of cardiac CINE MRI (40). CMT MRI can be considered to be analogous to dynamic imaging with z table position as the continuous variable and hence stands to benefit from GA sampling. In this paper, we present phantom and whole-body human results comparing GA to LA radial CMT MRI with identical image acquisition parameters (TR, TE, flip angle, in-plane resolution and bandwidth) at 3 Tesla.
METHODS
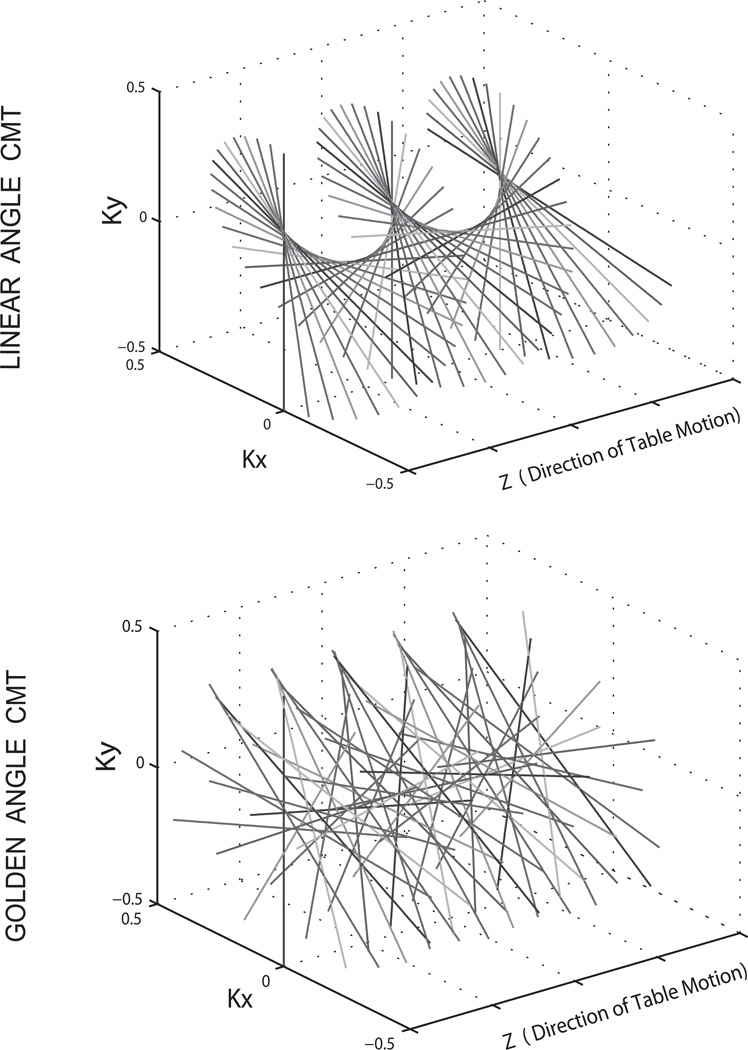
CMT MRI was implemented on a Philips Achieva whole-body 3 Tesla scanner (Philips Healthcare, Best, The Netherlands) with a 2-channel transmit and receive body coil. Software modifications enabled table motion during a scan with inputs of extended z direction field of view (zFOV), one of three table speeds (20, 90, or 180 mm/s) and table motion direction (into or out of the bore). No hardware changes were performed for this setup. CMT MRI was implemented as a continuous single slice axial radial scan with the total number of profiles (N) derived from Eqn. 1 for the extended z direction field of view. The table was moved to the fully extended position after the scan preparation phases, which were performed with the table centered at the landmark position. Scanning was performed continuously using the dual channel body coil with concurrent table movement. To maximize sampling in the z direction, the scanner’s full control gradient mode was utilized which allowed maximum gradient strengths and slew rates of 40 mT/m and 200 mT/m/s. Figure 1 shows the k-space trajectories of the CMT scans with LA and GA schemes.
Figure 1.
Linear Angle and Golden Angle radial CMT MRI data sampling patterns in normalized k space units. Table motion occurs in the Z direction.
CMT Experiments
Phantom Data Acquisition
Radial gradient recalled echo imaging was performed on an extended multi -phantom setup, which included the American College of Radiology (ACR, http://www.acr.org/~/media/ACR/Documents/Accreditation/MRI/LargePhantomInstructions.pdf) MRI phantom. The imaging parameters were : Full zFOV = 1500 mm, table speed = 20 mm/sec, in-plane FOV = 400 × 400 mm2, transverse orientation, in-plane voxel size = 1.56 × 1.56 mm2, TR/TE = 2.7/1.15 msec, flip angle = 20°, radial readout points= 256, excited slice thickness = 8 mm, total scan time = 75 sec. Power optimization was performed on the ACR phantom and all shims were set to zero current to maintain a globally acceptable shim across the extended zFOV.
LA and GA CMT scans were performed with a total of 27,778 equidistant projections per scan. For the LA setting, four scans were performed with 256, 185, 148 and 92 profiles acquired per 180° sweep and the same excited slice thickness of 8 mm. These profile values were derived from Eqn.1 for targeted slice reconstructions of 13.8 mm, 10.0 mm, 8.0 mm and 5.0 mm thicknesses, which matched the table movement per 180° sweep. This resulted in pitch values of 1.725, 1.25,1 and 0.625 for the four scans. To correct for trajectory misplacements along the readout direction, the readout direction was alternated (41). For the GA case, only a single scan was performed with profiles azimuthally stepped by 111.246° at the 2.7 msec TR and no readout alternation. In addition to the CMT LA and GA scans, a static multislice radial image of the ACR phantom was also acquired with the same TR/TE to serve as the gold standard image for comparison.
Human Data Acquisition
One male human volunteer was scanned with informed IRB consent at 3 Tesla. Whole-body scans were performed with the following parameters optimized for in-vivo imaging: Full zFOV = 1800 mm, table speed = 20 mm/sec, in-plane FOV = 400 × 400 mm2, transverse orientation, in plane voxel size = 1.56 × 1.56 mm2, TR/TE = 3.7/1.35 msec, flip angle = 15°, radial readout points= 256, excited slice thickness = 12 mm and readout bandwidth = 854 Hz/pixel, total scan time = 90 sec. The volunteer was positioned in the supine position and entered the magnet feet first with arms at his side. Pre-scan optimization consisting of center frequency and RF drive scale determination was performed at the level of the head. After the preparation phase, the table extended fully inwards such that the head was slightly inferior to the z position at iso-center, followed by the CMT scan covering the 1800 mm FOV. The volunteer was asked to hold his breath when the torso crossed the magnet isocenter to minimize motion artifacts. Four scans were performed for the LA setting, with table motion (targeted reconstruction slice thicknesses) of 18.9 mm, 15.0 mm, 9.0 mm and 5.0 mm, corresponding to 256, 203, 122 and 68 profiles per 180° sampling (nominal pitches of 1.575, 1.25, 0.75 and 0.42). Only a single scan was performed for the GA setting. In addition to the CMT scans, a static multislice Cartesian volume was also acquired at the same location with a 12 mm excitation thickness and same TR, TE, flip angle and in-plane resolution for comparison.
Data Reconstruction
Data processing and reconstruction was similar for both the phantom and human experiments. Complex images were reconstructed offline for both LA and GA cases. Slice wise image reconstructions were performed with slice centers separated by 1.56 mm, matching the in-plane resolution. For LA reconstructions from the four different scans, the corresponding numbers of profiles (256,185,148 or 92 for phantoms and 256, 203, 122 and 68 for humans) were included per slice. Shifts in the k-space readouts were compensated by calculating the 0th and 1st order phase shifts between alternating profiles in the spatial domain and correcting the profiles by phase multiplication in the spatial domain (41). In addition, the phase of the DC point in k-space was zeroed (42). The continuous movement of the table in CMT causes every profile to be acquired at a different z location and in order to reconstruct a slice accurately, all the profiles within that slice have to be interpolated to the slice center location. This was performed in k-space, where each profile within a given slice and the nearest anti parallel profile (profile with least absolute azimuthal separation and opposite readout direction) were used in a weighted linear interpolation to the slice center position, where the weights were the distances of the complementary profiles from the slice center. The anti parallel profile was chosen such that the slice center profile fell within the profile-anti parallel profile pair, a strategy that allowed picking the closest pair of profiles for interpolation. Following interpolation in k-space, standard radial reconstruction methods were applied. The data were pre-weighted using the sample density correction scheme of Pipe & Menon 1999, which minimized the streaking artifacts in the reconstructions at the slight expense of overall image sharpness, especially at higher degrees of azimuthal undersampling (43). The weighted data were gridded slice-by-slice using a custom gridding code written in Python (Anaconda version 3.4.2, Continuum Analytics, Austin, TX). The gridding kernel was a circular Kaiser-Bessel function with radius 4 and oversampling factor 2.0. The kernel β was calculated according to Eq. 5 of Beatty et al. (44). The gridded data were transformed using a 2D FFT and then roll-off corrected using the same kernel.
For the GA reconstructions, all four slice thicknesses were reconstructed from the same data set. For correction of k-space shifts, an analysis was performed to identify the projection that was most anti parallel to the profile being corrected while also being least distant in the z direction. An analysis of the GA series gives a deterministic candidate solution for this neighboring projection as being the 34th profile away from current profile. This profile is angled at 177.65° from the corrected profile, while being at a z distance of 34*TR*v (1.8 mm in this case) from it. For every profile therefore, this solution was used for correction of k-space shifts as described above. No data interpolation was performed in the GA case. The remainder of the reconstruction proceeded as in the LA case. A visual description of the reconstruction process has been included in the online supporting material.
RESULTS
Figure 2a–c shows reconstructed axial slices through the ACR phantom containing fine features and contrasting regions. The columns represent the four LA acquisitions (2a), one GA (2b) acquisition and one reference static radial scan (2c). The rows represent the data reconstructed at the four different slice thicknesses, of 13.8 mm, 10 mm, 8 mm and 5 mm. The GA scheme allows the selection of the profile set for reconstruction of a slice at all the slice thicknesses from a single data volume. GA images are seen to be of comparable quality to the fully sampled LA images (diagonal entries) at all slice thicknesses. LA data reconstructed at thicknesses lower than nominal present expected reconstruction artifacts, demonstrating the inability of the LA acquisition scheme to produce a slice of thickness lower than determined apriori. Also, for reconstructions of LA slice thicknesses above the acquired setting, images show a higher degree of blurring in comparison to the exact (diagonal entries) LA and the GA images. Therefore, a strategy of acquiring LA CMT images at a lower radial percentage to allow slice reconstructions at nominal and higher slice thicknesses will also fail, due to the inherently reduced azimuthal sampling. In contrast, GA sampling ensures optimized K space filling as the number of profiles per slice is increased.
Figure 2.
Panels showing axial CMT MRI image reconstructions. A slice through the ACR phantom, which includes the crossing 45° wedge features, is chosen for comparison. (a) 4×4 panel showing slices reconstructed at 13.8 mm, 10 mm 8 mm and 5 mm thicknesses (rows) from LA data acquired at the respective z spans over 180 degrees of radial coverage (columns). Diagonal entries with white enclosing boxes in the 4×4 matrix represent the nominal reconstructions from the four LA scans. Non-diagonal elements show over or under-sampled reconstructions. (b) Four GA reconstructions at the same slice thicknesses from the single GA data set. (c) Static radial images at the nearest slice position for comparison. GA provides complete flexibility of slice reconstruction, while LA suffers when under-sampled (severe streaking artifacts) or oversampled (loss of image sharpness).
Figure 3a shows full zFOV reformatted coronal images for the LA and GA scans. GA images show high quality at all four slice widths. LA coronal reformats suffer from stair- step artifact, which is often encountered in helical, single detector based computed tomography (45). The artifacts are evident in spite of interpolation in the table motion direction, mainly due to the large table pitch stemming from the relatively high table speed of 20 mm/s. The artifact level reduces with the reconstructed slice thickness. Importantly, the GA method does not suffer from this drawback and features, including the ring in the ACR phantom are clearly resolved in the z direction. In Figure 3b, a section through the ACR phantom at the level of a grid feature and adjacent spherical phantom is displayed for comparison. The ACR phantom grid is constructed of 1.35 mm thick separators at a uniform distance of 15 mm. The grid is clearly visualized in the GA reconstructions, especially in the 10, 8 and 5 mm slice thickness volumes while the LA images fail to display the grid accurately. LA images are degraded by severe stair step artifacts, which impair the resolution of the grid walls, especially in the direction of table motion. The clear resolution of the grid with the GA approach is noteworthy considering the large excited slice thickness of 8 mm.
Figure 3.
Coronal reformatted images of the phantom setup. (a) Panel showing full-extended 1500 mm field of view for 13.8 mm, 10 mm 8 mm and 5 mm thicknesses for LA and GA data. Stair step artifact is observed in the LA setting. GA images show excellent image quality with clear depiction of the ring feature in the ACR phantom. White arrow shows direction of table motion. (b) Coronal zoomed in sections showing comparisons of a grid feature in the ACR phantoms. Grid separators (15 mm apart, 1.35 mm thickness) are resolved clearly in the GA images. LA images show stair-step artifacts and the grid is not clearly resolved even in the 5 mm reconstruction. A profile across the grid feature along the z direction of table motion is displayed for each image.
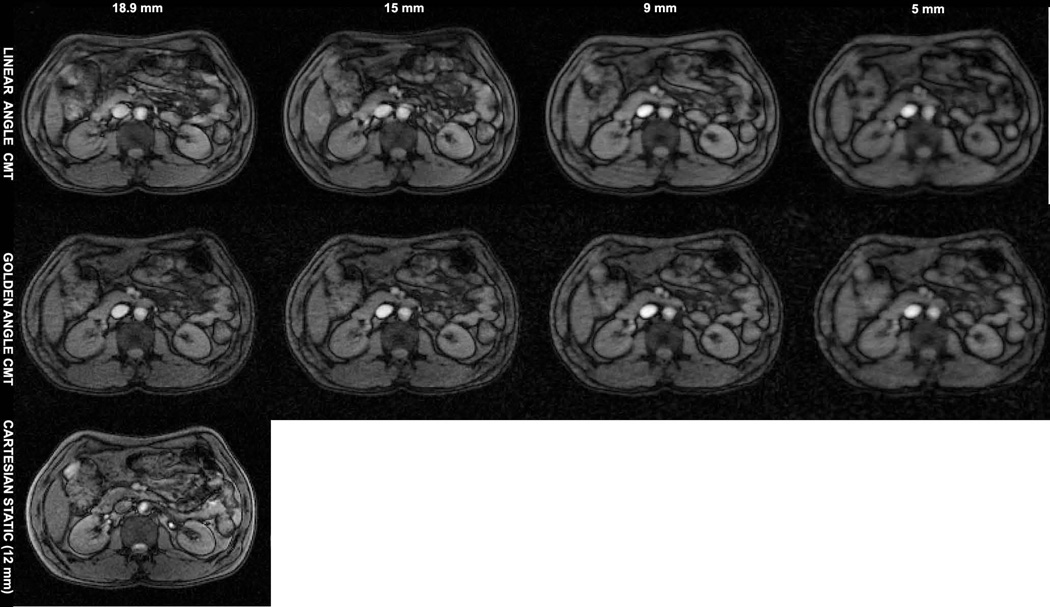
Figure 4 shows axial images at the level of the abdomen from the whole-body CMT scans of the human volunteer. The top row in 4a shows images from four separate LA acquisitions for slice thicknesses, 18.9 mm, 15mm, 9mm and 5mm. The bottom row shows the corresponding GA images from the single data set. High image quality is obtained from the GA CMT scan with clear depiction of anatomical details in the lower abdomen, even though image contrast is restricted due to the use of minimum TR and TE in both LA and GA scans. A nearest matching cartesian static image acquired with a slice thickness of 12 mm is shown for comparison.
Figure 4.
Axial slice comparisons at the level of the abdomen. High image quality is obtained with GA at all reconstructed slice thicknesses; despite the relatively high table speed of 20 mm/sec. A static Cartesian image at a closest matching location acquired with a slice excitation thickness of 12 mm matching the CMT acquisitions is shown for comparison.
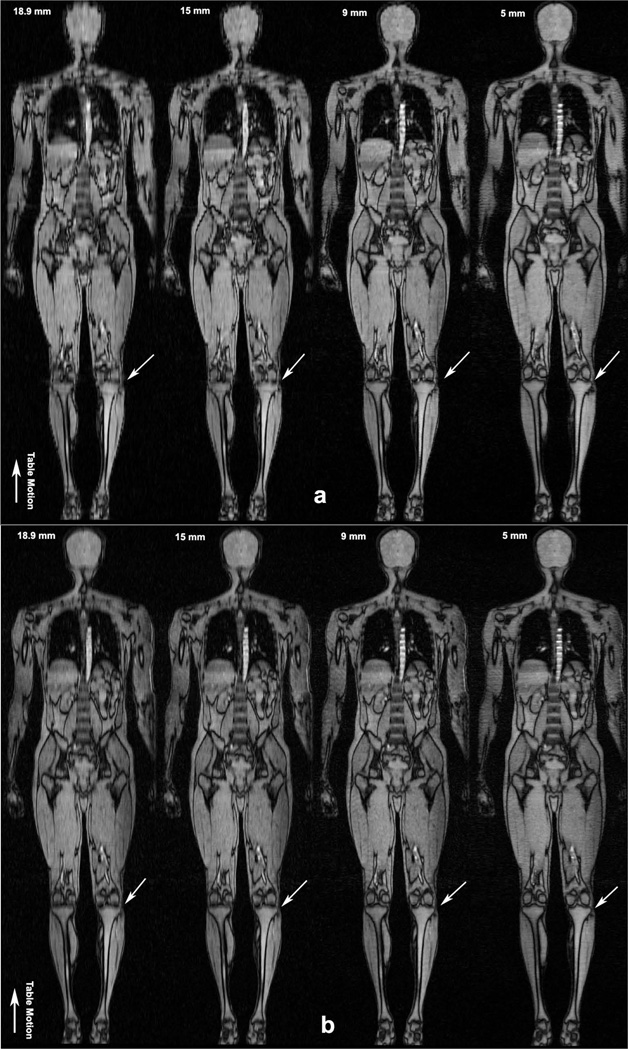
Figures 5a and 5b show coronal reformatted whole-body images of the LA and GA acquisitions at the four slice thicknesses, Progressively fine anatomical detail is seen in the GA reconstructions with decreasing slice thickness, for example, as indicated in the knee by white arrows. In comparison, the LA images are seen to suffer from stair-step artifacts, especially in the 18.9 mm, 15 mm and 9 mm volumes. Stair-step artifacts are not apparent at the lower slice thicknesses for LA CMT. However, improvement in coronal image quality comes at the price of increased in-plane artifacts as seen in Figure 4, due to the low number of profiles per slice.
Figure 5.
Coronal reformatted whole body images of the human volunteer (a) Four separate LA CMT MRI scans. Depiction of fine detail in the knee is limited compared to the GA images in Figure 5b, especially in the 18.9 mm, 15 mm and 9 mm volumes. (b) Coronal reformatted whole body images with GA CMT MRI from a single scan. Excellent image quality is obtained with the GA technique without stair-step artifacts seen in the LA case. No interpolation was performed on the GA data sets. Progressively finer detail is observed with the reconstruction of thinner axial slices as pointed out in the knee by small white arrows. Direction of table motion is indicated by large arrow.
Human data with 12 mm and 6 mm slice thicknesses and a fly through movie of the whole body at 18.9 mm have been included as online supporting material. In support MRM’s mission of reproducible research, the source code and data are freely available for download at https://github.com/senguptasaikat/MRM_Sengupta_Moving_Table_Golden_Angle_MRI (SHA-1 hash = 31b0d2d016b4c1f0535e2bcdfa14d9f245cf66fd)
DISCUSSION
Continuously moving table MRI is a powerful technique for high throughput whole-body examination. In this article, we have presented the benefits of GA CMT MRI over LA CMT MRI at 3 Tesla. While both LA and GA based CMT MRI produce good image quality, GA sampling introduces significant flexibility to CMT MRI. Particularly, it affords free choice of reconstructed slice thickness from a single scan, which is not possible with a single LA acquisition or with existing Cartesian CMT methods. This flexibility afforded by GA sampling can prove to be valuable in many clinical applications, which warrant for example, focused examination of small pathologies.
The unique sampling scheme of GA ensures that fine moving features along most directions are well encoded, which is not the case for LA, particularly at higher table speeds. LA CMT reformats also suffer from stair-step artifacts for larger table pitches and although the artifact levels reduce with lower pitches and thinner slices, reducing the pitch beyond a limit degrades in-plane image quality in both LA and GA due to the low number of profiles per slice. Therefore, GA sampling scheme allows a larger bandwidth of tolerable table pitches and therefore underlying table speeds, compared to LA CMT. In our experiments, the effect of excitation thickness on CMT image quality was not investigated. Use of other excitation thicknesses and pitches might result in changes in the image quality performance of LA vis-à-vis GA CMT MRI. One possible drawback of GA sampling however, might be stronger eddy current and residual echo effects in comparison to LA due to faster angular rotation of the gradients.
Increased tissue T1 relaxation times at 3 Tesla create novel technical challenges for CMT MRI, especially if table speeds are limited. A table speed slower than the 20 mm/s used in this study will therefore be critical in boosting signal levels at 3 Tesla. Another challenge at 3 Tesla is the increased field inhomogeneity, which can give rise to a range of off-resonance artifacts. One strategy of dealing with field inhomogeneities along the extent of the body would be to perform continuous B0 shimming optimized to the region of the body being imaged. Our initial results of this dynamic shimming approach in CMT MRI are promising, and show the potential for whole-body slice wise field optimization (46). Furthermore, B1 field variations along the extent of the body may also be minimized in a slice specific manner. Increased chemical shift at 3 Tesla may also introduce image artifacts, especially in locations of the body with significant adipose tissue depots. The tuning and loading the body coil as well as specific absorption rate (SAR) limits are additional factors, which may depend of the table position. These were however not accounted for in the current work. The single slice CMT MRI approach employed in this work is highly efficient since it does not require lead-in or lead-out phases as in sliding multslice acquisitions or initial filling of the data matrix as in 3D CMT MRI. Whole body water/fat composition imaging is a primary potential application of the single slice GA technique presented in this paper, However, the single slice approach might be limited in its extension to other contrasts, requiring longer TRs. Generation of other contrasts while maintaining GA sampling in z space allowing for slice reconstruction flexibility may necessitate multi slice imaging or slice following techniques. Though the results presented in this work were obtained on a 3 Tesla scanner, the GA CMT approach should be useful at other static field strengths including lower fields such as 1.5 T and higher fields such as 7 T. Clinical body MRI is still dominated by 1.5 T scanners, and GA CMT MRI offers new flexibility for faster scanning and slice reconstruction. Body imaging at higher fields, such as 7 T, relies on other technological developments related to parallel transmit coils and B1 correction methods. However, GA CMT could improve high field MRI covering the extended FOV of the body by using the most homogeneous region of the B0 and B1 fields in the axial plane near isocenter.
Our future work will focus on the integration of contrast generation methodologies with GA based CMT MRI, including long TR scans, interleaved multislice imaging, dynamic scanner adjustments, multichannel coil reconstruction, integration of parallel imaging and compressed sensing reconstruction techniques, as well as clinical application of this technology.
CONCLUSION
GA sampling affords powerful flexibility to radial whole-body CMT MRI. From a single scan, GA CMT MRI allows the reconstruction of arbitrary slice thicknesses with excellent image quality and no increase in imaging time. Further developments in image contrast generation; parameter optimization and multicoil acquisition are needed to fully exploit the benefits of this technique.
Supplementary Material
ACKNOWLEDGEMENTS
We thank the Peter Koken and Peter Bornert from Philips Research, Hamburg, Germany for their help in the implementation of CMT MRI. We also acknowledge funding from NIDDK/NIH R21 DK096282.
Footnotes
Supporting Figure S1. Reconstruction flow for linear and golden angle CMT MRI.
Supporting Figure S2. Interpolation scheme For Linear Angle CMT MRI.
Supporting Figure S3. Anti-parallel profile selection for k space shift correction in golden angle CMT MRI.
Supporting Figure S4. Linear Angle coronal reformats for human data, 6 different slice thicknesses.
Supporting Figure S5. Golden Angle coronal reformats for human data, 6 different slice thicknesses.
Contributor Information
Saikat Sengupta, Email: saikat.sengupta@vanderbilt.edu.
David S. Smith, Email: david.smith@vanderbilt.edu.
E. Brian Welch, Email: brian.welch@vanderbilt.edu.
REFERENCE
- 1.Brennan DD, Whelan PF, Robinson K, Ghita O, O'Brien JM, Sadleir R, Eustace SJ. Rapid automated measurement of body fat distribution from whole-body MRI. AJR Am J Roentgenol. 2005;185:418–423. doi: 10.2214/ajr.185.2.01850418. [DOI] [PubMed] [Google Scholar]
- 2.Ho KY, Leiner T, de Haan MW, Kessels AG, Kitslaar PJ, van Engelshoven JM. Peripheral vascular tree stenoses: evaluation with moving-bed infusion-tracking MR angiography. Radiology. 1998;206:683–692. doi: 10.1148/radiology.206.3.9494486. [DOI] [PubMed] [Google Scholar]
- 3.Wang Y, Lee HM, Khilnani NM, Trost DW, Jagust MB, Winchester PA, Bush HL, Sos TA, Sostman HD. Bolus-chase MR digital subtraction angiography in the lower extremity. Radiology. 1998;207:263–269. doi: 10.1148/radiology.207.1.9530326. [DOI] [PubMed] [Google Scholar]
- 4.Earls JP, DeSena S, Bluemke DA. Gadolinium-enhanced three-dimensional MR angiography of the entire aorta and iliac arteries with dynamic manual table translation. Radiology. 1998;209:844–849. doi: 10.1148/radiology.209.3.9844685. [DOI] [PubMed] [Google Scholar]
- 5.Takahara T, Imai Y, Yamashita T, Yasuda S, Nasu S, Van Cauteren M. Diffusion weighted whole-body imaging with background body signal suppression (DWIBS): technical improvement using free breathing, STIR and high resolution 3D display. Radiat Med. 2004;22:275–282. [PubMed] [Google Scholar]
- 6.Li S1, Sun F, Jin ZY, Xue HD, Li ML. Whole-body diffusion-weighted imaging: technical improvement and preliminary results. J Magn Reson Imaging. 2007;26:1139–1144. doi: 10.1002/jmri.21074. [DOI] [PubMed] [Google Scholar]
- 7.Padhani AR, Makris A, Gall P, Collins DJ, Tunariu N, de Bono JS. Therapy monitoring of skeletal metastases with whole-body diffusion MRI. J Magn Reson Imaging. 2014;39:1049–1078. doi: 10.1002/jmri.24548. [DOI] [PubMed] [Google Scholar]
- 8.Lauenstein TC, Goehde SC, Herborn CU, Goyen M, Oberhoff C, Debatin JF, Ruehm SG, Barkhausen J. Whole-body MR imaging: evaluation of patients for metastases. Radiology. 2004;233:139–148. doi: 10.1148/radiol.2331030777. [DOI] [PubMed] [Google Scholar]
- 9.Nakanishi K, Kobayashi M, Nakaguchi K, Kyakuno M, Hashimoto N, Onishi H, Maeda N, Nakata S, Kuwabara M, Murakami T, Nakamura H. Whole-body MRI for detecting metastatic bone tumor: diagnostic value of diffusion-weighted images. Magn Reson Med Sci. 2007;6:147–155. doi: 10.2463/mrms.6.147. [DOI] [PubMed] [Google Scholar]
- 10.Schmidt GP, Baur-Melnyk A, Herzog P, Schmid R, Tiling R, Schmidt M, Reiser MF, Schoenberg SO. High-resolution whole-body magnetic resonance image tumor staging with the use of parallel imaging versus dual-modality positron emission tomography-computed tomography: experience on a 32-channel system. Invest Radiol. 2005;40:743–753. doi: 10.1097/01.rli.0000185878.61270.b0. [DOI] [PubMed] [Google Scholar]
- 11.Stehling MJ, Howseman AM, Ordidge RJ, Chapman B, Turner R, Coxon R, Glover P, Mansfield P, Coupland RE. Whole-body echo-planar MR imaging at 0.5 T. Radiology. 1989;170:257–263. doi: 10.1148/radiology.170.1.2909106. [DOI] [PubMed] [Google Scholar]
- 12.Lauenstein TC, Semelka RC. Emerging techniques: whole-body screening and staging with MRI. J Magn Reson Imaging. 2006;24:489–498. doi: 10.1002/jmri.20666. [DOI] [PubMed] [Google Scholar]
- 13.Börnert P, Aldefeld B. Principles of whole-body continuously-moving-table MRI. J Magn Reson Imaging. 2008;28:1–12. doi: 10.1002/jmri.21339. [DOI] [PubMed] [Google Scholar]
- 14.Barkhausen J, Quick HH, Lauenstein T, Goyen M, Ruehm SG, Laub G, Debatin JF, Ladd ME. Whole-body MR imaging in 30 seconds with real-time true FISP and a continuously rolling table platform: feasibility study. Radiology. 2001;220:252–256. doi: 10.1148/radiology.220.1.r01jn07252. [DOI] [PubMed] [Google Scholar]
- 15.Johnson KM, Leavitt GD, Kayser HW. Total-body MR imaging in as little as 18 seconds. Radiology. 1997;202:262–267. doi: 10.1148/radiology.202.1.8988221. [DOI] [PubMed] [Google Scholar]
- 16.Schaefer AO, Langer M, Baumann T. Continuously moving table MRI in oncology. Rofo. 2010;182:954–964. doi: 10.1055/s-0029-1245727. [DOI] [PubMed] [Google Scholar]
- 17.Sommer G, Schaefer A-O, Baumann T, Ludwig Ua, Fautz H-P. Sliding multislice MRI for abdominal staging of patients with pelvic malignancies: a pilot study. J. Magn. Reson. Imaging. 2008;27:666–672. doi: 10.1002/jmri.21279. [DOI] [PubMed] [Google Scholar]
- 18.Horvath LJ, Burtness BA, McCarthy S, Johnson KM. Total-body echo-planar MR imaging in the staging of breast cancer: comparison with conventional methods--early experience. Radiology. 1999;211:119–128. doi: 10.1148/radiology.211.1.r99ap33119. [DOI] [PubMed] [Google Scholar]
- 19.Baumann T, Ludwig U, Pache G, Fautz H-P, Kotter E, Langer M, Schaefer O. Continuously moving table MRI with sliding multislice for rectal cancer staging: image quality and lesion detection. Eur. J. Radiol. 2010;73:579–587. doi: 10.1016/j.ejrad.2008.12.008. [DOI] [PubMed] [Google Scholar]
- 20.Kullberg J, Johansson L, Ahlström H, Courivaud F, Koken P, Eggers H, Börnert P. Automated assessment of whole-body adipose tissue depots from continuously moving bed MRI: a feasibility study. J Magn Reson Imaging. 2009 Jul;30(1):185–193. doi: 10.1002/jmri.21820. [DOI] [PubMed] [Google Scholar]
- 21.Börnert P, Keupp J, Eggers H, Aldefeld B. Whole-body 3D water/fat resolved continuously moving table imaging. J Magn Reson Imaging. 2007;25:660–665. doi: 10.1002/jmri.20861. [DOI] [PubMed] [Google Scholar]
- 22.Kruger DG, Riederer SJ, Grimm RC, Rossman PJ. Continuously moving table data acquisition method for long FOV contrast-enhanced MRA and whole-body MRI. Magn Reson Med. 2002;47:224–231. doi: 10.1002/mrm.10061. [DOI] [PubMed] [Google Scholar]
- 23.Kruger DG, Riederer SJ, Polzin Ja, Madhuranthakam AJ, Hu HH, Glockner JF. Dual-velocity continuously moving table acquisition for contrast-enhanced peripheral magnetic resonance angiography. Magn. Reson. Med. 2005;53:110–117. doi: 10.1002/mrm.20324. [DOI] [PubMed] [Google Scholar]
- 24.Kruger DG, Riederer SJ, Rossman PJ, Mostardi PM, Madhuranthakam AJ, Hu HH. Recovery of phase inconsistencies in continuously moving table extended field of view magnetic resonance imaging acquisitions. Magn. Reson. Med. 2005;54:712–717. doi: 10.1002/mrm.20573. [DOI] [PubMed] [Google Scholar]
- 25.Madhuranthakam AJ, Kruger DG, Riederer SJ, Glockner JF, Hu HH. Time-resolved 3D contrast-enhanced MRA of an extended FOV using continuous table motion. Magn Reson Med. 2004;51:568–576. doi: 10.1002/mrm.10729. [DOI] [PubMed] [Google Scholar]
- 26.Madhuranthakam AJ, Hu HH, Kruger DG, Riederer SJ. Numerical equilibration of signal intensity and spatial resolution in time-resolved continuously moving table imaging. Magn Reson Med. 2006;55:694–699. doi: 10.1002/mrm.20800. [DOI] [PubMed] [Google Scholar]
- 27.Sabati M, Lauzon ML, Frayne R. Space-time relationship in continuously moving table method for large FOV peripheral contrast-enhanced magnetic resonance angiography. Phys. Med. Biol. 2003;48:2739–2752. doi: 10.1088/0031-9155/48/17/301. [DOI] [PubMed] [Google Scholar]
- 28.Sabati M, Lauzon ML, Mahallati H, Frayne R. Interactive continuously moving table (iCMT) large field-of-view real-time MRI. Magn. Reson. Med. 2006;55:1202–1209. doi: 10.1002/mrm.20848. [DOI] [PubMed] [Google Scholar]
- 29.Han Y, Weigel M, Huff S, Ludwig U. Whole-body diffusion-weighted imaging with a continuously moving table acquisition method: preliminary results. Magn Reson Med. 2011;65:1557–1563. doi: 10.1002/mrm.22833. [DOI] [PubMed] [Google Scholar]
- 30.Ludwig U, Sommer G, Zaitsev M, Ghanem N, Hennig J, Fautz HP. 2D axial moving table acquisitions with dynamic slice adaptation. Magn Reson Med. 2006;55:423–430. doi: 10.1002/mrm.20779. [DOI] [PubMed] [Google Scholar]
- 31.Zhu Y, Dumoulin CL. Extended field-of-view imaging with table translation and frequency sweeping. Magn Reson Med. 2003;49:1106–1112. doi: 10.1002/mrm.10470. [DOI] [PubMed] [Google Scholar]
- 32.Aldefeld B, Börnert P, Keupp J. Continuously moving table 3D MRI with lateral frequency-encoding direction. Magn Reson Med. 2006;55:1210–1216. doi: 10.1002/mrm.20876. [DOI] [PubMed] [Google Scholar]
- 33.Sommer G, Fautz H-P, Ludwig U, Hennig J. Multicontrast sequences with continuous table motion: a novel acquisition technique for extended field of view imaging. Magn. Reson. Med. 2006;55:918–922. doi: 10.1002/mrm.20838. [DOI] [PubMed] [Google Scholar]
- 34.Keupp J, Aldefeld B, Börnert P. Continuously moving table SENSE imaging. Magn Reson Med. 2005;53:217–220. doi: 10.1002/mrm.20313. [DOI] [PubMed] [Google Scholar]
- 35.Hu HH, Madhuranthakam AJ, Kruger DG, Glockner JF, Riederer SJ. Continuously moving table MRI with SENSE: application in peripheral contrast enhanced MR angiography. Magn Reson Med. 2005;54:1025–1031. doi: 10.1002/mrm.20639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Fain SB, Browning FJ, Polzin JA, Du J, Zhou Y, Block WF, Grist TM, Mistretta CA. Floating table isotropic projection (FLIPR) acquisition: a time-resolved 3D method for extended field-of-view MRI during continuous table motion. Magn Reson Med. 2004;52:1093–1102. doi: 10.1002/mrm.20235. [DOI] [PubMed] [Google Scholar]
- 37.Scheffler K. Fast Volume Coverange using Sliding, Nonuniform Angular Sampling The Spiral CT Approach with Projection FLASH and TrueFISP Sequences. Proceedings of the 9th Annual Meeting of ISMRM; Glasgow, Scotland. 2001. p. 1774. [Google Scholar]
- 38.Rasche V, Holz D, Schepper W. Improved acquisition and reconstruction schemes in helical imaging. Proceedings of the 13th Annual Meeting of SMRM; San Francisco CA, USA. 1994. p. 78. [Google Scholar]
- 39.Shankaranarayanan A, Herfkens R, Hargreaves BM, Polzin JA, Santos JM, Brittain JH, Helical MR. continuously moving table axial imaging with radial acquisitions. Magn Reson Med. 2003;50:1053–1060. doi: 10.1002/mrm.10621. [DOI] [PubMed] [Google Scholar]
- 40.Winkelmann S, Schaeffter T, Koehler T, Eggers H, Doessel O. An optimal radial profile order based on the Golden Ratio for time-resolved MRI. IEEE Trans Med Imaging. 2007;26:68–76. doi: 10.1109/TMI.2006.885337. [DOI] [PubMed] [Google Scholar]
- 41.Rasche V, Holz D, Proksa R. MR fluoroscopy using projection reconstruction multi-gradient-echo (prMGE) MRI. Magn Reson Med. 1999;42:324–334. doi: 10.1002/(sici)1522-2594(199908)42:2<324::aid-mrm15>3.0.co;2-r. [DOI] [PubMed] [Google Scholar]
- 42.Shankaranarayanan A, Wendt M, Levin JS, Duerk JL. Two-Step navigatorless correction algorithm for radial k-space MRI acquisitions. Magn Reson Med. 2001;45:277–288. doi: 10.1002/1522-2594(200102)45:2<277::aid-mrm1037>3.0.co;2-1. [DOI] [PubMed] [Google Scholar]
- 43.Pipe JG, Menon P. Sampling density compensation in MRI: rationale and an iterative numerical solution. Magn Reson Med. 1999;41:179–186. doi: 10.1002/(sici)1522-2594(199901)41:1<179::aid-mrm25>3.0.co;2-v. [DOI] [PubMed] [Google Scholar]
- 44.Beatty PJ, Nishimura DG, Pauly JM. Rapid gridding reconstruction with a minimal oversampling ratio. IEEE Trans Med Imaging. 2005;24:799–808. doi: 10.1109/TMI.2005.848376. [DOI] [PubMed] [Google Scholar]
- 45.Gnanasegaran G1, Cook G, Adamson K, Fogelman I. Patterns, variants, artifacts, and pitfalls in conventional radionuclide bone imaging and SPECT/CT. Semin Nucl Med. 2009 Nov;39(6):380–395. doi: 10.1053/j.semnuclmed.2009.07.003. [DOI] [PubMed] [Google Scholar]
- 46.Sengupta S, Smith DS, Welch EB. Dynamic Slice-Optimized Shimming in Continuous Moving bed MRI. Proc of the Int Socy of Proc. Int. Soc. Magn. Reson. Med. 2014:1625. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.