Abstract
Citrate is one of the most important organic acids in many fruits and its concentration plays a critical role in organoleptic properties. The regulation of citrate accumulation throughout fruit development, and the origins of the phenotypic variability of the citrate concentration within fruit species remain to be clarified. In the present study, we developed a process-based model of citrate accumulation based on a simplified representation of the TCA cycle to predict citrate concentration in fruit pulp during the pre- and post-harvest stages. Banana fruit was taken as a reference because it has the particularity of having post-harvest ripening, during which citrate concentration undergoes substantial changes. The model was calibrated and validated on the two stages, using data sets from three contrasting cultivars in terms of citrate accumulation, and incorporated different fruit load, potassium supply, and harvest dates. The model predicted the pre and post-harvest dynamics of citrate concentration with fairly good accuracy for the three cultivars. The model suggested major differences in TCA cycle functioning among cultivars during post-harvest ripening of banana, and pointed to a potential role for NAD-malic enzyme and mitochondrial malate carriers in the genotypic variability of citrate concentration. The sensitivity of citrate accumulation to growth parameters and temperature differed among cultivars during post-harvest ripening. Finally, the model can be used as a conceptual basis to study citrate accumulation in fleshy fruits and may be a powerful tool to improve our understanding of fruit acidity.
Introduction
Citrate is one of the most important organic acids in many fruits [1], and its concentration in the pulp plays a critical role in organoleptic properties [2–5]. The citrate concentration varies considerably among cultivars of many fruit species including citrus [6], peach [7], pineapple [8], and banana [5]. The accumulation of citrate in fruit cells is a complex phenomenon because it involves several metabolic pathways and transport mechanisms across different compartments, mainly cytosol, mitochondria, and vacuole (for review see [9]). Ongoing transcriptomic [10], metabolomic [11], proteomic [12], and QTL studies [13] have begun to elucidate the complexity of the mechanisms involved in citrate accumulation. However, the regulation of citrate accumulation throughout fruit development, and the origins of the phenotypic variability of the citrate concentration within fruit species remain to be clarified. Given the complexity of the processes involved, ecophysiological process-based simulation models (PBSMs) could advance our understanding of the physiological mechanisms underlying citrate accumulation [14]. PBSMs could also help to elucidate the differences in citrate accumulation among and within fruit species, as it is the case for sugar accumulation in peach [15], and grape berry [16].
Attempts to mechanistically model citrate accumulation in fruits are rare. Lobit et al. [17] proposed a mechanistic model to simulate the dynamics of citrate concentration in peach fruit. This model was based on the assumption that in fleshy fruits, citrate accumulation is driven by the TCA cycle located in the mitochondria, which is a convincing hypothesis [9]. This model was used to analyze the effects of temperature and pulp growth on citrate concentrations in two cultivars of peach [17, 18], and appeared to provide a good framework to study citrate accumulation in fleshy fruit. However, the approach used to solve the system of equations derived from the model led to a simple equation to predict the rate of net citrate production with parameters that had lost their real biological meaning. Thus, despite its good predictive quality, this model did not allow a complete study of the behavior and regulation of fruit mitochondrial citrate metabolism.
In the present study, we built a new, more mechanistic, model of citrate accumulation, with parameters that have biological meaning, based on a simplified representation of the TCA cycle adopted by Lobit et al. [17], to predict citrate concentration in fruit during the pre- and post-harvest stages. Banana fruit was taken as a reference because it has the particularity of having separate growth and post-harvest ripening stages, during which citrate concentration undergoes substantial changes [19]. Moreover, the concentration of citrate in banana pulp varies greatly among cultivars which make possible to use the model as a tool to analyze the genotypic variability [5, 20]. The physiological age of the fruit at harvest is known to affect the concentration of citrate in banana pulp during post-harvest ripening [21]. Fruit pruning and potassium fertilization, two cultural practices commonly used by banana growers, can also impact the concentration of citrate in fleshy fruits (for review see [9]). Consequently, we chose to calibrate and validate the model on three cultivars with contrasting citrate accumulation, grown under different fruit loads and potassium supplies, and harvested at different stages to study how these growing conditions affect citrate metabolism (or not). Model parameterization, model selection, and test of fit are presented for the pre- and post-harvest phases. The sensitivity of the model to the input variables was analyzed during the pre- and post-harvest stages. The model enabled us to (i) advance our understanding of citrate metabolism during growth and post-harvest ripening of banana fruit; (ii) propose a possible explanation for differences in citrate accumulation among cultivars and identify potential genotypic parameters (i.e. genotype-dependent parameters); and (iii) study the effects of fruit growth conditions on citrate metabolism. Finally, the model can be used as a conceptual basis to study citrate accumulation in pre- and post-harvest stages in fleshy fruits and thus may be a powerful tool to improve our understanding of fruit acidity.
Materials and Methods
Description and units of parameters, constants and variables used throughout the text are summarized in S1 Table.
Model description
Model hypothesis
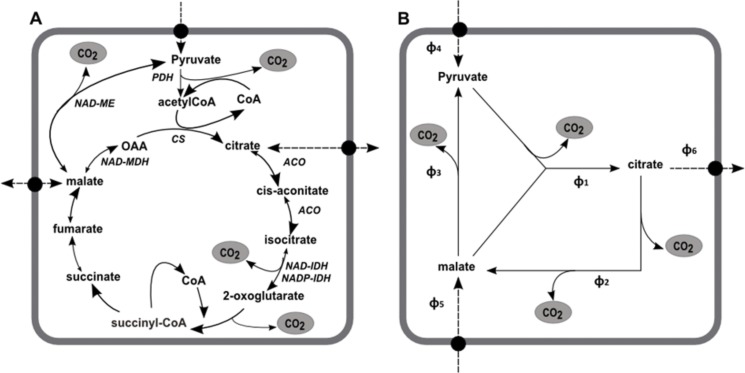
The accumulation of citrate in fruit cells involves several metabolic pathways and transport mechanisms across different compartments, mainly cytosol, mitochondria, and vacuole. Nevertheless, we showed in a previous paper [9] that the accumulation of citrate in the vacuole is unlikely to be limited by thermodynamic conditions, on the contrary to malate [22]. Therefore, it is likely that citrate accumulation in the vacuole is controlled by its cytosolic concentration and consequently by its metabolism. Among several possible pathways related to citrate metabolism, the TCA cycle is the only one that allows citrate synthesis. Therefore, the present model is based on the assumption that citrate accumulation in fleshy fruit is driven by the TCA cycle located in the mitochondria. The TCA cycle results in the oxidation of pyruvate into CO2 and a reduction in co-enzymes through a series of conversions between organic acids including malate and citrate (Fig 1A). The maintenance of the pools of TCA cycle intermediates implies that for each metabolite exported, one is imported, and vice versa. These exchanges are achieved by a variety of mechanisms mediated by mitochondrial carrier proteins (for reviews, see [23, 24]). The model presented here is based on the simplified representation of the TCA cycle used in the model of Lobit et al. [17] (Fig 1B). The only metabolites considered, pyruvate, malate and citrate, were chosen because they are at branch points between several reactions and because they are exchanged between the cytosol and the mitochondria. Pulp fruit was considered as a single big cell with mitochondrial and cytosolic compartments. We did not consider the compartmentalization of citrate in the vacuole because as we mentioned above we assumed that this step is not limiting for citrate accumulation in fruit cells.
Fig 1. Schematic representation of the TCA cycle.
(A) Reactions of the TCA cycle in the mitochondria and (B) the simplified model of Lobit et al. (2003). Enzymes are in italics: ACO, aconitase; CS: citrate synthase; NAD-ME, NAD-malic enzyme; NAD-IDH, NAD-isocitrate dehydrogenase; NADP-IDH, NADP- isocitrate dehydrogenase; NAD-MDH, NAD-malate dehydrogenase; PDH, pyruvate dehydrogenase. Dashed arrows indicate transport across the mitochondrial membrane.
Stoichiometric equations
The maintenance of the pools of metabolic intermediates imposes, for any given metabolite, that the sum of metabolic fluxes that synthesizes it and the sum of metabolic fluxes that degrades it are equal (Fig 1B).
| (1) |
| (2) |
| (3) |
The respiratory flux, approximated as the flux of CO2 produced by the TCA cycle, is:
| (4) |
where Mpyrmt, Mmalmt, and Mcitmt (mmol) are respectively the amount of pyruvate, malate and citrate in the pulp mitochondrial compartment, φi are the metabolic fluxes of the TCA cycle (mmol day-1), and Resp is the respiratory flux of the pulp mitochondrial compartment (mmol day-1).
Mathematical representations of enzymatic reactions
The metabolic flux between two compounds is described by enzyme kinetic rate laws, as a function that depends on the concentration of the reactants and on the ki parameters called rate constants [25].
| (5) |
| (6) |
| (7) |
where k1 (L2 day-1 mmol-1), k2 (L day-1), k3 (L day-1) are the rate constants, and Cmalmt, Cpyrmt, Ccitmt are the concentrations of malate, pyruvate and citrate in the pulp mitochondrial compartment, respectively (mmol L-1).
Mathematical representations of transport reactions
Several carriers are present on the inner membrane of plant cell mitochondria and allow the exchange of metabolites of the TCA cycle between the cytosol and the mitochondrial matrix (for review see [24]). For the sake of simplicity, we assumed that the transport of citrate, malate and pyruvate across the mitochondria depends mainly on the concentration gradients of the species transported between the cytosol and the mitochondrial matrix. Therefore, the formalism adopted to model the transport reactions was derived from Fick’s law, which states that the diffusion flux of a compound is proportional to the concentration gradient of this compound across the membrane.
| (8) |
| (9) |
| (10) |
where K4, K5, K6 are membrane permeability (L day-1); and Cmalcyt, Cpyrcyt, Ccitcyt are the respective concentrations of malate, pyruvate and citrate in the pulp cytosolic compartment (mmol L-1).
Solving the system and expressing the rate of net citrate production φ6 (mmol day-1)
Replacing the expressions of the different metabolic fluxes in Eq 1 to 4 gives the following system:
| (11) |
| (12) |
| (13) |
| (14) |
where Cpyrmt, Cmalmt, Ccitmt, Ccitcyt are the unknowns of the system, and Ki, ki, Cpyrcyt, Cmalcyt are parameters.
The system was solved by using the software Maple (Maple (16). Maplesoft, a division of Waterloo Maple Inc., Waterloo, Ontario). The solutions of Ccitmt and Ccitcyt were put into Eq 10 which gave the following expression for φ6:
| (15) |
Pulp respiration
Pulp respiration during fruit growth was calculated using the growth-maintenance equation [26]. Growth respiration is considered to be proportional to the fruit growth rate and maintenance respiration to dry mass and temperature [27, 28]. The effect of temperature is described with the Q10 concept. Pulp respiration (mmol CO2 day-1) was calculated as the sum of growth and maintenance respiration:
| (16) |
where qg is the growth respiration coefficient (mmol CO2 g-1), qm is the maintenance coefficient at 20°C (mmol CO2 g-1 day-1), Q10 is the temperature ratio of maintenance respiration (dimensionless), DW is the pulp dry weight (g) and Ѳ is the temperature (°C).
Pulp respiration during post-harvest ripening was calculated by considering growth respiration equal to zero, since the fruit was detached.
Calculation of the concentration of citrate in the pulp
Citrate concentration in the fruit was obtained by integrating φ6 over the monitored period starting with citrate content observed at the beginning of the period, and by dividing it by the pulp fresh weight.
| (17) |
where Ccit (mmol 100g FW-1) is the citrate concentration in the pulp, Mcitto (mmol fruit-1) is the amount of citrate in the pulp at t0, FW is pulp fresh weight (g), t is the time (days after bloom or days after ethylene treatment), to is the time of the beginning of the experiment, and φ6 the rate of net citrate production (mmol day-1).
Rate constants (ki) and membrane permeability (Ki)
We hypothesized that ki depends on enzyme activity, and Ki on transporter activity during fruit development. The activities of the TCA cycle enzymes and of the mitochondrial organic acid transporters can vary or remain constant during fruit growth [11, 29–31], and postharvest ripening [32–34], suggesting that ki and Ki are likely to vary during fruit growth and post-harvest ripening. During fruit growth, variations in ki and Ki may be due to changes in the number of mitochondria on one hand, and to the regulation of enzymes and transporter activities on the other hand. The first source of variation, i.e. the number of mitochondria, is likely to increase during fruit growth due to cell division and enlargement. Indeed, Winter et al. (1993 and 1994) found a positive linear relationship between the section area of the mitochondrial compartment and the section area of the leaf cells. Therefore, we chose to symbolize the link between the number of pulp mitochondria, and ki and Ki by representing their variations during fruit growth as a function of the structural dry weight of the pulp, which represents the constitutive part of pulp cells and is therefore an indicator of pulp cell growth. Concerning the second source of variation, it is known that mitochondrial enzymes and transporters can be regulated by allosteric and post translational regulation, but little information is available on this subject (for review see [35]). Therefore, for the sake of simplicity, we included a regulatory factor (mi) to modulate the relationship between the ki and Ki, and the structural dry weight of the pulp:
| (18) |
| (19) |
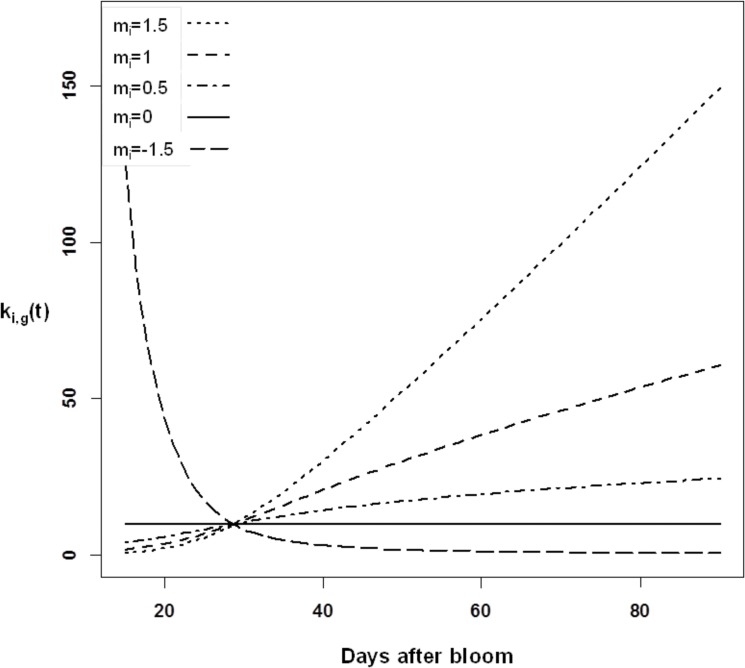
where SDW is the structural dry weight of the pulp (g); SDWref is a reference structural dry weight equal to 1 g; k i,g (L day-1 or L2 day-1 mmol-1), K i,g (L day-1), and m i (dimensionless) are fixed parameters, with k i,g and K i,g positives, and m i positive, null or negative. Depending on the values of the parameter m i, the patterns of ki,g(t) and Ki,g(t) can remain constant, increase, or decrease, as shown in Fig 2.
Fig 2. Hypothetical changes in the rate constant ki,g(t) during fruit growth as a function of parameter mi.
ki,g(t) = k i,g*SDWmi, with k i,g arbitrarily equal to 10 and SDW (pulp structural dry weight) taking values of the PL cultivar. The different values of mi correspond to the following situations: mi<0: enzyme inhibition exceeds the increase in the number of mitochondria; mi = 0: enzyme inhibition compensates for the increase in the number of mitochondria; 0<mi<1: enzyme inhibition under-compensates for the increase in the number of mitochondria; mi>1: activation of enzyme along with the increase in the number of mitochondria.
During postharvest ripening, the number of mitochondria of the pulp is likely to vary little since the fruit is no longer growing. Thus, changes in ki and Ki are likely to be only due to the regulation of enzymes and transporters. We chose to represent the putative variations of ki and Ki during banana post-harvest ripening as a function of the number of days after ethylene treatment using the following mathematical expression:
| (20) |
| (21) |
where DAE is the day after ethylene treatment; DAEref is a reference day after ethylene treatment equal to 1; k i,r (L day-1 or L2 day-1 mmol-1), K i,r (L day-1), and j i (dimensionless) are fixed parameters, with k i,r and K i,r positives, and j i positive, null or negative. Depending on the values of the parameter j i, ki,r(t) and Ki,r(t) can remain constant, increase, or decrease during ripening.
Model inputs and initial conditions
The model used daily pulp fresh weight, and daily pulp structural dry weight as input variables. Initial values were the amount of citrate in the fruit pulp on the first date of the modeled period. Eq 17 was numerically solved using the ‘lsoda’ function of the package ‘dsolve’ of the R software with a one-day time step [36].
Daily pulp dry weight was estimated by fitting a growth expolinear function to pulp dry weight data [37].
| (22) |
where Cm is the maximum absolute growth rate of pulp dry weight (g day-1), Rm is the maximum relative growth rate of pulp dry weight (g g-1 day-1), tb is the x axis intercept of the linear growth phase of pulp dry weight (day).
Daily pulp fresh weight was estimated using an empirical relationship with pulp dry weight (R² = 0.99 and n = 488):
| (23) |
Daily pulp structural dry weight was estimated using an empirical relationship with pulp dry weight (R² = 0.98 and n = 454):
| (24) |
Plant materials and experimental conditions
All experiments were conducted at the Campus Agro-Environnemental Caraïbe (CAEC, Martinique, French West Indies; latitude 14°37N, longitude 60°58W, altitude 16m) using three dessert banana cultivars (Musa spp.) diploids AA, that differ in their predominant organic acid at the eating stage: Indonesia 110 (IDN) which has a balanced ratio of citrate: malate, Pisang Jari Buaya (PJB) which is citrate dominant, and Pisang Lilin (PL) which is malate dominant (S1 Fig) [5]. In addition, these three cultivars present the advantage to be resistant to Black Leaf Streak Disease and Sigatoka Disease, two diseases known to affect banana fruit quality [38]. Experiments were conducted during the 2011 and 2012 growing seasons on continental alluvial soil. For the two growing seasons, irrigation was adjusted to the amount of rainfall to supply at least 5 mm of water per day, and non-systemic fungicide was applied to control foliar diseases. The mean daily temperature was 27 ± 1.2°C and 26± 0.9°C during the 2011 (March–November) and 2012 (February-August) growing season, respectively. In the 2011 experiment, 18 plants of each cultivar with high fruit load were used as the control treatment, and 18 other plants were highly pruned i.e. low fruit load. Fruit pruning was calculated so as to increase the leaf area: fruit ratio by approximately 2.5 for each cultivar (detailed in Etienne et al., 2014). In the 2012 experiment, two contrasted levels of potassium fertilization were applied: for each cultivar, one plot received 124 g of potassium per plant (high potassium fertilization) at 4-week intervals, while the other received no potassium at all (detailed in Etienne et al., 2014).
Fruit growth monitoring
In the two growing seasons, six bunches of each cultivar*treatment combination were selected. One fruit located in the internal row of the second proximal hand was collected for analyses every 15 days. Natural ripening on standing plants, i.e. when the first yellow finger appears, determined the end of sampling.
Monitoring of post-harvest ripening
Two harvest stages were studied in the 2011 experiment. The harvest stages were calculated for each cultivar to be 70% and 90% of the average flowering-to-yellowing time (FYT) of the bunch on the plant. For each harvest stage, six bunches of each cultivar*treatment combination were harvested. In the 2012 experiment, only one harvest stage was studied. The harvest stage was calculated for each cultivar to be 75% of the average FYT of the bunch on the plant. Six bunches of each cultivar*treatment combination were harvested. After the bunches were harvested, the second proximal banana hand per bunch was rinsed and dipped in fungicide (bitertanol, 200 mg L−1) for 1 min. The fruits were placed in a plastic bag with 20 μm respiration holes and stored in boxes for 6 days at 18°C. The fruits were then stored in a room at 18°C and underwent ethylene treatment (1 mL L−1 for 24 h) to trigger the ripening process. After 24 h, the room was ventilated. Bananas were maintained at 18°C for 13 days. A banana fruit was sampled before ethylene treatment, and at day 3, 6, 9 and 13 after ethylene treatment.
Biochemical and respiration measurements
For each fruit sampled, the fresh and dried pulp were weighed. The dried pulp was then mixed to obtain dry powder and to allow biochemical measurements. Citrate concentration was assessed according to the method described in Etienne et al. [19] using an enzymatic method and a microplate reader. Pulp structural dry weight was calculated as the difference between pulp dry weight and the sum of the weights of the main non-structural compounds (soluble sugars, starch, acids). To this end, concentrations of malate were assessed according to the method described in Etienne et al. [19], and concentrations of starch and soluble sugars (glucose, fructose, sucrose) were assessed according to Gomez et al. [39], using an enzymatic method and a microplate reader. For measurements of respiration, each sampled fruit was placed in a closed plastic jar. The temperature of the room was set at 18°C. After 1 hour, CO2 concentration was measured with a gas analyzer (Vigaz, CANAL120).
Model parameterization
Based on information found in the literature, the value of Cmalcyt was set at 1 mM [40, 41], and the value of Cpyrcyt was set at 0.5 mM [42, 43].
Parameters of the pulp dry weight growth model (Cm, Rm, tb) were estimated for each banana plant using a nonlinear least-squares regression method [44]. The model explained 99% of the pulp dry weight variance in the three cultivars and in the two years of the experiment, and the RRMSE was satisfactory with mean values of 0.1 (S2 Fig).
According to the literature, the temperature ratio of maintenance respiration Q10 was set at 2 [45]. The growth respiration coefficient of the pulp (qg) was derived from construction cost measurements on banana pulp. In the three cultivars, the total nitrogen, carbon and ash concentration of the banana pulp were measured at three different stages of fruit growth. The construction cost (CC; g glucose g-1) was calculated as a function of the carbon (C; g g DW-1), nitrogen (N; g g DW-1), and ash (A; g g DW-1) concentrations of banana pulp, and of the energetic costs of N assimilation and carbohydrate translocation [46, 47]:
| (25) |
where fNh is the fraction of N used in growth that is assimilated heterotrophically, assumed to be equal to 1 for fruits [47], and rT is the added cost of translocating photosynthetates from sources to sinks, assumed to be equal to 5.3% [46].
The coefficient qg (mmol CO2 g-1) was calculated using the following formula [48]:
| (26) |
where αCC is the carbon construction cost (α = 0.4 is the concentration of carbon in glucose), and MC is the molar mass of carbon equal to 12 g mol-1.
The calculated values of qg were found to not significantly differ among cultivars and among developmental stages (data not shown). Thus, for qg a value common to all cultivars and developmental stages was chosen as the mean value of the calculated values which was qg = 13 mmol CO2 g-1 ±1. This value is in the range of values found for tomato (9.3 mmol CO2 g-1; [49]), peach (7.0 mmol CO2 g-1; [50]), and mango (3.0 mmol CO2 g-1; [48]).
The maintenance respiration coefficient (qm) of the pulp during banana growth and post-harvest ripening were calculated respectively from measurements of respiration in harvested green fruits and in fruits subjected to ethylene treatment in the 2012 experiment (n = 180). Since the fruits were harvested, we assumed that the measured respiration corresponded only to maintenance respiration. Therefore, by inverting Eq 16, qm was calculated as follows:
| (27) |
The value of qm during fruit growth was estimated at qm = 0.15 mmol CO2 g-1 day-1 ±0.02 for the three cultivars, a value close to those estimated for tomato (0.27 mmol CO2 g-1 day-1; [51]), peach (0.05 mmol CO2 g-1 day-1; [50]), and mango (0.09 mmol CO2 g-1 day-1; [48]).
The values of calculated qm during postharvest ripening were plotted as a function of the number of days after ethylene treatment. In all three cultivars, qm increased dramatically during the first two days after ethylene treatment, and then remained constant until the end of ripening (S3 A,S3 B and S3 C Fig). An appropriate expression to represent qm was:
| (28) |
where DAE is the day after ethylene treatment, and qm1, qm2, and qm3 are fitted coefficients.
The values of qm differed significantly among cultivars, so we decided to fit the model of Eq 28 to the three cultivars separately. Thus, parameters qm1, qm2, and qm3 were estimated for each cultivar by using a nonlinear least-squares regression method on the 2012 data [44] (Table 1). The model allowed satisfactory prediction of fruit respiration during postharvest ripening (R² = 0.72; RRMSE = 0.10) (S3 D Fig).
Table 1. Estimated parameter values and standard errors (in parentheses) of the qm model during postharvest ripening in cultivars IDN, PJB, and PL.
| qm1
(mmol CO2 g-1 day-1) |
qm2
(dimensionless) |
qm3
(dimensionless) |
|
|---|---|---|---|
| IDN | 0.61 (0.01) | 0.71 (0.04) | 1.08 (0.18) |
| PJB | 0.48 (0.01) | 0.68 (0.05) | 0.65 (0.13) |
| PL | 0.52 (0.01) | 0.68 (0.04) | 0.87 (0.13) |
Parameters were estimated using the data from 2012 post-harvest ripening.
Model calibration
Every parameters related to reaction rates ki(t) and membrane permeability Ki(t) were estimated by fitting the predicted citrate concentrations to observed values of the 2011 dataset separately for each cultivar and developmental stage (60 data per cultivar during growth and 96 data per cultivar during post-harvest ripening) using the hydroPSO function of the R software [52]. The hydroPSO function uses the computational method of particle swarm optimization (PSO) that optimizes a problem by iteratively trying to improve a candidate solution with regard to a given measure of quality. Parameters were estimated by minimizing the following criterion:
| (29) |
where xij is the predicted value, and yij is the observed value of the fruit of the jth banana plant at date ti, and σj is the standard deviation of the observed values of the fruit of the jth banana plant.
The model obtained, in which all the estimated parameters were different among cultivars, was named Model 1.
Model selection
We used model selection to detect significant differences in parameter values among cultivars. Model 1 in which all the ki,g(t) and Ki,g(t) were specific to cultivars were compared to reduced models in which some of the parameters were supposed to be the same for some of the cultivars, thus reducing the number of parameters to be estimated. For two models that do not significantly differ in fit quality, the one with fewer parameters is always preferred. The best model was named Model 2.
Models were selected using the Akaike information criterion (AIC), which allows the comparison of nested and non-nested models. In our case, the number of parameters exceeded n/40 (where n is sample size), so a second order derivative AICc, which contained a bias correction term for small sample size, was applied, as suggested by Johnson and Omland [53]. The model with smaller AICc was preferred.
| (30) |
where n is the number of observations, RSS is the residual sum of squares, and k is the number of estimated parameters of the model.
Sensitivity analysis of the model to pulp growth, respiration and temperature
A sensitivity analysis of the model was conducted in order to get insights into the effects of pulp growth, respiration and temperature on citrate accumulation during fruit growth and post-harvest maturation. We linked the pre- and post-harvest stages by taking into account the six days of fruit storage at 18°C between harvest and ethylene treatment, and assumed that, during that period, fruit respiration was equal to growth maintenance respiration. The sensitivity of the model was quantified by normalized sensitivity coefficients (SC), defined as the ratio between variation in the citrate concentration (ΔC) relative to its standard value (C), and variation in growth parameters, respiration parameters, and temperature (ΔP) relative to its standard value (P) [54].
| (31) |
The interpretation of SC is referred to as local sensitivity analysis since these coefficients provide information on the effect of small changes in the parameters (or inputs) on the response of the model. They do not provide information on the effect of simultaneous or large changes in parameters (or inputs). SCs were calculated by altering one parameter (or input) by ±0.1% while maintaining all the other parameters at default values. A positive and negative sign of SC correspond, respectively, to a response in the same or reverse direction as the variation in the parameter (or input). The larger the absolute value of SC, the more sensitive the model is to the parameter (or input). Since the SC behaved similarly between years for a given cultivar, only results in 2011 are presented. For the sensitivity analysis during postharvest ripening, the SCs behaved similarly between the two harvest stages in a given cultivar, so only results for 70% of FYT are presented.
Goodness-of-fit and predictive quality of the model
The goodness-of-fit of the model was evaluated using two commonly used criteria, the root mean squared error (RMSE) and the relative root mean squared error (RRMSE), to compare the mean difference between simulated and observed results [55]. The smaller the value of RMSE and RRMSE, the better the fit.
| (32) |
where Yi is the predicted value of the fruit i, and Xi is the measured value of the fruit i. n is the number of data.
| (33) |
where is the mean of all observed values.
The predictive quality of the model, which ascertains the validity of the model in different scenarios, was quantified by the RMSE and RRMSE calculated on the 2012 data set.
Results
Overview of cultivar and treatment effects
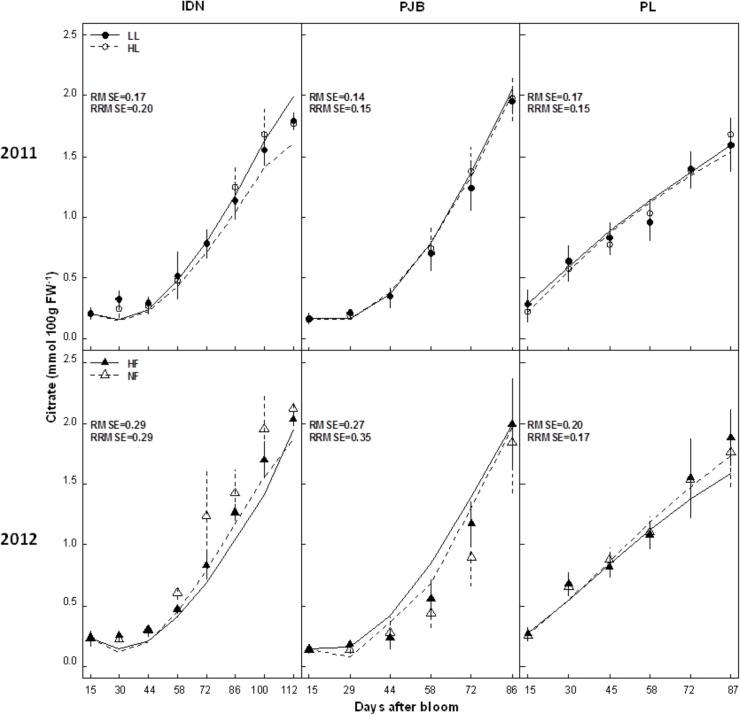
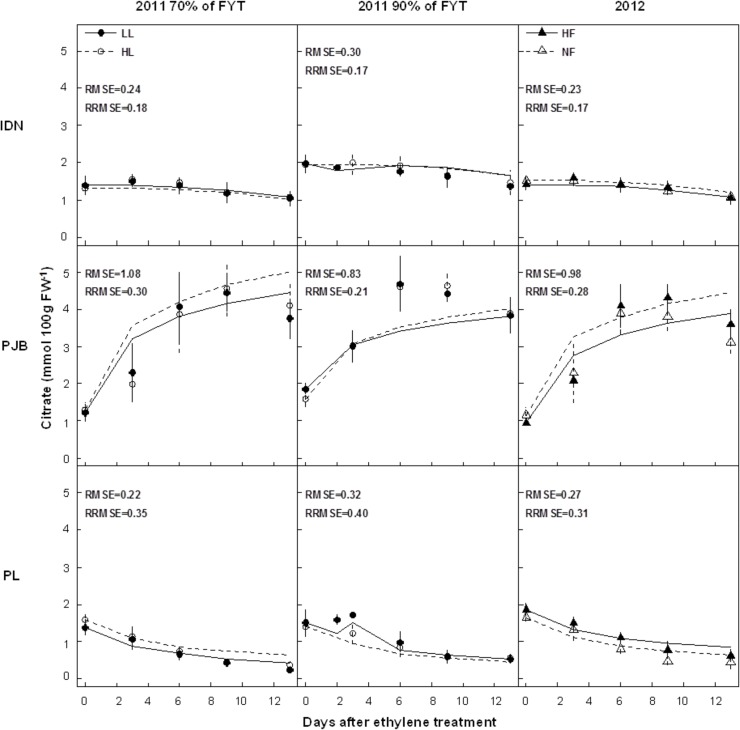
The effects of cultivar and treatments on citrate concentration in banana pulp during the pre- and post-harvest stages are detailed in a previous paper [20], so only the main conclusions are presented here. During banana growth, citrate concentration increased and was significantly affected by cultivar both in 2011 and 2012. The PL cultivar had significantly higher citrate concentration in the pulp than the IDN and PJB cultivars (Fig 3). During banana post-harvest ripening, both the ripening stage and the cultivar had a significant effect on the concentrations of citrate in 2011 and 2012. The pattern of citrate concentration in the pulp were the same in the IDN and PL cultivars with an overall decrease during ripening, whereas there was an overall increase in the PJB cultivar (Fig 4). At the end of ripening, PJB had the highest citrate concentration and PL the lowest. Fruits harvested later (at 90% of flowering-to-yellowing time (FYT)) had significantly higher concentration of citrate throughout ripening in the three cultivars. Low fruit load significantly increased the pulp fresh weight in all three cultivars but had no effect on the concentration of citrate during either growth or post-harvest ripening. Potassium fertilization significantly increased the pulp fresh weight in cultivars PJB and PL, whereas the opposite was the case for fruits from the IDN cultivars. However, potassium fertilization had no effect on the concentration of citrate during either growth or post-harvest ripening in all three cultivars.
Fig 3. Measured (dots) and simulated (lines) citrate concentrations in the pulp of cultivars IDN, PJB, and PL during fruit growth.
The cultivars were grown under two contrasted fruit loads in 2011 (LL: low fruit load; HL: high fruit load), and two contrasted levels of potassium fertilization in 2012 (NF: no potassium fertilization; HF: high level of potassium fertilization). Data are means ± s.d (n = 6). The RMSE (mmol 100g FW-1) and RRMSE are indicated in each graph.
Fig 4. Measured (dots) and simulated (lines) citrate concentrations in the pulp of cultivars IDN, PJB, and PL during fruit post-harvest ripening.
The cultivars were grown under two contrasted fruit loads in 2011 (LL: low fruit load; HL: high fruit load), and two contrasted levels of potassium fertilization in 2012 (NF: no potassium fertilization; HF: high level of potassium fertilization). In 2011, fruits were harvested at two different stages: early stage (70% of FYT) and late stage (90% of FYT). Data are means ± s.d (n = 6). The RMSE (mmol 100g FW-1) and RRMSE are indicated in each graph.
Model calibration and selection
Model 1 was fitted to observed data by estimating 48 parameters (16 per cultivar), and predictions were in good agreement with observed 2011 data for the three cultivars (mean RRMSE = 0.23). Comparison of model 1 with several reduced models was made based on the AICc criterion (data not shown). We selected the reduced model 2. In model 2, during the pre-harvest stage, m 1, m 3 and m 4 were fixed at 0 for the three cultivars; k 1,g, k 3,g, K 4,g were the same for the three cultivars; and K 5,g and m 5 were specific to cultivars, thus reducing the number of estimated parameters to nine (Table 2). During the post-harvest stage, j 1 were fixed at 0 for PJB, j 3 and j 4 were fixed at 0 for the three cultivars, j 5 were fixed at 0 for IDN and PL; and K 4,r and K 5,r were the same for cultivars IDN and PL, reducing the number of estimated parameters to 13 (Table 2). Values of the 22 estimated parameters of model 2 are summarized in Table 3.
Table 2. Results of model selection between full and reduced models using AICc criteria.
| Model | AICc | Stage | Estimated parameters | Fixed parameters |
|---|---|---|---|---|
| 1 | -665 | Pre-harvest | k1,g idn,m1 idn,k3,g idn,m3 idn,K4,g idn,m4 idn,K5,g idn,m5 idn,k1,g pjb,m1 pjb,k3,g pjb,m3 pjb,K4,g pjb,m4 pjb,K5,g pjb,m5 pjb,k1,g pl,m1 pl,k3,g pl,m3 pl,K4,g pl,m4 pl,K5,g pl,m5 pl | |
| Post-harvest | k1,r idn,j1 idn,k3,r idn,j3 idn,K4,r idn,j4 idn,K5,r idn,j5 idn, k1,r pjb,j1 pjb,k3,r pjb,j3 pjb,K4,r pjb,j4 pjb,K5,r pjb,j5 pjb, k1,r pl,j1 pl,k3,r pl,j3 pl,K4,r pl,j4 pl,K5,r pl,j5 pl | |||
| 2 | -729 | Pre-harvest | k1,g idn = k1,g pjb = k1,g pl,k3,g idn = k3,g pjb = k3,g pl, K4,g idn = K4,g pjb = K4,g pl, K5,g idn,m5 idn,K5,g pjb,m5 pjb,K5,g pl,m5 pl | m1 idn = m1 pjb = m1 pl = 0, m3 idn = m3 pjb = m3 pl = 0, m4 idn = m4 pjb = m4 pl = 0 |
| Post-harvest | k1,r idn,j1 idn,k3,r idn,k1,r pl,j1 pl,k3,r pl, k1,r pjb,k3,r pjb,K4,r pjb,K5,r pjb,j5 pjb, K4,r idn = K4,r pl,K5,r idn = K5,r pl | j1 pjb = 0,j5 idn = j5 pl = 0, j4 idn = j4 pjb = j4 pl = 0, j3 idn = j3 pjb = j3 pl = 0 |
The superscript names following the parameters refer to banana cultivars IDN, PJB and PL. The best model is Model 2.
Table 3. Selected rate constants and membrane permeability for the cultivars IDN, PJB, and PL according to the best model (Model 2).
| Rate constants (ki) and membrane permeability (Ki) | Unit | Equation | ||
|---|---|---|---|---|
| PL | IDN | PJB | ||
| Pre-harvest | ||||
| k1,g(t) | L².day-1.mmol-1 | 9000 | ||
| k3,g(t) | L.day-1 | 2 | ||
| K4,g(t) | L.day-1 | 4000 | ||
| K5,g(t) | L.day-1 | 0.0048*SDW(t)0.98 | 0.0012*SDW(t)1.99 | 0.0017*SDW(t)1.95 |
| Post-harvest | ||||
| k1,r(t) | L².day-1.mmol-1 | 5634*t1.36 | 4904*t-1.99 | 9887 |
| k3,r(t) | L.day-1 | 531 | 0.17 | 0.08 |
| K4,r(t) | L.day-1 | 3965 | 6889 | |
| K5,r(t) | L.day-1 | 1.0*10–4 | 1.03*t-1.26 | |
Evaluation of the model
Citrate concentrations simulated by model 2 were in good agreement with 2011 values observed in the three cultivars (RMSEs and RRMSEs ranged between 0.14 and 1.08 mmol 100g FW-1, and between 0.15 and 0.40 respectively) (Figs 3 and 4). Model validation on data from 2012 was also satisfactory, as revealed by RMSEs and RRMSEs of predictions, with values ranging between 0.20 and 0.98 mmol 100g FW-1, and between 0.17 and 0.35 respectively. Statistical analysis revealed that the model correctly simulated the strong effect of cultivar and fruit age (S2 and S3 Tables). The model predicted little effect of fruit load and potassium fertilization, consistent with observed data. The model predicted a small effect of harvest stage, consistent with observed data, but was not able to simulate the minor differences correctly (data not shown).
Predictions of metabolic fluxes
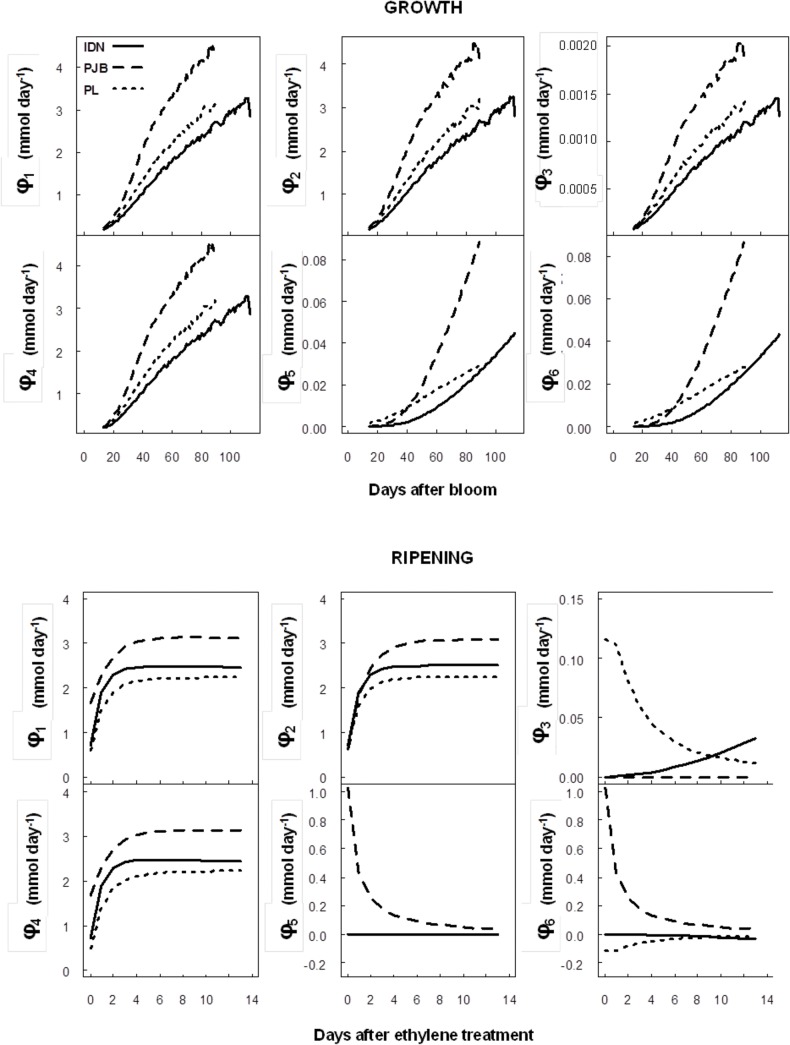
The metabolic fluxes of the TCA cycle predicted by the model are presented in Fig 5 for the three cultivars. During banana growth, all the metabolic fluxes underwent a continuous increase in the three cultivars. φ1, φ2, φ3, and φ4 followed the same pattern, but φ3 was a lot lower. φ5 and φ6 followed another pattern. All the metabolic fluxes were highest in cultivar PJB, then in cultivar PL and lastly in cultivar IDN. During post-harvest ripening, φ1, φ2, and φ4 dramatically increased in the first two days after ethylene treatment and then remained constant in all three cultivars. φ1, φ2, and φ4 were highest in cultivar PJB, then in cultivar IDN and lastly in cultivar PL. There were great differences in the pattern of φ3, φ5, and φ6 among cultivars during ripening. φ3 was close to zero for PJB, was positive and increased for IDN, and was positive and decreased for PL. φ5 and φ6 were close to zero for IDN and PL, and were high for PJB at the beginning of ripening but then decreased to 0.
Fig 5. Metabolic fluxes of the TCA cycle predicted by the citrate model during fruit growth and post-harvest ripening for the cultivars IDN, PJB, and PL.
Sensitivity analysis to growth, respiration and temperature
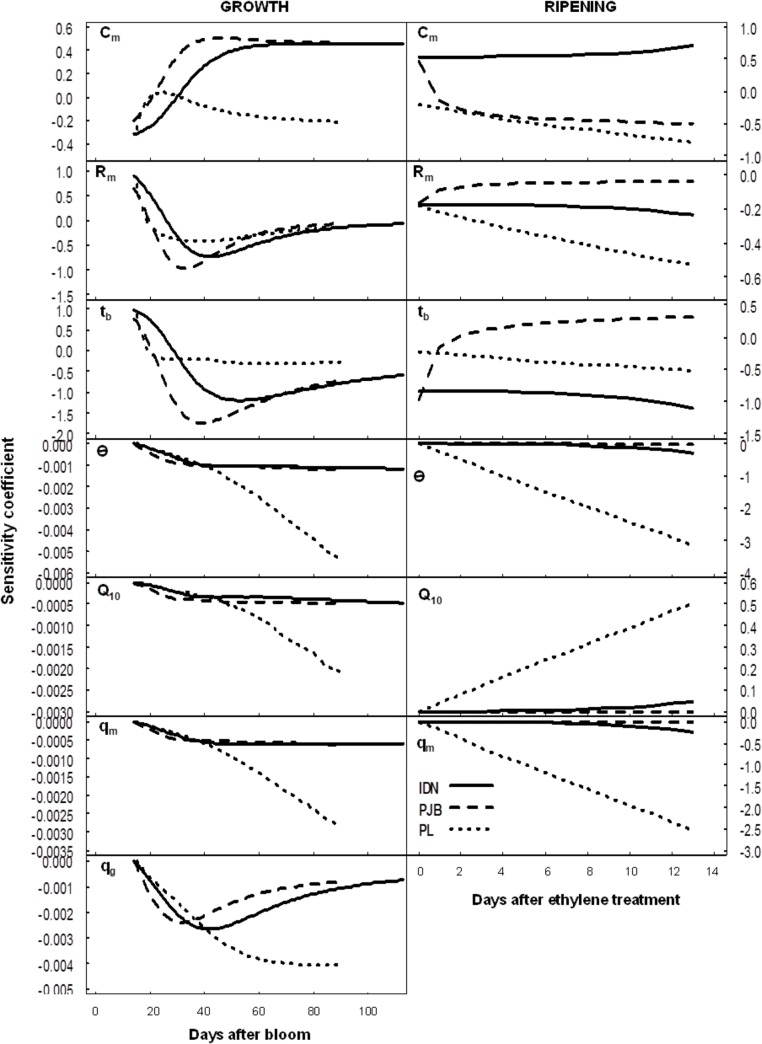
During banana growth, pulp growth parameters influenced citrate concentration in a cultivar dependent manner (Fig 6). The sensitivity of the model to Cm was higher in cultivars IDN and PJB, than in cultivar PL. The SC of Cm increased in the first part of growth, and remained almost constant thereafter. The model was very sensitive to Rm and tb at the beginning of growth, and less at the end. During postharvest ripening, Cm had a positive effect on citrate concentration in the cultivar IDN, and a negative effect in cultivars PJB and PL. Rm had a negative effect on citrate concentration in all three cultivars. tb had a negative effect on citrate concentration in cultivar IDN, and a positive effect in cultivars PJB and PL.
Fig 6. Normalized sensitivity coefficients of citrate concentration to the growth parameters, temperature, and respiration parameters during growth and post-harvest ripening in the cultivars IDN, PJB, and PL.
Temperature refers to air temperature during fruit growth, and to storage temperature during fruit ripening.
During banana growth, respiration parameters and temperature had no effect on citrate concentration in any of the three cultivars (Fig 6). During post-harvest ripening, qm and storage temperature greatly influenced citrate accumulation in a negative way in cultivar PL but had no effect in cultivars IDN and PJB. Q10 had a positive effect on citrate accumulation in cultivar PL, and no effect in cultivars IDN and PJB. The reason why Q10 had a positive effect was that storage temperature was lower than 20°C (see Eq 16).
Discussion
Metabolism more than dilution by growth was responsible for the genotypic variability in citrate concentration
The concentration of citrate in fruit pulp is the result of several processes. First, the metabolic processes of citrate control the amount of citrate in the pulp (for review see [9]). Second, the accumulation of water and dry matter in the fruit influences the concentration of citrate in the pulp due to dilution caused by change in fruit volume [56]. Pulp fresh weight increased during the pre-harvest stage for the three cultivars [20] but not sufficiently to induce a decrease in the concentration of citrate in the pulp. Thus, during the pre-harvest stage, citrate concentration was mainly linked to its metabolism. This result is in accordance with Wu et al. [18] who showed that peach citrate concentration was mainly linked to its metabolism during the green stage. As a consequence, the differences in the concentration of citrate in banana pulp among cultivars were mainly the result of differences in metabolism rather than in dilution [20]. During post-harvest ripening, since pulp fresh weight did not change anymore, the main component affecting citrate concentration and consequently responsible for genotypic variability was metabolism.
Potential role for NAD-malic enzyme and mitochondrial malate carriers in the genotypic variability of citrate metabolism during the pre- and post-harvest stages
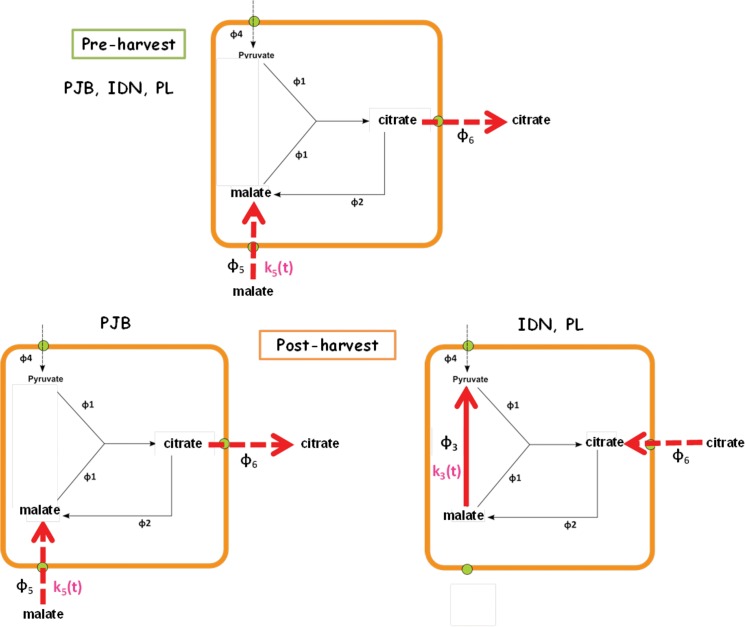
The model gives a possible explanation for differences in citrate metabolism between the pre- and post-harvest stages, and among cultivars (Fig 7 ). During fruit growth, the model predicted a common metabolic scheme for the three cultivars with the flux of malate conversion into pyruvate (φ3) close to zero, and consequently the flux of net citrate production (φ6) was equal to the flux of malate imported into mitochondria (φ5). Thus, during the pre-harvest stage, the import of malate into the mitochondria drove citrate production. The model suggested that differences in citrate accumulation among cultivars during fruit growth were due to differences in φ5, and in particular in K5,g(t), which reflects the activity of malate mitochondrial transporters. In the three cultivars, K5,g(t) increased during banana growth but increased more in cultivar PJB than in the two other cultivars. It is known that the expression of mitochondrial malate transporters varies during fruit development [31]. The absence of φ3 suggests that the pyruvate imported into the mitochondria through φ4 could completely satisfy the fruit energy demand, with no need to produce any pyruvate via the mitochondrial malic enzyme reaction.
Fig 7. Schematic diagram of the differences in organic acid metabolism predicted by the model among the three cultivars during the pre and post-harvest stages.
Red arrows indicate major fluxes involved in citrate accumulation. The genotypic parameters identified by the model are represented in pink.
During post-harvest ripening, the model predicted the same metabolic scheme as during growth in the cultivar PJB, i.e. the import of malate into the mitochondria drove citrate production. In cultivar PJB, K5,r(t) was important at the beginning of ripening and then decreased dramatically, explaining why the concentration of citrate increased significantly in the first days after ethylene treatment and then remained almost constant. In cultivars IDN and PL, φ3 was positive and φ5 was equal to zero during post-harvest ripening. Consequently, φ6 was equal to-φ3 and was therefore negative (in particular for PL; φ6 was close to zero for IDN), explaining the decrease in citrate concentration. Model selection indicated that k3,r(t), which reflects mitochondrial NAD-malic enzyme activity, can be assumed to remain constant during post-harvest ripening in the three cultivars, suggesting that NAD-malic enzyme activity is likely to vary little during this stage. Borsani et al. [33] observed no significant changes in NAD-malic enzyme activity during post-harvest ripening in peach. Differences in citrate concentrations between cultivars IDN and PL were due to differences in φ3, and in particular in k3,r(t). There is no information in the literature concerning the possible involvement of mitochondrial NAD-malic enzyme in the difference in acidity among fruit cultivars, but the model suggests this could be an interesting avenue to explore. In the end, it appears that screening for a genotype with low mitochondrial malate transport activity or high mitochondrial NAD-malic enzyme activity could be the most promising way to achieve a low citrate concentration in ripe fruit.
Pulp growth affected citrate metabolism in a cultivar-dependent manner
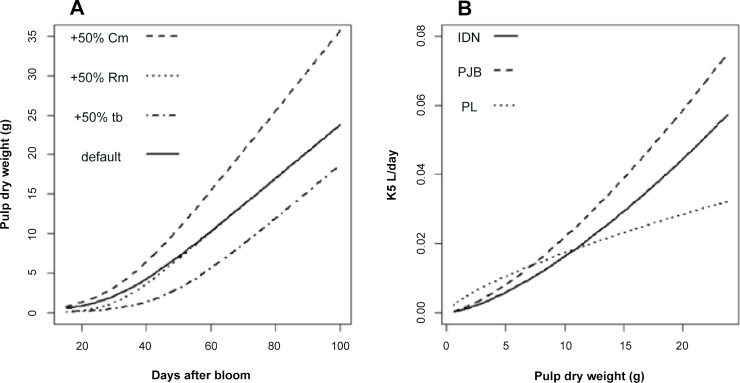
The effect of fruit load on citrate concentration predicted by our model was the result of modifications in banana pulp growth (S4 Table). Increasing pulp growth parameters affected pulp dry weight, and consequently pulp fresh weight, in different ways (Fig 8A) with consequences on citrate metabolism. During fruit growth, φ6 was equal to φ5 for the three cultivars, which means that φ6 depended on K5,g(t) and Malmt (see Eq 9). Increasing pulp dry weight increased K5,g(t) (Fig 8B). Malmt was positively related to dry weight through respiration. Nevertheless since Malmt was negligible compared to Malcyt (data not shown), respiration had no impact on φ6. Therefore, increasing pulp dry weight increased the weight of citrate in the pulp due to the increase in K5,g(t). In the end, the effect of pulp growth parameters on citrate concentration in the pulp depended on whether the effect on citrate production was greater than the effect on fresh weight (or not), explaining why the sensitivity coefficients of citrate concentration in the pulp varied so much during fruit growth. Wu et al. [18] used the citrate model of Lobit et al. [17] to study the effect of peach mesocarp growth on citrate concentration. They showed that an increase of pulp dry weight increased both fresh weight and citrate production, which increased citrate concentration at the beginning of fruit development and decreased it near maturity depended on whether the effect on citrate production was greater than the effect on fresh weight (or not). The fact that respiration had no impact on banana citrate concentration during the pre-harvest stage explains why the SCs of respiration parameters were close to zero which was similar to the results on peach maintenance respiration parameters obtained by Wu et al. [18]. However our results on banana growth respiration coefficient contrasted with the results on peach which showed that increasing growth respiration coefficient increased citrate concentration in particular at the beginning of fruit growth [18].
Fig 8. Changes in pulp dry weight in response to (A) growth parameters and (B) K5,g(t) for the three cultivars.
Growth parameters were increased one at a time by 50% of their default value. K5,g(t) were calculated for each cultivar using the equations presented in Table 3.
During post-harvest ripening, bigger fruits had higher respiration which had cultivar-dependent consequences on post-harvest citrate metabolism. For PL, φ6 was equal to-φ3 and was therefore negative. Since φ3 was positively related to Malmt, itself positively related to respiration, fruits with higher respiration had higher rate of citrate degradation. This explains why increasing qm, as well as decreasing Q10, decreased citrate concentration. For IDN, φ6 was close to zero and was therefore not affected by respiration. For PJB, φ6 was equal to φ5. Therefore, increasing respiration had no effect on citrate production because K5,r(t) only depended on time during post-harvest ripening (see Eq 21). The effect of pulp growth parameters on the concentration of citrate in the pulp during post-harvest ripening depended on their effects on citrate concentration at harvest (i.e. during the pre-harvest stage), on citrate metabolism after ethylene treatment and on fresh weight. All these combined effects explain why the SCs of citrate concentration to pulp growth parameters changed during post-harvest ripening. The minor effect of potassium fertilization on citrate concentration predicted by the model during post-harvest ripening was the result of small modifications in pulp growth. Fruits grown under contrasted potassium fertilization had different growth parameters (S5 Table) that affected citrate concentration during post-harvest ripening in a cultivar dependent manner.
The model predicted a cultivar-dependent response of citrate concentration to storage temperature
During fruit growth, the model predicted no effect of temperature on the concentration of citrate in the pulp for the three cultivars, whereas it showed a cultivar-dependent response to storage temperature during post-harvest ripening. A negative effect of storage temperature was predicted on the concentration of citrate for cultivar PL but none for cultivars IDN and PJB. This is an interesting outcome of the model since storage temperature is a variable easy to control, however these results need to be checked experimentally. The negative effect of temperature on citrate concentration predicted for cultivar PL is in accordance with the fact that, as frequently observed in field experiments, high temperatures reduce fruit acidity (for review see [9]). Moreover, Bugaud et al. [57] observed that banana harvested during the cold season had the highest concentration of citrate. The cultivar dependency of citrate concentration to temperature has also been simulated by Wu et al. [18] on peach using the model of Lobit et al. [17]. This model predicted that raising mean temperature during ripening increased citrate concentration for cv. Fidelia whereas it had almost no effect for cv. Suncrest. The main reason was that for cv. Fidelia, a parameter k3 related to temperature was additionally included in the model, compared with the model for cv. Suncrest. In our model, temperature affected citrate concentration only through modification of respiration. We did not consider any effect of temperature on enzyme and transporter activities but it is known that temperature controls the reaction rates of glycolysis and of the TCA cycle [35] by modifying enzyme activities [58], and also the kinetic properties of the mitochondrial transport systems involved [59]. Therefore, a possible improvement of the citrate model could be to take into account the temperature dependency of enzyme and transporter activity.
Model validity
We assumed that citrate accumulation is driven by the TCA cycle located in the mitochondria. This assumption is in fact a simplification of the complex carbon metabolism that takes place in fleshy fruit (for review see [9]). The model was based on a simplified representation of the TCA cycle and several processes were not considered, like the regulation of TCA cycle by coenzymes among others. The validity of flux predictions could be tested by comparing them to experimental measurements of metabolic fluxes. This kind of approach is commonly used to model metabolic flux and helps constrain the flux solution space [60]. Moreover, Sweetlove et al. [60] suggested that metabolic input and output are the key drivers of flux distribution, more than enzyme regulation. Consequently, the precise determination of the input metabolites considered in our model (cytosolic malate and pyruvate concentrations) should help improve metabolic predictions. In the present model, cytosolic malate and pyruvate concentrations were assumed to be constant during banana development, whereas in reality they certainly fluctuate since they play a role in the regulation of cytosolic pH [61]. Further work will be required to validate the main conclusions of the model with experimental results (i.e. measurements of enzyme activities or mRNA levels), as e.g. the possible involvement of mitochondrial NAD-malic enzyme in the difference in acidity among fruit cultivars.
Conclusion
The model of TCA cycle functioning proposed in this study satisfactorily simulated the dynamics of citrate concentration during the pre- and post-harvest stages of fruit development in a range of cultivars. This model turned out to be an interesting tool to dissect the effects of genotypic and environmental factors on citrate concentration. In particular, the model suggested major differences in TCA cycle functioning among cultivars during post-harvest ripening of banana, and pointed to the potential role of NAD-malic enzyme and mitochondrial malate carriers in the genotypic variability of citrate concentration. The next step will be to validate these assumptions experimentally. Given that the TCA cycle is a universal feature of fruit metabolism, the present model can be used as a conceptual basis for modeling citrate accumulation in other fruit species. In the future, linking such models with a model for malate [22], and a model relating titratable acidity and pulp composition [19], would be a powerful tool for fruit quality improvement.
Supporting Information
(XLSX)
(TIF)
(TIF)
(TIF)
(PDF)
(PDF)
(PDF)
(PDF)
(PDF)
Acknowledgments
We thank Dr. Hubert Vincent Varella for critical reading of model calibration, model selection and sensitivity analysis methodology.
Data Availability
All relevant data are within the paper and its Supporting Information files.
Funding Statement
Financial support for this study was provided by Structural European Funds. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Seymour GB, Taylor J, Tucker GA. Biochemistry of fruit ripening Chapman & Hall; London; 1993. [Google Scholar]
- 2. Esti M, Cinquanta L, Sinesio F, Moneta E, Di Matteo M. Physicochemical and sensory fruit characteristics of two sweet cherry cultivars after cool storage. Food Chem. 2002; 76: 399–405. [Google Scholar]
- 3. Harker F, Marsh K, Young H, Murray S, Gunson F, Walker S. Sensory interpretation of instrumental measurements 2: sweet and acid taste of apple fruit. Postharvest Biology and Technology. 2002; 24: 241–250. [Google Scholar]
- 4. Tieman D, Bliss P, McIntyre LM, Blandon-Ubeda A, Bies D, Odabasi AZ, et al. The chemical interactions underlying tomato flavor preferences. Curr Biol. 2012; 22: 1035–1039. 10.1016/j.cub.2012.04.016 [DOI] [PubMed] [Google Scholar]
- 5. Bugaud C, Cazevieille P, Daribo MO, Telle N, Julianus P, Fils-Lycaon B, et al. Rheological and chemical predictors of texture and taste in dessert banana (Musa spp.). Postharvest Biol Technol. 2013; 84: 1–8. [Google Scholar]
- 6. Sadka A, Dahan E, Or E, Roose ML, Marsh KB, Cohen L. Comparative analysis of mitochondrial citrate synthase gene structure, transcript level and enzymatic activity in acidless and acid-containing Citrus varieties. Funct Plant Biol. 2001; 28: 383–390. [Google Scholar]
- 7. Moing A, Svanella L, Monet R, Rothan C, Just D, Diakou P, et al. Organic acid metabolism during the fruit development of two peach cultivars. Acta Horticulturae. 1998; 465: 425–430. [Google Scholar]
- 8. Saradhuldhat P, Paull RE. Pineapple organic acid metabolism and accumulation during fruit development. Sci Hortic-Amsterdam. 2007; 112: 297–303. [Google Scholar]
- 9. Etienne A, Génard M, Lobit P, Mbeguié-A-Mbéguié D, Bugaud C. What controls fleshy fruit acidity? A review of malate and citrate accumulation in fruit cells. J Exp Bot. 2013; 64: 1451–1469. 10.1093/jxb/ert035 [DOI] [PubMed] [Google Scholar]
- 10. Cercos M, Soler G, Iglesias DJ, Gadea J, Forment J, Talon M. Global analysis of gene expression during development and ripening of citrus fruit flesh. A proposed mechanism for citric acid utilization. Plant Molecular Biology. 2006; 62: 513–527. [DOI] [PubMed] [Google Scholar]
- 11. Katz E, Boo KH, Kim HY, Eigenheer RA, Phinney BS, Shulaev V, et al. Label-free shotgun proteomics and metabolite analysis reveal a significant metabolic shift during citrus fruit development. J Exp Bot. 2011; 62: 5367–5384. 10.1093/jxb/err197 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Katz E, Fon M, Lee Y, Phinney B, Sadka A, Blumwald E. The citrus fruit proteome: insights into citrus fruit metabolism. Planta. 2007; 226: 989–1005. [DOI] [PubMed] [Google Scholar]
- 13. Schauer N, Semel Y, Roessner U, Gur A, Balbo I, Carrari F, et al. Comprehensive metabolic profiling and phenotyping of interspecific introgression lines for tomato improvement. Nature biotechnology. 2006; 24: 447–454. [DOI] [PubMed] [Google Scholar]
- 14. Martre P, Bertin N, Salon C, Génard M. Modelling the size and composition of fruit, grain and seed by process-based simulation models. New Phytologist. 2011; 191: 601–618. 10.1111/j.1469-8137.2011.03747.x [DOI] [PubMed] [Google Scholar]
- 15. Wu BH, Quilot B, Genard M, Li S, Zhao J, Yang J, et al. Application of a SUGAR model to analyse sugar accumulation in peach cultivars that differ in glucose–fructose ratio. Journal of Agricultural Science-London. 2012; 150: 53–63. [Google Scholar]
- 16. Dai ZW, Vivin P, Robert T, Milin S, Li SH, Génard M. Model-based analysis of sugar accumulation in response to source–sink ratio and water supply in grape (Vitis vinifera) berries. Funct Plant Biol. 2009; 36: 527–540. [DOI] [PubMed] [Google Scholar]
- 17. Lobit P, Génard M, Wu BH, Soing P, Habib R. Modelling citrate metabolism in fruits: responses to growth and temperature. J Exp Bot. 2003; 54: 2489–2501. [DOI] [PubMed] [Google Scholar]
- 18. Wu BH, Génard M, Lobit P, Longuenesse JJ, Lescourret F, Habib R, et al. Analysis of citrate accumulation during peach fruit development via a model approach. J Exp Bot. 2007; 58: 2583–2594. [DOI] [PubMed] [Google Scholar]
- 19. Etienne A, Génard M, Bancel D, Benoit S, Bugaud C. A model approach revealed the relationship between banana pulp acidity and composition during growth and post harvest ripening. Sci Hortic-Amsterdam. 2013; 162: 125–134. [Google Scholar]
- 20. Etienne A, Génard M, Bancel D, Benoit S, Lemire G, Bugaud C. Citrate and malate accumulation in banana fruit (Musa sp. AA) is highly affected by genotype and fruit age, but not by cultural practices Sci Hortic-Amsterdam. 2014; 169: 99–110. [Google Scholar]
- 21. Bugaud C, Chillet M, Beaute MP, Dubois C. Physicochemical analysis of mountain bananas from the French West Indies. Sci Hortic-Amsterdam. 2006; 108: 167–172. [Google Scholar]
- 22. Etienne A, Génard M, Lobit P, Bugaud C. Modeling the vacuolar storage of malate shed lights on pre- and post-harvest fruit acidity BMC Plant Biology. 2014; 14 10.1186/s12870-014-0310-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Laloi M. Plant mitochondrial carriers: an overview. Cellular and Molecular Life Sciences. 1999; 56: 918–944. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Haferkamp I, Schmitz-Esser S. The plant mitochondrial carrier family: functional and evolutionary aspects. Frontiers in plant science. 2012; 3: 1–19. 10.3389/fpls.2012.00001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Schallau K, Junker BH. Simulating plant metabolic pathways with enzyme-kinetic models. Plant Physiol. 2010; 152: 1763–1771. 10.1104/pp.109.149237 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Cannell M, Thornley J. Modelling the components of plant respiration: some guiding principles. Ann Bot-London. 2000; 85: 45–54. [Google Scholar]
- 27.Penning de Vries F, Laar Hv. Simulation of growth processes and the model BACROS. In: F. W. T. P. d. V. a. H. H. V. L. Pudoc, editor editors. Simulation of plant growth and crop production. Wageningen; 1982 pp. 114–135.
- 28. Thornley JH, Johnson IR. Plant and crop modelling: a mathematical approach to plant and crop physiology Oxford university press; New York: 1990. [Google Scholar]
- 29. Chen FX, Liu XH, Chen LS. Developmental changes in pulp organic acid concentration and activities of acid-metabolising enzymes during the fruit development of two loquat (Eriobotrya japonica Lindl.) cultivars differing in fruit acidity. Food Chem. 2009; 114: 657–664. [Google Scholar]
- 30. Iannetta PPM, Escobar NM, Ross HA, Souleyre EJF, Hancock RD, Witte C-P, et al. Identification, cloning and expression analysis of strawberry (Fragaria × ananassa) mitochondrial citrate synthase and mitochondrial malate dehydrogenase. Physiol Plantarum. 2004; 121: 15–26. [DOI] [PubMed] [Google Scholar]
- 31. Regalado A, Pierri CL, Bitetto M, Laera VL, Pimentel C, Francisco R, et al. Characterization of mitochondrial dicarboxylate/tricarboxylate transporters from grape berries. Planta. 2013; 237: 693–703. 10.1007/s00425-012-1786-8 [DOI] [PubMed] [Google Scholar]
- 32. Liu S, Yang Y, Murayama H, Taira S, Fukushima T. Effects of CO2 on respiratory metabolism in ripening banana fruit. Postharvest Biology and Technology. 2004; 33: 27–34. [Google Scholar]
- 33. Borsani J, Budde CO, Porrini L, Lauxmann MA, Lombardo VA, Murray R, et al. Carbon metabolism of peach fruit after harvest: changes in enzymes involved in organic acid and sugar level modifications. J Exp Bot. 2009; 60: 1823–1837. 10.1093/jxb/erp055 [DOI] [PubMed] [Google Scholar]
- 34. Jeffery D, Smith C, Goodenough P, Prosser I, Grierson D. Ethylene-Independent and Ethylene-Dependent Biochemical Changes in Ripening Tomatoes. Plant Physiol. 1984; 74: 32–38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Araujo WL, Nunes-Nesi A, Nikoloski Z, Sweetlove LJ, Fernie AR. Metabolic control and regulation of the tricarboxylic acid cycle in photosynthetic and heterotrophic plant tissues. Plant, Cell & Environment. 2012; 35: 1–21. [DOI] [PubMed] [Google Scholar]
- 36. Soetaert K, Petzoldt T, Setzer RW. Solving differential equations in R: Package deSolve. Journal of Statistical Software. 2010; 33: 1–25. 20808728 [Google Scholar]
- 37. Goudriaan J, Monteith J. A mathematical function for crop growth based on light interception and leaf area expansion. Ann Bot-London. 1990; 66: 695–701. [Google Scholar]
- 38. Castelan F, Saraiva L, Lange F, de Bellaire LdL, Cordenunsi B, Chillet M. Effects of black leaf streak disease and sigatoka disease on fruit quality and maturation process of bananas produced in the subtropical conditions of southern Brazil. Crop Protection. 2012; 35: 127–131. [Google Scholar]
- 39. Gomez L, Bancel D, Rubio E, Vercambre G. The microplate reader: an efficient tool for the separate enzymatic analysis of sugars in plant tissues—validation of a micro-method. J Sci Food Agric. 2007; 87: 1893–1905. [Google Scholar]
- 40. Gerhardt R, Heldt HW. Measurement of subcellular metabolite levels in leaves by fractionation of freeze-stopped material in nonaqueous media. Plant Physiol. 1984; 75: 542–547. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Gout E, Bligny R, Pascal N, Douce R. 13C nuclear magnetic resonance studies of malate and citrate synthesis and compartmentation in higher plant cells. Journal of Biological Chemistry. 1993; 268: 3986–3992. [PubMed] [Google Scholar]
- 42. Beaudry RM, Severson RF, Black CC, Kays SJ. Banana ripening: implications of changes in glycolytic intermediate concentrations, glycolytic and gluconeogenic carbon flux, and fructose 2, 6-bisphosphate concentration. Plant Physiol. 1989; 91: 1436–1444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Kubicek C, Röhr M. The role of the tricarboxylic acid cycle in citric acid accumulation by Aspergillus niger. European journal of applied microbiology and biotechnology. 1978; 5: 263–271. [Google Scholar]
- 44. Fox J. Non linear regression and non linear least squares In: oaks T., editor editors. Appendix to an R and S-PLUS companion to applied regression. CA: Sage publications; 2002. [Google Scholar]
- 45. Turner D. The response of the plant to the environment In: G. S., editor editors. Bananas and Plantains. London: Chapman & Hall; 1995. pp. 206–229. [Google Scholar]
- 46. Vertregt N, Penning de Vries F. A rapid method for determining the efficiency of biosynthesis of plant biomass. Journal of Theoretical Biology. 1987; 128: 109–119. [Google Scholar]
- 47. Wullschleger S, Norby R, Love J, Runck C. Energetic Costs of Tissue Construction in Yellow-poplar and White Oak Trees Exposed to Long-term CO2 Enrichment. Ann Bot-London. 1997; 80: 289–297. [Google Scholar]
- 48. Léchaudel M, Génard M, Lescourret F, Urban L, Jannoyer M. Modeling effects of weather and source–sink relationships on mango fruit growth. Tree Physiology. 2005; 25: 583–597. [DOI] [PubMed] [Google Scholar]
- 49. Penning de Vries F. Simulation of ecophysiological processes of growth in several annual crops IRRI; Wageningen; 1989. [Google Scholar]
- 50. DeJong T, Goudriaan J. Modeling peach fruit growth and carbohydrate requirements: reevaluation of the double-sigmoid growth pattern. Journal of the American Society for Horticultural Science. 1989; 114: 800–804. [Google Scholar]
- 51. Walker A, Thornley J. The tomato fruit: import, growth, respiration and carbon metabolism at different fruit sizes and temperatures. Ann Bot-London. 1977; 41: 977–985. [Google Scholar]
- 52.Zambrano-Bigiarini M, Rojas R, Zambrano-Bigiarini MM. Package ‘hydroPSO’. 2013.
- 53. Johnson JB, Omland KS. Model selection in ecology and evolution. Trends in ecology & evolution. 2004; 19: 101–108. [DOI] [PubMed] [Google Scholar]
- 54. Monod H, Naud C, Makowski D. Uncertainty and sensitivity analysis for crop models Elsevier; Amsterdam; 2006. [Google Scholar]
- 55. Kobayashi K, Salam MU. Comparing simulated and measured values using mean squared deviation and its components. Agron J. 2000; 92: 345–352. [Google Scholar]
- 56. Génard M, Baldazzi V, Gibon Y. Metabolic studies in plant organs: don't forget dilution by growth. Frontiers in plant science. 2014; 5: 1–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57. Bugaud C, Daribo M-O, Beauté M-P, Telle N, Dubois C. Relative importance of location and period of banana bunch growth in carbohydrate content and mineral composition of fruit. Fruits. 2009; 64: 63–74. [Google Scholar]
- 58. Lakso AN, Kliewer WM. The influence of temperature on malic acid metabolism in grape berries: I. Enzyme responses 1. Plant Physiol. 1975; 56: 370–372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59. Halestrap AP. The mitochondrial pyruvate carrier. Biochem J. 1975; 148: 85–96. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60. Sweetlove LJ, Obata T, Fernie AR. Systems analysis of metabolic phenotypes: what have we learnt?. Trends in Plant Science. 2014; 19: 222–230. 10.1016/j.tplants.2013.09.005 [DOI] [PubMed] [Google Scholar]
- 61. Smith FA, Raven JA. Intracellular pH and its regulation. Annual review of plant physiology and plant molecular biology. 1979; 30: 289–311. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
(XLSX)
(TIF)
(TIF)
(TIF)
(PDF)
(PDF)
(PDF)
(PDF)
(PDF)
Data Availability Statement
All relevant data are within the paper and its Supporting Information files.