In Situ Quantification of Protein Binding to the Plasma Membrane

Abstract

This study presents a fluorescence-based assay that allows for direct measurement of protein binding to the plasma membrane inside living cells. An axial scan through the cell generates a fluorescence intensity profile that is analyzed to determine the membrane-bound and cytoplasmic concentrations of a peripheral membrane protein labeled by the enhanced green fluorescent protein (EGFP). The membrane binding curve is constructed by mapping those concentrations for a population of cells with a wide range of protein expression levels, and a fit of the binding curve determines the number of binding sites and the dissociation coefficient. We experimentally verified the technique, using myosin-1C-EGFP as a model system and fit its binding curve. Furthermore, we studied the protein-lipid interactions of the membrane binding domains from lactadherin and phospholipase C-δ1 to evaluate the feasibility of using competition binding experiments to identify specific lipid-protein interactions in living cells. Finally, we applied the technique to determine the lipid specificity, the number of binding sites, and the dissociation coefficient of membrane binding for the Gag matrix domain of human T-lymphotropic virus type 1, which provides insight into early assembly steps of the retrovirus.

Introduction

The attachment of peripheral membrane proteins to lipid bilayers plays a critical role in many cellular functions, such as lipid metabolism, cytoskeletal structure, vesicle trafficking, signal transduction, cell differentiation, growth, and apoptosis (1–3). Because membrane binding is crucial for the cellular function of these proteins, characterization of the membrane binding curve is a prerequisite for understanding the function and regulation of peripheral membrane proteins. Most studies of protein-lipid interactions are based on in vitro assays with membranes in the form of lipid vesicles, supported lipid bilayers, or lipid monolayers (4–6). In some cases isolated membranes have been used to go beyond simple lipid membranes (7,8). However, these traditional assays study the protein and membrane ex situ, and are unable to reproduce the native conditions that give rise to the complex organization and dynamic behavior of cellular membranes. Thus, a technique that directly studies the membrane binding curve of proteins in living cells is highly desirable, not only to validate previous ex situ results, but also to explore the binding process in its natural environment.

This work describes a method for measuring the binding of a fluorescently labeled protein with the plasma membrane of a living cell. The technique utilizes an axial scan through the cell to generate a z-scan fluorescence intensity profile. The intensity profile is deconvolved into its cytoplasmic and membrane-bound fluorescence contributions by accounting for the local cell height and the point spread function (PSF) of the instrument. The membrane binding curve is generated from the deconvolved cytoplasmic and membrane intensity contributions for a population of cells covering a sufficiently wide range of protein expression levels. We further converted fluorescence intensities into concentrations in the cytoplasm and at the membrane by applying the brightness of the fluorescent-label enhanced fluorescent green protein (EGFP). Information about the binding affinity and the number of binding sites was recovered from a fit of the experimental data with a Langmuir isotherm. Moreover, competition binding experiments with different peripheral membrane proteins provided information about specific protein-lipid interactions at the plasma membrane.

Our approach, which we call z-scan fluorescence profile deconvolution (FPD), is related to z-scan fluorescence fluctuation spectroscopy and earlier work by Benda et al. (9). However, unlike z-scan fluorescence fluctuation spectroscopy (10,11), which characterizes the axial dependence of intensity fluctuations, z-scan FPD focuses specifically on information contained within the axial fluorescence intensity profile to generate the experimental binding curve. We applied z-scan FPD to investigate the interaction of myosin-1C with the plasma membrane, generated the experimental membrane binding curves, and determined its binding parameters. We also performed binding experiments with a variety of peripheral membrane proteins with known lipid targets to demonstrate the feasibility of competitive binding assays in the cell. Finally we applied our technique to study the membrane interactions of the matrix domain of human T-cell leukemia virus type 1 (HTLV-1) Gag. We previously observed that the Gag polyprotein and matrix (MA), its membrane-binding domain, of HTLV-1 interact with the plasma membrane at low cytoplasmic concentrations, which is in stark contrast with the corresponding proteins of the human immunodeficiency virus type 1 (HIV-1) (11–13). Here we expand our investigation of HTLV-1 virus assembly by characterizing the membrane binding curve for the MA domain of HTLV-1 Gag and the lipid-specificity of the interaction.

Materials and Methods

Experimental setup

Experiments were carried out on a modified two-photon microscope, as described previously in MacDonald et al. (10) and Chen et al. (14). Data were taken with a 63× C-Apochromat water immersion objective (NA = 1.2) at an excitation wavelength of 1000 nm and an average power of ∼0.3–0.4 mW after the objective (Carl Zeiss, Oberkochen, Germany). Photon counts were detected by an avalanche photodiode (SPCM-AQ-141; Perkin-Elmer, Dumberry, Quebec), recorded by a Flex02-01D card (correlator.com, Bridgewater, NJ), and analyzed with programs written in IDL 8.3 (Research Systems, Boulder, CO). For dual-channel measurements, a dichroic mirror with a center wavelength of 580 nm split the fluorescence emission into two detection channels. The green channel had an additional 84-nm-wide bandpass filter centered at 510 nm (Semrock, Rochester, NY) to eliminate the reflected fluorescence of mCherry.

Z-scans were performed by using an arbitrary waveform generator (Model No. 33250A; Agilent Technologies, Santa Clara, CA) to move the PZ2000 piezo stage (ASI, Eugene, OR) along the z axis. The driving signal from the arbitrary waveform generator was a linear ramp function with a peak-to-peak amplitude of 2.4 V and a period of 10 s. The peak-to-peak voltage corresponded to 24.1 μm of axial travel with the cells occupying roughly 5 μm in the center of each pass. Data were acquired at a frequency of 20 kHz for either a single z-scan or multiple z-scans.

Sample preparation and plasmid construction

The pEGFP-C1 and pEGFP-N1 plasmids were purchased from Clontech (Mountain View, CA) and the mCherry-C1 plasmid has been previously described in Wu et al. (15). The EGFP-H-Ras plasmid was a gift from Dr. Phillips (New York University School of Medicine, New York, NY). The Myosin1C-EGFP (Myo1C-EGFP) plasmid and the EGFP-labeled PH domain of Phospholipase C-delta (EGFP-PLCδ-PH) plasmid were gifts from Dr. Albanesi (University of Texas Southwestern Medical Center, Dallas, TX). The EGFP-labeled C2 domain of lactadherin (Lact-C2-EGFP) plasmid was purchased from Addgene (Plasmid 22852; Cambridge, MA). The Lact-C2-mCh plasmid was subcloned from the Lact-C2-EGFP plasmid into a mCherry-c1 backbone. The miniGAP-EGFP plasmid (the first 10 amino acids of GAP43) was a gift from Dr. Digman (University of California-Irvine, Irvine, CA). The miniGAP-mCh plasmid was cloned from miniGAP-EGFP and amplified by PCR with a 5′ primer that encodes an XhoI restriction site and a 3′ primer that encodes an EcoRI site. The HTLV-1 MA-EGFP plasmid has been previously described in Smith et al. (11). All sequences were verified by automatic sequencing.

All cellular studies were performed using transiently transfected U2OS cells that were obtained from ATCC (Manassas, VA) and maintained in 10% fetal bovine serum (Hyclone Laboratories, Logan, UT) and DMEM medium. Cells were subcultured in eight-well cover-glass chamber slides (Nalge Nunc International, Rochester, NY) 12 h before transfection. Transient transfections were carried out 24 h before measurement using GeneJET (Thermo Scientific, Carlsbad, CA) according to the manufacturer’s instructions. Immediately before measurement, the growth medium was replaced with Dulbecco’s PBS (phosphate-buffered saline) with calcium and magnesium (BioWhittaker, Walkerville, MD). For binding competition studies, cotransfections were performed with the two plasmid types mixed together at a given mole ratio before adding GeneJET (Thermo Fisher Scientific). Specifically, pLact-C2-EGFP: pLact-C2-mCh was mixed at a 1:3 ratio, while for all other competition experiments plasmids were mixed at a 1:6 (EGFP-labeled/mCh-labeled) ratio. During measurement, the fluorescence intensity ratio of the green and red detection channel was used to select cells expressing both proteins at a concentration ratio that matched or exceeded the plasmid ratio (15,16). This selection ensured that each measured cell contains a sufficient excess of the competitor over the probed protein.

Z-scan calibration of PSF

The PSF for our two-photon microscope is well approximated by the modified squared Gaussian-Lorentzian point-spread function (mGL-PSF),

$$PSF\left(\rho ,\zeta \right)={\left(\frac{z_0^2}{z_R^2+{\zeta }^2}\right)}^{\left(1+y\right)}\text{exp}\left(-\frac{4z_R^2}{w_0^2}\frac{{\rho }^2}{z_R^2+{\zeta }^2}\right),$$ (1)

as originally described by MacDonald et al. (10). The radial and axial beam waist are characterized by w₀ and z_R. The y parameter adjusts the axial decay of the PSF while maintaining a Gaussian cross section. The PSF parameters were determined by a z-scan calibration procedure as previously reported (10), which provided values of z_R = 1.02 ± 0.1 μm, y = 2.20 ± 0.3, and w₀ = 0.47 ± 0.05 μm. The mGL-PSF volume is determined by

$$V_{\infty }=\left(\frac{1}{4}\pi w_0^2{z}_R\right)\frac{\sqrt{\pi }\text{Γ}\left(y-\frac{1}{2}\right)}{\text{Γ}\left(y\right)},$$

and the cross-sectional area at the center of the PSF is given by $A_0=\left(\pi w_0^2/4\right)$ (10).

The z-scan intensity profile

Modeling of the z-scan intensity profile is based on the radially integrated PSF given by

$$\text{RIPSF}\left(\zeta \right)={\int }_0^{\infty }\text{PSF}\left(\rho ,\zeta \right)2\pi \rho d\rho .$$

It is convenient to use the radially integrated PSF to define a scaled volume function

$${\tilde{v}}_V\left(z;z_B,z_T\right)=\frac{1}{V_{\infty }}{\int }_{z_B-z}^{z_T-z}\text{RIPSF}\left(\zeta \right)d\zeta$$

and a scaled-area function

$${\tilde{v}}_A\left(z;z_M\right)=\frac{1}{A_0}\text{RIPSF}\left(z_M-z\right)$$

(10). The z-scan fluorescence intensity profile F(z) can be represented using the scaled volume and scaled area functions. For a cytoplasmic protein with the top and bottom membrane located at z_B and z_T, the intensity profile is given by $F\left(z\right)=F_0{\tilde{v}}_V\left(z;z_B,z_T\right)$, while the intensity profile of a protein bound to a membrane located at z_M is given by $F\left(z\right)=F_0{\tilde{v}}_A\left(z;z_M\right)$ (10,11).

Calculating the RIPSF function for the mGL-PSF described by Eq. 1 yields

$$\text{RIPSF}\left(z\right)=\frac{\pi w_0^2}{4}{\left(1+{\left(z/z_R\right)}^2\right)}^{-y}.$$

Evaluating the scaled volume function for the mGL-PSF leads to (10)

$${\tilde{v}}_V\left(z;z_B,z_T\right)=\frac{\text{Γ}\left(y\right)}{\sqrt{\pi }\text{Γ}\left(y-\frac{1}{2}\right)}\left(\text{Ψ}\left(y,\frac{z_T-z}{z_R}\right)-\text{Ψ}\left(y,\frac{z_B-z}{z_R}\right)\right),$$ (2)

with Ψ(y,x) = ₂F₁(1/2,y,3/2;−x²)x and ₂F₁(a,b,c,x) representing the hypergeometric function. The scaled area function is given by

$${\tilde{v}}_A\left(z,z_M\right)={\left(1+{\left(\frac{z_M-z}{z_R}\right)}^2\right)}^{-y}.$$ (3)

The scaled volume and area function were implemented in IDL 8.3 (Research Systems, Boulder, CO) for data analysis.

Z-scan data analysis

The photon counts sampled at 20 kHz were rebinned by a factor of 80 by software, which corresponds to a z-scan sampling time of T_z = 4 ms. The z-scan speed v_z = 4.82 μm/s resulted in a step size Δz = v_zT_z = 19.3 nm between binned photon counts k_z. Fluorescence intensity was determined by F(z) = k_z/T_z. The experimental z-scan intensity profile F(z) was analyzed in IDL 8.3 by least-squares fitting to Eq. 4 with a Levenberg-Marquardt algorithm, where the PSF parameters z_R and y were fixed to the calibrated values, and the standard deviation σ_binned of the binned photon counts was estimated from the SD σ_K of the unbinned counts by ${\sigma }_{\text{binned}}={\sigma }_k\sqrt{N_B}$, with N_B = 80 representing the number of samples in a single bin. In addition, brightness measurements inside the cytoplasm have been carried out as previously described in MacDonald et al. (10) and Smith et al. (11) in the thick section of 10–20 cells expressing EGFP. The average brightness λ from this calibration experiment was computed (17,18) and served as the monomeric brightness value to convert intensities into concentrations.

Results

Z-scan intensity profile of a peripheral membrane protein

A scan of the excitation spot along the z axis of a cell records the fluorescence intensity profile F(z) of the labeled protein. The intensity profile of a protein found at the plasma membrane and in the cytoplasm contains the signal contributions from three distinct cellular layers. The first layer is given by the bottom plasma membrane located at z_B, followed by a cytoplasmic layer and the top plasma membrane located at z_T. The fluorescence intensity profile of this geometry, which we refer to as a delta-slab-delta profile, has been recently described in Smith et al. (11) as

$$F_{\text{dsd}}\left(z\right)=F_B{\tilde{v}}_A\left(z;z_B\right)+F_{C\text{yto},\infty }{\tilde{v}}_V\left(z;z_B,z_T\right)+F_T{\tilde{v}}_A\left(z;z_T\right),$$ (4)

with F_B and F_T being the maximum fluorescence intensity at the membrane layers and F_Cyto,∞ representing the limiting intensity of a thick cytoplasmic layer. The scaled volume ${\tilde{v}}_V$ and area ${\tilde{v}}_A$ function are defined by Eqs. 2 and 3.

We measured z-scan intensity profiles from U2OS cells expressing Myo1C-EGFP. The panels of Fig. 1 display intensity profiles taken from two cells that differ in their protein expression level. Each experimental intensity profile (solid line) was fit to Eq. 4 to isolate the fluorescence contributions from each membrane (dotted line) and from the cytoplasm (dotted-dashed line), which are represented by the three terms of Eq. 4. The sum of these three terms determines the fitted z-scan intensity profile (shaded line). The relative contributions to the intensity profile from membrane-bound and cytosolic protein differ significantly for the two cells. Deconvolving the intensity profile into its components allowed us to quantify these differences. We will follow this approach in the rest of the article to generate a membrane binding curve, by analyzing intensity profiles from a cell population made up of cells that individually display different levels of protein expression.

Figure 1.

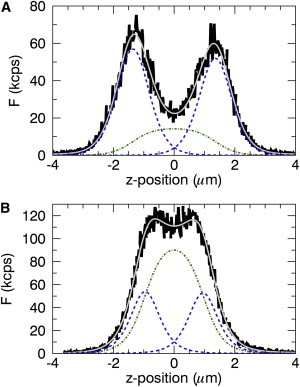
Z-scan intensity profile (solid line) for Myo1C-EGFP in two U2OS cells. The fit (shaded line) to Eq. 4 together with the membrane intensity components (dashed lines) and cytoplasmic component (dotted-dashed line). (A) Profile from a cell with a low cytoplasmic intensity and fit (χ²_red = 1.4, F_Cyto,∞ = 14.8 kcps, F_T = 51.9 kcps, F_B = 56.9 kcps). (B) Profile from a cell with a high cytoplasmic intensity and fit (χ²_red = 1.5, F_Cyto,∞ = 103 kcps, F_T = 52.6 kcps, F_B = 53.9 kcps). To see this figure in color, go online.

We expect the fluorescence intensity values to stay constant if the binding process of the peripheral membrane protein is at equilibrium. As a control, we performed repeated z-scans on cells expressing H-Ras-EGFP over extended time periods. Each z-scan is fit by Eq. 4 to identify the cell height and the fluorescence intensities in each of the three layers, as illustrated in Fig. 2. The top (Fig. 2 A, dashed) and bottom (solid) membrane intensity, as well as the cytosolic intensity (Fig. 2 B, dotted-dashed), remained remarkably stable even when the cell height (Fig. 2 C, solid) changed during the experiment. The fluorescence intensities at the top and bottom membrane were matched, which suggests that the affinity of binding to either membrane was the same. The concentration c_Cyto of cytoplasmic H-Ras-EGFP is determined from the cytosolic fluorescence intensity by F_Cyto,∞ = c_CytoλV_∞, where V_∞ is the PSF volume and λ represents the brightness of the EGFP protein that was measured by an independent control experiment. The protein concentration σ_M at the membrane is determined from the intensity F_M at the membrane by a similar relation, F_M = σ_MλA₀, where V_∞ is replaced by the PSF area A₀. Applying these relations to the data of Fig. 2 yielded surface concentrations of σ_B = 900 μm⁻² and σ_T = 920 μm⁻² for the bottom and top membranes and a cytoplasmic concentration c_Cyto = 71 μm⁻³.

Figure 2.

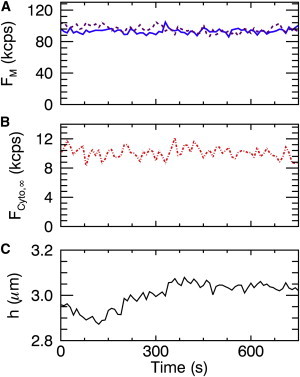
Fit parameters of consecutive z-scan intensity profiles taken in an U2OS cell expressing EGFP-H-Ras. (A) Fluorescence intensities at the top (dashed line) and bottom (solid line) membrane remain stable (F_B = 93.7 ± 3.2 kcps, F_T = 95.6 ± 4.3 kcps). (B) Cytoplasmic intensity (dot-dashed line) is constant (F_Cyto,∞ = 10.0 ± 0.8 kcps). (C) The cell thickness (solid line) changed within the first few minutes and then remained approximately constant. To see this figure in color, go online.

Membrane binding curve

Cells transiently transfected with EGFP-labeled Myo1C were selected and their z-scan intensity profile measured. The membrane and cytoplasmic intensity were determined by a fit of the intensity profile and are plotted in Fig. 3 A. The uncertainty in the fitted membrane and cytoplasmic intensities was on the order of, or smaller than, the symbol size, and was not plotted. The same condition applied to all membrane binding plots shown in this work. The membrane fluorescence intensity versus cytoplasmic fluorescence intensity displays a concentration-dependent response, which saturates at high cytoplasmic intensities. Fluorescence intensities from the bottom membrane (open triangles) and the top membrane (solid triangles) are in close agreement. The data represent the binding curve F_M(F_Cyto,∞) of the peripheral membrane protein to the plasma membrane. To model the experimental data, consider a cytoplasmic protein P that binds a free membrane binding site M with dissociation coefficient K to become a membrane-associated protein MP, $M+P\stackrel{K}{\rightleftarrows }MP$. The fractional saturation θ of the membrane binding sites is described by the Langmuir isotherm,

$$\theta =\frac{{\sigma }_M}{{\sigma }_0}=\frac{c_{\text{Cyto}}}{K+c_{\text{Cyto}}},$$ (5)

where c_Cyto and σ_M are the cytoplasmic and membrane-bound protein concentrations, while σ₀ represents the concentration of the total number of membrane binding sites M₀ = M + MP.

Figure 3.

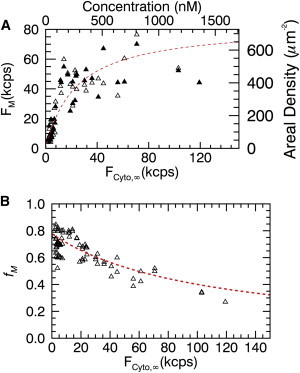
Fluorescence membrane binding curve of Myo1C-EGFP in U2OS cells. (A) Fluorescence intensity at the bottom (open triangles) and top (solid triangles) membrane versus fluorescence intensity in the cytoplasm. The fit (dotted line) to Eq. 6 recovers F₀ = 83 kcps and F_K = 24 kcps. (Top and right axes) Cytoplasmic and membrane-bound protein concentrations. (B) Membrane intensity fraction versus fluorescence intensity in the cytoplasm (open triangles) is well approximated by Eq. 8 (dotted line) with the same F₀ and F_K as determined in the top panel. To see this figure in color, go online.

We relate the Langmuir-isotherm to fluorescence intensities to facilitate the analysis of the data in Fig. 3 A. The cytoplasmic and membrane-bound protein concentrations are connected to the fluorescence intensities as described earlier, F_Cyto,∞ = c_CytoλV_∞ and F_M = σ_MλA₀. We further introduce the saturating fluorescence intensity at the membrane, F₀ = σ₀λA₀, and F_K = KλV_∞, to relate both the maximum binding site concentration and the dissociation coefficient to an intensity. Inserting these relations into Eq. 5 provides an alternate formulation of the Langmuir isotherm in terms of fluorescence intensities,

$$F_M=\theta F_0=\frac{F_0{F}_{\text{Cyto},\infty }}{F_K+F_{\text{Cyto},\infty }}.$$ (6)

A fit of the intensity data in Fig. 3 A to Eq. 6 with F₀ and F_K as free parameters is shown as a solid line with F_K = 24 ± 5 kcps and F₀ = 83 ± 10 kcps. We use the EGFP brightness λ, the PSF volume V_∞, and the area A₀ to convert these values into the dissociation coefficient K = 160 ± 30 μm⁻³ = 270 ± 50 nM and saturation concentration σ₀ = 750 ± 90 μm⁻².

An alternate way to represent membrane binding is to graph the membrane intensity fraction

$$f_M=\frac{F_M}{F_M+F_{\text{Cyto},\infty }}$$ (7)

versus the cytoplasmic intensity F_Cyto,∞. Because the z-scan intensity profile distinguishes between the bottom and top membrane, we further introduce the intensity fraction f_B of the bottom membrane and the intensity fraction f_T of the top membrane, which are defined by replacing F_M with F_B and F_T in Eq. 7, respectively. The membrane intensity fraction of the Myo1C data as a function of cytoplasmic intensity is shown in Fig. 3 B. The dashed line in Fig. 3 represents the Langmuir isotherm model,

$$f_M=\frac{F_0}{F_K+F_{\text{Cyto},\infty }+F_0},$$ (8)

with values for F₀ and F_K as determined above. The membrane intensity fraction decays monotonically with cytoplasmic concentration, because an increase in protein concentration leads to a further depletion of the available membrane binding sites. Evaluating Eq. 8 for a cytoplasmic concentration F_Cyto,∞ = 0 determines the maximum limiting value

$${\overline{f}}_M=\frac{F_0}{F_K+F_0}$$

for the membrane intensity fraction, which for the Myo1C data is 0.78. Thus, the saturation concentration σ₀ and the dissociation coefficient K are not independent variables, but linked by ${\overline{f}}_M$. If the data of the fluorescence membrane binding curve F_M(F_Cyto,∞) are insufficient to identify σ₀ and K unambiguously, an extrapolation of the measured fractional membrane intensity f_M can be used to identify the ratio of both parameters, which for intensity-based notation is given by $F_K/F_0=\left(1-{\overline{f}}_M\right)/{\overline{f}}_M$.

Lipid binding protein domains

Lactadherin is a peripheral membrane protein shown to interact with PS (phosphatidylserine) lipids through its C2 domain (19,20). We measured U2OS cells transiently transfected with an EGFP-labeled Lact-C2 fragment (Lact-C2-EGFP) and determined the experimental membrane-binding curve (see Fig. 4, open triangles). A fit (solid line) to the Langmuir-isotherm binding model leads to a saturation concentration σ₀ = 4100 ± 1100 μm⁻² and a dissociation coefficient K = 700 ± 310 nM. In a followup experiment, we cotransfected Lact-C2-EGFP and Lact-C2-mCh using a plasmid ratio of 1:3. We selected cells that express both proteins and measured the membrane-binding curve (open squares) of Lact-C2-EGFP from the fluorescence intensity traces in the green detection channel. The membrane saturation intensity F₀ is much lower than in the previous experiment, reflecting the presence of Lact-C2-mCh that competes with the green-labeled protein. We divided the amplitude of the Lact-C2-EGFP Langmuir-isotherm curve (solid line) by 4 to account for the binding site competition provided by Lact-C2-mCh. The binding curve (dashed line) with the rescaled amplitude is in good agreement with the experimental data, and illustrates the feasibility of binding competition assays.

Figure 4.

Fluorescence membrane binding curve (open triangles) for LactC2-EGFP in U2OS cells with fit (solid line) to Eq. 6 (F₀ = 530 kcps, F_K = 68 kcps). Competitive binding curve for LactC2-EGFP coexpressed with LactC2-mCh at a ratio of 1:3 (open squares) agrees with predicted binding curve (dashed line). To see this figure in color, go online.

We also examined the plasma-membrane binding curve of the PH domain of phospholipase C-delta 1 (PLCδ-PH), which is known to interact with PI(4,5)P₂ (phosphatidylinositol 4,5-bisphosphate) lipids (21). The experimental membrane-binding data (Fig. 5 A, open circles) of EGFP-labeled PLCδ-PH were determined in U2OS cells and fit to a Langmuir isotherm model (solid line) with σ₀ = 6200 ± 1300 μm⁻² and K = 5.3 ± 1.4 μM. Next, we coexpressed EGFP-PLCδ-PH with miniGAP-mCh. We selected cells that express both proteins and determined the membrane-binding curve (Fig. 5 A, solid stars) of the EGFP-PLCδ-PH from the intensity signal of green detection channel. The presence of miniGAP led to a drastic change in the binding curve for PLCδ-PH, which was also reflected by the fit of the binding data to a Langmuir isotherm model (dashed line). Plotting the same data with a reduced scale allowed the behavior at low intensities to be more clearly visualized (see Fig. S1 in the Supporting Material). The marked decrease in the amplitude of the binding curve implied that miniGAP and PLCδ-PH compete for the same binding sites at the membrane. This observation is consistent with the fact that both proteins are known to interact with PI(4,5)P₂ (22,23).

Figure 5.

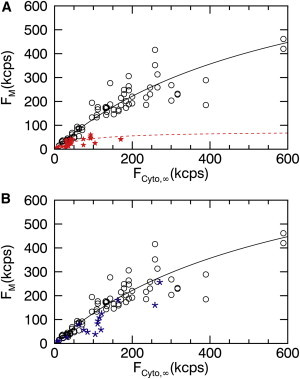
Fluorescence membrane binding curves in U2OS cells. (A) Binding curve for EGFP-PLC-PH (open circles) and fit (solid line) by Eq. 6 (F₀ = 909 kcps, F_K = 620 kcps). Competitive binding curve for EGFP-PLC-PH coexpressed with MiniGAP-mCh (solid stars) and fit (dotted line) by Eq. 6 (F₀ = 76 kcps, F_K = 71 kcps). (B) Binding curve for EGFP-PLC-PH (open circles) and fit (solid line) as shown in (A). Competitive binding curve for EGFP-PLC-PH coexpressed with LactC2-mCh (asterisks) closely tracks the binding curve for EGPF-PLC-PH alone. To see this figure in color, go online.

For a control experiment, we coexpressed EGFP-PLCδ-PH and Lact-C2-mCh in U2OS cells. The data in Fig. 5 B revealed that the experimental membrane-binding data of EGFP-PLCδ-PH in the presence (asterisks) or absence (open circles) of Lact-C2, closely track one another. In vitro studies have reported that PLCδ-PH interacts with PI(4,5)P₂, while Lact-C2 interacts with PS (19,20). Thus, both proteins are expected to target different binding sites at the membrane, which is corroborated by our experimental binding data.

HTLV-1 matrix

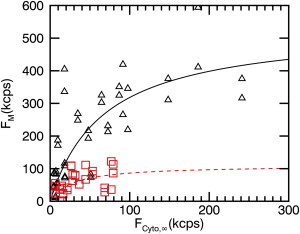
We recently investigated the MA domain of Gag in an effort to uncover the initial assembly steps of the retrovirus HTLV-1 Gag (11–13). MA was chosen as a simplified test system for initial studies of the assembly process, because it is the primary driver of Gag association with the inner leaflet of the plasma membrane, but lacks the ability to associate into large multimers (24,25). Previous work has shown that HTLV-1 MA Gag forms homo-complexes at the plasma membrane, but is monomeric in the cytoplasm (11–13,26). Because the membrane binding mechanism of HTLV-1 MA is not well understood, we decided to investigate the lipid specificity, binding affinity, and saturation concentration of the process. We transiently transfected U2OS cells with EGFP-labeled MA and determined the cytoplasmic and membrane-bound fluorescence intensities from multiple cells. The data (Fig. 6 A, open triangles) show a concentration-dependent increase in the fluorescence signal at the membrane. A fit (solid line) of the data to a Langmuir-isotherm resulted in a dissociation coefficient of K = 230 ± 130 nM and a membrane saturation concentration of σ₀ = 2800 ± 700 μm⁻².

Figure 6.

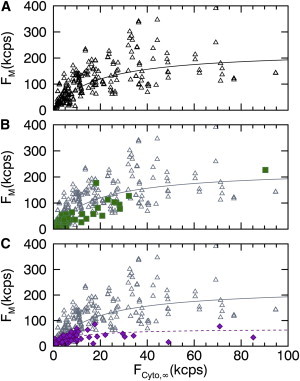
(A) Fluorescence membrane binding curve (triangles) for HTLV-1 MA-EGFP expressed in U2OS cells. (Shaded symbols) Same data are shown in (B) and (C). The fit (solid line) to Eq. 6 leads to F₀ = 288 kcps and F_K = 18 kcps. (B) Competitive binding curve (solid squares) of MA-EGFP coexpressed with miniGAP-mCh. (C) Competitive binding curve (solid diamonds) of MA-EGFP coexpressed with LactC2-mCh and fit (dashed line) to Eq. 6 (F₀ = 68 kcps, F_K = 8 kcps). To see this figure in color, go online.

Further, we performed competition studies to probe the lipid specificity of HTLV-1 MA binding to the plasma membrane. We first coexpressed HTLV-1 MA-EGFP with miniGAP-mCh to probe binding to PI(4,5)P₂. In Fig. 6 B, the binding curve (solid squares) of HTLV-1 MA-EGFP in the presence of miniGAP-mCh overlaps with the binding data (open triangles) taken for HTLV-1 MA-EGFP alone. This observation suggests that PI(4,5)P₂ is not the main lipid target of HTLV-1 MA. We next coexpressed HTLV-1 MA-EGFP with Lact-C2-mCh to probe PS binding. The presence of Lact-C2-mCh led to a strong change in the binding curve of HTLV-1 MA-EGFP (Fig. 6 C, solid diamonds) as compared to HTLV-1 MA-EGFP alone (open triangles). This result indicates that PS lipids are an important binding target of HTLV-1 MA. The dashed line represents the fit curve to a Langmuir-isotherm with a dissociation coefficient of K = 130 ± 16 nM and a membrane saturation concentration of σ₀ = 840 ± 110 μm⁻².

Discussion

Our data demonstrate that it is feasible to measure the membrane binding curve of fluorescently-labeled proteins inside living cells with z-scan FPD analysis. The technique relies on the deconvolution of the intensity profile with the help of an accurately parameterized PSF. We have found that the modified Gaussian-Lorentzian model provides a very faithful representation of the PSF for the two-photon instruments in our lab (10,11). An additional consideration is the cell height at the scan position, which must be sufficiently large to distinguish membrane and cytoplasmic contributions by the deconvolution process. In our experience, the cell thickness should be at least twice the axial beam waist z_R of the PSF, which implies a minimum thickness of ∼2 μm for our setup, a condition that was satisfied for all cell measurements presented in this study. Thus, while our study focused on U2OS cells, z-scan FPD has the potential to be expanded to other cell types as long as their minimum height is ∼2 μm.

Analysis of z-dependent intensity distributions of fluorescently labeled cells is not a novel concept in itself. For example, z-stack image analysis has been widely used in the fluorescence field to determine protein localization, which includes work from Aisiku et al. (27) and Dowal et al. (28), where they segment the z-dependent intensity distribution of Gα_q and Phospholipase Cβ into membrane and cytoplasmic regions. However, segmentation does not result in a quantitative separation of fluorescence signals from different compartments, because the PSF blurs the signal contributions. Modeling approaches have been used to account for the effect of the PSF, including recent work that used a three-dimensional Gaussian PSF to identify the membrane-bound and free intensities of tBid in an in vitro environment (29). However, an accurate and quantitative analysis requires a parameterized PSF to avoid systemic biases. Z-scan FPD achieves this goal and partitions the intensity profile into its membrane and cytoplasmic components. While this study was performed on a two-photon microscope, we expect that the same types of experiments are feasible on a one-photon confocal instrument. Extension of the z-scan method only requires a proper parameterization of the one-photon observation volume O (30), which replaces the PSF of two-photon excitation.

In this work we focused on the binding of a number of different protein domains to PI(4,5)P₂ and PS lipids. It has been estimated that the surface density of PI(4,5)P₂ lipid on the cell membrane is between 3000 and 5000 molecules/μm² (31) and that PLCδ-PH binds to PI(4,5)P₂ with a dissociation coefficient ranging from 2 to 3 μM in vitro (21,32). Fitting the binding curve of EGFP-PLCδ-PH (see Fig. 5 B) determined a surface concentration of 6200 ± 1300 molecules/μm² and a binding dissociation coefficient of K = 5.3 ± 1.4 μM in situ, which are close to the previously reported in vitro values. We also applied our technique to study the binding of Lact-C2-EGFP to PS lipids. Estimates of the lipid composition at the plasma membrane indicate that PS is more abundant than PI(4,5)P₂ (31). Thus, we expected to measure a higher surface density than for EGFP-PLCδ-PH, but experimentally observed a surface density of 4100 molecules/μm² for Lact-C2-EGFP (see Fig. 5 A), which is less than what we measured for EGFP-PLCδ-PH. However, the z-scan binding assay does not measure the lipid concentration, but the protein concentration at the membrane. Thus, accessibility to the targeted lipid as well as competition for binding sites from other cellular proteins will modulate the saturation concentration at the membrane. The binding affinity of LactC2 for PS on lipid vesicles has been measured by FRET experiments with reported in vitro dissociation coefficients of K = 290–350 nM (33,34), which agrees within a factor of 2 with our result.

Myo1C, a member of the myosin I superfamily, is known to associate with plasma membrane lipids (PI(4,5)P₂ and PS) through electrostatic interactions involving the tail domain (35,36). Hokanson and Ostap (37) and Hokanson et al. (38) studied the binding of the Myo1C tail fragment to large unilaminar vesicles containing 2% PI(4,5)P₂, and reported K_D values that depended on labeling and ranged from 230 to 530 nM. We determined a K = 270 nM for full-length Myo1C-EGFP in U2OS cells, which is in close agreement with the in vitro results from the Myo1C fragments. Finding the same affinity for the fragment and the full-length protein suggests that the tail domain of Myo1C is the main determinant for the membrane binding energy. This property has also been found in other proteins. For example, PLCδ and its PH domain bind with a very similar affinity (39).

We used the matrix domain of HTLV-1 Gag to probe the early assembly steps of this retrovirus. The MA domain of Gag contain a myristoyl moiety and a highly basic region, which are each important for membrane binding (reviewed in Hamard-Peron and Muriaux (40)). For HIV-1 the MA domain and full length Gag only associate with the plasma membrane at high protein concentrations, where protein-protein interactions trigger the exposure of the sequestered myristoyl moiety (13,40). In contrast, the MA domain and full-length Gag of HTLV-1 have been found to associate with the plasma membrane even at the lowest measurable fluorescence intensities (13). While this observation seems to imply a very high binding affinity, the data in Fig. 6 indicate a dissociation constant of several hundred nanomolar, which is a lower affinity than originally expected. This apparent inconsistency can be resolved by considering the limiting value ${\overline{f}}_M$ of the membrane fraction as the cytoplasmic protein concentration approaches zero, which depends on the surface concentration of binding sites and the affinity. The fit parameters of the binding curve for MA result in ${\overline{f}}_M=0.92$, which reflects the large ratio of F₀ to F_K. In other words, a sufficient high number of binding sites compensates for a lower binding affinity and results in a significant population of membrane-bound proteins even at the lowest expression levels. In the case of MA, >90% of the protein is at the plasma membrane at very low cytoplasmic protein concentrations.

The membrane binding partner of HTLV-1 Gag is still an open question. It has been shown that HIV-1 Gag binding with PI(4,5)P₂ is essential for function (25). However, when Inlora et al. (41) studied the interaction between PI(4,5)P₂ and the MA domain of HTLV-1, they concluded that PI(4,5)P₂ was not essential for particle assembly. This finding is corroborated by our in situ competitive binding assay (see Fig. 6 B), which demonstrates that PI(4,5)P₂ is not an essential binding partner of MA. Instead, we found that HTLV-1 MA-EGFP binds to PS lipid at the plasma membrane (Fig. 6 C). This observation agrees with in vitro work reporting that HTLV-1 Gag binds to liposomes containing PS (41).

The same study argued that HTLV-1 MA interacts with lipids primarily through electrostatic and not lipid-specific interactions. If electrostatic interactions are the main driver for membrane association, we would expect to observe competition for the PI(4,5)P₂ binding site, because the net charge of PI(4,5)P₂ at neutral pH is expected to be −3 or −4 (39), while for PS it is −1. However, the data in Fig. 6 B show no or at best only weak interaction between HTLV-1 MA and PI(4,5)P₂, because the competitive binding curve (solid squares) is only slightly lower than the binding curve for MA alone (open triangles). A potential explanation for the stronger interaction with PS lipids might be found in the distribution of basic residues in the matrix protein. Unlike HIV-1 MA, the basic residues of HTLV-1 MA are distributed throughout the sequence (42). The higher abundance of PS over PI(4,5)P₂ at the inner leaflet of the plasma membrane might lead to a larger number of local interactions with the distributed basic residues of the protein, which would result in an increased binding energy. Thus, our data suggest that interaction with PS lipids at the membrane plays an important role in the early assembly step of the HTLV-1 virus.

We briefly note that it is important to choose a suitable scan location within the cell. If the protein of interest is excluded from certain cellular compartments, then the presence of such a compartment along the scan trajectory will lead to a dip in the intensity profile, provided the compartment is comparable in size to the PSF. We use a bright-field image of the cell to find a position that avoids large structures such as the nucleus and the surrounding endomembrane system. We further perform at least two successive z-scans at each scan location, because movement of vesicles or other compartments between two successive scans introduces changes in the intensity profile. We only accept data where the intensity profile remains unchanged between scans. While these methods have proven sufficient for studying protein binding to the plasma membrane, a more sophisticated approach will be needed for proteins that interact with internal membranes to account for their complex spatial distribution inside the cell.

FPD analysis of the z-scan intensity profile separates membrane-bound and cytoplasmic protein components in terms of intensity. To translate these intensities into absolute concentrations requires an additional conversion factor from an independent experiment. In this work, we used the brightness of monomeric EGFP (determine from an independent control experiment) as our conversion factor to identify concentrations. However, even in the absence of a conversion factor, it is still possible to quantitatively compare intensity-based binding curves because the concentration and intensity are linearly related. This point is illustrated by the competition experiments depicted in Figs. 4–6.

The heterogeneity of the cytoplasm introduces uncertainty in brightness experiments and therefore in the determination of protein concentration, an issue that has been studied early on (43). We have found that the uncertainty of brightness measurements in cells is ∼10% (10), which implies an ∼10% uncertainty in determining the concentration. Similarly, we also observed a brightness uncertainty of ∼10% at the plasma membrane (11). This study generated membrane binding curves through single-point z-scan measurements taken over a sample of cells. However, the scatter in the data points of the measured binding curves appears much larger than the measurement uncertainty. This spread of intensities at the membrane for a given cytoplasmic concentration might reflect cell-to-cell variations or be caused by spatial heterogeneity at the cell membrane. To address this issue, we plan to expand the z-scan technique by combining it with x-y scans to explore small regions of the plasma membrane. This approach should allow us to investigate the origin of the scatter in the binding curve and potentially expand the reach of the technique to study binding of proteins with a nonuniform spatial distribution at the plasma membrane. While these developments will strengthen the technique, the results obtained from simple z-scans are already impressive. Single-point z-scans have proven to be sufficient for quantitative analysis of the binding and competition experiments shown here.

In summary, z-scan FPD offers a method for characterizing binding curves of peripheral membrane proteins within their native environment. The technique not only offers a way to test the binding results from ex situ studies within a cellular system, but also promises to reveal novel features. For example, competition assays can be performed to identify specific lipid-protein binding partners. We anticipate that the ability to quantitatively monitor membrane binding in situ should prove useful for functional studies of membrane-binding proteins.

Author Contributions

E.M.S. designed experiments, performed experiments, analyzed data, and wrote the article; J.H. performed experiments and analyzed data for H-Ras-EGFP; Y.C. designed experiments and contributed analysis tools; and J.D.M. designed experiments, analyzed data, and wrote the article.