Significance
Prediction is an essential part of life. However, are we really “good” at making predictions? More specifically, are pieces of our brain close to being optimal predictors? To assess the efficiency of prediction, we need to measure the information that neurons carry about the future of our sensory experiences. We show how to do this, at least in simplified contexts, and find that groups of neurons in the retina indeed are close to maximally efficient at separating predictive information from the nonpredictive background. Efficient coding of predictive information is a principle that can be applied at every stage of neural computation.
Keywords: neural coding, retina, information theory
Abstract
Guiding behavior requires the brain to make predictions about the future values of sensory inputs. Here, we show that efficient predictive computation starts at the earliest stages of the visual system. We compute how much information groups of retinal ganglion cells carry about the future state of their visual inputs and show that nearly every cell in the retina participates in a group of cells for which this predictive information is close to the physical limit set by the statistical structure of the inputs themselves. Groups of cells in the retina carry information about the future state of their own activity, and we show that this information can be compressed further and encoded by downstream predictor neurons that exhibit feature selectivity that would support predictive computations. Efficient representation of predictive information is a candidate principle that can be applied at each stage of neural computation.
Almost all neural computations involve making predictions. Whether we are trying to catch prey, avoid predators, or simply move through a complex environment, the data we collect through our senses can guide our actions only to the extent that these data provide information about the future state of the world. Although it is natural to focus on the prediction of rewards (1), prediction is a much broader problem, ranging from the extrapolation of the trajectories of moving objects to the learning of abstract rules that describe the unfolding pattern of events around us (2–4). An essential aspect of the problem in all these forms is that not all features of the past carry predictive power. Because there are costs associated with representing and transmitting information, it is natural to suggest that sensory systems have optimized coding strategies to keep only a limited number of bits of information about the past, ensuring that these bits are maximally informative about the future. This principle can be applied at successive stages of signal processing, as the brain attempts to predict future patterns of neural activity. We explore these ideas in the context of the vertebrate retina, provide evidence for near-optimal coding, and find that this performance cannot be explained by classical models of ganglion cell firing.
Coding for the Position of a Single Visual Object
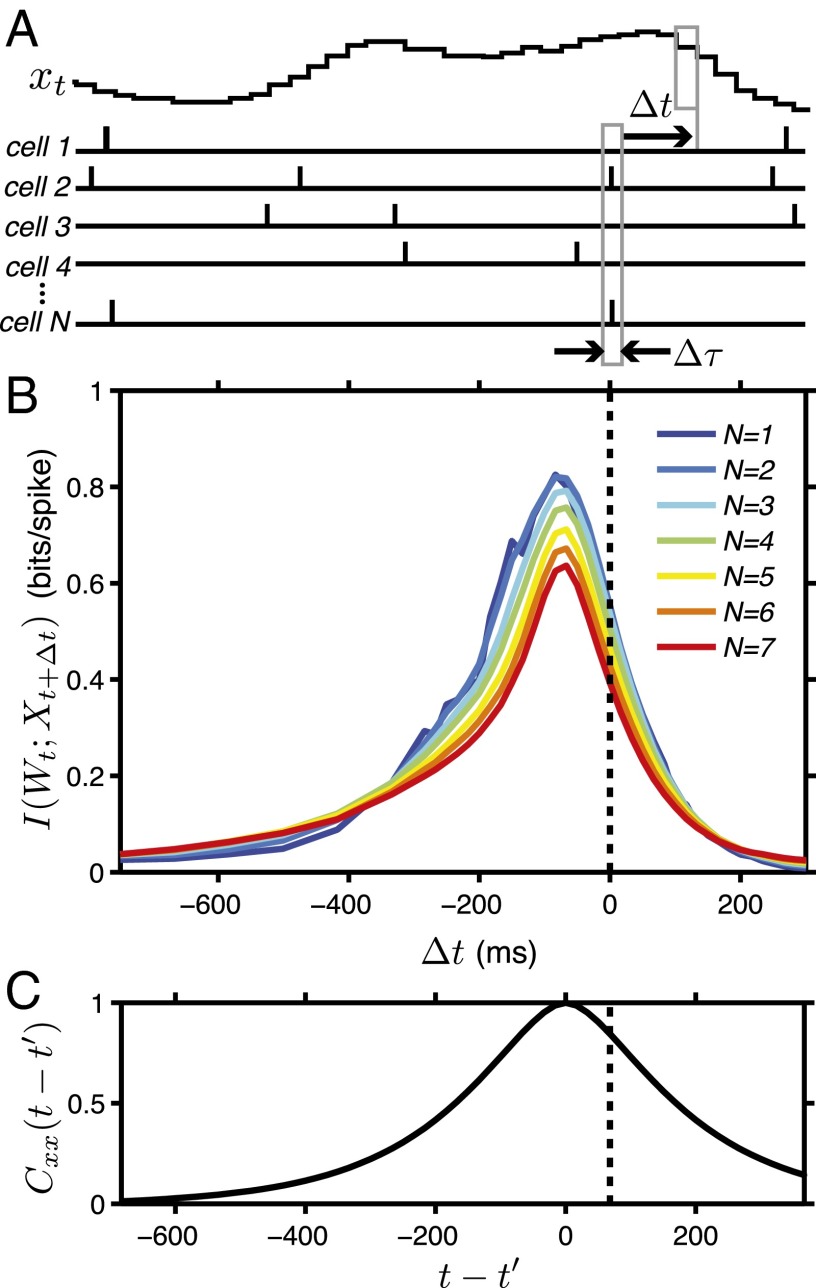
The structure of the prediction problem depends on the structure of the world around us. In a world of completely random stimuli, for example, prediction is impossible. Consider a simple visual world such that, in the small patch of space represented by the neurons from which we record, there is just one object (a dark horizontal bar against a light background) moving along a trajectory . We want to construct trajectories that are predictable, but not completely; the moving object has some inertia, so that the velocities are correlated across time, but is also “kicked” by unseen random forces. A mathematically tractable example (Eqs. 4 and 5 in Materials and Methods) is shown in Fig. 1A, along with the responses recorded from a population of ganglion cells in the salamander retina.
Fig. 1.
Information about position of a moving bar. (A) Trajectory and spiking responses recorded from several cells simultaneously (36); responses in a single small window of time can be expressed as binary words . (B) Information that N-cell words provide about bar position (Eq. 1), as a function of the delay , averaged over many N-cell groups. Estimation errors and SEMs over groups both are negligible (∼0.01 bits/spike); we stop at to avoid undersampling. (C) Normalized autocorrelation of the trajectory, , vs. time delay, . The peak has been shifted to align with the peak information in B.
If we look at neural responses in small windows of time, e.g., , almost all ganglion cells generate either zero or one action potential. Thus, the activity of a single neuron, labeled , can be represented by a binary variable when the cell spikes at time t and when it is silent. The activity of N neurons then becomes a binary “word” . If we (or the brain) observe the pattern of activity at time t, how much do we know about the position of the moving object? Neurons are responding to the presence of the object, and to its motion, but there is some latency in this response, so that will be maximally informative about the position of the object at some time in the past, . On the other hand, we know that the brain is capable of predicting the future position of moving objects and that these ganglion cells provide all of the visual data on which such predictions are based, so it must be true that also provides some information about .
We can make these ideas precise by estimating, in bits, the information that the words provide about the position of the object at time (5–8):
| [1] |
where describes the overall distribution of words generated by the neural population, describes the distribution of positions of the object across the entire experiment, and is the probability of finding the object at position x at time given that we have observed the response at time t. Results are shown in Fig. 1B, where we put the information carried by different numbers of neurons on the same scale by normalizing to information per spike.
As expected, the retina is most informative about the position of the object in the past. At this point, the information carried by multiple retinal ganglion cells is, on average, redundant, so that the information per spike declines as we examine the responses of larger groups of neurons. Although the details of the experiments are different, the observation of coding redundancy at is consistent with many previous results (9–17). However, the information that neural responses carry about position extends far into the past, , and more importantly this information extends into the future, so that the neural response at time t predicts the position of the object at times . This broad window over which we can make predictions and retrodictions is consistent with the persistence of correlations in the stimulus, as it must be (Fig. 1C). As we extrapolate back in time, or make predictions, the redundancy of the responses decreases, and there are hints of a crossover to synergistic coding of predictions far in the future, to which we return below.
Bounds on Predictability
Even if we keep a perfect record of everything we have experienced until the present moment, we cannot make perfect predictions: all of the things we observe are influenced by causal factors that we cannot observe, and from our point of view the time evolution of our sensory experience thus has some irreducible level of stochasticity. Formally, we imagine that we are sitting at time and have been observing the world, so far, for a period of duration T. If we refer to all our sensory stimuli as , then what we have access to is the past . What we would like to know is the future, . The statement that predictive power is limited is, quantitatively, the statement that the predictive information, , is finite (4). This is the number of bits that the past provides about the future, and it depends not on what our brain computes but on the structure of the world.
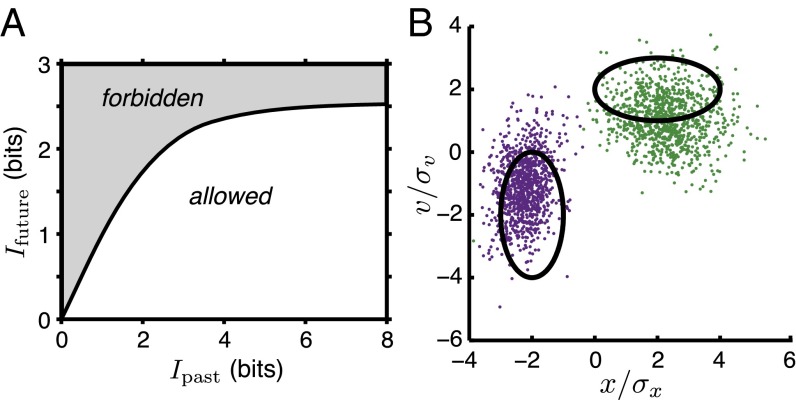
Not all aspects of our past experience are useful in making predictions. Suppose that we build a compressed representation Z of our past experience, keeping some features and throwing away others. We can ask how much predictive information is captured by these features, . Notice that, in building the representation Z, we start with our observations on the past, and so there is some mapping ; this feature extraction captures a certain amount of information about the past, . The crucial point is that, given the statistical structure of our sensory world, and are related to one another. Specifically, if we want to have a certain amount of predictive power , we need to capture a minimum number of bits about the past, . Conversely, if we capture a limited number of bits about the past, there is a maximum amount of predictive power that we can achieve, , and we can saturate this bound only if we extract the most predictive features. Thus, we can plot information about the future vs. information about the past, and in any particular sensory environment this plane is divided into accessible and impossible regions; this is an example of the information bottleneck problem (18, 19). In Fig. 2A, we construct this bound for the simple sensory world of a single moving object used in our experiments (see Materials and Methods for details). To be optimally efficient at extracting information is to build a representation of the sensory world that is close to the bound that separates the allowed from the forbidden.
Fig. 2.
Bounds on predictive information. (A) Any prediction strategy defines a point in the plane Ifuture vs. Ipast. This plane is separated into allowed and forbidden regions by a bound, , shown for the sensory world of a moving bar following the stochastic trajectories of Fig. 1. (B) We can capture the same information about the past in different ways, illustrated by the black “error ellipses” in the position/velocity plane. If we know that the trajectory is inside one of these ellipses, we have captured Ipast = 0.42 bits. However, points inside these ellipses propagate forward along different trajectories, and after , these trajectories arrive at the points shown in purple and green. Using the same number of bits to make more accurate statements about position leads to more predictive information (purple; ) than if we use these bits to make more accurate statements about velocity (green; ).
Building the maximally efficient predictor is nontrivial, even in seemingly simple cases. For an object with trajectories as in Fig. 1, knowledge of the object’s position and velocity at time t provides all of the information possible about the future trajectory. However, knowing position and velocity exactly requires an infinite amount of information. If, instead, we know the position and velocity only with some errors, we can draw an error ellipse in the position–velocity plane, as shown in Fig. 2B, and the area of this ellipse is related to the information that we have captured about the past. Points inside the error ellipse extrapolate forward to a cloud of possible futures. The key point is that error ellipses with the same area but different shapes or orientations—using, for example, the limited number of available bits to provide information about position vs. velocity—extrapolate forward to clouds of different sizes. Thus, to make the best predictions, we have to be sure that our budget of bits of about the past is used most effectively, and this is true even when prediction is “just” extrapolation.
Direct Measures of Predictive Information
The statement that the neural response w provides information about a feature f in the stimulus means that there is a reproducible relationship between these two variables (5–8). To probe this reproducibility, we must present the same features many times, and sample the distribution of responses . The information that w provides about f is as follows:
| [2] |
where the features are drawn from the distribution , and the overall distribution of responses is given by the following:
| [3] |
In the case of interest here, the feature f is the future of the stimulus. To measure the information that neural responses carry about the future, we thus need to repeat the future. More precisely, we need to generate stimulus trajectories that are different but converge onto the same future. Given that we can write the distribution of trajectories , we can draw multiple independent trajectories that have a “common future,” as shown schematically in Fig. 3A (20) (Materials and Methods).
Fig. 3.
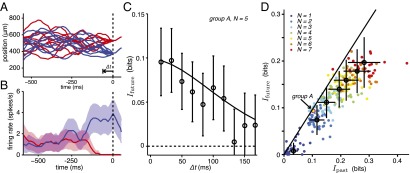
Direct measures of the predictive information in neural responses. (A) Many independent samples of the trajectory converge onto one of several common futures, two of which are shown here (red and blue). The time of convergence is indicated by the vertical dashed line. (B) Mean spike rates of a single neuron in response to the stimuli in A. Shaded regions are ±1 SEM. (C) Information about the common future for one group of five cells, as a function of the time, , until convergence. Solid line shows the bound on for this group’s . (D) Information about the future vs. information about the past, for many groups of different size, N with Δt = 1/60 s; group A as in C. Error bars include contributions from the variance across groups and the SD of the individual information estimates. Solid line is the bound from Fig. 2A.
If trajectories converge onto a common future at time , then for the neural responses will be independent of the future, and we can see this in single cells as a probability of spiking that is independent of time or of the identity of the future (Fig. 3B). As we approach , the neurons respond to aspects of the stimulus that are themselves predictive of the common future stimulus, and hence the probability of spiking becomes modulated. Quantitatively, we can use Eq. 2 to estimate the information carried by responses from neurons about the future, as shown in Fig. 3C for a particular five-cell group. This group of cells captures of information about the past of the sensory stimulus, or , computed by taking the stimulus feature, f, to be the past. Fig. 2A tells us that this amount of information about the past can lead to a maximum of about the future. We can compute the predictive information in this group of cells via Eq. 2 and compare it to this bound. In fact, this group of cells achieves , so that it is within error bars of being optimal. We can also generalize the bound in Fig. 2, to ask what happens if we make predictions not of the entire future, but only starting ahead of the current time; we see that the way in which predictive power decays as we extrapolate further into the future follows the theoretical limit set by the structure of the sensory inputs (Fig. 3C).
The results for the five-cell group in Fig. 3C, which has a modest amount of information about the future, are not unusual. For each of the 53 neurons in the population that we monitor, we can find the group of cells, including this neuron, that has the most future information. These groups also operate close to the bound in the plane, as shown in Fig. 3D. Not all groups that contain this neuron sit near the bound, but we do not expect a random sampling of cells to have this property. For example, two cells might sample different parts of visual space that are not connected via a predictable stimulus trajectory. The fact that every cell in this recording participated in some group that sits near the bound is intriguing. This continues to be true as we look at larger and larger groups of cells, until our finite dataset no longer allows effective sampling of the relevant distributions. At least under these stimulus conditions, populations of neurons in the retina thus provide near-optimal representations of predictive information, extracting from the visual input precisely those bits that allow maximal predictive power.
Could near-optimal prediction result from known receptive field properties of these cells? To test this, we have made conventional linear/nonlinear (LN) models of the individual neurons in our dataset (21, 22): image sequences are projected linearly onto a template (spatiotemporal receptive field), and the probability of spiking is a nonlinear function of this projection. We fit these models to the responses of each neuron to a long movie with same statistics as in Fig. 3, and we adjust the nonlinearity to match the mean spike probability and the information captured about the past by single cells (details in Linear–Nonlinear Model). We then analyzed the performance of the model populations in exactly the same way that we analyzed the real populations. Populations of LN neurons fall far below the bound on predictive information, and this gap grows with the number of neurons (Fig. S1), in marked contrast to the real data (Fig. 3D). Interestingly, the models are not so far from the performance of an optimal system that has access only to data from ∼100 ms in the past, comparable to the delay one might guess from Fig. 1B. Rather than being a consequence of the receptive fields for individual neurons, the near-optimal performance that we see in Fig. 3D thus is evidence that conventional models are missing the ability of the retina to overcome apparent delays in the encoding of dynamic inputs.
Predicting the Future State of the Retina
It seems natural to phrase the problem of prediction in relation to the visual stimulus, as in Fig. 3, but the brain has no direct access to visual stimuli except that provided by the retina. Could the brain learn, in an unsupervised fashion, to predict the future of retinal outputs? More precisely, if we observe that a population of retinal ganglion cells generates the word at time t, what can we say about the word that will be generated at time in the future? The answer to this question is contained in the conditional distribution of one word on the other, .
In Fig. 4A, we show an example of for cells, as the retina responds to naturalistic movies of underwater scenes (see Materials and Methods for details). This conditional distribution is very different from the prior distribution of words (shown to the right), which means that there is significant mutual information between and . In Fig. 4B, we show the distribution of this predictive information between words, for groups of , , and cells. We have normalized the information in each group by the mean number of spikes, and we see that the typical bits per spike is growing as we look at larger groups of cells. Thus, the total predictive information in the patterns of activity generated by N cells grows much more rapidly than linear in N: predictive information is encoded synergistically.
Fig. 4.
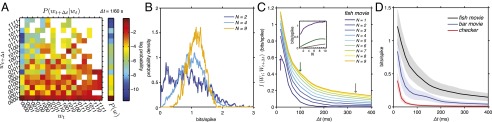
Mutual information between past and future neural responses. (A) Conditional distribution , at time , for the group of four cells with the maximum information (1.1 bits/spike), in response to a natural movie. The prior distribution of words, , is shown adjacent to the conditional. Probabilities are plotted on a log scale; blank bins indicate zero samples. (B) Distributions of for , , and cells, with . (C) Information between words as a function of . Inset shown information vs. N at marked by arrows. (D) Information between words for groups of , as a function for different classes of stimuli: a natural movie, the moving bar from Fig. 1, and a random flickering checkerboard refreshed at 30 fps. Shaded regions indicate SD across different groups of cells.
With these naturalistic stimuli, larger groups of cells carry predictive information for hundreds of milliseconds, as shown in Fig. 4C, and the maximum predictive information is above 1 bit/spike on average across the thousands of groups that we sampled. Smaller groups of cells do not carry long-term predictive power, and for short-term predictions they carry roughly one-half the information per spike that we see in larger groups.
The large amounts of predictive information that we see in neural responses are tied to the structure of the sensory inputs (Fig. 4D). Naturalistic movies generate the most powerful, and most long-ranged, predictable events; the responses to random checkerboard movies lose predictability within a few frames; and motion of a single object (as in Fig. 1) gives intermediate results. The internal dynamics of the retina could generate predictable patterns of activity even in the absence of predictable structure in the visual world, but this does not seem to happen. This raises the possibility that trying to predict the future state of the retina from its current state can lead us (or the brain) to focus on patterns of activity that are especially informative about the visual world.
The predictive information carried by N neurons is more than N times the information carried by single neurons, but even at it is less than 1 bit in total. Can a neuron receiving many such ganglion cell inputs compress the description of the state of the retina at time t, while preserving the information that this state carries about what will happen at time in the future? That is, can we do for the retinal output what the retina itself does for the visual input? In particular, if we can write down all of the predictive information in one bit, then we can imagine that there is a neuron inside the brain that takes the N cells as inputs, and then a spike or silence at the output of this “predictor neuron” captures the available predictive information.
Compressing our description of input words down to 1 bit means sorting the words into two groups . If this grouping is deterministic, then with neurons there are possible groupings, and so we can test all of the possibilities (Stimulus Information in σout for One Group and Fig. S2.). It indeed is possible to represent almost all of the predictive information from four neurons in the spiking or silence of a single neuron, and doing this does not require the predictor neuron to generate spikes at anomalously high rates; this result generalizes across many groups of cells (Fig. 5A). We also find that the optimal rules can be well approximated by the predictor neuron thresholding an instantaneous weighted sum of its inputs—a perceptron (Fig. 5B)—suggesting that such predictor neurons are not only possible in principle, but biologically realizable.
Fig. 5.
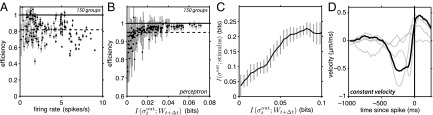
Predictor neurons. (A) Maximum efficiency as a function of the output firing rate, for 150 four-cell groups. Average over all groups is indicated by the dashed line; solid black line indicates perfect capture of all of the predictive information. (B) Efficiency of a perceptron rule relative to the best possible rule, for the same groups as in A. (C) The information that provides about the visual stimulus grows with the predictive information that it captures. Results shown are the means over all possible output rules, for 150 four-cell input groups; error bars indicate SDs across the groups. (D) Average velocity triggered on a spike of the predictor neuron for one four-cell group; light gray lines show the triggered averages for the input spikes; the predictor neuron selects for a long epoch of constant velocity. In A–C, Δt = 1/60 s; in D, Δt = 1/30 s.
Predictor neurons are constructed without reference to the stimulus—just as the brain would have to do—but by repeating the same naturalistic movie many times, we can measure the information that the spiking of a predictor neuron carries about the visual input, using standard methods (15, 23). As we see in Fig. 5C, model neurons that extract more predictive information also provide more information about the visual inputs. There is some saturation in this relationship, perhaps because the most effective predictor neurons are more efficient in selecting the relevant bits of the past. Nonetheless, it is clear that, by solving the prediction problem, the brain can “calibrate” the combinations of spiking and silence in the ganglion cell population, grouping them in ways that capture more information about the visual stimulus.
If we return to the simple world of a single bar moving on the screen, as above, then we can see that the spikes in predictor neurons are associated with interesting patterns of motion. One example is in Fig. 5D, where we see that a spike corresponds to an exceptionally long period of nearly constant velocity motion, followed by a reversal. Other examples include periods of high speed, independent of direction, or moments where the bar is located at a particular position with very high precision (see Feature Selectivity in Predictor Neurons and Fig. S3 for details). These results, which need to be explored more fully, support the intuition that the visual system computes motion not for its own sake, but because, in a world with inertia, motion estimation provides an efficient way of representing the future state of the world.
Discussion
Information theory defines the capacity of a signal to carry information (the entropy), but information itself is always information about something; successful applications of information theoretic ideas to biological systems are cases where it is clear which information is relevant. However, how can we use information theory to think about neural coding and computation more generally? It is difficult to guess how organisms will value information about particular features of the world, but value can be attached only to bits that have the power to predict the organism’s future experience. Estimating how much information neural responses carry about the future of sensory stimuli, even in a simple world, we have found evidence that the retina provides an efficient, and perhaps nearly optimal, representation of predictive information (Fig. 3).
Efficient representation of predictive information is a principle that can be applied at every layer of neural processing. As an illustration, we consider the problem of a single neuron that tries to predict the future of its inputs from other neurons, and encodes its prediction in a single output bit—spiking or silence. This provides a way of analyzing the responses from a population of neurons that makes no reference to anything but the responses themselves, and in this sense provides a model for the kinds of computations that the brain can do. Predictive information in the patterns of activity is coded synergistically (Fig. 4), maximally efficient representations of this information involve spiking at reasonable rates, without any further constraints, and the optimal predictor neurons are efficient transmitters of information about the sensory input, even though the rules for optimal prediction are found without looking at the stimulus (Fig. 5). Thus, solving the prediction problem would allow the brain to identify features of the retina’s combinatorial code that are especially informative about the visual world, without any external calibration.
The idea that neural coding of sensory information might be efficient, or even optimal, in some information theoretic sense, is not new. Individual neurons have a capacity to convey information that depends on the time resolution with which spikes are observed, and one idea is that this capacity should be used efficiently (24, 25), in part by adapting coding strategies to the distribution of the inputs (26–28). Another idea is that the neighboring cells in the retina should not waste their capacity by transmitting redundant signals, and minimizing this redundancy may drive the emergence of spatially differentiating receptive fields (29, 30). Similarly, temporal filtering may serve to minimize redundancy in time (31), and this is sometimes called “predictive coding” (32). Reducing redundancy requires removing any predictable components of the input, keeping only the deviations from expectation. In contrast, immediate access to predictive information requires an encoding of those features of the past that provide the basis for optimal prediction. The retina actively responds to predictable features of the visual stimulus (33) and, in the case of smooth motion, can anticipate an object’s location in a manner that corrects for its own processing delay (34, 35). Our current results suggest that, even for irregular motion, the retina can efficiently extract the features of the stimulus that allow it to encode all available predictive information. Efficient coding of predictive information is therefore a very different principle from most of those articulated previously, and one that illustrates the surprising computational powers of local neural circuits, like the retina.
Although there has been much interest in the brain’s ability to predict particular things, our approach emphasizes that prediction is a general problem, which can be stated in a unified mathematical structure across many contexts, from the extrapolation of trajectories to the learning of rules (20). Our results on the efficient representation of predictive information in the retina thus may hint at a much more general principle.
Materials and Methods
Multielectrode Recordings.
Data were recorded from larval tiger salamander retina using the dense 252-electrode arrays with 30-μm spacing, as described in ref. 36. A piece of retina was freshly dissected and pressed onto the multielectrode array. While the tissue was perfused with Ringer’s solution, images from a computer monitor were projected onto the photoreceptor layer via an objective lens. Voltages were recorded from the 252 electrodes at 10 kHz throughout the experiments, which lasted 4–6 h. Spikes were sorted conservatively (36), yielding populations of 49 or 53 identified cells from two experiments, from which groups of different sizes were drawn for analysis.
Stimulus Generation and Presentation.
Movies were presented to the retina from -pixel display, with 8 bits of grayscale. Frames were refreshed at 60 fps for naturalistic and moving bar stimuli, and at 30 fps for randomly flickering checkerboards. The monitor pixels were square and had a size of 3.81 μm on the retina. The moving bar (Fig. 1) was 11 pixels wide and black (level 0 on the grayscale) against a background of gray (level 128). The naturalistic movie was a 19-s clip of fish swimming in a tank during feeding on an algae pellet, with swaying plants in the background, and was repeated a total of 102 times. All movies were normalized to the same mean light intensity.
Motion Trajectories.
The moving-bar stimulus was generated by a stochastic process that is equivalent to the Brownian motion of a particle bound by a spring to the center of the display: the position and velocity of the bar at each time t were updated according to the following:
| [4] |
| [5] |
where is a Gaussian random variable with zero mean and unit variance, chosen independently at each time step. The natural frequency ω = 2π × (1.5 s−1) rad/s, and the damping ; with , the dynamics are slightly overdamped. The time step matches the refresh time of the display, and we chose to generate a reasonable dynamic range of positions. Positions at each time were rounded to integer values, and we checked that this discretization had no significant effect on any of the statistical properties of the sequence, including the predictive information.
Common Futures.
To create trajectories in which several independent pasts converge onto a common future, we first generated a single very long trajectory, comprised of time steps. From this long trajectory, we searched for segments with a length of 52 time steps such that the last two positions in the segment were common across multiple segments, and we joined each of these “pasts” on to the same future, generated with the common endpoints as initial conditions; matching two successive points is sufficient given the Markovian structure of Eqs. 4 and 5. Thirty such distinct futures with 100 associated pasts were displayed in pseudorandom order. Both the past and the future segments of the movie were each in duration.
Estimating Information.
For all mutual information measures, we followed ref. 37: data were subsampled via a bootstrap technique for different fractions f of the data, with 50 bootstrap samples taken at each fraction. For each sample, we identify frequencies with probabilities, and plug into the definition of mutual information to generate estimates . Plots of vs. were extrapolated quadratically to infinite sample size , and the intercept is our estimate of the true information; errors were estimated as the SD of at , divided by . Information estimates also were made for randomly shuffled data, which should yield zero information. If the information from shuffled data differed from zero by more than the estimated error, or by more than absolute cutoff of , we concluded that we did not have sufficient data to generate a reliable estimate. In estimating information about bar position (Fig. 1), we compressed the description of position into equally populated bins and checked that the information was on a plateau vs. K, meaning that we had enough adaptive bins to capture all of the entropy in the original position variable. When we compute the information that neural responses carry about the past stimulus, we follow refs. 15 and 23, making use of the repeated “futures” in the common future experiment.
Information Bottleneck.
Information about the future of the stimulus is bounded by the optimal compression of the past, for each given compression amount. Formally, we want to solve the “bottleneck problem” (18):
| [6] |
where we map pasts into some compressed representation , using a probabilistic mapping . The parameter sets the trade-off between compression [reducing the information that we keep about the past, ] and prediction [increasing the information that we keep about the future, ]. Once we find the optimal mapping, we can plot vs. for the one parameter family of optimal solutions obtained by varying . In general, this is a hard problem. Here, we are interested in trajectories such that position and velocity (together) are both Gaussian and Markovian, from Eq. 4. The Markovian structure means that optimal predictions can always be based on information contained at the most recent point in the past, and that prediction of the entire future is equivalent to prediction one time step ahead. Thus, we can take and . The fact that all of the relevant distributions are Gaussian means that there is an analytic solution to the bottleneck problem (38), which we used here. Further details are provided in Bound Calculation.
Supplementary Material
Acknowledgments
We thank E. Schneidman, G. J. Stephens, and G. Tkačik for useful discussions; and G. W. Schwartz, D. Amodei, and F. S. Soo for help with the experiments. We also thank the Aspen Center for Physics, supported by National Science Foundation (NSF) Grant PHY-1066293, for its hospitality. The work was supported by NSF Grants IIS-0613435, PHY-0957573, PHY-1305525, and CCF-0939370; by National Institutes of Health Grant EY-014196; by Novartis (through the Life Sciences Research Foundation); by the Swartz Foundation; and by the W. M. Keck Foundation.
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1506855112/-/DCSupplemental.
References
- 1.Schultz W, Dayan P, Montague PR. A neural substrate of prediction and reward. Science. 1997;275(5306):1593–1599. doi: 10.1126/science.275.5306.1593. [DOI] [PubMed] [Google Scholar]
- 2.Montague PR, Sejnowski TJ. The predictive brain: Temporal coincidence and temporal order in synaptic learning mechanisms. Learn Mem. 1994;1(1):1–33. [PubMed] [Google Scholar]
- 3.Rao RP, Ballard DH. Predictive coding in the visual cortex: A functional interpretation of some extra-classical receptive-field effects. Nat Neurosci. 1999;2(1):79–87. doi: 10.1038/4580. [DOI] [PubMed] [Google Scholar]
- 4.Bialek W, Nemenman I, Tishby N. Predictability, complexity, and learning. Neural Comput. 2001;13(11):2409–2463. doi: 10.1162/089976601753195969. [DOI] [PubMed] [Google Scholar]
- 5.Shannon CE. 1948. A mathematical theory of communication. Bell Sys Tech J 27:379–423, 623–656.
- 6.Cover TM, Thomas JA. Elements of Information Theory. 2nd Ed Wiley-Interscience; Hoboken, NJ: 2006. [Google Scholar]
- 7.Rieke F, Warland D, de Ruyter van Steveninck RR, Bialek W. Spikes: Exploring the Neural Code. MIT; Cambridge, MA: 1997. [Google Scholar]
- 8.Bialek W. Biophysics: Searching for Principles. Princeton Univ Press; Princeton: 2012. [Google Scholar]
- 9.Reich DS, Mechler F, Victor JD. Independent and redundant information in nearby cortical neurons. Science. 2001;294(5551):2566–2568. doi: 10.1126/science.1065839. [DOI] [PubMed] [Google Scholar]
- 10.Petersen RS, Panzeri S, Diamond ME. Population coding of stimulus location in rat somatosensory cortex. Neuron. 2001;32(3):503–514. doi: 10.1016/s0896-6273(01)00481-0. [DOI] [PubMed] [Google Scholar]
- 11.Puchalla JL, Schneidman E, Harris RA, Berry MJ., II Redundancy in the population code of the retina. Neuron. 2005;46(3):493–504. doi: 10.1016/j.neuron.2005.03.026. [DOI] [PubMed] [Google Scholar]
- 12.Narayanan NS, Kimchi EY, Laubach M. Redundancy and synergy of neuronal ensembles in motor cortex. J Neurosci. 2005;25(17):4207–4216. doi: 10.1523/JNEUROSCI.4697-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Chechik G, et al. Reduction of information redundancy in the ascending auditory pathway. Neuron. 2006;51(3):359–368. doi: 10.1016/j.neuron.2006.06.030. [DOI] [PubMed] [Google Scholar]
- 14.Osborne LC, Palmer SE, Lisberger SG, Bialek W. The neural basis for combinatorial coding in a cortical population response. J Neurosci. 2008;28(50):13522–13531. doi: 10.1523/JNEUROSCI.4390-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Schneidman E, et al. Synergy from silence in a combinatorial neural code. J Neurosci. 2011;31(44):15732–15741. doi: 10.1523/JNEUROSCI.0301-09.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Soo FS, Schwartz GW, Sadeghi K, Berry MJ., 2nd Fine spatial information represented in a population of retinal ganglion cells. J Neurosci. 2011;31(6):2145–2155. doi: 10.1523/JNEUROSCI.5129-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Doi E, et al. Efficient coding of spatial information in the primate retina. J Neurosci. 2012;32(46):16256–16264. doi: 10.1523/JNEUROSCI.4036-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Tishby N, Pereira FC, Bialek W. 1999. The information bottleneck method. Proceedings of the 37th Annual Allerton Conference on Communication, Control and Computing (University of Illinois, Urbana, IL), Vol 37, pp 368–377.
- 19.Creutzig F, Globerson A, Tishby N. Past-future information bottleneck in dynamical systems. Phys Rev E Stat Nonlin Soft Matter Phys. 2009;79(4 Pt 1):041925. doi: 10.1103/PhysRevE.79.041925. [DOI] [PubMed] [Google Scholar]
- 20.Bialek W, de Ruyter van Steveninck RR, Tishby N. Proceedings of the International Symposium on Information Theory. IEEE; Piscataway, NJ: 2006. Efficient representation as a design principles for neural coding and computation; pp. 659–663. [Google Scholar]
- 21.Eggermont JJ, Johannesma PM, Aertsen AM. Reverse-correlation methods in auditory research. Q Rev Biophys. 1983;16(3):341–414. doi: 10.1017/s0033583500005126. [DOI] [PubMed] [Google Scholar]
- 22.Schwartz O, Pillow JW, Rust NC, Simoncelli EP. Spike-triggered neural characterization. J Vis. 2006;6(4):484–507. doi: 10.1167/6.4.13. [DOI] [PubMed] [Google Scholar]
- 23.Brenner N, Strong SP, Koberle R, Bialek W, de Ruyter van Steveninck RR. 2000. Synergy in a neural code. Neural Comp 12(7):1531–1552. [DOI] [PubMed]
- 24.MacKay D, McCulloch W. The limiting information capacity of a neuronal link. Bull Math Biophys. 1952;14(2):127–135. [Google Scholar]
- 25.Rieke F, Warland D, Bialek W. Coding efficiency and information rates in sensory neurons. Europhys Lett. 1993;22(2):151–156. [Google Scholar]
- 26.Laughlin S. A simple coding procedure enhances a neuron’s information capacity. Z Naturforsch C. 1981;36(9-10):910–912. [PubMed] [Google Scholar]
- 27.Smirnakis SM, Berry MJ, II, Warland DK, Bialek W, Meister M. Adaptation of retinal processing to image contrast and spatial scale. Nature. 1997;386(6620):69–73. doi: 10.1038/386069a0. [DOI] [PubMed] [Google Scholar]
- 28.Brenner N, Bialek W, de Ruyter van Steveninck R. Adaptive rescaling maximizes information transmission. Neuron. 2000;26(3):695–702. doi: 10.1016/s0896-6273(00)81205-2. [DOI] [PubMed] [Google Scholar]
- 29.Barlow HB. Possible principles underlying the transformation of sensory messages. In: Rosenblith W, editor. Sensory Communication. Wiley; New York: 1961. pp. 217–234. [Google Scholar]
- 30.Atick JJ, Redlich AN. What does the retina know about natural scenes? Neural Comput. 1992;4(2):196–210. [Google Scholar]
- 31.Dan Y, Atick JJ, Reid RC. Efficient coding of natural scenes in the lateral geniculate nucleus: Experimental test of a computational theory. J Neurosci. 1996;16(10):3351–3362. doi: 10.1523/JNEUROSCI.16-10-03351.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Srinivasan MV, Laughlin SB, Dubs A. Predictive coding: A fresh view of inhibition in the retina. Proc R Soc Lond B Biol Sci. 1982;216(1205):427–459. doi: 10.1098/rspb.1982.0085. [DOI] [PubMed] [Google Scholar]
- 33.Berry MJ, II, Schwartz G. The retina as embodying predictions about the visual world. In: Bar M, editor. Predictions in the Brain: Using Our Past to Generate a Future. Oxford Univ Press; Oxford: 2011. pp. 295–310. [Google Scholar]
- 34.Berry MJ, 2nd, Brivanlou IH, Jordan TA, Meister M. Anticipation of moving stimuli by the retina. Nature. 1999;398(6725):334–338. doi: 10.1038/18678. [DOI] [PubMed] [Google Scholar]
- 35.Trenholm S, Schwab DJ, Balasubramanian V, Awatramani GB. Lag normalization in an electrically coupled neural network. Nat Neurosci. 2013;16(2):154–156. doi: 10.1038/nn.3308. [DOI] [PubMed] [Google Scholar]
- 36.Marre O, et al. Mapping a complete neural population in the retina. J Neurosci. 2012;32(43):14859–14873. doi: 10.1523/JNEUROSCI.0723-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Strong SP, Koberle R, van Steveninck RRD, Bialek W. Entropy and information in neural spike trains. Phys Rev Lett. 1998;80(1):197–200. [Google Scholar]
- 38.Chechik G, Globerson A, Tishby N, Weiss Y. Information bottleneck for Gaussian variables. JMLR. 2005;6:165–188. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.