Effects of Age and Diabetes on Scleral Stiffness

Short abstract

The effects of diabetes on the collagen structure and material properties of the sclera are unknown but may be important to elucidate whether diabetes is a risk factor for major ocular diseases such as glaucoma. This study provides a quantitative assessment of the changes in scleral stiffness and collagen fiber alignment associated with diabetes. Posterior scleral shells from five diabetic donors and seven non-diabetic donors were pressurized to 30 mm Hg. Three-dimensional surface displacements were calculated during inflation testing using digital image correlation (DIC). After testing, each specimen was subjected to wide-angle X-ray scattering (WAXS) measurements of its collagen organization. Specimen-specific finite element models of the posterior scleras were generated from the experimentally measured geometry. An inverse finite element analysis was developed to determine the material properties of the specimens, i.e., matrix and fiber stiffness, by matching DIC-measured and finite element predicted displacement fields. Effects of age and diabetes on the degree of fiber alignment, matrix and collagen fiber stiffness, and mechanical anisotropy were estimated using mixed effects models accounting for spatial autocorrelation. Older age was associated with a lower degree of fiber alignment and larger matrix stiffness for both diabetic and non-diabetic scleras. However, the age-related increase in matrix stiffness was 87% larger in diabetic specimens compared to non-diabetic controls and diabetic scleras had a significantly larger matrix stiffness (p = 0.01). Older age was associated with a nearly significant increase in collagen fiber stiffness for diabetic specimens only (p = 0.06), as well as a decrease in mechanical anisotropy for non-diabetic scleras only (p = 0.04). The interaction between age and diabetes was not significant for all outcomes. This study suggests that the age-related increase in scleral stiffness is accelerated in eyes with diabetes, which may have important implications in glaucoma.

1. Introduction

In 2014, 12.3% of the American population of age 20 and older (28.9 million) had diabetes and 1.7 million new cases were diagnosed [1]. The estimated cost of diabetes in 2012 was $245 billion. Diabetes is associated with a number of sight-threatening ocular diseases, including diabetic retinopathy and cataract [2]. Whether diabetes is a risk factor for developing glaucoma remains a topic of intense scientific and clinical research. Glaucoma is the second leading cause of blindness worldwide [3,4]. The central event in the disease is a slow and irreversible damage to the retinal ganglion cell axons that transmit the visual information from the retina to the brain. Damage occurs at the optic nerve head (ONH), region of the posterior eye through which the axons exit the eye and converge to form the optic nerve. Although the mechanisms leading to vision loss in glaucoma are poorly understood, there is substantial evidence that excessive intra-ocular pressure (IOP)-induced deformation of the ONH impairs the normal function of the axons.

One argument supporting the detrimental role of diabetes in glaucoma is as follows: long-term diabetes causes micro-angiopathy, which compromises blood flow in the optic nerve and retina and should exacerbate glaucomatous damage. However, this argument is challenged by most of the recent population-based studies, which found no correlations between diabetes and glaucoma [5–9]. Further, people with diabetes have on average a higher IOP compared with those without diabetes [10] and should therefore be more at risk for glaucoma. The fact that this is not the case has led Quigley [11] to suggest that early diabetes may be neuroprotective for glaucoma.

This hypothesis was recently tested in a rat model of experimental glaucoma [12]. Hyperglycemic rats showed delayed axonal degeneration compared with normoglycemic rats. In a follow-up clinical study in humans with glaucoma, Casson et al. [13] showed that topical glucose improved visual parameters such as mean contrast sensitivity and suggested that glucose may help “sick” retinal ganglion cells recover their normal function. These studies are evidence that diabetes or elevated glucose may upregulate the release of trophic factors that are neuroprotective in glaucoma.

Alternatively, Quigley hypothesized that diabetic eyes are less susceptible to glaucomatous damage because they are stiffer [11]. In this framework, a stiffer eye would deform less under the insult of IOP and shield the ONH against excessive deformation that could potentially damage the axons. The stiffening of soft tissues in diabetes has been attributed to the accumulation of advanced glycation end-product (AGE) cross-links of collagen [14]. Diabetes-induced AGE accumulation occurs in tendons [15,16], arteries [17] and also in ocular tissues such as the cornea [18] and the ONH [19]. Associated stiffening was reported in many tissues including arteries [20], the skin [21], the cornea [22], and the ONH [23].

The sclera is a tissue of critical importance in glaucoma. The sclera is the white outer shell and principal load-bearing tissue of the eye. This tissue is made of collagen, mainly type I (90%) and type III (≤5%) fibers [24,25] that are embedded in a hydrated matrix of proteoglycans. The collagen fibers aggregate parallel to each other to form 50 μm thick lamellae superimposed in the scleral plane [26]. Recent modeling efforts have shown that scleral stiffness [27,28], thickness [29], and collagen fiber structure [30] significantly influence the response of the ONH tissues to changes in IOP. Therefore, we expect that any diabetes-related changes in the material properties or microstructure of the sclera would alter the biomechanical environment of the ONH. To the best of our knowledge, the effects of diabetes on the collagen structure and material properties of the human sclera are unknown. Although it is hypothesized that scleral stiffness is larger in diabetic eyes, this has never been demonstrated in the human eye.

In a recent publication, we developed experimental and modeling methods to study the biomechanics and collagen microstructure of the sclera. We found that older age was associated with a less aligned or more random collagen fiber structure in the peripapillary sclera, region closest to the ONH, and an increased matrix stiffness [31]. We attributed this increase in stiffness to an accumulation of nonenzymatic cross-links, similarly to that occurring in diabetes, but at a slower rate. Interestingly, in contrast to diabetes, older age is a major risk factor for glaucoma. One possible interpretation is that scleral stiffening may occur at a faster rate in the sclera of people with diabetes, protecting them earlier from glaucomatous damage. We propose to test this hypothesis in this study.

To that end, we estimated the effects of diabetes, age, and their interactions on the collagen fiber structure and material properties of the matrix and the collagen fibers of the human sclera. Five scleras from diabetic donors and seven scleras from non-diabetic donors of age ranging between 46 and 91 were subjected to inflation testing [32]. Full-field DIC-measured displacements of the scleral surface were recorded during pressure elevation. After testing, WAXS was used to map the preferred orientations and degree of alignment of the collagen fibers of each sclera [33]. The material properties of each specimen, i.e., the matrix and fiber stiffness, were calculated by fitting a distributed fiber model that incorporated the WAXS-measured orientation and distribution of collagen fibers to the experimental displacement fields of the inflation test.

2. Methods

2.1. General Approach.

Our objective was to determine the material behavior of the sclera. Postmortem eyes from donors with and without diabetes were inflated, and the surface displacements were optically measured using DIC. The stress state in the peripapillary sclera cannot be experimentally measured from the inflation experiments because of the presence of the compliant ONH and complex geometry in this region. Instead, we used an indirect method to estimate stresses and fit a constitutive model to the experimentally measured displacement fields. The constitutive model included a detailed description of the collagen micro-architecture of the sclera of each specimen, as measured by WAXS. The collagen micro-architecture, strain response, and material behavior were compared to evaluate the effects of diabetes. The methods have been described in previous reports [30–33] and are just briefly presented below.

2.2. Specimens.

Twelve human scleras were obtained from the National Disease Research Interchange from ten donors aged 46–91 (Table 1). Donors with a clinical diagnosis of glaucoma were excluded. Five of the specimens were from diabetic donors, as indicated in the hospital records.

Table 1.

Human scleras subjected to inflation testing and WAXS measurements of the collagen fiber structure. All donors except FAA74l (African American) were of Caucasian descent.

Sclera	Age	Right/Left	Sex	Diabetes diagnosis
MC46r a	46	Right	Male	Diabetes
MC46l a	46	Left	Male	Diabetes
FC53r	53	Right	Female	—
MC58l	58	Left	Male	—
FC67r	67	Right	Female	Diabetes
FC71r	71	Right	Female	—
FAA74l	74	Left	Female	Diabetes
FC74l	74	Left	Female	Diabetes
FC77r a	77	Right	Female	—
FC77l a	77	Left	Female	—
MC77r	77	Right	Male	—
FC91r	91	Right	Female	—

^aFor MC46 and FC77, both eyes were included in the study.

2.3. Inflation Testing.

The inflation testing protocol was described in previous publications [32,34] and a schematic is shown in Fig. 1. Briefly, the specimens were cleaned of extra orbital fat and muscle, glued on a custom-made holder 3 mm posterior to the equator, and mounted on a pressure chamber enclosed by a humidity chamber. They were inflated through pressure-controlled injection of a saline solution. Pressure in the chamber was elevated from the baseline pressure of 1.5 mm Hg to 30 mm Hg at a rate of 1 mm Hg/s. The pressure loading regimen covers the range of physiological pressures in normal (12–22 mm Hg) and hypertensive (22–30 mm Hg) eyes [35]. The sclera was speckled by dispersing graphite powder through a 62 μm mesh to provide a high contrast pattern for DIC. During inflation, two stereo cameras with a 15 deg tilt angle imaged the deforming sclera every 2 s. A stereoscopic DIC system (Vic3D, Correlated Solutions, Inc., Columbia, SC) with a 10 μm uncertainty in the out-of-plane displacement [32,36] was used to measure the 3D displacement field of the scleral surface. This estimation of the uncertainty was comparable to the measurements by Ke et al. [37] (between 10 and 20 μm at 20 deg stereo angle) and [38] (root-mean-square error between 5 and 20 μm at 20 deg stereo angle). Scleral thickness was measured at eight locations in the peripapillary sclera and eight locations in the midposterior sclera using an ultrasonic pachymeter.

Fig. 1.

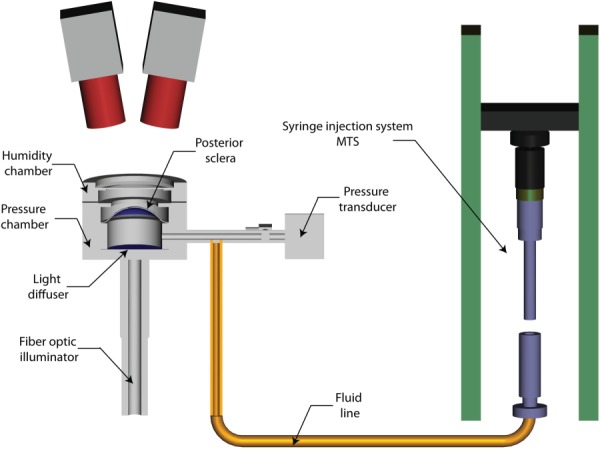
Schematic of the experimental apparatus used for the inflation test of the human sclera. The specimens were glued on a holder and placed on a pressure chamber. The pressure in the chamber was measured with a pressure transducer and changed by controlled-injection of PBS. During testing, the deforming scleral surface was imaged by two charge-coupled device cameras positioned 50cm above the specimen and oriented 15deg from the vertical axis on opposite sides. The white scleral surface was speckled by dispersing graphite powder through a 62 μm mesh to provide a high contrast pattern for DIC.

2.4. WAXS Measurements of the Fiber Structure.

After mechanical testing, the specimens were preserved in a 4% paraformaldehyde (PFA) solution until the time of X-ray measurements. A recent study showed that fixation of the tissue in PFA did not lead to significant alterations to the collagen fiber structure of the cornea [39]. A 15 mm circular specimen, centered on the ONH, was excised from each intact posterior sclera. WAXS was used to measure the through-thickness averaged distribution of fiber orientations at 0.5 mm intervals across the specimen following the methods fully described in Pijanka et al. [33] (Fig. 2(c)). The WAXS pattern from scleral tissue was dominated by a well-resolved equatorial (i.e., perpendicular to the fiber axis) reflection from the regular 1.6 nm spacing of the constituent collagen molecules aligned near axially within the scleral fibers (Fig. 2(a)). The collagen structure at one point of the sclera was described by the statistical distribution of collagen fibers D

Fig. 2.

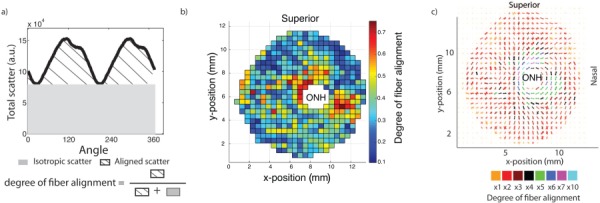
(a) Angular intensity profile for a single WAXS measurement located in the peripapillary sclera. The degree of fiber alignment, which was defined as the ratio of the aligned scatter to the total scatter, was calculated for each WAXS measurement and is mapped in (b) for FC74l. Scatter intensity plots from (a) can be represented as polar plots indicating the local preferred orientation (shape of the plot) and the degree of fiber alignment and assembled into polar plots as shown in (c).

$$D(\Phi )=\frac{I(\Phi )}{{\int }_0^{2\pi }I(\Phi )d\Phi }$$ (1)

where I is the total WAXS scatter, measured by increments of 1.4 deg in $\Phi$. As defined, $D(\Phi )d\Phi$ represents the number fraction of collagen fibers oriented between the angle $\Phi$ and $\Phi +d\Phi$. The degree of fiber alignment was calculated for every sampled point in the sclera by dividing the integral of the aligned scatter distribution by the corresponding integral of the total scatter, yielding a single value representing the proportion of fibers preferentially aligned at that point in the tissue (Fig. 2(a)). A contour of the degree of fiber alignment is shown in Fig. 2(b).

2.5. Estimation of Scleral Mechanical Properties by Inverse Finite Element Modeling.

The total strain energy density of the sclera was additively decoupled into a neo-Hookean deviatoric contribution parameterized by a shear modulus μ and a volumetric contribution parameterized by a bulk modulus κ representing the nonfibrillar collagen constituents (water, cells, elastin, and proteoglycans) and an integral contribution representing the collagen fibers, characterized by two parameters (α, β), where 4αβ represents the axial stiffness of a fiber [30,40,41]

$$W_{\mathrm{sclera}}(\mathbf{C},\mathbf{X})=\frac{\mu }{2}(\overline{I_1}-3)+\frac{\kappa }{4}(I_3-\ln (I_3)-1)+{\int }_0^{2\pi }\frac{\alpha }{\beta }[\exp \left(\beta ({\lambda }_{\mathrm{f}}^2-1)\right)-\beta {\lambda }_{\mathrm{f}}^2]D(\Phi ,\mathbf{X})d\Phi$$ (2)

where $I_1=\mathrm{tr}(\mathbf{C}),I_3=det(\mathbf{C})$ are two invariants of C, $\Phi$ is the orientation angle in the scleral plane, and ${\lambda }_{\mathrm{f}}(\Phi )$ represents the stretch of a fiber oriented in the ${\mathbf{e}}_{\Phi }$-direction, which was calculated as ${\lambda }_{\mathrm{f}}(\Phi )=\sqrt{{\mathbf{e}}_{\Phi }^{\top }.\mathbf{C}.{\mathbf{e}}_{\Phi }}$. Further,

• (1)A large bulk modulus κ = 100 MPa was used for all models to ensure that the volumetric deformation J ≤ 1.001 at the maximum pressure.
• (2)The matrix shear modulus μ and the fiber parameters (α, β) were assumed to be uniform across the sclera.
• (3)The normalized WAXS scatter intensity D (Eq. (1)) was used to describe the distribution of collagen fiber orientations. The spatial variations of D in the sclera were informed from the WAXS experiments.

In summary, the stiffness at a point of the sclera was dictated by the uniform scleral material parameters (μ, α, β) and the position-dependent fiber structure, described by the normalized WAXS scatter intensity.

The DIC-measured positions of the scleral surface at the baseline pressure and the thickness measurements were combined to create a specimen-specific mesh of the midposterior sclera [31] (Fig. 3). The mesh was extended from the outer peripapillary sclera to the ONH with a generic model. This model assumed that the thickness of the peripapillary sclera linearly decreased from the experimentally measured thickness at the outer peripapillary sclera (Fig. 3(b)) to the thickness at the scleral canal that was 0.4 mm for all specimens [42–44]. The geometry was descritized with hexahedron elements and three elements spanned the thickness. A different collagen fiber structure was used for each element and was defined using:

Fig. 3.

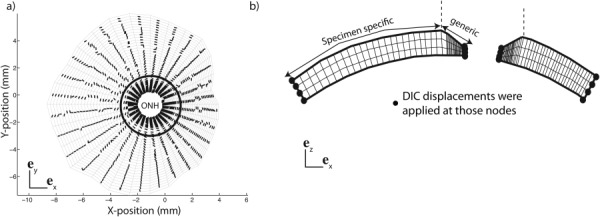
(a) Camera view of the specimen-specific mesh used for the inverse method for the specimen FC74l. The preferred fiber direction is represented for each element. (b) Side view showing the thickness variation close to the ONH. The thickness profile was created by linearly interpolating the 16 pachymeter measurements, made at two meridional positions and eight circumferential positions. The midposterior sclera was constructed from the DIC-measured position of the surface and the thickness data. DIC-displacements were applied at the edges of the mesh as kinematic boundary conditions. The boarder between the specimen-specific region and the generic region is marked with a circle in (a) and a vertical dashed line in (b).

• (1)Two vectors $({\mathbf{e}}_{\mathrm{f}},{\mathbf{e}}_{\mathrm{p}})$ of the scleral plane, where ${\mathbf{e}}_{\mathrm{f}}$ represents the local preferred fiber orientation and ${\mathbf{e}}_{\mathrm{p}}$ represents the direction normal to the local preferred fiber orientation in the scleral plane. The planar projections of the preferred fiber orientations are plotted in Fig. 3(a), and
• (2)The probability density function for fiber orientation D, which was the normalized scatter intensity of the colocalized WAXS measurement.

The same collagen fiber structure was assigned to the three elements through the thickness. A Cauchy traction boundary condition was prescribed on the inner surface using the time history of the applied pressure, and DIC-measured surface displacements were applied to the nodes throughout the thickness of the scleral canal and the outer edge as kinematic boundary conditions as described in Coudrillier et al. [31].

We used a global optimization algorithm to estimate the parameters $(\mu ,\alpha ,\beta )$ from the DIC-measured displacements of the inflation experiments, which was described and validated in Coudrillier et al. [31]. A dense grid of parameter estimates $({\mu }_i,{\alpha }_j,{\beta }_k)$ was generated, where (i, j, k) were simultaneously varied over a wide range of parameters spanning two orders of magnitude. For each parameter estimate, a finite element simulation was performed to compute the displacements at the nodes of the scleral surface. The accuracy of the model prediction was evaluated by calculating a scalar cost function, defined as the difference between DIC-measured and computed displacements, summed over every surface node, and 15 inflation pressure levels. The goal of the inverse method was to find the set of parameters $(\mu ,\alpha ,\beta )$, which minimized the cost function, by mapping the cost function over the parameter space.

2.6. Mechanical Anisotropy.

The sclera imposes IOP-induced tensile deformation to the ONH, which translates into an expansion of the scleral canal. The amount of scleral canal expansion is greatly determined by the mechanical anisotropy of the peripapillary sclera [28], which is defined as the ratio of scleral stiffness in the circumferential direction (i.e., parallel to the scleral canal) to scleral stiffness in the meridional direction (i.e., perpendicular to the scleral canal). The mechanical anisotropy depends on the structural anisotropy of the collagen fiber network and the mechanical properties of scleral tissue. For a nonlinear material, it also depends on the loading conditions. We used the experimental strains measured at 22.5 mm Hg averaged over 35 specimens in the circumferential and meridional directions [32] for the calculation of the local mechanical anisotropy. The mechanical anisotropy was defined as $\mathrm{MA}={\mathbb{C}}_{\mathrm{ffff}}/{\mathbb{C}}_{\mathrm{pppp}}$, where $\mathbb{C}=4({\partial }^2{W}_{\mathrm{sclera}}/\partial {\mathbf{C}}^2)$ is the fourth-order stiffness tensor, ${\mathbb{C}}_{\mathrm{ffff}}$ and ${\mathbb{C}}_{\mathrm{pppp}}$ are the moduli along the fiber and perpendicular directions calculated for $E_{\mathrm{f}}=1.1\%$ and $E_{\mathrm{p}}=1.9\%$, the averaged principal strains in the peripapillary sclera [32] (Fig. 4).

Fig. 4.

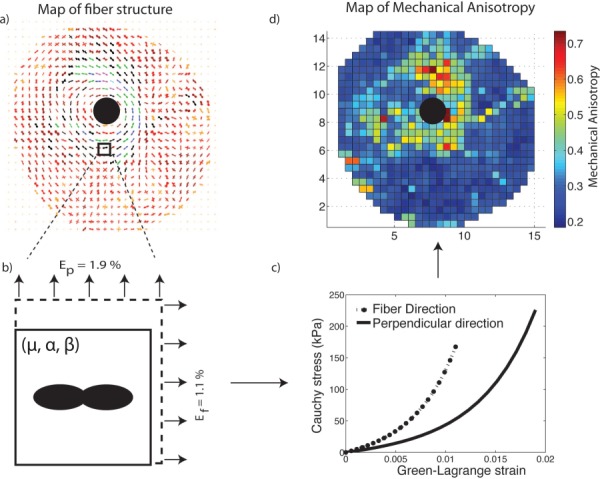
We modeled a biaxial stretch tension on finite element (b), which fiber structure was described using a single WAXS measurement (a). We used specimen-specific material properties and applied averaged circumferential and meridional strains measured in 35 specimens [] as boundary conditions. A representative stretch/stress curve is represented in (c). We repeated this simulation for every WAXS measurement to map the mechanical anisotropy across the posterior sclera as shown in (d).

2.7. Statistical Analyses.

Linear regression models were used to evaluate the effects of age, diabetes, and age–diabetes interactions on matrix and fiber stiffness. For the degree of fiber alignment and mechanical anisotropy, we collected 72 data points in the peripapillary sclera (region defined as being at a radial distance of 2 mm or less from the scleral canal) per specimen. Mixed linear models with spatial autocorrelation were used to evaluate the effects of age, diabetes, age–diabetes interaction, and peripapillary scleral quadrant taking account of the correlations among the repeat measurements for a specimen. For the degree of fiber alignment, a 2D exponential geometrically anisotropic autocorrelation structure was used for measurements from each specimen after examining the variogram and Akaikes information criteria [45]. Mechanical anisotropy did not exhibit spatial correlation, and a compound symmetry correlation structure was assumed. The Tukey–Kramer method [46] was used to adjust pairwise significance levels when comparing the effects of different scleral regions on fiber alignment and mechanical anisotropy. Note that correlations between the right and left eye of FC77 and MC46 were ignored.

We then calculated the power of our analyses to find statistically significant effects for diabetes and statistically significant differences in age effects between the diabetic and non-diabetic groups. For models with repeat measurements, the observed intracluster correlation coefficient assuming compound symmetry was used to obtain the effective sample size prior to calculating the power. For the degree of fiber alignment, the actual power may be lower than the power tabulated since repeat measurements were assumed to have a more complicated correlation structure. All analyses were performed using SAS 9.2 (SAS Institute, Cary, NC).

3. Results

3.1. Effects of Diabetes on the Collagen Fiber Structure.

For all specimens, mean degree of fiber alignment was lowest in the superior/nasal quadrant (adjusted p value ≤ 0.03, for the comparisons of the degree of fiber alignment in the SN with the three other quadrants). There were no differences in degree of fiber alignment between diabetic and non-diabetic scleras. Older age was associated with a lower degree of fiber alignment for both non-diabetic and diabetic specimens although the age effects were statistically significant for non-diabetic specimens only (p = 0.01). Figure 5 illustrates the relation between age and average degree of fiber alignment in the peripapillary sclera for both diabetic and non-diabetic groups. The effects of age were not significantly different between the two groups (p = 0.43 for the interaction between age and diabetes diagnosis) (Table 2).

Fig. 5.

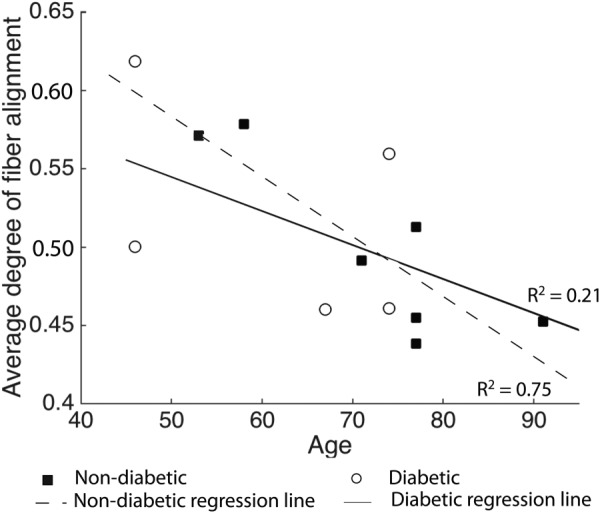
Degree of fiber alignment averaged over the entire peripapillary sclera for all specimens. Age was associated with a significant decrease in mean degree of fiber alignment for non-diabetic donors. Regression lines represent the age-related variation in degree of fiber alignment within the diabetic and non-diabetic groups.

Table 2.

Results of the multivariate model with spatial autocorrelation for the degree of fiber alignment in the peripapillary sclera with age, quadrant, diabetes diagnostic, and age–diabetes interaction as explanatory variables. The age–diabetes interaction was not significant (p = 0.43). The variogram for the degree of fiber alignment increased and then levels off as distance between two measurements of a same specimen increased, indicating spatial autocorrelation. S stands for superior, N for nasal, I for inferior, and T for temporal.

Degree of fiber alignment
Variable	Estimate (95% CI)	p value
Age (per 10-yr increase)
Specimen with a history of diabetes	−0.028 (−0.061, −0.005)	0.09
Specimen with no history of diabetes	−0.044 (−0.074, −0.014)	0.01
Diabetes		0.76
Yes	−0.008 (−0.069, 0.052)
No (reference)	0
Region		0.001
NI	−0.038 (−0.087, 0.012)
IT	−0.030 (−0.075, 0.014)
SN	−0.104 (−0.150, −0.058)
TS (reference)	0

p values in bold indicate statistical significance.

3.2. Effects of Diabetes on the Material Properties of the Matrix and Collagen Fibers.

The material parameters for the collagen fibers and matrix obtained after convergence of the IFEA are presented in Table 3. The results of the multivariate models for the material properties of the matrix and collagen fibers with age, diabetes, and age–diabetes interaction as explanatory variables are presented in Table 4. The interaction between age and diabetes was not significant (p = 0.28) for the matrix stiffness, but nearly significant for the fiber stiffness (p = 0.08). Older age was predictive of a larger matrix stiffness μ for both diabetic and non-diabetic donors although this result was statistically significant for diabetic donors only (p = 0.01, Fig. 6(a)). A linear regression of the effects of age on μ for non-diabetic scleras showed a 150% increase from age 40 to 90 with a correlation coefficient of R ²= 0.90. In a previous report that did not include diabetic donors, we found that older age was predictive of a significantly larger matrix stiffness [31]. Scleras from diabetic donors had a significantly larger matrix stiffness (p = 0.01). Older age was not associated with significant change in fiber stiffness 4αβ for non-diabetic donors (p = 0.60) but the age-related increase in fiber stiffness was borderline significant for donors with diabetes (p = 0.06, Fig. 6(b)).

Table 3.

Matrix modulus μ, parameters of the exponential fiber model (α, β), and fiber stiffness (4αβ) obtained by global optimization. Diabetic donors have their name in bold letters.

	μ	α	β	Fiber stiffness: 4αβ
	kPa	kPa	—	MPa
MC46r	125	5	65	1.300
MC46l	160	0.5	215	0.430
FC53r	100	204	11	8.976
MC58l	130	6	47	1.128
FC67r	175	10	100	4.028
FC71r	150	26.5	38	4.028
FC74r	300	15	141	8.460
FAA74l	470	40	42	6.730
FC77l	220	13.5	136	7.344
FC77r	225	15	145	8.70
MC77r	190	135	14	7.560
FC91r	250	2	137	1.096

Table 4.

Results of the multivariate model for the matrix and fiber stiffness with age, diabetes diagnostic, and age–diabetes interaction as explanatory variables. The age–diabetes interaction was not significant for the matrix stiffness (p = 0.28) and fiber stiffness (p = 0.08).

Outcome	Variable	Estimate (95% CI)	p value
Matrix stiffness μ (kPa)	Age (per 10-yr increase)
	Specimen with a history of diabetes	76.4 (24.1, 128.8)	0.01
	Specimen with no history of diabetes	40.8 (−6.8, 88.4)	0.08
	Diabetes		0.01
	Yes	130.6 (34.5, 226.6)
	No (ref)	0
Fiber stiffness 4αβ (MPa)	Age (per 10-yr increase)
	Specimen with a history of diabetes	2.27 (−0.15, 4.69)	0.06
	Specimen with no history of diabetes	−0.52 (−2.72, 1.69)	0.60
	Diabetes		0.92
	Yes	−0.19 (−4.63, 4.25)
	No (ref)	0

p values in bold indicate statistical significance.

Fig. 6.

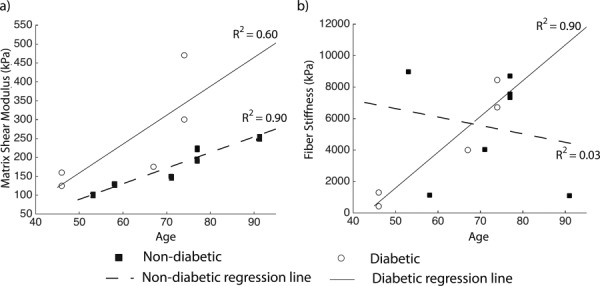
( a) Matrix shear modulus μ, (b) fiber stiffness 4αβ plotted versus age for diabetic and non-diabetic donors. Regression lines represent the age-related variation in stiffness within the diabetic and non-diabetic groups.

3.3. Effects of Age on the Mechanical Anisotropy of the Sclera.

In this section, we evaluate how the age-related changes in degree of fiber alignment and material properties combine to affect the mechanical anisotropy of scleral tissue. As expected, the mechanical anisotropy was highly correlated with the degree of fiber alignment (p < 0.0001). The mechanical anisotropy in the peripapillary sclera followed the pattern of the degree of fiber alignment, being largest in the temporal/superior quadrant (adjusted p value ≤ 0.02 for the comparison of TS with the three other quadrants) and lowest in superior/nasal quadrant (adjusted p value ≤ 0.02 for the comparison of SN with TS and NI, adjusted p value = 0.08 for the comparison of SN with IT).

Age was associated with a significant decrease in mechanical anisotropy for the non-diabetic donors (p = 0.04) but not for the diabetic donors (p = 0.87) as seen in Table 5 and Fig. 7. The age–diabetes interaction was not significant (p = 0.11).

Table 5.

Results of the multivariate model with compound symmetry correlation for mechanical anisotropy in the peripapillary sclera with age, quadrant, diabetes diagnostic, and age–diabetes interaction as explanatory variables. The age–diabetes interaction was not significant (p = 0.11). The variogram was flat for the mechanical anisotropy, indicating little or no spatial correlation. Mechanical anisotropy measurements from the same specimen were assumed to have the same correlation regardless of the distance between them. S stands for superior, N for nasal, I for inferior, and T for temporal. Observed mean mechanical anisotropy was 1.09 ± 0.68 in the NI, 1.06 ± 0.71 in the IT, 1.23 ± 0.77 in the TS, and 0.95 ± 0.58 in the SN.

Mechanical anisotropy
Variable	Estimate (95% CI)	p value
Age (per 10-yr increase)
Specimen with a history of diabetes	0.037 (−0.459, 0.534)	0.87
Specimen with no history of diabetes	−0.487 (−0.939, −0.035)	0.04
Diabetes		0.24
Yes	−0.5 (−1.42, 0.41)
No (reference)	0
Region:		<0.0001
NI	−0.150 (−0.249, −0.051)
IT	−0.180 (−0.278, −0.081)
SN	−0.301 (−0.400, −0.202)
TS (reference)	0

p values in bold indicate statistical significance.

Fig. 7.

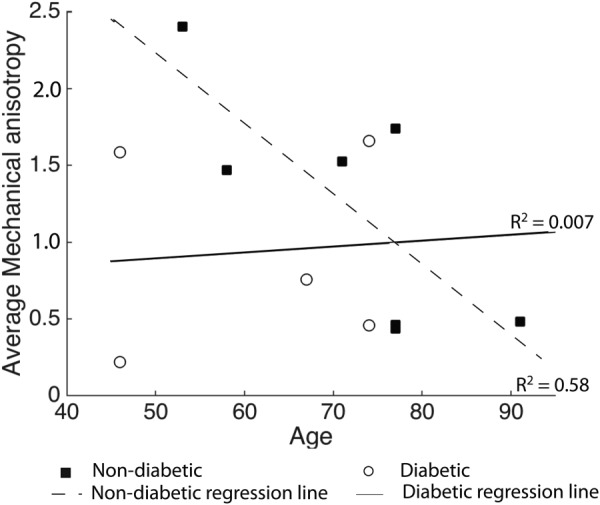
Average mechanical anisotropy in the peripapillary sclera plotted versus age for the diabetic and non-diabetic specimens. Regression lines represent the age-related variation in mechanical anisotropy within the diabetic and non-diabetic groups.

3.4. Power Analyses.

We calculated the statistical power of the models to detect significant diabetes effects for the fiber alignment, matrix and fiber stiffness, and mechanical anisotropy (Table 6). The sample size of this study was sufficiently large to detect significant diabetes effects in matrix stiffness (power > 0.80); however, we would need considerably more specimens to confidently estimate the effects of diabetes on the fiber stiffness, degree of fiber alignment, and mechanical anisotropy. We also calculated the power of the models to detect significant differences in age effects between the diabetic and non-diabetic groups. The outcome with highest power was the fiber stiffness (0.56). For this outcome, the power analysis estimated that we would need 19 specimens to detect a significant difference with 80% power.

Table 6.

Statistical power of the model to find statistically significant effects of diabetes for the different outcomes of this study

Outcome	Adjustment variables	Observed correlation between outcome and age	Observed intracluster correlation a	Power	Minimum # of specimens for at least 80% power b
Matrix stiffness	Age	0.70	—	0.86	11
Fiber stiffness	Age	−0.087	—	0.06	1034
Fiber alignment	Age and Ppscl quadrant	−0.041	0.075	0.08	410
Mechanical anisotropy	Age and Ppscl quadrant	−0.32	0.6	0.28	44

^aFor compound symmetry correlation structure.

^bTo find significant association given the observed partial correlation.

4. Discussion

In this study, we compared the collagen fiber structure and material properties of human scleras from diabetic and non-diabetic donors. The collagen fiber structure was measured using WAXS and the material properties were estimated by fitting a distributed fiber model to the displacement fields of an inflation test. The main findings of this study were

• (1)Older age was predictive of a lower peripapillary scleral degree of fiber alignment for both non-diabetic and diabetic scleras. However, the age effects were statistically significant for non-diabetic specimens only. There were no differences in degree of fiber alignment and age-related variations in degree of fiber alignment between the two groups.
• (2)Older age was predictive of a larger matrix stiffness for both non-diabetic and diabetic scleras. The age effects were significant for diabetic donors only and highly correlative for non-diabetic donors. Matrix stiffness was significantly larger in scleras of diabetic donors.
• (3)Older age was predictive of a larger fiber stiffness for diabetic specimens only. This study did not find any age-related variations in fiber stiffness for non-diabetic donors.
• (4)Older age was predictive of a larger scleral stiffness for diabetic specimens only.
• (5)Mechanical anisotropy was lower in older non-diabetic scleras only. No age-related effects were detected for diabetic donors.

We did not detect qualitative differences in collagen fiber orientation and quantitative differences in collagen fiber alignment between diabetic and non-diabetic scleras. The effects of diabetes on the collagen structure of soft tissues have not been studied extensively. One study used X-ray diffraction to measure the collagen structure of skin and tendons of baboons and also reported no diabetes-related changes in equatorial direction of collagen molecules in both tissues [47]. In our study, we found that the degree of fiber alignment was lower in older diabetic and non-diabetic scleras. The age-related decrease in the degree of fiber alignment in both groups indicates that the collagen fiber structure becomes more random; i.e., the relative number of circumferentially aligned fibers is lower in the older peripapillary scleras.

Diabetes had the largest effects on scleral stiffness, especially on the matrix part of the stiffness, which was larger in diabetic scleras (p = 0.01). Although the fiber stiffness was not significantly larger in diabetic scleras, the age-related variations in fiber stiffness were different between the two groups. In non-diabetic controls, the age-related variations in fiber stiffness were not significant. In contrast, the age-related increase in fiber stiffness was nearly significant among the diabetic specimens (p = 0.06). We previously discussed the age-related stiffening of the non-diabetic sclera [31]. The present findings seem to suggest that the age-related stiffening of the sclera occurs at a faster rate among the diabetic population, which is consistent with microstructural evidence of accelerated accumulation of intrafibrillar cross-links associated with diabetes [14]. As predicted by recent computational models, a stiffer sclera would protect ONH tissues from biomechanical insult [27,29,48]. There is also growing experimental evidence that the sclera becomes stiffer in glaucoma [32,49,50]. The finding of a stiffer sclera in glaucoma eyes after damage may be interpreted as a protective response. Although recent experimental findings suggested that having a stiffer sclera may accelerate axonal damage [51], others are investigating scleral crosslinking as a neuroprotective treatment for glaucoma [52]. Taken together, our study would suggest that diabetes-related stiffening of the sclera, at least in the early stage, provides a neuroprotective effect in glaucoma. Evidently, considering the low sample size of this study, this interpretation is still speculative and needs to be further evaluated.

Interestingly, the hypothesis that having diabetes is protective for glaucoma was also supported by our finding that mechanical anisotropy was lower in the older non-diabetic peripapillary scleras but not in the older diabetic peripapillary scleras. An age-related decrease in mechanical anisotropy would decrease the ability of the non-diabetic sclera to shield the ONH against excessive tensile deformation and may explain the increased susceptibility of the older non-diabetic eye to glaucoma.

The advantages and limitations of the techniques used in this study have been presented in detail elsewhere [30–33]. The main limitation pertaining to this study is the low sample size (12 specimens). Access to ultrabright X-ray sources, such as the diamond light source, is necessarily limited by high facility cost and demand, while lab-based X-ray sources are insufficiently powered for detailed investigation of hydrated biological tissues. In addition, we have insufficient data on diabetes exposure and duration. It is rare to obtain actual medical records documenting diabetes diagnosis and treatment because of privacy regulations and practical considerations. Further, about 37% of the diabetic population (or ∼3% of the U.S. population) is undiagnosed [1], and therefore it is possible that some of the donors categorized as non-diabetic had diabetes and were not aware of it. Despite those limitations, we were able to detect important differences between diabetic and non-diabetic scleras in matrix stiffness and age-related stiffening rates. It is interesting that we measured the most significant differences in age-effects of the matrix stiffness with diabetes, as one would expect the effects of diabetes to be stronger on the fiber stiffness because of the accelerated accumulation of fibrillar cross-links with diabetes. Further studies including more specimens from diabetic donors are needed to confirm the effects of diabetes on scleral stiffness. We observed large variability in the fiber stiffness between donors but also between the two eyes of the same donor (MC46). Previous studies in human scleral tissues have also reported similar level of variability between the left and right eye of the same donors [53,54]. The large differences in mechanical properties between the left and right eyes may be the result of the accumulated differences in remodeling over a person’s lifetime caused by differences in refractive errors and other physiological conditions.

The other limitations are briefly listed below. First, we assumed that the only cause of spatial variations in scleral mechanical properties was the variations in the collagen fiber structure. The mechanical behavior of the matrix and the fibers were identical in the peripapillary sclera and midposterior sclera. In this model, the matrix included the elastin fibers, which were assumed to be randomly oriented. Microscopy studies have showed that the matrix composition is different in the region closest to the ONH and the midperipheral regions of the sclera [55,56]. Different fiber material properties could have been assigned to different regions of the midposterior sclera. However, this would also have increased the number of parameters to optimize. With only three material parameters and the experimentally determined fiber structure, the model was able to accurately reproduce the experimental displacements.

Second, our WAXS method is very robust in regions where the fiber alignment is unidirectional, which includes the peripapillary region. The method becomes less robust in regions where there is a mixture of uni- and biaxial dominant orientations [57]. In addition, Pijanka et al. [33] carried out multiphoton microscopy to show that the circumferential alignment of the fibers in the peripapillary sclera is limited to the mid-to-outer 2/3 of the sclera and does not extend through the full thickness of the tissue. It should be remembered that our WAXS method yields thickness-averaged data. WAXS ignores out-of-plane tilt of fibers until the inclination angle is near-perpendicular to the tissue plane. This means that our results are practically unaffected by fiber-interlace.

Third, we used an idealized model geometry for the peripapillary sclera that was similar for the 12 specimens. The idealized geometry of the peripapillary sclera was based on the averaged measurements of Ren et al. [43], Norman et al. [58], and Vurgese et al. [44]. This most likely did not represent the specific geometry of each specimens and may have influenced the obtained material parameters.

Fourth, we used DIC to measure the surface displacements of the sclera. We and others have showed that the out-of-plane uncertainty in displacement calculation was around 10–15 μm [32,37,38]. We expect the experimental uncertainty in displacements to have little effects on the values of the material parameters, because our global optimizer minimized the averaged error between DIC-measured and model-predicted displacements over the entire surface and not the local nodal error.

In summary, the mechanical behavior and collagen fiber structure of 12 human scleras from diabetic and non-diabetic donors were characterized. Diabetes diagnosis was associated with a larger matrix stiffness and an increased scleral stiffening rate compared with non-diabetic control eyes.