Learning the Structure of Mixed Graphical Models

Abstract

We consider the problem of learning the structure of a pairwise graphical model over continuous and discrete variables. We present a new pairwise model for graphical models with both continuous and discrete variables that is amenable to structure learning. In previous work, authors have considered structure learning of Gaussian graphical models and structure learning of discrete models. Our approach is a natural generalization of these two lines of work to the mixed case. The penalization scheme involves a novel symmetric use of the group-lasso norm and follows naturally from a particular parametrization of the model. Supplementary materials for this paper are available online.

1 Introduction

Many authors have considered the problem of learning the edge structure and parameters of sparse undirected graphical models. We will focus on using the l₁ regularizer to promote sparsity. This line of work has taken two separate paths: one for learning continuous valued data and one for learning discrete valued data. However, typical data sources contain both continuous and discrete variables: population survey data, genomics data, url-click pairs etc. For genomics data, in addition to the gene expression values, we have attributes attached to each sample such as gender, age, ethniticy etc. In this work, we consider learning mixed models with both continuous Gaussian variables and discrete categorical variables.

For only continuous variables, previous work assumes a multivariate Gaussian (Gaussian graphical) model with mean 0 and inverse covariance Θ. Θ is then estimated via the graphical lasso by minimizing the regularized negative log-likelihood l(Θ) + λ ||Θ||₁. Several e cient methods for solving this can be found in Friedman et al. (2008a); Banerjee et al. (2008). Because the graphical lasso problem is computationally challenging, several authors considered methods related to the pseudolikelihood (PL) and nodewise regression (Meinshausen and Bühlmann, 2006; Friedman et al., 2010; Peng et al., 2009). For discrete models, previous work focuses on estimating a pairwise Markov random field of the form $p\left(y\right)\propto \exp {\sum }_{r\le j}{\varphi }_{rj}(y_r,y_i)$, where ϕ_rj are pairwise potentials. The maximum likelihood problem is intractable for models with a moderate to large number of variables (high-dimensional) because it requires evaluating the partition function and its derivatives. Again previous work has focused on the pseudolikelihood approach (Guo et al., 2010; Schmidt, 2010; Schmidt et al., 2008; Höfling and Tibshirani, 2009; Jalali et al., 2011; Lee et al., 2006; Ravikumar et al., 2010).

Our main contribution here is to propose a model that connects the discrete and continuous models previously discussed. The conditional distributions of this model are two widely adopted and well understood models: multiclass logistic regression and Gaussian linear regression. In addition, in the case of only discrete variables, our model is a pairwise Markov random field; in the case of only continuous variables, it is a Gaussian graphical model. Our proposed model leads to a natural scheme for structure learning that generalizes the graphical Lasso. Here the parameters occur as singletons, vectors or blocks, which we penalize using group-lasso norms, in a way that respects the symmetry in the model. Since each parameter block is of different size, we also derive a calibrated weighting scheme to penalize each edge fairly. We also discuss a conditional model (conditional random field) that allows the output variables to be mixed, which can be viewed as a multivariate response regression with mixed output variables. Similar ideas have been used to learn the covariance structure in multivariate response regression with continuous output variables Witten and Tibshirani (2009); Kim et al. (2009); Rothman et al. (2010).

In Section 2, we introduce our new mixed graphical model and discuss previous approaches to modeling mixed data. Section 3 discusses the pseudolikelihood approach to parameter estimation and connections to generalized linear models. Section 4 discusses a natural method to perform structure learning in the mixed model. Section 5 presents the calibrated regularization scheme, Section 6 discusses the consistency of the estimation procedures, and Section 7 discusses two methods for solving the optimization problem. Finally, Section 8 discusses a conditional random field extension and Section 9 presents empirical results on a census population survey dataset and synthetic experiments.

2 Mixed Graphical Model

We propose a pairwise graphical model on continuous and discrete variables. The model is a pairwise Markov random field with density p(x, y; Θ) proportional to

$$\exp \left(\sum _{s=1}^p\sum _{t=1}-\frac{1}{2}{\beta }_{st}{x}_s{x}_t+\sum _{s=1}^p{\alpha }_s{x}_s+\sum _{s=1}^p\sum _{j=1}^q{\rho }_{sj}\left(y_i\right)x_s+\sum _{j=1}^q\sum _{r=1}^q{\varphi }_{rj}(y_r,y_j)\right).$$ (1)

Here x_s denotes the sth of p continuous variables, and y_j the jth of q discrete variables. The joint model is parametrized by Θ = [{β_st}, {α_s}, {ρ_sj}, {ϕ_rj}]. The discrete y_r takes on L_r states. The model parameters are β_st continuous-continuous edge potential, α_s continuous node potential, ρ_sj(y_j) continuous-discrete edge potential, and ϕ_rj(y_r, y_j) discrete-discrete edge potential. ρ_sj(y_j) is a function taking L_j values ρ_sj(1), . . . , ρ_sj(L_j). Similarly, ϕ_rj(y_r, y_j) is a bivariate function taking on L_r × L_j values. Later, we will think of ρ_sj(y_j) as a vector of length L_j and ϕ_rj(y_r, y_j) as a matrix of size L_r × L_j.

The two most important features of this model are:

1. the conditional distributions are given by Gaussian linear regression and multiclass logistic regressions;

2. the model simplifies to a multivariate Gaussian in the case of only continuous variables and simplifies to the usual discrete pairwise Markov random field in the case of only discrete variables.

The conditional distributions of a graphical model are of critical importance. The absence of an edge corresponds to two variables being conditionally independent. The conditional independence can be read o from the conditional distribution of a variable on all others. For example in the multivariate Gaussian model, x_s is conditionally independent of x_t i the partial correlation coefficient is 0. The partial correlation coefficient is also the regression coefficient of x_t in the linear regression of x_s on all other variables. Thus the conditional independence structure is captured by the conditional distributions via the regression coefficient of a variable on all others. Our mixed model has the desirable property that the two type of conditional distributions are simple Gaussian linear regressions and multiclass logistic regressions. This follows from the pairwise property in the joint distribution. In more detail:

1. The conditional distribution of y_r given the rest is multinomial, with probabilities defined by a multiclass logistic regression where the covariates are the other variables x_s and y_\r (denoted collectively by z in the right-hand side):

   $$p(y_r=k\mid y_{\backslash r},x;ϴ)=\frac{\exp \left({\omega }_k^{T}z\right)}{{\sum }_{l=1}^{L_r}\exp \left({\omega }_l^{T}z\right)}=\frac{\exp \left({\omega }_{0k}+{\sum }_j{\omega }_{kj}{z}_j\right)}{{\sum }_{l=1}^{L_r}\exp \left({\omega }_{0l}+{\sum }_j{\omega }_{lj}+z_j\right)}$$ (2)

   Here we use a simplified notation, which we make explicit in Section 3.1. The discrete variables are represented as dummy variables for each state, e.g. $z_j=1[y_u=k]$, and for continuous variables z_s = x_s.
2. The conditional distribution of x_s given the rest is Gaussian, with a mean function defined by a linear regression with predictors x_\s and y_r.

   $$\begin{array}{cc}\hfill E(x_s\mid x_{\backslash s},y_r;ϴ)=& {\omega }^{T}z={\omega }_0+\sum _j{z}_j{\omega }_j\hfill \\ \hfill p(x_s\mid x_{\backslash r},y_r;ϴ)=& \frac{1}{\sqrt{2\pi }{\sigma }_s}\exp \left(-\frac{1}{2{\sigma }_s^2}{(x_s-{\omega }^{T}z)}^2\right).\hfill \end{array}$$ (3)

   As before, the discrete variables are represented as dummy variables for each state $z_j=1[y_u=k]$ and for continuous variables z_s = x_s.

The exact form of the conditional distributions (2) and (3) are given in (11) and (10) in Section 3.1, where the regression parameters w_j are defined in terms of the parameters Θ.

The second important aspect of the mixed model is the two special cases of only continuous and only discrete variables.

1. Continuous variables only. The pairwise mixed model reduces to the familiar multivariate Gaussian parametrized by the symmetric positive-definite inverse covariance matrix B = {β_st and mean μ = B⁻¹α,

   $$p\left(x\right)\propto \exp \left(-\frac{1}{2}{(x-B^{-1}\alpha )}^{T}B(x-B^{-1}\alpha )\right).$$
2. Discrete variables only. The pairwise mixed model reduces to a pairwise discrete (second-order interaction) Markov random field,

   $$p\left(y\right)\propto \exp \left(\sum _{j=1}^q\sum _{r=1}^q{\varphi }_{rj}(y_r,y_j)\right).$$

Although these are the most important aspects, we can characterize the joint distribution further. The conditional distribution of the continuous variables given the discrete follow a multivariate Gaussian distribution, $p(x\mid y)=\mathcal{N}(\mu \left(y\right),B^{-1})$. Each of these Gaussian distributions share the same inverse covariance matrix B but differ in the mean parameter, since all the parameters are pairwise. By standard multivariate Gaussian calculations,

$$p(x\mid y)=\mathcal{N}(B^{-1}\gamma \left(y\right),B^{-1})$$ (4)

$${\left\{\gamma \left(y\right)\right\}}_s={\alpha }_s+\sum _j{\rho }_{sj}\left(y_j\right)$$ (5)

$$p\left(y\right)\propto \exp \left(\sum _{j=1}^q\sum _{r=1}^j{\varphi }_{rj}(y_r,y_j)+\frac{1}{2}\gamma {\left(y\right)}^T{B}^{-1}\gamma \left(y\right)\right)$$ (6)

Thus we see that the continuous variables conditioned on the discrete are multivariate Gaussian with common covariance, but with means that depend on the value of the discrete variables. The means depend additively on the values of the discrete variables since ${\left\{\gamma \left(y\right)\right\}}_s={\sum }_{j=1}^r{\rho }_{sj}\left(y_j\right)$. The marginal p(y) has a known form, so for models with few number of discrete variables we can sample efficiently.

2.1 Related work on mixed graphical models

Lauritzen (1996) proposed a type of mixed graphical model, with the property that conditioned on discrete variables, $p(x\mid y)=\mathcal{N}(\mu \left(y\right),\Sigma \left(y\right))$. The homogeneous mixed graphical model enforces common covariance, Σ(y) ≡ Σ. Thus our proposed model is a special case of Lauritzen's mixed model with the following assumptions: common covariance, additive mean assumptions and the marginal p(y) factorizes as a pairwise discrete Markov random field. With these three assumptions, the full model simplifies to the mixed pairwise model presented. Although the full model is more general, the number of parameters scales exponentially with the number of discrete variables, and the conditional distributions are not as convenient. For each state of the discrete variables there is a mean and covariance. Consider an example with q binary variables and p continuous variables; the full model requires estimates of 2^q mean vectors and covariance matrices in p dimensions. Even if the homogeneous constraint is imposed on Lauritzen's model, there are still 2^q mean vectors for the case of binary discrete variables. The full mixed model is very complex and cannot be easily estimated from data without some additional assumptions. In comparison, the mixed pairwise model has number of parameters O((p + q)²) and allows for a natural regularization scheme which makes it appropriate for high dimensional data.

An alternative to the regularization approach that we take in this paper, is the limited-order correlation hypothesis testing method Tur and Castelo (2012). The authors develop a hypothesis test via likelihood ratios for conditional independence. However, they restrict to the case where the discrete variables are marginally independent so the maximum likelihood estimates are well-defined for p > n.

There is a line of work regarding parameter estimation in undirected mixed models that are decomposable: any path between two discrete variables cannot contain only continuous variables. These models allow for fast exact maximum likelihood estimation through node-wise regressions, but are only applicable when the structure is known and n > p (Edwards, 2000). There is also related work on parameter learning in directed mixed graphical models. Since our primary goal is to learn the graph structure, we forgo exact parameter estimation and use the pseudolikelihood. Similar to the exact maximum likelihood in decomposable models, the pseudolikelihood can be interpreted as node-wise regressions that enforce symmetry.

After we proposed our model¹, the independent work of Cheng et al. (2013) appeared, which considers a more complicated mixed graphical model. Their model includes higher order interaction terms by allowing the covariance of the continuous variables to be a function of the categorical variables y, which results in a larger model similar to Lauritzen's model. This results in a model with O(p²q+q²) parameters, as opposed to O(p²+q²) in our proposed pairwise model. We believe that in the high-dimensional setting where data sparsity is an issue a simpler model is an advantage.

To our knowledge, this work is the first to consider convex optimization procedures for learning the edge structure in mixed graphical models.

3 Parameter Estimation: Maximum Likelihood and Pseudolikelihood

Given samples ${(x_i,y_i)}_{i=1}^n$, we want to find the maximum likelihood estimate of Θ. This can be done by minimizing the negative log-likelihood of the samples:

$$\ell \left(ϴ\right)=-\sum _{i=1}^n\log p(x_i,y_i;ϴ)\text{where}$$ (7)

$$\log p(x,y;ϴ)=\sum _{s=1}^p\sum _{t=1}^p-\frac{1}{2}{\beta }_{st}{x}_s{x}_t+\sum _{s=1}^p{\alpha }_s{x}_s+\sum _{s=1}^p\sum _{j=1}^q{\rho }_{sj}\left(y_j\right)x_s+\sum _{j=1}^q\sum _{r=1}^j{\varphi }_{rj}(y_r,y_j)-\log Z\left(ϴ\right)$$ (8)

The negative log-likelihood is convex, so standard gradient-descent algorithms can be used for computing the maximum likelihood estimates. The major obstacle here is Z(Θ), which involves a high-dimensional integral. Since the pairwise mixed model includes both the discrete and continuous models as special cases, maximum likelihood estimation is at least as difficult as the two special cases, the first of which is a well-known computationally intractable problem. We defer the discussion of maximum likelihood estimation to the supplementary material.

3.1 Pseudolikelihood

The pseudolikelihood method Besag (1975) is a computationally efficient and consistent estimator formed by products of all the conditional distributions:

$$\tilde{\ell }(ϴ\mid x,y)=-\sum _{s\backslash 1}^p\log p(x_s\mid x_{=s},y;ϴ)-\sum _{r=1}^q\log p(y_r\mid x,y_{\backslash r};ϴ)$$ (9)

The conditional distributions p(x_s|x_\s, y; θ) and p(y_r = k|y_\r,, x; θ) take on the familiar form of linear Gaussian and (multiclass) logistic regression, as we pointed out in (2) and (3). Here are the details:

• The conditional distribution of a continuous variable x_s is Gaussian with a linear regression model for the mean, and unknown variance.

  $$p(x_s\mid x_{\backslash s},y;ϴ)=\frac{\sqrt{{\beta }_{ss}}}{\sqrt{2\pi }}\exp \left(\frac{-{\beta }_{ss}}{2}{\left(\frac{{\alpha }_s+{\sum }_j{\rho }_{sj}\left(y_j\right)-{\sum }_{t\ne s}{\beta }_{st}{x}_t}{{\beta }_{ss}}-x_s\right)}^2\right)$$ (10)
• The conditional distribution of a discrete variable y_r with L_r states is a multinomial distribution, as used in (multiclass) logistic regression. Whenever a discrete variable is a predictor, each of its levels contribute an additive effect; continuous variables contribute linear effects.

  $$p(y_r\mid y_{{\backslash }_r,},x;ϴ)=\frac{\exp \left({\sum }_s{\rho }_{sr}\left(y_r\right)x_s+{\varphi }_{rr}^{}(y_r,y_r)+{\sum }_{j\ne r}{\varphi }_{rj}(y_r,y_j)\right)}{{\sum }_{l=1}^{L_r}\exp \left({\sum }_s{\rho }_{sr}\left(l\right)x_s+{\varphi }_{rr}(l,l)+{\sum }_{j\ne r}{\varphi }_{rj}(l,y_j)\right)}$$ (11)

  Taking the negative log of both gives us

  $$-\log p(x_s\mid x_{\backslash s},y;ϴ)=-\frac{1}{2}\log {\beta }_{ss}=\frac{{\beta }_{ss}}{2}{\left(\frac{{\alpha }_s}{{\beta }_{ss}}+\sum _j\frac{{\rho }_{sj}\left(y_j\right)}{{\beta }_{ss}}-\sum _{t\ne s}\frac{{\beta }_{st}}{{\beta }_{ss}}{x}_t-x_s\right)}^2$$ (12)

  $$-\log p(y_r\mid y_{{\backslash }_r,},x;ϴ)=-\log \frac{\exp \left({\sum }_s{\rho }_{sr}\left(y_r\right)x_s+{\varphi }_{rr}^{}(y_r,y_r)+{\sum }_{j\ne r}{\varphi }_{rj}(y_r,y_j)\right)}{{\sum }_{l=1}^{L_r}\exp \left({\sum }_s{\rho }_{sr}\left(l\right)x_s+{\varphi }_{rr}(l,l)+{\sum }_{j\ne r}{\varphi }_{rj}(l,y_j)\right)}$$ (13)

  A generic parameter block, θ_uv, corresponding to an edge (u, v) appears twice in the pseudolikelihood, once for each of the conditional distributions p(z_u|z_v) and p(z_v|z_u).

Proposition 1. The negative log pseudolikelihood in (9) is jointly convex in all the parameters {β_ss, β_st, α_s, ϕ_rj, ρ_sj} over the region β_ss > 0.

We prove Proposition 1 in the Supplementary Materials.

3.2 Separate node-wise regression

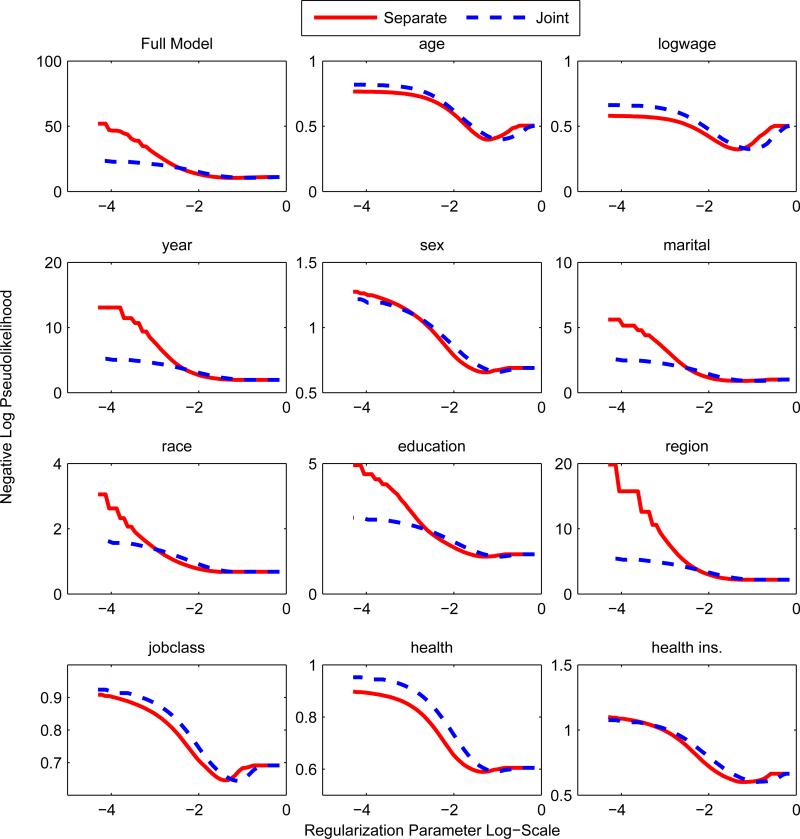
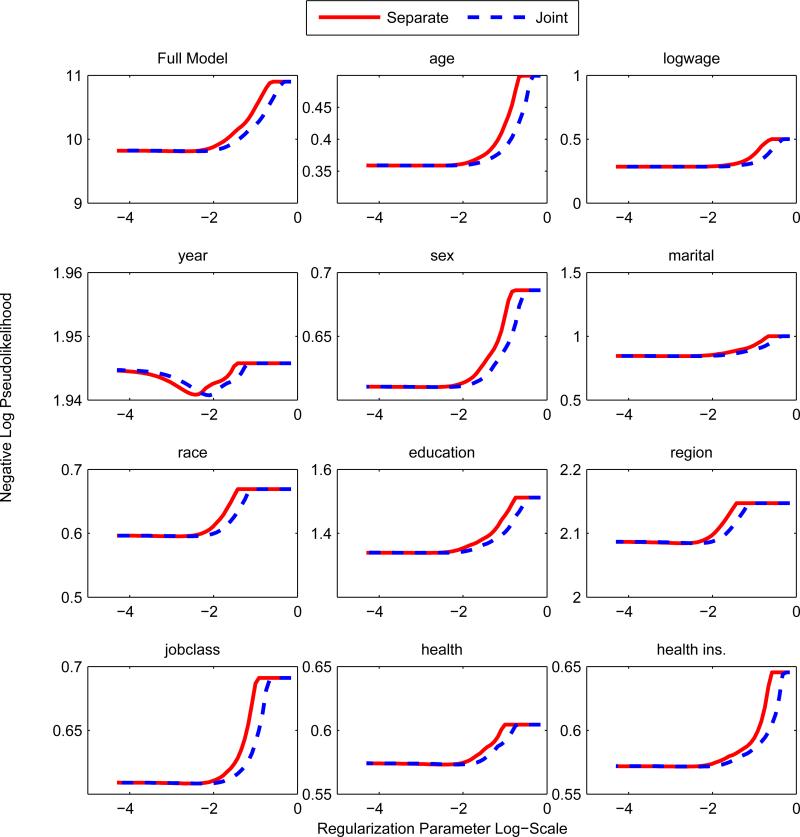
A simple approach to parameter estimation is via separate node-wise regressions; a generalized linear model is used to estimate p(z_s|z_\s) for each s. Separate regressions were used in Meinshausen and Bühlmann (2006) for the Gaussian graphical model and Ravikumar et al. (2010) for the Ising model. The method can be thought of as an asymmetric form of the pseudolikelihood since the pseudolikelihood enforces that the parameters are shared across the conditionals. Thus the number of parameters estimated in the separate regression is approximately double that of the pseudolikelihood, so we expect that the pseudolikelihood outperforms at low sample sizes and low regularization regimes. The node-wise regression was used as our baseline method since it is straightforward to extend it to the mixed model. As we predicted, the pseudolikelihood or joint procedure outperforms separate regressions; see top left box of Figures 5 and 6. Liu and Ihler (2012, 2011) confirm that the separate regressions are outperformed by pseudolikelihood in numerous synthetic settings.

Figure 5.

Separate Regression vs Pseudolikelihood n = 100. y-axis is the appropriate regression loss for the response variable. For low levels of regularization and at small training sizes, the pseudolikelihood seems to overfit less; this may be due to a global regularization effect from fitting the joint distribution as opposed to separate regressions.

Figure 6.

Separate Regression vs Pseudolikelihood n = 10, 000. y-axis is the appropriate regression loss for the response variable. At large sample sizes, separate regressions and pseudolikelihood perform very similarly. This is expected since this is nearing the asymptotic regime.

Concurrent work of Yang et al. (2012, 2013) extend the separate node-wise regression model from the special cases of Gaussian and categorical regressions to generalized linear models, where the univariate conditional distribution of each node p(x_s|x_\s) is specified by a generalized linear model (e.g. Poisson, categorical, Gaussian). By specifying the conditional distributions, Besag (1974) show that the joint distribution is also specified. Thus another way to justify our mixed model is to define the conditionals of a continuous variable as Gaussian linear regression and the conditionals of a categorical variable as multiple logistic regression and use the results in Besag (1974) to arrive at the joint distribution in (1). However, the neighborhood selection algorithm in Yang et al. (2012, 2013) is restricted to models of the form p(x) ∝ exp(Σ_s θ_sx_s + Σ_s,t θ_stx_sx_t + Σ_s C(x_s)). In particular, this procedure cannot be applied to edge selection in our pairwise mixed model in (1) or the categorical model in (2) with greater than 2 states. Our baseline method of separate regressions is closely related to the neighborhood selection algorithm they proposed; the baseline can be considered as a generalization of Yang et al. (2012, 2013) to allow for more general pairwise interactions with the appropriate regularization to select edges. Unfortunately, the theoretical results in Yang et al. (2012, 2013) do not apply to the baseline nodewise regression method, nor the joint pseudolikelihood.

4 Conditional Independence and Penalty Terms

In this section, we show how to incorporate edge selection into the maximum likelihood or pseudolikelihood procedures. In the graphical representation of probability distributions, the absence of an edge e = (u, v) corresponds to a conditional independency statement that variables x_u and x_v are conditionally independent given all other variables (Koller and Friedman, 2009). We would like to maximize the likelihood subject to a penalization on the number of edges since this results in a sparse graphical model. In the pairwise mixed model, there are 3 type of edges

1. β_st is a scalar that corresponds to an edge from x_s to x_t. β_st = 0 implies x_s and x_t are conditionally independent given all other variables. This parameter is in two conditional distributions, corresponding to either x_s or x_t is the response variable, p(x_s|x_\s, y; Θ) and p(x_t|x_\t, y; Θ).

2. ρ_sj is a vector of length L_j. If ρ_sj(y_j) = 0 for all values of y_j, then y_j and x_s are conditionally independent given all other variables. This parameter is in two conditional distributions, corresponding to either x_s or y_j being the response variable: p(x_s|x_\s, y; Θ) and p(y_j|x, y_\j; Θ).

3. ϕ_rj is a matrix of size L_r × L_j. If ϕ_rj(y_r, y_j) = 0 for all values of y_r and y_j, then y_r and y_j are conditionally independent given all other variables. This parameter is in two conditional distributions, corresponding to either y_r or y_j being the response variable, p(y_r|x, y_\r; Θ) and p(y_j|x, y_\j; Θ).

For conditional independencies that involve discrete variables, the absence of that edge requires that the entire matrix ϕ_rj or vector ρ_sj is 0.² The form of the pairwise mixed model motivates the following regularized optimization problem

$$\underset{ϴ}{\mathrm{minimize}}{\ell }_{\lambda }\left(ϴ\right)=\ell \left(ϴ\right)=\lambda \left(\sum _{s<t}1[{\beta }_{st}\ne 0]+\sum _{sj}1[{\rho }_{sj}\not\equiv 0]+\sum _{r<j}1[{\varphi }_{rj}\not\equiv 0]\right).$$ (14)

All parameters that correspond to the same edge are grouped in the same indicator function. This problem is non-convex, so we replace the l₀ sparsity and group sparsity penalties with the appropriate convex relaxations. For scalars, we use the absolute value (l₁ norm), for vectors we use the l₂ norm, and for matrices we use the Frobenius norm. This choice corresponds to the standard relaxation from group l₀ to group l₁/l₂ (group lasso) norm (Bach et al., 2011; Yuan and Lin, 2006),

$$\underset{ϴ}{\mathrm{minimize}}{\ell }_{\lambda }\left(ϴ\right)=\ell \left(ϴ\right)+\lambda \left(\sum _{s=1}^p\sum _{t=1}^{s-1}\mid {\beta }_{st}\mid +\sum _{s=1}^p\sum _{j=1}^q{\Vert {\rho }_{sj}\Vert }_2+\sum _{j=1}^q\sum _{r=1}^{j-1}{\Vert {\varphi }_{rj}\Vert }_F\right).$$ (15)

5 Calibrated regularizers

In (15) each of the group penalties are treated as equals, irrespective of the size of the group. We suggest a calibration or weighting scheme to balance the load in a more equitable way. We introduce weights for each group of parameters and show how to choose the weights such that each parameter set is treated equally under p_F , the fully-factorized independence model.³

$$\underset{ϴ}{\mathrm{minimize}}\ell \left(ϴ\right)+\lambda \left(\sum _{t=1}^p\sum _{t=1}^{s-1}{w}_{st}\mid {\beta }_{st}\mid +\sum _{s=1}^p\sum _{j=1}^q{w}_{sj}{\Vert {\rho }_{sj}\Vert }_2+\sum _{j=1}^q\sum _{r=1}^{j-1}{w}_{rj}{\Vert {\varphi }_{rj}\Vert }_F\right)$$ (16)

Based on the KKT conditions (Friedman et al., 2007), the parameter group θ_g is non-zero if

$$\Vert \frac{\partial \ell }{\partial {\theta }_g}\Vert >\lambda w_g$$

where θ_g and w_g represents one of the parameter groups and its corresponding weight. Now $\frac{\partial \ell }{\partial {\theta }_g}$ can be viewed as a generalized residual, and for different groups these are different dimensions—e.g. scalar/vector/matrix. So even under the independence model (when all terms should be zero), one might expect some terms $\Vert \frac{\partial \ell }{\partial {\theta }_g}\Vert$ to have a better random non-zero of being non-zero (for example, those of bigger dimensions). Thus for all parameters to be on equal footing, we would like to choose the weights w_g such that

$$w_g=E_{p_F}\Vert \frac{\partial \ell }{\partial {\theta }_g}\Vert \times \text{constant},$$ (17)

where p_F is the fully factorized (independence) model. We will refer to these as the exact weights. We do not have a closed form expression for computing them, but they can be easily estimated by a simple null-model simulation. We also propose an approximation that can be computed exactly. It is straightforward to compute $E_{p_F}{\Vert \frac{\partial \ell }{\partial {\theta }_g}\Vert }^2$ in closed form, which leads to approximate weights

$$w_g\propto \sqrt{E_{p_F}{\Vert \frac{\partial \ell }{\partial {\theta }_g}\Vert }^2}$$ (18)

In the supplementary material, we show that for the three types of edges this leads to the expressions

$$\begin{array}{cc}\hfill w_{st}=& {\sigma }_s{\sigma }_t,\hfill \\ \hfill w_{sj}=& {\sigma }_s\sqrt{\sum _a{p}_a(1-p_a)},\text{and}\hfill \\ \hfill w_{rj}=& \sqrt{\sum _a{p}_a(1-p_a)\sum _b{q}_b(1-q_b)},\hfill \end{array}$$ (19)

where σ_s is the standard deviation of the continuous variable x_s, p_a = Pr(y_r = a) and q_b = Pr(y_j = b). For all 3 types of parameters, the weight has the form of $w_{uv}=\mathbf{tr}\left(\mathbf{cov}\left(z_u\right)\right)\mathbf{tr}\left(\mathbf{cov}\left(z_v\right)\right)$, where z represents a generic variable and cov(z) is the variance-covariance matrix of z.

We conducted a small simulation study to show that calibration is needed. Consider a model with 4 independent variables: 2 continuous with variance 10 and 1, and 2 discrete variables with 10 and 2 levels. There are 6 candidate edges in this model and from row 1 of Table 1 we can see the sizes of the gradients are different. In fact, the ratio of the largest gradient to the smallest gradient is greater than 4. The edges ρ₁₁ and ρ₁₂ involving the first continuous variable with variance 10 have larger edge weights than the corresponding edges, ρ₂₁ and ρ₂₂ involving the second continuous variable with variance 1. Similarly, the edges involving the first discrete variable with 10 levels are larger than the edges involving the second discrete variable with 2 levels. This reflects our intuition that larger variance and longer vectors will have larger norm.

Table 1.

Penalty weights in a six-edge model.

	${\Vert \frac{\partial \ell }{\partial {\varphi }_{12}}\Vert }_F$	${\Vert \frac{\partial \ell }{\partial {\rho }_{11}}\Vert }_2$	${\Vert \frac{\partial \ell }{\partial {\rho }_{21}}\Vert }_2$	${\Vert \frac{\partial \ell }{\partial {\rho }_{12}}\Vert }_2$	${\Vert \frac{\partial \ell }{\partial {\rho }_{22}}\Vert }_2$	$\mid \frac{\partial \ell }{\partial {\beta }_{12}}\mid$
Exact weights wg (17)	0.18	0.63	0.19	0.47	0.15	0.53
Approximate weights wg (19)	0.13	0.59	0.18	0.44	0.13	0.62

Row 1 shows the exact weights w_g computed via (17) using Monte Carlo simulation. Row 2 shows the approximate weights computed via (19). Note that the weights are far from uniform, and the approximate weights are close to the exact weights.

The approximate weights from Equation (19) are a very good approximation to ||∇l||. Since the weights are only defined up to a proportionality constant, the cosine similarity is an appropriate measure of the quality of approximation. For this simulation, the cosine similarity is

$$sim(w,\Vert \nabla \ell \Vert )=.993,$$

which is extremely close to 1.

Using the weights from Table 1, we conducted a second simulation to record which edge would enter first when the four variables are independent. The results are shown in Table 2. Both exact and approximate calibration perform much better than no calibration, but neither deliver the ideal 1/6th probabilities one might desire in a situation like this. Of course, calibrating to the expectations of the gradient does not guarantee equal entry probability, but it brings them much closer.

Table 2.

Fraction of times an edge is the first selected by the group lasso regularizer, based on 1000 simulation runs.

	ϕ 12	ρ 11	ρ 21	ρ 12	ρ 22	β 12
No Calibration wg = 1	0.000	0.487	0.000	0.163	0.000	0.350
Exact wg (17)	0.101	0.092	0.097	0.249	0.227	0.234
Approximate wg (19)	0.144	0.138	0.134	0.196	0.190	0.198

Ideally each edge should be first 1/6th of the time (0.167), with a standard error of 0.012. The group lasso with equal weights (first row) is highly unbalanced. Using the exact weights from (17) is quite good (second row), while the approximate weighing scheme of (19) (third row) appears to perform the best.

The exact weights do not have simple closed-form expressions, but they can be easily computed via Monte Carlo. This can be done by simulating independent Gaussians and multinomials with the appropriate marginal variance σ_s and marginal probabilities p_a, then approximating the expectation in (17) by an average. The computational cost of this procedure is negligible compared to fitting the mixed model, so in practice either the exact or approximate weights can be used.

6 Model Selection Consistency

In this section, we study the model selection consistency, whether the correct edge set is selected and the parameter estimates are close to the truth, of the pseudolikelihood and maximum likelihood estimators. Consistency can be established using the framework first developed in Ravikumar et al. (2010) and later extended to general m-estimators by Lee et al. (2013). Instead of stating the full results and proofs, we will illustrate the type of theorems that can be shown and defer the rigorous statements to the Supplementary Material.

First, we define some notation. Recall that Θ is the vector of parameters being estimated {β_ss, β_st, α_s, ϕ_rj, ρ_sj}, Θ* be the true parameters that estimated the model, and Q = ∇²l(Θ*). Both maximum likelihood and pseudolikelihood estimation procedures can be written as a convex optimization problem of the form

$$\mathrm{minimize}\ell \left(ϴ\right)+\lambda \sum _{g\in G}{\Vert {ϴ}_g\Vert }_2$$ (20)

where l(θ) = {l_ML, l_PL} is one of the two log-likelihoods. The regularizer

$$\sum _{g\in G}\Vert {ϴ}_g\Vert =\lambda \left(\sum _{s=1}^p\sum _{t=1}^{s-1}\mid {\beta }_{st}\mid +\sum _{s=1}^p\sum _{j=1}^q{\Vert {\rho }_{sj}\Vert }_2+\sum _{j=1}^q\sum _{r=1}^{j-1}{\Vert {\varphi }_{rj}\Vert }_F\right).$$

The set G indexes the edges _st, ρ_sj, and ϕ_rj, and Θ_g is one of the three types of edges. Let A and I represent the active and inactive groups in Θ, so ${ϴ}_g^{\star }\ne 0$ for any g ∈ A and ${ϴ}_g^{\star }=0$ for any g ∈ I.

Let $\widehat{ϴ}$ be the minimizer to Equation (20). Then $\widehat{ϴ}$ satisfies,

1. ${\Vert \widehat{ϴ}-{ϴ}^{\star }\Vert }_2\le C\sqrt{\frac{\mid A\mid \log \mid G\mid }{n}}$

2. ${\widehat{ϴ}}_g=0\text{for}g\in I$ The exact statement of the theorem is given in the Supplementary Material.

7 Optimization Algorithms

In this section, we discuss two algorithms for solving (15): the proximal gradient and the proximal newton methods. This is a convex optimization problem that decomposes into the form f(x) + g(x), where f is smooth and convex and g is convex but possibly non-smooth. In our case f is the negative log-likelihood or negative log-pseudolikelihood and g are the group sparsity penalties.

Block coordinate descent is a frequently used method when the non-smooth function g is the l₁ or group l₁. It is especially easy to apply when the function f is quadratic, since each block coordinate update can be solved in closed form for many different non-smooth g (Friedman et al., 2007). The smooth f in our particular case is not quadratic, so each block update cannot be solved in closed form. However in certain problems (sparse inverse covariance), the update can be approximately solved by using an appropriate inner optimization routine (Friedman et al., 2008b).

7.1 Proximal Gradient

Problems of this form are well-suited for the proximal gradient and accelerated proximal gradient algorithms as long as the proximal operator of g can be computed (Combettes and Pesquet, 2011; Beck and Teboulle, 2010)

$$pro{x}_t\left(x\right)=\underset{u}{\mathrm{argmin}}\frac{1}{2t}{\Vert x-u\Vert }^2+g\left(u\right)$$ (21)

For the sum of l₂ group sparsity penalties considered, the proximal operator takes the familiar form of soft-thresholding and group soft-thresholding (Bach et al., 2011). Since the groups are non-overlapping, the proximal operator simplifies to scalar soft-thresholding for β_st and group soft-thresholding for ρ_sj and ϕ_rj.

The class of proximal gradient and accelerated proximal gradient algorithms is directly applicable to our problem. These algorithms work by solving a first-order model at the current iterate x_k

$$\underset{u}{\mathrm{argmin}}f\left(x_k\right)+\nabla f{\left(x_k\right)}^T(u-x_k)+\frac{1}{2t}{\Vert u-x_k\Vert }^2+g\left(u\right)$$ (22)

$$=\underset{u}{\mathrm{argmin}}\frac{1}{2t}{\Vert u-(x_k-t\nabla f\left(x_k\right))\Vert }^2+g\left(u\right)$$ (23)

$$=pro{x}_t(x_k-t\nabla f\left(x_k\right))$$ (24)

$$\underset{u}{\mathrm{argmin}}f\left(x_k\right)+\nabla f{\left(x_k\right)}^T(u-x_k)+\frac{1}{2t}{(u-x_k)}^{T}H(u-x_k)+g\left(u\right)$$ (25)

The proximal gradient iteration is given by x_k+1 = prox_t (x_k − t∇f(x_k)) where t is determined by line search. The theoretical convergence rates and properties of the proximal gradient algorithm and its accelerated variants are well-established (Beck and Teboulle, 2010). The accelerated proximal gradient method achieves linear convergence rate of O(c^k) when the objective is strongly convex and the sublinear rate O(1/k²) for non-strongly convex problems.

The TFOCS framework (Becker et al., 2011) is a package that allows us to experiment with 6 different variants of the accelerated proximal gradient algorithm. The TFOCS authors found that the Auslender-Teboulle algorithm exhibited less oscillatory behavior, and proximal gradient experiments in the next section were done using the Auslender-Teboulle implementation in TFOCS.

7.2 Proximal Newton Algorithms

The class of proximal Newton algorithms is a 2nd order analog of the proximal gradient algorithms with a quadratic convergence rate (Lee et al., 2012; Schmidt, 2010; Schmidt et al., 2011). It attempts to incorporate 2nd order information about the smooth function f into the model function. At each iteration, it minimizes a quadratic model centered at x_k

$$=\underset{u}{\mathrm{argmin}}\frac{1}{2t}{(u-x_k+t{H}^{-1}\nabla f\left(x_k\right))}^{T}H(u-x_k+t{H}^{-1}\nabla f\left(x_k\right))+g\left(u\right)$$ (26)

$$=\underset{u}{\mathrm{argmin}}\frac{1}{2t}{\Vert u-(x_k-t{H}^{-1}\nabla f\left(x_k\right))\Vert }_H^2+g\left(u\right)$$ (27)

$$≔Hpro{x}_t(x_k-t{H}^{-1}\nabla f\left(x_k\right))\text{where}H={\nabla }^{2}f\left(x_k\right)$$ (28)

$$f(x_k+t{p}_k)+g(x_k+t{p}_k)\le f\left(x_k\right)+g\left(x_k\right)-\frac{t\alpha }{2}{\Vert p_k\Vert }^2$$

The Hprox operator is analogous to the proximal operator, but in the ||·||_H-norm. It simplifies

Algorithm 1.

Proximal Newton

repeat

Solve subproblem $p_k=Hpro{x}_t(x_k-t{H}_k^{-1}\nabla f\left(x_k\right))-x_k$ using TFOCS.

Find t to satisfy Armijo line search condition with parameter α

$f(x_k+t{p}_k)+g(x_k+t{p}_k)\le f\left(x_k\right)+g\left(x_k\right)-\frac{t\alpha }{2}{\Vert p_k\Vert }^2$

Set xk+1 = xk + tpk

k = k + 1

until $\frac{\Vert x_k-x_{k+1}\Vert }{\Vert x_k\Vert }<tol$

to the proximal operator if H = I, but in the general case of positive definite H there is no closed-form solution for many common non-smooth g(x) (including l₁ and group l₁). However if the proximal operator of g is available, each of these sub-problems can be solved efficiently with proximal gradient. In the case of separable g, coordinate descent is also applicable. Fast methods for solving the subproblem Hprox_t(x_k − tH⁻¹∇rf(x_k)) include coordinate descent methods, proximal gradient methods, or Barzilai-Borwein (Friedman et al., 2007; Combettes and Pesquet, 2011; Beck and Teboulle, 2010; Wright et al., 2009). The proximal Newton framework allows us to bootstrap many previously developed solvers to the case of arbitrary loss function f.

Theoretical analysis in Lee et al. (2012) suggests that proximal Newton methods generally require fewer outer iterations (evaluations of Hprox) than first-order methods while providing higher accuracy because they incorporate 2nd order information. We have confirmed empirically that the proximal Newton methods are faster when n is very large or the gradient is expensive to compute (e.g. maximum likelihood estimation). Since the objective is quadratic, coordinate descent is also applicable to the subproblems. The hessian matrix H can be replaced by a quasi-newton approximation such as BFGS/L-BFGS/SR1. In our implementation, we use the PNOPT implementation (Lee et al., 2012).

7.3 Path Algorithm

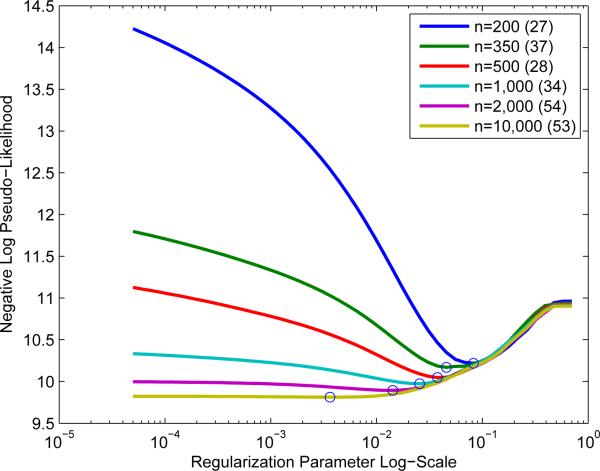
Frequently in machine learning and statistics, the regularization parameter λ is heavily dependent on the dataset. λ is generally chosen via cross-validation or holdout set performance, so it is convenient to provide solutions over an interval of [λ_min, λ_max]. We start the algorithm at λ₁ = λ_max and solve, using the previous solution as warm start, for λ₂ > . . . > λ_min. We find that this reduces the cost of fitting an entire path of solutions (See Figure 4). λ_max can be chosen as the smallest value such that all parameters are 0 by using the KKT equations (Friedman et al., 2007).

Figure 4.

Model selection under different training set sizes. Circle denotes the lowest test set negative log pseudolikelihood and the number in parentheses is the number of edges in that model at the lowest test negative log pseudolikelihood. The saturated model has 55 edges.

8 Conditional Model

In addition to the variables we would like to model, there are often additional features or covariates that affect the dependence structure of the variables. For example in genomic data, in addition to expression values, we have attributes associated to each subject such as gender, age and ethnicity. These additional attributes affect the dependence of the expression values, so we can build a conditional model that uses the additional attributes as features. In this section, we show how to augment the pairwise mixed model with features.

Conditional models only model the conditional distribution p(z|f), as opposed to the joint distribution p(z, f), where z are the variables of interest to the prediction task and f are features. These models are frequently used in practice Lafferty et al. (2001).

In addition to observing x and y, we observe features f and we build a graphical model for the conditional distribution p(x, y|f). Consider a full pairwise model p(x, y, f) of the form (1). We then choose to only model the joint distribution over only the variables x and y to give us p(x, y|f) which is of the form

$$p(x,y\mid f;ϴ)=\frac{1}{Z(ϴ\mid f)}\exp \left(\sum _{s=1}^p\sum _{t=1}^p-\frac{1}{2}{\beta }_{st}{x}_s{x}_t+\sum _{s=1}^p{\alpha }_s{x}_s+\sum _{s=1}^p\sum _{j=1}^q{\rho }_{sj}\left(y_j\right)x_s+\sum _{j=1}^q\sum _{r=1}^j{\varphi }_{rj}(y_r,y_j)+\sum _{l=1}^F\sum _{s=1}^p{\gamma }_{ls}{x}_s{f}_l+\sum _{l=1}^F\sum _{r=1}^q{\eta }_{lr}\left(y_r\right)f_l\right)$$ (29)

We can also consider a more general model where each pairwise edge potential depends on the features

$$p(x,y\mid f;ϴ)=\frac{1}{Z(ϴ\mid f)}\exp \left(\sum _{s=1}^p\sum _{t=1}^p-\frac{1}{2}{\beta }_{st}\left(f\right)x_s{x}_t+\sum _{s=1}^p{\alpha }_s\left(f\right)x_s+\sum _{s=1}^p\sum _{j=1}^q{\rho }_{sj}(y_j,f)x_s+\sum _{j=1}^q\sum _{r=1}^j{\varphi }_{rj}(y_r,y_j,f)\right)$$ (30)

(29) is a special case of this where only the node potentials depend on features and the pairwise potentials are independent of feature values. The specific parametrized form we consider is ϕ_rj(y_r, y_j, f) ≡ ϕ_rj(y_r, y_j) for r ≠ j, ρ_sj(y_j, f) ≡ ρ_sj(y_j), and β_st(f) = β_st. The node potentials depend linearly on the feature values, ${\alpha }_s\left(f\right)={\alpha }_s+{\sum }_{l=1}^F{\gamma }_{ls}{x}_s{f}_l$, and ϕ_rr(y_r, y_r, f) = ϕ_rr(y_r, y_r) + Σ_l η_lr(y_r).

9 Experimental Results

We present experimental results on synthetic data, survey data and on a conditional model.

9.1 Synthetic Experiments

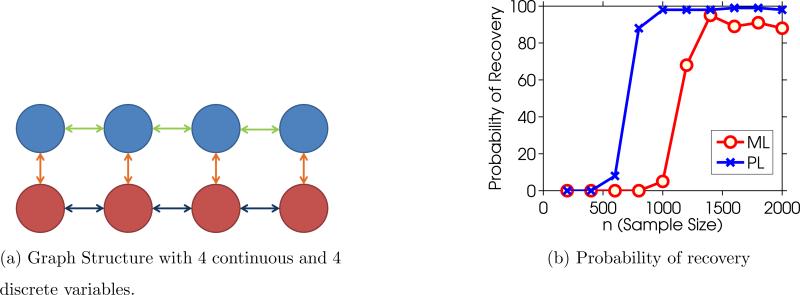
In the synthetic experiment, the training points are sampled from a true model with 10 continuous variables and 10 binary variables. The edge structure is shown in Figure 2a. λ is chosen proportional to $\sqrt{\frac{\log (p+q)}{n}}$ as suggested by the theoretical results in Section 6. We experimented with 3 values $\lambda =\{1,5,10\}\sqrt{\frac{\log (p+q)}{n}}$ and chose $\lambda =5\sqrt{\frac{\log (p+q)}{n}}$ so that the true edge set was recovered by the algorithm for the sample size n = 2000. We see from the experimental results that recovery of the correct edge set undergoes a sharp phase transition, as expected. With n = 1000 samples, the pseudolikelihood is recovering the correct edge set with probability nearly 1. The maximum likelihood was performed using an exact evaluation of the gradient and log-partition. The poor performance of the maximum likelihood estimator is explained by the maximum likelihood objective violating the irrepresentable condition; a similar example is discussed in (Ravikumar et al., 2010, Section 3.1.1), where the maximum likelihood is not irrepresentable, yet the neighborhood selection procedure is. The phase transition experiments were done using the proximal Newton algorithm discussed in Section 7.2.

Figure 2.

Figure 2a shows the graph used in the synthetic experiments for p = q = 4; the experiment actually used p=10 and q=10. Blue nodes are continuous variables, red nodes are binary variables and the orange, green and dark blue lines represent the 3 types of edges. Figure 2b is a plot of the probability of correct edge recovery, meaning every true edge is selected and no non-edge is selected, at a given sample size using Maximum Likelihood and Pseudolikelihood. Results are averaged over 100 trials.

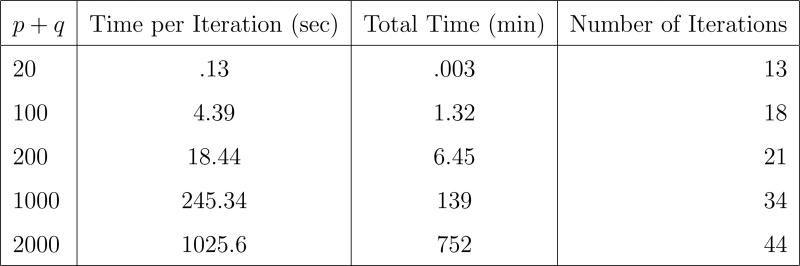
We also run the proximal Newton algorithm for a sequence of instances with p = q = 10, 50, 100, 500, 1000 and n = 500. The largest instance has 2000 variables and takes 12.5 hours to complete. The timing results are summarized in Figure 3.

Figure 3.

Timing experiments for various instances of the graph in Figure 2a. The number of variables range from 20 to 2000 with n = 500.

9.2 Survey Experiments

The census survey dataset we consider consists of 11 variables, of which 2 are continuous and 9 are discrete: age (continuous), log-wage (continuous), year(7 states), sex(2 states),marital status (5 states), race(4 states), education level (5 states), geographic region(9 states), job class (2 states), health (2 states), and health insurance (2 states). The dataset was assembled by Steve Miller of OpenBI.com from the March 2011 Supplement to Current Population Survey data. All the evaluations are done using a holdout test set of size 100, 000 for the survey experiments. The regularization parameter λ is varied over the interval [5 × 10⁻⁵, 0.7] at 50 points equispaced on log-scale for all experiments. In practice, λ can be chosen to minimize the holdout log pseudolikelihood.

9.2.1 Model Selection

In Figure 4, we study the model selection performance of learning a graphical model over the 11 variables under different training samples sizes. We see that as the sample size increases, the optimal model is increasingly dense, and less regularization is needed.

9.2.2 Comparing against Separate Regressions

A sensible baseline method to compare against is a separate regression algorithm. This algorithm fits a linear Gaussian or (multiclass) logistic regression of each variable conditioned on the rest. We can evaluate the performance of the pseudolikelihood by evaluating − log p(x_s|x_\s, y) for linear regression and − log p(y_r|y_\r, x) for (multiclass) logistic regression. Since regression is directly optimizing this loss function, it is expected to do better. The pseudolikelihood objective is similar, but has half the number of parameters as the separate regressions since the coefficients are shared between two of the conditional likelihoods. From Figures 5 and 6, we can see that the pseudolikelihood performs very similarly to the separate regressions and sometimes even outperforms regression. The benefit of the pseudolikelihood is that we have learned parameters of the joint distribution p(x, y) and not just of the conditionals p(x_s|y, x_\s). On the test dataset, we can compute quantities such as conditionals over arbitrary sets of variables p(y_A, x_B|y_A^C, x_B^C ) and marginals p(x_A, y_B) (Koller and Friedman, 2009). This would not be possible using the separate regressions.

9.2.3 Conditional Model

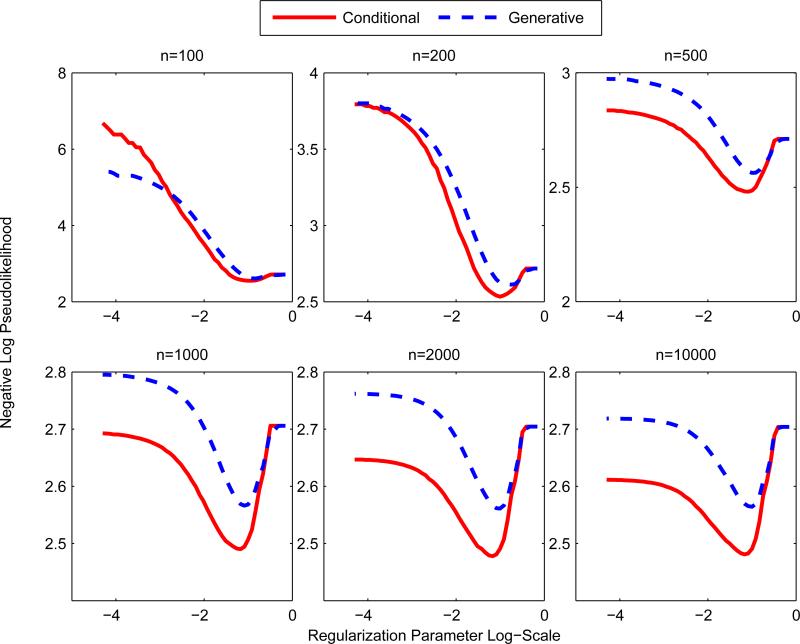
Using the conditional model (29), we model only the 3 variables logwage, education(5) and jobclass(2). The other 8 variables are only used as features. The conditional model is then trained using the pseudolikelihood. We compare against the generative model that learns a joint distribution on all 11 variables. From Figure 7, we see that the conditional model outperforms the generative model, except at small sample sizes. This is expected since the conditional distribution models less variables. At very small sample sizes and small λ, the generative model outperforms the conditional model. This is likely because generative models converge faster (with less samples) than discriminative models to its optimum.

Figure 7.

Conditional Model vs Generative Model at various sample sizes. y-axis is test set performance is evaluated on negative log pseudolikelihood of the conditional model. The conditional model outperforms the full generative model at except the smallest sample size n = 100.

9.2.4 Maximum Likelihood vs Pseudolikelihood

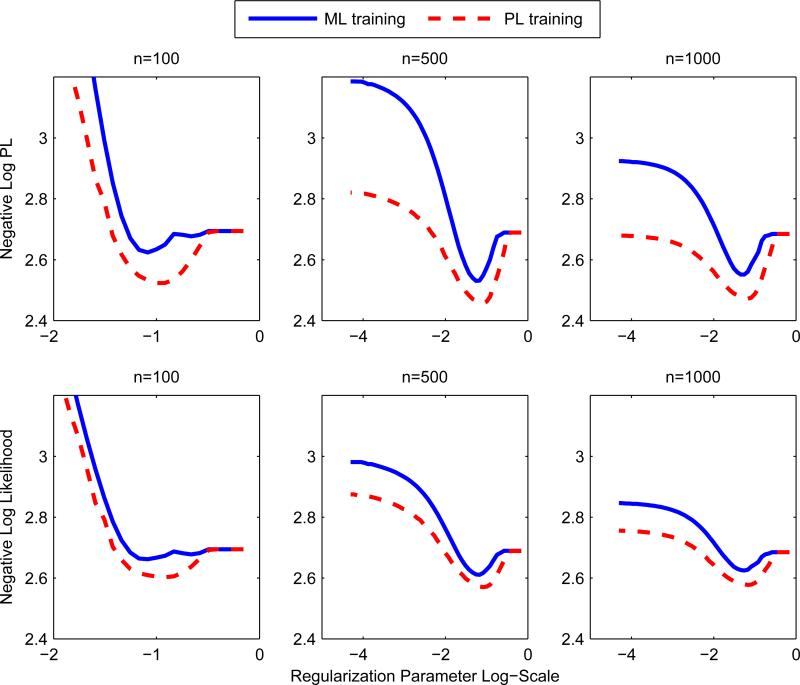
The maximum likelihood estimates are computable for very small models such as the conditional model previously studied. The pseudolikelihood was originally motivated as an approximation to the likelihood that is computationally tractable. We compare the maximum likelihood and maximum pseudolikelihood on two different evaluation criteria: the negative log likelihood and negative log pseudolikelihood. In Figure 8, we find that the pseudolikeli-hood outperforms maximum likelihood under both the negative log likelihood and negative log pseudolikelihood. We would expect that the pseudolikelihood trained model does better on the pseudolikelihood evaluation and maximum likelihood trained model does better on the likelihood evaluation. However, we found that the pseudolikelihood trained model outperformed the maximum likelihood trained model on both evaluation criteria. Although asymptotic theory suggests that maximum likelihood is more efficient than the pseudolikeli-hood, this analysis is applicable because of the finite sample regime and misspecified model. See Liang and Jordan (2008) for asymptotic analysis of pseudolikelihood and maximum likelihood under a well-specified model. We also observed the pseudolikelihood slightly outperforming the maximum likelihood in the synthetic experiment of Figure 2b.

Figure 8.

Maximum Likelihood vs Pseudolikelihood. y-axis for top row is the negative log pseudolikelihood. y-axis for bottom row is the negative log likelihood. Pseudolikelihood outperforms maximum likelihood across all the experiments.

10 Conclusion

This work proposes a new pairwise mixed graphical model, which combines the Gaussian graphical model and discrete graphical model. Due to the introduction of discrete variables, the maximum likelihood estimator is computationally intractable, so we investigated the pseudolikelihood estimator. To learn the structure of this model, we use the appropriate group sparsity penalties with a calibrated weighing scheme. Model selection consistency results are shown for the mixed model using the maximum likelihood and pseudolikelihood estimators. The extension to a conditonal model is discussed, since these are frequently used in practice.

We proposed two efficient algorithms for the purpose of estimating the parameters of this model, the proximal Newton and the proximal gradient algorithms. The proximal Newton algorithm is shown to scale to graphical models with 2000 variables on a standard desktop. The model is evaluated on synthetic and the current population survey data, which demonstrates the pseudolikelihood performs well compared to maximum likelihood and nodewise regression.

For future work, it would be interesting to incorporate other discrete variables such as poisson or binomial variables and non-Gaussian continuous variables. This would broaden the scope of applications that mixed models could be used for. Our work is a first step in that direction.

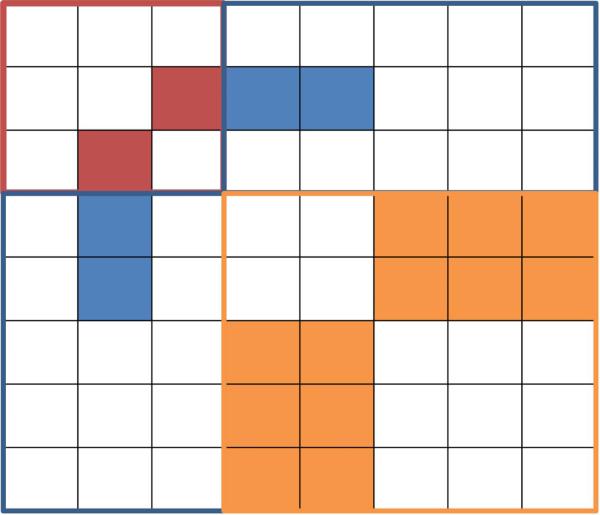
Figure 1.

Symmetric matrix represents the parameters Θ of the model. This example has p = 3, q = 2, L₁ = 2 and L₂ = 3. The red square corresponds to the continuous graphical model coefficients B and the solid red square is the scalar β_st. The blue square corresponds to the coefficients ρ_sj and the solid blue square is a vector of parameters ρ_sj(·). The orange square corresponds to the coefficients ϕ_rj and the solid orange square is a matrix of parameters ϕ_rj(·, ·). The matrix is symmetric, so each parameter block appears in two of the conditional probability regressions.