Significance
Neurons represent both signal and noise in binary electrical discharges termed action potentials. Hence, the standard signal-to-noise ratio (SNR) definition of signal amplitude squared and divided by the noise variance does not apply. We show that the SNR estimates a ratio of expected prediction errors. Using point process generalized linear models, we extend the standard definition to one appropriate for single neurons. In analyses of four neural systems, we show that single neuron SNRs range from −29 dB to −3 dB and that spiking history is often a more informative predictor of spiking propensity than the signal or stimulus activating the neuron. By generalizing the standard SNR metric, we make explicit the well-known fact that individual neurons are highly noisy information transmitters.
Keywords: SNR, signal-to-noise ratio, neuron, simulation, point processes
Abstract
The signal-to-noise ratio (SNR), a commonly used measure of fidelity in physical systems, is defined as the ratio of the squared amplitude or variance of a signal relative to the variance of the noise. This definition is not appropriate for neural systems in which spiking activity is more accurately represented as point processes. We show that the SNR estimates a ratio of expected prediction errors and extend the standard definition to one appropriate for single neurons by representing neural spiking activity using point process generalized linear models (PP-GLM). We estimate the prediction errors using the residual deviances from the PP-GLM fits. Because the deviance is an approximate χ2 random variable, we compute a bias-corrected SNR estimate appropriate for single-neuron analysis and use the bootstrap to assess its uncertainty. In the analyses of four systems neuroscience experiments, we show that the SNRs are −10 dB to −3 dB for guinea pig auditory cortex neurons, −18 dB to −7 dB for rat thalamic neurons, −28 dB to −14 dB for monkey hippocampal neurons, and −29 dB to −20 dB for human subthalamic neurons. The new SNR definition makes explicit in the measure commonly used for physical systems the often-quoted observation that single neurons have low SNRs. The neuron’s spiking history is frequently a more informative covariate for predicting spiking propensity than the applied stimulus. Our new SNR definition extends to any GLM system in which the factors modulating the response can be expressed as separate components of a likelihood function.
The signal-to-noise ratio (SNR), defined as the amplitude squared of a signal or the signal variance divided by the variance of the system noise, is a widely applied measure for quantifying system fidelity and for comparing performance among different systems (1–4). Commonly expressed in decibels as 10log10(SNR), the higher the SNR, the stronger the signal or information in the signal relative to the noise or distortion. Use of the SNR is most appropriate for systems defined as deterministic or stochastic signals plus Gaussian noise (2, 4). For the latter, the SNR can be computed in the time or frequency domain.
Use of the SNR to characterize the fidelity of neural systems is appealing because information transmission by neurons is a noisy stochastic process. However, the standard concept of SNR cannot be applied in neuronal analyses because neurons transmit both signal and noise primarily in their action potentials, which are binary electrical discharges also known as spikes (5–8). Defining what is the signal and what is the noise in neural spiking activity is a challenge because the putative signals or stimuli for neurons differ appreciably among brain regions and experiments. For example, neurons in the visual cortex and in the auditory cortex respond respectively to features of light (9) and sound stimuli (10) while neurons in the somatosensory thalamus respond to tactile stimuli (11). In contrast, neurons in the rodent hippocampus respond robustly to the animal’s position in its environment (11, 12), whereas monkey hippocampal neurons respond to the process of task learning (13). As part of responding to a putative stimulus, a neuron’s spiking activity is also modulated by biophysical factors such as its absolute and relative refractory periods, its bursting propensity, and local network and rhythm dynamics (14, 15). Hence, the definition of SNR must account for the extent to which a neuron’s spiking responses are due to the applied stimulus or signal and to these intrinsic biophysical properties.
Formulations of the SNR for neural systems have been studied. Rieke et al. (16) adapted information theory measures to define Gaussian upper bounds on the SNR for individual neurons. Coefficients of variation and Fano factors based on spike counts (17–19) have been used as measures of SNR. Similarly, Gaussian approximations have been used to derive upper bounds on neuronal SNR (16). These approaches do not consider the point process nature of neural spiking activity. Moreover, these measures and the Gaussian approximations are less accurate for neurons with low spike rates or when information is contained in precise spike times.
Lyamzin et al. (20) developed an SNR measure for neural systems using time-dependent Bernoulli processes to model the neural spiking activity. Their SNR estimates, based on variance formulae, do not consider the biophysical properties of the neuron and are more appropriate for Gaussian systems (16, 21, 22). The Poisson regression model used widely in statistics to relate count observations to covariates provides a framework for studying the SNR for non-Gaussian systems because it provides an analog of the square of the multiple correlation coefficient (R2) used to measure goodness of fit in linear regression analyses (23). The SNR can be expressed in terms of the R2 for linear and Poisson regression models. However, this relationship has not been exploited to construct an SNR estimate for neural systems or point process models. Finally, the SNR is a commonly computed statistic in science and engineering. Extending this concept to non-Gaussian systems would be greatly aided by a precise statement of the theoretical quantity that this statistic estimates (24, 25).
We show that the SNR estimates a ratio of expected prediction errors (EPEs). Using point process generalized linear models (PP-GLM), we extend the standard definition to one appropriate for single neurons recorded in stimulus−response experiments. In analyses of four neural systems, we show that single-neuron SNRs range from −29 dB to −3 dB and that spiking history is often a more informative predictor of spiking propensity than the signal being represented. Our new SNR definition generalizes to any problem in which the modulatory components of a system’s output can be expressed as separate components of a GLM.
Theory
A standard way to define the SNR is as the ratio
| [1] |
where is structure in the data induced by the signal and is the variability due to the noise. To adapt this definition to the analysis of neural spike train recordings from a single neuron, we have: to (i) define precisely what the SNR estimates; (ii) extend the definition and its estimate to account for covariates that, along with the applied stimulus or signal input, also affect the neural response; and (iii) extend the SNR definition and its estimate so that it applies to point process models of neural spiking activity.
By analyzing the linear Gaussian signal plus noise model (Supporting Information), we show that standard SNR computations (Eq. S5) provide an estimator of a ratio of EPEs (Eq. S4). For the linear Gaussian model with covariates, this ratio of EPEs is also well defined (Eq. S6) and can be estimated as a ratio of sum of squares of residuals (Eq. S7). The SNR definition further extends to the GLM with covariates (Eq. S8). To estimate the SNR for the GLM, we replace the sums of squares by the residual deviances, their extensions in the GLM framework Eqs. S9 and S10. The residual deviance is a constant multiple of the Kullback−Leibler (KL) divergence between the data and the model. Due to the Pythagorean property of the KL divergence of GLM models with canonical link functions (26–28) evaluated at the maximum likelihood estimates, the SNR estimator can be conveniently interpreted as the ratio of the explained KL divergence of the signal relative to the noise. We propose an approximate bias correction for the GLM SNR estimate with covariates (Eq. S11), which gives the estimator better performance in low signal-to-noise problems such as single-neuron recordings. The GLM framework formulated with point process models has been used to analyze neural spiking activity (5–7, 29). Therefore, we derive a point process GLM (PP-GLM) SNR estimate for single-neuron spiking activity recorded in stimulus−response experiments.
A Volterra Series Expansion of the Conditional Intensity Function of a Spiking Neuron.
Volterra series are widely used to model biological systems (30), including neural spiking activity (16). We develop a Volterra series expansion of the log of the conditional intensity function to define the PP-GLM for single-neuron spiking activity (31). We then apply the GLM framework outlined in Supporting Information to derive the SNR estimate.
We assume that on an observation interval we record spikes at times . If we model the spike events as a point process, then the conditional intensity function of the spike train is defined by (5)
| [2] |
where is the number of spikes in the interval for and is the relevant history at t. It follows that for small,
| [3] |
We assume that the neuron receives a stimulus or signal input and that its spiking activity depends on this input and its biophysical properties. The biophysical properties may include absolute and relative refractory periods, bursting propensity, and network dynamics. We assume that we can express in a Volterra series expansion as a function of the signal and the biophysical properties (31). The first-order and second-order terms in the expansion are
| [4] |
where is the signal at time t, is the increment in the counting process, is the one-dimensional signal kernel, is the one-dimensional temporal or spike history kernel, is the 2D signal kernel, is the 2D temporal kernel, and is the 2D signal−temporal kernel.
Eq. 4 shows that up to first order, the stimulus effect on the spiking activity and the effect of the biophysical properties of the neuron, defined in terms of the neuron’s spiking history, can be expressed as separate components of the conditional intensity function. Assuming that the second-order effects are not strong, then the approximate separation of these two components makes it possible to define the SNR for the signal, also taking account of the effect of the biophysical properties as an additional covariate and vice versa. We expand the log of the conditional intensity function in the Volterra series instead of the conditional intensity function itself in the Volterra series to ensure that the conditional intensity function is positive. In addition, using the log of the conditional intensity function simplifies the GLM formulation by using the canonical link function for the local Poisson model.
Likelihood Analysis Using a PP-GLM.
We define the likelihood model for the spike train using the PP-GLM framework (5). We assume the stimulus−response experiment consists of independent trials, which we index as . We discretize time within a trial by choosing large and defining the subintervals . We choose large so that each subinterval contains at most one spike. We index the subintervals and define to be if, on trial , there is a spike in the subinterval ((ℓ−1)Δ,ℓΔ) and it is otherwise. We let be the set of spikes recorded on trial in . Let be the relevant history of the spiking activity at time . We define the discrete form of the Volterra expansion by using the first two terms of Eq. 4 to obtain
| [5] |
where , , and , and hence the dependence on the stimulus goes back a period of , whereas the dependence on spiking history goes back a period of . Exponentiating both sides of Eq. 5 yields
| [6] |
The first and third terms on the right side of Eq. 6 measure the intrinsic spiking propensity of the neuron, whereas the second term measures the effect of the stimulus or signal on the neuron’s spiking propensity.
The likelihood function for given the recorded spike train is (5)
| [7] |
Likelihood formulations with between-trial dependence (32) are also possible but are not considered here.
The maximum likelihood estimate of can be computed by maximizing Eq. 7 or, equivalently, by minimizing the residual deviance defined as
| [8] |
where and is the saturated model or the highest possible value of the maximized log likelihood (26). Maximizing to compute the maximum likelihood estimate of is equivalent to minimizing the deviance, because is a constant. The deviance is the generalization to the GLM of the sum of squares from the linear Gaussian model (33).
As in the standard GLM framework, these computations are carried out efficiently using iteratively reweighted least squares. In our PP-GLM likelihood analyses, we use Akaike’s Information Criterion (AIC) to help choose the order of the discrete kernels and (34). We use the time-rescaling theorem and Kolmogorov−Smirnov (KS) plots (35) along with analyses of the Gaussian transformed interspike intervals to assess model goodness of fit (36). We perform the AIC and time-rescaling goodness-of-fit analyses using cross-validation to fit the model to half of the trials in the experiments (training data set) and then evaluating AIC, the KS plots on the second half the trials (test data set). The model selection and goodness-of-fit assessments are crucial parts of the SNR analyses. They allow us to evaluate whether our key assumption is valid, that is, that the conditional intensity function can be represented as a finite-order Volterra series whose second-order terms can be neglected. Significant lack of fit could suggest that this assumption did not hold and would thereby weaken, if not invalidate, any subsequent inferences and analyses.
SNR Estimates for a Single Neuron.
Applying Eq. S11, we have that for a single neuron, the SNR estimate for the signal given the spike history (biophysical properties) with the approximate bias corrections is
| [9] |
and that for a single neuron, the SNR estimates of the spiking propensity given the signal is
| [10] |
where is the dimension or the number of parameters in . Application of the stimulus activates the biophysical properties of the neuron. Therefore, to measure the effect of the stimulus, we fit the GLM with and without the stimulus and use the difference between the deviances to estimate the (Eq. 9). Similarly, to measure the effect of the spiking history, we fit the GLM with and without the spike history and use the difference between the deviances to estimate the (Eq. 10).
Expressed in decibels, the SNR estimates become
| [11] |
| [12] |
Applications
Stimulus−Response Neurophysiological Experiments.
To illustrate our method, we analyzed neural spiking activity data from stimulus−response experiments in four neural systems. The stimulus applied in each experiment is a standard one for the neural system being studied. The animal protocols executed in experiments 1–3 were approved by the Institutional Animal Care and Use Committees at the University of Michigan for the guinea pig studies, the University of Pittsburgh for the rat studies, and New York University for the monkey studies. The human studies in experiment 4 were approved by the Human Research Committee at Massachusetts General Hospital.
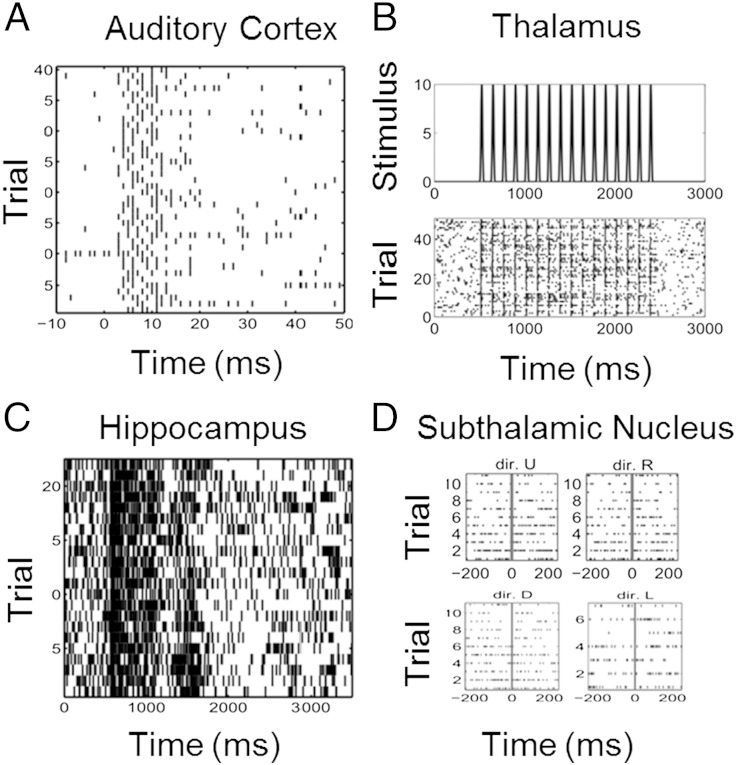
In experiment 1 (Fig. 1A), neural spike trains were recorded from 12 neurons in the primary auditory cortex of anesthetized guinea pigs in response to a 200 μs/phase biphasic electrical pulse at 44.7-μA applied in the inferior colliculus (10). Note that the neural recordings were generally multi-unit responses recorded on 12 sites but we refer to them as neurons in this paper. The stimulus was applied at time 0, and spiking activity was recorded from 10 ms before the stimulus to 50 ms after the stimulus during 40 trials. In experiment 2, neural spiking activity was recorded in 12 neurons from the ventral posteromedial (VPm) nucleus of the thalamus (VPm thalamus) in rats in response to whisker stimulation (Fig. 1B) (11). The stimulus was deflection of the whisker at a velocity of 50 mm/s at a repetition rate of eight deflections per second. Each deflection was 1 mm in amplitude and began from the whiskers' neutral position as the trough of a single sine wave and ended smoothly at the same neutral position. Neural spiking activity was recorded for 3,000 ms across 51 trials.
Fig. 1.
Raster plots of neural spiking activity. (A) Forty trials of spiking activity recorded from a neuron in the primary auditory cortex of an anesthetized guinea pig in response to a 200 μs/phase biphasic electrical pulse applied in the inferior colliculus at time 0. (B) Fifty trials of spiking activity from a rat thalamic neuron recorded in response to a 50 mm/s whisker deflection repeated eight times per second. (C) Twenty-five trials of spiking activity from a monkey hippocampal neuron recorded while executing a location scene association task. (D) Forty trials of spiking activity recorded from a subthalamic nucleus neuron in a Parkinson's disease patient before and after a hand movement in each of four directions (dir.): up (dir. U), right (dir. R), down (dir. D), and left (dir. L).
In experiment 3 (Fig. 1C), neural spiking activity was recorded in 13 neurons in the hippocampus of a monkey executing a location scene association task (13). During the experiment, two to four novel scenes were presented along with two to four well-learned scenes in an interleaved random order. Each scene was presented for between 25 and 60 trials. In experiment 4, the data were recorded from 10 neurons in the subthalamic nucleus of human Parkinson's disease patients (Fig. 1D) executing a directed movement task (15). The four movement directions were up, down, left, and right. The neural spike trains were recorded in 10 trials per direction beginning 200 ms before the movement cue and continuing to 200 ms after the cue.
The PP-GLM was fit to the spike trains of each neuron using likelihood analyses as described above. Examples of the model goodness of fit for a neuron from each system is shown in Supporting Information. Examples of the model estimates of the stimulus and history effects for a neuron from each system are shown in Fig. 2.
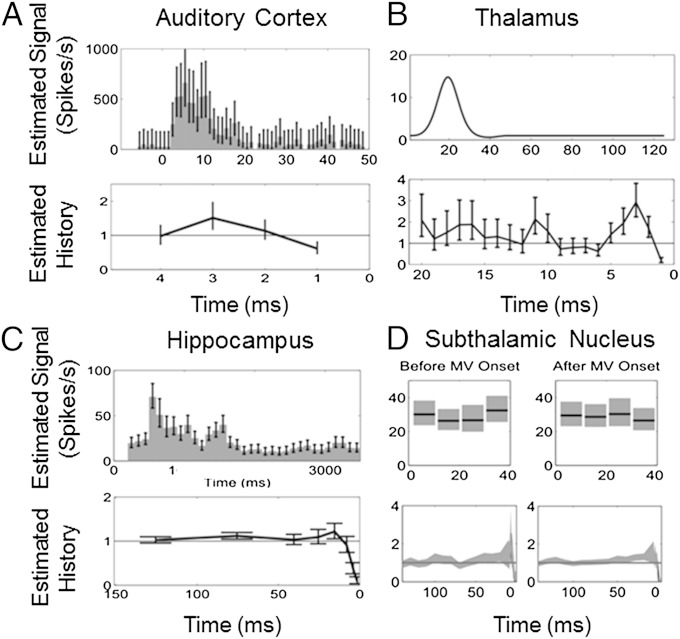
Fig. 2.
Stimulus and history component estimates from the PP-GLM analyses of the spiking activity in Fig. 1. (A) Guinea pig primary auditory cortex neuron. (B) Rat thalamic neuron. (C) Monkey hippocampal neuron. (D) Human subthalamic nucleus neuron. The stimulus component (Upper) is the estimated stimulus-induced effect on the spike rate in A, C, and D and the impulse response function of the stimulus in B. The history components (Lower) show the modulation constant of the spike firing rate.
SNR of Single Neurons.
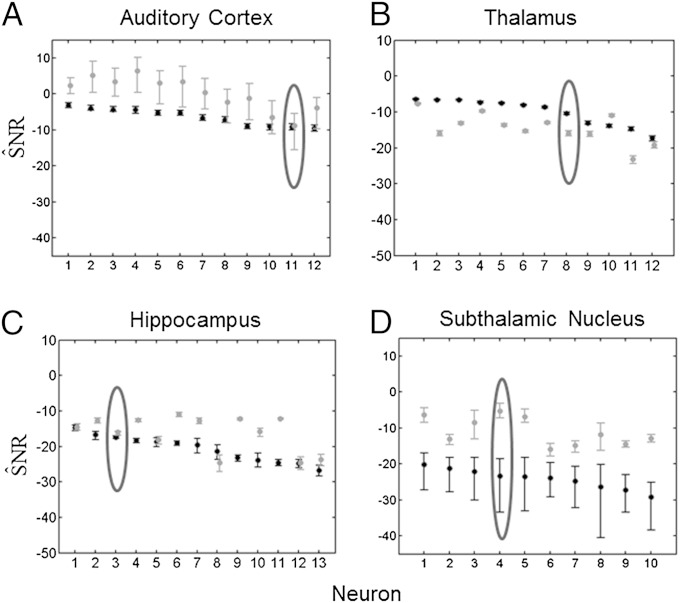
We found that the estimates (Eq. 11) of the stimulus controlling for the effect of the biophysical model properties were (median [minimum, maximum]): −6 dB [−10 dB, −3 dB] for guinea pig auditory cortex neurons; −9 dB [−18 dB, −7 dB] for rat thalamic neurons; −20 dB [−28 dB, −14 dB] for the monkey hippocampus; and −23 dB [−29 dB, −20 dB] for human subthalamic neurons (Fig. 3, black bars). The higher SNRs (from Eq. 11) in experiments 1 and 2 (Fig. 3 A and B) are consistent with the fact that the stimuli are explicit, i.e., an electrical current and mechanical displacement of the whisker, respectively, and that the recording sites are only two synapses away from the stimulus. It is also understandable that SNRs are smaller for the hippocampus and thalamic systems in which the stimuli are implicit, i.e., behavioral tasks (Fig. 3 C and D).
Fig. 3.
KL-based SNR for (A) 12 guinea pig auditory cortex neurons, (B) 12 rat thalamus neurons, (C) 13 monkey hippocampal neurons, and (D) 10 subthalamic nucleus neurons from a Parkinson's disease patient. The black dots are , the SNR estimates due to the stimulus correcting for the spiking history. The black bars are the 95% bootstrap confidence intervals for . The gray dots are , the SNR estimates due to the intrinsic biophysics of the neuron correcting for the stimulus. The gray bars are the 95% bootstrap confidence intervals for . The encircled points are the SNR and 95% confidence intervals for the neural spike train raster plots in Fig. 1.
We found that estimates (from Eq. 12) of the biophysical properties controlling for the stimulus effect were: 2 dB [−9 dB, 7 dB] for guinea pig auditory cortex; −13 dB [−22 dB, −8 dB] for rat thalamic neurons; −15 dB [−24 dB, −11 dB] for the monkey hippocampal neurons; and −12 dB [−16 dB, −5 dB] for human subthalamic neurons (Fig. 3, gray bars). They were greater than for the guinea pig auditory cortex (Fig. 3A), the monkey hippocampus (Fig. 3C), and the human subthalamic experiments (Fig. 3D), suggesting that the intrinsic spiking propensities of neurons are often greater than the spiking propensity induced by applying a putatively relevant stimulus.
A Simulation Study of Single-Neuron SNR Estimation.
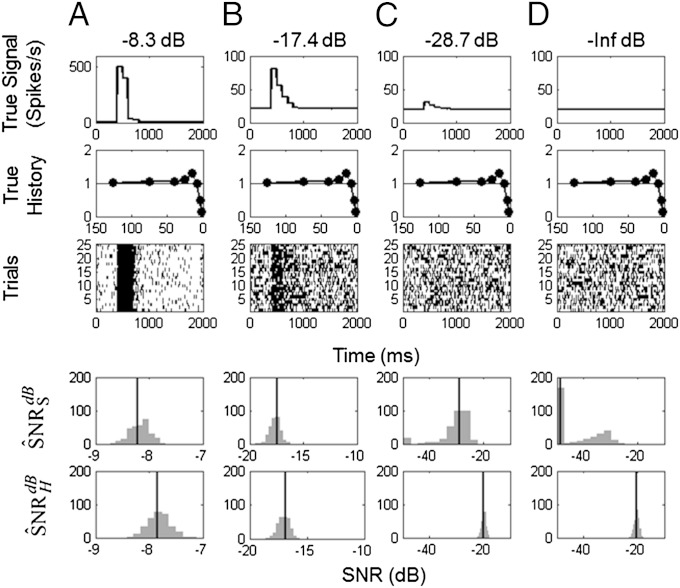
To analyze the performance of our SNR estimation paradigm, we studied simulated spiking responses of monkey hippocampal neurons with specified stimulus and history dynamics. We assumed four known SNRs of −8.3 dB, −17.4 dB, −28.7 dB, and –∞ dB corresponding, respectively, to stimulus effects on spike rates ranges of 500, 60, 10, and 0 spikes per second (Fig. 4, row 1). For each of the stimulus SNRs, we assumed spike history dependence (Fig. 4, row 2) to be similar to that of the neuron in Fig. 1C. For each of four stimulus effects, we simulated 300 experiments, each consisting of 25 trials (Fig. 4, row 3). To each of the 300 simulated data sets at each SNR level, we applied our SNR estimation paradigm: model fitting, model order selection, goodness-of-fit assessment, and estimation of (Fig. 4, row 4) and (Fig. 4, row 5).
Fig. 4.
KL-based SNR of simulated neurons with stimulus and history components. The stimulus components were set at four different SNRs: (A) −8.3 dB, (B) −17.4 dB, (C) −28.7 dB, and (D) –∞ dB, where the same spike history component was used in each simulation. For each SNR level, 300 25-trial simulations were performed. Shown are (row 1) the true signal; (row 2) the true spike history component; (row 3) a raster plot of a representative simulated experiment; (row 4) histogram of the 300 , the SNR estimates due to the stimulus correcting for the spiking history; and (row 5) histogram of the 300 , the SNR estimates due to the intrinsic biophysics of the neuron correcting for the stimulus. The vertical lines in rows 4 and 5 are the true SNRs.
The bias-corrected SNR estimates show symmetric spread around their true SNRs, suggesting that the approximate bias correction performed as postulated (Fig. 4, rows 4 and 5). The exception is the case in which the true SNR was and our paradigm estimates as large negative numbers (Fig. 4D, row 4). The are of similar magnitude as the SNR estimates in actual neurons (see SNR = −18.1 dB in the third neuron in Fig. 3C versus −17.4 dB in the simulated neuron (Fig. 4B).
A Simulation Study of SNR Estimation for Single Neurons with No History Effect.
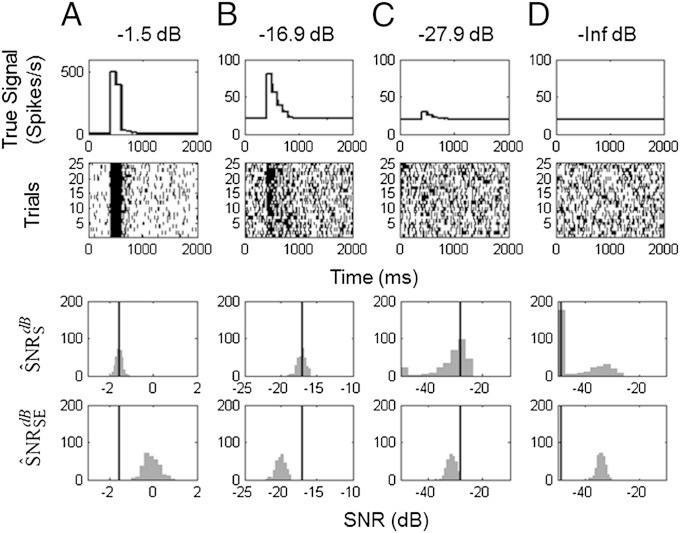
We repeated the simulation study with no spike history dependence for the true SNR values of −1.5 dB, −16.9 dB, −27.9 dB, and –∞ dB, with 25 trials per experiment and 300 realizations per experiment (Fig. 5). Removing the history dependence makes the simulated data within and between trials independent realizations from an inhomogeneous Poisson process. The spike counts across trials within a 1-ms bin obey a binomial model with n = 25 and the probability of a spike defined by the values of the true conditional intensity function times 1 ms. Hence, it is possible to compute analytically the SNR and the bias in the estimates. We used our paradigm to compute . For comparison, we also computed the variance-based SNR proposed by Lyamzin et al. (20) Both and the variance-based estimates were computed from the parameters obtained from the same GLM fits (see Eq. S16). For each simulation in Fig. 5, the true SNR value based on our paradigm is shown (vertical lines).
Fig. 5.
A comparison of SNR estimation in simulated neurons. The stimulus components were set at four different SNRs: (A) −1.5 dB, (B) −16.9 dB, and (C) −27.9 dB with no history component. For each SNR level, 300 25-trial simulations were performed. Shown are (row 1) the true signal; (row 2) a raster plot of a representative simulated experiment; (row 3) histogram of the 300 KL-based SNR estimates, ; and (row 4) histogram of the 300 squared error-based SNR estimates, (20). The vertical lines in rows 3 and 4 are the true SNRs.
The histograms of (Fig. 5, row 3) are spread symmetrically about the true expected SNR. The variance-based SNR estimate overestimates the true SNR in Fig. 5A and underestimates the true SNR in Fig. 5 B and C. These simulations illustrate that the variance-based SNR is a less refined measure of uncertainty, as it is based on only the first two moments of the spiking data, whereas our estimate is based on the likelihood that uses information from all of the moments. At best, the variance-based SNR estimate can provide a lower bound for the information content in the non-Gaussian systems (16). Variance-based SNR estimators can be improved by using information from higher-order moments (37), which is, effectively, what our likelihood-based SNR estimators do.
Discussion
Measuring the SNR of Single Neurons.
Characterizing the reliability with which neurons represent and transmit information is an important question in computational neuroscience. Using the PP-GLM framework, we have developed a paradigm for estimating the SNR of single neurons recorded in stimulus response experiments. To formulate the GLM, we expanded the log of the conditional intensity function in a Volterra series (Eq. 4) to represent, simultaneously, background spiking activity, the stimulus or signal effect, and the intrinsic dynamics of the neuron. In the application of the methods to four neural systems, we found that the SNRs of neuronal responses (Eq. 11) to putative stimuli—signals—ranged from −29 dB to −3 dB (Fig. 1). In addition, we showed that the SNR of the intrinsic dynamics of the neuron (Eq. 12) was frequently higher than the SNR of the stimulus (Eq. 11). These results are consistent with the well-known observation that, in general, neurons respond weakly to putative stimuli (16, 20). Our approach derives a definition of the SNR appropriate for neural spiking activity modeled as a point process. Therefore, it offers important improvements over previous work in which the SNR estimates have been defined as upper bounds derived from Gaussian approximations or using Fano factors and coefficients of variation applied to spike counts. Our SNR estimates are straightforward to compute using the PP-GLM framework (5) and public domain software that is readily available (38). Therefore, they can be computed as part of standard PP-GLM analyses.
The simulation study (Fig. 5) showed that our SNR methods provide a more accurate SNR estimate than recently reported variance-based SNR estimate derived from a local Bernoulli model (20). In making the comparison between the two SNR estimates, we derived the exact prediction error ratios analytically, and we used the same GLM fit to the simulated data to construct the SNR estimates. As a consequence, the differences are only due to differences in the definitions of the SNR. The more accurate performance of our SNR estimate is attributable to the fact that it is based on the likelihood, whereas the variance-based SNR estimate uses only the first two sample moments of the data. This improvement is no surprise, as it is well known that likelihood-based estimates offer the best information summary in a sample given an accurate or approximately statistical model (34). We showed that for each of the four neural systems, the PP-GLM accurately described the spike train data in terms of goodness-of-fit assessments.
A General Paradigm for SNR Estimation.
Our SNR estimation paradigm generalizes the approach commonly used to analyze SNRs in linear Gaussian systems. We derived the generalization by showing that the commonly computed SNR statistic estimates a ratio of EPEs (Supporting Information): the expected prediction of the error of the signal representing the data corrected for the nonsignal covariates relative to the EPE of the system noise. With this insight, we used the work of ref. 26 to extend the SNR definition to systems that can be modeled using the GLM framework in which the signal and relevant covariates can be expressed as separate components of the likelihood function. The linear Gaussian model is a special case of a GLM. In the GLM paradigm, the sum of squares from the standard linear Gaussian model is replaced by the residual deviance (Eq. S10). The residual deviance may be viewed as an estimated KL divergence between data and model (26). To improve the accuracy of our SNR estimator, particularly given the low SNRs of single neurons, we devised an approximate bias correction, which adjusts separately the numerator and the denominator (Eqs. 9 and 10). The bias-corrected estimator performed well in the limited simulation study we reported (Figs. 4 and 5). In future work, we will replace the separate bias corrections for the numerator and denominator with a single bias correction for the ratio, and extend our paradigm to characterize the SNR of neuronal ensembles and those of other non-Gaussian systems.
In Supporting Information, we describe the relationship between our SNR estimate and several commonly used quantities in statistics, namely the R2, coefficient of determination, the F statistic, the likelihood ratio (LR) test statistic and f2, Cohen’s effect size. Our SNR analysis offers an interpretation of the F statistic that is not, to our knowledge, commonly stated. The F statistic may be viewed as a scaled estimate of the SNR for the linear Gaussian model, where the scale factor is the ratio of the degrees of freedom (Eq. S21). The numerator of our GLM SNR estimate (Eq. S9) is a LR test statistics for assessing the strength of the association between data Y and covariates X2. The generalized SNR estimator can be seen as generalized effect size. This observation is especially important because it can be further developed for planning neurophysiological experiments, and thus may offer a way to enhance experimental reproducibility in systems neuroscience research (39).
In summary, our analysis provides a straightforward way of assessing the SNR of single neurons. By generalizing the standard SNR metric, we make explicit the well-known fact that individual neurons are noisy transmitters of information.
Supplementary Material
Acknowledgments
This research was supported in part by the Clinical Eye Research Centre, St. Paul’s Eye Unit, Royal Liverpool and Broadgreen University Hospitals National Health Service Trust, United Kingdom (G.C.); the US National Institutes of Health (NIH) Biomedical Research Engineering Partnership Award R01-DA015644 (to E.N.B. and W.A.S.), Pioneer Award DP1 OD003646 (to E.N.B.), and Transformative Research Award GM 104948 (to E.N.B.); and NIH grants that supported the guinea pig experiments P41 EB2030 and T32 DC00011 (to H.H.L.).
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1505545112/-/DCSupplemental.
References
- 1.Chen Y, Beaulieu N. Maximum likelihood estimation of SNR using digitally modulated signals. IEEE Trans Wirel Comm. 2007;6(1):210–219. [Google Scholar]
- 2.Kay S. Fundamentals of Statistical Signal Processing. Prentice-Hall; Upper Saddle River, NJ: 1993. [Google Scholar]
- 3.Welvaert M, Rosseel Y. On the definition of signal-to-noise ratio and contrast-to-noise ratio for FMRI data. PLoS ONE. 2013;8(11):e77089. doi: 10.1371/journal.pone.0077089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Mendel J. Lessons in Estimation Theory for Signal Processing, Communications, and Control. 2nd Ed Prentice-Hall; Upper Saddle River, NJ: 1995. [Google Scholar]
- 5.Truccolo W, Eden UT, Fellows MR, Donoghue JP, Brown EN. A point process framework for relating neural spiking activity to spiking history, neural ensemble, and extrinsic covariate effects. J Neurophysiol. 2005;93(2):1074–1089. doi: 10.1152/jn.00697.2004. [DOI] [PubMed] [Google Scholar]
- 6.Brillinger DR. Maximum likelihood analysis of spike trains of interacting nerve cells. Biol Cybern. 1988;59(3):189–200. doi: 10.1007/BF00318010. [DOI] [PubMed] [Google Scholar]
- 7.Brown EN, Barbieri R, Eden UT, Frank LM. Likelihood methods for neural data analysis. In: Feng J, editor. Computational Neuroscience: A Comprehensive Approach. CRC; London: 2003. pp. 253–286. [Google Scholar]
- 8.Brown EN. Theory of point processes for neural systems. In: Chow CC, Gutkin B, Hansel D, Meunier C, Dalibard J, editors. Methods and Models in Neurophysics. Elsevier; Paris: 2005. pp. 691–726. [Google Scholar]
- 9.MacEvoy SP, Hanks TD, Paradiso MA. Macaque V1 activity during natural vision: Effects of natural scenes and saccades. J Neurophysiol. 2008;99(2):460–472. doi: 10.1152/jn.00612.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Lim HH, Anderson DJ. Auditory cortical responses to electrical stimulation of the inferior colliculus: Implications for an auditory midbrain implant. J Neurophysiol. 2006;96(3):975–988. doi: 10.1152/jn.01112.2005. [DOI] [PubMed] [Google Scholar]
- 11.Temereanca S, Brown EN, Simons DJ. Rapid changes in thalamic firing synchrony during repetitive whisker stimulation. J Neurosci. 2008;28(44):11153–11164. doi: 10.1523/JNEUROSCI.1586-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Wilson MA, McNaughton BL. Dynamics of the hippocampal ensemble code for space. Science. 1993;261(5124):1055–1058. doi: 10.1126/science.8351520. [DOI] [PubMed] [Google Scholar]
- 13.Wirth S, et al. Single neurons in the monkey hippocampus and learning of new associations. Science. 2003;300(5625):1578–1581. doi: 10.1126/science.1084324. [DOI] [PubMed] [Google Scholar]
- 14.Dayan P, Abbott LF. Theoretical Neuroscience. Oxford Univ Press; London: 2001. [Google Scholar]
- 15.Sarma SV, et al. Using point process models to compare neural spiking activity in the subthalamic nucleus of Parkinson’s patients and a healthy primate. IEEE Trans Biomed Eng. 2010;57(6):1297–1305. doi: 10.1109/TBME.2009.2039213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Rieke F, Warland D, de Ruyter van Steveninck RR, Bialek W. Spikes: Exploring the Neural Code. MIT Press; Cambridge, MA: 1997. [Google Scholar]
- 17.Optican LM, Richmond BJ. Temporal encoding of two-dimensional patterns by single units in primate inferior temporal cortex. III. Information theoretic analysis. J Neurophysiol. 1987;57(1):162–178. doi: 10.1152/jn.1987.57.1.162. [DOI] [PubMed] [Google Scholar]
- 18.Softky WR, Koch C. The highly irregular firing of cortical cells is inconsistent with temporal integration of random EPSPs. J Neurosci. 1993;13(1):334–350. doi: 10.1523/JNEUROSCI.13-01-00334.1993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Shadlen MN, Newsome WT. The variable discharge of cortical neurons: Implications for connectivity, computation, and information coding. J Neurosci. 1998;18(10):3870–3896. doi: 10.1523/JNEUROSCI.18-10-03870.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Lyamzin DR, Macke JH, Lesica NA. Modeling population spike trains with specified time-varying spike rates, trial-to-trial variability, and pairwise signal and noise correlations. Front Comput Neurosci. 2010;4(144):144. doi: 10.3389/fncom.2010.00144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Soofi ES. Principal information theoretic approaches. Am Stat. 2000;95(452):1349–1353. [Google Scholar]
- 22.Erdogmus D, Larsson EG, Yan R, Principe JC, Fitzsimmons JR. Measuring the signal-to-noise ratio in magnetic resonance imaging: A caveat. Signal Process. 2004;84(6):1035–1040. [Google Scholar]
- 23.Mittlböck M, Waldhör T. Adjustments for R2-measures for Poisson regression models. Comput Stat Data Anal. 2000;34(4):461–472. [Google Scholar]
- 24.Kent JT. Information gain and a general measure of correlation. Biometrika. 1983;70(1):163–173. [Google Scholar]
- 25.Alonso A, et al. Prentice’s approach and the meta-analytic paradigm: A reflection on the role of statistics in the evaluation of surrogate endpoints. Biometrics. 2004;60(3):724–728. doi: 10.1111/j.0006-341X.2004.00222.x. [DOI] [PubMed] [Google Scholar]
- 26.Hastie T. A closer look at the deviance. Am Stat. 1987;41(1):16–20. [Google Scholar]
- 27.Simon G. Additivity of information in exponential family probability laws. J Am Stat Assoc. 1973;68(342):478–482. [Google Scholar]
- 28.Cameron AC, Windmeijer FAG. An R-squared measure of goodness of fit for some common nonlinear regression models. J Econom. 1997;77(2):329–342. [Google Scholar]
- 29.Paninski L. Maximum likelihood estimation of cascade point-process neural encoding models. Network. 2004;15(4):243–262. [PubMed] [Google Scholar]
- 30.Marmarelis VZ. Nonlinear Dynamic Modeling of Physiological Systems. John Wiley; Hoboken, NJ: 2004. [Google Scholar]
- 31.Plourde E, Delgutte B, Brown EN. A point process model for auditory neurons considering both their intrinsic dynamics and the spectrotemporal properties of an extrinsic signal. IEEE Trans Biomed Eng. 2011;58(6):1507–1510. doi: 10.1109/TBME.2011.2113349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Czanner G, Sarma SV, Eden UT, Brown EN. A signal-to-noise ratio estimator for generalized linear model systems. Lect Notes Eng Comput Sci. 2008;2171(1):1063–1069. [Google Scholar]
- 33.McCullagh P, Nelder JA. Generalized Linear Models. Chapman and Hall; New York: 1989. [Google Scholar]
- 34.Pawitan Y. In All Likelihood. Statistical Modelling and Inference Using Likelihood. Oxford Univ Press; London: 2013. [Google Scholar]
- 35.Brown EN, Barbieri R, Ventura V, Kass RE, Frank LM. The time-rescaling theorem and its application to neural spike train data analysis. Neural Comput. 2002;14(2):325–346. doi: 10.1162/08997660252741149. [DOI] [PubMed] [Google Scholar]
- 36.Czanner G, et al. Analysis of between-trial and within-trial neural spiking dynamics. J Neurophysiol. 2008;99(5):2672–2693. doi: 10.1152/jn.00343.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Sekhar SC, Sreenivas TV. Signal-to-noise ratio estimation using higher-order moments. Signal Process. 2006;86(4):716–732. [Google Scholar]
- 38.Cajigas I, Malik WQ, Brown EN. nSTAT: Open-source neural spike train analysis toolbox for Matlab. J Neurosci Methods. 2012;211(2):245–264. doi: 10.1016/j.jneumeth.2012.08.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Collins FS, Tabak LA. Policy: NIH plans to enhance reproducibility. Nature. 2014;505(7485):612–613. doi: 10.1038/505612a. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.