On the question of whether lubricants fluidize in stick–slip friction

Significance

The costs to developed economies of friction and wear in technology are some 4–6% of their gross national product, so improved understanding of frictional dissipation can lead to substantial benefits. A widespread mode of friction is the intermittent motion (stick–slip) between sliding solid surfaces (such as the squeak of hinges, or a bow running over a cello string), which can persist even on adding lubricants, but its origins are not well understood. We now show directly, by capturing the fleeting, individual slip events at millisecond and subnanometer resolution, that, in contrast to accepted and long-standing belief, shear melting (fluidization) of thin lubricant layers does not occur in stick–slip sliding. This new insight may open the way to improved lubricant design.

Abstract

Intermittent sliding (stick–slip motion) between solids is commonplace (e.g., squeaking hinges), even in the presence of lubricants, and is believed to occur by shear-induced fluidization of the lubricant film (slip), followed by its resolidification (stick). Using a surface force balance, we measure how the thickness of molecularly thin, model lubricant films (octamethylcyclotetrasiloxane) varies in stick–slip sliding between atomically smooth surfaces during the fleeting (ca. 20 ms) individual slip events. Shear fluidization of a film of five to six molecular layers during an individual slip event should result in film dilation of 0.4–0.5 nm, but our results show that, within our resolution of ca. 0.1 nm, slip of the surfaces is not correlated with any dilation of the intersurface gap. This reveals that, unlike what is commonly supposed, slip does not occur by such shear melting, and indicates that other mechanisms, such as intralayer slip within the lubricant film, or at its interface with the confining surfaces, may be the dominant dissipation modes.

Intermittent sliding (stick–slip) of solids in contact is an everyday effect, such as in the squeak of hinges or the music of violins, when the bow slides past the strings, or, at a different scale, in earthquakes (where tectonic plates slide past each other). Such solid sliding is a major cause of frictional dissipation, and can persist even in the presence of lubricants (1). At a nanotribological level, surface force balance (SFB) measurements, supported by theory and computer simulations, have shown that when simple organic liquids are confined between atomically smooth, solid (mica) surfaces to films thinner than some six to eight molecular layers, they may become solid-like, and are often layered (2–14). Subsequent sliding of the surfaces across such films when they are subjected to shear may then take place via stick–slip motion (15, 16). During the stick part, the surfaces are in rigid contact until the shear force between them exceeds the static friction, at which point they slip rapidly past each other (relaxing the shear stress) and then stick again, in a repeating cycle. The issue of how the confined (lubricant) layer progressively yields and then becomes rigid again during such stick–slip sliding has been intensely studied over the past several decades, not least because a better understanding may result in improved lubrication approaches.

The molecular basis of the stick–slip cycle in sheared solid-like lubricant films as described above is not well understood (17–28). This is at least in part because, experimentally, it is very challenging to capture what happens to the lubricant layer during the fleeting, individual slip events taking place in the nanometrically confined film. Even when measured under controlled conditions, as in the SFB, these slip events are not only of very short duration [ca. 20 ms (18)] but generally occupy only a tiny fraction of the stick–slip cycle, with the surfaces in nonsliding contact (stick) for almost the entire cycle period. For this reason, much of our understanding has been derived from theoretical modeling and computer simulation studies (17, 19–25, 27–29). Classically, these almost all suggest that the stick–slip motion involves periodic shear melting transitions and resolidification of the film as it undergoes transition between solid-like and liquid-like phases during sliding. Even where there is some disagreement in the model details [for example, on the precise mechanism by which the films solidify at the end of the slip (22, 25)], they maintain the essential idea of fluidization of the lubricant layers during the slip part of the stick–slip cycle. In the shear-induced solid to liquid transition (fluidization), a density change is also expected because the fluidized phase is less dense than the solid phase. This leads to a volumetric expansion and contraction cycle (corresponding respectively to slip and stick), with a dilation of the thin lubricant film during the slip event (17, 23, 25, 27). Some more recent simulations suggest that slip may occur at the wall–fluid interfaces or via interlayer slip within the film rather than via film melting (19, 27, 28), although the scenario of lubricant fluidization during slip is the generally accepted mechanism.

There have been few experimental studies on individual slips during stick–slip sliding across lubricant films, and none where the film thickness in such fleeting events has been examined (15, 16, 18, 30–32). Clues may also be extracted from stick–slip motion of confined granular systems under shear, where numerical simulations (33, 34) and some experiments (35–37) suggest that fluidization and dilation may play a role in the stick–slip instability. While this is suggestive, differences between granular layers and lubricant films include not only five orders of magnitude between size of grains and of molecules but, in particular, the issue of molecular interactions, negligible in granular shear but all-important when shearing lubricants.

In the present study, we examine directly the individual slip events during stick–slip sliding across thin lubricant films, and in particular the issue of film dilation during the fleeting slip motion itself. This is done to provide “smoking gun” evidence concerning the issue of film fluidization, where such dilation is expected to be a clear signature. We confine a thin (few nanometers) model liquid film between smooth solid surfaces in an SFB, shear it, and monitor the film thickness during stick–slip sliding via fast video microscopy. To overcome the major challenge presented by the shortness of the slip events, which occupy only some 1% of the stick–slip cycle over which a subnanometer dilation needs to be detected against a comparable level of noise, we analyze our data using tools from classical signal detection theory to correlate the slip events with the instantaneous value of the film thickness.

Results and Discussion

We confine a film of the model liquid octmethylcyclotetrasiloxane (OMCTS; see Materials and Methods) between molecularly smooth mica surfaces in an SFB (Materials and Methods). The OMCTS is known to undergo layering and solidification in thin enough films (when the number of layers n ≤ 6), and subsequent sliding of the confining mica surfaces when a shear force is applied proceeds via stick–slip motion. We monitor the film thickness D during the stick–slip via fast video recording. Since fluidization involves a change in density of the OMCTS film as it goes from solid (during the stick part of the motion) to liquid (during the slip), and since the liquid is essentially incompressible (38, 39), this will be manifested as a dilation δD in the confined film thickness each time a slip event occurs. As the film solidifies again at the end of the slip, it should return to its former density and thickness D. Thus, we look for an increase δD in the film thickness that is correlated with the fleeting slip events.

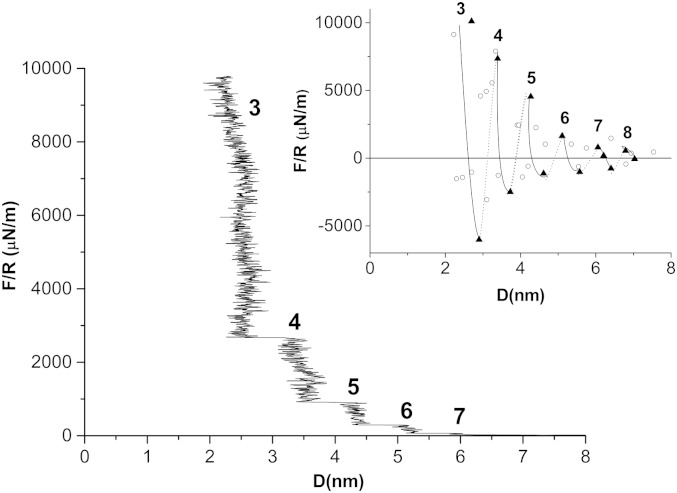
At the beginning of each SFB experiment, the normal force profiles across the OMCTS (Materials and Methods) were determined, and only experiments confirming the existence of the characteristic oscillatory force profiles expected for confined OMCTS were continued. Such oscillatory profiles are a signature of the system purity, as even trace amounts of contamination suppress the oscillations (7). The oscillations occur because the OMCTS forms a layered structure between the confining mica surfaces and, on approach, the layers are squeezed out one by one. Typical oscillatory normal force profiles between two atomically flat bare mica surfaces across purified, freshly distilled OMCTS are shown in Fig. 1 (see Materials and Methods for purification procedure). Normal profiles on approaching and receding of the surfaces were recorded both manually, by measuring the fringe position in a quasistatic point-by-point approach, and via a dynamic approach using fast video recording as the surfaces are compressed (Materials and Methods). Fig. 1 shows the step-like approach of the surfaces revealed by the dynamic approach method; steps are of one molecular diameter (ca. 0.85 nm) as the layers are being squeezed out one by one while increasing the applied pressure, in agreement with earlier studies (7, 15, 40, 41). The quasistatic profiles (Fig. 1, Inset) show more clearly the oscillatory forces in good agreement with these earlier studies. Both types of measurement (dynamic and quasistatic) reveal the characteristic layered structure of the confined OMCTS, with the numbers in Fig. 1 indicating the number n of molecular layers corresponding to the force maxima before layer squeezeout occurs. We note that in independent experiments, the step-like approach was reproducible (with steps of ca. 0.8–0.9 nm), although the absolute mean layer thickness for a given n could vary by up to ±0.2–0.3 nm due to uncertainties in the zero of calibration, in line with earlier studies of oscillatory forces (42). As noted, for n ≤ 6, the confined OMCTS behaves in a solid-like manner, i.e., it is capable of sustaining a finite shear stress before yielding when the shear stress exceeds the static friction force, and subsequent sliding takes place via stick–slip motion (7).

Fig. 1.

Typical normal forces vs. surface separation between two mica surfaces across OMCTS. F_n(D)/R profiles measured in a dynamic approach (Supporting Information) [in the Derjaguin normalization, F_n(D)/R = 2πE(D), where R is the mean surface curvature and E(D) the interaction energy per unit area between flat parallel surfaces obeying the same force laws]. (Inset) Open circles represent F_n(D)/R measured in a quasistatic approach. Solid triangles are data from ref. 7. The numbers adjacent to the profile at the force maxima indicate the number of OMCTS molecular layers at the corresponding separations.

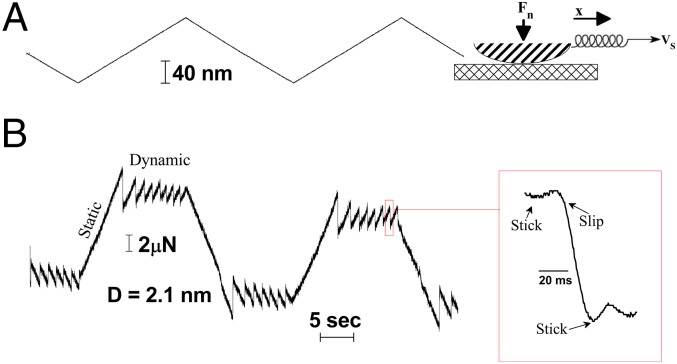
Once system purity was established via the oscillatory normal force F_n(D) profiles as in Fig. 1, lateral motion is applied to the top mica surface at different separations D corresponding to the different numbers of OMCTS layers, establishing a lateral shear stress across the confinement-solidified liquid. The subsequent sliding proceeds via typical stick–slip motion, and the resulting frictional shear force F_s is recorded (Materials and Methods). Typical variation of applied and sliding motion with time are shown in Fig. 2. Fig. 2A shows the back-and-forth lateral motion applied to the top mica surface at surface separation D = D₃ = 2.1 ± 0.3 nm (n = 3, Fig. 1). Fig. 2B is the corresponding stick–slip pattern seen in the friction force measured by the bending of the SFB shear spring. Fig. 2B, Inset provides details of a single slip event on an expanded time scale, showing that its duration is ca. 20 ms.

Fig. 2.

Shear interactions between two mica surfaces across OMCTS (D = D₃ = 2.1 ± 0.2 nm). Top trace (A) is the lateral back and forth motion applied to the top mica surface at v_s (∼ 12 nm/s) via the shear spring as indicated in the schematic on the right. Bottom trace (B) is the shear force corresponding to the spring extension. A characteristic stick–slip sliding pattern is demonstrated, with Inset showing one slip event on an expanded time scale.

To determine whether slip events as shown in Fig. 2 are correlated with dilation of the OMCTS film, we monitor simultaneously both the stick–slip sliding via F_s and the D values via the fast video recording. Typical results are shown in Fig. 3.

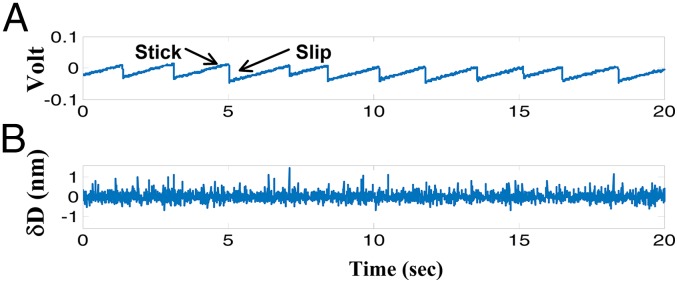
Fig. 3.

Simultaneous recording of (A) oscilloscope output proportional to friction force F_s during stick–slip sliding across a D = D₅ = 4.5 ± 0.3-nm-thick OMCTS film (corresponding to n = 5; see Fig. 1) and (B) variation δD of surface separation relative to D = D₅, from the interference fringe tip position (Materials and Methods).

A visual inspection of Fig. 3B indicates no signal in δD above the noise level (of peak-to-peak amplitude ca. 1 nm) that is correlated with the slip events indicated in Fig. 3A (which are the vertical parts of the trace in Fig. 3A as indicated). To proceed, we use a signal detection approach (43) based on a Generalized Likelihood Ratio Test (GLRT) with a Constant False Alarm Rate (CFAR; see Materials and Methods) that is capable of correlating the slip events during a stick–slip run such as in Fig. 3A, with small changes δD in D (Fig. 3B). We bear in mind that the individual slip events are of only ca. 20 ms duration (Fig. 2), while the stick events are on average about two orders of magnitude longer (e.g., ca. 1.8 s for the run in Fig. 3A). First, we estimate the range of dilations δD that we might expect for fluidization of the solidified OMCTS films. The range of relevant solidified film thicknesses is n = 3 to n = 6 molecular layers, corresponding to D ≈ 2.4–5.1 nm, and, for a density difference of ca. 10% between solid and liquid OMCTS (38, 39), we would expect dilations of ca. 0.2–0.5 nm as the solid OMCTS film fluidizes. Thus, we need to be able to detect temporally fleeting fluidization-induced dilations of this magnitude over a background of surface separation D that is undilated for almost the entire duration (∼99%) of the stick–slip run, and where the noise (ca. 1 nm peak-to-peak) is comparable with the signal sought.

We first establish the ability of the signal detection approach to correlate signals as in Fig. 3 A and B (assuming such a correlation exists), and to determine its resolution in detecting such correlated δD values. Assuming that each slip event corresponds to dilation in D of duration 20 ms (Fig. 2B, Inset), we carried out the following calibration measurements. To mimic the rigid coupling between the two mica surfaces arising from confinement of the OMCTS in its solidified phase, we clamped the lower surface in the SFB (Materials and Methods), so that the two surfaces were rigidly mounted with respect to each other in the normal direction. To mimic the sought dilation signals δD in Fig. 3A, we hold the surfaces apart in air and apply vertical displacement pulses (via the piezo tube mounting the top surface, Materials and Methods) of duration 20 ms at frequency 0.5 Hz and different amplitudes δD₀ = 0.126 ± 0.01 nm, 0.32 ± 0.01 nm, and 1.26 ± 0.01 nm. Simultaneously, we measure the surface separation via fast video recording of the interference fringes, as in Fig. 3B. Our aim is to check whether the resulting change δD recorded from the interference fringe position can be correlated with the δD₀ pulses. This is shown in Fig. 4.

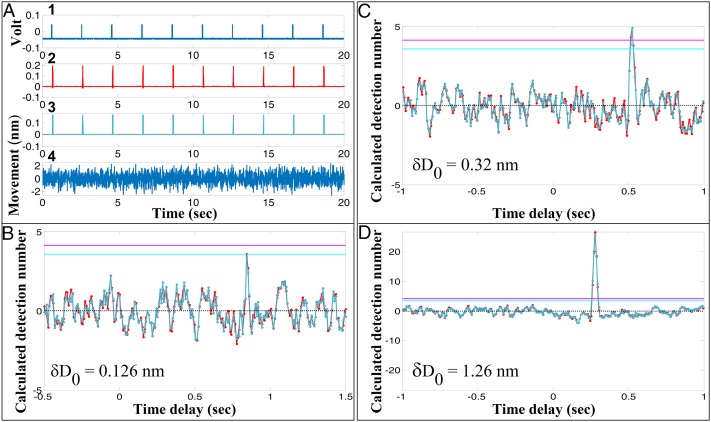
Fig. 4.

Correlation detection of fleeting applied dilation signals δD₀ with changes δD in recorded gap separation. (A, 1) Normal motion δD₀ (dilation of gap D) applied by voltage pulses on PZT (see Supporting Information and Fig. S1). (2) The natural signal (obtained for these control experiments by applying sampling rate conversion and normalization to the signal in 1; Materials and Methods and Supporting Information). (3) The functional signal, obtained by applying thresholding operations to the natural signal in 2 (Materials and Methods). (4) The fringe movement recorded by video. For this example, δD₀ = 0.126 ± 0.01 nm. See Materials and Methods for details of signal processing. (B) Correlation of natural (red) and functional (blue) dilation signals with changes δD in the intersurface gap D, for δD₀ = 0.126 nm, from A, as a function of synchronization delay time. Turquoise and purple horizontal lines are, respectively, the 1% and 0.1% false alarm probabilities. (C) As in B, but for δD₀ = 0.32 ± 0.01 nm applied amplitude. (D) As in B, but for δD₀ = 1.26 ± 0.01 nm applied amplitude. The presence at an appropriate delay time of a single detection number peak above the background, with a value reaching or exceeding the 1% false alarm probability, indicates correlation between the applied (δD₀) and detected (δD) signals.

In Fig. 4A, 1 shows a typical time trace of applied displacement pulses δD₀, in terms of the calibrated voltage pulse applied to the SFB piezo tube on which the upper mica surface is mounted (in air) (δD₀ = 0.126 ± 0.01 nm for this example). Fig. 4A, 2, the so-called “natural” signal, is for these control experiments, obtained by applying sampling rate conversion and normalization to the signal in Fig. 4A, 1 (Materials and Methods). Fig. 4A, 3 is the so-called “Functional” signal, obtained by applying thresholding operations to the natural signal of Fig. 4A, 2 (Materials and Methods). Finally, Fig. 4A, 4 gives the values of δD determined via fast video microscopy during the period of the applied displacements. We use the GLRT/CFAR protocol (Materials and Methods) to correlate the natural and the functional signals, derived from δD₀ (Fig. 4A, 2 and 3), with the δD signal of Fig. 4A, 4. Essentially, this is a convolution of the two sets of signals, whose output is a detection number. The value of the detection number is compared with a threshold, which is determined according to the noise statistics and is set such that the false alarm probability is 1% or 0.1%. Possible synchronization mismatch between applied signal, Fig. 4A, 1, and detected signal, Fig. 4A, 4, which may arise from nonsimultaneous commencement of the recording of the signals, is taken into account by repeating the convolution with delay increments (of 8 ms, the period of a single video frame), over a ca. 1-s range either side of the nominal start of the signal recording. Positive correlation between the applied δD₀ signal (Fig. 4A, 2 and 3) and the detected δD signal (corresponding to the change in surface separation, Fig. 4A, 4) is manifested as a single peak in the detection number above the background values (at the appropriate delay that precisely synchronizes the two sets of signals), whose value equals or exceeds the false alarm threshold. Full details are provided in Materials and Methods.

In Fig. 4 B–D, we plot the detection number for applied displacement pulses δD₀ = 0.126 nm, 0.32 nm, and 1.26 nm as a function of the time delay. We note at once that in all three cases, there is a marked single peak of the detection number for the particular time delay that synchronizes the signals, well above the background of (uncorrelated) detection numbers at different delay times; and that this peak—which we may call the correlation peak—reaches or exceeds the 1% or lower threshold for false alarm probability. A plot showing the variation of maximal detection number on δD₀ is shown in Fig. S2. We conclude that our experimental and signal processing system is clearly capable finding a correlation between applied δD₀ dilation pulses in the surface separation with amplitudes down to 1.2 Å and the changes in the surface separation as determined by fast video recording of the interference fringe positions. Moreover, the pulse duration, 20 ms, and 0.5-Hz frequency are comparable to the duration and frequency of slip events in stick–slip sliding, Figs. 2 and 3. We emphasize also that the noise level in the fringe position of these control experiments in air is, with peak-to-peak amplitude of ca. 2 nm (Fig. 4A, 4), significantly larger than the noise level when OMCTS is confined between the surfaces (Fig. 5), as there is little damping of ambient vibrations by the material (air) in the gap. The fact that we clearly observe correlations at this noise level even for the δD₀ = 0.126 nm and 0.32 nm applied signals reinforces our conclusion that in the stick–slip sliding, where the noise level is generally much lower, any such correlations would be easily identified.

Fig. 5.

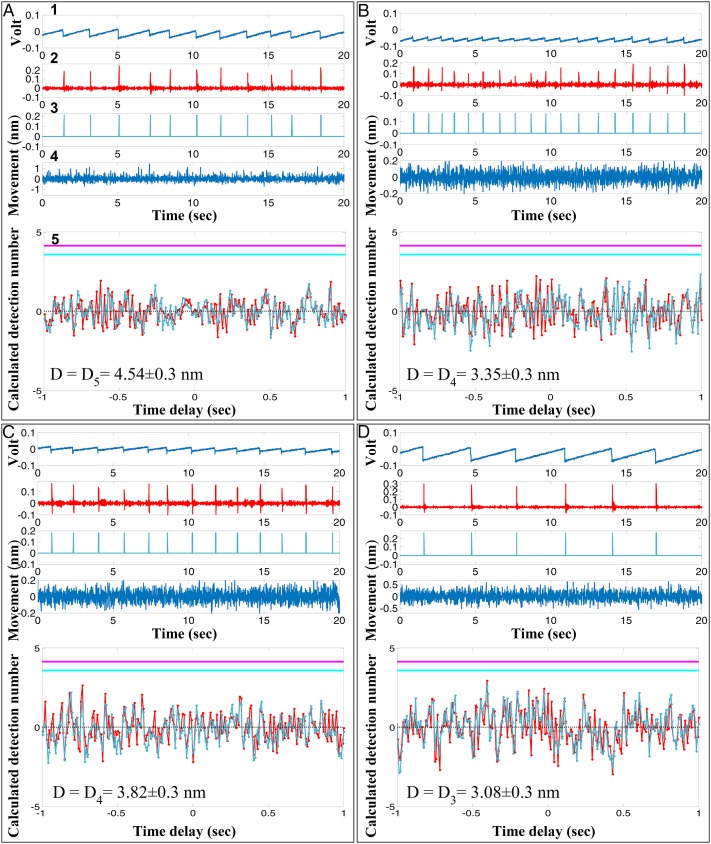
Correlation detection of slip events, during stick–slip sliding across OMCTS films of thickness D, with changes δD in gap separation. In each panel, 1 shows the stick–slip sliding trace as in Fig. 3A. Plots 2–4 are analogous to 2–4 in Fig. 4A, and consist, respectively, of the natural signal (obtained by taking the derivative of the stick–slip trace in 1), the functional signal based on 2, and the corresponding change δD in the OMCTS film thickness determined via simultaneous fast video recording. Plot 5 shows the detection number variation with delay time, analogous to Fig. 4 B–D, and indicates also the OMCTS thickness as D = D_n, where n is the number of confined layers. A–D show data from different contact points and experiments, where each panel shows the corresponding thickness of OMCTS film (data in this figure are taken from three independent experiments). The absence of a single correlation peak reaching the false alarm 1% threshold in any of the detection number vs. delay time plots indicates, in comparison with Fig. 4, that the slip events are not correlated with any dilation of the OMCTS film that is larger than ca. 0.1 nm.

This shows that we can with confidence apply this correlation-determining protocol to data such as in Fig. 3, where the stick–slip trace, Fig. 3A, should—if shear fluidization and consequent film dilation of a few angstroms occur at the slip events—provide a detection number trace with a clear correlation peak at an appropriate delay time, just as in Fig. 4. This was done in 15 independent measurements (different contact points in three independent experiments, i.e., different pairs of mica sheets, where layering was clearly evident) of stick–slip sliding across OMCTS films (thickness D) and simultaneous fast video recordings of the corresponding surface separations. Fig. 5 presents four typical measurements, taken from different experiments and across different thicknesses (and number of layers, n = 3–5) of the confined OMCTS showing the stick–slip traces, the corresponding fast video recordings of the surface separations, and the resulting detection number variation with delay time.

Inspection of Fig. 5 shows at once that there is no singular correlation peak approaching the 1% false alarm probability threshold in any of the detection number vs. delay time plots for the four stick–slip traces shown. This was the case with all 15 independent stick–slip traces measured. Comparing with the clear correlation peaks seen in Fig. 4 resulting from gap dilations δD₀ = 0.126 nm and δD₀ = 0.32 nm (let alone δD₀ = 1.26 nm), this demonstrates that there are no dilations, down to the ca. 0.1-nm level, that are correlated with the slip events in the stick–slip sliding. Since, for the film thicknesses D in the range 3–4.5 nm shown in Fig. 5, we expect fluidization during slip to result in a 10% dilation, or ca. 0.3–0.45 nm, this shows clearly that no fluidization of the confined OMCTS occurs during the slip events.

This unambiguous finding for a model lubricant system goes against the generally assumed scenario (17, 21–23, 25), that stick–slip sliding across a confinement-solidified lubricant film proceeds by fluidization (and accompanying dilation) of the film during the slip events. At the same time, we recall that there have not, to date, been measurements of the thickness of such films during the fleeting slip events themselves, so that our finding is, to our knowledge, the first direct experimental investigation of this. The inference from our results is that, at least for the model system studied here, stick–slip motion does not occur via repeating cycles of shear fluidization (slip) followed by solidification (stick), as such cycles should be correlated with film dilation, but by some other mode. It is appropriate to recall here an earlier investigation of single slip events in stick–slip sliding across confined OMCTS (18), where an “effective viscosity” of the sheared film was estimated by analyzing the relative motion during the slip (similar to that shown in Fig. 3B). This indicated a value some orders of magnitude higher than the bulk viscosity of the lubricant, but it may well be that a slip mechanism not involving shear melting could also explain the relative motion without the need to invoke shear-induced melting (19, 27). It is also of interest that a number of more recent theoretical and simulation studies of stick–slip across lubricant films have indeed indicated the possibility that the slip events take place via slip of the solidified film at the confining surfaces, or within the solidified film itself (between its layers), without fluidization (19, 27, 28). According to these (19), the energy required for shear melting exceeds the frictional dissipation energy during a slip, so that fluidization of the film does not occur. It may well be that the slip observed in our experiments takes place via such a mechanism. The simulation study of ref. 29, in which stick–slip behavior was observed between two surfaces sliding across a confined organic film whose density was kept constant (i.e., the surface separation did not change during the sliding, as in our experiments), is clearly also consistent with our findings. Given the increasing computing power enabling progressively more realistic calculations (19, 21, 25, 44, 45), a detailed simulation study of such slip, possibly emulating in detail the OMCTS/mica configuration described here, would yield considerable microscopic insight into this very common effect.

Materials and Methods

Materials.

All solvents used were analytical grade or purified water, while the OMCTS was highly purified by distillation. More details are provided in Supporting Information.

SFB Measurements.

The detailed experimental procedures used to measure the normal and shear forces between mica surfaces using an SFB, shown schematically in Fig. 6A, have been described in detail elsewhere (7), including the stringent cleaning procedures, and are detailed in Supporting Information.

Fig. 6.

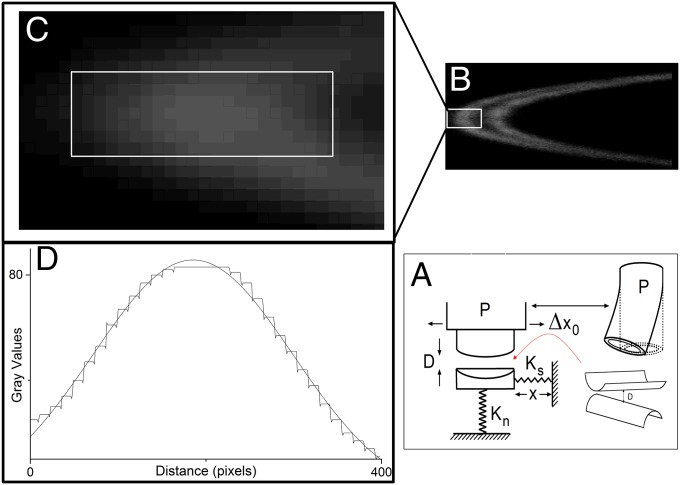
(A) Schematic of the SFB. The sectored piezoelectric tube on which the top mica surface is mounted is capable of both normal and lateral motion, the latter by applying equal and opposite voltages on opposing sectors. Further details are provided in Supporting Information. (B) Fringes of equal chromatic order as video recorded. The doublet arises from the mica birefringence. (C) Enlargement of fringe edge in B. White box demonstrates the selected array of pixels used to calculate the center of mass position of the fringe. (D) A gray values plot of one line of pixels; the solid black line represents a Gaussian fit of the data.

Video Image Capture and Analysis.

To track the surface movement during the very short (ca. 20 ms; see Fig. 2B) slip events, we capture the movement of the fringes by using a Sony HC-HR70 camera, frame grabbing at a rate of 118 frames per second, i.e., 3–4 frames per slip event, and, simultaneously, the shear forces as revealed from the bending of the shear springs, monitored by the change in capacitance of the air gap capacitor probe.

In the video SFB recording system used in this study, one pixel is equivalent to ca. 0.3 nm in absolute surface separation. To improve the imaging resolution, we used a center of mass algorithm to follow the movement of the fringe (Fig. 6B) in each frame by calculating the position of the brightest point in an array of pixels, Fig. 6 C and D (instead of simply following the brightest single pixel position at the middle of the fringe), which can simply be determined by using a Gaussian fit as in Fig. 6D. Frame grabbing is automated, as is the conversion of the fringe pattern to D values via fast algorithms.

Signal Detection.

Our aim is to look for a slight movement of the fringes (corresponding to film dilation, if any) that is correlated with the fleeting slip events. The motion (signal) we are trying to detect, of amplitude <0.5 nm, is comparable with the noise level in the fringe position (with peak-to-peak amplitude ca. 1 nm; see Figs. 3–5). Since this movement is expected to occur only during the ca. 20 ms of the slip event, i.e., typically during 1–2% of a stick–slip cycle, correlation between the two signals is far from obvious merely by visually comparing the two time plots of the signals (indeed, it is this that has, to date, made detection of such slip-associated dilation such a challenge). We therefore use a detection theory-based analysis to reveal such correlation. To test the two hypotheses, H0 (the fringe movements are uncorrelated with the slip events) against H1 (the fringe movements are correlated with the slip events), we use tools from classical detection theory using a GLRT with a CFAR (see, e.g., refs. 43 and 46). The underlying mathematical–statistical principles are briefly outlined in Supporting Information. In the following, we describe the experiment and the ensuing statistical tests results.

The stick–slip signal and the movement of the fringe are recorded simultaneously, with a possible synchronization mismatch and at different sampling rates (Supporting Information). We carry out some standard preprocessing stages, which include sampling-rates conversion (aimed at obtaining both signals at similar sampling rates), trend removal (basically, eliminating drift), and scale normalization (Supporting Information).

The raw stick–slip signal recorded by the oscilloscope is shown in Fig. 3A and in Fig. 5 for several stick–slip runs. The signal consists of a (relatively) long period when the surfaces are rigidly coupled (stick) and a short period (slip) when they slide past each other (a single slip is seen at high time resolution at the right of Fig. 2B). To correlate the slip events alone with the δD (fringe movement) signal, we take the derivative of the stick–slip signal with respect to time, which yields short duration peaks corresponding to the individual slip events, and an essentially constant value (which may be set to zero) during the stick period. This derivative of the stick–slip signal is the natural signal used by the detecting algorithm, and its peaks are used to determine the timing of the slip events. Since the exact expected shape of the presumed movement signal is unknown, and might not precisely follow the derivative of the stick–slip signal, we also generated a clean so-called functional signal for alternative detection, by applying some thresholding operations to the natural signal (Supporting Information).

The fringe position recorded by video during the stick–slip sliding is shown, for example, in Fig. 3B or in Fig. 5 (4 in Fig. 5 A–D. The stick–slip signal and the movement of the fringe are recorded simultaneously, with a possible synchronization mismatch. This time delay mismatch is taken into account when looking for correlation between the signals, as shown in the detection number vs. delay time plots in Figs. 4 and 5. The detection algorithm generates the detection numbers in these plots essentially by convoluting the two sets of signals: It multiplies each properly delayed (−1-s to 1-s) version of the target signal (natural or functional) with the measured signal (fringe movement) and integrates (sums) over the product, yielding a detection number for each time delay, (in Figs. 4 and 5, natural or functional are represented in red or azure lines, respectively). This detection number is compared with a threshold, which is determined according to the noise statistics (Supporting Information) and is set such that the false alarm probability is 1% or 0.1%. Obtaining a detection level that exceeds the threshold, at a certain time delay (that which precisely synchronizes the two sets of signals), will indicate sufficient correlation between the two signals for reliable preference of hypothesis H1 over H0. If the detection value does not exceed the threshold for any of the tested time delays, reliable preference of hypothesis H0 over H1 is established.

To establish the detection limit of this protocol, a control experiment was conducted, as described in Results and Discussion and in Fig. 4. To determine the amplitude of the applied changes (δD₀) in surface separation in this controls experiment, we clamped the normal force spring, held the surfaces apart in air, and applied measurable normal movements larger than the noise level. For each applied voltage on the piezo, we calculated the average amplitude of 100 measurements and built a calibration graph that represents the relation between the applied voltage on the piezo and the actual amplitude of movement (see Fig. S1). Movements below 0.5–1 nm are within the noise level; thereafter, their values were extrapolated linearly from the calibration graph (Supporting Information). In this way, we were able to apply the small amplitudes (down to ca. 0.1 nm) shown in the control experiment of Fig. 4.