Population dynamics of cancer cells with cell state conversions

Abstract

Cancer stem cell (CSC) theory suggests a cell-lineage structure in tumor cells in which CSCs are capable of giving rise to the other non-stem cancer cells (NSCCs) but not vice versa. However, an alternative scenario of bidirectional interconversions between CSCs and NSCCs was proposed very recently. Here we present a general population model of cancer cells by integrating conventional cell divisions with direct conversions between different cell states, namely, not only can CSCs differentiate into NSCCs by asymmetric cell division, NSCCs can also dedifferentiate into CSCs by cell state conversion. Our theoretical model is validated when applying the model to recent experimental data. It is also found that the transient increase in CSCs proportion initiated from the purified NSCCs subpopulation cannot be well predicted by the conventional CSC model where the conversion from NSCCs to CSCs is forbidden, implying that the cell state conversion is required especially for the transient dynamics. The theoretical analysis also gives the condition such that our general model can be equivalently reduced into a simple Markov chain with only cell state transitions keeping the same cell proportion dynamics.

INTRODUCTION

One of the salient features suggested by cancer stem cell (CSC) theory [1–3] is the hierarchical cell-lineage structure in tumorigenesis [4] associated with normal tissue biology. That is, CSCs are capable of continuous proliferation and giving rise to the other non-stem cancer cells (NSCCs) but not vice versa. CSCs are therefore called tumor-forming cancer cells, and the central role of CSCs has also been supported in metastasis and cancer recurrence [5,6]. More effectively CSCs-targeted therapies thus hold hope for improving survival and quality of lives [7,8].

However, recent studies challenged the theory and claimed that the relation between CSCs and NSCCs could be much more complicated. It was reported that CSCs can be generated from more differentiated cell states [8–13]. In particular, the conversion from NSCCs to CSCs was in situ visualized in Yang et al’s work [13]. An alternative scenario of CSC theory was thus proposed that bidirectional interconversions between CSCs and NSCCs could happen [10]. Even though this scenario remains controversial [14] and its molecular mechanism is poorly understood, these new ideas may provide valuable insights into cancer biology and therapeutic strategy. In this study, we present a general mathematical investigation for a further understanding of the relation between CSCs and NSCCs, especially with the aim of investigating the role of cell state conversion from NSCCs to CSCs in regulating cellular population structure in cancer. Mathematical exploration of cancer has been an important part of cancer research since the 1950s [15–17]. In recent years, CSC theory has become one of the major topics in mathematical cancer study [18–21]. In particular, the hierarchical organization of cancer was widely investigated in previous work [22–29], where the role of asymmetric and symmetric divisions of CSCs in the processes of carcinogesis received special attention [23,24,29]. However, less attention was paid to bidirectional conversions between CSCs and NSCCs. As a pioneering work, Gupta et al. introduced a Markov chain model of stochastic transitions between different phenotypic states of cancer cells [10], for explaining the phenotypic equilibrium in cell state mixture in breast cancer cell lines. In their model, the dynamic changes of cell state proportions in cancer were only attributed to cell state transitions which are not biologically justified before, where cell divisions and death that have extensively been investigated in conventional CSC model were not accounted for. Therefore, it is not mechanistically distinguishable whether the cell state equilibrium can be the evidence supporting the existence of bidirectional cell state conversions, or can only be a result of conventional CSCs mechanisms.

To systematically describe the biological kinetics of cellular population in cancer, we built a compartmental cell model [30] entirely upon biologically known cellular mechanisms, such as symmetric and asymmetric cell divisions of CSCs, symmetric cell division of NSCCs, and phenotypic conversions between different cell states. In particular, we term the model with positive conversion rate from NSCCs to CSCs the bidirectional model, otherwise it is called unidirectional model, i.e., unidirectional model describes the conventional hierarchical structure of CSCs model. Therefore, our approach provides a unified framework to investigate both conventional and bidirectional relations between CSCs and NCSSs.

By comparing the equilibrium behavior of the bidirectional and unidirectional models, we found that they both can display phenotypic equilibria in the proportion of cells in various states. That is, whether or not the phenotypic equilibria arise, it cannot be used as a significant criterion for distinguishing the two models.

However, based on the dynamic analysis of the transient behavior of the two models, we found that they will differ in their transient dynamics even when they both tend to the same equilibrium state. In particular, starting from a purified NSCCs subpopulation, i.e., when the initial proportion of CSCs is very small, the bidirectional model predicted a rapid rise of CSCs proportion, whereas the CSCs proportion in the unidirectional model gradually increased to its final equilibrium. We showed that this disparity between the two models can be applied to investigate the existence of cell state conversion from NSCCs to CSCs.

When applying our model to recent experimental data on cancer cell lines: On one hand, the time series data was well predicted by our bidirectional model; on the other hand, just as our theoretical result showed, the conversion from NSCCs to CSCs contributes to the transient increase in CSCs proportion shortly after the isolation of the NSCCs subpopulation.

Moreover, comparing our model with the Markov chain with cell state transitions [10], it is shown that our model can be a generalization of the Markov chain model. In particular, our model will be equivalent to the Markov chain only if different cell states in the population can equally contribute to the growth of the whole population. Otherwise, the dynamics of the proportions in various cell states should be captured by nonlinear models. Meanwhile, it is also found that the linearity of the model corresponds to the exponential growth of the whole population with a constant rate, which is in line with their hypothesis and interpretation of the experimental result [10].

RESULTS

The models

To apply the compartmental cell model to investigate the dynamics of cancer, we treat cancer as a population of different cell states [31], where each cancer cell can be assigned to one of the several phenotypic states: CSC, NSCC₁, NSCC₂, …, NSCCm. To better illustrate our model, we consider three cell states: CSC, NSCC₁ and NSCC₂. In particular, CSCs can not only replicate themselves by symmetric cell division, they can also differentiate into other NSCCs by asymmetric cell divisions:

$$\mathrm{C}\mathrm{S}\mathrm{C}\stackrel{{\alpha }_1}{\to }\mathrm{C}\mathrm{S}\mathrm{C}+\mathrm{C}\mathrm{S}\mathrm{C};$$

$$\mathrm{C}\mathrm{S}\mathrm{C}\stackrel{{\alpha }_2}{\to }\mathrm{C}\mathrm{S}\mathrm{C}+\mathrm{N}\mathrm{S}\mathrm{C}{\mathrm{C}}_1;$$

$$\mathrm{C}\mathrm{S}\mathrm{C}\stackrel{{\alpha }_3}{\to }\mathrm{C}\mathrm{S}\mathrm{C}+\mathrm{N}\mathrm{S}\mathrm{C}{\mathrm{C}}_2;$$

where α_i represent the division rates accordingly. In addition, cell death is also included in our model:

$$\mathrm{C}\mathrm{S}\mathrm{C}\stackrel{{\alpha }_4}{\to }\varphi .$$

For NSCCs, besides the symmetric cell divisions and cell death, i.e.,

$$\mathrm{N}\mathrm{S}\mathrm{C}{\mathrm{C}}_1\stackrel{{\beta }_1}{\to }\mathrm{N}\mathrm{S}\mathrm{C}{\mathrm{C}}_1+\mathrm{N}\mathrm{S}\mathrm{C}{\mathrm{C}}_1;$$

$$\mathrm{N}\mathrm{S}\mathrm{C}{\mathrm{C}}_1\stackrel{{\beta }_2}{\to }\varphi ;$$

$$\mathrm{N}\mathrm{S}\mathrm{C}{\mathrm{C}}_2\stackrel{{\mathrm{\gamma }}_1}{\to }\mathrm{N}\mathrm{S}\mathrm{C}{\mathrm{C}}_2+\mathrm{N}\mathrm{S}\mathrm{C}{\mathrm{C}}_2;$$

$$\mathrm{N}\mathrm{S}\mathrm{C}{\mathrm{C}}_2\stackrel{{\mathrm{\gamma }}_2}{\to }\varphi ;$$

the spontaneous cell state conversions between different cell states are also accounted for:

$$\mathrm{N}\mathrm{S}\mathrm{C}{\mathrm{C}}_1\stackrel{{\beta }_3}{\to }\mathrm{C}\mathrm{S}\mathrm{C};$$

$$\mathrm{N}\mathrm{S}\mathrm{C}{\mathrm{C}}_1\stackrel{{\beta }_4}{\to }\mathrm{N}\mathrm{S}\mathrm{C}{\mathrm{C}}_2;$$

$$\mathrm{N}\mathrm{S}\mathrm{C}{\mathrm{C}}_2\stackrel{{\mathrm{\gamma }}_3}{\to }\mathrm{C}\mathrm{S}\mathrm{C};$$

$$\mathrm{N}\mathrm{S}\mathrm{C}{\mathrm{C}}_2\stackrel{{\mathrm{\gamma }}_4}{\to }\mathrm{N}\mathrm{S}\mathrm{C}{\mathrm{C}}_1;$$

where β₃ and γ₃ are the reaction rates of the conversions from NSCCs to CSCs. We term this type of reactions the dedifferentiation reaction; while β₄ and γ₄ are the transition rates between NSCC₁ and NSCC₂.

The above group of biochemical kinetics schemes can be extended to the general case of CSC, NSCC₁, NSCC₂, …, NSCCm, providing a systematic framework to investigate the population dynamics of various cell states in cancer. For example, the breast cancer cell lines SUM159 and SUM149 were studied [10] and three cancer cell states (stem-like, basal and luminal corresponding to CSC, NSCC₁ and NSCC₂ respectively in our framework) were identified via cell-surface markers.

Denote the number of CSCs, NSCC₁ and NSCC₂ at time t as S_t, $N_t^{(1)}$ and $N_t^{(2)}$ respectively. Note that the change of S_t can arise not only from symmetric cell division and death of CSCs, but also from cell state conversions from NSCC₁ and NSCC₂, so the rate of change in S_t consists of

$$({\alpha }_1-{\alpha }_4)S_t+{\beta }_3{N}_t^{(1)}+{\mathrm{\gamma }}_3{N}_t^{(2)},$$

where α₁ − α₄ can be seen as the net growth rate of S_t contributed by CSCs themselves. Similarly, we can have the rates of changes in $N_t^{(1)}$ and $N_t^{(2)}$, then the dynamics of this population can be described by a system of ordinary differential equations (ODEs) of (S_t, $N_t^{(1)},N_t^{(2)}$)

$$\{\begin{array}{c}\frac{\mathrm{d}{S}_t}{\mathrm{d}t}=({\alpha }_1-{\alpha }_4)S_t+{\beta }_3{N}_t^{(1)}+{\mathrm{\gamma }}_3{N}_t^{(2)}\hfill \\ \frac{\mathrm{d}{N}_t^{(1)}}{\mathrm{d}t}={\alpha }_2{S}_t+({\beta }_1-{\beta }_2-{\beta }_3-{\beta }_4)N_t^{(1)}+{\mathrm{\gamma }}_4{N}_t^{(2)}\hfill \\ \frac{\mathrm{d}{N}_t^{(2)}}{\mathrm{d}t}={\alpha }_3{S}_t+{\beta }_4{N}_t^{(1)}+({\mathrm{\gamma }}_1-{\mathrm{\gamma }}_2-{\mathrm{\gamma }}_3-{\mathrm{\gamma }}_4)N_t^{(2)}\hfill \end{array}$$ (1)

where β₁−β₂−β₃−β₄ is the net growth rate of $N_t^{(1)}$ contributed by NSCC₁ themselves (similar to the biological meaning of γ₁ − γ₂ − γ₃ − γ₄). If time series data of (S_t, $N_t^{(1)},N_t^{(2)}$) can be experimentally measured, we can estimate the values of the coeffcients in Eq. (1) by statistic method, but not all the α_i, β_i and γ_i individually. For example, the value of α₁ − α₄ can be estimated, but we cannot estimate α₁ and α₄ individually (the same as β₁ − β₂ − β₃ − β₄ and γ₁ − γ₂ − γ₃ − γ₄). In other words, based on population-level data, we can only estimate the net growth rates accordingly. With the development of single cell technology, we believe that stochastic cell based model would be established in future as a powerful approach to resolve the parameters individually [32].

Interestingly, however, the reaction rates of the cell state conversions, i.e., β₃, β₄, γ₃ and γ₄ are present as independent coeffcients, namely, we can estimate all the conversion rates individually from the time series data on cell populations. When focusing on the general cell lineage relation between CSCs and NSCCs, we simplify the model to a population composed of only two cell states: CSC and NSCC (denote the numbers of CSCs and NSCCs as S_t and N_t respectively). When the conversion rate from NSCCs to CSCs is positive, i.e., β₃ > 0, we have the bidirectional model:

$$\{\begin{array}{c}\frac{\mathrm{d}{S}_t}{\mathrm{d}t}=({\alpha }_1-{\alpha }_4)S_t+{\beta }_3{N}_t\hfill \\ \frac{\mathrm{d}{N}_t}{\mathrm{d}t}={\alpha }_2{S}_t+({\beta }_1-{\beta }_2-{\beta }_3)N_t\hfill \end{array}$$ (2)

when β₃ = 0, i.e., there is no conversion from NSCCs to CSCs, the model will become the conventional hierarchical model of cancer cells, we term it the unidirectional model:

$$\{\begin{array}{c}\frac{\mathrm{d}{S}_t}{\mathrm{d}t}=({\alpha }_1-{\alpha }_4)S_t\hfill \\ \frac{\mathrm{d}{N}_t}{\mathrm{d}t}={\alpha }_2{S}_t+({\beta }_1-{\beta }_2)N_t\hfill \end{array}$$ (3)

In fact, the existence of dedifferentiation reaction distinguishes the bidirectional model from the unidirectional one.

Instead of the absolute numbers of cell populations, however, only the proportions of various cell states are usually experimentally measured. Thus one often converts the population model to a proportion one. Let s_t be the proportion of CSCs, n_t = 1 − s_t be the proportion of NSCCs, then the dynamics of CSCs proportion can be captured by the following nonlinear ODE (Supplemental Materials):

$$\frac{\mathrm{d}{s}_t}{\mathrm{d}t}=-A{s}_t^2+B{s}_t+{\beta }_3,$$ (4)

where A = (α₁ + α₂ − α₄) − (β₁ − β₂) and B = (α₁ − α₄) − (β₁ + β₃ − β₂). In particular, the nonlinear term A measures the difference between the net growth rates of the whole population contributed by CSCs, i.e., α₁ + α₂−α₄, and by NSCCs, i.e., β₁ − β₂. When β₃ = 0, the model will become

$$\frac{\mathrm{d}{s}_t}{\mathrm{d}t}=-A{s}_t^2+B{s}_t.$$ (5)

Eq. (4) corresponds to the bidirectional model, and Eq. (5) is for the unidirectional model.

Theoretical analysis of the models

Equilibria in cell state mixture of the two models

Previous work [10,13] has reported that the populations of cancer cells can display equilibria in cell state proportions. In both of our bidirectional and unidirectional models, the CSCs proportions can tend towards equilibria over time, independent of their initial nonzero proportions (Supplemental Materials). For the unidirectional model, in particular, if the net growth rate contributed by the symmetric cell division of CSCs is larger than that by NSCCs, the population will tend to nonzero equilibrium of CSCs proportion; otherwise NSCCs will take up the whole population. Therefore, even without cell state conversion from NSCCs to CSCs, given the above condition, the population driven by the unidirectional model can still maintain the equilibrium of the cell state proportions. This suggests that the proportion equilibrium in cell states cannot distinguish the bidirectional model from the unidirectional one, and then may not be used as a significant criterion for investigating the existence of dedifferentiation from NSCCs to CSCs.

Differences between the two models on the transient dynamics starting from very small CSCs proportion

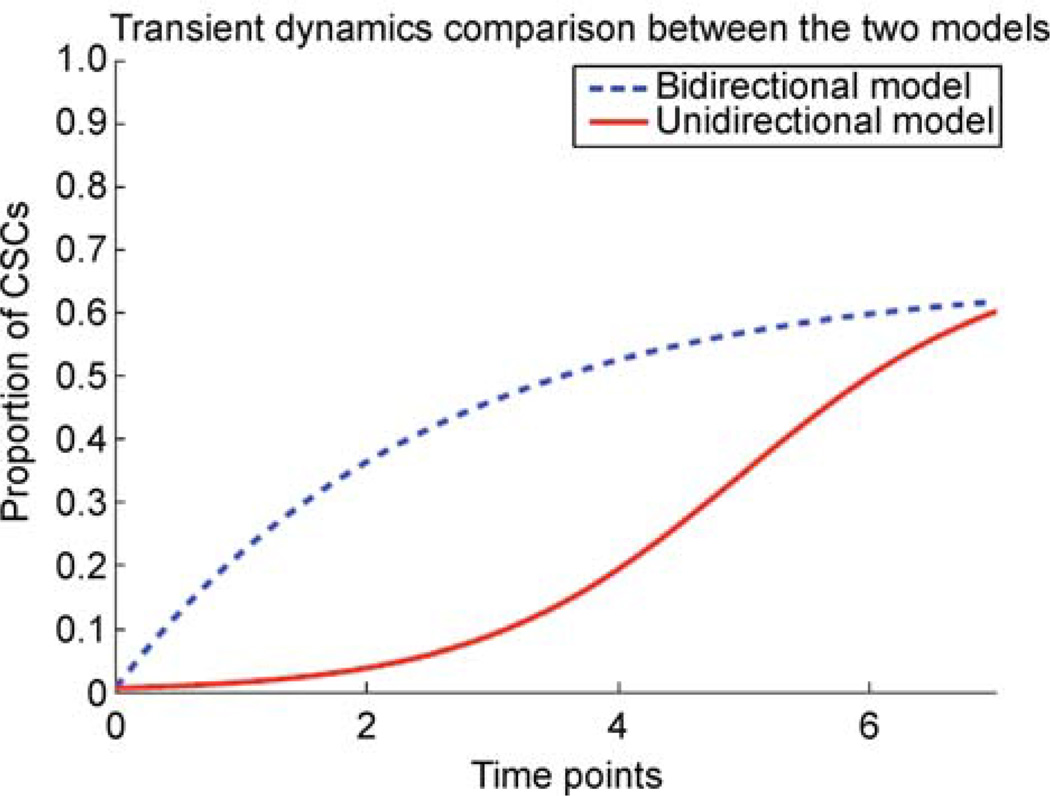
We now turn to the transient dynamics rather than the equilibrium behavior of the two models. Especially starting from a purified NSCCs population, i.e., when the initial value of CSCs proportion is very small, the two models differ a lot in their initial growth rates (Supplemental Materials). For the unidirectional model, the growth of CSCs is only contributed by the self-renewal of the residual CSCs themselves. Note that there are only a few residual CSCs shortly after the cell sorting of NSCCs subpopulation, and the initial growth of CSCs proportion should be very slow. Then the growth rate will gradually increase with the accumulation of CSCs. During this period, the trajectory of CSCs proportion is convex-like (Figure 1). Compared to the gradual increase predicted by the unidirectional model, the bidirectional model predicts a relatively rapid rise in CSCs proportion. This is due to the dedifferentiation reaction. Even though the amount of CSCs is very limited at the very beginning, the conversion from NSCCs to CSCs effectively speeds up the increase of CSCs in the population. From the example in Figure 1, it is shown that the disparity between the growths of the two models enlarges shortly after the initiation, and then gradually shrinks as they approach to their final equilibria. Note that after about 7 time points, the two dynamics would become essentially indistinguishable, and we call it the characteristic time before which the differences between the two models can be used to investigate the existence of cell state conversion from NSCCs to CSCs.

Figure 1. The comparison of the transient dynamics between bidirectional and unidirectional models.

To better illustrate our theoretical result, we set in this example that both models start from the same purity (about 99.5%) of NCSSs subpopultion, and end with the same equilibrium state (about 0.65). It is found that the two models differ in their transient dynamics. The disparity between the growths of the two models enlarges shortly after the initiation, and then gradually shrinks as they approach to their final equilibria. After about 7 time points, the two dynamics would become essentially indistinguishable.

The relation between our model and Markov chain model

To explain the phenotypic equilibrium in cell state mixture in breast cancer cell lines, Gupta et al. described the population dynamics of cancer cells by a Markov chain [10], where cell state transitions were the only biological mechanisms contributing to the dynamic change of cell state proportions, and the conventional cell divisions and death were totally ignored. We now discuss the relation between our model and theirs. Based on our theoretical analysis (Supplemental Materials), it is shown that their model can be a specific case of our framework only when the nonlinear terms in our model vanish. For the proportion model in Eq. (4), in particular, it could be equivalent to a Markov chain only when the nonlinear term A is negligible, implying that the trajectory of the cell proportions described in our model is exactly the same as the Markov chain with cell state transitions. Note that A = (α₁+ α₂ − α₄) − (β₁ − β₂) measures the difference between the contributions by CSCs and NSCCs to the whole population growth, and our result indicates that only if different cell states in the population can equally contribute to the growth of the whole population, the changes of cell state proportions can be equivalently described as a Markov chain only with cell state transitions. Otherwise, the Markov chain model cannot correctly capture the cellular kinetics. Considering the cell cycle time of CSCs and NCSSs can be different [33], one should be cautious about the scope of application of Markov chain method to the population modeling of cancer cells.

Nonlinear term

It was shown above that the nonlinear term plays a crucial role in determining whether our proportion model can be reduced into a Markov chain. Another biological significance of A is that, when A vanishes, not only will the proportion model be a linear equation, but the dynamics of the total population size will also be linear (Supplemental Materials), leading to the exponential growth of the whole population with a constant rate. In other words, when our proportion model can be equivalent to a Markov chain, the trajectories of the population dynamics will be exponential-like curves. It has been reported that the total population size of breast cancer cell line grew with constant doubling time [10], which is in line with the prediction of our theoretical result. Otherwise, when the nonlinear term are not negligible, the populations can be shown to grow as sigmoid-like curves (Supplemental Materials).

Model validation with experimental data

To validate our theoretical model with real experimental data, we now use two data sets of cancer cell lines from recent published work: SW620 colon cancer cell line [13], and SUM159 breast cancer cell line [10].

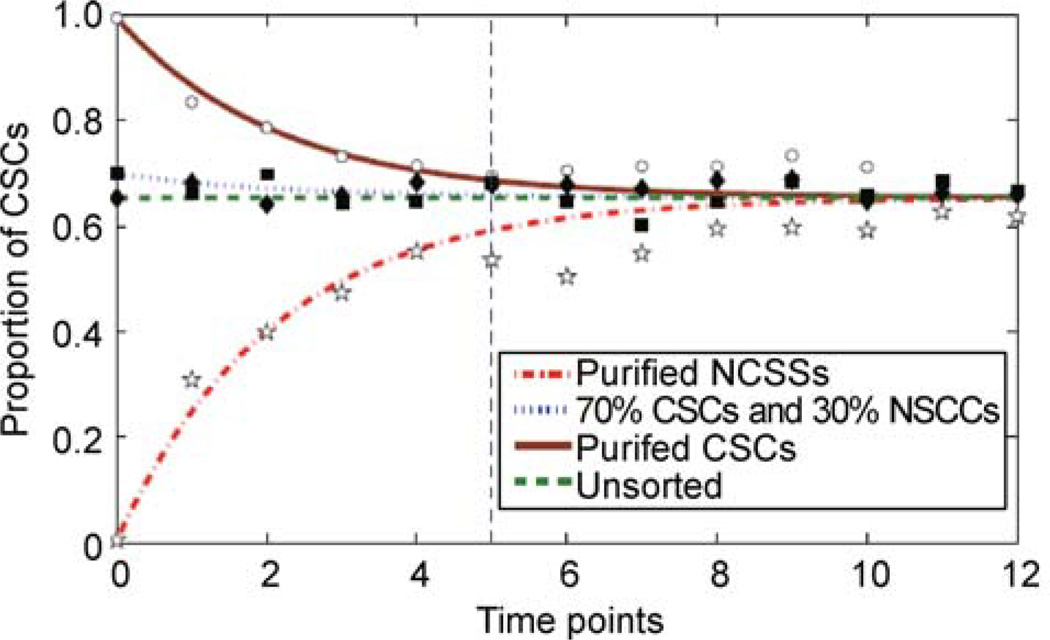
We first apply our model to the data on SW620 cell line (Figure 2). We estimated the parameters in Eq. (4) from the time series data on the first 6 (out of 13) time points by least squares method, and then predicted the values of CSCs proportion for the remaining time points. Figure 2 shows that the evolutions of CSCs proportions initiated from four different states can be well predicted by our model, where the best fit value of A is approximately zero. As discussed in the last section, A being zero corresponds to the well-balanced growth rates contributed by CSCs and NSCCs.

Figure 2. Validation of the bidirectional model (Eq. (4)) with the data on SW620 colon cancer cell line.

We trained our parameters with the data on the first 6 time points, then predicted the remaining time points of four different cases together with the best fitting parameters. The colorful lines are the trajectories predicted by the model, and the discrete dots are the experimental data accordingly. The best fitting parameters are A ≈ 0, B ≈ −0.40 and β₃≈0.26.

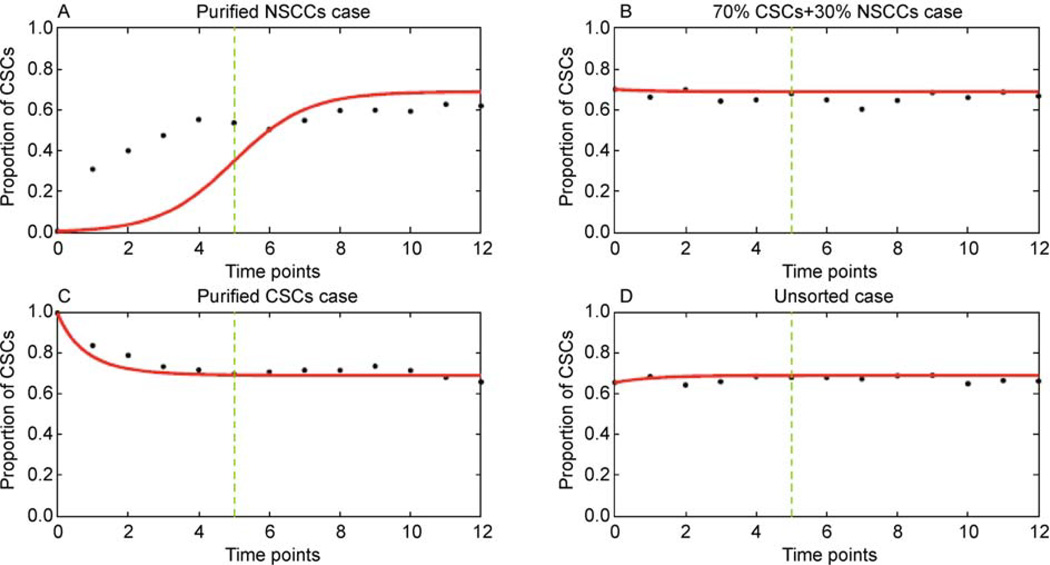
To further explore the role of dedifferentiation reaction in our model, we fitted the unidirectional model to the data. Except for the purified NSCCs case in Figure 3A, the other three cases in Figure 3B, C and D are still reasonably predicted by the model. For Figure 3A, in particular, we found that the increase of CSCs proportion in the first few days predicted by the unidirectional model is much slower than that measured on data. Actually, when initiated from the purified NSCCs, the increase of CSCs immediately after cell sorting could only be attributed to the self-renewal of the residual CSCs themselves when the conversion from NSCCs to CSCs was forbidden. However, based on the rate limitation of cell division cycle and the purity in the FACS experiment (at least 99% purity in Ref. [13]), even the most rapidly dividing human cells known cannot support such a rapid increase of cell state proportion [10,34]. It is thus suggested that the rapid increase of CSCs proportion in the transient dynamics could be conceptually explained by the dedifferentiation reaction. This is in line with our theoretical prediction.

Figure 3. Fitting the unidirectional model (Eq. (5)) to the data.

The red lines are the trajectories predicted by our unidirectional model, and the black dots are the experimental data. It is shown that in (B), (C) and (D), the predicted trajectories are in good accord with the data. In (A), however, we found that the increase of CSCs proportion predicted by our model is much slower than that shown on data in the first few days. The optimum parameters are A ≈ 1.39, B ≈ 0.96.

Similar results can be presented when we generalize our model to the case of three cell states (stem-like, basal and luminal) [10]. When applying our bidirectional model to their data on SUM159 cell line, we found that the trajectories predicted by our model are in good accord with theirs. We also fitted our unidirectional model with the data. The fitting result again implies that the conversion of NSCCs into CSCs is necessary for the transient dynamic regulation of cell population structure.

DISCUSSION

By adding cell state conversions into the conventional hierarchical organization of CSC paradigm, we have presented a mathematical framework that can provide theoretical insights into the population dynamics of cancer cells. It was found that the conversion from NCSSs to CSCs plays an important role in the transient dynamics, rather than the long-term equilibrium behavior. Growing evidence supports that cellular heterogeneity is essential in keeping cancer as an organic and adaptive complex system [35]. Our results support that the dedifferentiation mechanism could contribute to the robustness of cancer heterogeneity and survival after the perturbations (e.g., CSCs-targeted therapy) that try to eradicate CSCs. From an evolutionary point of view, bidirectional cell state conversions can be seen as a cooperative mechanism of different cancer cells that increases their collective fitness in the process of competing with various anticancer mechanisms [36]. This inspired us to rethink about therapeutic strategy of cancer. In particular, it is suggested that the targets of anticancer therapies should be balanced, that is, the effective therapies need to aim to the combination of CSCs and their niches.

Even though the bidirectional scenario has enriched the conventional CSC hypothesis, it seems to be too early to embrace the fundamental change in CSC theory. In particular, the molecular mechanism for the cell state conversion is poorly understood. It has been reported that TGF-β might have important roles in the conversion and homeostasis between CSCs and NSCCs through activating the process of epithelial mesenchymal transition (EMT) [13]. Further studies on related molecular-cellular systems should be important tasks in future. Currently, in particular, CSCs are often simply identified via one or several cell surface antigen markers (e.g., CD133 for SW620 colon cancer cell line [13]). With the rapid development of genomic and imaging techniques, it is believed that multi-dimensional genetic and epigenetic characteristics for different cell states will provide more detailed information to the researches of bidirectional conversions between CSCs and NSCCs in cancer.

Besides the deterministic models on cellular population level we studied in this work, stochastic molecular level models should be taken into account. From the viewpoint of stochastic dynamics, the cell state conversion can be seen as the stochastic transition from one epigenetic metastable state to another [37,38]. Therefore, with the accumulation of related high-throughput data, analytical and computational methods developed in stochastic network dynamics can be used to build reasonable models for interpreting the molecular mechanisms of the cell state conversions in cancer.

Moreover, according to the mathematical theory of nonequilibrium biochemical systems [39–41], our model can be shown not to satisfy the condition of detailed balance, implying that the process of our model shows time-irreversible complexity with associated cycle fluxes. The analysis of nonequilibrium properties in our model can also be interesting work in the future.