Limited Sampling Strategy and Target Attainment Analysis for Levofloxacin in Patients with Tuberculosis

Abstract

There is an urgent need to improve and shorten the treatment of tuberculosis (TB) and multidrug resistant tuberculosis (MDR-TB). Levofloxacin, a newer fluoroquinolone, has potent activity against TB both in vitro and in vivo. Levofloxacin dosing can be optimized to improve the treatment of both TB and MDR-TB. Levofloxacin efficacy is linked primarily to the ratio of the area under the concentration-time curve for the free fraction of drug (fAUC) to the MIC. Since obtaining a full-time concentration profile is not feasible in the clinic, we developed a limited sampling strategy (LSS) to estimate the AUC. We also utilized Monte Carlo simulations to evaluate the dosing of levofloxacin. Pharmacokinetic data were obtained from 10 Brazilian TB patients. The pharmacokinetic data were fitted with a one-compartment model. LSSs were developed using two methods: linear regression and Bayesian approaches. Several LSSs predicted levofloxacin AUC with good accuracy and precision. The most accurate were the method using two samples collected at 4 and 6 h (R² = 0.91 using linear regression and 0.97 using Bayesian approaches) and that using samples collected at 2 and 6 h (R² = 0.90 using linear regression and 0.96 using Bayesian approaches). The 2-and-6-h approach also provides a good estimate of the maximum concentration of the drug in serum (C_max). Our target attainment analysis showed that higher doses (17 to 20 mg/kg of body weight) of levofloxacin might be needed to improve its activity. Doses in the range of 17 to 20 mg/kg showed good target attainment for MICs from 0.25 to 0.50. At an MIC of 2, poor target attainment was observed across all doses. This LSS for levofloxacin can be used for therapeutic drug monitoring and for future pharmacokinetic/pharmacodynamic studies.

INTRODUCTION

Tuberculosis (TB) is the second leading cause of death from an infectious disease, behind HIV. In 2012, 8.6 million people developed TB, and 1.3 million died from it. Also, multidrug-resistant (MDR) and extensively drug-resistant (XDR) TB are on the rise. The WHO estimates that about 5% of the new TB cases globally are caused by MDR-TB, and of those, 9% are XDR-TB (1). This indicates that the current treatment is not adequate. The standard treatment of TB consists of rifampin, isoniazid, pyrazinamide, and ethambutol for 2 months, followed by rifampin and isoniazid for 4 to 7 months. The success rate for this regimen is relatively high (greater than 95%) based on per-protocol analyses of the initial clinical trials (2, 3). However, TB is still a worldwide pandemic, and even in the United States, with its excellent TB control efforts, only about 89% of patients complete treatment within 12 months, not 6 (4). Lack of adherence may lead to treatment failure and development of MDR TB.

The treatment of MDR-TB currently requires treatment for a minimum of 18 months with at least 4 drugs, including an injectable (aminoglycoside or polypeptide). Examples of second-line drugs used for MDR-TB include ethionamide, cycloserine, and p-aminosalicylic acid. Drugs that are used for MDR-TB are less effective and potentially more toxic than first-line drugs. Also, success rate for treatment of MDR-TB is low compared to drug-susceptible TB. The WHO estimates that success rate for MDR-TB is 48% (5). Therefore, it is important to improve and shorten the treatment of TB and MDR-TB.

Fluoroquinolones are commonly used for the treatment of TB and MDR-TB and have the potential to improve and shorten their treatment. Levofloxacin (LVX) is one of the preferred fluoroquinolones because of its potency and relative safety. LVX has both in vitro and in vivo efficacy against TB, with an MIC that ranges from 0.25 to 2.0 μg/ml (6, 7). Also, clinical trials suggest LVX has improved the treatment of MDR TB (8). However, the dosing of LVX currently used might be suboptimal (9, 10). Murine studies show that fluoroquinolones have dose-dependent activity against TB (6, 11). In the murine study by Shandil et al., ofloxacin (the racemic mixture which contains 50% LVX) was administered over a range of doses, and rather than reaching a plateau the log₁₀ CFU continued to decrease throughout the range of 2 to 320 for the ratio of the area under the concentration-time curve for the free fraction of drug (fAUC) to the MIC (11). Fluoroquinolones also clearly show dose-dependent activity when used to treat other bacterial infections. This dose-dependent activity is mainly driven by the fAUC/MIC ratio, followed by the fC_max/MIC ratio (11–13). The target fAUC/MIC ratio for fluoroquinolone bactericidal activity against infections with Gram-negative bacteria is 80 to 100. Schentag et al. suggested a higher fAUC/MIC ratio, >170, for more rapid killing of both Gram-negative and -positive pathogens (9, 10). A hollow-fiber study of moxifloxacin against TB suggested a fAUC/MIC ratio of 53 to completely suppress drug-resistant mutant population (12). Using these pharmacokinetic/pharmacodynamic (PK/PD) targets, the dosing of LVX can be optimized to maximize the exposure of LVX relative to its MIC. Monte Carlo simulation can be used to determine the optimal dose of LVX for a population. Also, dosing can be optimized at the individual level using therapeutic drug monitoring (TDM).

TDM can be used as a tool to determine plasma concentrations and to adjust doses based upon individual patient requirements. TDM has been shown to be beneficial in the treatment of TB (14–19). Additionally, several studies have shown that TB drug concentrations lower than the expected range are a risk factor for treatment failure (20–23). Also, LVX pharmacokinetics show moderate interindividual variability, which may pose additional challenges in LVX dose optimization. The AUC of LVX ranged from 103 to 358 μg · h/ml following a 1,000-mg dose in a previous pharmacokinetic study in TB patients (24).

During the TDM of LVX, blood samples usually are collected at 2 and 6 h postdose. The 2-h-postdose sample captures the C_max, and the 6-h sample distinguishes between delayed absorption and malabsorption (16). The suggested target range for LVX C_max LVX is 8 to 12 μg/ml. This corresponds to a C_max/MIC ratio of roughly 10 (16). However, as LVX efficacy is mainly linked to the fAUC/MIC ratio, it is important to have information regarding the LVX AUC. Since only limited samples are available during TDM, the estimation of LVX AUC can be a challenge. One approach to estimate the AUC is to use a well-designed, limited sampling strategy (LSS) (25, 26).

Two methods are available to develop a LSS: linear regression and Bayesian approaches. Linear regression has the advantage of simplicity, while Bayesian approaches are more accurate and robust but require the use of specialized pharmacokinetic software and training. As it is important to develop an approach to accurately estimate LVX AUC for patients with limited samples, in this study we remodeled a data set that we published previously to develop a LSS for LVX using linear regression and Bayesian approaches. We also utilized Monte Carlo simulations to evaluate the current dosing of LVX.

(Part of this work was presented at the 54th Interscience Conference on Antimicrobial Agents and Chemotherapy, Washington, DC, September 2014.)

MATERIALS AND METHODS

Study population and design.

The study included 10 newly diagnosed TB patients from Brazil (24). All patients were 18 to 65 years old and had relatively normal renal, hematologic, and hepatic functions. Patients received a 1,000-mg dose once daily and were sampled at 0, 1, 2, 4, 8, 12, 18, and 24 h after the fifth dose. Subjects fasted overnight before drug administration.

Analytical assay.

Samples were stored at –80°C until shipped to the United States. Samples were analyzed using a validated assay as previously described (24). In brief, we used a high-performance liquid chromatography (HPLC) system (Thermo-Finnigan, San Jose, CA) coupled with a FL3000 fluorescence detector (Thermo Electron Corporation, Waltham, MA). A six-point standard curve was used to determine unknown concentrations and ranged from 0.20 μg/ml to 15 μg/ml. The lower limit of quantification was 0.20 μg/ml. The overall validation precision for levofloxacin quality control samples was 0.76 to 4.83%. Accuracy was within 5% across the entire range of assay standards.

Model building.

We remodeled the data set using the parametric software Monolix (version 4.2). Monolix estimates model parameters using a maximum likelihood approach via the stochastic approximation expectation maximization algorithm (27). We used the same structural model as in the previous publication, a one-compartment model with first-order absorption and linear elimination (24). All pharmacokinetic parameters were assumed to be log-normally distributed. The residual variability was evaluated using constant, proportional, exponential, and combined error models. We also explored the possible correlation between pharmacokinetic parameters and covariates. Covariates included age, sex, body weight, and serum creatinine. Creatinine clearance (CL_CR) also was calculated using the Cockcroft-Gault equation. A stepwise regression using the likelihood ratio test was used to identify the significant covariates (a P value of 0.1 to be included in the model [forward addition] and a P value of 0.05 to be retained in the model [backward elimination]).

LSS.

The LSS was developed for LVX using both linear regression and a Bayesian approach. The final population pharmacokinetic model was used to simulate time-concentration profiles for 1,000 virtual patients. Concentrations were simulated at the following time points: 0, 1, 2, 4, 6, 8, 12, 18, and 24 h. Further, our lab has several data sets for TB patients from various countries, derived from other prospective studies (24, 28, 29). These data files were used to describe the patient demographics in the virtual population. The number of subjects included in the data set was 200. Each subject was replicated 5 times to get to 1,000 virtual patients. The averages (standard deviations) for age, weight, and serum creatinine were 38 years (13.5), 57.5 kg (10), 0.8 μg/ml (0.21), respectively. Females were 20% of the virtual population and on average had 15% lower body weight and 20% lower serum creatinine. The AUC from 0 to 24 h (AUC_0–24) for the simulated subjects was calculated using the trapezoidal rule (Phoenix software v.6.4). The main focus was to assess if samples collected at 2 and 6 h postdose accurately estimated the AUC_0–24. We also examined estimating the AUC_0–24 using different combinations of one or two samples collected between 1 and 6.

For the Bayesian approaches, pharmacokinetic parameters were fixed at the values obtained from the final model. Individual pharmacokinetic parameters were estimated for each individual using the limited samples design file that we created using Microsoft Excel. Bayesian estimation was obtained from following theorem:

$$P(\theta \hspace{0.17em}|\hspace{0.17em}x)=p(x\hspace{0.17em}|\hspace{0.17em}\theta )\times p\left(\theta \right)/p\left(x\right)$$

which states that the posterior probability [p(θ x)] of a pharmacokinetic parameter θ, given the data (x or measured concentration in a patient), is proportional to the product of the likelihood of the data [p(x | θ)] with the prior probability of the parameter p(θ).

In our study, the Bayesian (maximum a posteriori probability [MAP]) estimator for the ratio of clearance (CL) to F was used to predict the AUC for that individual as follows:

$${\text{AUC}}_{0-\tau }=\mathit{D}/\left(\frac{\text{Cl}}{\mathit{\text{F}}}\right)$$

For the linear regressing methods, AUC was regressed as a function of the concentrations at different time points. The observed AUC was considered the dependent variable, and LVX concentrations at different time points are the independent variables.

LSS validation and statistical analysis.

To assess the predictability of the strategy, we estimated the correlation coefficient between predicted and observed AUCs. The Bland-Altman plot was used to compare predicted and observed AUCs. We also calculated bias percent (mean prediction error) and precision percent (root mean squared error) as follows (30):

$$\text{Bias}\hspace{0.17em}\%=\frac{\mathrm{\Sigma }({\text{AUC}}_{\text{predicted}}-{\text{AUC}}_{\text{observed}})}{N}\times \left(\frac{100}{{\text{AUC}}_{\text{mean}}}\right)$$

$$\text{Precision}\hspace{0.17em}\%=\sqrt{\frac{\mathrm{\Sigma }{({\text{AUC}}_{\text{predicted}}-{\text{AUC}}_{\text{observed}})}^2}{N}}\times \left(\frac{100}{{\text{AUC}}_{\text{mean}}}\right)$$

Microsoft Excel and R software were used for all statistical analysis and plots (31).

Simulation and target attainment.

The final population pharmacokinetic model was used to perform simulations to help evaluate the dosing of LVX. The dosing regimens simulated were 11, 14, 17, and 20 mg/kg of body weight, rounded to the nearest 250. For a 70-kg individual, these doses approximately correspond to 750-, 1,000-, 1,250-, and 1,500-mg doses, respectively. The doses selected are the ones being evaluated by CDC TBTC study 32 (clinical trial NCT01918397).

The patient demographics used for the simulation were those used for the LSS. The data set contains 200 subjects, and it was replicated 50 times to get 10,000 virtual patients, using R software. The effect of covariates also was included in the simulations. From the simulated CL/F, we calculated the AUC for each virtual patient using equation 2.

Target attainment analysis was performed at MICs of 0.25, 0.5, 1, and 2 μg/ml. The protein binding for LVX was set at 0.4. Since no target has been validated for LVX against TB, we evaluated the target attainment at two different values (fAUC/MIC ratio of >53 or >100). Simulations and target attainment analysis were performed using the R software (31).

RESULTS

A total of 80 samples from TB patients were used for the development of the population pharmacokinetic model. The study included two females and eight males. The median body weight, age, and serum creatinine were 56 kg, 44 years, and 0.9 μg/ml, respectively.

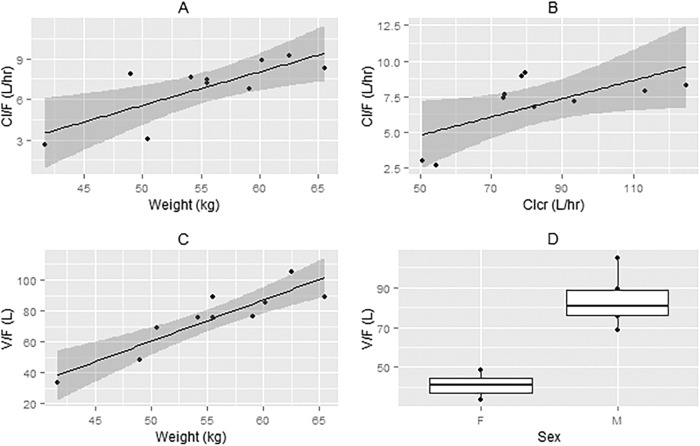
A one-compartment open model with linear elimination and first-order absorption adequately described the data. A combined error model best described the residual variability. Goodness-of-fit plots are shown in Fig. 1 and 2. Significant covariates included sex for the ratio of the volume of distribution (V) to F, body weight for V/F and CL/F, and CL_CR for CL/F (Fig. 3). The effect of body weight was modeled using a power function. The exponents were fixed at 1 and 0.75 for V/F and CL/F, respectively, and were scaled to the median body weight (56 kg). The effect of CL_CR on CL/F was modeled using a linear function and scaled to the median CL_CR (79 liters/h). Plots showing correlation between pharmacokinetic parameters and covariates are provided in the supplemental material. The final estimates for the model compared to the previous estimate from nonparametric expectation maximization (NPEM) are shown in Table 1.

FIG 1.

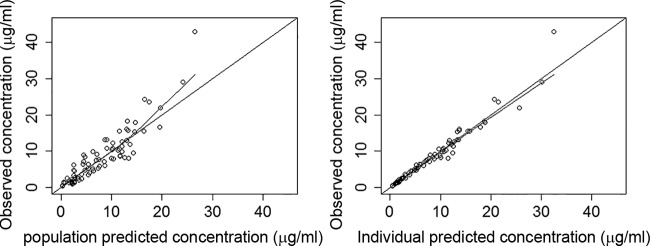
(Left) Population predicted versus population observed concentrations. (Right) Individual predicted versus individual observed concentrations.

FIG 2.

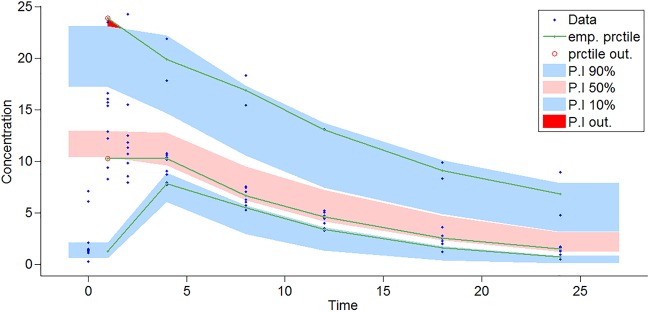
Visual predictive check (VPC) for LVX concentration (μg/ml) versus time (hours) based on 1,000 Monte Carlo simulations from the final population pharmacokinetic model. The solid green line represents the 10th, 50th, and 90th percentiles (prctile) of observed data. The shaded regions represent the 90% confidence interval around the 10th, 50th, and 90th percentiles of simulated data. The blue circles are observed concentrations. Abbreviations: emp. prctile, empirical percentile; P.I, prediction interval.

FIG 3.

Correlation between covariates and pharmacokinetic parameters. (A) Correlation between weight and CL/F. (B) Correlation between CL_CR and CL/F. (C) Correlation between weight and V/F. (D) Box plot of V/F by sex.

TABLE 1.

Parameter estimates for our final population pharmacokinetic model^a

Parameter	PK estimate from Monolix (RSE [%])	CV (%) (RSE [%])	Estimate from previous publication (24) using NPEM
Ka (h−1)	4.8	29.8 (128)	5.96
V/F (liters)		10.7 (32)	81.21
Male	79.1 (5)
Female	49.4 (9)
CL/F (liters/h)	6.22 (9)	26.4 (23)	7.63
Residual variability
a	0.0891 μg/ml (47)
b	11.6% (11)

^aAll pharmacokinetic parameters are expressed as medians. RSE, relative standard error; CV, coefficient of variation. The K_a estimate was capped at 5; the RSE was not estimated for K_a. Log(CL/F) = log(6.22) + 0.0107 * (CL_CR − 79.08) + 0.75 * [log(weight) − log(56 kg)]. Log(V/F) = log(79.1) − 0.472 * sex (female) + [log(weight) − log(56 kg)]; male was considered the reference population. For residual variability, a and b represent the constant and proportional parts of the residual variability, respectively.

LSS.

Tables 2 and 3 show the LSS results using both methods. The Bayesian estimator was consistently more accurate that the linear regression method. For the Bayesian approaches, a single time point collected at 6 h was the best predictor for AUC in terms of R² (R² = 0.95, bias = −0.32%, precision = 17%). For two sample time points, samples collected at 4 and 6 h were the best predictor of AUC in terms of R² (R² = 0.97, bias = −0.8%, precision = 10.5%). Samples collected at 2 and 6 h showed good predictability (R² = 0.96, bias = −0.6%, precision = 11.7%), with the 2-h sample providing a reasonable estimate of C_max.

TABLE 2.

LSS using Bayesian estimator

Sampling time(s) (h)	Bias (%)	Precision (%)	R2
1	−3.4	24.6	0.85
2	−1.5	21.2	0.88
4	−0.08	20.7	0.93
6	−0.32	17	0.95
1, 2	−1.5	19.8	0.90
1, 4	−0.007	15	0.94
2, 4	−0.5	14.3	0.94
2, 6	−0.6	11.7	0.96
4, 6	−0.8	10.5	0.97

TABLE 3.

LSS using linear regression

Sampling time(s) (h)	Equationa	Bias (%)	Precision (%)	R2
1	AUC = 19.4 + 7.8 C1	0	34	0.42
2	AUC = −1.16 + 10.4 C2	0	29	0.58
4	AUC = −10.4 + 14 C4	0	20	0.80
6	AUC = −2.1 + 16.6 C6	0	14	0.90
1, 2	AUC = −0.7 + −0.23 C1 + 10.7 C2	0	29	0.58
1, 4	AUC = −4 + −1.67 C1 + 15.8 C4	0	19.6	0.80
2, 4	AUC = −11 + 0.19 C2 + 13.9 C4	0	20	0.80
2, 6	AUC = −8.5 + 1.3 C2 + 15.4 C6	0	13.6	0.90
4, 6	AUC = −11 + 4 C4 + 12.7 C6	0	12.8	0.91

^aC1, C2, etc., are the concentration at 1 h, 2 h, etc.

For the linear regression methods, a single sample collected at 6 h was the best predictor for AUC in terms of R² (R² = 0.90, bias = 0%, precision = 14%). For the method using samples from two time points, samples collected at 4 and 6 h were the best predictors of AUC in terms of R² (R² = 0.91, bias = 0%, precision = 12.8%). Samples collected at 2 and 6 h showed good predictability (R² = 0.90, bias = 0%, precision = 13.6%). Figures 4 and 5 show the observed versus predicted AUC and Bland-Altman plot for predictions based on the 2- and 6-h sampling.

FIG 4.

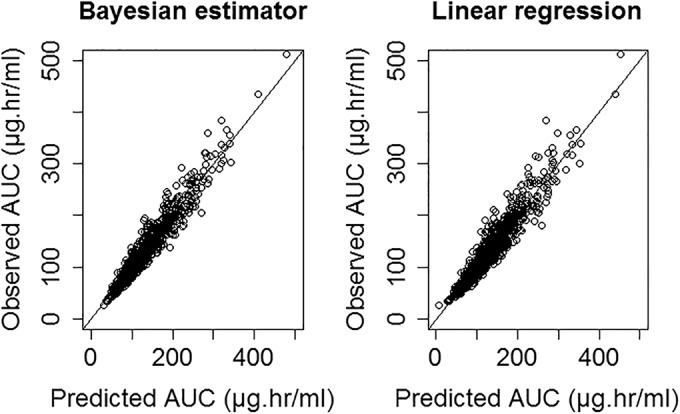
Observed versus predicted AUC using 2- and 6-h samples for both linear regression and Bayesian estimator.

FIG 5.

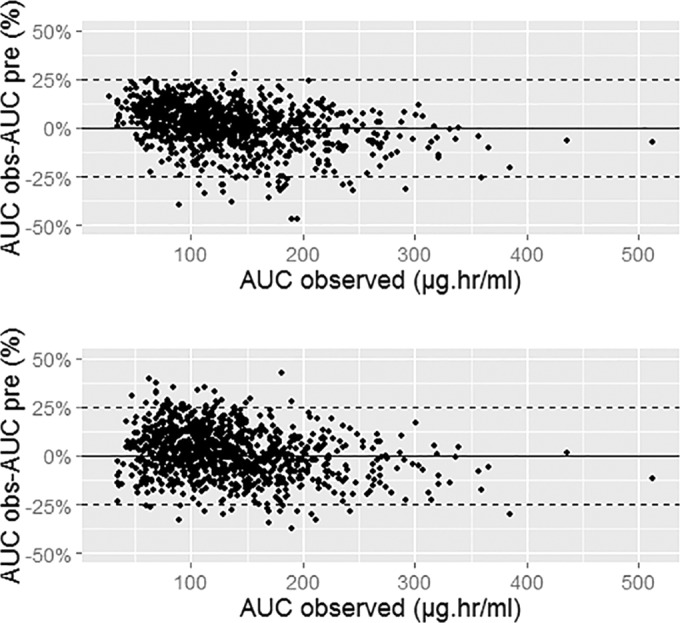
Bland-Altman plots using 2- and 6-h samples. (Top) Bayesian estimator; (bottom) linear regression-based method.

Simulation and target attainment analysis.

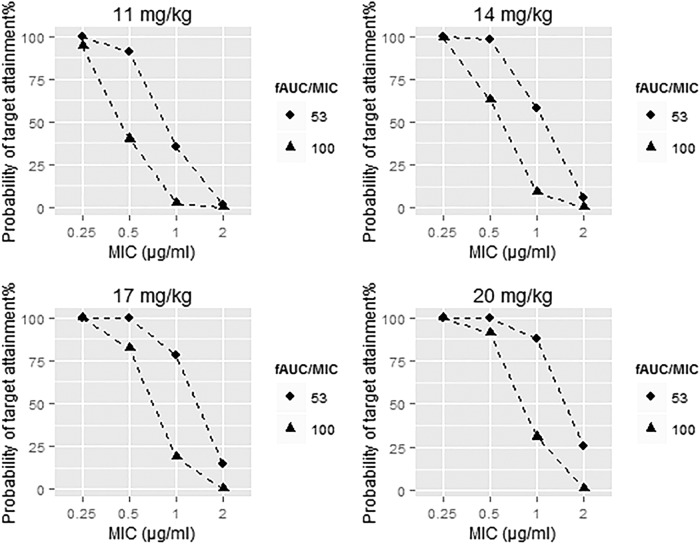
We utilized the final population pharmacokinetic model to simulate LVX AUCs at different dosing regimens and calculated target attainment at different MICs (Fig. 6). The equations and R code used for the simulations are shown in the supplemental material.

FIG 6.

Probability of target attainment for the different dosing regimens.

Target attainment was highly dependent on the MIC, as expected. At an MIC of 0.25 μg/ml, all four dosing regimens showed good target attainment at both targets (fAUC/MIC ratios of 53 and 100). At an MIC of 0.5 μg/ml, the 17- and 20-mg/kg doses showed good target attainment at both target ratios (53 and 100). At an MIC of 2 μg/ml, all dosing regimens showed poor target attainment, especially at the fAUC/MIC ratio of 100.

DISCUSSION

In our study we developed an LSS for LVX using both Bayesian approaches and linear regression. We focused on sampling strategies that utilize one or two samples collected 1 to 6 h postdose. This approach is feasible and can be applied in the clinic. When two samples were used for estimation of the AUC, the most accurate were those taken at 4 and 6 h postdose, followed by 2- and 6-h-postdose samples. The latter strategy, used at most centers for TDM of the TB drugs, offers a better estimate of C_max than does the 4-and-6-h sampling strategy. Optimal sampling strategy predicts that the latest possible measurable concentration would be the most highly correlated with CL/F and thus with AUC. In our case, a single-sample strategy was most accurate with a 6-h sample. However, this strategy does not offer clear information about C_max and cannot distinguish directly between delayed absorption and malabsorption. Our results also showed that the Bayesian estimator was more accurate than linear regression; however, linear regression methods are simpler and do not require experience in using pharmacokinetic software. The estimates can be determined using a spreadsheet or a handheld calculator.

Overall, this LSS can guide the TDM of LVX. One can use the LSS to achieve a desired AUC target for each patient. This would help minimize the variability in LVX AUC from patient to patient. Optimally, one would have both the individual MIC and the individual AUC for each patient. The objective would be to maximize the fAUC/MIC ratio to the desired, predefined number. Currently, MIC determinations and individual plasma protein binding studies are not a part of standard TB treatment. Until they become available, one would have to rely on locally reported values of MIC and literature values for protein binding (6). For example, assuming an MIC of 1, protein binding of 0.4, and a target fAUC/MIC of 53, the target AUC would be approximately 90. If the more stringent fAUC/MIC of 100 were desired, the target AUC would be approximately 170.

LSS models also can be used for pharmacokinetic/pharmacodynamic analyses. Several of the studies assessing the relationship between TB drug concentrations and outcome are based on routine TDM data. However, for most TB drugs, efficacy has been shown to be linked to the fAUC/MIC ratio (11, 32, 33). In order to do a more comprehensive concentration response analysis, one can utilize available LSS methods to calculate the AUC for patients with only sparse data. Several LSS methods have been developed for TB drugs, including rifampin, isoniazid, pyrazinamide, ethambutol, linezolid, and moxifloxacin (25, 34–36). However, unless MICs are determined, the exposure response analysis always will be limited.

The final estimates for our population pharmacokinetic model are similar to those in our previous publication (24) and other pharmacokinetic studies in different patient populations (37, 38). The CL/F for LVX was significantly influenced by both CL_CR and body weight. Therefore, weight-based dosing for LVX might be more appropriate. Also, it is important to consider renal function when dosing LVX. We used our final population pharmacokinetic model to perform target attainment analysis to evaluate the dosing of LVX. Doses in the range of 17 to 20 mg/kg showed good target attainment for MICs from 0.25 to 0.5 μg/ml. For an MIC of 1, only a 20-mg/kg dose showed good target attainment at the fAUC/MIC ratio of 53, while none showed good target attainment at the fAUC/MIC ratio of 100. At an MIC of 2 μg/ml, poor target attainment was observed across all doses, regardless of the target selected, suggesting that LVX might be less effective when the MIC is at 1 μg/ml or higher. The currently recommended dose of LVX is 500 to 1,000 mg daily. This dose corresponds to an 8- to 15-mg/kg dose for a 70-kg individual. Based on our simulations, these doses might be suboptimal, and using higher doses might be more efficacious. Also, using weight-based dosing instead of a fixed dose would decrease the variability in AUC. Another reason to emphasize using higher doses is to limit the risk of developing drug resistance. One concern with using fluoroquinolones is the rapid development of resistance (39, 40), especially given that TB patients are treated for longer periods than patients with other infections. The longer the patient is treated, the more likely resistance is to develop, especially with suboptimal dosing (41–45). The recent study by Cegielski et al. found that 11.2% of patients developed resistance to fluoroquinolones while on treatment for MDR-TB (46). Although dosing was not discussed in their paper as a possible cause for this, it likely was a factor in development of resistance to fluoroquinolones (47). Therefore, it is important to administer doses that are sufficient to kill and suppress the development of resistance. TBTC study 32 (clinical trial NCT01918397) is currently evaluating the efficacy of high-dose LVX in the treatment of MDR-TB. This study will help determine if using higher doses of LVX can help improve and shorten the treatment of MDR-TB.

One important limitation of our study is the small sample used for the population pharmacokinetic model. Also, all of our patients are from one site in Brazil, and our results might not be able to be generalized to all patients with TB/MDR-TB. To overcome the small sample size, we created a virtual population from our final model and developed the LSS from that population. The targets we utilized for our target attainment analysis have not been validated in clinical studies. The fAUC/MIC ratio of >53 is based on an in vitro study with moxifloxacin, and the fAUC/MIC ratio of >100 is extrapolated from other bacterial infections. We utilized these targets because of the lack of PK/PD studies for LVX against TB. Mycobacterium tuberculosis has a very low growth rate compared to other bacteria, and it not clear whether this target would also apply to Mycobacterium tuberculosis.

In conclusion, our analysis showed that LVX AUC can be estimated using limited samples in patients with TB. Our simulations also showed that doses higher than those currently used might be more efficacious. However, further investigations are warranted to better understand the pharmacokinetic/pharmacodynamics of LVX against TB to help its dose optimization.