CAN STABILITY REALLY PREDICT AN IMPENDING SLIP-RELATED FALL AMONG OLDER ADULTS?

Abstract

The primary purpose of this study was to systematically evaluate and compare the predictive power of falls for a battery of stability indices, obtained during normal walking among community-dwelling older adults. One hundred and eighty seven community-dwelling older adults participated in the study. After walking regularly for 20 strides on a walkway, participants were subjected to an unannounced slip during gait under the protection of a safety harness. Full body kinematics and kinetics were monitored during walking using a motion capture system synchronized with force plates. Stability variables, including feasible-stability-region measurement, margin of stability, the maximum Floquet multiplier, the Lyapunov exponents (short- and long-term), and the variability of gait parameters (including the step length, step width, and step time) were calculated for each subject. Accuracy of predicting slip outcome (fall vs. recovery) was examined for each stability variable using logistic regression. Results showed that the feasible-stability-region measurement predicted fall incidence among these subjects with the highest accuracy (68.4%). Except for the step width (with an accuracy of 60.2%), no other stability variables could differentiate fallers from those who did not fall for the sample studied in this study. The findings from the present study could provide guidance to identify individuals at increased risk of falling using the feasible-stability-region measurement or variability of the step width.

INTRODUCTION

Falls can result in injury, institutionalization, and even death in older adults (Bieryla et al., 2007). Slips during walking comprise 40% of outdoor falls among older adults (Luukinen et al., 2000). It is important to identify individuals at an elevated risk of falling before implementing effective fall prevention strategies. While it is logical to postulate that a person’s gait stability should yield useful clues as to the likelihood of falls (Hamacher et al., 2011), there is little consensus on how gait stability should be defined or measured. Though there are many measurements quantifying human gait stability, little evidences support their capability of actually predicting an impending fall.

The definition of a person’s stability can be based on the kinematic relationship between this person’s center of mass (COM) and its base of support (BOS) (Borelli, 1680), as it reflects a person’s ability to restore or maintain COM balance in upright posture without resorting to alter the existing BOS. Beyond the classical quantification of the limits of stability (i.e. within the confine of the BOS) which only deals with the relative position of COM to BOS, its extended conceptual framework measures the dynamic stability in terms of the relative motion state (i.e. the position and velocity) between COM and its BOS (Pai and Patton, 1997). Such conceptual framework has been used to estimate the feasible stability region (FSR) in the COM-BOS-state space in walking (Fig. 1). Two different methods: the 7-link model optimization (Yang et al., 2007) and a single-link pendulum model with a linear approximation of the equation of motion (Hof et al., 2005), have been used and different FSRs were established. The predictive measures characterized by these two methods will be named in the present study as FSR measurement and margin of stability, respectively.

Fig. 1.

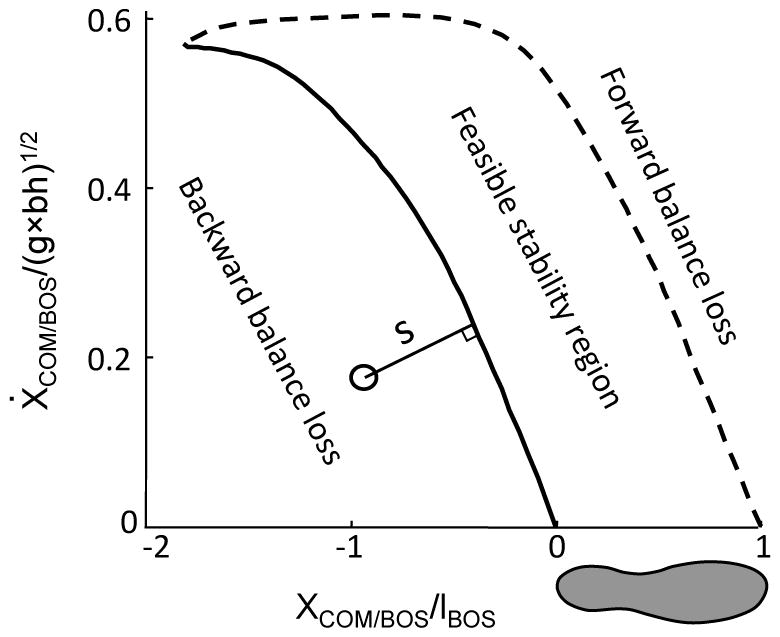
Schematic illustration of the feasible-stability-region (FSR) measurement (s). The thin solid line indicates the magnitude of the FSR measurement against backward balance loss, which was defined as the shortest distance from the given center of mass (COM) motion state (i.e., the combination of the COM anteroposterior position and forward velocity) to the limits against backward balance loss (the thick solid line). When the COM motion state is below/above the limits, the FSR measurement value is negative/positive, respectively. Also shown is the computer predicted FSR in the COM motion state space. The FSR is enclosed by two boundaries: the limits against backward balance loss and the one against forward balance loss (the thick dashed line). Position (X_COM/BOS) and velocity (Ẋ_COM/BOS) of the COM relative to the base of support (BOS) are dimensionless variables expressed as a fraction of l_BOS and $\sqrt{g\times bh}$, respectively, where l_BOS depicts the foot length, g is gravitational acceleration, and bh the body height.

Alternatively, gait variability has also been applied to quantify its stability. Based on the nonlinear dynamics theory for cyclical movement, variability in kinematics is indicative of stability (Dingwell et al., 2001; England and Granata, 2007; Hausdorff et al., 2001). Indices, such as the maximum Floquet multipliers (Dingwell et al., 2007) and Lyapunov exponents (Dingwell and Cusumano, 2000), have been employed to continuous joint or trunk kinematics (Bruijn et al., 2010; Dingwell and Kang, 2007) to respectively evaluate body orbital and local stability. During gait, perturbations can arise from internal (e.g. neuromuscular) and external sources (e.g. slip). Thus, the likelihood of falls is dependent not only on the individual’s neuro-musculoskeletal capacity, but on external factors like type and intensity of perturbations encountered in daily life. Indeed, some studies have proposed that the local stability (Lockhart and Liu, 2008) and the orbital stability (Grabiner et al., 2008; Hamacher et al., 2011) are able to differentiate fall-prone individuals from their health counterpart.

Further, simpler yet, descriptive spatiotemporal gait parameters such as the standard deviation of step length, step width or step/stride time can also yield useful information reflecting a person’s control of gait stability (Hausdorff et al., 2001; Owings and Grabiner, 2004; Woledge et al., 2005). It is unclear how well these methods can predict an impending slip-related fall in walking among community-dwelling older adults, and how well these approaches will fair relative to each other.

The purpose of this study was to evaluate the degree to which these stability measurements could predict an impending slip-related fall among community-dwelling older adults. We have been able to successfully induce inadvertent falls by initiating slips unknown to the walking older adults in a protective laboratory environment (Pai et al., 2014). The outcome from the gait-slip among older adults (fall vs. recovery) would be used to evaluate the capability of predicting slip-related falls for each one of these stability measurements.

METHODS

2.1 Subjects

One hundred and eighty seven community-dwelling older adults (age 71.9±5.1 years) participated in the gait-slip experiment (Table 1). All participants signed an informed consent form approved by the Institutional Research Board prior to participating in this study. They were free of any known neurological, musculoskeletal, or other systemic disorders that would have affected their postural control.

Table 1.

The demographics in mean ± SD and history of fall for both groups (fall vs. recovery).

Groups	Fall (n = 98)	Recovery (n = 89)	p value	Pooled (n = 187)
Age (years)	71.8 ± 5.5	71.9 ± 4.8	0.969	71.9 ± 5.1
Gender (female)	77 (78.6%)	52 (58.4%)	0.003 *	129 (69.0%)
Height (cm)	164.1 ± 7.5	168.8 ± 9.2	0.001	166.2 ± 8.6
Mass (kg)	75.8 ± 13.7	77.1 ± 14.0	0.515	76.4 ± 13.8
Fall history (%)	36.1	38.8	0.749 *	37.4

^*the χ² test was used.

2.2 Experimental set-up

An unannounced slip was induced as subjects walked along a 7-m instrumented pathway in which a sliding device was embedded. The device consisted of a side-by-side pair of movable platforms, firmly locked in place when subjects walked along the walkway during regular walking (Fig. 2) (Yang and Pai, 2007). They had a low profile approximately 6 mm above the walkway, and were mounted on top of a low-friction metal frame embedded in the walkway. The locks were electronically released, unknown to the person who stepped on the platform, to initiate a forward slip. The platforms were free to slide ≥0.75 m forward after release. During walking, all subjects wore a full-body safety harness which was connected to a bearing by shock-absorbing ropes at the shoulders and waist. This low-friction linear bearing moved smoothly along a ceiling-mounted track. The harness system protected subjects from any potential injuries during falling while imposing negligible resistance or constraint to their walking movement (Fig. 2).

Fig. 2.

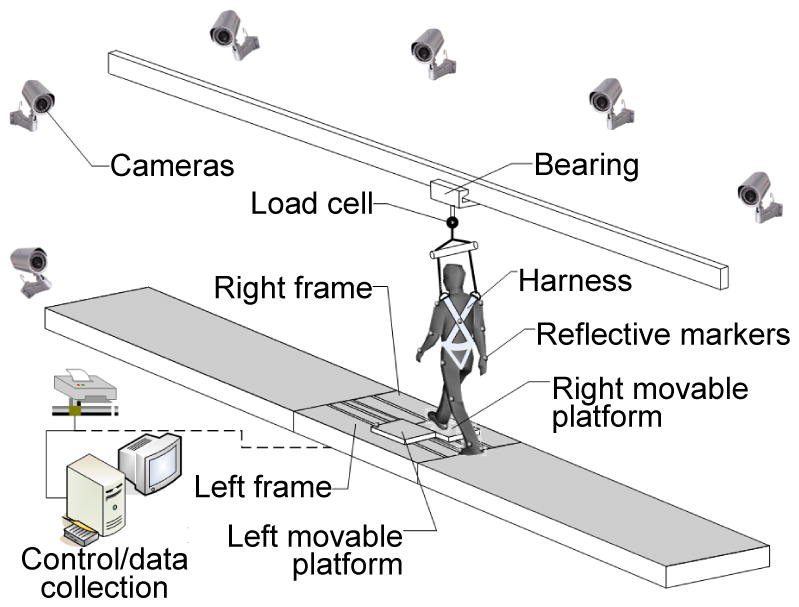
The diagrammatic representation of the experimental setup for inducing slip in gait. A slip is induced by releasing two low-friction movable platforms. Each of the two platforms is mounted on a frame with four linear bearings, and the frame was bolted to two force plates to measure the ground reaction force. The movable platforms were embedded in a 7-m walkway and made less noticeable to the subject by surrounding stationary decoy platforms. A set of 28 light-reflective markers were placed on bilateral upper and lower extremities, torso, and platforms. Their spatial positions were captured by an 8-camera motion capture system. The subjects were required to wear a safety harness which is individually adjusted to prevent a fall to the ground. A load cell was used to measure the force exerted on the harness.

Subjects were instructed to walk in their preferred speed. Although they were informed that a slip might occur later, they were not aware when, where, and how it would happen. They were also instructed to try to recover their balance after slipping and continue walking forward. After approximately 20 normal walking strides, the right platform was released immediately after the right (slipping) foot contacted it. The left platform would then be released once the subjects’ left (recovery) foot landed on it during the slip trial. The detection of foot contact was based on the measurement from four force plates (AMTI, Newton, MA) installed beneath the metal frames.

2.3 Data reduction

Full body kinematics data from 28 retro-reflective markers placed on the subjects’ body and platforms were gathered using an 8-camera motion capture system (MAC, Santa Rosa, CA) at 120Hz synchronized with the force plates and load cell at 600Hz. Locations of joint centers, heels, and toes were computed from the filtered marker positions. The body COM kinematics (including its position and velocity) was computed using gender-dependent segmental inertial parameters (de Leva, 1996) based on a distributed-mass human model. The trunk segment’s position and orientation were calculated from the joint centers of shoulders, hips and neck marker (C7) as well as sacrum marker (Online Supplement). The vertical component of the ground reaction force was used to identify the instants of touchdown in gait.

The outcome of slip was classified as a fall if the peak load cell force exceeded 30% body weight (bw) (Yang and Pai, 2011). The falls were confirmed via visual inspection of recorded video. A recovery occurred when the moving average of load cell force on the harness did not exceed 4.5%bw over any one second period after slip onset (Yang and Pai, 2011). If the average load cell force exceeded 4.5%bw over any one second period after the slip occurred, but the load cell force never reached a peak of 30%bw, this trial would be identified as harness assistance (Yang and Pai, 2011). The harness assistance trials would be excluded from further analysis due to the uncertainty of determining the slip outcome without the harness. No one was identified as harness-assistance trial in this study.

2.4 FSR measurement

The FSR measurement (s, the length of the thin solid line in Fig. 1) indicates the magnitude of the instantaneous dynamic stability of the COM against backward falling. The stability is calculated as the shortest Euclidean distance from the COM motion state to the limits against backward falling (thick line in Fig. 1) (Yang et al., 2008a; Yang et al., 2008b). The two components of the COM motion state, i.e. its position (X_COM/BOS) and velocity (Ẋ _COM/BOS) were calculated relative to the BOS and normalized by l_BOS and $\sqrt{g\times bh}$ respectively, where l_BOS represents the foot length, g is the gravitational acceleration and bh the body height (Fig. 1). The approaches to calculate the FSR measurement and their Matlab codes can be found in the supplemental material of our previous publication (Yang et al., 2008a). The FSR measurement was calculated at the instant of right foot touchdown immediately prior to the slip onset upon the slip trial.

2.5 Margin of stability

The margin of stability in the anteroposterior direction is calculated as the difference between the anteroposterior boundary of the BOS and the extrapolated impending COM location (X_COM) (Hof et al., 2005). The extrapolated COM can be calculated as

$$X_{\text{COM}}=x+\frac{v}{{\omega }_0}$$

where x denoted the anteroposterior position of the body COM, v represented the anteroposterior velocity of body COM, and ${\omega }_0=\sqrt{g/l}$; l was the equivalent pendulum length, which in this study was taken as the distance from the body COM to right ankle center. The margin of stability (b) was then defined as:

$$b=X_{\text{COM}}-X_{\text{BOS}}$$

where X _BOS was the backward boundary of the BOS (i.e. the right heel). The margin of stability was also calculated at the instant of right foot touchdown prior to slip onset in the slip trial.

2.6 Floquet multiplier

To assess the orbital (Floquet multiplier) and local (Lyapunov exponent) dynamic stability during gait, the trunk segment kinematics over all 20 cycles (or strides, from a touchdown to next touchdown of the same foot) during normal walking prior to the novel slip trial were used. The 6-dimensional state space was built for the trunk’s kinematics as (Kang and Dingwell, 2006):

$$\mathbf{S}(t)=[x,y,z,\theta ,\phi ,\psi ]\in {\mathfrak{R}}^6$$

where x/y/z represented the anteroposterior/mediolateral/vertical position of the trunk center; and θ/φ/ψ denoted the 3-dimensioal rotational movement of the trunk: roll/pitch/yaw. The details of calculating trunk kinematics were provided in Online Supplement.

The Floquet multiplier was estimated based on the well-developed method to characterize the orbital stability (Dingwell and Kang, 2007; Donelan et al., 2004; Hurmuzlu and Basdogan, 1994). First, the state space built above was partitioned into individual gait cycles and then each cycle was evenly divided into 100 intervals, corresponding to 0–100% of entire gait cycle (Dingwell and Kang, 2007). Poincare maps were then defined for each percent of the gait cycle as:

$${\mathbf{S}}_{i+1}=\mathbf{F}\left({\mathbf{S}}_i\right)$$

where S_i is the state of the system at strike i at each given Poincare section (i.e. at each percent of the gait cycle). Fixed points for each Poincare map (S*) were defined from the average trajectory across all strides. Thus:

$${\mathbf{S}}^{\ast }=\mathbf{F}\left({\mathbf{S}}^{\ast }\right)$$

The Floquet multiplier of the system was then estimated from a linearized approximation of the Poincare map:

$${\mathbf{S}}_{i+1}-{\mathbf{S}}^{\ast }\approx \mathbf{J}\left({\mathbf{S}}^{\ast }\right)\left({\mathbf{S}}_i-{\mathbf{S}}^{\ast }\right)$$

where, the J(S*) ∈ ℜ^6×6 is the Jacobian matrix of the system for each Poincare section (percent of the gait cycle). The Jacobian matrix was determined by solving above equation using a least squares algorithm (Bruijn et al., 2009; Hurmuzlu and Basdogan, 1994). The first 5 eigenvalues of J(S*) defined the Floquet multiplier (Bruijn et al., 2009; Donelan et al., 2004; Hurmuzlu and Basdogan, 1994; Kang and Dingwell, 2008; Kuo, 1999). The last (i.e., the 6^th) eigenvalue of J(S*) had a value of ~0 and was thus false (Kang and Dingwell, 2008). The magnitude of the maximum Floquet multiplier of each percent of the gait cycle was calculated. These Floquet multiplier values were then averaged to obtain the maximum Floquet multiplier over all strides, which were used in the present study.

2.7 Lyapunov exponents

Short-term and long-term Lyapunov exponents were calculated to quantify the local stability. From the constructed state spaces as mentioned above, Euclidean distances between neighboring trajectories in the state space were calculated as a function of time and averaged over all original nearest neighbor pairs to obtain the average exponential rate of divergence (Dingwell and Cusumano, 2000; Rosenstein et al., 1993):

$$y(i)=\frac{1}{\mathrm{\Delta }t}\langle ln\left[d_j(i)\right]\rangle =\left[{\lambda }^{\ast }\right]i+ln\left[d_{0j}\right]$$

where d_j (i) represents the Euclidean distance between the j^th pair of nearest neighbors after i discrete time steps (i.e. iΔt); 〈·〉 denotes the average over all values of j (Rosenstein et al., 1993), and d_{0 j} is the initial value of d_j. The slope of the mean logarithmic divergence curve is used as a measure of the divergence (Dingwell and Marin, 2006). Short-term exponents were calculated as the slopes of linear fits to the divergence curves between 0 and 0.5 stride, while long-term exponents were taken as the slopes between strides 4 and 10 (Bruijn et al., 2009; Dingwell and Cusumano, 2000).

2.8 Gait parameters

We first computed the step length, step width, and step time for those 20 normal walking strides (Owings and Grabiner, 2004; Woledge et al., 2005). The variability of these gait parameters was then calculated as the standard deviation of the step length, step width, and step time over all step cycles which started at the heel strike and finished at the next heel strike of the contralateral foot. The step length/step width was the anteroposterior/mediolateral distance between heels at touchdown. The step time was the time elapsed between two consecutive touchdowns. These measurements were assessed to evaluate the temporal and spatial aspects of the gait parameters.

2.9 Statistical analysis

Independent t-test and χ² test were used to examine whether the demographics and fall history were different between groups (fall vs. recovery, Table 1). Independent t-tests were also employed to identify if the eight predictors, including the FSR measurement, the margin of stability, the Floquet multiplier, the short-term Lyapunov exponent, the long-term Lyapunov exponent, and the variability in step length, step width, and step time, demonstrated significant outcome-related difference (Table 2). Logistic regression was then conducted to examine the prediction power of each variable with outcome (fall vs. recovery) as the dependent variables (Table 3). Sensitivity, specificity, and likelihood ratio analyses were performed for each predictive variable between fallers and those who did not fall based on the cutoff score predicted from the logistic regression (which was set at 0.5). Odds ratios were also calculated for each predictive variable based on the logistic regression coefficient and its standard deviation (SD) across all subjects (Table 4). All statistics were performed using SPSS 19.0 (IBM Corp., Armonk, NY), and a significance level of 0.05 was used throughout.

Table 2.

Comparisons of all predictive variables organized by slip outcome (fall vs. recovery).

Variables		Fall (n = 98)	Recovery (n = 89)	p value
Feasible-stability-region measurement		−0.181 ± 0.048	−0.156 ± 0.047	< 0.001
Margin of stability		0.039 ± 0.058	0.051 ± 0.052	0.162
Floquet multiplier		0.422 ± 0.044	0.432 ± 0.044	0.121
Lyapunov exponent	Short-term	0.671 ± 0.442	0.737 ± 0.587	0.383
	Long-term	0.034 ± 0.036	0.026 ± 0.045	0.205
Gait parameters variability	Step length (m)	0.070 ± 0.040	0.062 ± 0.035	0.113
	Step width (m)	0.031 ± 0.013	0.027 ± 0.010	0.009
	Step time (sec)	0.044 ± 0.020	0.041 ± 0.019	0.460

Table 3.

Prediction sensitivity, specificity, and likelihood ratios of slip outcomes (fall vs. recovery) from logistic regression analysis based on each predictive variable.

Predictive variables		Sensitivity		Specificity		Overall prediction (%)	Likelihood ratio		p value	Threshold
		Value (% fall)	95% CI	Value (% recovery)	95% CI		Value	95% CI
Feasible-stability-region measurement		68.4	58.6–76.7	56.2	45.8–66.0	62.6	1.56	1.19–2.05	< 0.001	−0.160
Margin of stability		71.4	61.8–79.4	36.0	26.8–46.3	54.5	1.12	0.91–1.36	0.166
Floquet multiplier		71.4	61.8–79.4	43.8	34.0–54.2	58.3	1.27	1.02–1.59	0.121
Lyapunov exponent	Short-term	84.7	76.3–90.5	15.7	9.61–24.7	51.9	1.01	0.89–1.14	0.383
	Long-term	65.3	55.5–74.0	48.3	38.2–58.6	57.2	1.26	0.99–1.62	0.205
Gait parameters variability	Step length	63.3	53.4–72.1	47.2	37.2–57.5	55.6	1.20	0.94–1.54	0.116
	Step width	60.2	50.3–69.3	48.3	38.2–58.6	54.5	1.17	0.90–1.51	0.011	0.026
	Step time	84.7	76.3–90.5	18.0	11.4–27.2	52.9	1.03	0.91–1.17	0.459

CI: confidence interval.

Table 4.

Odds ratio for slip-related falls for all predictive variables of slip outcome

Predictive variables		SD	Odds ratio	95% CI
Feasible-stability-region measurement		0.048	1.74	0.96–3.16
Margin of stability		0.055	1.22	0.66–2.26
Floquet multiplier		0.044	1.26	0.69–2.32
Lyapunov exponent	Short-term	0.516	1.14	0.52–2.51
	Long-term	0.041	1.22	0.68–2.20
Gait parameters	Step length (m)	0.066	1.27	0.71–2.28
	Step width (m)	0.029	1.50	0.92–2.93
	Step time (sec)	0.019	1.11	0.52–2.41

^*The odds ratio indicates the factor by which the fall probability increases with an increase (for Lyapunov exponents and gait parameters) or decrease (for the feasible-stability-region measurement, margin of stability, and Floquet multiplier) of 1SD in the variable across all subjects.

CI: confidence interval.

RESULTS

Ninety-eight people (52.4%) fell and 89 recovered successfully. The margin of stability, the Floquet multiplier, and both short- and long-term Lyapunov exponents were not significantly different between fallers and those who did not fall (Table 2, p>0.05 for all). Among the gait parameters, only the variability of the step width differed between falls and recoveries: fallers had greater variability in step width than those who did not fall (Table 2, p<0.01). However, fallers and those who recovered exhibited similar variability in step length and step time (Table 2, p>0.05). The FSR measurement was significantly different between the fall and recovery groups at touchdown during gait. Falls were more instable in comparison with recoveries at touchdown (Table 2, p<0.001).

The logistic regression model revealed the predictive ability of these variables (Table 3). The variability in step width, and the FSR measurement achieved significance level (p<0.01 for step width variability and p<0.001 for FSR measurement, Table 3) in predicting slip outcomes. Between these two predictors, FSR measurement was the one with the greater overall prediction accuracy (62.6%); followed by the variability in step width (54.5%). None of other variables reached the significance criterion (p>0.05). A decrease of 1SD (=0.048 across all subjects) in FSR measurement increased the probability of falling by 1.74 (Table 4). An increase of 1SD of variability in step width (=0.029m) increased the odds of falling by a factor of 1.50 (Table 4).

DISCUSSION

The results indicated that the FSR measurement offers the best prediction of the slip outcome during gait among older adults, followed by the variability of the step width. Both appear to have reasonable ability (62.6% and 54.5%, respectively) to predict an impending recovery or fall from a slip in gait. Other measurements failed to differentiate falls from recoveries.

The FSR measurement reflects the simultaneous control of both COM position and velocity relative to the BOS (Pai, 2003). The latter is critically dependent upon how well a person executes a protective stepping to recover from a severe postural perturbation such as gait-slip. A balance loss is a precursor of a fall during an unannounced novel slip (Yang et al., 2007). One of the criteria to derive the FSR was to prevent the person from a loss of balance during gait (Yang et al., 2008a). Nonetheless, not all loss of balance has led to an actual fall. An effective protective step can quickly restore stability after the slip, and this might explain why the FSR measurement only had a limited success (62.6%) in predicting the outcome from an impending falls. Previous empirical findings have demonstrated that together, FSR measurement and another measurement of a person’s limb support can nearly fully (~100%) account for the outcome following gait-slip among young adults (Yang et al., 2011).

The margin of stability was proposed based on a simplified inverted pendulum model with linear approximation of the solution of its equation of motion (Hof et al., 2005). While this approach is highly attractive due to its simplicity, the linearity may not quite accurately characterize the limits of stability at a movement speed range like that during walking (Hof et al., 2005). This might be why the margin of stability was not different between fallers and those who did not fall in this study (Table 2).

Increased variability in gait parameters has been prospectively associated with an increased risk of falls in elderly subjects (Hausdorff et al., 2001; Maki, 1997). Healthy elderly also exhibit increased step width variability (Owings and Grabiner, 2004). Consistent with the literature, the results from the present study indicated that gait variability, particularly in step width, was another variable showing significantly group-related difference. The variability of step width was able to correctly predict approximately 54.5% of the overall slip outcome in this study. The increased step width variability may have implications for the placement of feet and further the lateral instability during gait (Bauby and Kuo, 2000; Kuo, 1999). It has been proposed that lateral instability plays a critical role in predicting falls among older adults (Maki, 1997). Hence, the variability of step width in the current study shows evident predictive power of slip outcome. Although the predictive power of step width is slightly (8%) less than the FSR measurement, the variability in step width could still be an important predictor of potential falls due to its remarkable simplicity.

Both the local stability (Lyapunov exponents) and orbital stability (Floquet multiplier) failed to distinguish fallers from those who did not (Table 2). One potential reason could be that both of them did not directly account for the dynamic mechanisms underlying the variability (Beauchet et al., 2007). A dynamic system, especially a human body, can be described as a complex neurocontroller coupled with a nonlinear biomechanical system. Limit-cycle behavior generated by this system is influenced by input disturbances causing output variance. Therefore, output variability is a product (convolution) of input disturbances, neuromuscular control, and biomechanical dynamics. A basic assumption of these approaches is that an increased variability in walking pattern is indicative of impaired motor control. However, the extent to which this variability is equal to stability is not clear (England and Granata, 2007); there might be a difference between variability and instability (Beauchet et al., 2007). A person’s successful recovery from a slip perturbation was mainly controlled by the entire dynamic system. The probability of falls after slip will not only depend upon gait variability, but also on the placement of protective stepping after the onset of perturbation. It is possible that both FSR measurement and the variability of the step width reflect the foot placement that is associated with essential aspects of the impending stepping behavior (Bruijn et al., 2011; Yang et al., 2009).

Another possible explanation could be that both orbital and local stability reflect the response characteristics to a small external or internal disturbance of a dynamic system (Dingwell and Cusumano, 2000; Dingwell and Kang, 2007; Hurmuzlu and Basdogan, 1994). However, slip perturbations encountered in the present study (the maximum slip distance could reach 90cm) were considerably large in scale. Given such an intensive external perturbation, the orbital or local stability may not be able to detect a system’s perturbation response correctly. Consequently, both of them did not exhibit any group-related difference and failed to differentiate fallers from those who recovered. Further, due to its inherent cycle-to-cycle variability, human gait is neither strictly periodic (a requirement of orbital stability calculation) nor strongly aperiodic (an assumption of local stability computation) (McAndrew et al., 2011). These factors may also contribute to the failure of these two in predicting slip outcome.

Contrary to the present findings, some studies proposed that the local stability (Lockhart and Liu, 2008) and the orbital stability (Grabiner et al., 2008; Hamacher et al., 2011) are able to differentiate fall-prone individuals from their health counterpart. Several factors may contribute to such discrepancy. First, the subject selections were different between studies. The fall-prone older adults in previous studies (Grabiner et al., 2008; Lockhart and Liu, 2008) were identified by their history of falls (at least one fall within 6 months). Among our study participants, past fall incidence did not correlate with their immediate lab reproduced falls as evidenced by nearly equal past fall rates in both the fall and recovery groups (36.1% vs. 38.8%, Table 1). Although approximately 37% of our participants reported having had one fall in the past year; this would not be sufficient to classify them as being fall-prone. Further, the investigated falls were different between studies. The causes of falls for fall-prone people in previous studies could be any possible factors, not limited to slip (Grabiner et al., 2008; Lockhart and Liu, 2008).

Since over-ground walking is more natural, we collected the gait-slip date during over ground walking rather than on treadmill. However, this set-up limited our ability to collect sufficiently long data set because the person would “walk out” of the motion capture area. The limited data may not lead to accurate calculation of Floquet multipliers and Lyapunov exponents. This may further affect the predictive capability of slip-related falls for both orbital and local dynamic stabilities. To our best knowledge, there is no guideline or consensus on the minimal length of data series required to yield acceptable estimates (Bruijn et al., 2009). As the first attempt of its kind, the present study still shed light on the relative predictive power across various contemporary methods. To examine the predictive capability of falls for various stability indices based on huge amount of continuous strides would merit our further effort.

In summary, the study has indicated the FSR measurement provides the best prediction on falls or slip-recovery. On the other hand, the variability of the step width may be the most practical measurement due to its simplicity. The findings from the present study could provide guidance to identify individuals at raised fall risk using these two measurements of stability, especially among a seemingly non-symptomatic population (e.g. community-living older adults) before they actually experience an injurious fall, which would be essential for fall prevention.