Kernel Approach for Modeling Interaction Effects in Genetic Association Studies of Complex Quantitative Traits

Abstract

The etiology of complex traits likely involves the effects of genetic and environmental factors, along with complicated interaction effects between them. Consequently, there has been interest in applying genetic association tests of complex traits that account for potential modification of the genetic effect in the presence of an environmental factor. One can perform such an analysis using a joint test of gene and gene-environment interaction. An optimal joint test would be one that remains powerful under a variety of models ranging from those of strong gene-environment interaction effect to those of little or no gene-environment interaction effect. To fill this demand, we have extended a kernel-machine based approach for association mapping of multiple SNPs to consider joint tests of gene and gene-environment interaction. The kernel-based approach for joint testing is promising, since it incorporates linkage disequilibrium information from multiple SNPs simultaneously in analysis and permits flexible modeling of interaction effects. Using simulated data, we show that our kernel-machine approach typically outperforms the traditional joint test under strong gene-environment interaction models and further outperforms the traditional main-effect association test under models of weak or no gene-environment interaction effects. We illustrate our test using genome-wide association data from the Grady Trauma Project, a cohort of highly traumatized, at-risk individuals, which has previously been investigated for interaction effects.

INTRODUCTION

In recent years, many genetic studies of complex human traits have employed genome-wide association studies (GWAS) to enable near-comprehensive assessment of common genetic variation across the genome. Empirical evidence suggests that common genetic variation plays an important role in many complex traits and diseases, with common variants estimated to explain 25-33% of risk to schizophrenia [International Schizophrenia, et al. 2009; Lee, et al. 2012], 40% of risk for bipolar disorder [Lee, et al. 2011], and 50% of risk for autism spectrum disorder [Gaugler, et al. 2014], among other traits. However, even in studies involving tens of thousands of study subjects, the identification of specific common trait-influencing variation remains elusive. One potential reason for the lack of replicable GWAS hits is that a single-nucleotide polymorphism (SNP) may influence a trait but the effect is modified by an interaction with an environmental factor [Ioannidis 2007] such as age [Province, et al. 1989; Shi, et al. 2009; Simino, et al. 2014]. If one ignores the gene-environment interaction effect and considers only the marginal effect of the SNP, the causal SNPs might regrettably be disregarded. Additionally, the differences in the distribution of the environmental factor between the initial and validation studies could impede replication of the initial SNP finding. This possibility, along with the observation of gene-environment interactions in various genetic studies [Caspi, et al. 2002; Caspi, et al. 2003; Duncan and Keller 2011; Jarvik, et al. 1997; Ober and Vercelli 2011; Shaffer, et al. 2015; Uher 2014; Wilhelm, et al. 2006] has spurred interest in performing genome-wide association studies of complex traits that accounts for possible genetic modification of effect by environment [Gauderman, et al. 2013; Kim, et al. 2014; Xu, et al. 2013].

To account for possible modification of genetic effects by environment in candidate-gene and GWAS projects, one can apply a joint test of SNP main effect and SNP-environment interaction effect on phenotype. Such a joint test can be more powerful than a test of SNP main effect alone if an interaction exists [Chatterjee, et al. 2006; Kraft, et al. 2007]. A typical joint test involves fitting a regression model that accounts for the main effect of a single SNP, main effect of the environment, and a two-way interaction between the SNP and environment. One then constructs from the fitted regression model a two degree-of-freedom test of the joint null hypothesis that there is no SNP and no SNP-environment interaction effect, typically using a Wald or likelihood-ratio statistic [Kraft, et al. 2007; Wang, et al. 2008].

While some recent interaction findings using methods like the joint test as well as other procedures have been reported (e.g. [Binder, et al. 2008; Bradley, et al. 2013; Gauderman, et al. 2013; Kim, et al. 2014; Liao, et al. 2013; Shaffer, et al. 2015]), by and large the field has not matured in a way to match its propitious beginnings [Duncan and Keller 2011; Munafo, et al. 2014]. A possible explanation lies with an inherent motivation behind interaction studies: one reason to include a modifying effect of environment within a genetic analysis is to find subgroups of individuals where the genetic effects are of larger magnitude than the overall group as a whole, and thus gain power over genetic studies that fail to account for the environmental modifier. This gain in power occurs when the interaction effect is much larger than the main effect, such as when a genotype has an effect on phenotype in the presence of environmental effect but no effect in the absence of the exposure (termed “complete” interaction: see model M1 in Figure 1). However, when the interaction effect is of equal magnitude or smaller than the main SNP effect (see models M3-M5 in Figure 1), a main effect test (which has 1 degree of the freedom less than the joint test) might perform similarly or even better than the joint test [Kraft, et al. 2007; Zammit, et al. 2010].

Figure 1.

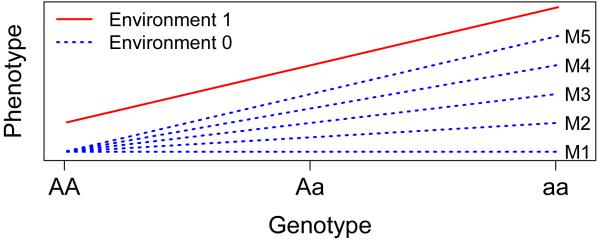
A range of possible gene and gene-environment models, from M1 (complete interaction) to M5 (no interaction). The red line represents genotypic effect among individuals who have been exposed to the environmental insult. The 5 blue lines represent possible genotypic effects for individuals who were not exposed to the environmental insult, resulting in models that range from complete interaction (M1) to no interaction (M5).

When there is interest in considering the modifying effects of genotype on phenotype in the presence of interaction with environment, an optimal joint association test would then be one that remains powerful under a variety of interaction models, ranging from those of strong interaction effect to little or no interaction effect [Hunter and Kraft 2007; Sullivan 2007; Zammit, et al. 2010]. To fill this demand, we present an approach to performing a joint test of gene and gene-environment interaction for common SNPs that builds upon the kernel-based methods introduced by Kwee et al. [Kwee, et al. 2008] and Wu et al. [Wu, et al. 2010] to test for genetic main effects. Our kernel-based approach for joint analysis begins by grouping SNPs into SNP sets based on prior biological knowledge. We then apply a kernel function that quantifies the pairwise similarity between subjects based on the genotypes of the SNPs falling within the set, as well as environmental exposure. By introducing a garrote parameter into the kernel function (as considered in Maity and Lin [Maity and Lin 2011] for microarray analysis), we can then construct a score statistic to assess whether pairwise genetic similarity in the presence of possibly modifying effects of environment correlates with phenotypic similarity.

The kernel-based approach to joint gene and gene-environment interaction testing is promising for three reasons. First, examining sets of SNPs rather than each SNP independently (as done in the methods of Kraft et al. [Kraft, et al. 2007] and Wang et al. [Wang, et al. 2008]) will greatly reduce multiple-testing burden. For example, in a GWAS, while the traditional single-SNP regression approach could result in millions of tests [Wang, et al. 2005], grouping all typed SNPs into genes and then implementing the kernel-based approach will result in ~20,000 tests [International Human Genome Sequencing Consortium 2004]. Second, since multiple typed markers are likely to be in linkage disequilibrium (LD) with the causal variant, joint consideration of these markers will capture the effect of a true causal variant more effectively than independent marker testing. Third, the kernel approach readily allows for inclusion of prior information (such as biological plausibility or association signals from prior association studies) in the form of weights to assist in the formation of the kernel matrix. SNP set methods have proved to be more powerful than univariate testing of main genetic effects [Kwee, et al. 2008; Tzeng, et al. 2011; Wu, et al. 2010] and we anticipate similar trends when considering joint tests of gene and gene-environment effects.

The remainder of this manuscript is organized as follows. We first describe our joint SNP set analysis framework, including how to form SNP sets and how to test SNP sets for association using a kernel framework that allows for potential modifying effects by an environmental factor. Next, we present simulation results comparing our joint approach both to traditional joint tests of gene and gene-environment interaction as well as to traditional tests of main genetic effects only. We then illustrate the kernel-machine approach using quantitative measures of post-traumatic stress disorder and depression collected as part of the Grady Trauma Project. We finish with concluding remarks and discuss potential extensions of our approach.

MATERIALS AND METHODS

Assumptions and Notation

Assume a population-based study that samples N unrelated subjects. For each subject j = 1,…,N, we let Y_j denote the continuous phenotype and X_j be a vector of covariates. We further define E_j to be a continuous or categorical environmental exposure of interest. Assume also that each subject has been genotyped at a collection of M common SNPs in a genetic region of interest. Define G_j = (G_j,1, G_j,2, …, G_j,m ) as the genotypes at the M SNPs for subject j, where G_j,m is coded as the number of copies of the minor allele that subject j possesses at variant m. The SNPs included in G will be referred to as the “SNP set.” Wu et al. [Wu, et al. 2010] suggest several ways for constructing SNP sets. A natural strategy is to group together all genetic variants that are located on or near a gene. However, we note that this strategy is reliant on the quality of the database used to define the SNPs that fall within the gene and may also result in the set harboring SNPs that are not necessarily in LD. Consequently, it may be advantageous to consider other SNP sets such as haplotype blocks or sliding windows. For illustration purposes in this manuscript, we will form SNP sets based on genes and consider all genotyped SNPs between the start and end of transcription, as well as variants within 2kb up- and down-stream from the gene to capture nearby regulatory regions.

Traditional Single-SNP Tests

We first describe two traditional tests that consider the analyses on the level of an individual SNP. First, if we believe a SNP has modest-to-no interaction with environment to influence outcome (see Models M4-M5 in Figure 1), we would typically apply a main-effects only model that implements a linear regression of the form

$$\mathbf{Y}=\mathbf{X}\gamma +{\beta }_{\mathrm{SNP}}{\mathbf{G}}_m+{\beta }_{\mathrm{ENV}}\mathbf{E}+e,$$ (1)

where Y is an N x 1 vector of phenotypes, X is an N x c vector of c covariates (including an intercept) with regression parameter vector γ, E denotes an N x 1 vector of the environmental exposure (considered a covariate and not an effect modifier) with regression coefficient β_ENV, and G_m denotes an N x 1 vector of SNP genotypes at SNP m with regression parameter β_SNP. Finally, the residual error e follows a MVN distribution, e~MVN(0,σ²I), where I denotes the NxN identity matrix. We then implement a likelihood ratio test to assess the null hypothesis of H₀ : β_SNP=0 for each SNP m. To adjust for multiple testing of M correlated SNPs, we could apply procedures like P_ACT [Conneely and Boehnke 2007] or use a permutation procedure that randomly shuffles the M genotypes of each subject as a unit (preserving the LD structure).

If we instead suspect sizable SNP-environment interaction (see models M1-M2 in Figure 1), we might then apply a joint test of SNP and SNP-environment interaction using the following modified model from (1)

$$\mathbf{Y}=\mathbf{X}\gamma +{\beta }_{SNP}{\mathbf{G}}_m+{\beta }_{\mathrm{ENV}}\mathbf{E}+{\beta }_{\mathrm{SNP}\ast \mathrm{ENV}}{\mathbf{G}}_m\mathbf{E}+e$$ (2)

where the notation is the same as defined in equation (1). The difference between model (2) and model (1) is the inclusion of a two-way interaction between G_m and E with regression parameter β_SNP*ENV. Using a likelihood ratio test, we can assess the null hypothesis H₀: β_SNP = β_BNP*ENV = 0. We repeat model (2) and obtain likelihood-ratio tests for each of the M genotyped SNPs. To adjust for multiple testing we require permutations, since P_ACT is only applicable to studies of main SNP effect. In performing permutations under the null hypothesis, one must take care to preserve the relationship between phenotype Y with the covariates X and the environmental predictor E; failure to preserve this relationship can lead to invalid inference [Buzkova, et al. 2011]. We preserve this relationship while also maintaining LD structure among SNPs by randomly permuting the M genotypes of each subject as a unit, acknowledging that such permutation assumes that the genotypes are uncorrelated with the environmental predictors in the population.

Two-way Interaction Kernels

Using kernel regression, Kwee et al. [Kwee, et al. 2008] and Wu et al. [Wu, et al. 2010] implemented mixed models for testing the effect of variant sets on complex human phenotypes. These approaches use a kernel function K(G_j ,G_k) to quantify the genetic similarity between subjects j and k across the M SNPs in the SNP set. We modify the methods described by Kwee et al. [Kwee, et al. 2008] and Wu et al. [Wu, et al. 2010] to permit joint gene and gene-environment interaction testing as follows. First, we select a kernel that appropriately models interactions. While many kernels are available [Schaid 2010], we explore the use of the joint weighted 2-way interaction kernel (W2WK) in this work. We define Z_j = (G_j, E_j) as the combined genetic and environmental information on each subject. We then define the weighted 2-way interaction kernel for subjects j and k as

$$K({\mathbf{Z}}_j,{\mathbf{Z}}_k)=(1+{\Sigma }_{m=1}^M{w}_m{G}_{jm}{G}_{km})(1+E_j{E}_k).$$ (3)

Under this kernel, weight for the m^th variant, w_m, reflects the relative contribution of that variant to our estimate of local genetic similarity between subjects j and k. Ideally, causal variants would receive a large weight, and noncausal SNPs would receive a weight close to zero, making the weight of these SNPs negligible. Although by nature we do not know which SNPs are causal, a careful weighting scheme can result in more power. Wu et al. [Wu, et al. 2010] and Schifano et al [Schifano, et al. 2012] provide nice discussions on relevant weighting approaches for common SNP analyses. For all simulations and analyses reported here, we implement a weighting scheme based on the minor-allele frequency (MAF) of each assayed SNP that weights rarer variants over more common ones; the particular weight we apply for the m^th variant is w_m = 1/√MAF_m.

Based on the chosen kernel function, we can then define the kernel matrix K as the NxN matrix, where the (j,k)^th element is equal to K(Z_j, Z_k). The resulting K matrix represents genomic and environmental likeness, as well as interaction between genotype and environment, between all pairs of individuals across the M variants in the SNP set. Once we construct K, we incorporate this kernel matrix within a mixed model that, for each pair of subjects, compares the genetic and environmental similarity to phenotypic similarity, adjusting for covariates. For continuous phenotypes, we can fit the mixed model as

$$\mathbf{Y}=\mathbf{X}\gamma +\mathbf{U}+e.$$ (4)

As with the traditional models described above, γ denotes a vector of regression parameters for fixed-effect covariates X and e is a vector of independent random errors that follows a normal distribution. U denotes a random effect affiliated with the variant set that follows the multivariate normal (MVN) distribution with a mean 0 and covariance matrix τK. Within this random effect, τ denotes the component of variance due to the effects of the environment, variants within the variant set, and the interactions between these factors.

When an interaction kernel is applied to the linear mixed model in equation (4) the environmental risk factors are a component of the random effects portion (U) of the model. Therefore, a null hypothesis of τ = 0 would correspond to testing if none of the genetic, environmental, or interaction factors within the kernel influences the trait. This null is not particularly interesting in genetic studies, since the test would be significant if only the environmental factors, and no genetic or gene-environment interaction factors, were associated with the phenotype of interest. We therefore modify the kernel such that a significant finding is due only to a genetic effect in the presence of a potential interaction with the modeled environmental factors. To do so, we use a strategy employed by Maity and Lin [Maity and Lin 2011] for microarray analysis and attach an extra “garrote” parameter, δ, to the genetic effects in the kernel function such that the weighted two-way interaction kernel becomes

$$k({\mathbf{Z}}_j,{\mathbf{Z}}_k)=(1+\delta {\Sigma }_{m=1}^M{w}_m{G}_{jm}{G}_{km})(1+E_j{E}_k).$$ (5)

With this reparameterization, we can then test for the effect of the gene in the presence of potential interactions with the environmental factors by considering the null hypothesis H₀ : δ=0 [Breiman 1995]. Maity and Lin [Maity and Lin 2011] demonstrate that the appropriate score test is

$$S={\widehat{\tau }}_0{(\mathbf{Y}-\mathbf{X}{\widehat{\beta }}_0)}^T{\mathbf{V}}^{-1}[d\mathbf{K}∕d{\delta }_0]{\mathbf{V}}^{-1}(\mathbf{Y}-\mathbf{X}{\widehat{\beta }}_0)∕2$$ (6)

where $\mathbf{V}={\widehat{\sigma }}_0^2+{\widehat{\tau }}_0{\mathbf{K}}_{(\delta =0)},\mathrm{and}d\mathbf{K}∕d{\delta }_0$ denotes the derivative of K with respect to δ under the null hypothesis. ($\left({\widehat{\beta }}_0\right),{\widehat{\tau }}_0,\mathrm{and}{\widehat{\sigma }}_0^2$) are estimators of (β,τ,σ²) under the null hypothesis, which can be estimated by applying restricted maximum likelihood (REML) procedures to the reduced form of the linear mixed model [Liu, et al. 2007]. The asymptotic distribution of the test S follows a complicated mixture of χ² distributions. We approximate the distribution using Welch-Satterthwaite’s method [Satterthwaite 1946], although we could also use Davies’ method [Davies 1980].

Simulations

To validate our method in terms of appropriate type I error and to assess its power compared to traditional joint and main-effect tests, we carry out simulation studies under a range of configurations. We perform simulations based on SNPs and LD patterns found 2 kb up- and down-stream from signal transducer and activator of transcription 3 (STAT3), a gene on chromosome 17q21.31. We show the pairwise LD structure of SNPs in STAT3 in Supplementary Figure 1. To incorporate observed LD patterns from HapMap samples, we used the HAPGEN package [Spencer, et al. 2009] to generate simulated SNP data. HAPGEN generates simulated genotype information for all SNPs identified in HapMap within the STAT3 gene; however, to better replicate real GWAS conditions, we applied the testing approaches only to those SNPs that would be typed on standard genotyping arrays. Although 27 common SNPs fall within the STAT3 gene, only 14 of the 27 are genotyped on the Illumina HumanOmni1-Quad genotyping platform. Thus, the 14 typed SNPs form the SNP set for the kernel approach, and only the 14 typed SNPs are tested for association using the traditional main and joint tests. Under simulations where the causal SNP is not genotyped, power to detect an association relies on LD between the causal SNP and typed SNPs.

Size and Statistical Power

We conducted simulations under four types of null linear models to verify that the joint W2WK approach properly controls the type I error rate. We assumed a model of Y_j = β_ENVE_j+e_j, where the error term, e_j, follows a standard normal distribution. E_j models an environmental exposure under a Bernoulli(0.5) distribution. We let β_ENV, the main effect size of the environment, be set to 0, 0.33, 0.67, and 1 (corresponding to R² values of approximately 0, 0.03, 0.11, and 0.25 respectively). For null simulations, we set sample size to N=250, 500, and 1000. For each of the four null models, we evaluated size using 5000 replicates of the data.

We next performed power calculations to compare the kernel approach to the traditional joint and main-effect tests under different levels of SNP-environment interaction. We simulate data for subject j under the model

$$Y_j+0.33E_j+\zeta G_{j,m}+(0.2-\zeta )G_{j,m}{E}_j+e_j$$ (7)

where E_j again models the environmental exposure under a Bernoulli(0.5) distribution, e_j follows a standard normal distribution, and G_j,_m is the allele count of the causal SNP in subject j. We set the values of ζ to the 5 different values (0.00, 0.05, 0.10, 0.15, and 0.20), which corresponds to simulation Models M1-M5, respectively (see Table 1). As ζ (and the model number) increases, the interaction effect decreases while the main effect increases. For instance, in Model 1, where ζ=0, we assume ‘complete’ interaction: the causal SNP affects phenotype exclusively through gene-environment interaction. Model 3 assumes that the genotypic effect is twice as large in exposed individuals compared with unexposed individuals. Model 5 assumes that the subgroups have the same mean genotypic effect; that is, there is no gene-environment interaction. For each of the 5 models, we allowed each of the 27 common SNPs in STAT3 to be causal in turn. We model genotypic effect acting first in an additive then in a dominant manner. For power simulations, we set sample size to N=500. As with the size simulations, we assumed only genotype information for the 14 SNPs on the Illumina HumanOmni1-Quad platform was available, and used only these SNPs to compute the test statistics. Power was estimated as the proportion of P-values <0.05 and was evaluated based on 500 replicates of the data per model.

Table I.

Models of gene-environment interaction

		Total Genetic Effect
Model	ζ	Exposed Subgroup	Unexposed Subgroup
M1	0.00	0.20	0.00
M2	0.05	0.20	0.05
M3	0.10	0.20	0.10
M4	0.15	0.20	0.15
M5	0.20	0.20	0.20

The five models of interaction considered in our simulations. Under M1, we assume that unexposed individuals have no genotypic effect. In M2, the genotypic effect in unexposed individuals is ¼ that of exposed individuals. In M3, unexposed individuals have on average half the genotypic effect of exposed individuals. In M4, unexposed individuals have ¾ the mean genotypic effect as the exposed subgroup. Finally, in M5, mean genotypic effect is equal across subgroups; no interaction effect is occurring.

RESULTS

Table II shows the empirical size for common variant analyses at α=0.05. Our simulations confirm that our 2-way interaction kernel approach maintains appropriate type-I error, regardless of main effect size of environment. The type-I error of the traditional main effect and traditional joint test were also appropriate.

Table II.

Controlling for Type I Error Rate: Empirical Size

Sample Size	250				500				1000
Environmental Effect	0.00	0.33	0.67	1.00	0.00	0.33	0.67	1.00	0.00	0.33	0.67	1.00
W2WK	0.043	0.045	0.050	0.049	0.050	0.050	0.051	0.047	0.049	0.046	0.051	0.052
Traditional Joint	0.051	0.052	0.056	0.053	0.051	0.048	0.052	0.049	0.052	0.051	0.050	0.047
Traditional Main	0.055	0.053	0.058	0.053	0.051	0.050	0.048	0.053	0.049	0.051	0.049	0.049

Empirical sizes for the W2WK, traditional joint, and traditional main-effect tests at the α=0.05 level. Sample sizes were set to N=250, 500, and 1000. Environmental main effect was allowed to vary from 0, 0.33, 0.67, and 1 (corresponding to R² values of approximately 0, 0.03, 0.11, and 0.25 respectively).

Figures 2-4 show the power results for models M1, M3, and M5, the effect of the SNP on outcome originated under either an additive genetic model (left) or a dominant model (right). Similar power results for models M2 and M4 are shown in Supplemental Figures 2 and 3, respectively. Power is plotted as a function of causal SNP, where the causal SNPs are ordered by genomic location. The genotyped SNPs (denoted by the ‘x’ on the bottom of the plots) were used to compute the test statistics, but each HapMap SNP (regardless of whether it is typed) is treated as causal in turn. Thus, in situations where the causal SNP is not typed, we rely on the correlation of the causal SNP with observed typed SNPs in the set to gain statistical power. The MAF of the SNPs is plotted below the power plot in the grey line. For example, SNP 9 (rs9909659) has a MAF 0.21 and is not genotyped on the Illumina array. However, as shown in Supplementary Figure 1, it is in strong LD with several SNPs that are typed (R²>0.9 for SNP 3 (rs3198502), SNP 4 (rs1053005), and SNP 6 (rs3744483)). Power to detect an effect of SNP 9 relies on LD among these genotyped SNPs.

Figure 2.

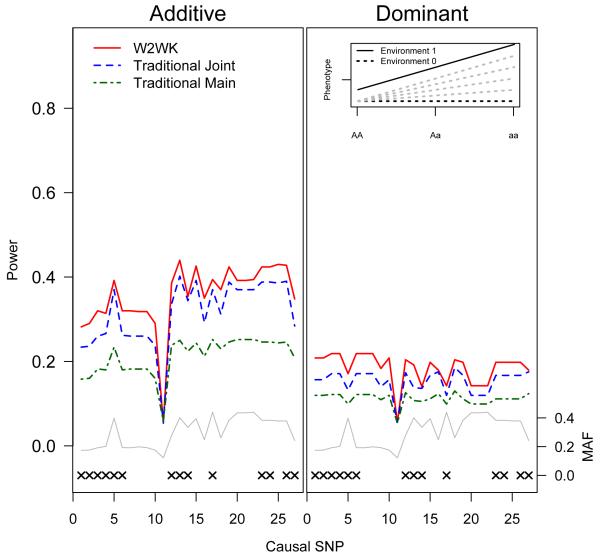
Power for the W2WK (red), traditional joint (blue), and traditional main effect (green) approaches by causal SNP under the M1 model. An “x” marks the 14 SNPs that were modeled as genotyped in our simulations. The MAF of each SNP (grey line) is along the right Y-axis. Plot on the left assumes an additive model; the plot on the right assumes the underlying model is dominant, but was tested as additive. Inset plot shows the underlying model (M1): solid black line represents genotypic effect among individuals who have been exposed to the environmental insult. Dotted black line shows genotypic effect of individuals who were not exposed to the environmental insult under the M1 model. Dotted grey lines indicate alternate models that are considered elsewhere in this manuscript.

Figure 4.

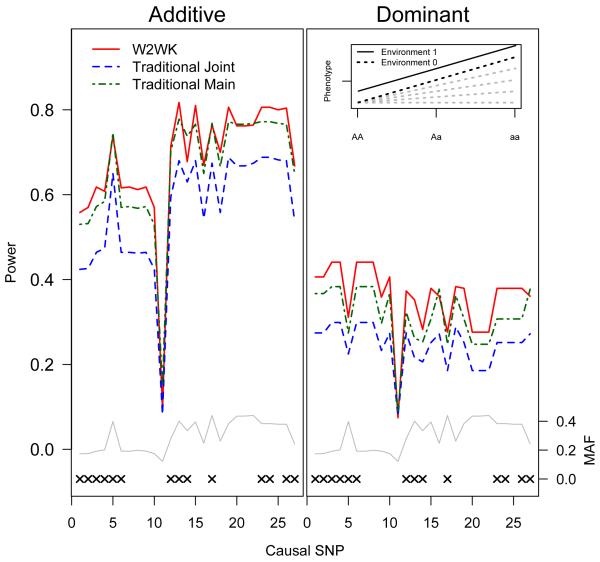
Power for the W2WK (red), traditional joint (blue), and traditional main effect (green) approaches by causal SNP under the M5 model. An “x” marks the 14 SNPs that were modeled as genotyped in our simulations. The MAF of each SNP (grey line) is along the right Y-axis. Plot on the left assumes an additive model; the plot on the right assumes the underlying model is dominant, but was tested as additive. Inset plot shows the underlying model (M5): solid black line represents genotypic effect among individuals who have been exposed to the environmental insult. Dotted black line shows genotypic effect of individuals who were not exposed to the environmental insult under the M5 model. Dotted grey lines indicate alternate models that are considered elsewhere in this manuscript.

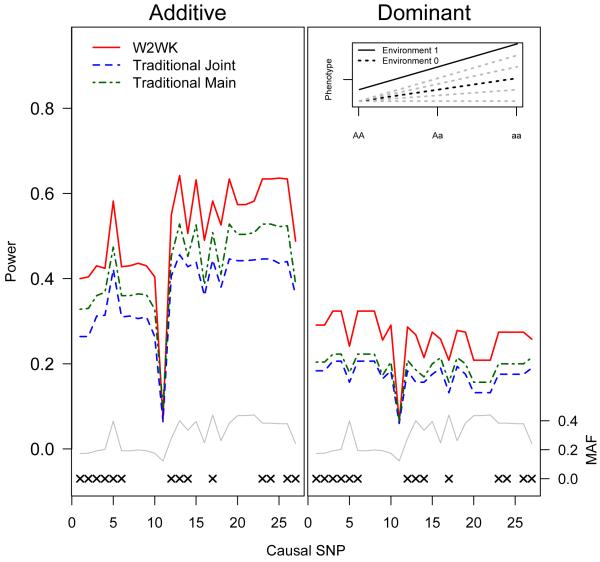
In our simulations, the traditional joint test did not always outperform the main-effect test, even when a significant interaction effect was present. Implementation of the traditional joint test resulted in considerable increases in power relative to the traditional main test only under models of complete interaction (model M1, Figure 2). Under the M2 model shown in Table I, despite the fact that the interaction effect is 4-fold larger than the genetic main effect in this model, the traditional joint test provides only a modest power gain over the traditional main effect test (Supplementary Figure 2). When the interaction effect is equal to or smaller than the genetic main effect (model M3-M5, Figures 3 & 4 and Supplementary Figure 3), the traditional main effect tests are consistently more powerful than the traditional joint tests.

Figure 3.

Power for the W2WK (red), traditional joint (blue), and traditional main effect (green) approaches by causal SNP under the M3 model. An “x” marks the 14 SNPs that were modeled as genotyped in our simulations. The MAF of each SNP (grey line) is along the right Y-axis. Plot on the left assumes an additive model; the plot on the right assumes the underlying model is dominant, but was tested as additive. Inset plot shows the underlying model (M3): solid black line represents genotypic effect among individuals who have been exposed to the environmental insult. Dotted black line shows genotypic effect of individuals who were not exposed to the environmental insult under the M3 model. Dotted grey lines indicate alternate models that are considered elsewhere in this manuscript.

Across all five models, for both additive and dominant assumptions, the joint W2WK approximately matches or outperforms the optimal traditional test. Under the complete and strong interaction models (models M1 and M2, Figure 2 and Supplementary Figure 2), the joint W2WK kernel matches or outperforms the traditional joint test across all SNPs. In models M3 and M4, although the main effect test outperforms the traditional joint test, the joint W2WK outperforms the main effect test (Figures 3 and Supplementary Figure 3). Even under the assumption of no gene-environment interaction occurring (M5, Figure 4), our joint W2WK approach remains somewhat more powerful or of approximately equal power when compared with the traditional main-effect test for the large majority of SNPs.

The power of our joint W2WK approach relies on LD existing between the causal SNP and genotyped SNPs in the sample. To examine the relationship between LD and power in our simulated datasets, we calculated the median squared correlation (median R²) of the causal SNP with genotyped SNPs in our SNP set across simulated datasets for a specific model. As shown in Supplementary Figure 4, our joint W2WK approach is least powerful compared with the traditional approaches when median R² between causal SNP and genotyped SNPs is close to 0 but becomes increasingly more powerful than these other approaches as the median R² increases. Our findings regarding the relationship between median R² and power for our joint W2WK test yield similar conclusions to those reported by Wu et al. [Wu, et al. 2010] and Schifano et al. [Schifano, et al. 2012] for SNP set analysis of main effects on phenotype.

The joint W2WK approach offers more power than the optimal traditional approach across a considerable range of causal SNP minor allele frequencies. Although all approaches are more powerful as the causal SNP’s MAF increases, there is no clear relationship between MAF and relative strength of our approach (Supplementary Figure 5). The weighting scheme we selected for the bulk of our simulations is an inverse relationship with MAF; this weighting scheme is most beneficial when the MAF of the causal SNP is rarer relative to the genotyped SNPs in the set. To examine if power of the joint W2WK approach is affected by the choice of MAF weight, we also performed an unweighted analysis that assumes equal contribution from all genotyped SNPs in the SNP set. We present these results in Supplementary Figure 5. Overall, power using the unweighted version of our approach was somewhat lower than from using the joint W2WK approach, except for causal SNPs that were quite common (MAF > 0.35). For these SNPs, the unweighted approach offered slightly more power to detect an effect than the joint W2WK.

Application to Grady Trauma Project Data

Depression is a moderately heritable disorder (h²≈0.30), yet, despite substantial interest in identifying genetic causes of the disorder, its genetic underpinnings remain largely unidentified [Flint, et al. 2008]. Research indicates a potential association between depression and genes in the cannabinoid receptor 1 (CB₁) pathway [Agrawal, et al. 2012; Barrero, et al. 2005; Monteleone, et al. 2010; Vinod and Hungund 2006]. The relationship between depression and CB₁ may be modified, however, by gender [Castelli, et al. 2013; Riebe, et al. 2010].

We applied our joint W2WK approach to a GWAS study of depression to assess the relationship between CB₁ genes and outcome, allowing for interaction with gender, and contrasted our results with those found under the traditional single-SNP tests. Data used in our analysis were collected as part of a larger study, called the Grady Trauma Project (GTP), which investigates the role for psychiatric disorders such as post-traumatic stress disorder and depression [Bradley, et al. 2008; Ressler, et al. 2011]. Participants in the GTP are served by the Grady Hospital in Atlanta, Georgia, and are predominantly urban, African American, and of low socioeconomic status. GTP staff approach subjects in the waiting rooms of Grady Primary Care and Obstetrics and Gynecology and obtain their written consent to participate. GTP staff conduct an extensive verbal interview, which includes demographic information, a history of stressful life events, and several psychological surveys. The GTP queries participants on the Beck Depression Inventory (BDI), a 21-item multiple-choice questionnaire that assesses symptoms of depression [Beck, et al. 1996]. Summing the responses yields a score ranging from 0-63, with scores higher than 28 being indicative of moderate to severe depression. We selected this score as a continuous outcome variable, transforming each individual’s BDI scores to y_i=ln(BDI_i + 1), where ln is the natural log, to uphold the normality assumption required for the traditional tests.

The GTP genotyped participants on the Illumina HumanOmni1-Quad array to permit GWAS analyses. For this work, we studied the Cannabinoid Receptor 1 gene (CNR1), on chromosome 6q14-q15, which encodes for the CB₁ receptor, and the Fatty Acid Amide Hydrolase gene (FAAH), on chromosome 1p35-p34, which breaks down the primary endocannabinoid in humans, as genes of interest. The HumanOmni1-Quad array genotypes 11 common SNPs within 2kb up- and downstream from CNR1, and 7 common polymorphisms in and near the FAAH gene. Additionally, we obtained the top 10 principal components (PCs) from the GWAS data, which we included as covariates in all models to account for population stratification. We obtained BDI scores, genotype, PCs, and gender information on 3475 subjects.

We applied our joint W2WK test, along with traditional joint and traditional main-effect tests, to the dataset. We observed that both the traditional main-effect and traditional joint tests indicated a nominal association between CNR1 and BDI scores, whether gender was included only as a covariate or as an effect modifier (P-values 0.007 and 0.024 respectively). The P-value testing this association using the joint W2WK approach yielded similar trends as the two other test but yielded a p-value that was at least 4-fold smaller than either traditional approach (P-value 0.0016). Evidence suggests that the association between CNR1 and BDI scores might be due to a blend of genetic main effect and interaction between CNR1 and gender, but is unlikely to be an example of complete or very strong interaction, since the P-values of the traditional main effect test is smaller than that of the traditional joint test). None of the three tests found a significant association between variants in the FAAH gene and BDI scores (Table III).

Table III: Analysis of the Grady Trauma Project Data

	Gene
	CNR1	FAAH
W2WK	0.002	0.406
Traditional Joint	0.024	0.407
Traditional Main	0.007	0.603

P-values using the joint W2WK, traditional joint, and traditional main-effect only tests on the Grady Trauma Project dataset. The joint W2WK and traditional joint analyses considered interactions with gender.

DISCUSSION

We have presented a kernel machine based framework for SNP set analysis for continuous outcomes when an interaction between genotype and an environmental insult is suspected. The proposed test is a variance component score test, which relies on fitting the null linear regression model to compute the test statistic. Since the P-values are computed analytically, our method allows faster analyses on a genomewide scale than the traditional regression approaches, which might rely on permutation procedures to establish significance. Analysis of simulated STAT3 data for 500 and 1000 subjects takes 30 seconds and 3.5 minutes, respectively, on a MacBook Pro possessing a 2.2 GHz processor and 8 GB of memory. If one were to parallelize the approach across 50 CPUs, one could complete a GWAS analysis of 20,000 gene sets with a sample size of 1000 in approximately one day. We provide R software implementing the approach on our website (see Web Resources) which can be run through PLINK, if desired.

In general, our joint W2WK approach has more power than the either the joint or main-effect traditional approaches. Since the magnitude and prevalence of interactions is largely unknown, we considered several models of gene and gene-environment interaction effects. When the underlying model is one of complete interaction, the joint W2WK outperforms the traditional joint test across a range of minor allele frequencies and LD patterns. Our approach performs particularly well relative to either traditional test when the underlying causal model involves a blend of both interaction and main genetic effects. We consider the power gains under these models to be especially noteworthy, since they are considered to be more biologically plausible than a model of complete interaction [Zammit, et al. 2010]. We lastly considered the scenario that no gene-environment interaction is occurring; that is, all the genotypic effect occurs through genetic main effect. Using traditional joint testing under this model would result in costly loss of power relative to the traditional main-effect test. However, across all modeled causal SNPs, the joint W2WK approach maintains power that rivals or even modestly outperforms the traditional main-effect test. We have also demonstrated that the joint W2WK approach has more power relative to the traditional approaches across all interaction models when the genetic effects are acting in a dominant fashion, but tested assuming an additive effect.

Our joint W2WK is explicitly designed to test for a joint effect of genetic main effect and interaction between gene and environment. If instead one is interested in testing exclusively for a gene-environment interaction effect using SNP sets, one can apply a related kernel procedure created by Lin et al. called GESAT. [Lin, et al. 2013]. Like W2WK, GESAT is a variance-component score test that utilizes a kernel function for analysis. However, while our joint W2WK procedure models genetic, environment, and gene-environment interaction effects as random effects via a kernel function in the mixed-model framework, GESAT only models the gene-environment interaction term as random and models the main genetic and environmental effects parametrically as fixed effects (estimated under the null using ridge regression). GESAT is useful when an interaction-only test is more desirable than a joint test, such as for detecting a crossover interaction (i.e. when the genetic effects change as a function of environment, such that the genotype conferring lowest risk in one environment confers highest risk in another environment).

Although the results presented here are focused on interaction between environment and common SNPs, the approach is readily extendible to rare variant gene-environment interaction analysis. The approach can also be used to simultaneously model multiple environmental exposures, which would be useful in cases where several environmental measurements might be expected to correlate with a true latent exposure that is interacting with genotype to influence outcome. We will explore these ideas more in future work.