A cross-population extended haplotype-based homozygosity score test to detect positive selection in genome-wide scans

Abstract

In this article, we developed a cross-population comparison test statistic to detect chromosome regions in which there is no significant excess homozygosity in one population but homozygosity remains high in the other. We treated an extended stretch of homozygosity as a surrogate indicator of a recent positive selection. Conditioned on existing linkage disequilibrium, we proposed to test the haplotype version of the Hardy–Weinberg equilibrium (HWE). For each population, we assumed that a random sample of unrelated individuals were typed on a large number of single nucleotide polymorphisms (SNPs). A pooled-test statistic was constructed by comparing the measurements of homozygosity of the two samples around a core SNP. In the chromosome regions where HWE is roughly true in one population and HWE is not true in the other, the pooled-test statistic led to significant results to detect the positive selection. We evaluated the performance of the test statistic by type I error comparison and power evaluation. We showed that the proposed test statistic was very conservative and it had good power when the selected allele remains polymorphic. Then, we applied the test to HapMap Phase II data to make a comparison with previous results and to search for new candidate regions.

1. INTRODUCTION

In the human genome, genetic variants (or new mutations) that increase the fitness of an individual in his/her environment might increase in frequency and these variants/mutations are termed as advantageous. The selection acting on advantageous alleles are so-called positive selection (Akey 2009 [1] and Nielsen 2005 [14]). In the neighborhood of the advantageous variants/mutations, the nearby alleles/variants may rise to high frequency rapidly due to strong linkage disequilibrium (LD). Therefore, positive selection may leave a haplotype signature of high frequencies and may lead to excess haplotype homozygosity. Since the new mutations can be related to complex traits, the excess haplotype homozygosity signature of positive selection may lead to the detection of important and interesting genetic variants. Thus, it is important to detect genomic regions of positive selection. With the advent of dense single nucleotide polymorphism (SNP) map across the human genome, there has been a great interest in the genome-wide scan of SNP data to detect important genetic variants. One interesting area is genome-wide scan of genetic regions of positive selection [12, 17].

There have been quite a few statistical methods to detect positive selection, such as Hanchard’s HS, Sabeti’s EHH, Tajima’s D test, Fu and Li’s D test, Fay and Wu’s H test, and Hudson’s haplotype-partition method [10, 8, 11, 16, 19, 7, 6]. All these methods basically used one sample from a population to build test statistics to detect selection signals. In Sabeti et al. (2007) [17], a cross-population extended haplotype homozygosity (xp-EHH) method was developed to detect selective sweeps in which the selected allele has approached or achieved fixation in one population but remains polymorphic in the other. The method is based on cross-population comparison of two populations to discover the important alleles. It is an extension based on Sabeti’s EHH [16] and logarithm transformation plus normalization to a standard normal distribution.

In Zhong et al. (2010) [22], the authors developed three homozygosity score statistics to detect positive selection. The statistics were designed to analyze a sample of a specific population. They depended on the length of homozygosity around a core SNP. We calculated the mean and variance of each statistic under the appropriate null hypothesis to facilitate computation of p-values by a normal approximation. The three tests included (a) an extended genotype-based homozygosity score test (EGHST), (b) a hidden Markov model score test (HMMST), and (c) an extended haplotype-based homozygosity score test (EHHST). The null hypothesis of EGHST assumed both Hardy–Weinberg equilibrium (HWE) and linkage equilibrium. The EHHST explicitly took into account multi-locus linkage disequilibrium. The HMMST occupied the intermediate ground of allowing for pairwise LD. In short, the EHHST was the most conservative test.

Under several demographic population models, we evaluated by simulation that the EHHST leads to appropriate false positive rates [22]. We investigated the power of EHHST by comparing with the popular methods. It was found that the EHHST is very robust in terms of correct type I error rates; in addition, it has higher or similar power as the existing popular methods such as Hanchard’s HS and Sabeti’s EHH. We also applied the tests to the previously studied HapMap Phase II data. Our results were consistent with previous findings across the genome and within specific candidate regions. We identified new candidate regions which were not reported before.

In this article, we developed a cross-population comparison test statistic to detect chromosome regions in which there is no significant excess homozygosity in one population but homozygosity remains high in the other. The idea was to extend the EHHST using two sample pooled t-test statistics and to build cross-population extended haplotype-based homozygosity score tests (xp-EHHST). Such as EHHST, we calculated the mean and variance of xp-EHHST under its null hypothesis to facilitate computation of p-values by a normal approximation and the approximation does not need other transformations like logarithm. All we assumed was that the sample size is relatively large such as the HapMap Phase II data. We evaluated the performance of xp-EHHST by type I error comparison and power evaluation. Then, we applied it to HapMap Phase II data to make a comparison with previous results and to search for new candidate regions.

2. METHODS

Before we introduce the cross-population score test statistic, we describe the haplotype data we intend to analyze, i.e., the whole-genome SNP data of HapMap Phase II [12]. This will be helpful for readers to understand the proposed cross-population score test statistics. Once one understands the data structure, it would not be hard to understand the construction of cross-population score test statistics.

2.1 HapMap Phase II data

The datasets include 3.1 million SNP genotypes from population samples of three continents: 60 CEPH Utah residents with ancestry from northern and western Europe (CEU), 60 Yoruba from Ibadan (YRI), Nigeria in Africa, and 45 Han Chinese from Beijing (CHB) and 45 Japanese from Tokyo (JPT) Japan of Asia. The two Asian samples are combined into one, and we refer hereafter to it as CHB+JPT as instructed by the HapMap Consortium. We used only the unrelated individuals from the three samples, omitting the children in the trio families from the CEU and YRI samples. The samples are downloaded from http://ftp.hapmap.org/downloads/phasing/2007-08rel22/phased/.

To understand the human haplotype data, look at the following example of the two haplotypes of an individual on one chromosome at 22 SNPs

$$\begin{array}{cccccccccccccccccccccc}1& 1& 1& 0& 0& 1& 1& 0& 0& 1& 1& 1& 0& 1& 1& 1& 1& 0& 1& 1& 1& 0\\ 1& 1& 1& 0& 1& 1& 1& 0& 0& 1& 1& 1& 0& 1& 1& 1& 1& 0& 0& 1& 1& 0\end{array}$$

Each row above is a haplotype of alleles at the 22 SNPs, and the haplotypes of the individual are given by the two rows. One allele from the top row and the corresponding allele on the bottom row consist of a genotype at a SNP. For instance, the genotype of the first SNP is 1/1 and the genotype of the last SNP is 0/0, where/divides the two alleles. At the first three SNPs, we have homozygous genotype 1/1; at the four SNP, we have a homozygous genotype 0/0; at the fifth SNP, we have a heterozygous genotype 0/1; and at next two SNPs, we have homozygous genotype 1/1, etc.

As shown above, the haplotypes of an individual on one chromosome can be expressed by two rows. Therefore, the haplotypes of the CEU sample consist of 120 rows for each chromosome and so the haplotypes of YRI sample, and the haplotypes of CHB+JPT sample consist of 180 rows for each chromosome.

2.2 Test statistic

The cross-population comparison score test statistic is defined with respect to two populations, A and B, at a given core SNP. First, only the SNPs for which there are data for both populations A and B are selected as core SNPs. Notice that only the core SNP needs to have data for both populations, and the other surrounding SNPs are not necessarily to have data for both populations.

Suppose the selected core SNP is SNP 0 which is the central SNP. For a specific population which is either population A or B, let us denote the SNPs around the core SNP 0 as k = …, −2, −1, 0, 1, 2, …. Let M be the indicator of whether the core SNP 0 is homozygous, let L be the number of consecutive homozygous SNPs flanking the SNP 0 on the left, and let R be the number of consecutive homozygous SNPs flanking the SNP 0 on the right. If the core SNP 0 is heterozygous (M = 0), then we define L = R = 0. Here one may need to do truncations if the core SNP 0 is on the boundary or is close to the boundary. The truncation means that we may need to stop to count for the numbers L and R of consecutive homozygous SNPs around the core SNP 0, if the core SNP 0 is on the boundary or is close to the boundary. For instance, if the core SNP is on the left boundary, L is equal to 0 due to truncation; if the core SNP is on the right boundary, R is 0. The extent of homozygosity is measured by the total T = L + M + R.

The quantities L, M, R, and T are random variables that vary from person to person. Since the variables L, M, R, and T are defined for either population A or B separately, the surrounding SNPs k = …, −2, −1, 1, 2, … of population A can be different from those of population B but we do need the core SNP 0 to be the same for both populations A and B. For population A, let us denote the mean and variance of T by μ_A and ${\sigma }_A^2$, respectively; similarly, let μ_B and ${\sigma }_B^2$ be the mean and variance of T for population B, respectively.

Next, we restrict our attention to the chromosome region around the core SNP to calculate its homozygosity score in population A. Consider a random sample of n_A unrelated individuals of population A typed on a large number of SNPs around the core SNP 0. Let T_Ai be the value of T for person i in the random sample. The summation ${\sum }_{i=1}^{n_A}{T}_{Ai}$ provides a measurement of total homozygosity in the sample. If there is no significant excess homozygosity, ${\sum }_{i=1}^{n_A}[T_{Ai}-{\mu }_A]$ tends to be close to 0; otherwise, it tends to be much larger than 0. Thus, ${\sum }_{i=1}^{n_A}[T_{Ai}-{\mu }_A]$ provides a measurement of excess homozygosity around the core SNP 0. We proceed analogously with respect to population B. Consider a random sample of n_B unrelated individuals of population B. Let T_Bj be the value of T for person j in the random sample of population B. The summation ${\sum }_{j=1}^{n_B}{T}_{Bj}$ provides a measurement of total homozygosity in the sample. Again, ${\sum }_{j=1}^{n_B}[T_{Bj}-{\mu }_B]$ tends to be close to 0 if there is no significant excess homozygosity in the sample; otherwise, it tends to be much larger than 0.

To test the excess homozygosity of one population against the other, a pooled-test statistic is defined as (1)

$$S_{AB}=\frac{{\sum }_{i=1}^{n_A}(T_{Ai}-{\mu }_A)/n_A-{\sum }_{j=1}^{n_B}(T_{Bj}-{\mu }_B)/n_B}{{\sigma }_P\sqrt{1/n_A+1/n_B}},$$ (1)

where ${\sigma }_P^2=\frac{(n_A-1){\sigma }_A^2+(n_B-1){\sigma }_B^2}{n_A+n_B-2}$ is the pooled-variance of random variable T for populations A and B. The pooled-test score S_AB is directional: a significant positive score suggests excess homozygosity in population A, whereas a significant negative score suggests excess homozygosity in population B. In practice, the mean and variance parameters μ_A, μ_B, ${\sigma }_A^2$ and ${\sigma }_B^2$ need to be estimated by empirical data. By doing so, the test statistic S_AB would follow a t-distribution with a degree of freedom of n_A + n_B − 2. For HapMap II data, the sample sizes are big enough that large sample theory applies (n_A + n_B is equal to or larger than 120). In this article, we assume that the score test S_AB approximately follows a standard normal distribution.

As in Zhong et al. (2010) [22], we were interested in three null hypotheses:

• Null hypothesis of EGHST: HWE and linkage equilibrium;

• Null hypothesis of HMMST: HWE and pairwise LD but no higher-order disequilibrium interactions;

• Null hypothesis of EHHST: HWE and arbitrary multi-locus LD.

In Zhong et al. (2010) [22], the authors calculated the mean and the variance of variable T for a specific population under each of the three null hypotheses. Under the null hypothesis of EHHST, arbitrary LD is allowed, while pair-wise LD is allowed under the null of HMMST and no LD is allowed under the null of EGHST. The EHHST is the most conservative. In this article, we only extend EHHST to cross-population test S_AB, which is called xp-EHHST, to take the conservative advantage of EHHST.

Under the null hypothesis of xp-EHHST S_AB, we assume that both populations reach HWE but arbitrary LD is allowed, i.e., both populations satisfy haplotype version of HWE. In the human genome, LD tends to extend the stretch of homozygosity surrounding a central selected marker given high density SNPs such as the HapMap Phase II data in one population but not in another population, i.e., one population satisfies the haplotype version of HWE but the other does not. Thus, high positive or lower negative values of S_AB in a genome region indicate a possibility of significant excess homozygosity in one of two populations.

To calculate the xp-EHHST S_AB, one needs to estimate the mean and variance parameters μ_A, μ_B, ${\sigma }_A^2$, and ${\sigma }_B^2$. These parameters can be calculated by the means and variance-covariances of L, M and R. The related technical materials can be found in Zhong et al. (2010) [22]. In the Supplementary I (http://www.intlpress.com/SII/p/2011/4-1/SII-4-1-ru-fan-supplement.zip), a rough description is provided for reader’s convenience.

3. RESULTS

3.1 Type I error rates

We evaluated the performance of xp-EHHST S_AB via empirical type I error calculations. We first used SelSim to simulate data under the neutral model [18]. A few fixed numbers 51, 61, 71, 81, 91 and 101 of SNPs were simulated in a genomic region. In addition, uniform recombination rates of ρ = 1.5, 3, 6 and 9 between SNPs were assumed. To calculate an empirical type I error rate, we simulated 2,500 random sample pairs of n = 60 or n = 100 individuals. In each sample pair, two independent samples were generated under the neutral model; one served as the population that the selected allele approached fixation and the other one served as a sample to calculate the false positive rates of S_AB. For each sample pair, an empirical S_AB value for the central SNP was calculated. The type I error rates at three nominal levels α = 0.05, α = 0.01, and α = 0.001 were reported in Table 1, which were the proportion of the S_AB values of the 2,500 sample pairs that exceeded 95th, 99th and 99.9th percentiles of the standard normal.

Table 1.

Type I error rates of the cross-population extended haplotype-based homozygosity score test (xp-EHHST).

Sample size n	# of SNPs	ρ	Nominal level			# of SNPs	ρ	Nominal level
			α=0.05	α=0.01	α=0.001			α=0.05	α=0.01	α=0.001
100	51	1.5	0.0684	0.0208	0.0068	61	1.5	0.0488	0.0096	0.0004
		3	0.0672	0.0188	0.0052		3	0.0340	0.0068	0.0004
		6	0.0612	0.0160	0.0040		6	0.0340	0.0056	0.0012
		9	0.0600	0.0180	0.0032		9	0.0348	0.0084	0.0004
	71	1.5	0.0344	0.0056	0.0004	81	1.5	0.0296	0.0056	0.0004
		3	0.0272	0.0044	0.0000		3	0.0304	0.0064	0.0004
		6	0.0256	0.0024	0.0004		6	0.0228	0.0056	0.0000
		9	0.0236	0.0044	0.0004		9	0.0196	0.0048	0.0000
	91	1.5	0.0336	0.0096	0.0008	101	1.5	0.0440	0.0088	0.0012
		3	0.0320	0.0064	0.0008		3	0.0360	0.0048	0.0000
		6	0.0244	0.0036	0.0008		6	0.0220	0.0028	0.0000
		9	0.0216	0.0032	0.0004		9	0.0200	0.0024	0.0004
60	91	1.5	0.0524	0.0088	0.0004	101	1.5	0.0500	0.0084	0.0012
		3	0.0400	0.0076	0.0012		3	0.0392	0.0064	0.0004
		6	0.0200	0.0056	0.0004		6	0.0320	0.0060	0.0004
		9	0.0216	0.0028	0.0000		9	0.0216	0.0024	0.0000

All results were based on 2,500 simulations using Software SelSim [18]

The results of Table 1 showed that the type I error rates were generally higher than the nominal levels when the number of SNPs is 51, for each of the four recombination rates. The type I error rates were deceasing when the number of SNPs increased, and the type I error rates were less than or around the nominal level when the number of SNPs was larger or equal to 61. Hence, the truncation at the boundary SNPs caused a problem of high false positives. In general, the xp-EHHST S_AB had appropriate type I error rates when it was used to calculate test scores of SNPs which were reasonably far away from the boundary (≥30). Compared with EHHST developed in Zhong et al. (2010) [22], the type I error rates of xp-EHHST were lower and so it was more robust. Possibly, this is due to that sample size is doubled in xp-EHHST to n_A + n_B − 2 = 2n − 2 (n = 100 or n = 60) for S_AB compared with a sample size n − 1 of EHHST.

To investigate the impact of demographic population history on the xp-EHHST S_AB, we performed coalescent simulations using ms [9]. We evaluated the type I error rates of xp-EHHST S_AB under a few plausible population genetic demographic models. Specifically, we considered four demographic models similarly as those considered in Hanchard et al. (2006) [8] and Zhong et al. (2010) [22]:

1. Population structure: two equal-sized sub-populations were simulated which exchanged migrants with a probability 0.1;

2. Population expansion: a rapid population growth was simulated with a current population size 10,000, and the population had a constant population size until 500 generations ago when it expanded exponentially by a factor of 100 to reach the current day population size 10,000;

3. Population bottleneck 150/300: a panmictic population was simulated which had a constant size 10,000 until T₁ = 300 generations ago when it underwent an instantaneous size reduction to 5,000, followed by a period of 150 generations of constant size, and then followed by a rapid exponential population expansion in the last T₂ = 150 generations to reach a current day size 20,000.

4. Population bottleneck 250/500: a population similar to the above Population bottleneck 150/300, except T₁ = 500 and T₂ = 250.

Now, a genomic region of 101 SNPs was simulated with four recombination fractions ρ = 1.5, 3, 6, and 9. In addition, 2,500 sample pairs of n = 60 or n = 100 were generated to calculate the empirical type I error rates one by one. The results were reported in Table 2. When the recombination fractions were 3, 6 or 9, the type I error rates were generally around or lower than the nominal levels. When the recombination fraction was ρ = 1.5, the type I error rates were around or lower than the nominal levels for two demographic models of population structure and population expansion, and higher than the nominal levels for the two demographic models of population bottleneck. In general, the xp-EHHST was reasonably robust for the four simple demographic models. Again, the type I error rates of xp-EHHST were lower than those of EHHST developed in Zhong et al. (2010) [22].

Table 2.

Type I error rates of the cross-population extended haplotype-based homozygosity score test (xp-EHHST).

Demographic model	Sample size n	ρ	Nominal level			Sample size n	ρ	Nominal level
			α=0.05	α=0.01	α=0.001			α=0.05	α=0.01	α=0.001
Population structure	100	1.5	0.0388	0.0116	0.0016	60	1.5	0.0468	0.0116	0.0016
		3	0.0316	0.0056	0.0008		3	0.0324	0.0084	0.0012
		6	0.0244	0.0045	0.0000		6	0.0232	0.0044	0.0004
		9	0.0164	0.0028	0.0000		9	0.0228	0.0052	0.0004
Population expansion	100	1.5	0.0432	0.0080	0.0008	60	1.5	0.0352	0.0056	0.0012
		3	0.0352	0.0052	0.0008		3	0.0264	0.0064	0.0012
		6	0.0252	0.0036	0.0004		6	0.0224	0.0048	0.0008
		9	0.0228	0.0052	0.0008		9	0.0148	0.0024	0.0000
Population bottleneck 150/300	100	1.5	0.0768	0.0184	0.0028	60	1.5	0.0732	0.0236	0.0056
		3	0.0420	0.0092	0.0012		3	0.0500	0.0116	0.0012
		6	0.0296	0.0052	0.0008		6	0.0324	0.0080	0.0012
		9	0.0264	0.0032	0.0004		9	0.0240	0.0048	0.0004
Population bottleneck 250/500	100	1.5	0.0692	0.0192	0.0028	60	1.5	0.0724	0.0184	0.0024
		3	0.0380	0.0068	0.0008		3	0.0404	0.0084	0.0012
		6	0.0340	0.0064	0.0008		6	0.0336	0.0056	0.0004
		9	0.0272	0.0028	0.0004		9	0.0292	0.0076	0.0004

All results were based on 2,500 simulations using software ms [10], and a genomic region of 101 SNPs was simulated

3.2 Power of xp-EHHST

Such as Zhong et al. (2010) [22] and Hanchard et al. (2006) [8], we performed coalescent simulations for power comparison by SelSim [18]. We simulated a genomic region comprising 101 SNPs instead of 50, to avoid a potential problem caused by truncation at the boundary (refer to Type I error rates). In the simulation of Hanchard et al. (2006) [8], three different uniform recombination rates, ρ = 4N₀r = 1.5, 3, and 6, between SNPs were used, and three different allele frequencies (0.1, 0.2 and 0.4) were used for the minor allele of the central SNP. Here N₀ is the diploid population size and r is the probability of cross-over per-generation between the SNPs.

To calculate an empirical power level, we simulated 2,500 sample pairs of 200 chromosomes or n = 100 individuals. In each sample pair, two independent samples were generated: the first one was generated under the neutral model which served as the population that the selected allele approached fixation; the second one is simulated using four recombination rates ρ = 1.5, 3, 6 and 9, and six present day population frequencies of the derived allele for the central SNP (0.1, 0.2, 0.4, 0.6, 0.8, and 0.9). As Hanchard et al. (2006) [8], a partial selective sweep was assumed for the central SNP by using a selection coefficient s = 500 for the second sample in a sample pair. The second sample served as a sample in which homozygosity remains high to calculate the empirical power of S_AB. For each sample pair, we calculated an empirical xp-EHHST value for the central SNP. Then, the empirical power was calculated as the proportion of the 2,500 xp-EHHST values that exceeded 95th, 99th and 99.9th percentiles of the standard normal. The results were reported in Table 3.

Table 3.

Power of the cross-population extended haplotype-based homozygosity score test (xp-EHHST).

Selection coefficient	Sample size n	Recombination rates ρ	Nominal level α	Present day popu. freq. of derived allele
				0.1	0.2	0.4	0.6	0.8	0.9
s=500	100	1.5#	0.05	0.9788	1.0000	1.0000	1.0000	0.9884	0.7880
			0.01	0.9320	0.9972	1.0000	1.0000	0.9584	0.5284
			0.001	0.8128	0.9900	1.0000	0.9996	0.8180	0.2044
		3#	0.05	0.9024	0.9960	1.0000	1.0000	0.9492	0.4844
			0.01	0.7512	0.9884	1.0000	0.9992	0.8336	0.1972
			0.001	0.4876	0.9500	0.9964	0.9896	0.5348	0.0440
		6#	0.05	0.7496	0.9840	0.9992	0.9964	0.9328	0.4604
			0.01	0.5108	0.9440	0.9952	0.9936	0.7836	0.1812
			0.001	0.2152	0.8148	0.9824	0.9668	0.4924	0.0428
		9	0.05	0.6444	0.9668	0.9980	0.9976	0.9152	0.4412
			0.01	0.4036	0.8968	0.9928	0.9868	0.7644	0.1888
			0.001	0.1500	0.7176	0.9668	0.9552	0.4852	0.0476
	60	1.5	0.05	0.8448	0.9908	0.9996	0.9992	0.9112	0.4832
			0.01	0.7008	0.9800	0.9992	0.9860	0.7320	0.2336
			0.001	0.4888	0.9444	0.9924	0.9300	0.3992	0.0644
		3	0.05	0.6524	0.9448	0.9992	0.9916	0.7168	0.2844
			0.01	0.4336	0.8608	0.9876	0.9532	0.4204	0.0960
			0.001	0.2032	0.6964	0.9472	0.8196	0.1516	0.0172
		6	0.05	0.4740	0.8676	0.9608	0.9792	0.6976	0.2540
			0.01	0.2400	0.6980	0.9336	0.9260	0.4468	0.0988
			0.001	0.0916	0.4280	0.8256	0.7660	0.1816	0.0168
		9	0.05	0.4736	0.8292	0.9828	0.9740	0.6744	0.2692
			0.01	0.2444	0.6352	0.9368	0.9144	0.4036	0.0904
			0.001	0.0864	0.3600	0.8016	0.7336	0.1684	0.0144

All results were based on 2,500 simulations using Software SelSim [18]. The rows marked by # contain results which were calculated using the same models and parameters as those of Figure 1 of Hanchard et al. (2006) [8]. Abbreviation: freq. — frequency, popu. —population

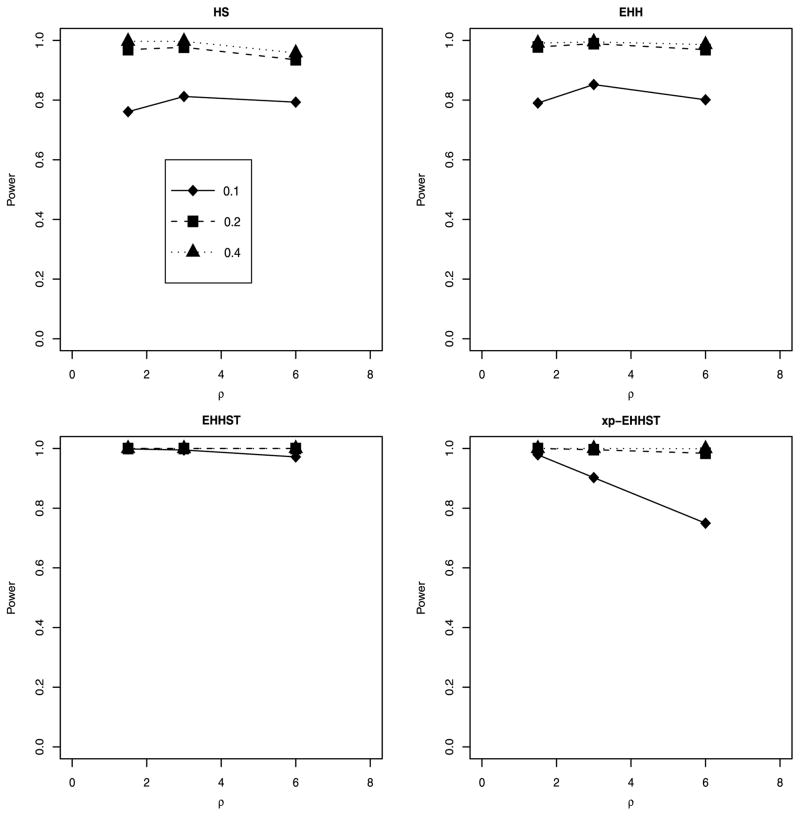
Using the results in Table 3, we first compared the performance of our xp-EHHST with Sabeti’s EHH and Hanchard’s HS. We showed the power comparison in Figure 1. The two plots on the top of Figure 1, i.e., EHH and HS plots, were taken from Hanchard et al. (2006) [8], Figure 1. The left plot on the bottom of Figure 1 was taken from Zhong et al. (2010) [22] which showed the empirical power of EHHST, and the right plot on the bottom showed the empirical power of xp-EHHST. The results of Figure 1 and Table 3 clearly showed that the xp-EHHST performed just as well as or even better than Hanchard’s HS and Sabeti’s EHH except for the case of allele frequency which was 0.1 and recombination rates ρ = 6.

Figure 1.

Power comparison of xp-EHHST with EHHST [22] and Sabeti’s EHH and Hanchard’s HS. The two plots on the top, i.e., EHH and HS plots, were taken from Hanchard et al. (2006) [8], Figure 1. The left plot on the bottom was taken from Zhong et al. (2010) [22].

Compared with EHHST developed in Zhong et al. (2010) [22], the power of xp-EHHST was lower or similar. For the two cases of population frequencies 0.2 and 0.4 of the derived allele of the central SNP, the power of xp-EHHST was similar to that of EHHST in Figure 1; the power of xp-EHHST was lower than that of EHHST when population frequency is 0.1 and recombination rates are ρ = 3, 6 in Figure 1. From the results of Table 3 of Zhong et al. (2010) [22] and Table 3, the power of xp-EHHST was similar to or slightly lower than that of EHHST for the two cases of population frequencies 0.4 and 0.6. For the other cases of population frequencies of the derived allele, the power of xp-EHHST could be lower than that of EHHST.

We calculated the empirical power by simulating 2,500 sample pairs of 120 chromosomes or n = 60 individuals. The HapMap data contained samples of size 60, and our results provided some insight about the samples. The results were reported in the bottom part of Table 3. The power of xp-EHHST was high for two present day population frequencies 0.4 and 0.6 of the derived allele of the central SNP. In the case of three present day population frequencies 0.1, 0.2, and 0.8, the xp-EHHST provided reasonably high power. For the present-day population frequency 0.9 of the derived allele, the empirical power of the xp-EHHST could be low. Therefore, the xp-EHHST has high power when the selected allele remains polymorphic, but it has little power when the selected allele has risen to high frequency or fixation in the populations.

3.3 Results in the candidate regions of HapMap Phase II data

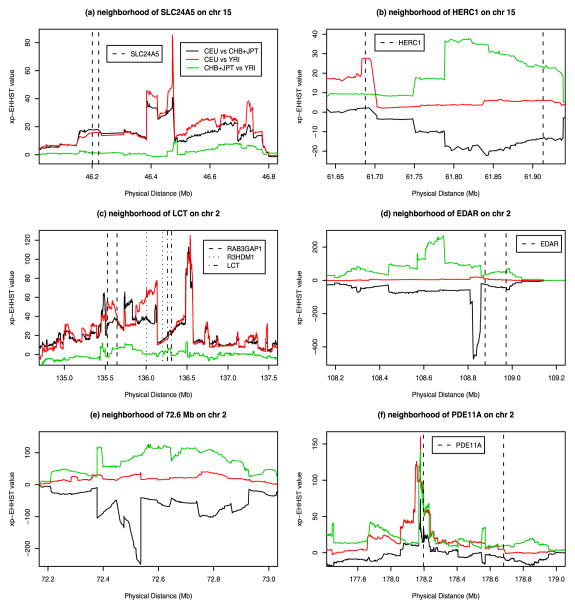
In the region of SLC24A5 gene on chromosome 15, a striking reduction in heterozygosity in the CEU sample was found, and this was treated as evidence of positive selection [17, 13]. Figure 2a showed that the xp-EHHST curves of CEU vs CHB+JPT and CEU vs YRI were high while the curve of CHB+JPT vs YRI was low. Hence, the results were consistent with those of Sabeti et al. (2007) and Lamason et al. (2005) [17, 13]. One may want to notice that the EHHST scores of CEU sample were high while those of CHB+JPT and YRI samples were very low in Zhong et al. (2010) [22].

Figure 2.

The xp-EHHST values of three population samples of HapMap Phase II data: Graph (a) in the region of SLC24A5 gene and Graph (b) in the region of HERC1 gene on chromosome 15, Graph (c) in the region of RAB3GAP1, R3HDM1, LCT genes, Graph (d) in the region of EDAR gene, Graph (e) in the region around 72.6 Mb, and Graph (f) in the region of PDE11A gene on chromosome 2.

In Table 1 of Sabeti et al. (2007) [17], CHB+JPT sample was showed to have signals of positive selection in a 200 kb region around gene HERC1 on chromosome 15, which was located between the dashed lines from 61.69 Mb to 61.91 Mb on the Figure 2b. The xp-EHHST values plotted in Figure 2b showed that the xp-EHHST values of CHB+JPT vs YRI were clearly highest or significantly positive within most parts of HERC1 gene, the xp-EHHST values of CEU vs CHB+JPT were clearly lowest or significantly negative, and the xp-EHHST values of CEU vs YRI were clearly around 0. Hence, the CHB+JPT sample showed long extended haplotype homozygosity in the gene region compared with the other two samples.

In a chromosome region around 136.0 on chromosome 2, CEU sample showed selective signals in the neighborhood of three genes: LCT gene located between 136.26 Mb and 136.32 Mb, RAB3GAP1 between 135.53 Mb and 135.64 Mb and R3HDM1 between 136.01 Mb and 136.20 Mb [17, 4, 5, 15]. Our xp-EHHST values of CEU vs CHB+JPT and CEU vs YRI plotted in Figure 2c were noticeably higher, confirming the previous results. In the meantime, the xp-EHHST values of CHB+JPT vs YRI were low and around 0.

Two other regions on chromosome 2, a 1.0 Mb region around the gene EDAR and an 800 kb region around 72.6 Mb, showed strong evidence of selection in CHB+JPT sample (Table 1, Sabeti et al., 2007 [17]). The xp-EHHST values plotted in Figure 2d–e confirmed the previous findings that the xp-EHHST values of CHB+JPT vs YRI were clearly highest or significantly positive in the two regions, the xp-EHHST values of CEU vs CHB+JPT were clearly lowest or significantly negative, and the xp-EHHST values of CEU vs YRI were clearly around 0.

In a 1.2 Mb region around the gene PDE11A, both the CHB+JPT and CEU samples were reported to have a strong signal of selection (Table 1, Sabeti et al. 2007 [17]). The xp-EHHST values plotted in Figure 2f showed that the xp-EHHST curves of CHB+JPT vs YRI and CEU vs YRI were high. This confirmed the previous results.

Figure 2 gave the xp-EHHST values in the candidate regions of chromosome 2 and chromosome 15 [17]. The results of xp-EHHST values in the other candidate regions reported in Table 1 of Sabeti et al. (2007) [17] were provided in Supplementary II (http://www.intlpress.com/SII/p/2011/4-1/SII-4-1-ru-fan-supplement.zip).

3.4 New candidate regions of HapMap Phase II data for further investigation based on the high xp-EHHST scores

By type I error evaluation, it was found that xp-EHHST was very conservative and it is even more robust than EHHST proposed in Zhong et al. (2010) [22]. The high absolute xp-EHHST values in a chromosome region indicated that there were likely long stretches of homozygosity in one population but not in the other. Therefore, we used xp-EHHST in search of new candidate regions for further investigations. Before selecting a candidate region, we first selected SNPs in a region as follows: 1) the selected SNP had high absolute xp-EHHST value of top one percentile, i.e., the absolute xp-EHHST value of the SNP is in the top one percentile of all SNPs of a chromosome in which the SNP was located, 2) the selected SNP had an allele which is likely to be newly derived by using the data from http://hg-wen.uchicago.edu/selection/frontpage.html of the University of Chicago [20], 3) the derived allele of the selected SNP had a high frequency which was larger than 0.5 in the tested population, 4) the derived allele of the selected SNP was likely to be highly differentiated among the three populations of CHB+JPT, CEU, and YRI, i.e., the F_st score of the SNP was in the top one percentile of all F_st scores of SNPs on a chromosome [2, 3, 21]. A candidate region was selected if there was a long list of SNPs which satisfied the four election criteria.

Based on the four criteria described above, 15 candidate regions were found for positive selection when the selected SNP had high absolute xp-EHHST value of top one percentile, Supplementary III (http://www.intlpress.com/SII/p/2011/4-1/SII-4-1-ru-fan-supplement.zip) and Table 4. In the 15 candidate regions, 2 are close to regions (chromosome 1, 167,445,196–167,764,984bp; chromosome 4, 41,521,093–41,849,931bp) reported in Sabeti et al. (2007) [17]; and 9 were not reported in Sabeti et al. (2007) [17]; we counted these 11 regions as new candidates. In the 11 new candidate regions, 2 were not reported in Zhong et al. (2010) [22], i.e., chromosome 7, 135,458,203–135,496,018bp and chromosome 12, 37,243,569–37,336,502bp. The remaining 4 regions were overlapped with the regions or were within regions reported in Sabeti et al. (2007) [17].

Table 4.

New candidate regions for positive selection identified by the four criteria described in the main text and Supplementary III (http://www.intlpress.com/SII/p/2011/4-1/SII-4-1-ru-fan-supplement.zip).

Region	Chr	Tested population	Starting and ending positions (bp)	Size (bp)	Number of SNPs	Genes in or near the region
1	1	CHB+JPT	75329244–75512920	183,676	11	LHX8, SLC44A5
2#	1	CHB+JPT	167443021–167764984	321,963	16	BLZF1, SLC19A2
3	2	CHB+JPT	103484100–103606852	122,752	16	SLC9A4, SLC9A2, MFSD9, TMEM182
4	3	CHB+JPT	106178646–106306013	127,367	22	ALCAM, CBLB
5	3	CHB+JPT	109117646–109578788	461,142	11	C3 or f66, DPPA2, DPPA4, RP11-702L6
6	3	CHB+JPT	17430401–17686131	255,730	19	PLCL2, TBC1D5
7#	4	CHB+JPT	41521093–41849931	328,838	76	SLC30A9, TMEM33, BEND4, WDR21B
8	5	CHB+JPT	117006587–117796132	789545	47
9	7	CEU	119168428–119351441	183,013	16	KCND2
10†	7	CHB+JPT	135458203–135496018	37,815	12	NUP205, SLC13A4, FAM180A, MTPN
11†	12	CEU	37243569–37336502	92,933	23

^#marks regions which are close to candidate regions reported in Table 1, Sabeti et al. (2007) [17].

^†marked regions which were not identified before in Sabeti et al. (2007) [17] or Zhong et al. (2010) [22].

The sixth column, Number of SNPs, gives number of SNPs which satisfied the four criteria in a region

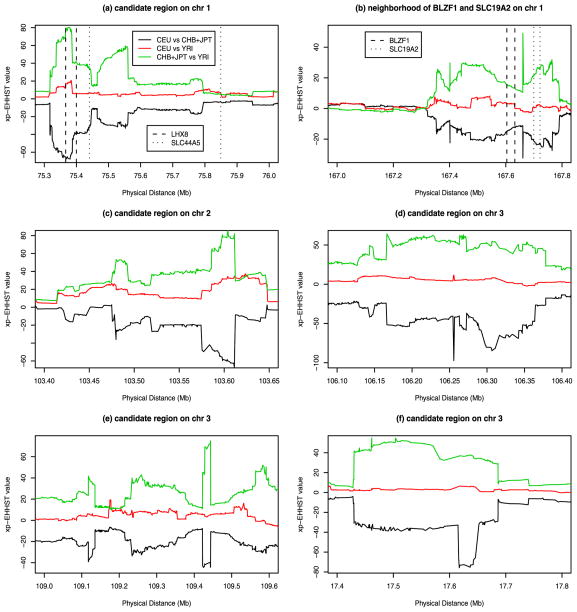
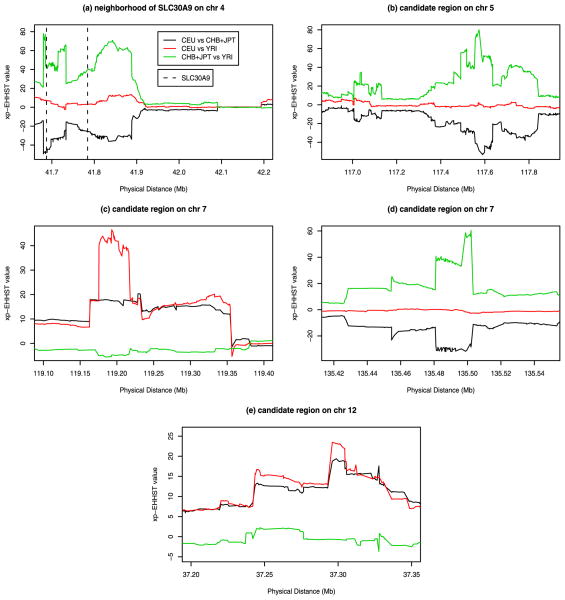
The regions containing the least number of SNPs satisfying the criteria (11 SNPs) were located on chromosomes 1 and 3, i.e., 75,329,244–75,512,920bp and chromosome 3, 109,117,646–109,578,788bp. Other regions contained 12 to 76 SNPs which satisfied the criteria. Figure 3 and Figure 4 presented the xp-EHHST values in the 11 new candidate regions. In the regions of Figures 3a–f and Figure 4a,b,d, the xp-EHHST values of CHB+JPT vs YRI were positively high and the xp-EHHST values of CEU vs CHB+JPT were negatively low, while those of CEU vs YRI were around 0; Thus, the CHB+JPT sample had long stretches of homozygosity in those regions which confirmed the findings in Table 4. In the two regions of Figure 4c,e, the xp-EHHST values of CEU vs CHB+JPT and CEU vs YRI were positively high, while those of CHB+JPT vs YRI were around 0; Thus, it is likely that there were selection signals for the CEU sample in the two candidate regions.

Figure 3.

The xp-EHHST values of three population samples of HapMap Phase II data in the candidate regions on chromosomes 1, 2, and 3 identified in Table 4.

Figure 4.

The xp-EHHST values of three population samples of HapMap Phase II data in the candidate regions on chromosomes 4, 5, 7, and 12 identified in Table 4.

3.5 Software and computational performance

Our C++ code for the proposed methods is freely available on request to Dr. Fan.

4. DISCUSSION

In this article, we developed a cross-population extended haplotype-based homozygosity score test statistic to detect excess homozygosity in one population using another population as a baseline which does not have significant excess homozygosity. Our xp-EHHST was constructed as a two-sample pooled t-test which has an approximate normal distribution as long as the sample size is relatively large, e.g., the HapMap II data. Such as the xp-EHH in Sabeti et al. (2007) [17], it is designed to detect selective sweeps in which the selected allele has risen to high frequency or fixation in one population but remains polymorphic in the other. Unlike the xp-EHH in Sabeti et al. (2007) [17], our xp-EHHST does not need logarithm transformation since it is an approximately normal score test.

By simulation studies, we showed that the xp-EHHST has correct type I error rates and it is very robust in the presence of population history of bottlenecks, expansions, and population structures. In Zhong et al. (2010) [22], we showed that EHHST was more robust than Hanchard’s HS and Sabeti’s EHH. Compared with EHHST, the empirical type I error rates of xp-EHHST are lower and so it is more conservative. Therefore, the xp-EHHST is the most conservative. For power comparison, we showed that xp-EHHST performed just as well or better than Hanchard’s HS and Sabeti’s EHH for most cases. The power of xp-EHHST was similar or lower than that of EHHST; thus, the robustness of xp-EHHST had a trade of lower power.

The xp-EHHST was applied to the HapMap II data; the results were consistent with previous results [17, 22]. We then applied xp-EHHST to search for new candidate regions of positive selection of the HapMap II data. Based on four rigorous criteria, 15 candidate regions were found to show excess homozygosity, in which 11 regions were new for further investigation and validation of positive selection since they were not identified in Sabeti et al. (2007) [17]. In the 11 new candidate regions, two regions were really new since they were not identified before in Sabeti et al. (2007) [17] or Zhong et al. (2010) [22]. In addition, two regions were close to candidate regions reported in Table 1, Sabeti et al. (2007) [17]. The remaining 4 regions were overlapped with the regions or were within regions reported in Sabeti et al. (2007) [17].

In this article, the xp-EHHST was applied to analyze the HapMap II data for a genome-wide scan in the candidate regions and to search for new regions for positive selections. In addition to the genome-wide scan, the proposed test statistic xp-EHHST can be used in fine mapping of positive selection. By fine mapping, we mean that one may type more SNPs in a candidate region for further high resolution detection of positive selection. In practice, xp-EHHST is computationally demanding and so it would be ideal to perform fast genome-wide scan via EHHST or Sabeti’s EHH. Then, the proposed xp-EHHST can be applied to the haplotype data for fine mapping based on the prior selection signals to get better results.

Under the assumption of no significant excess homozygosity in a chromosome region, HWE is roughly true in one population; on the other hand, the HWE is hardly true in the region if homozygosity remains high in the other population. The xp-EHHST was designed to detect genomic regions in which one population has extended stretches of homozygosity while the other does not. In those regions, the empirical values of xp-EHHST tends to be either significantly positive or significantly negative. The signals of significantly positive or negative xp-EHHST values in a regions can be treated as excess homozygosity for further investigation of positive selection.

In practice, both populations may have excess homozygosity in one genomic region, e.g., both CHB+JPT and CEU have strong selection signals in a 1.2 Mb region around the gene PDE11A on chromosome 2 (Figure 2f) [17, 22]. In this case, the absolute xp-EHHST values can be small such as the xp-EHHST curve of CEU vs CHB+JPT in Figure 2f since the measurements of homozygosity cancel each other in the numerator of xp-EHHST. Hence, a good practice in data analysis is to apply both one-population methods and cross-population methods simultaneously. For one-population methods, the choices can be Hanchard’s HS, Sabeti’s EHH, and our EHHST. For cross-population methods, only two approaches are available, i.e., Sabeti’s EHH and the proposed xp-EHHST. One may get a full picture by applying both one-population and two-population approaches to analyze the data.

The proposed test can be generalized to multiple populations to test if there is an excess homozygosity difference or not (say 3 or more populations), just as the generalization of two sample t-test to analysis of variance (ANOVA). Then, multiple population ANOVA F-test can be constructed to test if there is an excess homozygosity difference; and if there is a difference, one needs to find which populations have the excess homozygosity. Due to the length of the paper, we leave the possible extension for future research.