Design and analysis of large-scale biological rhythm studies: a comparison of algorithms for detecting periodic signals in biological data

Abstract

Motivation: To discover and study periodic processes in biological systems, we sought to identify periodic patterns in their gene expression data. We surveyed a large number of available methods for identifying periodicity in time series data and chose representatives of different mathematical perspectives that performed well on both synthetic data and biological data. Synthetic data were used to evaluate how each algorithm responds to different curve shapes, periods, phase shifts, noise levels and sampling rates. The biological datasets we tested represent a variety of periodic processes from different organisms, including the cell cycle and metabolic cycle in Saccharomyces cerevisiae, circadian rhythms in Mus musculus and the root clock in Arabidopsis thaliana.

Results: From these results, we discovered that each algorithm had different strengths. Based on our findings, we make recommendations for selecting and applying these methods depending on the nature of the data and the periodic patterns of interest. Additionally, these results can also be used to inform the design of large-scale biological rhythm experiments so that the resulting data can be used with these algorithms to detect periodic signals more effectively.

Contact: anastasia.deckard@duke.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Many methods for detecting periodicity or patterns in biological time series data exist, and these methods often come from scientific fields outside of biology. Although these methods may perform well for their original area of intended use, it is often unclear how well they will perform on a given biological dataset. In this study, we investigate the utility of four algorithms. Ours is not the first effort to tackle this question of algorithm selection:

In de Lichtenberg et al. (2005a), they compared the performance of their new method with five existing methods (visual inspection, Fourier and correlation scores, partial least squares regression, single-pulse model, cubic spline model and Bayesian model) on three cell cycle datasets from Saccharomyces cerevisiae by Spellman et al. (1998). They demonstrated that their new method outperformed these other methods at identifying genes from benchmark gene sets, which was attributed to including a measure of amplitude in their scoring. As in many such studies, they found that no single method performed the best across all their benchmark sets.

Dequéant et al. (2008) analyzed the performance of five algorithms [phase consistency, address reduction, cyclohedron test, stable persistence and Lomb–Scargle (LS)] on the outputs of the segmentation clock in Mus musculus. They compared the top results of the algorithms with benchmark sets of known cyclic genes. They then looked at the algorithm’s top genes that were not in the benchmark sets to see if they had a biological connection to known cyclic behaviors. Some methods performed better in the first task, others performed better in the second.

Zhao et al. (2008) analyzed the performance of three closely related spectral analysis schemes (LS, Capon and missing-data amplitude and phase estimation (MAPES)) on a cell cycle dataset in S.cerevisiae. For their benchmarks, they used the list of genes involved in the cell cycle from Spellman et al. (1998) and the list of genes not involved in the cell cycle from de Lichtenberg et al. (2005b). Their results showed that LS outperformed the other methods.

Each of these studies measured the performance of algorithms by how well they can identify known sets of genes for a given periodic process (cell cycle, somitogenesis, etc.). To avoid the potential biases and challenges in this approach, we augmented our study of biological data (Section 2.2) with a study on synthetic datasets (Section 2.1) so that we could quantify an algorithm’s performance against known ground truth. We used synthetic data to characterize algorithm performance for different signal shapes, noise levels and sampling rates that are present in different organisms and technologies. Synthetic data were also used to investigate the algorithm’s ability to recover period, phase and amplitude.

Previous studies generally focused on one type of periodic signal or one type of organism. Our goal is to study how algorithms perform across a variety of organisms and periodic processes. We used algorithms to analyze experimental data from several systems: the cell cycle (Orlando et al., 2008) and metabolic cycle (Tu et al., 2005) in S.cerevisiae, circadian rhythm (Hughes et al., 2009) in M.musculus and the root clock (Moreno-Risueno et al., 2010) in Arabidopsis thaliana. We focused on microarray datasets and designed the synthetic data to capture the characteristics of these data types.

After evaluating a large collection of algorithms, de Lichtenberg (DL) (de Lichtenberg et al., 2005a), LS (Lomb, 1976; Scargle, 1982), JTK_CYCLE (JTK) (Hughes et al., 2010) and persistent homology (PH) (Cohen-Steiner et al., 2010) were selected for comparison. Several other algorithms were evaluated but not included in further analysis because of similarity to tested algorithms, being too general, using pre-processing algorithms, lesser performance or no available implementation. These included, but were not limited to, COSOPT (Straume, 2004), ARSER (Yang and Su, 2010), LSPR (Yang and Zhang, 2011) and address reduction (Ahnert et al., 2006).

The four algorithms were chosen because they derive from four different mathematical methods for identifying periodicity. They were also selected for their ability to work on datasets with limited numbers of periods, as the microarray datasets we examine contain 2–3 periods. Each defines periodicity differently, weights aspects of rhythmicity differently (e.g. amplitude, profile shape) and responds differently to noise, irregular intervals and missing data. Periodic signals are often described using the properties of cosine curves: period, amplitude and phase shift. Period is the length of one cycle or, alternatively, the distance before a pattern repeats. Amplitude is one half the peak-to-trough height. Phase shift is the distance that the signal has been shifted in time. Each of these algorithms returns a list of P-values or scores for each of the time series evaluated based on some combination of periodicity and/or amplitude.

The LS method was developed in the field of astrophysics (Lomb, 1976; Scargle, 1982) as a Fourier style method, but was designed to deal with data that exhibit irregular sampling, which is typical of observational data in astronomy. It measures the correspondence to sinusoidal curves and determines their statistical significance (Glynn et al., 2006).

JTK has its origins in statistics but was adapted for biological data in Hughes et al. (2010). It correlates pairs of points and then computes the significance of the correlation to that of a reference curve.

The algorithm described by de Lichtenberg (DL) (de Lichtenberg et al., 2005b) was constructed specifically for the yeast cell cycle and thus comes directly from biology. It measures the periodicity of a signal, but also takes into account a measure of the amplitude. It uses permutations to generate a background distribution for measuring significance.

PH comes from the field of computational topology, an area that lies at the intersection of mathematics and computer science (Cohen-Steiner et al., 2010). PH examines persistence pairings of minima and maxima along the curve. A single minima and maxima is considered to be the ideal perfect oscillation; additional smaller oscillations create more minima and maxima that are interpreted as a less perfect curve.

2 RESULTS

2.1 Synthetic data

To quantify algorithm performance and to make valid comparisons between each algorithm’s results, we developed several sets of synthetic data to test the algorithms (Supplementary Tables S1 and S2). Four types of analysis were performed using synthetic data.

The synthetic dataset included non-periodic cases: flat and linear; and periodic cases: cosine, two cosines with different periods and amplitudes, cosine damped, cosine peaked, cosine with a linear trend and cosine with an exponential trend (Fig. 1). The start time was 0 and the end time was 200, with period lengths of 100 (two cycles in a profile), the amplitude at 50 (for peak to trough of 100), and the phase shifts were chosen on a uniform distribution of 0 to the selected period length. Gaussian noise was applied to the profiles with standard deviation = {0, 25, 50}. These data were sampled evenly with three different numbers of samples = {50, 25, 17}. This dataset was evaluated by each of the algorithms, which were run to search for a large range of periods, with period lengths between approximately 40 and 160 (except DL, which was set to the target period because it only searches for one period). Note that DL uses permutations on the entire dataset to compute periodicity scores, so its results can vary based on the profiles included in the dataset and the number of permutations.

Fig. 1.

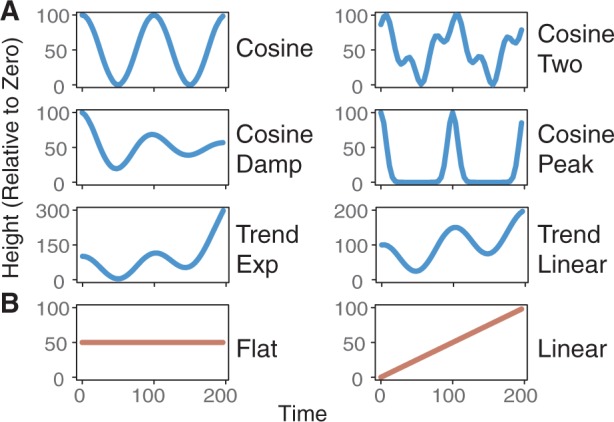
Test profiles for the synthetic datasets. The synthetic datasets include (A) periodic profiles and (B) non-periodic profiles

In the first analysis, we tested each algorithm’s performance on separating periodic from non-periodic signals with different signal shapes, noise levels and sampling rates. For each case, 1000 profiles were generated. We examined the ability of the algorithms to classify periodic versus non-periodic profiles using receiver operator characteristic (ROC) plots (Fig. 2 and Supplementary Figs S1–S3). ROC plots of algorithms visualize the sensitivity and specificity on discriminating between positive (periodic) cases and negative (non-periodic) cases as the P-value or score cutoff is varied. These plots can inform the selection of score or P-value cutoffs by looking at the trade-offs between maximizing the true-positive rate (sensitivity) and minimizing the false-positive rate (1−specificity). We examined degradation in classification performance due to noise by looking at increasing noise levels for a fixed number of samples (Fig. 2A). As expected, performance degraded as noise increased; however, the performance on cosine two, damped and peaked profiles degraded much more rapidly than for the other curves. We then examined the degradation in classification performance due to sampling rate by looking at decreasing numbers of samples for a fixed noise level (Fig. 2B). Again, performance degraded as sampling rate decreased. The performance on non-standard cosine curves (all but cosine) degraded much more rapidly than the performance on cosine curves. Both LS and JTK return P-values, which change based on number of samples (see Supplementary Table S3).

Fig. 2.

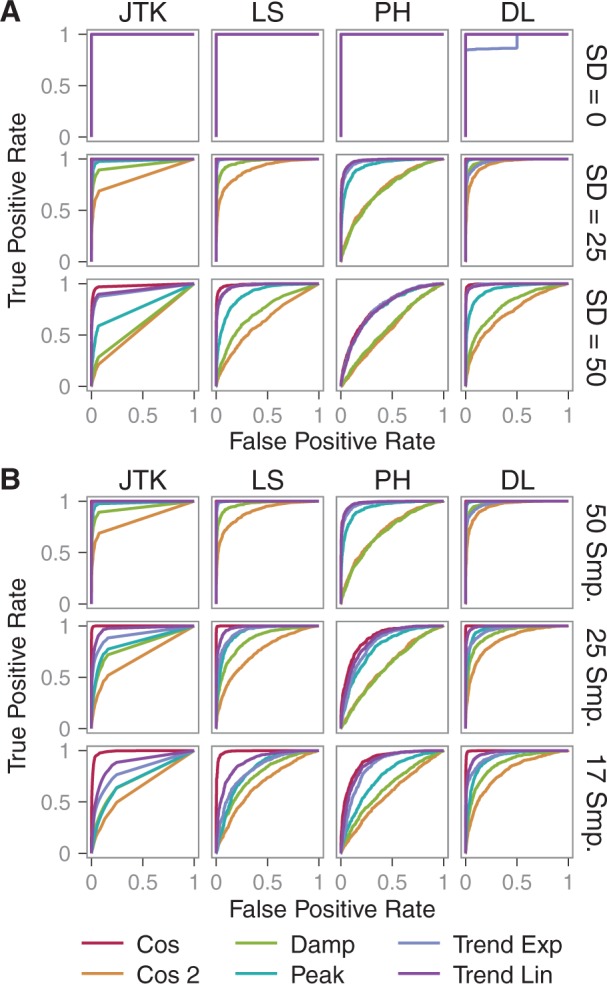
ROC plots showing algorithm performance on identifying periodic signals for different shapes, noise levels and sampling rates. (A) Performance for increasing Gaussian noise with SD = {0, 25, 50} and number of samples = 50. (B) Performance for decreasing sampling rates with number of samples = {50, 25, 17} and noise SD = 25. Used -ln (P-value or score)

The second analysis examined whether the algorithms exhibit a bias (for or against) any specific signal shapes. Each algorithm has its own definition of what it considers to be a periodic signal, which can be detected in how each algorithm scores different shapes (Fig. 3). To understand these preferences, the distributions of scores for each shape were plotted with no noise. This analysis demonstrated that with no noise, JTK, LS and PH all give cosine curves the highest scores. JTK’s next preference is for peaked profiles, whereas LS’s next preference is for damped profiles and cosine two. DL gave the best scores to some of the trended exponential (which had scores ranging from best to worst), followed closely by trended linear, and then similar scores for cosine, peaked, damped and cosine two. As noise increases, and to some extent as the number of samples decreases, the biases by shape become less distinct or shift as the scores of different shapes begin to overlap (Supplementary Fig. S4). However, LS does maintain more bias for cosine, especially compared with peaked shapes.

Fig. 3.

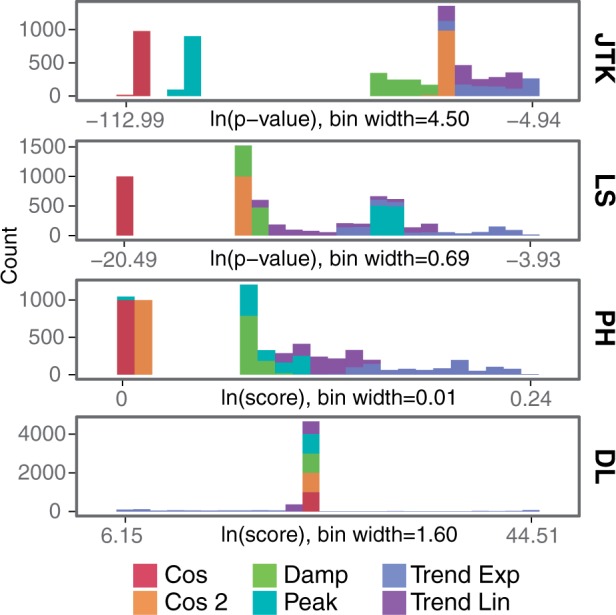
Algorithm biases for curve shapes. Histograms display scores returned for each different curve shape, for number of samples = 50 and no noise (Gaussian noise SD = 0). The x-axis shows the natural log of the scores, ranging from the lowest (best score) to the highest (worst score) returned by the algorithm. The y-axis shows the number of profiles receiving the score

In the fourth analysis, we explored each algorithm’s ability to recover the period length of the periodic signals. The ability to accurately recover period will help in selecting profiles that belong to a given periodic process. We constructed more synthetic datasets using the previous specifications, but with varying periods. We again applied increasing Gaussian noise with standard deviation = {0, 25, 50}. For each case, 100 profiles were generated. We examined the differences between the algorithms’ estimates and the actual parameters used (Fig. 4). The algorithms LS, JTK and PH all do well with no noise (SD = 0) for cosine and cosine damped. Estimates for peaked are slightly less accurate, and the trended curves are least accurate. As the noise increases, the accuracy of the period estimation for the damped and peaked curves degrades more rapidly than for the cosine curves. PH shows the most rapid degradation in period estimation under increasing noise levels. Period estimates for all curves are plotted, regardless of their periodicity score. In JTK, profiles with the worst P-value ( = 1) are assigned one period, creating a band across the plot. In LS and PH, many curves with poor periodicity scores have estimated periods that are lower than the actual periods. DL was not tested here as it only tests one target period. For analysis of phase shift, see Supplementary Figure S5.

Fig. 4.

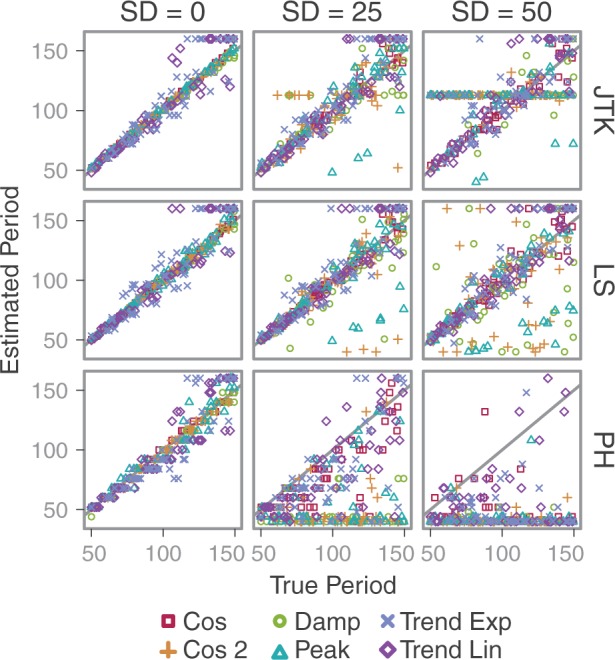
Period estimates for different profile shapes and noise levels. Estimates for all profiles are shown. The number of samples = 50 for times 0–200 and Gaussian noise with SD = {0, 25, 50}. The black line indicates estimate = true. Plots of the true period versus estimated period. The period lengths were 50–150

2.2 Biological data

For the biological data, we analyzed each algorithm’s ability to detect transcripts of a given periodic process. Experimental data from several systems were studied: the cell cycle (Orlando et al., 2008) and metabolic cycle (Tu et al., 2005) in S.cerevisiae, circadian rhythm (Hughes et al., 2009) in M.musculus and the root clock (Moreno-Risueno et al., 2010) in A.thaliana. Each dataset was run through the LS, JTK, DL and PH algorithms (Supplementary Table S4).

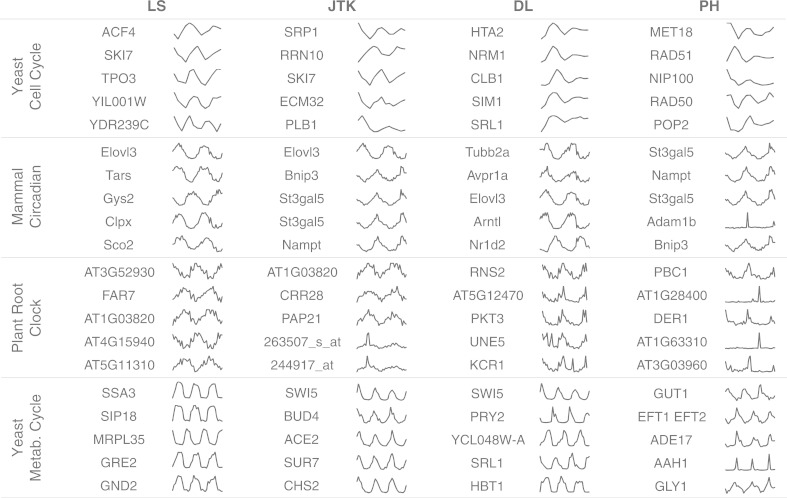
We use these results to illustrate what preferences the algorithms display for the four datasets. In Figure 5, the top five scoring profiles from each algorithm on each dataset are shown (Supplementary Figs S6–S9 for the top 20). All of the probes were rank ordered on P-value (LS, JTK) or score (DL, PH). In cases where several probes received the same score, we selected curves of interest (number of probes with the same top score: cell cycle PH: 253, metabolic cycle DL: 42, root DL: 530, circadian DL: 52). The results show how different the datasets are from one another (see Section 2 for more information). The yeast cell cycle data are less densely sampled than the other datasets (samples/cycles in the data: yeast cell cycle 13/2, yeast metabolic 36/3, root clock 39/2, mammal circadian 48/2). The plant root clock and mammal circadian data appear to be noisier than the yeast datasets.

Fig. 5.

The top five scoring gene expression profiles from each algorithm for each dataset. Algorithms are shown in columns and the datasets are in rows. All the expression profiles are normalized minimum to maximum for their amplitude

Shapes similar to cosine curves appear in the top scores from LS; but we can see curves that look equally periodic, although less similar to cosine shapes, in the other algorithms’ top scores. The DL algorithm prefers higher amplitude profiles, as measured by standard deviation, which works well for the yeast cell cycle data: two of the top five scores shown are cell cycle genes (NRM1 and CLB1). In the plant root clock, however, DL’s top scoring expression profiles appear to be noisier than JTK or LS’s top profiles. There are also many profiles that are more peaked, which both JTK and DL score well from the yeast metabolic cycle data. PH detects extremely peaked profiles, which works well in the yeast metabolic data, but returns results that do not appear to be periodic in the mammal circadian and the plant root clock. For example, the genes Adam1b in the mouse circadian and AT1G28400 in the root clock datasets appear to be singular peaks not associated with periodic expression. However, in the case of the yeast metabolic data, many of the top results show steep peaks (e.g. AAH1); these appear to be truly periodic profiles as they are regularly spaced and match the expected period.

In some cases, the rankings between algorithms are similar, whereas in other cases they can be dramatically different. One of LS’s top five for the yeast cell cycle, ACF4, was ranked in the best 5% by all algorithms. However, YDR239C was ranked in the best 5% by JTK and PH but was ranked in the worst 10% by DL.

To compare the algorithms that return significance measures, JTK and LS, we counted the number of genes at several cutoffs for P-values and q-values (Table 1). The q-values were calculated using Benjamini–Hochberg false discovery rate (FDR) (Benjamini and Hochberg, 1995). We used previously published information about the number of periodic genes associated with each of these processes for comparison. The number of genes considered to be periodically expressed can vary by the type of algorithm(s) applied, score/P-value cutoffs used, and any additional filtering on other characteristics of the expression profiles. For the yeast cell cycle data, 1271 genes were identified as having periodic transcription using the de Lichtenberg method (Orlando et al., 2008); 800 were identified using a Fourier algorithm with a correlation measurement on a different yeast cell cycle dataset (Spellman et al., 1998). For the yeast metabolic cycle, 3552 genes were called periodic using a combination of the LS periodogram and autocorrelation function (P < 0.05) (Tu et al., 2005). For the root clock data, the authors identified 3493 periodic genes using the intersection of LS (P < 0.015) and address reduction with filtering by fold change and expression value (Moreno-Risueno et al., 2010). For comparison, from our run of LS without filtering or other methods, there are 10 509 profiles that have P < 0.01. For the mouse liver circadian data, 3667 periodic genes were identified by the intersection of the Fisher’s G and COSOPT methods (q < 0.05) (Hughes et al., 2009); 5425 using JTK (BH Q < 0.05) (Hughes et al., 2010).

Table 1.

The number of genes considered periodic at various cutoffs on P-values and q-values

Dataset	Algorithm	P < 0.05	P < 0.01	q < 0.05	q < 0.01
Yeast cell cycle	LS	4	0	0	0
	JTK	800	208	0	0
Yeast metabolic cycle	LS	3744	2660	2918	1819
	JTK	4626	3828	4237	3396
Root clock	LS	12 518	10 509	11 677	9322
	JTK	13 364	11 990	12 894	11 491
Mammal circadian	LS	6570	3849	2845	1577
	JTK	9991	6204	5607	3935

When attempting to compare the results of several algorithms, selecting sets of periodic genes by P-value or score poses an interesting problem. Selecting one significance level can return genes sets with large differences in the number of genes considered periodic. For example, in the yeast cell cycle data, using P < 0.05 gives 800 genes from JTK but only four genes from LS. Additionally, the algorithms PH and DL do not return P-values. Therefore, it is difficult to directly compare P-values or scores returned by these algorithms. See Supplementary Figures S10–S13 for the distributions of P-values or scores.

2.3 Recommendations

From these results and literature on the algorithms, we have created a decision tree to recommend algorithms based on their ability to distinguish periodic from non-periodic profiles in synthetic data (Fig. 6). Sampling at least one full period is recommended, and sampling across two periods is strongly preferred, as periodicity means that values are repeated at regular intervals, which can only be verified with two full periods. LS can handle data with one or less periods, but JTK and PH require at minimum of one full period.

Fig. 6.

Recommendations for selecting an algorithm based on the dataset’s noise, sampling rate and expected curve shapes. Start on the left to select the type of noise, then sampling rate and then shape

Considering the interactions of noise, sampling rate and shape is complicated (See Supplementary Figs S1–S3 for ROC plots with area under curve (AUC)). In an ideal situation with no noise and high sampling rate, JTK, LS and PH performed well at distinguishing periodic from non-periodic signals. At low noise levels, PH worked well and its ignorance of shape can be used to find peaked profiles. However, PH’s performance degrades more rapidly than LS and JTK under increasing noise and decreasing sampling rate. As noise increases or sampling rate decreases, the ability to detect damped and peaked profiles degraded most rapidly for all the algorithms. Where the data are noisy (e.g. Gaussian noise SD = 50 with a peak-to-trough amplitude of 100) and low sampling rate (e.g. 17 samples across two periods), the algorithms perform most poorly in distinguishing damped, peaked and cosine two signals from non-periodic signals, but performed better on cosine and trended signals. In this case, it would be advisable to repeat the experiment with a higher sampling rate and/or lower noise levels. It would also be possible to apply algorithms to correct for other signals in the data, such as trending, damping or noise; however, we did not test these types of preprocessing on the performance of periodicity detection algorithms. Where high noise or low sampling rate (but not both) exists, JTK and LS are able to differentiate between periodic and non-periodic profiles for cosine. These algorithms also performed reasonably well for trended data, but their performance on damped or peaked data was much lower.

These algorithms also provide different features. Both LS and JTK return measures of significance, whereas DL and PH return scores. JTK is ignorant of amplitude, so it can be used to pick out profiles of low or high amplitude without bias (as much as those signals can stand out from noise). DL preferred high amplitude profiles, as measured by the standard deviation of the profiles. However, this can also lead to a preference for profiles with higher noise. Some algorithms can handle time series with missing time points, such as JTK, and/or unevenly spaced time points, such as LS. See Supplement for more information on their features (Section 1) and information on the execution times of their implementations (Section 2).

3 DISCUSSION

Our findings suggest that curve shape has the largest impact on the scoring of biological signals by these periodicity detection algorithms, especially under conditions of higher noise or lower sampling rate. Algorithms such as LS, DL and JTK rely on comparing data with reference curves (LS and DL assume a sinusoidal curve, JTK can use a user-specified curve); therefore, they will perform most accurately when the data match the assumptions specified by the reference curves. Additionally, as noise increases or sampling rate decreases, the ability of these algorithms to classify non-standard curve shapes degrades much more rapidly than for true cosine shapes. This is helpful when a specific type of shape is being sought and any other types should be filtered out, but is limited in a more exploratory setting when it is unknown what curve shapes a periodic process might produce.

This also brings up the question of preprocessing the data to remove factors external to the expression levels (noise, systematic error, population averaging effects, etc). To perform preprocessing, the type of external factor must be identified and quantitatively characterized in way that an algorithm can correct for it. Additionally, computationally fitting and resampling data at a higher rate can make a dataset more amenable to computational approaches, but in the case of LS and JTK, would alter the resulting P-values. Although these could increase performance of periodicity detection algorithms, caution should be exercised to avoid altering the underlying signal.

The applicability of the recommendations will vary depending on how well the characteristics in the data are known and how well the assumptions of these tests match these characteristics. In cases where the characteristics of noise, the number of cycles or shape are not known in the dataset, these recommendations should be relaxed and we suggest using several algorithms. Additionally, if the characteristics of the data are not similar to the synthetic signals (e.g. profiles are more similar to a square wave), then the recommendations may not perform as desired.

Given their different underlying ideas of periodicity, these algorithms could be used together to recover a more comprehensive set of periodic signals within a dataset. This is especially useful when the signal attributes are not known beforehand. Additionally, these algorithms also contain components for measuring phase shift and amplitude that could be used separately, and supplemented with other methods. Amplitude could be a useful measure of regulation, and phase shift is an important measure of timing. Being able to accurately estimate phase shifts between transcripts can allow us to reconstruct timing and suggest regulatory relationships.

Another issue is how to interpret and compare the P-values or scores that are returned by these methods. The work of Kallio et al. (2011) and Futschik and Herzel (2008) suggests that the significance of the results is generally overestimated in statistical methods where the null model may have more randomness than exists in the data. This causes the significance values to be excessively optimistic and overestimates the number of periodic genes. Additionally, LS and JTK return P-values, and these P-values change if the sampling density changes. Therefore, the periodicity of two identical profiles, one with twice as many time points as the other, is not directly comparable using the final P-values from these algorithms.

As we have seen in this study, there are several algorithms that could be run against biological datasets that will return results of interest. To improve these results, there must be an understanding of what information is available in the data, what answers are being sought in the data and which algorithms will be best able to bridge the gap between these two points.

4 MATERIALS AND METHODS

Lomb–Scargle (Lomb, 1976; Scargle, 1982): Sinusoidal curves of different periods are compared with the time series to generate a measure of correspondence. The significance of each of these is calculated, and the period of the most significant fit is returned. The implementation was in R and was from Glynn et al. (2006).

JTK_CYCLE (Hughes et al., 2010): A set of reference curves (sinusoidal, but can be defined) is generated to varying periods and phase shifts. A pair-wise comparison of all points in a curve calculates whether they are increasing or decreasing in relation to one another. The increasing/decreasing pattern of the time series is then compared with the increasing/decreasing pattern of each reference curve to determine the statistical significance of the correlation. The period and phase shift for the reference curve with the most significant correlation is returned. The authors of JTK (Hughes et al., 2010) provided an implementation in R.

de Lichtenberg (de Lichtenberg et al., 2005b): To measure the significance of periodicity, a background distribution is generated by creating a set of random profiles by permuting the profile’s expression values. The P-value is the proportion of permuted profiles with Fourier score at least as large as the original profiles observed Fourier score. For the significance of regulation, the gene expression profile is compared with a set of random profiles generated by selecting a value from a randomly selected gene profile at each time point. The P-value for regulation (amplitude) is measured as the proportion of permuted profiles with standard deviation at least as large as a time series’ observed standard deviation. The implementation in R from Orlando et al. (2008) was used (see Acknowledgements).

Persistent Homology (Cohen-Steiner et al., 2010): PH normalizes the data from 0 to 1, and then pairs (in a subtle way) minima and maxima of a time series. A measure is obtained by summing the differences (persistence) between the maximum and the minimum of each pair. If there is only one minimum and maximum pair, the measure is one, indicating a perfect oscillation. Additional oscillations in the time series will create more pairs, which will increase the score, indicating a less perfect curve. Sliding windows with widths equal to the range of periods are used; the period with the lowest score is returned. The last author of Cohen-Steiner et al. (2010) provided a C++ implementation of the PH algorithm (see Acknowledgements). See Supplement for additional details.

In the yeast cell cycle data (GSE8799) (Orlando et al., 2008), there is a stress response during the recovery period; we, therefore, ignored the first two time points and looked only at the last 13 time points. There were two replicates, for our analysis we used only the first replicate. The data were provided by the authors. For the yeast metabolic data (GSE3431) (Tu et al., 2005), we evened the sample times in the data by making the sampling at every 24 minutes. Any blanks in the data were filled with zeros. The data were downloaded from Gene Expression Omnibus. In the plant root clock data (GSE21611) (Moreno-Risueno et al., 2010), we applied evenly spaced time points to approximate the inferred timing. The data were provided by the authors. For the mammalian circadian rhythm data (GSE11923) (Hughes et al., 2009), the data were provided by the authors. See Supplement for additional details.