Spatial Control of Biochemical Modification Cascades and Pathways

Abstract

Information transmission in cells occurs through complex networks of proteins and genes and is relayed through cascades of biochemical modifications, which are typically studied through ordinary differential equations. However, it is becoming increasingly clear that spatial factors can strongly influence chemical information transmission in cells. In this article, we systematically disentangle the effects of space in signaling cascades. This is done by examining the effects of localization/compartmentalization and diffusion of enzymes and substrates in multiple variants of chemical modification cascades. This includes situations where the modified form of species at one stage 1) acts as an enzyme for the next stage; 2) acts as a substrate for the next stage; and 3) is involved in phosphotransfer. Our analysis reveals the multiple effects of space in signal transduction cascades. Although in some cases space plays a modulatory effect (itself of interest), in other cases, spatial regulation and control can profoundly affect the nature of information processing as a result of the subtle interplay between the patterns of localization of species, diffusion, and the nature of the modification cascades. Our results provide a platform for disentangling the role of space and spatial control in multiple cellular contexts and a basis for engineering spatial control in signaling cascades through localization/compartmentalization.

Introduction

Cells respond to their environment and regulate their internal functioning through complex and sophisticated networks of proteins and genes. Chemical information is transmitted in these networks via various sequences of chemical modifications. The nature of chemical information transmission in signaling cascades is the focus of a large body of work, which has revealed the effects of modifications, the enzymatic regimes, and the effects of enzyme and substrate sequestration.

However, sequences of chemical modifications often involve relevant species moving to different locations where other species may be localized (1). Thus, although modeling and understanding information transmission in signaling cascades through ordinary differential equations provides many useful insights, it completely ignores the spatial dimension of signal transduction. In most studies, spatial aspects are ignored, even if acknowledged, either because they are assumed a priori to be of secondary importance or because the available data are not spatially resolved. At the outset, an implicit assumption often made is that spatial effects can be easily subsumed within a kinetic description through the alteration of relevant kinetic constants, or that it plays a minor role in signal transduction. However, it is not at all clear whether that is indeed the case, or whether spatial factors may introduce important changes in information processing.

We examine the effects of space and localization in different signal transduction cascades. Spatial control through localization and compartmentalization is a recurrent theme in cell biology, observed in many signaling pathways; in addition, localization/compartmentalization through the creation of microcompartments is emerging as an experimental tool in synthetic biology (1–4). We systematically disentangle the interplay of localization, diffusion, and the nature of the modification cascades in a controlled in silico setting. By employing fairly general models and representative scenarios, we aim to tease out the effects of space in signaling cascades. This is contrasted with ordinary differential equation (ODE) models of the cascades, highlighting exactly when and how spatial factors significantly affect and shape signal transduction.

Materials and Methods

Our goal is to dissect the effects of space in modification cascades/pathways. One of the most widespread ways in which spatial effects come into play in cells is through localization of entities and modifications. Thus, we largely focus on the effects of space and localization/compartmentalization on various cascades, though we also briefly examine scenarios without localization.

Modification cascades/sequences can arise in different ways in cell signaling. One such scenario is when a modified substrate acts as an enzyme for a subsequent step. Another is when a modified substrate acts as a substrate for a subsequent modification. A third, distinct scenario of modification sequences is through phosphotransfer. These modification sequences are typically studied and understood through ODEs. Stochastic descriptions are invoked to study the effects of small numbers of molecules. Usually, however, the effects of space are ignored. We systematically examine the effects of space and spatial control on these modification sequences by constructing explicit spatial models incorporating the localization and transport of species. The analysis of these spatial models is compared with that of the default ODE models of these processes.

Model setting

We employ multiple models, each describing a different modification sequence. A basic component of most of these models is a covalent modification cycle. A spatial model of this basic enzymatic cycle is described in a standard way by incorporating enzyme binding to substrate (reversibly) to give rise to the complex, which gets irreversibly converted to the modified substrate. The conversion of a protein X to/from its modified version, X^∗, involving the kinase K and phosphatase P is described by

$$\frac{\partial \left[X\right]}{\partial t}=-k_1\left[X\right]\left[E\right]+k_{-1}\left[XK\right]+k_4\left[X^{\ast }P\right]+D_{\text{X}}\frac{{\partial }^2\left[X\right]}{\partial {\theta }^2}$$

$$\frac{\partial \left[X^{\ast }\right]}{\partial t}=-k_3\left[X^{\ast }\right]\left[P\right]+k_{-3}\left[X^{\ast }P\right]+k_2\left[XK\right]+D_{X^{\text{∗}}}\frac{{\partial }^2\left[X^{\text{∗}}\right]}{\partial {\theta }^2}$$

$$\frac{\partial \left[K\right]}{\partial t}=-k_1\left[X\right]\left[K\right]+k_{-1}\left[XK\right]+k_2\left[XK\right]+D_K\frac{{\partial }^2\left[K\right]}{\partial {\theta }^2}$$

$$\frac{\partial \left[P\right]}{\partial t}=-k_3\left[X^{\text{∗}}\right]\left[P\right]+k_{-3}\left[X^{\ast }P\right]+k_4\left[X^{\ast }P\right]+D_P\frac{{\partial }^2\left[P\right]}{\partial {\theta }^2}$$

$$\frac{\partial \left[XK\right]}{\partial t}=k_1\left[X\right]\left[K\right]-k_{-1}\left[XK\right]-k_2\left[XK\right]+D_{\text{XK}}\frac{{\partial }^2\left[XK\right]}{\partial {\theta }^2}$$

$$\frac{\partial \left[X^{\ast }P\right]}{\partial t}=k_3\left[X^{\text{∗}}\right]\left[P\right]-k_{-3}\left[X^{\ast }P\right]-k_4\left[X^{\ast }P\right]+D_{X^{\ast }P}\frac{{\partial }^2\left[X^{\ast }P\right]}{\partial {\theta }^2},$$

where k₁ and k₃ are the rate constants for binding of the enzymes and their substrate, k₋₁ and k₋₃ are the rate constants for the dissociation of the enzyme-substrate complexes, and k₂ and k₄ are the rate constants for product formation. θ is the spatial coordinate and D_j is the diffusion coefficient for species j. This model includes the diffusion of multiple species and is defined over the entire spatial domain (assumed, for simplicity, to be one-dimensional (1-D)). Different patterns of localization are possible in this cycle (e.g., see our previous work (6)). One scenario corresponds to all species nondiffusible and localized in the same subdomain. Another scenario relevant here is where the entire cycle is localized in a subdomain, apart from one species that exits the domain. The species that are localized in a given region are regarded as nondiffusible (variants of the model involving species diffusing but being prevented from exiting the subdomain are also possible, but these distinctions are not needed here). By allowing X^∗ alone to diffuse, we then obtain a scenario where X^∗ can exit the subdomain while other species remain localized. We now turn to the kinetic description of cascades, before describing spatial models.

Enzymatic cascade

When the modified substrate X^∗ at the first stage is an enzyme for a second modification cycle, the second cycle is described in an analogous way, with X^∗ playing the role of a kinase, mediating the conversion of Y to Y^∗, and the reverse conversion mediated by a phosphatase, P2. The kinetic equations for all modification cascades are presented in Section 1 of the Supporting Material. Having components of both modification cycles in the same subdomain, with all species nondiffusible (and present uniformly initially in this subdomain), corresponds to having a localized cascade in a single compartment. This corresponds to an ODE description of the cascade. A schematic of enzymatic cascades is shown in Fig. 1 A.

Figure 1.

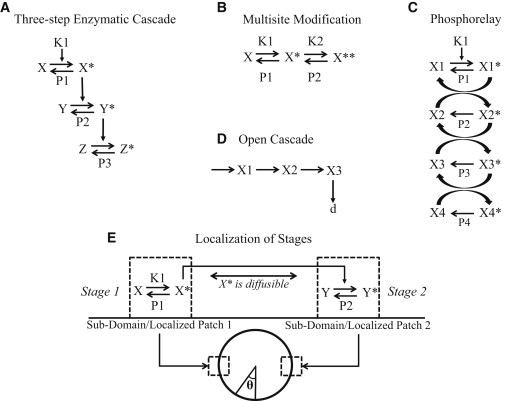
Schematic of different kinds of cascades and their localization. (A) The three-step enzymatic cascade. The modified substrate in the preceding step acts as the enzyme in the next step. (B) Multisite modification. The steps leading to successive modification of a substrate are shown. The relevant enzymes (kinases/phosphatases) for different modifications can be either different (as shown here) or the same. (C) Phosphorelay. Shown here is a cascade of four phosphotransfer reactions where the modified substrate transfers its phosphoryl group to the subsequent substrate species. In addition, phosphatases that remove the phosphoryl group may also be present. A special case of this cascade where the phosphatase of the last stage is the kinase of the first stage is also studied. (D) Open cascade. A three-stage open cascade is depicted. (E) A schematic of the spatial domain and the compartmentalization of a two-step enzymatic cascade in the two subdomains. X^∗ is the communicating species and diffuses in the spatial domain.

Modification sequence with a common substrate

A different modification sequence results when a modified substrate is modified subsequently by other enzymes. The modification status of a substrate is sometimes referred to as a molecular bar code. If all enzymes and substrates are localized in the same subdomain, assuming a specific ordering to the modification, the modification of X to X^∗ mediated by the enzyme pair K1, P1 and the conversion of X^∗ to X^∗∗ mediated by the pair K2, P2 can be described by a basic ODE model. Each elementary modification cycle is described by unpacking the covalent modification cycle in a standard way, as described above. The combination of the description of the two modification cycles provides the ODE model for the sequence of modifications (see Fig. 1 B).

Phosphotransfer mechanism

Another basic mechanism of chemical information transmission is via a phosphotransfer. In a two-step phosphorelay, the substrate in the first step, X1, is phosphorylated by an enzyme (K1). The phosphorylated form, X1^∗, transfers its phosphate group to the substrate of the second step, X2, producing X2^∗, resulting in X1^∗ converting back to X1. A phosphatase catalyzes the dephosphorylation of X2^∗ to X2. Different variants of phosphotransfer models exist that vary depending on whether phosphatases exist for individual steps in the cascade (5). We consider a scenario where individual steps have phosphatases, and so X1^∗ can be dephosphorylated by a phosphatase P1 and so on. The ODE model describing the kinetics is presented in the Supporting Material. Other variants of phosphotransfer models were also examined (discussed subsequently). We study the two-step phosphorelay and a four-step phosphorelay (which is observed in nature). Fig. 1 C is a schematic of a four-step phosphorelay.

Spatial model

We study spatial models of the above cascades, focusing on the effects of spatially compartmentalizing individual stages. This is done as follows. The first set of modifications and relevant species (one part of the cascade) is localized in one patch/subdomain, and the second set of modifications and relevant species (the other part of the cascade) is localized in a second patch/subdomain (of equal size to the first), diametrically opposite to the first (Fig. 1 E). If no species diffuses, the two patches are isolated with no communication and the modification sequence is broken.

We examine the most natural spatial versions of these cascades by allowing the common species of the two different parts of the cascade to diffuse in the spatial domain and reach the second region to effect the next step in the modification sequence. Thus, in the case of the two-step enzymatic modification cascade mentioned above, X^∗ diffuses out of the first location, reaching the second location, where it catalyzes the modification of the next stage. The species X, K1, XK1, and X^∗P1 all belong in subdomain 1, whereas Y, X^∗Y, Y^∗P2, and P2 all remain in subdomain 2. The species X^∗ is present in both patches as well as the intervening spatial region. In the case where the modified substrate at the first stage serves as a substrate for the next stage, the modified substrate X^∗ diffuses in the spatial domain. All other species are present in either the first or the second subdomain. In the two-stage phosphotransfer model, the modified form of the first stage, X1^∗, diffuses and reaches the second domain and transfers a phosphate group to X2, which is localized there. Fig. 1 E depicts a two-step cascade with localization, illustrating how different stages are localized in different locations and the connecting agent diffuses through the spatial domain.

We analyze these spatial models (see Section 1 in the Supporting Material), contrasting them with ODE models of these cascades, which correspond to all steps localized in the same location. Note that in the above description individual stages are localized in different locations and we have one species that diffuses to effect a communication between the two locations. Naturally, it is possible to consider more complex scenarios where multiple species may be diffusing, and these can easily be analyzed by simply making other species diffuse in our modeling framework. In this article, we largely restrict ourselves to the scenario described above, as the simplest nontrivial spatial depiction of the cascade. We discuss some aspects of multiple species diffusing in the text and in Section 2.4 of the Supporting material.

The model is cast, for simplicity, in a 1-D spatial domain with periodic boundary conditions (results analogous to those presented here have been obtained for no-flux boundary conditions). Note that the two patches are of equal size and are symmetrically located at diametrically opposite points on the circle (Fig. 1 E). Therefore, for the scenarios considered here, the results are exactly equivalent to those with no-flux boundary conditions in a domain half the size. Thus, all essential results are equally valid for both cases and could be relevant to situations involving modification and diffusion of species in the membrane or the cytosol.

Inputs

The modification sequences are initiated by the presence of enzymes for the first stage. These enzymes are assumed to be localized in the first domain and their concentration is varied as part of our analysis.

Parameters

The models of the various cascades involve various kinetic parameters, which can affect enzymatic regimes and information processing. Our approach regarding parametric choices is dictated by the questions of interest. Since the main focus here is on the role of space, and our analysis contrasts the spatial and ODE models, we approach this as follows. We choose a basal set of kinetic parameters (in enzymatic modification/phosphotransfer), which represents enzymatic modification in a generic parameter regime. We separately examine special parameter regimes, such as mass-action or ultrasensitive regimes, to check that similar trends (where applicable) apply here as well. The remaining parameters are the diffusivity of relevant species and the relative sizes of the patches and the overall domain. Again, we choose representative basal values for these parameters. We study the effect of these latter parameters in our analysis. Since we contrast PDE models with ODE models with the same kinetic parameters, we can directly assess the effects of these spatial parameters. In most cases, we perform analytical work to explicitly reveal the influence of parameters and ensure that the essential conclusions are independent of specific kinetic parameters. We emphasize that for the kinds of investigations performed and the nature of conclusions drawn, this approach suffices. If, in some case, a detailed parametric analysis is warranted, it is performed. Parameter values are presented in the Supporting Material.

Numerical method

The PDEs were discretized using finite difference equations and results were checked by doubling the discretization. All simulations were performed in MATLAB using ode15s. In addition, we were able to compare the kinetic parts of our MATLAB models with corresponding models in COPASI (which are automatically generated) for model checking.

Results and Discussion

Structure of results

Our results for each type of cascade are presented as follows. 1) We examine the behavior of the spatially distributed cascade (in particular, the concentration of the cascade output, which is typically localized) contrasted with ODE models of the cascade that correspond to all stages colocalized; thus, we compare local concentrations. 2) We vary suitable spatial parameters such as the size of the patches or separation between patches, as appropriate. 3) We analyze enzymatic modification cascades, multisite enzymatic and phosphotransfer mechanisms, starting with basic mechanisms and subsequently exploring biologically motivated variations of each of these. 4) We present computational results backed up by analytical work and tables, presented in the Supporting Material.

The spatial separation of stages of a cascade leads to a dilution effect

We begin by discussing a two-step enzymatic signaling cascade, examining the effect of localization of the two different stages of the cascade at different locations, contrasting this with the situation where all elements are colocalized (Fig. 2 A). By contrasting the two situations, we find that the concentration of the output of the cascade (Y^∗) is reduced when the modifications occur in different locations. This is understood by noting that when the modification steps are separated, the modified species at the first step, X^∗, must diffuse to complete the second modification—as a result, its concentration is spread over the domain, leading to a dilution effect. The concentration of X^∗ available to the second step is less compared to the scenario where all modifications occur in the same region. Although the concentration of this communicating species increases when the size of the subdomains increases (or the separation decreases), the concentration of the output of the cascade will always be lower for the scenario where the modifications are separated (Fig. 2 B). If the separation between the subdomains increases, the output of the cascade will further decrease, as X^∗ will be spread over a longer domain. The dilution effect occurs because in the course of signaling, the communicating species has to spread in the spatial domain. If there is no de novo production of this species, this spreading results in a decrease of its local concentration. This is demonstrated analytically in Section 2.1 of the Supporting Material.

Figure 2.

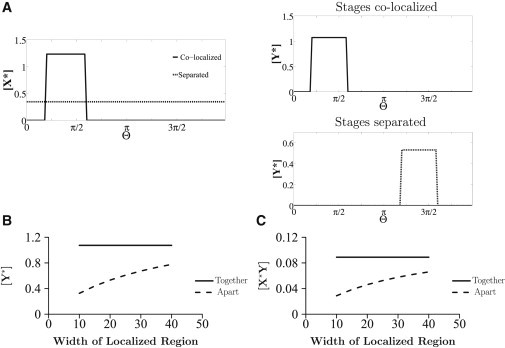
Localization in the two-step cascade. Spatial concentration profiles of species in scenarios of complete colocalization and spatial separation of stages are shown. (A) In the spatial separation scenario, the concentration of Y^∗ is reduced as a result of separation of the steps of the cascade, whereas X^∗ attains a uniform profile. (B) [Y^∗] is compared between the colocalized (solid line) and separated (dashed line) scenarios for a range of widths of the localized patches in the domain (as a fraction of total domain size). In the latter case, as the width of the localized region is increased, [Y^∗] increases, but it is still less than [Y^∗] when all reactions are colocalized. (C) The concentration of the complex [X^∗Y] in these two cases is shown. A reduction of the steady state [X^∗Y] concentration is seen when the stages are separated, implying a reduction in retroactive effects.

A second point related to the dilution effect is worth mentioning. We find that when the components of the cascade are separated, the effect of retroactivity is reduced. Specifically, the amount of species X^∗ sequestered in the downstream complex at steady state is reduced when compared to the case of the completely colocalized cascade. The effect of the second layer of the cascade on the first layer is studied by monitoring the concentration of the complex X^∗Y. We find that the retroactivity effect is significantly weakened when compared to the scenario where all species are together (Fig. 2 C). This is understood by noting that spatial separation significantly reduces the amount of X^∗ in the second domain, as discussed, and hence also reduces the amount of X^∗ sequestered in the second step of the cascade. In Section 2.1 of the Supporting Material, we analytically demonstrate this.

The above discussion reveals the presence of a tradeoff when the two stages of the cascade are separated; at steady state, the output is reduced, and the back-propagating effect of the second stage on the first is also reduced.

The dilution effect can be mitigated under different conditions

The effect of spatial segregation on the steady-state behavior of the cascade discussed above can be reduced under certain conditions. One obvious way to do this is to reduce the spatial separation between the two subdomains. A second way is by designing/operating the cascade in a regime so that the concentration of the communicating species, X^∗, is sufficiently low. This can be achieved, for instance, by having a high amount of phosphatase P1 in the first domain. In such a situation, the output of the spatially separated cascade does not deviate much from that of the colocalized cascade. The reason for this can be explained analytically. 1) At steady state, X^∗ attains a uniform profile. This is seen by adding all the equations for the species X, X^∗, and their complexes. The kinetic terms cancel out, leaving the diffusion term for X^∗, and so at steady state, X^∗ is spatially uniform. 2) If cascade parameters are such that X^∗ is sufficiently low, this means that the amount of species X that has leaked out of the first compartment is small (relative to the total amount of X species there). The leaking out of X^∗ results in a modified total concentration of species X in the first domain. 3) The steady states of all X species can be determined from the steady state of the ODEs of the first stage of the cascade, with the modified total X in domain 1, accounting for the leakage. Thus, when the total concentration of species X in domain 1 is modified to a small degree, the steady state of all X species (including X^∗) is close to the situation where no X^∗ exits (the situation of a colocalized cascade). Therefore, the effect on the cascade output, Y^∗, induced by spatial separation is negligible, both in absolute and relative terms. This is discussed further analytically in Section 2.1 of the Supporting Material, with Table S1 showing how increasing the phosphatase concentration in domain 1 can result in attenuation of the dilution effect.

Cascades with a Goldbeter-Koshland-type switch

A special case of a cascade is one where an individual stage operates in the ultrasensitive regime. A two-step cascade, where the first step is in the ultrasensitive parameter regime (9) and (for simplicity) the second step operates in the mass-action kinetic regime, with all components colocalized exhibits a switch-like response of the output, Y^∗, to the input. In the spatially separated case, this switch-like effect is typically severely attenuated (Fig. S2). This is because the enzymatic cascade at the first layer is now an open system, and the leaking out (due to diffusion) of X^∗ works against switch-like behavior, in effect making more phosphatase P1 available (moving it away from the ultrasensitive regime). It is therefore of interest to see when the switch-like behavior can be maintained in a spatially distributed cascade. One way to achieve this is if the diffusing species is not directly involved in the realizing of the switch. Having an intermediate layer with species I that is modified to I^∗ catalyzed by X^∗ (through mass-action kinetics) and I^∗ diffusing to the new domain (and modifying Y to Y^∗ there), the switch-like effect can indeed be seen (see Section 2.1 in the Supporting Material). In this case, the input to the diffusing stage of the cascade (the intermediate layer) already contains the switch-like effect: the diffusing stage of the cascade can be treated exactly like the first stage of the cascade we studied previously. However, the amplitude of the switch is reduced due to dilution. This illustrates an aspect relevant to the propagation of switch-like effects in spatially separated enzymatic cascades, where the switch behavior arises primarily from one stage: keeping the factors responsible for a switch localized (negligible leaking out), and propagating the effect via downstream pathways close to mass-action kinetics works to maintain the integrity of the switch.

Three-step cascades with switch-like behavior

We now examine three-step cascades with switch-like behavior, as an extension of the two-step cascades. As a starting point, we use a model of the MAPK cascade developed and analyzed elsewhere (7,8): this describes the three-tier modification cascade of MAPK signaling. We note that some aspects of MAPK signaling, such as the distributive multisite modification at different stages, are not included here. For the purpose of our study, we examine this cascade as an example of one with switch-like behavior. In the model, each modification step is described in the standard way (with explicit description of complexes) and the kinetic parameters employed are from Ventura et al. (8). The ODE model corresponds to the scenario of all species localized in the same domain. Model analysis shows that the cascade exhibits switch-like behavior. In addition, analysis (8) shows that incorporating multisite modification at the second and third stages results in the same qualitative behavior with further sharpening of the switch.

Since the three-tier cascade has three distinct stages, it is clear that there are a number of combinations or spatial designs to spatially partition the cascade. For example, the first stage, associated with modifications of species X, may occur in one location, and those associated with species Y and Z could occur in another location. Another possibility involves stages associated with species X and Y localized in one location and that associated with species Z in another. In the former case, X^∗ would have to diffuse to the second location to catalyze the modification of Y and in the latter, Y^∗ would have to diffuse to the second location to complete the modification cascade. Fig. 3 A shows four different spatial designs denoted I–IV, involving two different compartments. With an increased possibility of spatial designs, a cell may have more room to exert spatial control over the interactions and achieve a variety of distinct responses.

Figure 3.

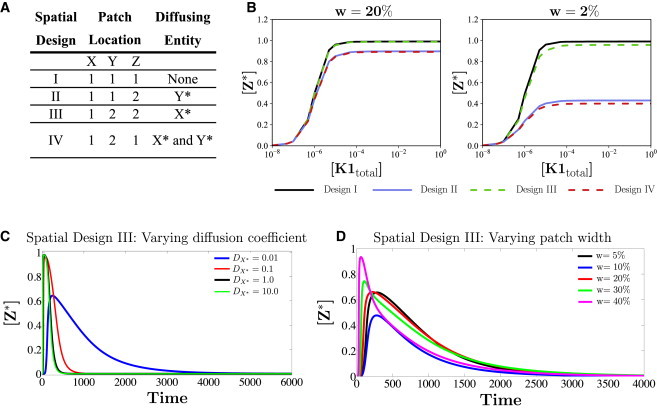
Three-step cascade with switch-like behavior: (A) Four examples of different spatial compartmentalizations (designs) of the cascade are shown: I) species X, Y, and Z are all together in subdomain 1; II) X and Y are in subdomain 1 and Z is in subdomain 2; III) X is in subdomain 1 and Y and Z are in subdomain 2; IV) X and Z are in subdomain 1 and Y is in subdomain 2. (B) Two sets of steady-state input-output curves are shown, one when the width (w) of each localized patch is one-fifth of the domain size (left) and the other when the width is one-fiftieth of the domain size (right). These plots show that when patch size is smaller (right), spatial designs II and IV have a significant effect on the input-output curve. In the larger-patch plot (left), the curve for design III is practically indistinguishable from the colocalized case (design I), and the curves for designs II and IV are also practically indistinguishable. For both domain sizes, design III has steady-state input-output curves similar to that of design I. (C and D) Transient signal input to the cascade, shown for spatial design III. (C) The effect of diffusivity of the communicating species (similar trends are seen for other designs) on the transient behavior of the output. (D) The duration of the pulse and diffusivity of the communicating species: X^∗ is fixed. As the patch width increases, a nonmonotonic response is seen: the amplitude of Z^∗ (shown for the middle of location 2) initially decreases and then increases.

Input-output responses can be distorted differently with different spatial partitioning of the cascade

The steady-state behavior of the cascade for spatial designs I–IV is examined. This was done for two different relative sizes of the patches (i.e., two different separation distances between them). When the modifications occur in one place, the input-output relationship at steady state is sigmoidal. For the case of a smaller separation (larger relative size of patches), for spatial design II and III, the input-output relationship is largely maintained and still appears sigmoidal. The input-output relationship is distorted significantly in the case of larger separation of patches for spatial design II, and the input-output curve becomes much less sigmoidal. However, even with increased separation, for spatial design III, the input-output curve is less distorted and still sigmoidal (Fig. 3 B). This shows how different spatial designs can have both subtle and strong effects on cascade behavior (Fig. 3 B). It demonstrates that it is possible to design a spatially separated cascade that can largely retain the basic input-output characteristics of the colocalized cascade. The fact that spatial design III leads to a small distortion of the switch can be understood from our analysis of two-step cascades. Here, the kinetic parameters are such that the concentration of the communicating species X^∗ is typically low relative to total concentrations of species X (this is true in the ODEs, too).This is true across the entire range of cascade input where Z^∗ is sensitive with switch-like behavior. Thus, diffusion of X^∗ leads to negligible distortion of steady-state input-output characteristics, for the same reason discussed above. For a high enough input, the concentration of X^∗ can be such that dilution may play a role, but this corresponds to input (and [X^∗]) ranges where Z^∗ is relatively insensitive.

Responses to transient inputs

Our studies of cascades so far have focused on steady states. We now briefly examine pulse inputs of the enzyme K1 to the cascade. Here, we assume, for simplicity, that the input modifies the first stage via mass-action kinetics (this has a very minor effect on the qualitative behavior incidentally), focusing on the concentration of Z^∗ for different diffusivities of the diffusing species and other spatial parameters.

The effect of diffusivity of communicating species for fixed pulse input

In this section, we examine transient aspects of signaling in spatial design III, subject to a pulse input, focusing on the effect of diffusivity of X^∗. As the diffusivity increases, the transient peak concentration of Z^∗ attained is higher, and the time taken to reach steady state also decreases. Typically, there is appreciable sensitivity of peak concentration for low diffusivities, whereas less difference is seen between the transient peak concentrations for intermediate and high diffusion coefficient values (Fig. 3 C). A similar trend is seen in other designs as well. This indicates how transient behavior of the module output may be shaped by the diffusivity of the communicating species, and that slowly diffusing species can result in strong distortions of transient signaling. This can impose a nontrivial constraint in feasible spatial designs of signaling cascades, for instance in synthetic biology.

The effect of patch size for fixed-pulse duration and diffusivity of communicating species

Note that patch size has no effect when all stages are colocalized together. The transient peak concentration of Z^∗ typically increases with increasing patch size. Nonmonotonic trends can also be seen in spatial designs III (Fig. 3 D) and IV (Fig.S3 a). In spatial design III, we find that when the diffusivity of the communicating species is low, as the patch size increases, the transient peak concentration of Z^∗ first decreases and then increases. Increasing patch size reduces the separation between patches but increases species amounts. The increase in the amount of downstream species can, in a transient regime, result in a reduction of peak Z^∗ concentration (through sequestration effects).

Switch-like behavior in cascades can arise for particular combinations of parameters, such as the MAPK model parameters. Although numerical results in general can depend on parameters, our analysis shows 1) how switch-like behavior can be significantly distorted, and 2) how it can largely be maintained in a spatial cascade. In the latter case, our analysis of two-step cascades provides relevant insights. Also, similar effects can be expected when the multistep modification at different stages is included (in fact, since the multisite modifications occur in stages 2/3, the minor distortion result in design III is relevant here, too). Our approach provides a framework for elucidating the effects of spatial partitioning in more complex cascades and engineering spatial design of cascades like the MAPK cascade.

Multisite modification

In this module (Fig. 1 B), the modified form at the first stage is the substrate for the next step. When the modifications occur in different compartments, the product of the first stage, X^∗, has to diffuse to the second location, where the enzymes that catalyze the second modification are present, to complete the sequence of modifications. Having multiple modifications increases the number of spatial designs similar to enzymatic cascades. We focus on the two-site modification module.

The enzymes (kinase, phosphatase) for the first and second modifications are (K1,P1) and (K2,P2), respectively. The ODE model corresponds to all species/modifications in the same compartment. The spatially segregated scenario corresponds to K1, P1 being present in one location and K2, P2 in the second location. In the colocalized scenario, the concentration of X^∗∗ is greater than that of the spatial segregated scenario. Similar to the enzymatic cascade, the dilution effect of the diffusing species, X^∗, plays a role. The local concentration of X^∗, when it diffuses, is lower everywhere in the spatial domain, and hence, less is available for its conversion to X^∗∗. Decreasing the separation between the subdomains, or increasing the size of these subdomains, results in an increase in the steady-state concentration of X^∗∗, which is, however, still lower than the colocalized scenario (Fig. 4 A). Examining the spatial average concentration of X^∗ (averaged over the full domain), we find in the spatially segregated scenario that the average concentration of this phosphoform is higher than in the colocalized scenario (Fig. 4 B). In fact, the average concentration of X^∗ increases with spatial separation (these points are discussed in Section 2.2 in the Supporting Material, with analytical work).

Figure 4.

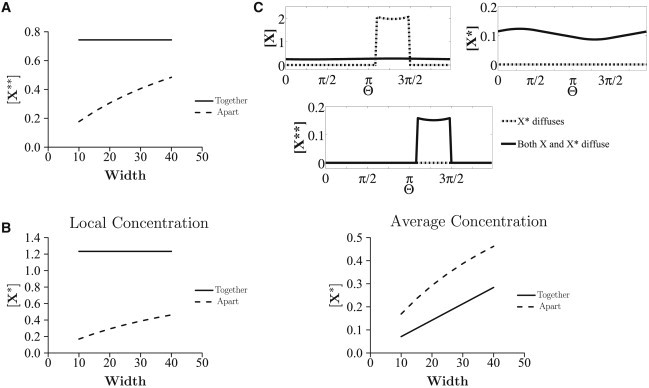
Multisite modification. (A and B) The kinase and phosphatase pairs are different for the two modification steps (K1, P1 and K2, P2). (A) [X^∗∗] is plotted against the width of the localized patch (expressed as a fraction of total domain length): [X^∗∗] is always higher when the modifications occur in the same location. The X^∗∗ concentration increases with the width of the patch. (B) The average (over the full domain) and local concentrations of X^∗ are compared in these cases. The average concentration of X^∗ is greater when modifications are in different compartments, implying a higher total production of X^∗ in this case. (C) When the kinases for both modification steps are different but the phosphatases are the same (and the modifications take place in separate compartments), at steady state, the concentration of X^∗∗ will be zero if X^∗ is the only communicating species (dash-dotted line), leaving only X in the second compartment. A way to overcome this locational constraint is by having both X and X^∗ diffuse in the domain (solid line).

We consider a variant of the above case: the first and second modifications are catalyzed by two kinases, K1 and K2, respectively, and the same phosphatase P1 catalyzes the reverse reactions. When the modifications are in separate locations, the steady-state concentration of X^∗∗ (and X^∗) is zero. This is due to the presence of the enzyme P1. P1 converts X^∗∗ to X^∗ and also converts X^∗ to X in the second location, leaving only unmodified substrate X in the second location at steady state (Fig. 4 C). When the modifications occur in the same compartment, both the modifying enzymes, K1 and K2, are present together with P1 to compensate for the reverse reaction. Thus, nonzero steady states are observed for X^∗ and X^∗∗. Thus, the segregated scenario creates an impediment to obtaining nonzero steady-state response for modified substrates. Alternatively, this segregated scenario may be regarded as creating a new capability for the module, a way to achieve a purely transient/adaptive response (a transient increase in X^∗∗ in the second location before it falls back down to zero), something which would not occur in the colocalized scenario. If viewed as an impediment, a way in which this can be bypassed is by having both X and X^∗ diffuse (Fig. 4 C). This ensures a continuous cycling of X and X^∗ between the two patches, resulting in nonzero concentrations of X^∗∗ at the second location.

We discuss another aspect of spatial control in the case of multisite modification. Our model assumes a specific order for multisite modification, which is implicit in Fig. 1: the modification of the substrate occurs first via K1, before K2 (and the reverse for the phosphatases). If we examine a random multisite modification mechanism (i.e., either modification can occur first), we see that the spatial separation of kinase-phosphatase pairs we have studied automatically imposes an order for modification, if the unmodified substrate is initially present in one of the compartments. Thus, multisite modification via a random mechanism would still proceed in a specific order. If the substrate modified by the second kinase remains localized in the second compartment, this order is maintained and reflected in both transient and steady-state behavior. Spatial control in multisite modification can also occur through localization of kinase(s) and phosphatase(s) at different locations, with substrate cycling between these locations. We briefly discuss this in Section 2.6 in the Supporting Material.

Phosphorelays

In this cascade, an enzyme catalyzes the first phosphorylation step. The product of this step transfers its phosphoryl group to the substrate of the next step, and so on. Phosphatases may be present at every stage. The product of the last step is typically dephosphorylated by a phosphatase. We study two-step relays before turning to four-step relays.

The concentration of the output of the two-step relay, X2^∗, is compared in the colocalized and spatially segregated scenarios. In the segregated scenario, X1^∗ (product of the first step) diffuses to a different location and transfers its P group to X2 (getting converted back to X1). The phosphatase P2 dephosphorylates X2^∗ back to X2; at steady state, both X1^∗ and X2^∗ attain a steady-state value of zero. Eventually, only X1 and X2 are present at steady state at the second location. All the X1^∗ diffuses out of the first location and gets converted back to X1 at the second location, resulting in a zero steady state for X1^∗ and the relay stalling (Fig. 5 A, SM 2.2).

Figure 5.

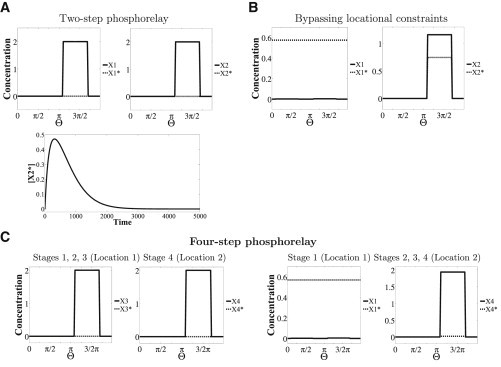
Phosphorelay. (A and B) A two-step phosphorelay (first two stages in Fig. 1C) is considered. (A) When the relay steps occur in separate locations (dashed line), [X2^∗] only transiently increases (lower; [X2^∗] in the middle of the second domain is shown); its steady-state concentration is zero; the steady state of [X1^∗] is also zero. (B) A possible way to sustain a nonzero level of X2^∗ and bypass this locational constraint is by having a uniform input signal/input at both locations. Shown is the case of a uniform input signal revealing a nonzero output of the cascade. (C) A case where the phosphorelay has four steps and the input kinase is a bifunctional enzyme that acts as the kinase (in the first step) and the phosphatase (in the last step) as well is shown. Two spatial designs are shown. In Design 1 (left), X1, X2, and X3 are in domain 1 and X4 is in domain 2, with X3^∗ the communicating/diffusing species. Here, [X4^∗] is zero at steady state. In Design 2 (right), X1 is in domain 1 and X2, X3, and X4 are in domain 2. X1^∗ is the communicating species. Here, the steady state of X4^∗ is nonzero (though small). This is because the bifunctional enzyme will ensure that an equilibrium between X1^∗ and X1 exists at the second location, preventing the relay from stalling. Note that [X1] is low but nonzero in both locations in (B) and in (C, right).

Again, spatial segregation creates a constraint. In contrast to the colocalized scenario, in the segregated case, the concentration of output (X2^∗) only transiently increases at the second location. This holds true for three- and four-step relays as well (with different spatial designs). Ways to bypass this constraint in two-step relays include 1) removing the phosphatase of the second step; 2), having X1 diffuse (in addition to X1^∗), which ensures continuous cycling of X1 and X1^∗ between the locations; and 3) having the input signal itself be present everywhere in the spatial domain, or at least at the second location (Fig. 5 B); this can reconvert X1 to X1^∗ in the second domain.

An interesting variation of phosphorelays occurs when the input enzyme of the phosphorelay is also the phosphatase of the last step, a situation which can arise through the presence of bifunctional kinases. Such scenarios have been observed in nature (11). We consider spatially distributed phosphorelays, as before, with this enzyme present at both locations (the input and output ends). If we consider a four-step relay and examine the situation where the first three stages occur in one location and the last stage in a different location (X3^∗ diffuses, effecting the communication), we find that X4^∗ at steady state is zero (Fig. 5 C). In contrast, in a two-step cascade with a bifunctional kinase of this kind, the output, X2^∗, can be nonzero, because the bifunctional enzyme at the second location can trigger conversion of X1 back to X1^∗ at this location. Thus, the presence of a bifunctional enzyme of this kind can allow for nonzero steady states from the output of the phosphorelay. However, in the case of a four-step relay, depending on the spatial partitioning of the cascade, this may or may not be possible. If more than one stage of the relay is localized in the first location, then the presence of a bifunctional enzyme at the second location cannot be used for the purposes of activation (because there is no X1 species in this location) and sustaining the phosphorelay. However, this can happen if only the first stage is localized in the first location and all other stages are localized in the second location, with X1^∗ diffusing, effecting the communication (see Fig. 5 C). This reveals another facet of spatial control of modification cascades.

Open cascades

The examples above involved fixed total amounts of substrates in the spatial domain, whether or not species entered or exited compartments. As a final example, we consider a modification sequence that involves a steady supply of substrate entering and leaving the domain. For concreteness, we examine the irreversible conversion of X1 to X2 to X3 with inflow of X1 and outflow of X3 (Fig. 1 D). Such modification sequences have been studied via ODEs. If a signal causes the conversion of either X1 or X2, the output of the system X3 at steady state is independent of the signal level, and this is thus an example of adaptation: the output recovers to its original prestimulus level, after a step input. This happens irrespective of the position in the cascade where the signal acts.

We now study spatially segregated scenarios. In all cases, X1 is present in location 1 and X3 in location 2. We first consider the case where the signal modifies X2 to X3 (in location 2). X2, which is produced in the first compartment, diffuses to the other, causing a modification to X3 (Fig. S4). An analysis of this scenario shows that in this case, X3 does not exhibit (exact) adaptive behavior locally in the second compartment. In fact, X3 exhibits spatial variation in the second compartment, whose amplitude is dependent on the signal and diffusivity of X2. A simple analysis (Section 2.3 in the Supporting Material) shows that the spatial average of X3 is independent of the signal. This shows how localization and spatial separation can change (local) adaptive behavior into nonadaptive behavior, even though adaptation of the average amount of X3 occurs. If the diffusion coefficient of X2 becomes high, then this effect is reduced. On the other hand, when the signal acts to convert X1 to X2 (in location 1), we find that the steady-state X3 reaches a steady state independent of the signal value, demonstrating that such a spatially distributed open cascade can adapt to signals at certain positions in the cascade. In general, in a cascade of this form, the spatially segregated scenario results in a loss of exact adaptation if the signal acts to convert the diffusible entity.

Conclusions

Information processing in cells occurs largely through chemical means and involves the movement of molecules to appropriate locations (1,12–15). Nevertheless, the default method of conceptualizing and understanding information processing in cellular systems is through ODEs, with a few studies focusing on the role of stochasticity. The effect of spatial factors has not been investigated in depth, even though it is clear that spatial control is an important aspect of cellular information processing networks.

One of the most common ways in which spatial control functions in cells is through localization and compartmentalization of components (2,16–18). There are multiple biological examples of this, which echo some of the scenarios we have studied. In enzymatic modification cascades in MAPK signaling and Fox-O signaling, certain entities in the cascade translocate to a new location (e.g., the nucleus) to complete the cascade (17,19,20). In general, the phosphorylation/modification status of a protein is a natural chemical mechanism to control its transport, especially out of/into compartments, and there are multiple examples of this both in single-site and multisite phosphorylation (21–25). The phosphorylated protein may be further modified in the new compartment. Cascades and pathways with phosphorelays are encountered in bacteria, in some cases with spatial control (26). Open cascades have been implicated and studied in the context of homeostatic mechanisms (27–29). We focused on the effect of localization/compartmentalization on modification cascades by creating and analyzing explicit spatial models of these cascades, incorporating localization of species in different locations, providing an appropriate controlled setting. This is relevant both for understanding existing cascades/pathways in cells and imposing spatial control of pathways by synthetic and other means.

Although some studies of compartmentalization/spatial behavior of cascades exist (30–32), our study brings together a global view of spatial control by considering different scenarios, explicit spatial description, and a framework through which we can study the effects of both compartmentalization and diffusion, as well as their interplay (also see our previous article (33)). Although we largely focused on localization, we also studied the effects of diffusion in enzymatic cascades without localization, revealing retroactive effects of species diffusion (see Section 2.5 in the Supporting Material). The global approach undertaken reveals parallels and essential differences between different modification cascades. Through explicit spatial models, we can dissect the effect of many factors, including compartment size and separation, diffusivity of one or more species, etc. Although compartmental ODE models can provide useful insights in some cases, explicit spatial models are necessary for any systematic understanding of spatial regulation and localization, some aspects of which cannot be captured properly in simple compartmental ODE models (e.g., transient effects or effects of intervening medium). This is especially relevant in the cascades/pathways studied, where nonlinearity, conservation of species, and their interplay play vital roles. Although we briefly discuss the effects of multiple species diffusion (see Section 2.4 in the Supporting Material), our framework allows for a systematic exploration to be undertaken in the future. Our models have been developed in 1-D, and as such, they capture the interplay of basic spatial effects that are equally relevant in 2-D and 3-D. Naturally, there are different aspects in 2-D and 3-D that will need additional investigation through dedicated 2-D/3-D models, which can build on the insights obtained here and may be facilitated by software such as Virtual Cell (vcell.org).

Our study of enzymatic cascades reveals firstly that localization of stages at different spatial locations can result in a strongly diminished response. Second, by tuning kinetic parameters/phosphatase concentrations in the cascade, it is possible to buffer against this to a large extent. Third, we find that localization and separation of stages in a cascade can reduce steady state retroactive effects. It is likely that this may be a basic mechanism by which retroactivity is reduced and/or suppressed in multiple cellular contexts. By studying three-step cascades, we find that spatial separation can strongly reduce switch-like behavior in cascades, in agreement with Takahashi et al. (10). We find here that depending on the spatial design of the cascade, it is possible that the switch-like characteristic is largely preserved. These results point to different aspects of the interplay between enzymatic cascades and spatial organization.

Our analysis of multisite-modification mechanisms reveals that through compartmentalization, a random enzymatic modification mechanism (with multiple enzymes) can be converted to an ordered mechanism. In addition, spatially averaging the results across the domain (done when measurements are taken at the cellular level) masks and distorts important aspects of the behavior of these pathways. If different modifications involve a common phosphatase, then the spatially separated modification scheme results in a purely transient increase of the modified phosphoforms, settling at a zero steady state, completely converse to the ODE models. This results from the fact that at the downstream location, the phosphatase is able to reverse phosphorylation for both the full and partial phosphoforms. In such cases, an additional cellular mechanism is then needed to synthesize/transfer relevant substrate to the original location to replenish it. Phosphorelay cascades (in contrast to enzymatic cascades) again reveal similar behavior if different steps of the cascade are separated. Interestingly, a phosphorelay cascade with the phosphatase of the last step acting as a bifunctional kinase (a design observed in nature) can allow the phosphorelay to function (in certain cases) even with compartmentalization, relieving the above constraint.

Space, and in particular spatial localization, is a recurrent theme in cellular systems. Its importance has been acknowledged in the biological literature, and yet the consequences of localization have not been examined systematically across different kinds of cascades. Spatial localization and control of signaling is relevant from multiple viewpoints: as a basic ingredient in the evolution of information processing networks, as a source of complexity in elucidating information processing and decision making in cells, and as a new mode of control for synthetic biology. We discuss the consequences of our results in relation to these themes.

The evolution of biological networks has resulted in a marked increase in the complexity of signaling pathways as one progresses from bacteria to eukaryotes. This is due to an increased number of components, new modes of interaction, increased feedback regulation, and new entities that are parts of the signaling pathways. Even though localization is present in bacteria as well, it is clear that there are many additional ways of compartmentalization/localization in eukaryotes with the increased number of compartments possible. This indicates that with all the additional complexity of signaling components in eukaryotes, spatial localization may provide important capabilities for realizing different modes of information processing while also bypassing existing constraints. Of course, depending on the context, localization may itself impose important constraints in information processing.

At the outset, it is not easy to guess the rules by which evolution works. The general belief is that evolution works by tinkering with existing networks and circuits, refining, adding and perhaps deleting elements. Naturally, with a substantially increased number of components and possibility of interactions, the complexity of a signal transduction network greatly increases, also increasing the possibility of undesirable interactions. One basic capability provided by localization of components in different places is the insulation of parts of a pathway from the other, minimizing extraneous interactions and unwanted cross talk. Thus, even for a desired mode of information processing (e.g., a switch) the spatially distributed solution may provide a new, more robust alternative. For such a spatially distributed design, our analysis provides insights into how a spatially distributed cascade (with the same kinetic properties) may be organized or optimally partitioned to give rise to a switch. Correspondingly, if the spatially distributed nature of a pathway is given, it may be possible to make local kinetic refinements and arrive at a robust switch-like behavior of the cascade that works around the spatial constraints. In addition, as we have discussed, it is possible to use localization as a mechanism to generate new modes of signal transduction as well, without extraneous kinetic interactions. It is then possible to employ additional refinements to such mechanisms to generate new, more robust circuits exhibiting this behavior.

A default method for studying information processing in signaling pathways is through ODEs. ODEs make an assumption about well-mixed systems with sufficient numbers of molecules so as to justify the kinetic descriptions. Even in some cases where these assumptions may not strictly be met, the ODE description may provide an adequate initial description of the system, essentially because the ODE encodes a form of causal interaction that is the dominant factor in the information processing. The ODEs may be modeled and the results compared with data that implicitly make similar assumptions. Tools of reverse engineering of networks make similar assumptions. Although a widespread, and generally sensible, approach is to develop a model (and employ an appropriate framework) based on the available data, it is also important to examine the actual combination of factors that gives rise to the relevant behavior. As our study indicates, spatial localization results in both modulatory and drastic changes in signal transduction characteristics. Although in some cases a spatial model may be essentially subsumed within a kinetic description, in other cases, as we have seen, this is simply not the case. Modeling such processes with ODEs may then involve invoking additional pathways/feedback effects that may simply be incorrect. Likewise, making measurements using spatial averages (as is done by lysing cells) may simply distort the actual picture.

These aspects come to the fore especially in the presence of strong nonlinearity, which is, of course, a basic and widespread element in signaling pathways. Likewise, other tools for analyzing circuits, including the robustness of circuits, usually employ ODE models. It is very possible that spatial localization and compartmentalization may in fact be a key aspect relevant to the robustness of the circuit. It is also interesting to note that one of the recurrent themes in signal transduction has been the effects of sequestration (34–38) and how this can result in monostable switches (through molecular titration), retroactivity and even bistability (through enzyme sharing for instance). When we examine spatially distributed signaling pathways, we find that some of these effects may in fact be reduced simply due to the spatial compartmentalization and separation, which results in open systems. On the other hand, it may also happen that spatial separation can actually work to accentuate some of this behavior. For instance, spatial separation and the dilution effect discussed above can result in altered availability of enzymes in one compartment, allowing for a regime of bistability, if this is an intrinsic capability of the enzymatic mechanism (as in multisite phosphorylation by a single kinase/phosphatase pair).

Another tool being used to understand different aspects of cellular decision making is information theory (39). Information theory itself relies on some basic abstractions and assumptions, describing the communication process in unidirectional terms, incorporating information encoding, transmission, and decoding. The spatially localized and separate steps we have studied in some respects come close to depicting such a scenario. Our studies demonstrate that specific physiochemical aspects such as the nature of the chemical modification, the spatial location of auxilliary chemical entities, and the size of the domain play a vital role in how chemical information is actually transmitted and processed.

The spatial regulation of information is also directly relevant to spatial control of pathways through synthetic and other means. In the recent past, experimental approaches in synthetic biology have employed scaffolds to manipulate and shape signal transduction (40). The recent development of microcompartments is another step in this direction (4,41–43). The development of a theoretical framework allows for a systematic exploration of capabilities and constraints associated with the spatial manipulation of information processing, using building blocks available to cells along with additional engineered components. It brings to light hidden tradeoffs involved in this process, and could suggest ways to design synthetic circuits engineered with explicit spatial organization. In combination with new and emerging experimental capabilities, it provides a systematic platform for employing tools that harness or manipulate spatial aspects to shape signal transduction and pathway behavior in general. Finally, this is also relevant in related emerging areas, such as molecular communication and chemical information processing/computing (44,45), each of which deals with the transmission of information through molecular transport and interaction.

Author Contributions

Both authors designed the study, performed the research, and directly contributed to the results presented; J.K. wrote the article with input from A.A-N.

Editor: Stanislav Shvartsman.