Summary
Envelope glycoprotein gp120 of HIV-1 possesses several variable regions whose precise structure has been difficult to establish. We report a new model of gp120, in complex with antibodies CD4 and 17b, complete with its variable regions. The model was produced by a computational protocol which uses cryo-electron microscopy (EM) maps, atomic-resolution structures of the core, and information of binding interactions. Our model has excellent fit with EMD5020 (Liu et al., 2008), is stereochemically and energetically favorable, and has the expected binding interfaces. Comparison of the ternary arrangement of the loops in this model with those bound to PGT122 (Julien et al., 2013a) and PGV04 (Lyumkis et al., 2013) suggested a possible motion of the V1V2 away from the CCR5 binding site and towards CD4. Our study also revealed that the CD4-bound state of the V1V2 loop is not optimal for gp120 bound with several neutralizing antibodies.
Introduction
Elucidating functionally important structural details at finer resolutions of highly flexible proteins or glycoproteins with large variable domains remains an elusive task. It is difficult to discern a complete and high resolution structure of such glycoproteins in their native state. For such glycoproteins, x-ray crystallography reports atomic resolution structure, but often cannot resolve the variable regions, or has to remove those regions entirely before the glycoprotein becomes amenable to crystallization. Additionally, the crystallization process can also cause conformational changes. On the other hand, electron-microscopy (EM) can often produce a lower resolution model of the entire glycoprotein in its in-situ state. Here, we report a computational protocol that can model protein complexes including the variable domains at atomic resolution with high statistical confidence, while ensuring that the conformation of the complex matches its EM model, and that stereochemical constraints are not violated. Hence, the protocol promises to greatly accelarate structural and functional study of molecular complexes.
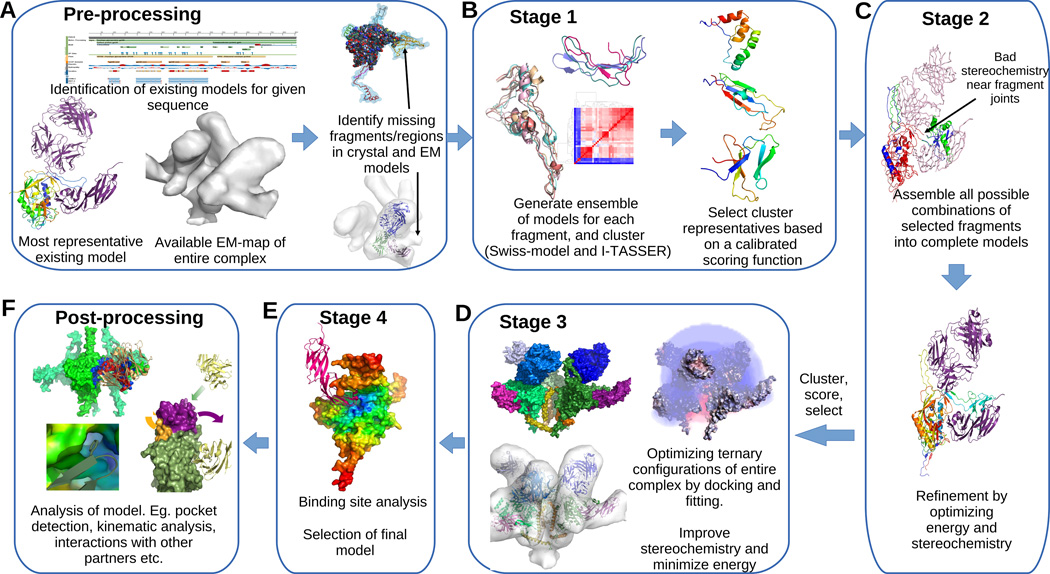
Our comprehensive computational protocol (Figure 1) completes partial atomic resolution x-ray structures by integrating available data from other x-ray structures, coarse resolution EM models, as well as stoichiometry and binding site information. It first generates an ensemble of feasible structural models for each missing fragment, and then clusters, ranks and assembles them into complete models while optimizing a multi-term scoring function that takes into account the agreement of the complete structure with the EM model, the feasibility of the interfaces between the fragments and other ligands, and stereochemistry.
Figure 1. Integrative refinement and validation protocol for modeling proteins with variable domains.
(A) Given a sequence we identify candidate partial crystal structures and EM-maps for the protein and identify the fragments that are missing in the crystal structure and locate corresponding empty regions in the EM. (B) Threading and homology modeling are used to generate an ensemble of candidate models for each fragment. Existing partial crystal structures, known binding interfaces, prior knowledge about residue contacts and stereochemical properties of proteins are used to calibrate a multi-term scoring function, which is used to rank the clusters and select small number of models for each fragment. The same scoring model is used in ranking and selecting models in the remaining steps as well. (C) Fragments are assembled in all possible combinations to generate a large set of complete models, which are then refined iteratively in terms of both the energy and stereochemistry. (D) A small set of refined models are co-optimized with other chains in the complex to improve the ternary interfaces and fitting to the EM-map. A single model (E) is chosen based on the scoring function and binding site analysis. (F) Further analytics are performed to validate the model, to compare with previous models and also to infer new kinematic, energetic, and binding information.
Our protocol bridges a gap between ab-initio loop/fragment modeling and threading/homology modeling. Ab-initio loop modelers can accurately predict or model loops that are fairly short, but fail for longer loops. For example, among the most popular loop modelers ModLoop (Fiser & Sali, 2003) and FREAD (Choi & Deane, 2010) support loops up to 20 residues long, FALC-Loop (Lee et al., 2010) supports loops between 4–12 residues, and YASARA, based on Canutescu and Dunbrack’s algorithm (Canutescu & Dunbrack, 2003), supports loops of up to 18 residues. This makes it impossible to directly use such tools to model large variable regions (e.g. the V1V2 loop of gp120). Threading and homology modeling, on the other hand, have been successful (Wu et al., 2007; Schwede et al., 2003; Eswar et al., 2007) in modeling small to medium sized proteins (about 100 residues). This range is sufficient for modeling the missing portions of most complexes. However, the current tools do not take into account the interplay between multiple chains in a complex, and hence are not applicable for modeling complexes with more than one chain. There are some recently reported integrative modeling tools (Lasker et al., 2012; Velzquez-Muriel et al., 2012; Hashem et al., 2013) that can handle multiple chains. They separately model components (protein chains or RNA) of a macro-molecular assembly by homology and/or threading, segment the EM map of the complete macro-molecule, and then fit the individual homology models into different segments of the EM model. While these methods improve the tertiary arrangements, they do not address modelling partial fragments of proteins, loop closure, and satisfaction of local stereochemical constraints. In our paper, we address this limitation. Also, our method does not require pre-segmentation of the EM model, which can become arbitrary and error-prone.
Our protocol was calibrated on a control set of high resolution structures of gp120 and achieved statistically significant correlation with ground truth. Finally, the calibrated protocol was used to generate a complete structural model of the envelope glycoprotein gp120 of HIV (including all its variable loops) in complex with CD4 and 17b.
The protein complex gp160, is the only solvent accessible glycoprotein of the mature HIV-1, forming spikes protruding outside a bi-layer lipid membrane (envelope). It is cleaved by a subtilisin-like protease at position 512 into a membrane extremal gp120 chain and a partially buried gp41 chain. gp120 itself has a relatively conserved core and several variable regions named V1, V2, V3, V4 and V5, spanning residues 131–156, 157–196, 297–330, 385–418 and 461–471 respectively. gp120 is believed to be instrumental in the initiation of the process of infecting a cell (Pantophlet & Burton, 2006). It first binds with the primary receptor CD4 present on the surface of T-cells and then binds with chemotaxis receptor CCR5. This induces conformational changes to gp120 and then to gp41, which starts to fuse with the membrane of the host cell, and the RNA of the virus is released into the cell (Karlsson Hedestam et al., 2008). Understanding the structural basis of these interactions and designing antibodies to disrupt them have been the mainstay of anti-HIV research for almost 30 years.
Elucidating the structure of gp120 in its native state has proved extremely challenging since the variable domains V1-V2, V3, V4 and V5 are highly flexible and the surface is heavily glycosylated. Both of these make it hard to purify and crystallize gp120, and also introduce heterogeneity in EM imaging leading to low resolution reconstruction. All of the previously reported x-ray models of the complex of gp120 with CD4 and 17b, are missing the V1-V2 and V3 loops. Out of around 480 residues of gp120, only 321 are present in x-ray models 1G9M, 1GC1 and 1RZJ (Kwong et al., 1998; Huang et al., 2004) deposited in the protein data bank (PDB). Other x-ray models in the PDB are missing even more residues (please see Discussion). At the low resolution end, there exist EM models, for example EMD:5020 (Liu et al., 2008) is a 20Å resolution model of the same complex (gp120+CD4+17b). Although the resolution is insufficient to correctly identify locations of secondary structural components or for manually grafting missing fragments, it does provide coarse spatial restraints. For instance, rigidly fitting 1GC1 into EMD5020 validates that the relative orientations of the three molecules in the x-ray model are close to their in-situ state, and at the same time reveals large unoccupied portions of the EM map where the variable missing loops are expected to be (Figure 2D). This provides the starting point of our protocol.
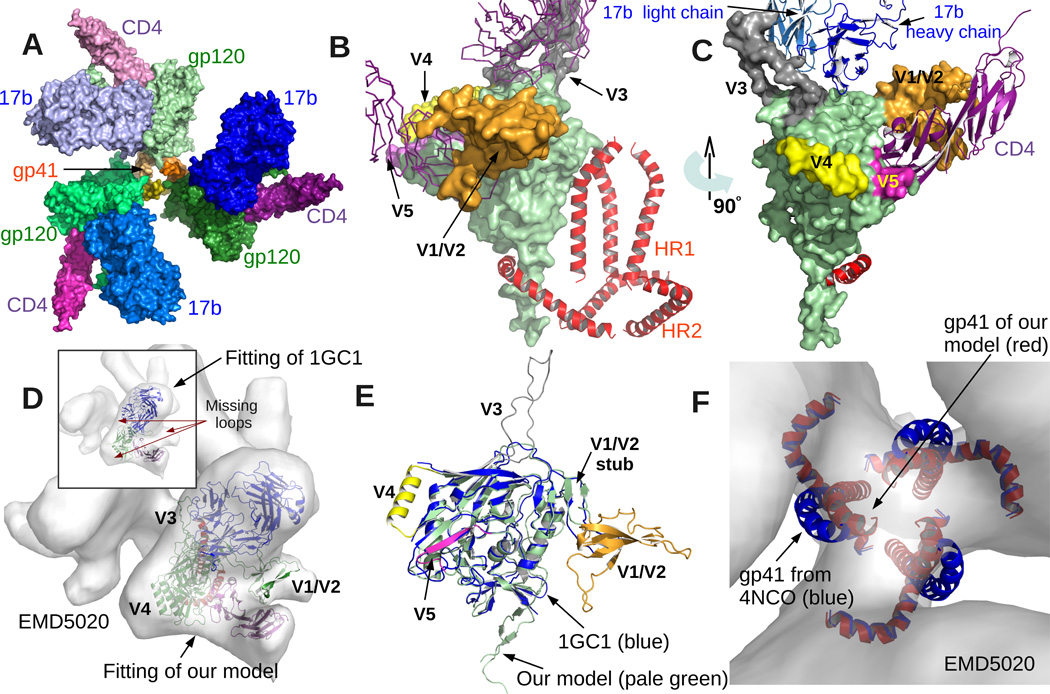
Figure 2. Model Overview.
(A) Quaternary architecture of the model shows that three copies of gp120 and gp41 form the central part of a trimer (3-fold cyclic symmetry). Also three copies of CD4 and 17b are attached to the three gp120s. A small opening through the center along the symmetry axis is also visible. (B) shows the model from a direction orthogonal to the symmetry axis. gp120 is rendered using smooth surface representation. The core is colored pale green and the variable loops are highlighted using different colors. The gp41 model occupies the center of the trimer (all three copies are shown). Notice that all the variable regions (except V3) are away from the central area. (C) provides a different view of the same. (D) shows the fitting of our model into EM density map EMD5020 (Liu et al., 2008). Our model includes the variable loops that are missing in previously reported x-ray structures of the same complex (e.g. 1GC1 (Kwong et al., 1998) as shown in the inset). (E) compares the gp120 model from 1GC1 with our model. Note that the core as well as the V1/V2 stub align almost perfectly. Finally, (F) compares the gp41 model from 4NCO (Julien et al., 2013a). Although we used the same models for the two heptad-repeats (HR1 and HR2), to improve the fitting with EMD5020 while maintaining a favorable interface with gp120, our algorithm moved the HR1 part slightly closer to the center of the trimer. But there is still an opening as seen in (A).
In the final model we report here, all the variable loops occupy the vacant regions of the EM map. Moreover the model has an improved interface of gp120 with CD4 and 17b. The tertiary architecture of the variable loops in our model mostly agrees with recently submitted complete models of gp120 complexed with PGV04 and PGT122 (Lyumkis et al., 2013; Julien et al., 2013a). However there are natural differences of the ternary arrangement of the loops with respect to each other and especially with respect to 17b. These all reinforce previous observations (e.g. (Stanfield et al., 1999) that the loops undergo large conformational changes when bound to different partners. Our model also shows some new residue-residue contacts of CD4 and 17b with gp120, which upon experimental validation (e.g. isothermal titration calorimetry), could lead to new insights for neutralizing antibody design. Our comprehensive computational protocol, can additionally be applied to generate complete and improved resolution structural models of gp120 in complex with other partners leveraging recently reported EM-maps with resolutions ranging between 6–25 Angstroms (Bartesaghi et al., 2013; Tran et al., 2012; Klasse et al., 2013; Khayat et al., 2013; Sanders et al., 2013).
Results
Multi-stage integrative modeling and refinement protocol
Given the sequences of one or more chains and a low resolution EM map of a complex, we first identify the best representative atomic structure of the complex involving the chains in the protein data bank, and fit the structure into the density map (Figure 1A). Then we identify fragments of the sequence for which atomic structure is missing, identify corresponding locations in the fitted density map, and then generate and fit multiple models for each fragment (Figure 1B). In the second stage, a diverse subset of the fragments are chosen (Figure 1C) by clustering based on structural similarity, ranking clusters by average score, and selecting highest scoring models from the clusters. The selected fragments are then assembled in all possible combinations to generate an ensemble of complete models (Figure 1C). In the third stage, after structural optimization and energy minimization (Chopra et al., 2010) of the complete models a small, diverse, and high-scoring subset is selected. Then Local refinement-based docking (Chowdhury et al., 2013) and fitting (Bettadapura et al., 2012; Bajaj et al., 2013), together with energy minimization is used to improve the binding interactions of chains in the selected models (Figure 1D).
If multiple candidates recieve high scores, our protocol applies a final binding site analysis to rank them (Figure 1E). Note that in some cases, especially if other experimental validation tools are available or if there is not much difference in the scores of the top few models, then considering multiple high ranked models out of this protocol is advised.
The scoring function we developed rewards favorable fitting with a EM density map of the protein complex, favorable interactions of the fragments with the partial chains derived from the protein data bank, lower energy (under the GBSA model), and better stereochemistry (measured as a consensus of a large set of protein structure quality assessment tools). We have primarily two different types of scoring terms- sinternal and sexternal. sinternal is a combination of a set of quality metrics which assess the stereochemistry and tertiary folds using state of the art structure validation tools, namely Verify3D, PROCHECK, ERRAT, ProSA, ModEval, and MolProbity (Luthy et al., 1992; MacArthur et al., 1993; Colovos & Yeates, 1993; Sippl, 1993; Shen, 2006; Davis et al., 2007). sexternal is another set of terms, developed by us, to evaluate the ternary interactions and fitting to a density map (Chowdhury et al., 2013; Bahadur & Zacharias, 2008; Glaser et al., 2001; Shatsky et al., 2008; Vasishtan & Topf, 2011) (see supplement for details). The first rewards appropriate refinement, and the second rewards agreement with experimental data (EM, existing co-crystal structures etc.). The quality of a structure X for a specific term is defined as sX – µX/σX where sX is the raw score of the model, and µX and σX are the expected value and standard deviation of the raw scores over all structures in a control set. Note that a positive score for a term indicates a model have better than the expected (or average) quality in terms of that specific criteria. The overall quality of the model is a sum of the qualities for each term.
Our search and scoring protocol was tested on 20 existing crystal structures of gp120 complexed with CD4 and/or 17b. It successfully predicted a near-native pose as the top-ranked solution in 13/16 cases for gp120-17b interactions and 11/16 cases for gp120-CD4 interactions (with 3 more cases having a correct solution within top 10 predictions). While this is not perfect, it is significantly accurate as far as the current state of the art in initial stage protein-protein docking. Also, in 18 out of the overall 32 cases, our method picked the lowest RMSD solution as the top solution. These results provide strong indication that the scoring model clearly distinguishes between native and non-native poses, and the algorithm successfully and sufficiently samples the conformational space to find near-native conformations.
Protocol calibration for modeling gp120
Here, we discuss the preparation of benchmarks and the calculations of µX and σX for different scoring terms.
PSVS (Bhattacharya et al., 2007) computed and reported µX and σX for PROCHECK g-factors, Verify3D, ProSA and MolProbity composite scores, for a large set of non-redundant proteins. We verified if the distribution of the scores reported in PSVS accurately represents the quality of the structures in our control set (see Figure S2). We found that most of the structures in our benchmark had scores that lie within 2σ from the mean score (μ) for structures in the low-resolution class of PSVS (resolution between 2.5–3.5Å). The actual resolution of the structures in our set (Figure S2) range from 1.89 to 3.51, and hence the z-scores and ranges prescribed by PSVS are validated. More importantly, we found that sinternal can correctly distinguish between low and high resolution crystal structures within the control set. The Pearson correlation coefficient of sinternal and corresponding resolutions across the 20 models is −0.5927, which corresponds to a tail probability of 0.006175. The correlation is statistically significant and hence if the sinternal of a model is higher than the average value (−8.14) of the control set, we can accept it, with high confidence, as a high resolution and stereochemically accurate model.
The objective of sexternal is to distinguish between correct and incorrect interfaces/sites offered to the binding partners (e.g. CD4 and 17b), and correct and incorrect conformations for fitting/alignment to the EM map. For each term in sexternal, we computed the distribution of values observed on a control set of 20 existing crystal structures of gp120. Then the mean µ, min m, max M and standard deviation σ of these raw scores were used to define z-scores. Usually, a model with an average score gets a z-score of 0 by definition. However, since complete gp120 models will have more than 100 extra residues as compared to the partial models in the control set, it is expected that the interface area, MIS (which is maximized when larger portion of the density map is covered by a model upon fitting) and residue-contacts (negative and positive) for the complete models will be higher than all the models in the control set. Hence, we use the extreme values (min or max) of the control set as the expected value when computing z-scores for these terms. For example, the z-score for MIS, zMIS, is defined as sMIS – MMIS/σMIS (see Figure S2). While this ensures that all positive z-scores represent better than average quality, they are no different in their application to ranking and comparison of models if the mean were used instead. The last column in Figure S2 shows which gp120 models were co-crystallized with CD4 and 17b and hence have a correct site topology. The correlation between this labeling and sexternal is 0.7363 and is statistically even more significant than the one for sinternal.
In conclusion, if a model is rated as high quality under both sinternal and sexternal, then the model is indeed high quality with high probability.
Modeling gp120 in complex with CD4 and 17b
We applied our calibrated integrative protocol to model missing fragments of gp120 in their bound state with 17b and CD4. EMD5020 at 20Å resolution was used to provide a coarse spatial constraint and 1GC1 was used as the base atomic structure. Swiss Model Schwede et al. (2003) and I-TASSER Roy et al. (2010) were used to generate ensembles of models for each missing regions, and after clustering the best ranked representatives (according to the calibrated scoring method described above) were combined in all possible ways. This resulted in 56 composite models. Among these 56 composite models, we observed eight predominant clusters, four of which did not contain any high scoring models. Two representatives each from the best two clusters (by average score), and one each from the next two best clusters were picked for refinement via energy minimization. After the refinement, we found two models to be quite similar in score, and one of them, dubbed Model31, was chosen as the best candidate based on binding site analysis, and in the remaining part of the article this chosen model is referred to as the new model or the final model. Please see supplement for detailed report on the outcome of different stages of the protocol.
Structure of gp120 in complex with CD4 and 17b
The final structural model consists of a cleaved gp120 bound to CD4, 17b and a peptide model of gp41 (Figure 2A). The model fits well (Figure 2D) into the density map EMD5020 (Liu et al., 2008). We use two metrics to quantitatively assess the quality of fitting- excluded total ratio (ETR) and mutual information score (MIS). Low ETR indicates that a smaller fraction of backbone atoms lie outside a specific boundary representation of the EM model. High MIS indicates that larger portion of the EM model is occupied. Our complete gp120 model has an ETR score of 0.064. The optimized configurations of 17b and CD4 chains also show excellent fitting accuracy with ETRs 0.086 and 0.015 respectively. For comparison, the best rigid body fitting of 1GC1 with the density map has ETR scores of 0.005, 0.112 and 0.03 for the gp120, 17b and CD4 chains respectively. The overlap scores (MIS) for the gp120, 17b and CD4 in the new model are 61.03, 50.88 and 54.99 respectively (compared to 53. 85, 49.65 and 53.78 respectively for 1GC1).
Note that the variable regions not only fit well with the density, but also lie on the periphery of the complex (Figures 2B-C). This agrees with previous reports (Liu et al., 2008; Tran et al., 2012; Bartesaghi et al., 2013) regarding the expected positions of the variable loops in the open conformation (when bound to CD4 and 17b). The general configuration of CD4 and 17b in the trimer also matches well with the EM map, as well as with previously reported models of gp120 co-crystallized with CD4 and 17b. However, in comparison with 1GC1, our model of 17b undergoes a small shearing motion (small tilt and twist w.r.t. the binding site). The footprint on the core remains almost identical, but the light chain comes in contact with the V3 loop (Figure 3A). The model of gp41 is based on the one in 4NCO (Julien et al., 2013a). Application of our fitting protocol to optimize the correlation with EMD5020 while preserving favorable contacts with gp120 resulted in a configuration of the HR1 helix is a slightly shifted location as compared to the one reported in 4NCO (see Figure 2F). A manual alignment of the gp120-HR1 complex from 4NCO with our gp120, actually results in poor ETR. We chose to keep the model predicted by the algorithm, i.e. the one that best explains the EM data (EMD5020) for the modeled complex, instead of manually intervening.
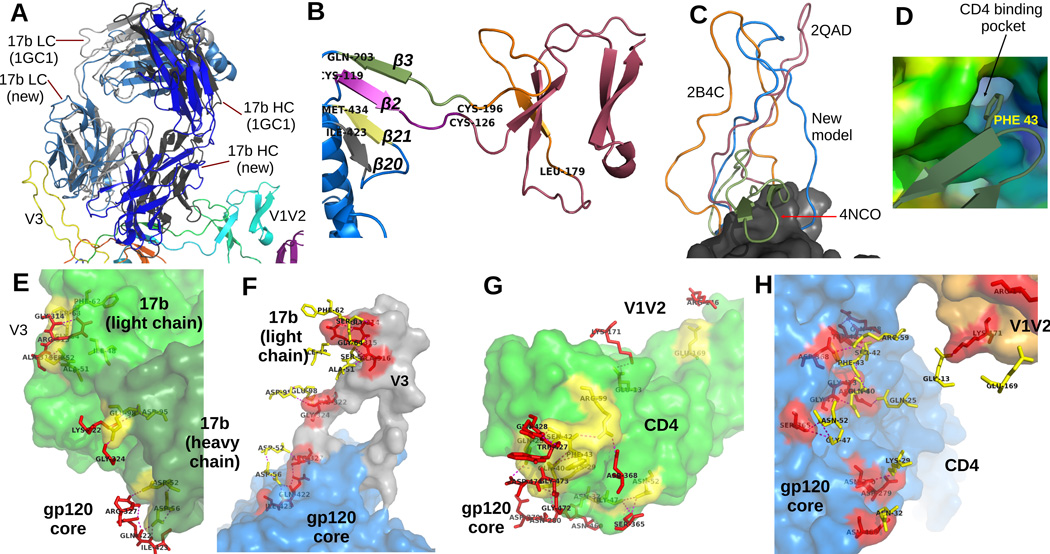
Figure 3. A closer look at the model.
(A) We superimposed the position of 17b derived from 1GC1 on our model of 17b to contrast them. Our model of 17b is colored in shades of blue, and the 17b model from 1GC1 is colored using shades of gray. (B) A detailed look at the conformation of the V1V2 loop and stub. Notice the 4 anti-parallel beta sheets between residues 126–178, which is similar to the 4 anti-parallel ’Greek-key’ formation reported in (McLellan et al., 2011). The β2 and β3 sheets at the stub shows the same orientation w.r.t. β20 and β21 as reported in existing crystal structures, but opposite of the models in 4NCO and 3J5M. (C) V3 loops from 3 existing structures are compared with our model (the models are superimposed by aligning the cores). The conformation from 3J5M covers the 17b site and also contains beta sheets. Our model is conformationally closest to the V3 of 2B4C. (D) shows the nestling of the PHE43 ring of CD4 inside the CD4 binding pocket of our gp120 model. Figures (E) and (F) show the contacts between 17b and gp120. In these figures, the residues in contact are rendered as sticks. Contact residues belonging to gp120 are colored red, and those belonging to 17b are colored yellow. gp120 itself is colored blue, with the V1V2 and V3 loops highlighted in orange and gray colors. 17b is colored green. The dashed lines indicate polar contacts. To clearly display the residues on the contact region, the two figures show the same set of contacts from two different perspectives. In E, the camera is inside gp120 whose surface is not rendered, and in F, the camera is inside 17b. Figures (G) and (H) show the contacts between CD4 and gp120 in a similar manner.
Our model also preserves the binding interactions (residue contacts) at the gp120-CD4 interface as well as places the PHE43 ring of CD4 into the CD4 binding pocket (Figure 3D). Even though we used the x-ray model 1GC1 fitted to EMD 5020 as the starting point of our protocol, repeated application of flexible fitting and local refinement docking resulted in relative orientations between gp120-CD4-17b that is slightly different from the corresponding orientations present in 1GC1 (Figure 3A). This change of orientation, together with minor side chain movements for energy minimization and stereochemistry corrections, resulted in small changes to binding contacts between gp120 core with CD4 and 17b (see Figure 3E-H). Finally, our model also has disulphide bonds at expected locations (between residues 119–205, 218–247, 228–239, 296–331, 378–445 and 385–418).
Quality assessment of the model
In the previous section we have reported the ETR and MIS as measures of the quality of the agreement of our model with EMD5020. The model also has better docking/complementarity score than existing models of the same complex. For example, 1GC1 has 64 atom-atom clashes between gp120 and CD4, but the new model has none. At the same time, the 1GC1 model has a residue contact potential value (Glaser et al., 2001) of 190.9, while the new model has 196. The overall free energy, computed under the PBSA model using the MolEnergy package (Bajaj et al., 2011), were -2033.04 and -4306.45 kCal/Mol respectively for 1GC1, and the new model. Further quality assessment can be found in Figure S2-S4 and tables ST3, ST4.
Now we consider the internal quality. Ramachandran plot analysis by Procheck (MacArthur et al., 1993) showed 89.6% residues in most favored, 7.6% in additionally allowed, 1.4% in generously allowed and only 1.4% in disallowed regions (see Figure S5). Overall Procheck g-factor is -0.22 for ϕ – ψ angles only and −0.04 for all, both of which is extremely favorable and correspond to high resolution (< 2Å) structures (Bhattacharya et al., 2007). In total only 10 bad contacts were reported and 3.6% residues were found to have bad planarity. ProsaII (Sippl, 1993) composite score for the model is 0.76, which is also representative of high resolution structures (Bhattacharya et al., 2007). MolProbity (Davis et al., 2007) composite score for the model is 30.44 (z-score -3.70), which in general indicates that a model is in the low resolution range. However, we note that among existing x-ray models of gp120, 1G9M, 1G9N, 1GC1, 1RZJ and 3RJQ all have worse MolProbity scores. Verify3D (Luthy et al., 1992) reports that more than 71% of the residues have a 1D-3D score above 0.2, which is in acceptable range according to Verify3D’s guidelines. Please refer to our paper’s supplement, especially Figure S2-S4, for a more detailed analysis of the quality in comparison with existing crystal structures of gp120, and models produced by naive application of homology/threading.
Since all the quality metrics mentioned above have also been used as part of the optimization routine (except the PBSA), we also used the PDB validation software (ADIT), Modeval (Shen, 2006) and Qmean z-score (Benkert et al., 2011) to provide independent validation of the quality. PDB validation software (ADIT) reported RMS deviation for bond angles at 0.7 degrees and bond length deviation of 0.003Å, both of which is quite acceptable. ModEval (Shen, 2006) predicted an RMSD of 3.378 (for the gp120 chain only). The Qmean z-score combines stereochemistry, secondary structure level agreement, electrostatics and solvation energies. The Qmean z-score for the new model was -1.666 (compared to -2.96 for 1GC1). This is within the acceptable range for a protein of this size. A plot showing the quality of our model with respect to existing x-ray models in terms of Q-mean z-scores in given in Figure S5.
Discussion
Significance of the new model
The new model adds to the current understanding of the interaction of gp120 with CD4 and 17b. None of the previously reported crystal structures of gp120, in complex with either or both of CD4 and 17b, includes the variable loops V1V2 and V3 (see Figure 4B and S1). Among models bound to other partners, only 2B4C and 4JM2 contain the V4 loop, and only 2B4C and 2QAD contain the V3 loop. The parts of gp120 that are in contact with gp41 (mostly the residues at the start and end of the chain) are also reported only in a few structures (e.g. 3JWD (Pancera et al., 2010). There are two recent models (PDBID: 3J5M and 4NCO) of gp120 in complex with antibodies PGV04 and PGT122 (Lyumkis et al., 2013; Julien et al., 2013a) that include all the variable regions (though with missing fragments of V2 and V4). However, a study of existing structures revealed that even the structure of the relatively conserved core region of gp120 depends on the binding partner (see Figure 4A and Supplement). This was further highlighted when we aligned the gp120 model in 3J5M (which contains the variable loops complexed with PGV04) to 1GC1 (which does not have the variable loops but is bound to CD4 and 17b). We found that the conformation of the V1/V2 and V3 loops of 3J5M is occluding the binding site of 17b (Figure 4C) and hence cannot possibly be the correct configuration of the loops when gp120 is bound to CD4 and 17b. Finally, even though there have been previous attempts (Wang et al., 2013; Guan et al., 2013) at modeling gp120 with variable loops, their protocols depended on manually grafting loop fragments extracted from other crystal structure to the core without rigorous validation, refinement and fitting. Also, direct application of state of the art homology modeling/threading tools produce energetically and stereochemically favorable models, but cannot correctly handle ternary constraints (see Supplement for details). In summary, we present the first stereochemically sound and complete model of gp120 in complex with CD4 and 17b that includes refined model structures of the loops, and satisfies/agrees with currently available experimental data of the same complex.
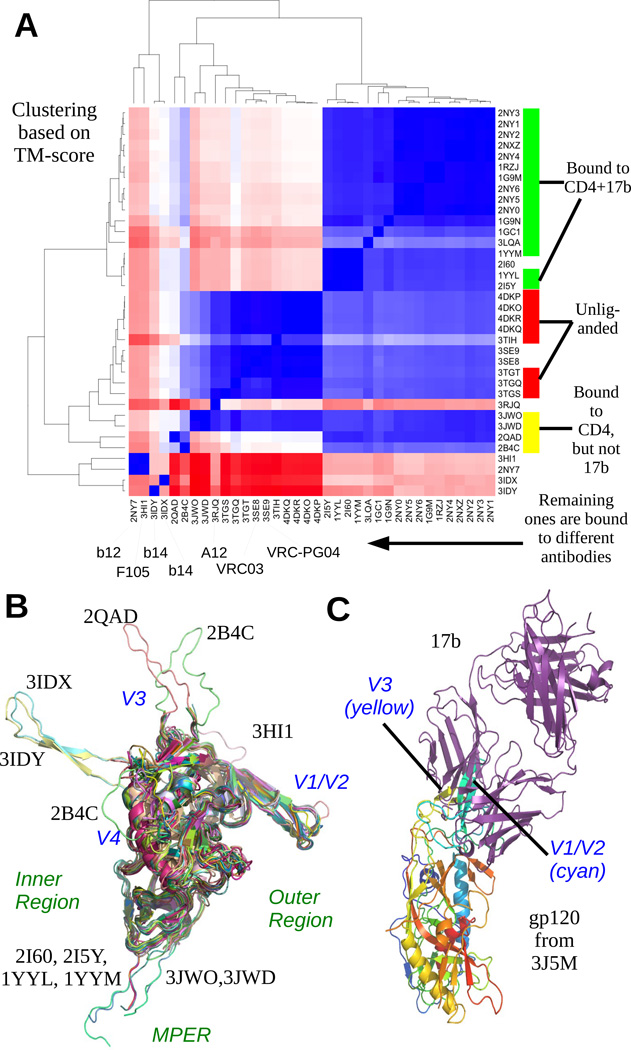
Figure 4. Summary of existing gp120 structure models.
(A) A heatmap based on TM-score of alignment and corresponding clustering of the gp120 models shows that the clusters are completely correlated with the partners of gp120 in different models; models with same partners or partners with same binding site are clustered together. In (B), all the structures (except 4NCO and 3J5M) have been superimposed. The variable regions are marked out. The inner and outer regions refers to whether that part is buried/exposed when gp120 forms a trimer, the inner part being closer to the axis of symmetry. From this figure, it is immediately clear that the core is more conserved than the variable regions. (C) superposing the cores of 3J5M and 1GC1 gives us a relative configuration of the gp120 chain of 3J5M and the 17b from 1GC1. The V1V2 and V3 loops of 3J5M are occupying the binding site of 17b and hence are not in a configuration amenable for binding with 17b.
Comparison of new model with existing atomic models
To compare our model with existing x-ray structures, we aligned our gp120 model with 42 different x-ray structures available in the Protein Data Bank (PDB) using TM-Align (Zhang & Skolnick, 2005). TM-Align uses a scoring scheme called TM-score (Xu & Zhang, 2010), which has better accuracy than RMSD in identifying alignments that correctly superimposes the structural motifs. A TM-score higher than 0.5 indicates two proteins have the same fold. The core of our model has very high similarity with the x-ray models where gp120 is in bound state with CD4 and 17b, and also where gp120 is unliganded (cf. Figure 2E). For this class, the average TM score is 0.9545 and average RMSD is 1.575. However, our model is different from the cores of 3HI1, 2NY7, 3IDX and 3IDY where gp120 is in bound state with fab F105, b12, b13 and b13. The average TM-score and RMSD in this case are 0.8452 and 2.526 respectively.
The V1V2 region of the new model forms 4 beta sheets between residues 126-178, which is similar to the conformations observed in 4NCO, 3J5M and 3U4E (Julien et al., 2013b; Lyumkis et al., 2013; McLellan et al., 2011) (note that the V1V2 conformation reported in (McLellan et al., 2011) does not include the core). However, the lengths of the beta sheets in our model are somewhat shorter. The orientation of the β2 and β3 sheets (the V1V2 stub) w.r.t. the β20 and β21 sheets observed in both 4NCO and 3J5M, are flipped compared to other crystal structures (e.g. 1GC1) containing the V1V2 stubs. Our model however has the same orientation as in 1GC1 (Figure 3B). The V3 variable region of our model does not contain any sheets or helices, similar to the models reported in 2B4C and 2QAD and moreover the ternary configuration is also quite similar. However it differs from the PGV04 and PGT122 bound models reported in 3J5M and 4NCO respectively (Julien et al., 2013b; Lyumkis et al., 2013), where the V3 region contains two small anti-parallel beta sheets (Figure 3C).
CD4-induced conformational change of variable loops
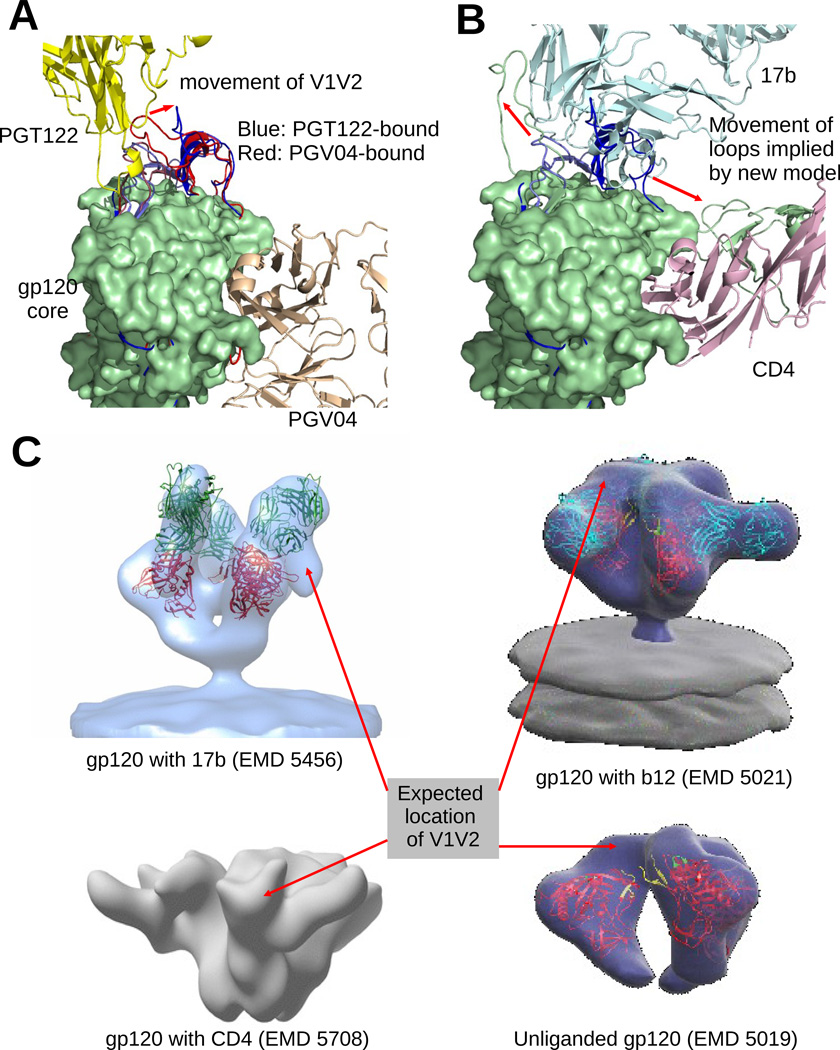
In both 4NCO and 3J5M, the V1V2 and V3 loops are bundled together and covers the 17b binding site (Figure 5A). In 4NCO, we notice that to allow the binding of PGT122, the V1V2 loop shifts a little bit. Despite this shift, both of these configurations of the V1V2 loop remain quite far from PGV04 or CD4 binding site. However, this configuration of the loops occludes the expected binding site of 17b (Figure 4C). We note that even though PGT122 binds near the V3 loop, it has a very small footprint on gp120 itself and the binding is heavily glycan-dependent. On the other hand, 17b has a large footprint on the core of gp120 (as reported in many x-ray models including 1GC1, 1G9M, 1RZJ etc. (Kwong et al., 1998,2000; Huang et al., 2004), as well as on the V3 loop, as seen in our model. In our model the V1V2 loop is pushed off from the 17b site and squeezed into the space between 17b and CD4 (Figure 5B). Such a configuration of the V1V2 loop is further validated from EMD5456 (Tran et al., 2012) and EMD5708 (Klasse et al., 2013) where gp120 is bound with only 17b, and with only CD4 respectively (Figure 5C). However, the configuration is vastly different from the un-liganded, or b12-bound state seen in EMD5019 and EMD5021 (Liu et al., 2008) respectively. A similar conclusion was reached by Guttman et al. (2014) based on different EM models and hydrogen-deuterium exchange experiments. It was reported in (Liu et al., 2008) that gp120 undergoes a twisting motion around the trimer symmetry axis to expose the CD4 binding site. Our results further implies that motion of V1V2 induced by CD4 actually enables CCR5 binding. Also, EMD5021 and the footprint analysis (below) show that other antibodies might not induce or even prevent a similar motion of the V1V2 loop.
Figure 5. Model suggests probable flexible movement of gp120 variable loops.
(A) Superposition of the gp120 models from 4NCO and 3J5M (blue and red), bound to PGT122 and PGV04 respectively. The V1/V2 and V3 loops occupy the same general location in both cases. But in the PGT122 bound configuration, the V1V2 loop has a noticeable shift to avoid clash with PGT122. In (B), we see that 17b, which binds on the core near the V3 loop has large clash with both V1V2 and V3 loops of 4NCO (blue), and to allow the binding of 17b, both loops must move away to the configuration observed in our model (green). (C) We compared the expected locations of the V1V2 loops in several EM models of gp120. The expected locations are identified by locating large vacant space in the EM map near the V1V2 stem of a fitted atomic model of gp120. EM model of gp120 bound with only 17b (EMD 5456 shows a movement of the V1V2 loop (similar to our reported model) away from the ‘top’ region of gp120. Interestingly, gp120 bound with only soluble CD4 (EMD 5708 also indicates a similar motion. So, the movement of V1V2 is not only a result of repulsion by 17b, but maybe also due to an attraction towards CD4. On the other hand, b12, which also binds at the same site as CD4, does not allow/require V1V2 to move away from its unliganded configuration
Configuration of the V1V2 loops with respect to antibodies binding at CD4bs
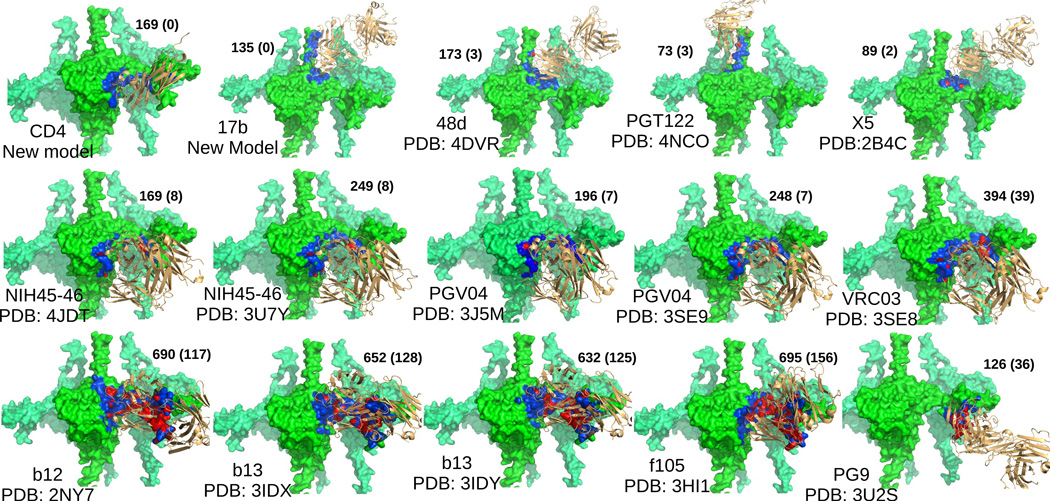
We computed the footprint of different antibodies whose x-ray structures in bound state with gp120 (core or complete) are available. We transformed the bound gp120-antibody complex such that the gp120 chain aligns with our gp120 model. Alignment was performed using PyMOL (Schrödinger, LLC, 2010). Then, for each antibody, all heavy atoms of our gp120 model were classified as in-contact, clashing and far based on the distance between the atom and the closest atom on the antibody. Figure 6 shows the results by coloring gp120 using blue, red and green for the three classes, and also shows the number of atoms in-contact and clashing. The notable aspect is that even though NIH45-46, PGV04, VRC03 and b12 bind at the same site as CD4, they clash with the V1V2 loop. Hence, the configuration of V1V2 we found, as optimal for CD4+17b binding, is not optimal for those antibodies. So the model of the V1V2 reported here is specific to the CD4-bound state only. To gain insight into the interactions of the CD4bs antibodies and the V1V2 loop, one could apply our protocol to the EM maps of those complexes.
Figure 6. Binding footprints, and clashes for different antibodies.
The footprints (see text) of different antibodies on our gp120 model are shown. In each figure, gp120 is colored lime, and the antibody is colored light orange (and rendered as ribbons). The parts of gp120 in contact with the antibody are colored blue, and the parts that have steric clash are colored red. In each figure, the name of the antibody is given. The numbers beside the figure report the number of atoms of gp120 that come in contact, and the numbers inside the braces report the number of atoms, of gp120, that have a clash with the antibody (please see Figure S6 for details).
On sampling the space of configurations
In any ensemble based modeling approach, ensuring that the discrete samples are diverse and cover the space of configurations uniformly is necessary to ensure that at least one model is close to the native state. For hierarchical modeling protocols, the space of configuration also need to be defined hierarchically.
In stage 1, to sample the space of internal flexibilities at atomic resolution (backbone torsions), we relied on the sampling mechanisms of I-TASSER and Swiss-model, whose efficacy have been established before (Roy et al., 2010; Schwede et al., 2003).
In stage 2, we cluster and sample a small set of candidates for each variable region, and then assemble them into complete models. Note that the framents that do not fit well into the EM map, or do not have favorable contacts with partners CD4 and 17b are discarded. We performed halfset tests to verify the diversity and coverage of the retained assembled models. We carried out 10000 experiments. In each experiment, the samples are randomly grouped into two sets S1 and S2. Then we computed d S1, d S2 and d S1, S1 representing the average distance (in terms of RMSD) between the models in set S1, the average distance between the models in set S2, and the average distance between the models in set S1 to the models in set S2 respectively. Ideally, we want the difference δd=|d S1 – d S2| to be close to zero, and d S1, S1 close to the average distance between models in the entire set d C . Table 1 summarizes the findings. The data indicates fairly uniform sampling has been achieved.
Table 1.
Result of halfset tests to quantify the diversity of samples for different ensembles. Please see text for definitions of d C, d S1, S1 , and | d S1 – d S2 |
| Ensemble | d C | d S1,S1 | δd |
|---|---|---|---|
| SwissTasser | 3.05336 | 3.05349 | 0.185896 |
| V1V2 fragments | 4.22266 | 4.22255 | 0.053789 |
| V3 fragments | 2.90354 | 2.90353 | 0.085899 |
| Spliced models | 2.10545 | 2.10545 | 0.154006 |
Stage 3 co-optimizes each model in complex with CD4 and 17b. In this stage the focus of the sampling is on the space of orientations between the components. Both our docking and fitting tools (Chowdhury et al., 2013) use exhaustive uniform sampling of the Euclidean group. In conclusion, in each stage of the hierarchical sampling and search, the space of configurations (for the degrees of freedom relevant for the stage) is sampled uniformly.
Even low resolution EM maps can help guide hierarchical modeling
While a EM map at 20Å resolution cannot, on its own, be relied upon to identify even secondary structural components, it can still help resolve coarser level details, like the expected location of larger domains (e.g. the entire V1V2 loop). We have already discussed how our scoring model, which incorporates multiple metrics which measures different aspects of model quality, leads to a fine resolution model with high confidence. Here, we explore the effect of taking out the ETR and MIS terms, in effect trying to model without using the EM map. Since our pipeline uses the scores for the purpose of ranking, and selecting models for the next stage, we consider the rankings of the ensemble of models at each stage with and without the ETR and MIS terms in sexternal. Specifically, we compare the correlation of the two ranked lists. The rankings after stage 1 (swiss and I-TASSER based models) had a high correlation ,0.69, and had one false positive. This was due to the factor that all the I-TASSER models which had poor ETR and MIS scores also had poor clash scores, and hence the outcome did not change too much. However, when we compared the rankings of the spliced models (stage 2), the correlation was small, −0.0124. Since the spliced models all have better clash scores than the stage 1 models, EM-based scores started to be a discriminating factor between models. In fact, in the second list, the best scoring model would have a V1V2 configuration that lies completely outside the prescribed isocontour of the EM map (see Figure S6 in supplement).
Experimental Procedures
Protocol Details
Stage 1: Fragment Modeling
For each fragment of gp120 (core, v1v2, v3, and v4), we used two of the state-of-the-art homology/threading platforms, namely Swiss-Model (Schwede et al., 2003) and I-TASSER (Roy et al., 2010), to generate multiple initial models, based on different templates and having different folds. Each model was then flexibly fit using PF3Fit (Bettadapura et al., 2012; Bajaj et al., 2013) into EMD5020 (Liu et al., 2008). The fitted models were next clustered based on their fold similarity (measured using TM-score (Xu & Zhang, 2010)), and the best scoring models from each cluster were picked (Figures 1A-B).
Stage 2: Chain Modeling
The selected fragments were assembled in all possible combinations to form a large ensemble set of complete models. Initially, these assembled structures are not stereo-chemically sound as the bond lengths/angles at the joints are too far from ideal (Figure 1C for example). To remove the gaps in the chain and improve the stereo-chemistry, we used the threading pipeline of Swiss-model (Schwede et al., 2003) where the assembled model was specified as a template to generate a new model with better local stereo-chemistry but whose 3D folds exactly match the assembled model (Figure 1C). Then energy minimization was performed on the new model using KoBaMin (Chopra et al., 2010). These two steps were repeated until no significant improvement was observed. A few of the improved models were selected after clustering and ranking based on their scores.
Stage 3: Co-optimization and Trimer Modeling
In the previous steps, only the structure of gp120 was optimized and evaluated, while CD4 and 17b were kept fixed at their gp120 bound configuration in 1GC1 (Kwong et al., 1998). Each of the models generated in the pipeline was aligned with the gp120 core of 1GC1 to evaluate the quality of the interface with CD4 and 17b. In this third stage, we applied a multi-scale docking protocol, F2Dock (Chowdhury et al., 2013), to refine the configuration of CD4 and 17b for each of the selected models. For some of the models, the refined configurations removed all clashes and also improved residue contacts. The complete model of the complex (for each selected model) was energy-minimized using KoBaMin (Chopra et al., 2010) (Figure 1D). Finally, one model was chosen and the trimeric complex was formed by fitting. If multiple optimized candidates have comparable scores, and the user wishes to choose only one model, our pipeline offers a binding site analysis as a last ranking tool.
Stage 4: Binding Site Analysis
The binding site analysis applies our exhaustive docking protocol (Chowdhury et al., 2013) and verifies that known binding sites remain the most favorable binding sites even after the missing regions have been added. We consider the top 1000 docking results and for each residue Ri on the receptor (gp120), we count the number Ci of poses of the ligand (CD4 or 17b), for which the residue is on the contact region (Figure 1E). Then we define the probability of the residue Ri being part of the binding site as Pi = Ci /1000. These statistical inference of binding site is then compared to known binding site data available from known bound structures (in which variable regions are missing). Let, 𝔹 𝕊 be the set of residues that belong to the binding site of the known structure, and ℕ𝔹 𝕊 be the set of residues that do not. Then the quality of a complete model is defined as
Details of the application of the protocol for modeling gp160+CD4+17b complex can be found in our paper supplement.
Software Availability
The software used in the protocol for computing the quality of fitting, and the quality of quaternary contacts are available under academic use license at http://cvcweb.ices.utexas.edu/cvcwp/software under the PF2 Fit and F2 Dock packages respectively.
Supplementary Material
Highlights.
Our protocol had significant accuracy in scoring existing x-ray structures of gp120
Reported gp120 model with all variable loops have excellent fit with EM-map EMD 5020
Reported gp120 model is stereochemically and energetically favorable
Structure suggests possible movement of the loops induced by binding with CD4 and 17b
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Bahadur RP, Zacharias M. The interface of protein-protein complexes: analysis of contacts and prediction of interactions. CMLS. 2008;65:1059–1072. doi: 10.1007/s00018-007-7451-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bajaj C, Bauer B, Bettadapura R, Vollrath A. Nonuniform Fourier Transforms for Rigid-Body and Multi-Dimensional Rotational Correlations. SIAM J. of Sc. Comput. 2013;35:B821–B845. doi: 10.1137/120892386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bajaj C, Chen S-C, Rand A. An efficient higher-order fast multipole boundary element solution for Poisson-Boltzmann based molecular electrostatics. SIAM J. Sci. Comput. 2011;33:826–848. doi: 10.1137/090764645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bartesaghi A, Merk A, Borgnia MJ, Milne JLS, Subramaniam S. Prefusion structure of trimeric HIV-1 envelope glycoprotein determined by cryo-electron microscopy. Nature Struct. Mol. Biol. 2013;20:1352–1357. doi: 10.1038/nsmb.2711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benkert P, Biasini M, Schwede T. Toward the estimation of the absolute quality of individual protein structure models. Bioinformatics. 2011;27:343–350. doi: 10.1093/bioinformatics/btq662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bettadapura R, Bajaj C, Vollrath A. Technical Report 12–18. UT at Austin: ICES; 2012. PF3Fit: Hierarchical Flexible Fitting in 3D EM. [Google Scholar]
- Bhattacharya A, Tejero R, Montelione GT. Evaluating protein structures determined by structural genomics consortia. Proteins. 2007;66:778–795. doi: 10.1002/prot.21165. [DOI] [PubMed] [Google Scholar]
- Canutescu AA, Dunbrack RL. Cyclic coordinate descent: A robotics algorithm for protein loop closure. Prot. Sc. 2003;12:963–972. doi: 10.1110/ps.0242703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choi Y, Deane CM. FREAD revisited: Accurate loop structure prediction using a database search algorithm. Proteins. 2010;78:1431–1440. doi: 10.1002/prot.22658. [DOI] [PubMed] [Google Scholar]
- Chopra G, Kalisman N, Levitt M. Consistent refinement of submitted models at CASP using a knowledge-based potential. Proteins. 2010;78:2668–2678. doi: 10.1002/prot.22781. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chowdhury R, Rasheed M, Keidel D, Moussalem M, Olson A, Sanner M, Bajaj C. Protein-Protein Docking with F2Dock 2.0 and GB-Rerank. PLoS ONE. 2013;8:e51307. doi: 10.1371/journal.pone.0051307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Colovos C, Yeates TO. Verification of protein structures: patterns of nonbonded atomic interactions. Prot. Sc. 1993;2:1511–1519. doi: 10.1002/pro.5560020916. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davis IW, Leaver-Fay A, Chen VB, Block JN, Kapral GJ, Wang X, Murray LW, Arendall WB, Snoeyink J, Richardson JS, et al. MolProbity: all-atom contacts and structure validation for proteins and nucleic acids. Nuc Acids Res. 2007;35:W375–W383. doi: 10.1093/nar/gkm216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eswar N, Webb B, Marti-Renom MA, Madhusudhan MS, Eramian D, Shen M-Y, Pieper U, Sali A. Comparative protein structure modeling using MODELLER. Chapter 2. Curr. Prot. in Protein Sc. 2007;(Unit 2.9) doi: 10.1002/0471140864.ps0209s50. [DOI] [PubMed] [Google Scholar]
- Fiser A, Sali A. ModLoop: automated modeling of loops in protein structures. Bioinformatics. 2003;19:2500–2501. doi: 10.1093/bioinformatics/btg362. [DOI] [PubMed] [Google Scholar]
- Glaser F, Steinberg DM, Vakser IA, Ben-Tal N. Residue Frequencies and Pairing Preferences at Protein-Protein Interfaces. Proteins. 2001;43:89–102. [PubMed] [Google Scholar]
- Guan Y, Pazgier M, Sajadi MM, Kamin-Lewis R, Al-Darmarki S, Flinko R, Lovo E, Wu X, Robinson JE, Seaman MS, et al. Diverse specificity and effector function among human antibodies to HIV-1 envelope glycoprotein epitopes exposed by CD4 binding. PNAS. 2013;110:E69–E78. doi: 10.1073/pnas.1217609110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guttman M, Garcia NK, Cupo A, Matsui T, Julien J-P, Sanders RW, Wilson IA, Moore JP, Leeemail KK. CD4-Induced Activation in a Soluble HIV-1 Env Trimer. Structure. 2014;22:974–984. doi: 10.1016/j.str.2014.05.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hashem Y, Georges Ad, Fu J, Buss SN, Jossinet F, Jobe A, Zhang Q, Liao HY, Grassucci Ra, Bajaj C, et al. High-resolution cryo-electron microscopy structure of the Trypanosoma brucei ribosome. Nature. 2013;494:385–389. doi: 10.1038/nature11872. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang C-c, Venturi M, Majeed S, Moore MJ, Phogat S, Zhang M-Y, Dimitrov DS, Hendrickson WA, Robinson J, Sodroski J, et al. Structural basis of tyrosine sulfation and VH-gene usage in antibodies that recognize the HIV type 1 coreceptor-binding site on gp120. PNAS. 2004;101:2706–2711. doi: 10.1073/pnas.0308527100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Julien J-P, Cupo A, Sok D, Stanfield RL, Lyumkis D, Deller MC, Klasse P-J, Burton DR, Sanders RW, Moore JP, et al. Crystal Structure of a Soluble Cleaved HIV-1 Envelope Trimer. Science. 2013a;342:1–12. doi: 10.1126/science.1245625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Julien J-P, Sok D, Khayat R, Lee JH, Doores KJ, Walker LM, Ramos A, Diwanji DC, Pejchal R, Cupo A, et al. Broadly neutralizing antibody PGT121 allosterically modulates CD4 binding via recognition of the HIV-1 gp120 V3 base and multiple surrounding glycans. PLoS Path. 2013b;9:e1003342. doi: 10.1371/journal.ppat.1003342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karlsson Hedestam GB, Fouchier RAM, Phogat S, Burton DR, Sodroski J, Wyatt RT. Nature Rev. The challenges of eliciting neutralizing antibodies to HIV-1 and to inuenza virus. Nature Rev. Microbiol. 2008;6:143–155. doi: 10.1038/nrmicro1819. [DOI] [PubMed] [Google Scholar]
- Khayat R, Lee JH, Julien J-P, Cupo A, Klasse PJ, Sanders RW, Moore JP, Wilson Ia, Ward AB. Structural characterization of cleaved, soluble HIV-1 envelope glycoprotein trimers. J. Vir. 2013;87:9865–9872. doi: 10.1128/JVI.01222-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klasse PJ, Depetris RS, Pejchal R, Julien J-P, Khayat R, Lee JH, Marozsan AJ, Cupo A, Cocco N, Korzun J, et al. Influences on trimerization and aggregation of soluble, cleaved HIV-1 SOSIP envelope glycoprotein. J. Vir. 2013;87:9873–9885. doi: 10.1128/JVI.01226-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kwong PD, Wyatt R, Majeed S, Robinson J, Sweet RW, Sodroski J, Hendrickson WA. Structures of HIV-1 gp120 envelope glycoproteins from laboratory-adapted and primary isolates. Structure. 2000;8:1329–1339. doi: 10.1016/s0969-2126(00)00547-5. [DOI] [PubMed] [Google Scholar]
- Kwong PD, Wyatt R, Robinson J, Sweet RW, Sodroski J, Hendrickson WA. Structure of an HIV gp120 envelope glycoprotein in complex with the CD4 receptor and a neutralizing human antibody. Nature. 1998;393:648–659. doi: 10.1038/31405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lasker K, Frster F, Bohn S, Walzthoeni T, Villa E, Unverdorben P, Beck F, Aebersold R, Sali A, Baumeister W. Molecular architecture of the 26S proteasome holocomplex determined by an integrative approach. PNAS. 2012;109:1380–1387. doi: 10.1073/pnas.1120559109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee J, Lee D, Park H, Coutsias EA, Seok C. Protein loop modeling by using fragment assembly and analytical loop closure. Proteins. 2010;78:3428–3436. doi: 10.1002/prot.22849. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu J, Bartesaghi A, Borgnia MJ, Sapiro G, Subramaniam S. Molecular architecture of native HIV-1 gp120 trimers. Nature. 2008;455:109–113. doi: 10.1038/nature07159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luthy R, Bowie JU, Eisenberg D. Assessment of protein models with three-dimensional profiles. Nature. 1992;356:83–85. doi: 10.1038/356083a0. [DOI] [PubMed] [Google Scholar]
- Lyumkis D, Julien J-P, Val Nd, Cupo A, Potter CS, Klasse P-J, Burton DR, Sanders RW, Moore JP, Carragher B, et al. Cryo-EM Structure of a Fully Glycosylated Soluble Cleaved HIV-1 Envelope Trimer. Science. 2013:1484. doi: 10.1126/science.1245627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacArthur MW, Moss DS, Laskowski RA, Thornton JM. PROCHECK: a program to check the stereochemical quality of protein structuresJApp. Cryst. 1993;26:283–291. [Google Scholar]
- McLellan JS, Pancera M, Carrico C, Gorman J, Julien J-P, Khayat R, Louder R, Pejchal R, Sastry M, Dai K, et al. Structure of HIV-1 gp120 V1/V2 domain with broadly neutralizing antibody PG9. Nature. 2011;480:336–343. doi: 10.1038/nature10696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pancera M, Majeed S, Ban Y-EA, Chen L, Huang C-c, Kong L, Kwon YD, Stuckey J, Zhou T, Robinson JE, et al. Structure of HIV-1 gp120 with gp41-interactive region reveals layered envelope architecture and basis of conformational mobility. PNAS. 2010;107:1166–1171. doi: 10.1073/pnas.0911004107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pantophlet R, Burton DR. GP120: target for neutralizing HIV-1 antibodies. Ann. Rev. of Immun. 2006;24:739–769. doi: 10.1146/annurev.immunol.24.021605.090557. [DOI] [PubMed] [Google Scholar]
- Roy A, Kucukural A, Zhang Y. I-TASSER: a unified platform for automated protein structure and function prediction. Nat. Prot. 2010;5:725–738. doi: 10.1038/nprot.2010.5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanders RW, Derking R, Cupo A, Julien JP, Yasmeen A, Val Nd, Kim HJ, Blattner C, Pena ATdl, Korzun J, et al. A Next-Generation Cleaved, Soluble HIV-1 Env Trimer, BG505 SOSIP.664 gp140, Expresses Multiple Epitopes for Broadly Neutralizing but Not Non- Neutralizing Antibodies. PLoS Path. 2013;9:1–20. doi: 10.1371/journal.ppat.1003618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schrödinger LLC. The PyMOL molecular graphics system. version 1.3r1. 2010 [Google Scholar]
- Schwede T, Kopp J, Guex N, Peitsch MC. SWISS-MODEL: An automated protein homology-modeling server. Nuc. Acids Res. 2003;31:3381–3385. doi: 10.1093/nar/gkg520. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shatsky M, Hall R, Brenner S, Glaeser R. A method for the alignment of heterogeneous macromolecules from electron microscopy. Journal of Structural Biology. 2008;166:67–78. doi: 10.1016/j.jsb.2008.12.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen M. Statistical potential for assessment and prediction of protein structures. Prot. Sc. 2006;15 doi: 10.1110/ps.062416606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sippl MJ. Recognition of errors in three-dimensional structures of proteins. Proteins. 1993;17:355–362. doi: 10.1002/prot.340170404. [DOI] [PubMed] [Google Scholar]
- Stanfield R, Cabezas E, Satterthwait A, Stura E, Profy A, Wilson I. Dual conformations for the HIV-1 gp120 V3 loop in complexes with different neutralizing fabs. Structure. 1999;7:131–142. doi: 10.1016/s0969-2126(99)80020-3. [DOI] [PubMed] [Google Scholar]
- Tran EEH, Borgnia MJ, Kuybeda O, Schauder DM, Bartesaghi A, Frank GA, Sapiro G, Milne JLS, Subramaniam S. Structural mechanism of trimeric HIV-1 envelope glycoprotein activation. PLoS Path. 2012;8:37. doi: 10.1371/journal.ppat.1002797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vasishtan D, Topf M. Scoring functions for cryoEM density fitting. Journal of Structural Biology. 2011;174:333–343. doi: 10.1016/j.jsb.2011.01.012. [DOI] [PubMed] [Google Scholar]
- Velzquez-Muriel J, Lasker K, Russel D, Phillips J, Webb BM, Schneidman-Duhovny D, Sali A. Assembly of macromolecular complexes by satisfaction of spatial restraints from electron microscopy images. PNAS. 2012;109 doi: 10.1073/pnas.1216549109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang W, Nie J, Prochnow C, Truong C, Jia Z, Wang S, Chen XS, Wang Y. A systematic study of the N-glycosylation sites of HIV-1 envelope protein on infectivity and antibody-mediated neutralization. Retrovirology. 2013;10:14. doi: 10.1186/1742-4690-10-14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu S, Skolnick J, Zhang Y. Ab initio modeling of small proteins by iterative TASSER simulations. BMC Biol. 2007;5:17. doi: 10.1186/1741-7007-5-17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu J, Zhang Y. How significant is a protein structure similarity with TM-score = 0.5? Bioinformatics. 2010;26:889–895. doi: 10.1093/bioinformatics/btq066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y, Skolnick J. TM-align: a protein structure alignment algorithm based on the TM-score. Nuc. Acids Res. 2005;33:2302–2309. doi: 10.1093/nar/gki524. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.