Identifying localized changes in large systems: Change-point detection for biomolecular simulations

Significance

With data proliferating across many disciplines, data analysts often wish to identify abrupt changes in complex systems with many measured quantities—a problem complicated by the fact that a given change might affect only a few of these quantities. We developed a method that accurately identifies changes in such systems by searching concurrently for change times and the subset of measured quantities that change at each of these times. This work was motivated by the challenge of detecting biologically interesting structural changes in proteins, but our method may prove useful in diverse application domains.

Abstract

Research on change-point detection, the classical problem of detecting abrupt changes in sequential data, has focused predominantly on datasets with a single observable. A growing number of time series datasets, however, involve many observables, often with the property that a given change typically affects only a few of the observables. We introduce a general statistical method that, given many noisy observables, detects points in time at which various subsets of the observables exhibit simultaneous changes in data distribution and explicitly identifies those subsets. Our work is motivated by the problem of identifying the nature and timing of biologically interesting conformational changes that occur during atomic-level simulations of biomolecules such as proteins. This problem has proved challenging both because each such conformational change might involve only a small region of the molecule and because these changes are often subtle relative to the ever-present background of faster structural fluctuations. We show that our method is effective in detecting biologically interesting conformational changes in molecular dynamics simulations of both folded and unfolded proteins, even in cases where these changes are difficult to detect using alternative techniques. This method may also facilitate the detection of change points in other types of sequential data involving large numbers of observables—a problem likely to become increasingly important as such data continue to proliferate in a variety of application domains.

Change-point detection—the problem of detecting abrupt changes in temporal or other sequential data—represents a long-standing research area in statistics, with applications in fields ranging from manufacturing and economics to climatology and genetics (1). Although an extensive body of literature addresses this problem, most of it concerns the detection of changes in a single, univariate observable (1–5).

With the proliferation of data across scientific and engineering disciplines, many modern applications require the ability to identify changes in complex systems with large numbers of observables. Such complex systems often have the property that each change affects only a (potentially small) subset of observables. In geophysical or climate data, for example, a change may affect measurements in a particular geographic region; in public health monitoring, a disease outbreak may primarily affect a particular community; and in social media, various events may affect the activity of particular subsets of users. A number of change-point detection methods have been developed for multivariate data (6–13), but most of these methods focus on detecting substantive changes in the joint distribution of all observables and are thus ill suited for applications in which a change might involve only a small subset of observables.

Our own work is motivated by the detection of structural changes in proteins, a challenging change-point detection problem in which the essential characteristics of each biologically interesting change may typically be characterized in terms of a limited subset of a large number of observables. The atoms within a protein fluctuate constantly, but occasionally a protein undergoes a structural transition from one set of structurally similar, rapidly interconverting atomic arrangements to another. These transitions, or “conformational changes,” are often of biological importance, allowing the protein to act as a nanoscale machine that carries out specific tasks within a cell. The study of such conformational changes may often be facilitated by atomic-level molecular simulation techniques, such as molecular dynamics (MD) simulation. These simulations, which have grown longer and more plentiful in recent years (14, 15), provide a means to capture the motions of individual atoms in a protein or other biomolecule at fine temporal resolution.

Identifying conformational changes in proteins given the positions of each atom over time represents a challenge for several reasons (16–19). First, although a conformational change is characterized by a difference in the atomic position distributions of certain atoms before and after the change, this difference may be small relative to the magnitude of an ever-present background of rapid fluctuations in the positions of all atoms in the protein.

Second, a typical protein comprises thousands of atoms, and a large number of univariate observables (e.g., Cartesian coordinates or interatomic distances) are required to fully specify the positions of all of these atoms. It is often difficult to find one or a few summary measurements that capture all of the important conformational changes in a biomolecular simulation without prior knowledge of the nature of those changes.

Finally, many biologically interesting conformational changes occur within localized regions of the protein that may each encompass as few as 1–2% of its atoms and thus a relatively small fraction of the observables. Identifying small subsets of observables whose distributions change simultaneously can be like searching for a needle in a haystack, and classical change-point detection methods are generally not well suited to this task.

To address these challenges, we developed a statistical method that, given time series for a large number of observables, searches concurrently for both change times and the subset of observables that change at each of these times. We refer to our approach as the “simultaneous penalized likelihood estimation” (SIMPLE) change-point detection method.

We show that SIMPLE detects important and often subtle conformational changes in real MD simulations of folded and unfolded proteins, reproducing observations made through painstaking manual analysis and also revealing previously unnoticed changes. SIMPLE automatically attributes detected conformational changes to subsets of input observables corresponding to specific regions of the protein molecule, facilitating the interpretation of results. In quantitative tests performed on synthetic MD trajectories with known change points, we find that SIMPLE detects conformational changes more accurately than various methods currently used for biomolecular simulation analysis.

Several other change-point detection methods recently introduced in the statistics literature, including those by Zhang, Siegmund, and coworkers (20–23), Bleakley and Vert (24), and Jeng et al. (25), are also designed to detect changes involving subsets of multiple observables, and they have largely been applied to the detection of DNA copy number variants in genomics data. These methods focus primarily on detecting points in the genomic sequence or in time at which changes occur, addressing only heuristically the problem of identifying which observables change at each of those points, or choosing them in a simple greedy fashion. SIMPLE, by contrast, formulates the problem as an explicit and concurrent optimization over all possible change times and all possible sets of observables that may change at each of those times. SIMPLE also allows for greater flexibility in the statistical model of the data distribution and can incorporate prior knowledge about which groups of observables are likely to change together (such as those corresponding to neighboring atoms in proteins). Our results indicate that, for certain difficult change-point detection problems in our application domain, SIMPLE achieves a substantial accuracy advantage over these alternative methods.

The formulation of the SIMPLE method is sufficiently general to allow its application in a variety of other domains that require the detection of change points in subsets of large numbers of observables. SIMPLE may thus help address the challenges posed by the proliferation of “big data” not only in scientific fields such as genomics, neuroscience, and particle physics, but also in areas such as business analytics, network security, and quality control.

Overview of Method

SIMPLE takes as input multiple time series representing the values of a set of observables or measurements over a common sequence of points in time. When applying the method to simulations of biomolecules such as proteins, we typically use time series representing distances between pairs of atoms, or positions of atoms under global structural alignment. The method could be easily adapted to use other observables, such as torsion angles.

SIMPLE’s output is a set of change points for each observable. We wish to choose these change points such that the values of an observable between any two successive change points are likely to come from a single probability distribution—in other words, such that the statistics do not change substantially from one part of that interval to another. To avoid spurious change-point detections, we wish to select as few change points as possible. We also wish to exploit the fact that a single change is likely to involve multiple observables, and thus multiple observables will often have simultaneous change points. In biomolecular simulations, observables corresponding to neighboring regions of a molecule are particularly likely to have such simultaneous change points.

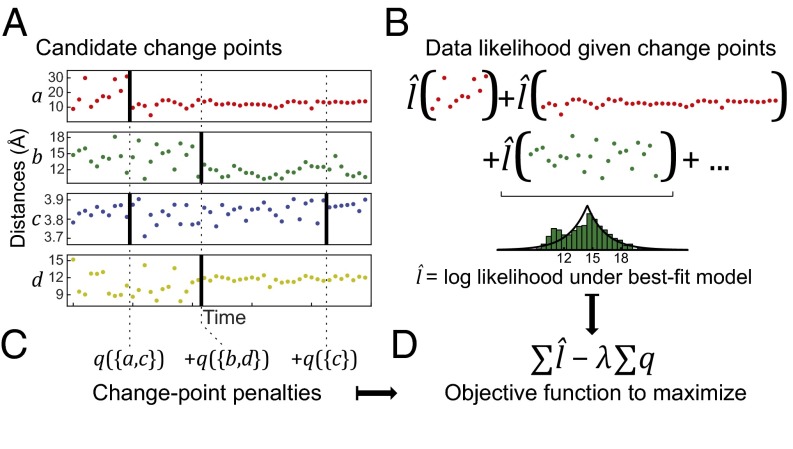
SIMPLE formulates the problem as an optimization over all possible change-point selections given the observed data (Fig. 1). In particular, it attempts to select a set of change points that maximizes an objective function of the form

$$\begin{array}{l}\text{log}\left(\text{max}\hspace{0.17em}\text{likelihood}\hspace{0.17em}\text{of}\hspace{0.17em}\text{data}\hspace{0.17em}\text{given}\hspace{0.17em}\text{these}\hspace{0.17em}\text{change}\hspace{0.17em}\text{points}\right)\\ -\hspace{0.17em}\lambda \times \left(\text{penalty}\hspace{0.17em}\text{function}\hspace{0.17em}\text{for}\hspace{0.17em}\text{these}\hspace{0.17em}\text{change}\hspace{0.17em}\text{points}\right),\end{array}$$ [1]

where λ is a positive constant. The first term is obtained by fitting the data for each observable between each consecutive pair of change points to a single probability distribution from a given family. This term increases as more change points are added. The penalty function in the second term is constructed to increase as new change points are added, but less quickly if the added change points are simultaneous with existing ones in other observables. For biomolecular simulation data, we use penalty functions that penalize simultaneous changes less if they involve observables representing spatially proximate regions of a molecule.

Fig. 1.

Given many noisy observables, the SIMPLE method detects change points for each one by maximizing a penalized-likelihood objective function that reflects the assumption that each change likely involves multiple observables. For (A) any candidate set of change points, (B) a statistical model is fitted to the data between each pair of change points in each observable, and the log-likelihood values are summed over all data segments and all observables. (C) A penalty for each set of simultaneous change points is summed over all change times. (D) The objective function is the total log-likelihood minus a sensitivity parameter, λ, times the total penalty.

The constant λ acts as a sensitivity parameter. Decreasing λ weakens the effect of the penalty function, yielding a larger number of detected change points, including points corresponding to smaller, shorter-lived changes. Increasing λ strengthens the effect of the penalty term, reducing the number of changes detected and restricting them to larger, longer-lived changes.

To ensure that SIMPLE detects not only changes in average structure but also changes in the degree of fluctuation about that structure, we fit the data using a family of probability distributions with two parameters representing average and spread, respectively. The method is thus unaffected by scaling and shifting transformations of any individual time series input. We typically use Laplace distributions, which provide greater robustness to outliers than Gaussian distributions by allowing the method to detect changes in median rather than mean.

Under a broad set of conditions discussed in a later section (Mathematical and Algorithmic Formulation of Method), the solution to the optimization problem of Eq. 1 using the Laplace distribution model is provably asymptotically consistent. That is, if there are true changes in the probability distribution that is assumed to generate the input data, then the solution correctly identifies these changes (and only these changes), given a sufficient number of independent data points between the change times. Importantly, this result holds even when the true distribution of the data does not fit a Laplace model, as long as the true data distribution has tails that decay exponentially or faster and satisfies certain other general properties.

Eq. 1 leads to a complicated optimization problem. SIMPLE approximates its solution using an iterative algorithm (SI Text) that leverages a recently developed, fast optimization method for univariate data (26). This iterative algorithm produces good results in practice and is both efficient and parallelizable. Even on a single processor, it can be readily applied to large datasets involving thousands of time series.

Application to Molecular Dynamics Simulation Data

Simulations of Protein Folding and Unfolding.

To illustrate the application of SIMPLE, we first consider the MD simulation trajectories presented by Lindorff-Larsen et al. (27) in which 12 proteins spontaneously and repeatedly fold to their native structures from an unfolded state. For each protein, we applied SIMPLE to time series of distance measurements between all pairs of alpha-carbon atoms, using a single penalty function that promotes simultaneous detection of changes in adjacent amino acid residues (details in SI Text). This choice of input time series and penalty function represents our default recommendation for analyses focused on conformational changes of the protein backbone. We chose values of the sensitivity parameter λ to yield ∼100 detected changes per simulation.

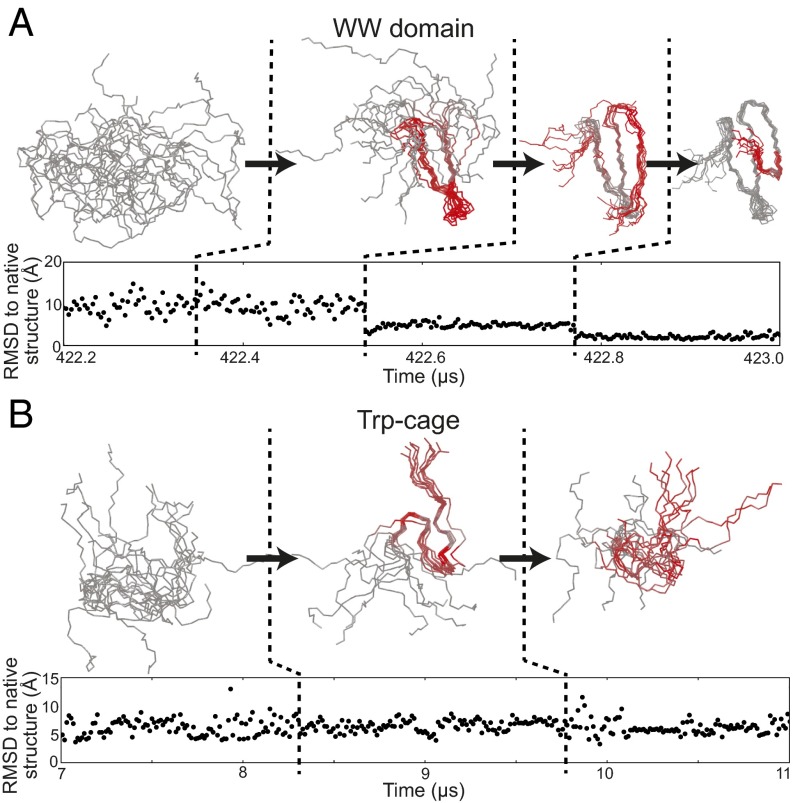
SIMPLE not only detects the folding and unfolding transitions but also automatically segments many of them into several steps corresponding to the formation and loss of metastable structure, as illustrated in Fig. 2A for a simulation of a WW domain. This and similar simulations of the WW domain have been the subject of extensive previous manual, visual, and automated analysis (27–30), and SIMPLE’s results correspond closely to the results of these previous analyses. SIMPLE also indicates which of its input distance measurements are involved in each change, allowing one to highlight the residues that best characterize each change.

Fig. 2.

Results from application of SIMPLE to equilibrium protein-folding simulation trajectories. (A) Three consecutive detected conformational changes in the WW domain reveal a folding pathway. (B) Two consecutive detected conformational changes in Trp-cage during the unfolded state reveal transient formation of a metastable structure that does not lie along the overall folding pathway. Several of these changes are not evident in the time series of RMSD to the native structure, which is often used in the analysis of protein simulations. Aligned ensemble images are shown for the protein backbone structures between each successive pair of detected changes, with red color used to indicate the spatial location of the change between the current ensemble and the previous ensemble as indicated by SIMPLE’s output (SI Text). As inputs to SIMPLE, we used 595 interatomic distance observables across ∼65,000 time points for the WW domain trajectory and 190 interatomic distance observables across ∼21,000 time points for the Trp-cage trajectory (SI Text). Changes detected over the full lengths of these simulation trajectories are shown in Figs. S1 and S2. The average number of observables found to change distribution at each change point was 205 for the WW domain trajectory and 69 for the Trp-cage trajectory.

For most of the simulated proteins, SIMPLE also identifies changes within the folded and unfolded states that reveal partial folding events, partial unfolding events, and formation of misfolded metastable structures. Many of these changes have not been identified previously. Detection of conformational changes within the unfolded state is particularly challenging, because such changes are often masked by large, rapid fluctuations in the unstructured regions of the protein and because global structural descriptors such as root-mean-square deviation (RMSD) from the native structure tend to be less informative in such cases (Fig. 2B).

Simulations of a Folded Protein.

Next, we illustrate the application of SIMPLE to a set of simulations in which the β₂-adrenergic receptor (β₂AR), a protein that serves as a target of beta blockers and other widely used drugs, transitions spontaneously from one experimentally observed conformational state (the “active state”) to another (the “inactive state”). These simulations were used by Dror et al. (31) to elucidate the mechanism of receptor activation, which required the determination of key conformational changes through painstaking manual analysis and examination.

These simulations differ from those of the previous example in two important ways. First, each β₂AR simulation captures only a single transition from the initial to the final conformational state. These simulations are thus representative of most MD simulations in the literature, in that each simulation visits most of the relevant conformational states only once.

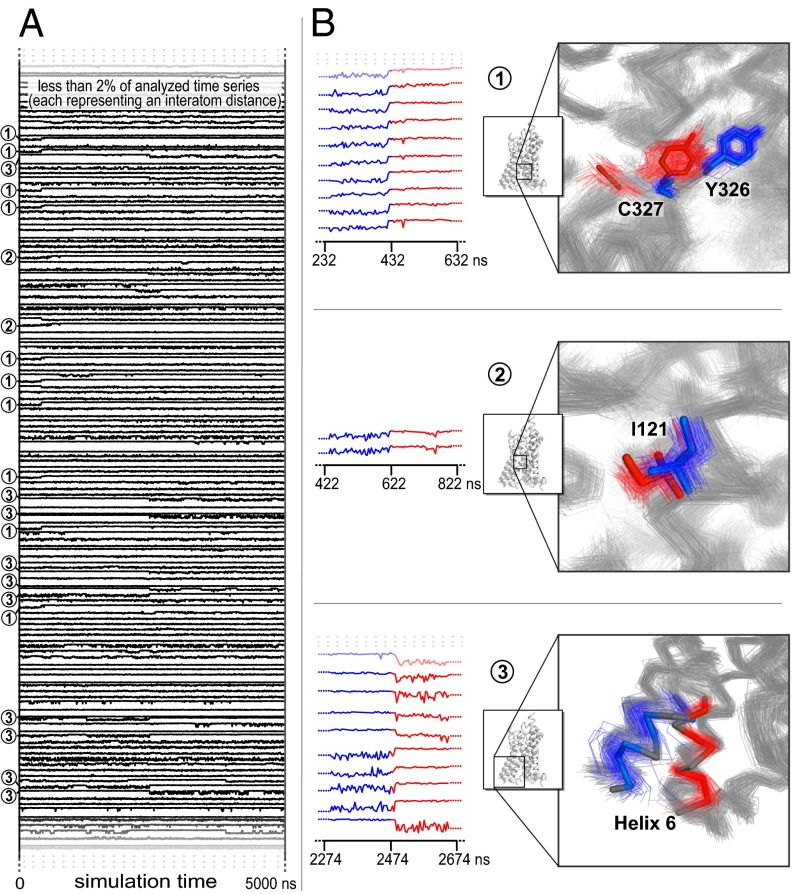
Second, the β₂AR remains fully folded throughout the simulations, and the conformational changes that take place are subtle, often involving only amino acid side chains. To ensure sensitivity to such side-chain motions, we used as time series inputs to SIMPLE the distances between each pair of atoms that came into contact with one another at any point during a simulation—a total of ∼14,000 pairs of atoms (Fig. 3A). We applied a fixed nonlinear transformation to each distance to emphasize formation and breakage of direct contacts between pairs of atoms, as such contacts are often functionally important in proteins. The penalty function was chosen to promote the simultaneous detection of changes involving distances between atoms from the same pair of protein residues. This choice of input time series and penalty function represents our default recommendation for analyses of simulation trajectories in which side-chain motions may be of interest (details in SI Text).

Fig. 3.

Application of SIMPLE to a simulation of the β₂-adrenergic receptor transitioning spontaneously from its active state to its inactive state. (A) We used as inputs ∼14,400 observables across ∼1,000 time points. Each observable represented the distance between one pair of atoms, after application of a nonlinear transformation that emphasizes formation and breakage of direct contacts between atoms. (B) Three of the four conformational changes detected at a sensitivity parameter setting of λ = 1,300. Multiple simulation snapshots before and after each change are superimposed. The residues found to be involved in each change are shown in blue before each change and in red afterward. The remainder of the protein is shown in gray both before and after the change. The conformational changes illustrated are detected as simultaneous changes of 17, 2, and 122 input observables, respectively. The only detected change that is not displayed, a motion of residue Tyr219 and nearby residues, takes place about 50 ns before the third change displayed and is detected as a simultaneous change of 65 input observables. The detected conformational changes correspond closely to those identified by Dror et al. (31) through painstaking manual and visual analysis.

Fig. 3B illustrates the results of SIMPLE for one of the β₂AR trajectories. The detected conformational changes correspond very closely to the changes identified by Dror et al. (31) through manual and visual analysis as the key conformational changes in the β₂AR’s transition from its active state to its inactive state. In particular, these conformational changes match the major changes of the connector region and G-protein–binding site illustrated in figure 2 of that paper, except that SIMPLE recognizes that the final change—an inward motion of helix 6 accompanied by a repositioning of Tyr219 on helix 5—actually involves two steps in this trajectory, with the helix 6 motion following the Tyr219 motion. These changes were also detected by SIMPLE in the other 11 active-to-inactive state simulation trajectories shown in figure 3 of Dror et al. (31) (details in SI Text).

Comparison of Performance with That of Other Methods

To measure the performance of various methods for detecting conformational changes, we generated synthetic MD simulation trajectories where changes in the atomic position distributions occur at known times (there is no such “ground truth” for actual MD trajectories). We took care to preserve key properties of actual MD trajectories. In particular, we created synthetic trajectories, using a stationary bootstrap of the actual millisecond-long MD trajectory of the bovine pancreatic trypsin inhibitor (BPTI) reported by Shaw et al. (28), so that the noise distributions and short-timescale autocorrelations of the atomic positions were similar to those observed in the real trajectory. The synthetic trajectories transition among four conformational states modeled on ones described by Shaw et al. (28), with the transitions selected according to a Markov chain. We created 25 synthetic trajectories, each with four state transitions. Each trajectory was analyzed independently.

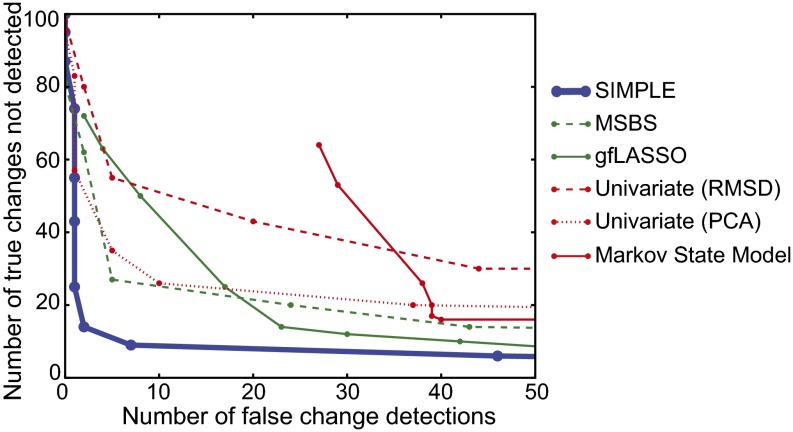
Fig. 4 compares various methods according to the number of correct and incorrect detections of change times, adjusting λ in SIMPLE and a sensitivity parameter in each of the other methods to control the total number of detections (more detail in SI Text). All other SIMPLE parameters were set to their default values for analyses focused on conformational changes of the protein backbone. According to these criteria, SIMPLE, shown in blue in Fig. 4, substantially outperforms both methods previously developed for or used in the context of MD simulation analysis (red) and other methods from the statistics literature (green). SIMPLE also identifies the observables that change at each time, but we do not include this in our comparisons because most other methods do not return this information.

Fig. 4.

Comparison of the performance of various methods for detecting conformational changes in synthetic protein trajectories in which the conformational changes take place at predetermined times. SIMPLE (blue) outperforms several methods previously published in the biomolecular simulation literature (red), including a state identification method involving Markov state models (32) and a univariate change-point detection method (17) applied to time series of either the RMSD from native structure (“RMSD”) or the coefficient of the first principal component (“PCA”). SIMPLE also outperforms certain related change-point detection methods described in the recent statistics literature (green), including the group-fused LASSO (gfLASSO) approach of Bleakley and Vert (24) and an adaptation of the multisample binary segmentation (MSBS) approach of Zhang et al. (20).

Many common analyses of MD trajectories rely on a single, generic summary measurement such as the RMSD to the native structure or the coefficient of the first principal component of the aligned atomic positions. Certain conformational changes, however, prove difficult to detect using such summary measurements. To quantify this limitation, we applied a state-of-the-art univariate change-point detection method described in the MD literature (17) to the time series for each of these summary measurements and found that it underperformed most of the multivariate methods we examined (Fig. 4).

In multivariate analyses of MD trajectories, change-point detection methods are generally passed over in favor of state identification methods, which aim to explicitly identify the conformational states visited during a simulation. These range from basic clustering techniques to sophisticated algorithms for building Markov state models (MSMs) (32–35). Fig. 4 shows the results of using a leading MSM method, MSMBuilder2 (32), to yield a parsimonious set of state transition times for each trajectory (SI Text). SIMPLE performs substantially better in our tests than the MSM method. It should be noted that for an alternative synthetic dataset consisting of a long equilibrium trajectory that visits each conformational state dozens of times, the MSM method is competitive with SIMPLE (Fig. S3). The vast majority of real-world MD simulations, however, do not visit every state many times. Our comparison also gives the MSM approach some artificial advantages (details in SI Text). State identification is of interest in its own right, and MSM methods are invaluable for that purpose, but our results show that one may be able to detect conformational changes more accurately using change-point detection methods without identifying states.

We also compared SIMPLE to the recently published change-point detection methods of Zhang et al. (20) and Bleakley and Vert (24), which we adapted to the analysis of MD simulations (Fig. 4, Fig. S3, and SI Text). These methods—which were also designed to detect changes involving subsets of observables, but do not perform concurrent optimization over change times and subsets of changed observables—perform relatively well in our tests, but do not detect as many of the true changes as SIMPLE at any given false-positive rate.

Mathematical and Algorithmic Formulation of Method

Detailed Formulation of Penalized-Likelihood Optimization.

Consider $J$ time series observables of $T$ data points each, indexed as ${\left\{{\left\{Y_{j,t}\right\}}_{t=1}^T\right\}}_{j=1}^J$. Let ${\left\{{\tau }_i\right\}}_{i=1}^K$ denote a sequence of $K$ candidate change times with $S_i\subset \{1,\dots ,J\}$ the candidate observables that change at time ${\tau }_i$. For each $j$, let the candidate change times in observable $j$ be denoted as ${\left\{{\tau }_{j,i}\right\}}_{i=1}^{K_j}$, with ${\tau }_{j,0}=0$ and ${\tau }_{j,K_j+1}=T$. SIMPLE detects change points in the data by solving the optimization problem

$$\widehat{K},\left\{{\widehat{\tau }}_i\right\},\left\{{\widehat{S}}_i\right\}=\text{arg}\underset{K,\hspace{0.17em}\left\{{\tau }_i\right\},\left\{S_i\right\}}{\text{max}}{\displaystyle \sum }_{j=1}^J{\displaystyle \sum }_{i=0}^{K_j}\widehat{l}\left(Y_{j,{\tau }_{j,i}+1},\dots ,Y_{j,{\tau }_{j,i+1}}\right)-\lambda {\displaystyle \sum }_{i=1}^{K}q\left(S_i\right).$$ [2]

Here, $\widehat{l}\left(Y_{j,{\tau }_{j,i}+1},\dots ,Y_{j,{\tau }_{j,i+1}}\right)$ is the maximum log-likelihood, under some statistical model, of data in an observable between two candidate change points of that observable. $q:2^{\left\{1,\dots ,J\right\}}\to \mathbf{R}$ is a strictly increasing penalty function on subsets of observables that satisfies the property $q\left(S_1\bigsqcup S_2\right)<q\left(S_1\right)+q\left(S_2\right)$ whenever $S_1$ and $S_2$ are nonempty and disjoint, so that simultaneous change points incur a smaller penalty than change points of the same observables at differing times. In the special case where $J=1$, $\lambda =\text{log}T$, and the likelihood model is Gaussian with shared variance across segments, our objective function reduces to the univariate problem studied by Yao (4).

In our applications, we use the Laplace distribution model

$$\widehat{l}\left(Y_{j,{\tau }_{j,i}+1},\dots ,Y_{j,{\tau }_{j,i+1}}\right)=\underset{\mu ,v}{\text{max}}\text{log}\left({\displaystyle \prod }_{k={\tau }_{j,i}+1}^{{\tau }_{j,i+1}}\frac{1}{2v}\text{exp}\left(-\frac{\left|Y_{j,k}-\mu \right|}{v}\right)\right),$$ [3]

and we perform the optimization in Eq. 2 under the constraint that change times ${\tau }_{j,i}$ and ${\tau }_{j,i+1}$ are separated by at least two data points (to avoid degeneracies in the maximum-likelihood value). We note that the likelihood model implied by Eqs. 2 and 3 treats data between change points in each observable as independent and Laplace distributed with unknown median and scale and also treats observables as independent of one another. However, SIMPLE is effective even when some of these assumptions are not satisfied. We observe below that the method is asymptotically consistent even when the data are not Laplace distributed and when observables may be correlated with each other, as long as the median and/or mean absolute deviation of the marginal distributions of some observables change at each change point. Empirically, we also observe that the data model of Eq. 3 yields reasonable performance in the presence of weak autocorrelation within each observable between change points. In applications where data are instead strongly autocorrelated, we would advocate applying SIMPLE using an autoregressive or other time-series likelihood model in place of Eq. 3.

For analysis of biomolecular simulation data, we use penalty functions of the form $q\left(S\right)={\left({{\displaystyle {\sum }_i\left|S{\displaystyle \cap }{G}_i\right|}}^{\beta }\right)}^{\alpha }$ for parameters $0<\alpha ,\beta <1$, where $G_i\subset \{1,\dots ,J\}$ are groups of observables representing spatially proximate locations on the protein molecule. Each term ${\left|S{\displaystyle \cap }{G}_i\right|}^{\beta }$ promotes simultaneous detection of changes in the observable group $G_i$, and the summation and exponentiation by $\alpha$ promotes simultaneous detection of changes across all observables. Our recommended (default) choices of the parameters $\alpha$ and $\beta$ and groups $G_i$, based on qualitative performance in real-data examples, are discussed in SI Text. We find that, in our synthetic-data experiments, the performance of SIMPLE is relatively stable under different choices of $\alpha$ and $\beta$ and groups $G_i$ (Fig. S4).

For application domains where prior knowledge is not available to guide the construction of observable groups, we suggest using the generic penalty function $q\left(S\right)={\left|S\right|}^{\alpha }$. The single tuning parameter α controls the extent to which change points are detected as simultaneous across observables. It takes on a value between 0 and 1 and may be set closer to 1 if each change is expected to involve few observables or closer to 0 if each change is expected to involve most of the observables. In the absence of prior knowledge, we suggest a default value of 0.7.

Asymptotic Consistency Under General Distributional Assumptions.

Theorem. Let the data ${\left\{Y_{\cdot ,t}\right\}}_{t=1}^T$ be $T$ independent random vectors of $J$ (not necessarily independent) observables. Suppose there exist $K^0$ true change times ${\left\{{\tau }_i^0\right\}}_{i=1}^{K^0}$ with changed observable sets ${\left\{S_i^0\right\}}_{i=1}^{K^0}$, such that data for observable $j$ between change points $i$ and $i+1$ of that observable are marginally distributed according to some distribution $F_{j,i}$. Assume the following conditions hold:

• i)Each $F_{j,i}$ has tails that decay at least exponentially, i.e., $F_{j,i}\left(-x\right)+\left(1-F_{j,i}\left(x\right)\right)\le A{e}^{-Bx}$ for some $A,B>0$ and all $x\in \mathbf{R}$. Each $F_{j,i}$ has density $f_{j,i}$ bounded below by some $m>0$ in a neighborhood of its median and above by some $M<\infty$ over all of $\mathbf{R}$.
• ii)Each $F_{j,i}$ differs from $F_{j,i+1}$ in its median and/or mean absolute deviation from the median.
• iii)For any disjoint nonempty sets $S_1,S_2\subset \{1,\dots ,J\}$, $q\left(S_1\right)+q\left(S_2\right)>q\left(S_1\bigsqcup S_2\right)>q\left(S_1\right)$.
• iv)The minimum separation between change times satisfies ${\text{liminf}}_{T\to \infty }\left(\left({\text{min}}_i{\tau }_{i+1}^0-{\tau }_i^0\right)/T\right)>0$, and the penalty magnitude satisfies ${\text{lim}}_{T\to \infty }\left(\lambda \left(T\right)/T\right)=0$ and $\lambda \left(T\right)\ge C{\left(\text{log}T\right)}^2$ for some $C>0$.
• v)There exists a known upper bound $K_{\text{max}}\ge K^0$ (independent of $T$).

Let $\widehat{K},\left\{{\widehat{\tau }}_i\right\},\left\{{\widehat{S}}_i\right\}$ be the solution to the optimization problem in Eq. 2 with the Laplace data model of Eq. 3, under the constraints $\left|{\tau }_{i+1}-{\tau }_i\right|\ge 2$ and $K\le K_{\mathit{max}}$. Then, for some sufficiently large $C$ in condition iv and any $\epsilon >0,$

$$\underset{T\to \infty }{\text{lim}}\mathrm{Pr}\left(\widehat{K}=K^0,\hspace{0.17em}{\widehat{S}}_i=S_i^0\hspace{0.17em}\text{and}\hspace{0.17em}\frac{\left|{\widehat{\tau }}_i-{\tau }_i^0\right|}{T}<\epsilon \hspace{0.17em}\text{for}\hspace{0.17em}\text{all}\hspace{0.5em}1\le i\le K^0\right)=1.$$

This Theorem ensures that, in the limit of infinite data between change times, the solution to the SIMPLE optimization problem using the Laplace likelihood model has the correct number of true change times with arbitrarily small relative errors in those times, as well as the correct subsets of changed observables. This asymptotic consistency result holds even if the $J$ observables are not Laplace distributed or are not independent. Indeed, we use the Laplace model simply as a robust tool for detecting changes in median and in mean absolute deviation from median, whether or not the data actually follow a Laplace distribution. A proof and further discussion are provided in SI Text.

Overview of Algorithmic Approach.

Although the optimization problem in Eq. 2 is conceptually simple, it may be difficult to solve exactly even for datasets of moderate size. We propose an iterative algorithm to approximate its solution, which yields good results in our tested applications. Empirically, this algorithm appears to require close to linear (in the total size JT of the input data matrix) runtime per iteration and terminates in a small number of iterations.

The key idea underlying the algorithm is that if candidate change points in all but one observable are held fixed, then the optimization problem for change points in the last observable reduces to a univariate penalized-likelihood optimization problem with time-varying penalties. A pruned dynamic programming algorithm recently developed by Killick et al. (26) may be applied to efficiently and exactly solve this univariate problem. To approximate the solution to Eq. 2, we use an iterative approach in which, at each iteration, we solve this univariate problem for each observable by treating as fixed the changes in the other observables from the preceding iteration. To prevent the algorithm from reaching a poor local maximum, we include an additional step in each iteration that can adjust the detected time of a change in multiple observables. The algorithm is easily parallelizable, and a parallel implementation using MPI is available at https://github.com/DEShawResearch/SIMPLEchangepoint. Further details are provided in SI Text.

Concluding Remarks

Although we have emphasized the application of the SIMPLE method for the detection of conformational changes in biomolecular simulation data, the method is quite general in its formulation and should be applicable to many other problems in which one wishes to detect changes affecting subsets of many observables. Potential applications include the detection of distributed denial-of-service (DoS) attacks in computer networks (36), of weather and climate changes from meteorological data (37), and of disease outbreaks from surveillance data collected at multiple locations (38). These problems are similar to that of detecting conformational changes in biomolecules in that a distributed DoS attack, climate change, or disease outbreak is likely to cause a simultaneous change in a number of the monitored observables. In each case, the total number of monitored observables is potentially very large, and spatial or graphical relationships among them could be exploited through an appropriate choice of penalty function in SIMPLE. Some of these applications place a premium on the detection of a change as soon as it occurs, and this remains an important topic for future work.

Researchers have previously noted that classical multivariate change-point detection methods often fail to detect changes that involve only a small number of observables. Rogerson and Yamada, for example, applied univariate and multivariate cumulative sum methods to disease surveillance and concluded that neither is completely satisfactory, as “the univariate method is generally better at detecting changes ... that occur in a small number of regions; the multivariate is better when change occurs in a large number of regions” (ref. 38, p. 2195). We believe that SIMPLE, which is designed to identify changes involving any number of observables, could help fill this gap between classical univariate and multivariate approaches, providing an analytical tool that could prove increasingly useful as new data acquisition technologies continue to drive an explosive proliferation in the number and size of datasets involving large numbers of observables.