Small Temperature Dependence of the Kinetic Isotope Effect for the Hydride Transfer Reaction Catalyzed by Escherichia coli Dihydrofolate Reductase

Abstract

The H/D primary kinetic isotope effect (KIE) for the hydride transfer reaction catalyzed by Escherichia coli dihydrofolate reductase (ecDHFR) is calculated as a function of temperature employing ensemble-averaged variational transition-state theory with multidimensional tunneling. The calculated KIEs display only a small temperature dependence over the temperature range of 5 to 45 °C. We identify two key features that contribute to canceling most of the temperature dependence of the KIE that would be expected on the basis of simpler models. Related issues such as the isotope effects on Arrhenius preexponential factors, large differences between free energies of activation and Arrhenius activation energy, and fluctuations of effective barriers are also discussed.

This paper presents a theoretical explanation of the unusual temperature dependence¹ of the kinetic isotope effect (KIE) for the hydride transfer chemical step of the reaction catalyzed by E. coli dihydrofolate reductase (ecDHFR). The explanation identifies two general features that may be important in interpreting enzymatic kinetic isotope effects more generally.

Many enzyme reactions involve hydron transfer (transfer of H⁺, H⁻, or H^•). Such reactions have significant contributions from zero-point energy and tunneling; KIEs have been extensively used to study these effects.^1–7 Surprisingly, a number of enzymes have been found to display almost temperature-independent KIEs,^1–4 which are contrary to experience with small-molecule chemistry or simple tunneling models. Recent multidimensional tunneling calculations have been successfully used to study tunneling effects on enzymatic KIEs, but the most accurate methods have so far been applied only at a single temperature.⁸

DHFR catalyzes the reduction of 7,8-dihydrofolate (DHF) to 5,6,7,8-tetrahydrofolate (THF) with the key chemical step being the transfer of a hydride ion from the nicotinamide ring of the cofactor nicotinamide adinine dinucleotide phosphate (NADPH). At pH ≅ 7, product release is partly rate-limiting⁹ and the H/D kinetic isotope effect is about 1.1–1.3, but the intrinsic KIE on the hydride transfer step is >3.¹⁰ Furthermore, at 25 °C, the phenomenological free energy of activation derived from the rate constant⁹ by using transition-state theory is 13.4 kcal/mol,⁷ and the free energy of reaction calculated from the experimental equilibrium constant⁹ is −4.4 kcal/mol.⁷

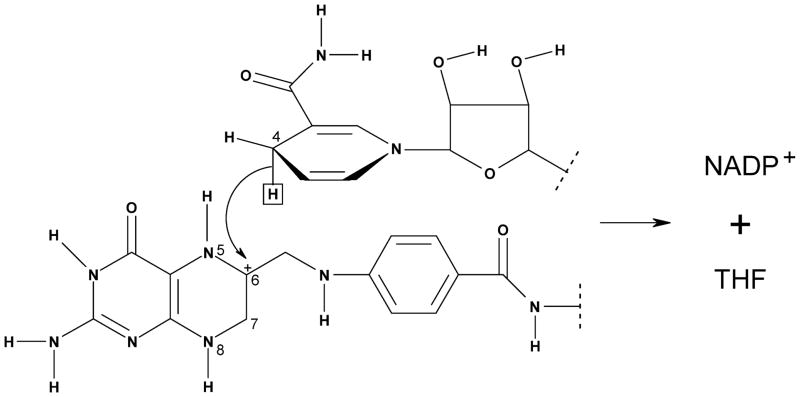
Here, we report a dynamical simulation of the ecDHFR system using a combined quantum mechanical and molecular mechanical (QM/MM) approach. As depicted in Figure 1, the reactive fragment that involves transferring a hydride ion from the C4 position of NADPH (the cofactor) to the C6 in N5-preprotonated DHF (the substrate) to form THF (the product) is treated quantum mechanically. The hydride transfer KIEs at 5 and 45 °C and 1 atm are calculated using ensemble-averaged variational transition-state theory with multidimensional tunneling (EA-VTST/MT).⁶ As explained in the original papers,⁶ the calculations include the potential of mean force (PMF) based on umbrella sampling, quantization of bound vibrations based on ensemble-averaged instantaneous normal-mode analyses, and quantum effects on the reaction coordinate based on optimized multidimensional tunneling calculations. A key feature is the ensemble average that samples different transition paths in the enzyme active site; this allows the inclusion of classical recrossing effects that could also¹¹ be treated as nonequilibrium bath effects. With one exception (a more accurate fitting procedure for quantized vibrational energy as a function of reaction coordinate), we follow the computational procedures that have been described in a previous paper,⁷ where KIEs of the ecDHFR-catalyzed reaction were calculated at 25 °C.

Figure 1.

The QM fragment used in the present study to describe the hydride transfer reaction catalyzed by ecDHFR (top, NADPH; bottom, N5-preprotonated DHF). The QM/MM boundaries are indicated by dotted lines.

The goal is to rationalize the unusual temperature dependence of the unimolecular hydride transfer KIE. The first-stage calculated rate constant with quantized vibrations is

$$k^{\text{VTST}}=\frac{k_{\mathrm{B}}T}{h}exp[-\mathrm{\Delta }{G}_{\text{QC}}^{\text{SRC}}/RT]$$ (1)

where k_B is the Boltzmann constant, h is Planck’s constant, T is temperature, R is the gas constant, and $\mathrm{\Delta }{G}_{\text{QC}}^{\text{SRC}}$ is the single-reaction-coordinate quasiclassical free energy of activation, calculated by adding quantization effects¹² to the classical PMF as a function of the reaction coordinate z, which is the difference between the hydrogen-to-donor-carbon distance and the hydrogen-to-acceptor-carbon distance. Note that $\mathrm{\Delta }{G}_{\text{QC}}^{\text{SRC}}$ is evaluated at the maximum of the sum of the PMF and the quantized vibration correction; the ensemble of geometries corresponding to this maximum is called the transition state or the dynamical bottleneck. Coupling the reaction coordinate z to other degrees of freedom for each member of the transition-state ensemble allows us to obtain more highly optimized reaction paths for the protein environment at instantaneous times during the molecular dynamics simulation and then to estimate an ensemble-averaged recrossing correction

$$\mathrm{\Gamma }=\frac{1}{M}\sum _{i=1}^M{\mathrm{\Gamma }}_i$$ (2)

where Γ_i is the recrossing transmission coefficient for ensemble member i of the quasiclasical transition-state ensemble,⁶ and M is the number of ensemble members in the average (M = 20 in the present work). This leads to an improved rate constant that corrects for dynamic recrossing events on the basis of a different reaction coordinate for each member of the transition-state ensemble

$$k_{\text{QC}}=\mathrm{\Gamma }{k}^{\text{VTST}}$$ (3)

where k_QC denotes the ensemble-averaged quasiclassical rate constant. Finally, we calculate a transmission coefficient κ_i for quantum effects (tunneling and nonclassical reflection) on the optimized reaction coordinate of each member of the quasi-classical transition-state ensemble, and a final estimate of the rate constant is given by

$$k=\gamma k^{\text{VTST}}$$ (4)

where

$$\gamma =\frac{1}{M}\sum _{i=1}^M{\mathrm{\Gamma }}_i{\kappa }_i$$ (5)

The individual κ_i values were calculated by microcanonically optimizing the tunneling paths between small-curvature tunneling paths and large-curvature tunneling paths.¹³ However, the results would be only 2% smaller for H⁻ transfer (and the same for D⁻ transfer) if we had limited the calculation to small-curvature tunneling paths.

Figure 2 displays the computed classical mechanical PMF (relative to reactants) along the hydride transfer reaction coordinate z. Our simulation shows that both the transition state and the product state are destabilized, relative to reactants, when temperature is increased. The position of the transition state shifts toward the product side at higher temperatures, in accordance with Hammond’s postulate.¹⁴ Concomitantly, the effective barrier top becomes narrower and more symmetric as T increases.

Figure 2.

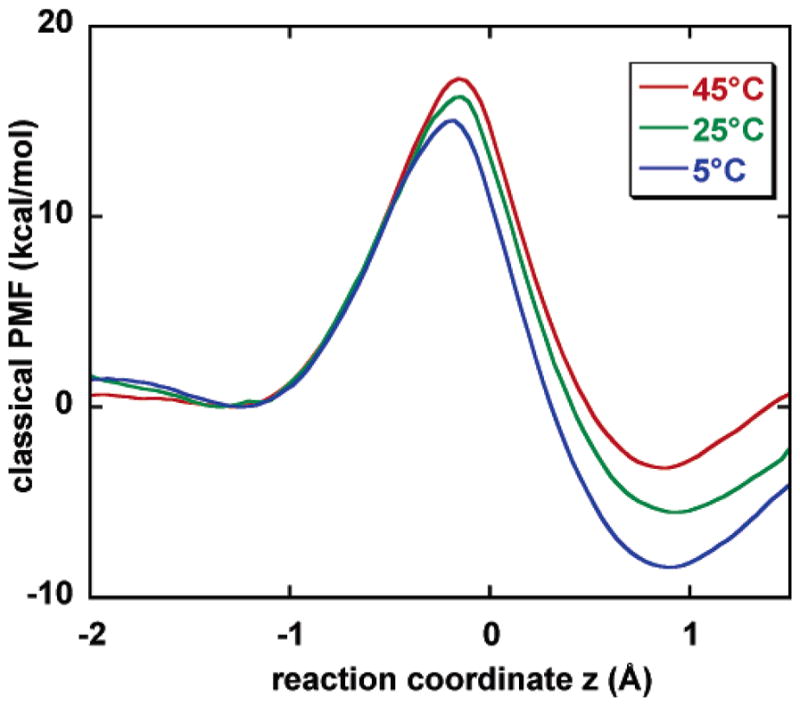
Computed classical mechanical potential of mean force (PMF) at 5, 25, and 45 °C. The 25 °C result is from ref 7.

As is common in the enzyme kinetics literature, we report our calculated rate constants k’s as free energies of activation by using the relation

$$k=\frac{k_{\mathrm{B}}T}{h}exp[-\mathrm{\Delta }{G}_T^{\text{act}}/RT]$$ (6)

where $\mathrm{\Delta }{G}_T^{\text{act}}$ is the phenomenological free energy of activation at temperature T. The free energies of activation for H⁻ transfer, the H/D KIEs, and the changes in KIEs from 5 to 45 °C at various levels of theory are given in Table 1 (the final column of the table is explained later), and the free energies of activation for D⁻ transfer are in Table 2. Including quantized vibrational contributions, dynamical recrossing, and multidimensional tunneling yields KIEs of 3.22 and 3.01 at 5 and 45 °C, respectively, in rough agreement with experiment.¹ The temperature variation of the KIE is −2.8% and −6.5% without and with tunneling. Although there is still a small temperature variation in the computed KIE, this is almost within the error bar of the experimental results¹ (+1.1 ± 6.2%). The key point we want to emphasize here is not the temperature independence but rather the smallness of the temperature dependence. The small temperature dependence results not from some intrinsically temperature-independent mechanism but rather from a near-cancellation of competing temperature-dependent effects. In such a case, the remaining temperature dependence is hard to predict with high precision, since it has the nature of the difference of two large numbers that accidentally nearly cancel.

TABLE 1.

Calculated Free Energies of Activation (kcal/mol) for H⁻ Transfer, H/D KIEs, and Isotope Effects on the Arrhenius Preexponetial Factor (A_H/A_D)

level	278 K (5 °C)		318 K (45 °C)		change in KIE	AH/AD
	barrier	KIE	barrier	KIE
classical	14.5		16.7
+ quantized vib.	12.2	2.83	14.0	2.81	−0.02	2.7
+ recrossinga	12.3	2.86	14.1	2.78	−0.08	2.3
+ tunnelinga	11.6	3.22	13.5	3.01	−0.21	1.9
experiment		3.54 ± 0.16		3.58 ± 0.15		4.0 ± 1.5

^aAveraged over 20 reaction coordinates.

TABLE 2.

Free Energies of Activation (kcal/mol) for Deuteride Transfer

T (K)	$\mathrm{\Delta }{G}_T^{\text{act}}$
278	12.2
318	14.2

If we had neglected corner-cutting in the tunneling calculations (that is, if we neglect reaction-path curvature in the tunneling calculations), the calculated KIEs would have dropped to 2.78 and 2.73 at 5 and 45 °C, respectively, in poorer agreement with experiment. This zero-curvature calculation corresponds to a temperature dependence of −1.8%.

Table 3 gives the overall ensemble-averaged transmission coefficients, the transmission coefficient components due to recrossing and tunneling, and their standard deviations at 5 and 45 °C for both H and D isotopes. This table shows that including tunneling increases the rate constants by factors of 2.6–3.8, where the light isotope tunnels more than the heavier one. The tunneling transmission coefficients for both isotopes at 45 °C are smaller than those at 5 °C, indicating a reduced relative extent of tunneling when the system temperature is raised, as usual.

TABLE 3.

Calculated Transmission Coefficients^a and their Standard Deviations

level	278 K (5 °C)		318 K(45 °C)
	H	D	H	D
recrossing (Γ)	0.79 [0.27]	0.78 [0.25]	0.85 [0.21]	0.86 [0.17]
tunneling (κ)	3.77 [1.94]	3.48 [1.24]	2.84 [0.73]	2.59 [0.58]
overall (γ)	3.12 [1.89]	2.74 [1.16]	2.48 [0.95]	2.32 [0.62]

^aAveraged over 20 reaction coordinates; standard deviations are given in brackets.

Although special models based on gated motions coupled to low-frequency modes along the reaction coordinate have been proposed³ to interpret temperature-independent KIEs, we note that the present calculations include such effects, as well as vibrationally enhanced tunneling and environmentally coupled tunneling, automatically without special assumptions. Table 3 shows that the transmission coefficients at 45 °C display smaller standard deviations than those at 5 °C, reflecting less fluctuation in the effective barriers at the high temperature, although structural fluctuations of an enzyme are typically expected to increase as the temperature is increased.

A widely used method of inferring the importance of tunneling in experimental results is based on fitting the results to the Arrhenius equation

$$k=Aexp[-E_{\mathrm{a}}/RT]$$ (7)

where A is the Arrhenius preexponential factor, and E_a is the Arrhenius activation energy. Unlike $\mathrm{\Delta }{G}_T^{\text{act}}$, the parameter E_a is a constant. Table 4 reports the Arrhenius parameters obtained from the present calculation, and Table 1 gives the intermediate results for A_H/A_D. The A_H/A_D ratios computed by including quantized vibrations, quantized vibrations plus recrossing, and quantized vibrations with recrossing and tunneling are 2.7, 2.3, and 1.9, respectively. These results qualitatively reproduce the large experimental A_H/A_D ratio (4.0 ± 1.5)¹ that is beyond the so-called semiclassical limit¹⁵ of 1.41 for H/D isotope effects. It is interesting to note that an A_H/A_D ratio outside the range of 0.7–1.3¹⁶ has widely been accepted¹⁷ as an indicator of quantum mechanical tunneling; however, the reliability of using this criterion has recently been questioned by Tautermann and coworkers.¹⁸ Our results show that large A_H/A_D values can be obtained with a moderate amount of tunneling, since the tunneling transmission coefficients are about 3 for the ecDHFR catalyzed hydride transfer over the temperature range being investigated, and Table 1 shows that an even larger A_H/A_D ratio is obtained without considering tunneling contributions than when it is included, which is the typical situation for moderate tunneling.¹⁵

TABLE 4.

Arrhenius Parameters

isotope	A (s−1)	Ea (kcal/mol)
H	702	−1.0
D	372	−0.7
AH/AD; Ea,H–Ea,D	1.9	0.3

An Arrhenius plot of the calculated KIE is shown in Figure 3, where the results for a gas-phase hydrogen transfer reaction¹⁹ with a similar magnitude of the KIE are included for comparison. This illustrates that the KIEs for the nonenzyme reaction display a greater temperature dependence than those of the enzyme system. How does ecDHFR make the KIE less dependent on temperature? Our calculations identify two main contributing factors.

Figure 3.

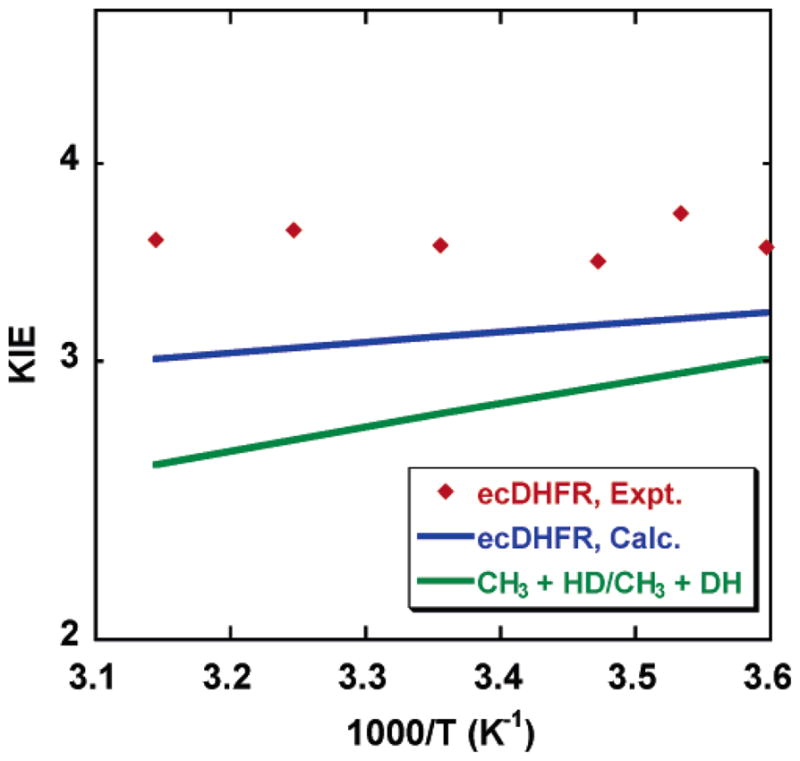
Temperature dependence of KIEs for the ecDHFR-catalyzed and a gas-phase hydrogen transfer reaction with a similar magnitude to that of the KIEs.

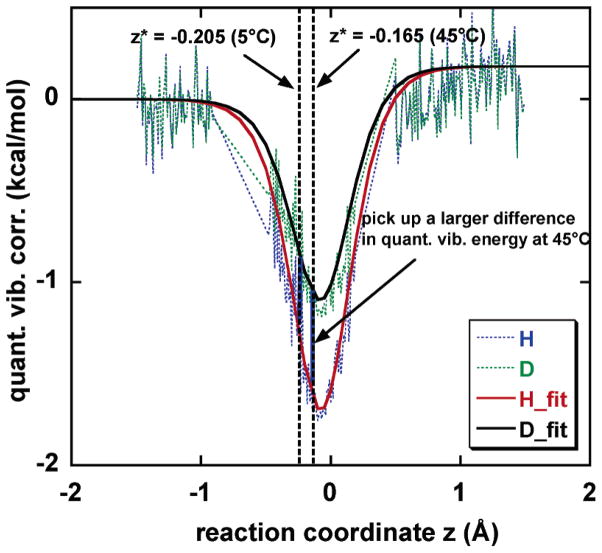
First, we found that there is a significant change in the position along the reaction coordinate of the transition state, affecting the computed KIE as a function of temperature. Figure 4 shows the effect of quantization on the vibrational free energies for hydride and deuteride transfer as functions of z. The H/D KIE depends exponentially on the difference between the H and D curves at their respective transition states, that is, at their respective dynamical bottlenecks. If the position of the transition state were independent of T, the KIE would be expected to decrease with increasing temperature.¹⁷ However, the location of the dynamical bottleneck depends on temperature (Figure 2). In particular, using the quantized PMF (row 2 of Table 1), we find that the transition state is at z = −0.205 Å at 5 °C and at z = −0.165 Å at 45 °C, so that there is greater vibrational free-energy difference at higher temperatures than at lower ones (Figure 4). (Note that, in ref 7, the quantized vibration correction curve along the reaction coordinate was fitted to a fifth-order polynomial, and consequently, the transition state on the quantized PMF was located at z = −0.145 Å at 25 °C. In the present calculation, to monitor the transition state shift more accurately when temperature changes, we use the same methodology as ref 7 except that a more physical approach is adopted to obtain the quantized vibration correction as a function of the reaction coordinate. In particular, we fit the quantized vibration correction curve into an inverted Eckart function (see Figure 4), and this improvement accounts for the numerical difference in the transition-state positions of ref 7 and this work.) The sliding of the transition state toward the product side provides a mechanism for obtaining an invariant KIE or small change in KIE because of a greater isotopic difference in vibrational free energy at the high temperature. At this stage, the KIE is predicted to decrease by 1% over 5–45 °C, whereas if we had used the quantized energy requirement at 5 °C for the 45 °C KIE, it would have decreased by 8%. This kind of change in the transition-state location over a small temperature interval may often be more significant for enzymes than for small molecules, because entropic contributions of the enzyme cooperative motions may change significantly with even a small deviation from physiological temperature.²⁰

Figure 4.

Quantized vibrational energy requirements (relative to the classical ones) at 5 and 45 °C; the transition states, which are the locations of the maxima of $\mathrm{\Delta }{G}_{\text{QC}}^{\text{SRC}}$, are indicated by vertical dotted lines. The results are fit to Eckart functions.

Second, tunneling is sensitive to the shape and barrier height of the mean effective potential along the reaction coordinate, which can be temperature dependent for condensed-phase reactions.^6,21 To illustrate this importance of this effect, in Figure 5, we compare the calculated free-energy profiles along the reaction coordinate of the ecDHFR-catalyzed hydride transfer at 5 and 45 °C with those of the hydrogen transfer reaction between CH₃ and H₂ in the gas phase.19 In Figure 5, all free-energy barriers are normalized at the barrier top so that one can easily monitor differences in the barrier shape as temperature changes. For the gas-phase reaction of CH₃ + H₂, the free-energy profile retains its shape from 5 to 45 °C; in fact, our calculation indicated that the free energy of activation profile, normalized at the top, does not change enough with temperature for the change to be visible in the plot, and the position of the dynamical bottleneck does not move over 5–45 °C for this reaction, in contrast to the large transition-state shift that has been observed for the ecDHFR-catalyzed hydride transfer in the present study. Remarkably, as shown in Figure 5, the ecDHFR system displays significant changes in the free-energy barrier shape over the 5–45 °C temperature range, which is quite different behavior from the gas-phase reactive system. Typically, tunneling becomes relatively less important at higher temperatures where overbarrier processes can compete better. If the barrier becomes more amenable to tunneling as T is raised, this shape effect can cancel part of the usual²² temperature dependence of the tunneling transmission coefficient. To reveal the effect of the change in barrier shape with T, we simulated an imaginary tunneling experiment (denoted by T_A/T_B) where the enzymatic system is allowed to tunnel at one temperature (T_A) through an effective barrier that is determined from the simulation carried out in another temperature (T_B). The 5/45 system tunnels more than the 5/5 system, suggesting that the effective barrier determined at 45 °C has a thinner shape, which is consistent with the finding in the classical PMF simulation. Table 5 gives the ensemble-averaged tunneling transmission coefficients obtained from one of these imaginary systems compared to the results of consistent tunneling calculations. If a T-independent barrier model is used with the 45 °C barrier, the tunneling contribution to the KIE decreases 5% over the 5–45 °C interval. However, the effect is only 3% when each calculation is carried out with its appropriate barriers.

Figure 5.

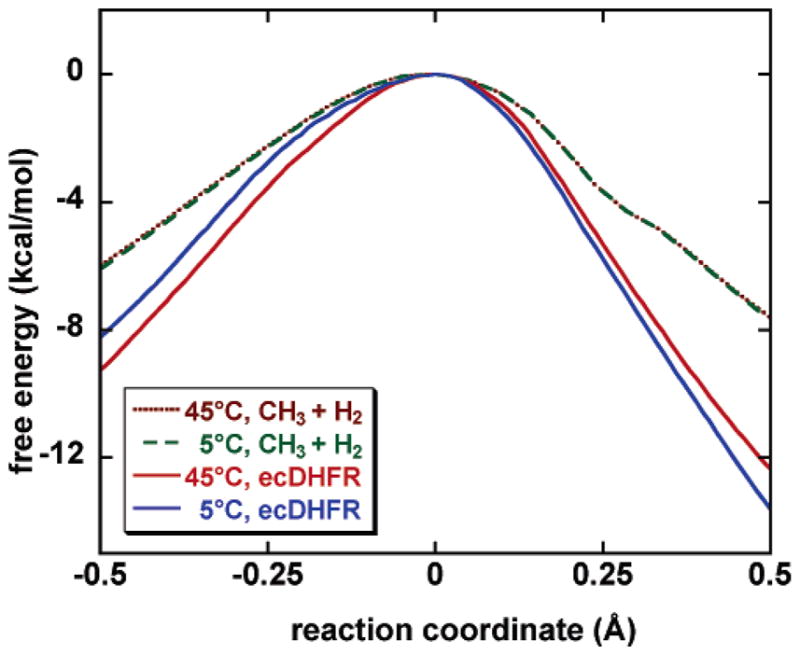
Computed free-energy profiles (with quantized vibration contributions included) along the reaction coordinate for the ecDHFR catalyzed reaction at 5 and 45 °C. The same profiles for the gas-phase hydrogen transfer reaction of CH₃ + H₂ are shown for comparison, where the reaction coordinate is distance along the mass-scaled minimum-energy path (scaled to mass of 1 amu). All curves have been normalized at the top to emphasize the difference in the barrier shape as temperature changes.

TABLE 5.

Tunneling Transmission Coefficients (κ’s) and KIEs for Systems to Tunnel through Different Effective Potential Barriers

TA/TB	κH	κD	KIE
45/45	2.85	2.71	1.05
5/45	4.13	3.77	1.10
5/5	3.77	3.48	1.08

Another interesting aspect of the present results is the temperature dependence of the rate constant itself. For H⁻ transfer, the calculated rate constant decreases from 4.4 × 10³ s⁻¹ at 5 °C to 3.5 × 10³ s⁻¹ at 45 °C; this small decrease is associated with a negative activation energy, as shown in Table 4. Thus, E_a is 14 kcal/mol lower than $\mathrm{\Delta }{G}_T^{\text{act}}$, a surprisingly large difference. A surprisingly small E_a was recently found4 experimentally for the similar hydride transfer catalyzed by thymidylate synthase. In fact, the temperature dependence of the rate constant has been measured²³ for ecDHFR, and the rate was found to have a small but non-monotonic dependence on temperature, increasing by a factor of 2.1 from 15 to 35 °C, then decreasing by a factor of 1.4 from 35 to 45 °C. Reference 1 also mentioned an initial velocity measurement of the hydride transfer step of ecDHFR at pH 9 (where hydride transfer is more rate-limiting) that yields a phenomenological E_a of 3.7 ± 0.3 kcal/mol (see ref 25 of ref 1). Thus, our calculation agrees qualitatively with experiment in that the T dependence is unexpectedly small or unexpectedly negative for a reaction with such a large free energy of activation.

In summary, two features have been identified that may reduce the temperature dependence of KIEs for enzymatic reactions as compared to small-molecule reactions, namely (1) variation of the transition-state position and (2) temperature dependence of the effective potential barrier for tunneling. An EA-VTST/MT calculation including these effects predicts a KIE that changes by only 6.5% over the 5–45 °C interval for the hydride transfer catalyzed by ecDHFR, which is only slightly larger than the experimental uncertainty on the KIE. Without these two mechanisms, it would have decreased by 16%. Our calculations reproduce the nonclassical isotope effect found experimentally for the Arrhenius preexponential factors. Furthermore, we find larger fluctuations in the tunneling ensemble at 5 °C than at 45 °C, and we find an Arrhenius activation energy about 14 kcal/mol lower than the free energy of activation.