Light scattering study of the normal human eye lens: Elastic properties and age dependence

Abstract

The human ocular lens is a tissue capable of changing its shape to dynamically adjust the optical power of the eye, a function known as accommodation, which gradually declines with age. This capability is the response of the lens tissue to external forces which, in turn, is modulated by the biomechanical characteristics of lens tissues. In order to investigate the contributions of lens sclerosis to loss of accommodation, we report on in vitro confocal Brillouin light scattering studies of human ocular lenses spanning over a 30-70 year age range. Using this non-destructive measurement method, we determined that the longitudinal bulk modulus (average ± SD) of the lens nucleus (2.79±0.14 GPa) was consistently greater than the bulk modulus of the lens cortex (2.36±0.09 GPa). Moreover, our results showed that these differences were not age dependent over the 40 year age range that we evaluated using healthy lens tissues. Our results are consistent with the hypothesis that an age-dependent change in the bulk modulus of lens tissues does not fully account for the natural decline of accommodation.

I. Introduction

The young human eye can adjust its focal power so that images of both distant and near objects can be focused on the retina—a process known as accommodation. During accommodation, changes in the focal power of the lens result from changes in the shape of the crystalline lens [1]. The material properties of the lens are an important factor that determines the responsiveness of this tissue to the external forces that reshape the lens during lenticular accommodation. Understanding the material properties of the lens, their correspondence with the known anatomical structure and how these material properties change with age is critical for understanding the forces required to alter the shape of the lens, the mechanism of accommodation and its age-related decline. The objectives of the current study were to evaluate regional differences in the material properties of the human lens ex-vivo using a non-destructive test method — Brillouin light scattering (BLS) — and to determine if there are any measureable age dependent changes using this technique.

The lens is a biconvex spheroidal tissue encapsulated within an elastic collagenous outer membrane of varying thickness [2], [3]. During accommodation, external forces are translated to the internal mass of the lens tissue through the lens capsule. This causes the lens to thicken in its anterior-posterior dimension and asymmetrically steepens the curvature of the external surfaces.

Lens tissue is formed by lens fiber cells, which are highly differentiated epithelial cells containing few organelles, no cell nucleus and a relatively high proportion of specialized cytoplasmic proteins (∼65% water and ∼35% protein) [4]. Because of its high water content, the Poisson ratio ν, of the lens is ∼0.5 [5]. The body of the lens is comprised of several structurally distinct regions that may be generally divided into an inner nucleus and outer cortex. Lens fibers continue to grow throughout life, adding volume to the lens cortex [6]. The nucleus is developmentally older than the cortex and, although it is formed by the same lens epithelial fibers, the nucleus lacks the visibly distinct lamellar organization of lens fibers seen in the cortex [7] and it does not increase in thickness with age [6]. These morphological and ultrastructural differences may confer different material properties to each region of this tissue that may also differ by age [7]. With increasing age, the ability to accommodate to near targets gradually diminishes resulting in the need for reading glasses or bifocals by the age of 45 years—a condition known as presbyopia. The mechanisms underlying presbyopia are equivocal. Helmholtz's theory states that a stiffening of the crystalline lens is responsible, although differences between the central nucleus and outer cortex of the lens and their separate roles in relation to presbyopia have not yet been fully addressed. A non-invasive technique capable of probing the elastic properties of different segments of the lens would be especially valuable in identifying contributions to the lens deformations and their evolution with age.

Here we report on the application of Brillouin scattering to probe the axial spatial variation (or gradient) of the lens's mechanical properties. Brillouin light scattering (BLS) is the inelastic scattering of light waves caused by interactions of the electric field of the light with acoustic modes of materials. The expansions and contractions created in the material by propagating acoustic waves result in spatial and temporal modulations of the material density. The resulting time dependent changes in the electromagnetic characteristics, such as the refractive index of the material, underlie the coupling of the light to the acoustic modes. Conversely, the electric field of an incident light wave can induce spatially varying and temporally periodic elastic strains and initiate acoustic waves in materials. The corresponding loss of energy from the light wave to the material results in a down shift of the photon frequency (Stokes scattering), while the transfer of energy from existing acoustic waves in a material to the incident light wave results in a light frequency upshift (anti-Stokes scattering). These transfers of energy result in modulations of the scattered light wave with discrete sum (anti-Stokes) and difference (Stokes) frequencies impressed upon the frequency of the incident light wave, leading to the characteristic Brillouin doublets evident in the spectra presented below. The downward and upward shifts in the light frequencies correspond to the creation and annihilation of discrete acoustic vibrations (phonons) with resulting Brillouin scattering conforming to the conservation of total energy and momentum. Since, for well defined acoustic waves to propagate, there must exist appreciable coupling of neighboring atoms and/or other structural elements (i.e. mechanical properties) of the material, detection of these acoustic waves by a technique such as BLS, provides direct access to its elastic properties.

The low energies of acoustic vibrations in materials, compared to light waves, are related to their relative propagation speeds. This ratio is typically 10^-5. Since the 514.5 nm laser light utilized in this study has a frequency of about 10¹⁴ Hz (100 THz), the frequency shifts of the incident light produced by the photon-acoustic wave interactions is of the order of 10⁹ Hz (GHz). Such small frequency shifts from the incident light, requires a means to isolate and analyze the Brillouin scattered signal against a strong background of elastically scattered laser light. This requires a high-resolution dispersive unit such as Fabry-Perot interferometers with high light throughput and superior extinction (contrast) characteristics. The multi-pass tandem interferometer system utilized in this study provides these features with a contrast ratio of over 10¹⁰.

Brillouin scattering is distinct from other types of light scattering phenomena. In Raman scattering, while formally identical to Brillouin scattering, the energy transfer between the light and the material often involve vibrational modes (optic phonons) of the material. These are excitations that lie in the terahertz range, and are distinct from their acoustic mode counterparts. In contrast, photoacoustic spectroscopy requires a laser source that thermally excites acoustic waves in the material which are subsequently detected by a sensitive acoustic transducer. Fluorescence spectroscopy involves the interchange of energy between light and electronic energy levels of the material.

There are numerous advantages of Brillouin scattering, especially from biological tissues. Since the acoustic waves in a BLS measurement are induced at ambient temperature without the need for external transducers, this non-contact, non-destructive confocal technique is especially suited to investigate the biomechanical properties of the lens. In addition to not requiring any special tissue preparation, strong Brillouin spectral features are acquired within seconds and with low laser power levels that when refined, may be suitable for use in vivo. Most previously reported methods of measuring the elastic properties of the lens are either destructive [4], [8], [9], or at least disruptive [10] of the normal lens structure. Thus the BLS technique has numerous advantages over other techniques for determining the regional material properties of the lens.

The Brillouin light scattering technique has been applied to many conventional condensed matter systems [11], heterostructures [12] and to monitor the pressure dependence of compressional acoustic modes supported in solutions [13]. The high precision of the method is evident in its application to supported films [14] and free standing, 100 nm thick, membranes [15] to non-destructively measure the sound velocity, and hence the elastic properties of these ultrathin systems. It has also been successfully applied to completely characterize the elastic properties of highly anisotropic laminar structures [16].

In general, the propagation speed U of a longitudinal acoustic wave in a viscoelastic medium of density ρ is given by $U^2=\frac{(K+\frac{4}{3}G)}{\rho }$ where the medium is determined by a combination of the bulk modulus (K) and shear modulus (G). In the case of the eye lens, G is much smaller than K, and thus the variation of the bulk modulus with depth is determined by the expression K = U²ρ. In Brillouin scattering, the speed of the acoustic wave is given by U = λf/2n where λ = 514.5 nm is the illumination laser wavelength, f is the average of the backscattered Stokes and Anti-Stokes Brillouin frequency shifts, and n the refractive index of the lens. Thus the spatial variation of the bulk modulus K = ρλ²f²/4n² is directly obtained from the measured Brillouin shift f, and knowledge of n and ρ as the incident laser beam probes different positions within the lens.

The precision and accuracy with which Brillouin scattering has been successfully applied to determine all of the independent elastic constants of highly anisotropic [16] materials can, in general, be also applicable to biological tissues. In the case of the eye lens however, the very low values for its shear modulus that arise from its large water content, would make a complete characterization of the elastic properties by this method difficult. For instance a G = 10² kPa, would yield Brillouin frequencies of the order of megahertz which is below the range accessible with our interferometer system. Instead the method offers excellent opportunities to fully characterize the compressional moduli, and thus to evaluate their role in reshaping the lens during accommodation. This study takes advantage of the high spatial resolution, non-invasive and non-destructive features offered by Brillouin scattering to probe the spatial gradients of the longitudinal bulk modulus within the lens and its age dependence.

II. Materials and Methods

Fig. 1 illustrates schematically the backscattering geometry and the holder for the eye lens under study. Fresh and otherwise healthy human crystalline lenses were provided by the Ohio Lions Eye Bank, Columbus, Ohio already placed in a storage media consisting of a balanced salt solution with an osmolarity similar to that of the aqueous humor (290 millimoles) of the following composition (in g/l): NaCl 8.0, KCl 0.4, Na₂HPO₄ 0.1, glucose 1.0, Hepes 2.38, and buffered with 8 ml of 0.5 M NaOH to a pH of 7.4. The lenses were obtained at most 3 days postmortem, and stored in solution at a temperature below 60°F. A total of 29 lenses from 22 subjects spanning an age range of 30-70 years were used. The lenses evaluated had intact capsules, were not diseased, and the lens tissue from these eyes had no clinically visible signs of cataract. No lenses within intact enucleated eyes were studied.

Fig 1.

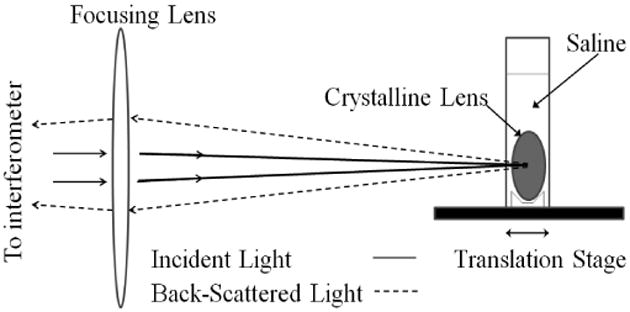
Schematic diagram of the backscattering geometry for measurements from the eye lens placed within a holder containing 0.9% saline solution. The holder, mounted on a programmable linear translation stage, enables the lens to be translated parallel to the optic axis for consecutive measurements with high precision.

The Brillouin measurements were performed along the central axis through the geometric center of the lens, with the reflected laser beam traveling along the backscattered path that overlapped with the incident beam as illustrated in Fig.1. Spectra were recorded with 2 - 10 mW of λ = 514.5 nm laser radiation focused to spot of about 35 to 50 microns in diameter. The lenses were placed in a custom made square holder containing 0.9 % saline solution. In order to conveniently maintain normal incidence of the incoming laser light to the lens tissue, no measurements were made along the lateral dimension as that would be sensitive to the equatorial curvature of the lens.

Spectra were measured as a function of depth within the lens in 25 ± 1 μm step sizes, starting from the anterior surface, proceeding through the lens tissue, and ending at the posterior surface. As schematically illustrated in Fig. 2, the scattered radiation was dispersed by a 6-pass tandem Fabry-Perot interferometer (JRS Scientific Tandem Fabry-Perot Interferometer TFP-1) with 450 μm entrance pinhole that determines the axial spatial resolution of the measurement. Further reduction of the pinhole size to 150 μm did not improve the axial spatial resolution that we estimated as 100 μm. For a lateral spot size of 35 to 50 μm in diameter, we had a total probe volume between 4 to 8 × 10^-4 mm³ for our measurements. The lower limit for the frequency measurement for our interferometer system was 1 GHz. A baseline measurement was first recorded with saline in the holder prior to recording spectra from the lens. Each scan was integrated for 20-100 seconds depending upon the depth of the probe region within the lens, for an average total time of 35 minutes. Data acquisition times as low as five seconds were possible, without overly compromising the accuracy of the results. On average approximately 60 scans were taken with each lens to characterize a single complete depth profile starting from the anterior and moving toward the posterior pole of the lens. Often the measurements were repeated from the same lens to ensure reproducibility of the Brillouin data, with no significant differences observed between the different sets of measurements. The Brillouin doublets for each scan were fitted by Gaussian profiles and the average of the two peak frequencies were taken.

Fig 2.

Schematic of the experimental setup showing tandem Fabry-Perot interferometer (FP), eye lens in holder sample (S) and various optical components (L: Lens, M: Mirror). The sample is placed on a linear translation stage at a location where the focal spot of the incident light is confocal to the entrance pinhole P of the FP. The translation stage enables sampling desired positions within the lens while maintaining the confocal arrangement.

III. Experimental Results

Fig. 3 illustrates the scattering configuration in relation to the lens and representative Brillouin spectra recorded from different segments of the lens. The right panel shows typical Brillouin modes in the outer (cortex) section of a 31 year old lens at 7.8 GHz. This mode is identified as the longitudinal acoustic phonon of the local region being studied; the corresponding transverse mode is not evident due to the low value of the shear modulus. Also, the thickness of the lens as determined from the Brillouin data at the front and posterior of the lens is in agreement with the value of 3.5 mm obtained from direct measurement, where the lens was viewed against a ruler scale after the Brillouin measurements were made further confirming that the source of the Brillouin scattering was coincident with the anatomical boundaries of the lens. From the work of Brown and others the anterior to posterior thickness of the lens for a 29 year old is apporoximately 3.75 mm [17], [18], [19]. Our observations for the maximum Brillouin frequency at 9.0 GHz (2.2 mm deep to the anterior lens surface), agree with estimates of Brown for the location of the lens nucleus (0.68 mm to 3.28 mm deep) to the anterior pole of the lens, left panel Fig. 3). Upon moving the focus of the probe laser further within the lens (3.3 mm), the spectra demonstrate a shift that corresponds well with Brown's expected location of the transition from the nucleus to the posterior cortex. The spectra shown in Fig. 3 were typical for the lenses evaluated. The axial location of the spectral shift between the nucleus and cortex differed between samples and the thickness of the anatomical regions corresponded with age of the sample. Of particular interest as discussed in detail below, are the distinct frequencies in the cortex and nucleus as well as the doublet structure evident in the cortex-nucleus transition region (center panel Fig. 3).

Fig 3.

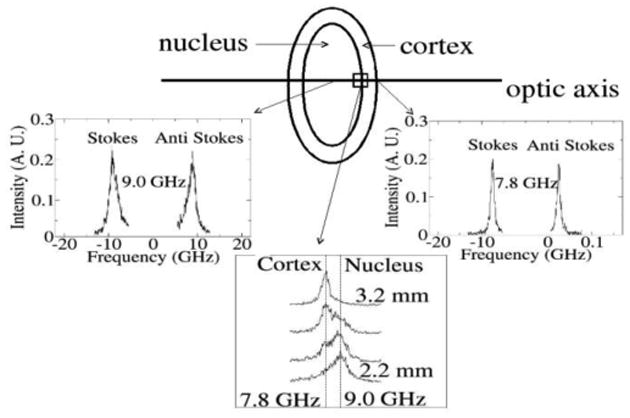
Representative Brillouin spectra from different sections of the right (OD) lens from a 31 year old measured along the primary optic axis showing characteristic Stokes, anti-Stokes Brillouin doublet. The modes are associated with the longitudinal acoustic phonon of the tissue. In addition to spectra from the cortex (right panel) and nucleus (left panel), modes in the vicinity of the nucleus-cortex interface are shown. As the transition is made out of the nucleus into the cortex, (curves 2.2 mm to 3.2 mm center panel), two distinct peaks are evident whose spectral weight gradually makes a transition from high frequency (nucleus) to low frequency (cortex).

The mode frequencies, which are directly dependent on the elastic properties of the lens, provide a map of the bulk modulus of the lens. A compilation of a sequence of Brillouin spectra from a 41 year old lens is illustrated in Fig. 4 and shows the transformations of the mode within the lens. Fig. 5 summarizes the Brillouin frequencies for the cortex and nucleus for the entire age range of lenses investigated. Two features are clearly evident. First, the frequency of the longitudinal acoustic phonon within the cortex is lower than the corresponding mode in the nucleus for all age groups. The average frequency of 7.85 GHz (cortex) and 8.80 GHz (nucleus) over the entire age range had standard deviations of 0.14 GHz and 0.22 GHz respectively. This variation within the nucleus and cortex may be attributed to real variations observed within the population studied, e.g. biological variability, as well as experimental sources of error. Despite our efforts to control them, the precision of axial and lateral alignment, the possible degeneration of tissue condition between the time of collection and our experiments, and other factors may also have contributed to our observations. Second, there is little variation in the magnitude of each frequency over the entire age range, a behavior consistent with the absence of change in the bulk modulus of the cortex and nucleus of the lenses over an age span of four decades. The observed frequency shift in the lens cortex was unrelated to age (slope = −0.005 GHz/year, 95% CI = −0.012 to +0.002; P = 0.18). Likewise, the observed frequency shift in the lens nucleus was unrelated to age (slope = −0.001 GHz/year; 95% CI = −0.006 to +0.004; P = 0.62).

Fig 4.

Sequence of Brillouin light scattering spectra recorded from the eye lens of a 41 year old man. From bottom (anterior) to top (posterior), the Stokes/anti-Stokes doublet represent scans recorded along the primary axis in incremental steps of 0.100 mm. The modes progressively increase from 7.80 GHz in the cortex to 8.90 GHz in the nucleus and then steadily recover back to 7.80 GHz when transitioned to the posterior of the lens. The uncertainty of the frequency measurements is ±0.05 GHz.

Fig 5.

Age dependence of the longitudinal acoustic phonon frequency in the cortex and nucleus of the lens. For all ages, the frequency of the acoustic mode associated in the cortex is always smaller than the corresponding mode in the nucleus. The lines correspond to the average frequency, 7.85 GHz (cortex) and 8.80 GHz (nucleus), values of the data set. The standard deviation from the average is 0.14 GHz (cortex), and 0.22 GHz (nucleus).

The variation of the bulk modulus (K) within the nucleus and cortex may be calculated from the dependence of the frequency shift on the probe spot within the lens. The refractive index for human lenses was taken as n = 1.42 for the nucleus, and 1.37 for the cortex [20]. Bulk moduli were calculated from the mode frequency f, where the density ρ for the lens was taken to be approximately 1,085 kg/m³. The results are presented in Fig. 6. For all ages, the bulk modulus in the cortex is always smaller than the corresponding modulus in the nucleus. The average bulk modulus is 2.36 GPa (cortex) and 2.79 GPa (nucleus) with standard deviations of 0.09 GPa and 0.14 GPa respectively.

Fig 6.

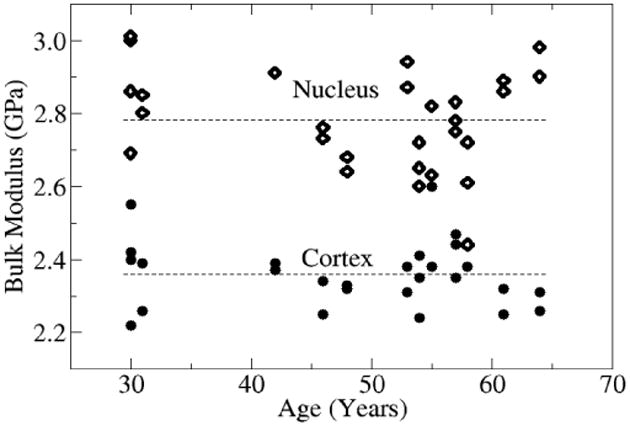
Age dependence of the bulk modulus in the cortex and nucleus of the lens. For all ages, the bulk modulus in the cortex was always smaller than the corresponding modulus in the nucleus. The modulus is determined from the phonon frequencies of Fig. 5. The lines correspond to the average bulk modulus values 2.36 GPa (cortex) and 2.79 GPa (nucleus) of the data set. The standard deviation from the average is 0.09 GPa (cortex), and 0.14 GPa (nucleus).

IV. Discussion

Our results demonstrate a depth dependent regional variation in the bulk modulus of the ocular lens tissue with an average value for the cortex lying below that of the nucleus. These results agree with the bulk moduli calculated from the data of Vaughan and Randall [21], who were the first to use BLS to deduce the longitudinal bulk modulus of the crystalline lens, but did not evaluate the age or depth dependent spatial variation of these moduli. The regional variation in the bulk modulus that we found are consistent with what others have reported—that the cortex modulus is less than the nucleus modulus [22], [23], [24]. In a re-analysis of Fishers original estimates [4] of the Elastic moduli for the lens cortex and nucleus, Burd and colleagues [23] argue that the original analysis of data collected by Fisher was flawed and that the correct interpretation of this data suggests a greater Young's modulus (E) for the lens nucleus than the outer cortex, which is in agreement with our results. We also find no age dependence for the bulk modulus in either the cortex or nuclear lens tissues. Hence our findings are consistent with the hypothesis that the underlying cause for presbyopia is not due to changes in the bulk modulus of the lens with age. Beers and van der Heijde evaluated the velocity of ultrasound propagation in lens tissue. This tissue velocity is governed by the same principles as BLS and is dependent upon Young's modulus and material density. As in our results, they found no age dependent change in ultrasound velocity in healthy lens tissues [25]. Our findings on the differences between the cortex and nuclear bulk modulus lend additional support to the work of others who have used different techniques to show that the lens and its material properties cannot be accurately modeled as a simple or homogenous structural entity [2], [10], [23], [25], [26].

Irrespective of these results, understanding the age-related decline in accommodation may be more complicated than simply knowing the mechanical properties of the lens tissues. For example, some have argued that hardening of the lens nucleus can explain presbyopia [26]. Koopmans and colleagues have demonstrated that replacement of lens tissues with softer deformable gel materials results in a decreased amplitude of accommodation in adolescent monkeys, in-vivo. Others have suggested that a decline in the elasticity of the lens capsule or that reduced zonular tension with age-related increased lens mass may contribute to presbyopia. It is possible that several of these factors may conspire to reduce accommodation in middle age. For instance, in spite of the lack of changes to the bulk modulus with age, changes to the shear modulus of the lens that we were unable to measure through Brillouin light scattering could contribute to presbyopia.

The Brillouin light scattering technique offers a number of advantages over previously employed indentation and micro bubble techniques [8], [9], [14], which are destructive or at least disruptive to the anatomical structure of the lens tissue. BLS is a non-destructive probe of the elastic properties of the crystalline lens over a microscopic volume (4 to 8 × 10^-4 mm³), a scale over which the properties of these tissues are thought to vary [22]. By comparison the micro-indentation techniques of Heys and colleagues used a 0.5 mm cylindrical indenter that probed the lens tissue at a depth of 0.5 mm and therefore had a sample volume of approximately 0.4 mm³, nearly 1000 times the sample volume of our method. The BLS technique has also recently been successfully used to evaluate the lens of the mouse eye [27]. Additional work is needed to evaluate the shear modulus of the lens, the role of visco-elastic properties of the biological tissue and the biomechanical characteristics of the lens capsule by BLS. Further development and refinements of this technique may permit the evaluation of biomechanical characteristics of these and other ocular tissues in-vivo.

The recent work of Weeber et al. [9] and Heys et al. [8], shows a “massive increase” in lens shear modulus with age, from frozen, non-fresh tissue samples. These mechanical probes reveal a shear modulus gradient across the lens. Weeber et al. found shear moduli values in the 1 - 100 kPa range with the shear modulus of both the center (nucleus) and periphery (cortex) increasing by a factor of 10⁴ and 10² respectively over the measured age range. These results reveal a cross-over around 45 – 50 years where the youngest lenses had a minimum central shear modulus, to older lenses having a maximum [9]. It is noted that the consequence of freezing the specimen and subsequent sectioning on the measured moduli remain unknown [29]. Studies using differing techniques have yielded mixed results ranging from only limited increases in lens stiffness before the age where accommodation is lost [28], [30], [31], [32], to a “massive increase” in nuclear stiffness [8], [9].

It is difficult to compare published experimental results because of the wide variety of experimental approaches: some were not conducted on human eyes, were performed on donor tissues, or were based on assumptions of mathematical modeling. The increase in lens stiffness as a function of age reported by some studies is exponential, contrary to the linear age-related decline of accommodation that is observed clinically. Likewise, the major increases in lens stiffness occur beyond the age of 50 years, long after the majority of accommodative function is lost [5].

We note that the term “stiffness” has been widely used in the context of the eye lens and subject to broad interpretation. It is therefore important that measured parameters are precisely identified within the framework of terminology of elasticity theory such as stiffness, hardness, as well as shear (G), bulk (K) and Young's (E) modulus used to characterize tissue mechanics. Moreover, elastic modulus and elasticity are often utilized inappropriately for the Young's modulus E. The various moduli can, in principle, be compared through relations amongst the different elastic constants. For instance in an isotropic system, the bulk modulus K is related to the shear modulus G and Poisson ratio ν through the equation, $K=\frac{2G(1+\nu )}{3(1-2\nu )}$. In the case of a highly hydrated tissue which can be characterized as incompressible (i.e. ν∼ 0.5), it follows that the bulk modulus can be very large while the shear modulus (G) remains small. It is thus not unusual for the human eye lens to have shear modulus values G ∼ 10² – 10³ Pa, while bulk moduli are in the giga-pascal (i.e. K ∼ 10⁹ Pa) range, as found in this study. The term stiffness has often been identified with the shear modulus. For instance, in the study of Heys et al. [8], the local stiffness of the lens was related to G based on an assumed a linear relationship between the applied force and shear modulus.

In light of a growing body of evidence the loss of elasticity of the surrounding capsule and the lens matrix must be considered as a, if not the, major factor in the loss of accommodation. Fisher indicates that the ability of the capsule to mould the lens wanes as we get older [33]. Thus, depending on the compliancy of the lens matrix to the moulding pressure of the capsule, the decline in near focusing ability with age could be associated with the decline in the ability of the lens system to both apply moulding pressure and to respond to this pressure. As noted above, as in the case of water, supporting no shear with a finite (2.2 GPa) bulk modulus, a hydrated tissue like the lens nucleus with 64% water by weight and cortex (69%) [34] could have widely differing shear and compressive moduli. The high protein content of the lens tissue leads, as observed in our study, to a substantial shift of the longitudinal acoustic phonon frequency from that of water. This behavior is consistent with a lens structure of concentric layers of closely apposed fiber cells that forms a complex protein gel with an overall protein content that is about one-third of the lens mass. Light and electron microscopy studies of the lens structure [35] reveal numerous interdigitations between lens fibers that presumably stabilize the lens mass, resist deformation during accommodation and help account for the low shear modulus that would be consistent with our study. Our approach yields a description of the local constitutive compressional properties of the lens fibers.

One approach to the analysis of the biomechanical characteristics of the lens is the use of finite element modeling [36], [37]. The success of this approach depends largely upon accurate estimates of the elemental properties of the lens material as well as correct characterization of how the gross structure of the lens is derived from organization and interaction of these individual elements. Our results not only provide an estimate of the elemental physical characteristics of the lens material, but suggest a plausible explanation for how these observed physical characteristics may be reconciled with the known anatomical structure of the lens. Our results show that on a microscopic level, the lens material is relatively incompressible, a hydraulic characteristic that is desirable for translating forces efficiently and effectively. This further suggests an important role for the interaction of the individual lens fibers and the shear forces generated between them during accommodation. Characterization of these forces will require a different approach.

As described above, our computation of the bulk modulus of the lens depends directly upon the sample density and inversely upon the index of refraction. By this expression, either a decrease in tissue density or an increase in the index of refraction of the sample would lead to a corresponding decrease in the calculated bulk modulus (K). Our current methods do not account for the effects of viscoelasticity or the influence of anisotropic structure, which is known to exist in biological tissues. Age associated lens changes such as an increase in insoluble protein fraction or a change in the index gradient [38], [39], [40], [41], would lead to offsetting effects on our calculated bulk modulus that would proportionally favor the influence of an increasing index of refraction and thus a lower calculated bulk modulus of older eyes. However, a recent study concluded that age dependence of the central refractive index, showed no statistical significance [42]. It should be emphasized that all of the lenses evaluated in this study were from normal eyes that showed no evidence of clinically defined cataracts. Additional experiments with lenses from older eyes and from eyes with cataracts are needed to understand how our observations would differ with the onset of age associated nuclear sclerosis or disruption of the normal lens morphology that occurs with cataracts.

At present we are witnessing development of additional treatments for presbyopia. For example, the lens capsule could be refilled with biocompatible and optically suitable clear gel creating a new physiological lens in situ [43]. The arrest or reversal of age related hardening of the lens cortex is a theory being pursued aggressively by a number of groups [44]. An alternative approach is to pharmacologically manipulate lens elasticity [45], [46]. While such surgical or pharmacological alterations of lens elasticity can be assessed by measuring a patient's amplitude of accommodation, a non-invasive objective measurement of lens elasticity would be beneficial. When suitably modified, the light scattering approach presented here, could offer a means of quantifying the age-associated biomechanical properties of the lens.

V. Conclusion

In conclusion, Brillouin light scattering studies were conducted to determine the variation of the bulk modulus within the human crystalline lens and to determine if this variation depended on age. Spectra recorded from the anterior through the posterior of the lens revealed that the nucleus was characterized by a higher longitudinal acoustic phonon frequency, and thus bulk modulus, than the surrounding cortex for all ages. Moreover, there was little variation in these longitudinal elastic properties over four decades. These findings contrast recent results based on dynamic mechanical probes that reveal the shear modulus of frozen lens specimens to increase exponentially with age. Our results are consistent with the hypothesis that an age-dependent change in the bulk modulus of lens tissues does not fully account for the natural decline of accommodation. The non-invasive feature of the BLS technique has the potential to provide a detailed in-vivo measure of the bulk modulus of the lens measured through the cornea and aqueous humor.

Biographies

Sheldon T. Bailey received B.S. degree in physics from Penn State University, The Behrend Campus, Erie, Pennsylvania, USA, in 2005. He is now pursuing a Ph.D. in physics at The Ohio State University, Columbus, Ohio.

Michael D. Twa received the B.A. degree in biology from The University of California, San Diego in 1986 and the O.D. degree in physiological optics and optometry from the University of California at Berkeley in 1990. He received the M.S. degree in 2002 and Ph.D. in 2006 in vision science from The Ohio State University.

He was a Senior Optometrist and Clinical Instructor of Ophthalmology at the University of California, San Diego and later appointed as a Research Assistant Professor at The Ohio State University. He is now an Assistant Professor at the University of Houston College of Optometry where his research interests include biomedical imaging and tissue biomechanics. Dr. Twa is a Fellow of the American Academy of Optometry and member of the Association for Research and Vision in Ophthalmology.

Jared C. Gump recieved his BS in Physics from West Virginia University in 1996 and his PhD from The Ohio State University in 2002. His graduate work focused on Brillouin scattering studies of chalgogenide glasses and the human lens. Currently Dr. Gump is a researcher at the Indian Head Division of the Naval Surface Warfare Center where he explores the properties of energetic materials. His research includes high-pressure and temperature studies using x-ray diffraction and time-resolved spectroscopy.

Manoj Venkiteshwar received the B.S. degree in optometry from the Birla Institute of Technology and Science, Pilani, India in 1999. He was awarded the M.S. degree in 2001 and Ph.D. in 2006 in vision science from The Ohio State University. He is currently the Manager of Medical Affairs at Alcon Research in Texas (since 2009). His research interests include accommodation and presbyopia management, and visual performance testing.

Mark A. Bullimore, MCOptom, PhD, FAAO is a Professor at The Ohio State University College of Optometry where he teaches a number of courses, including ophthalmic optics. He received his Optometry degree and PhD in Vision Science from Aston University in Birmingham, England in 1984 and 1987 respectively. Prior to joining the faculty at OSU, he spent 8 years at the University of California at Berkeley. His research interests include myopia, low vision, presbyopia, and refractive surgery.

He is the Development Director and former President of the American Optometric Foundation, a philanthropic organization devoted to the advancement of optometric education and research. He is the former Editor of Optometry and Vision Science, the Journal of the American Academy of Optometry. He served a four-year term on the U.S. Food and Drug Administration's Ophthalmic Devices Panel and is a consultant to a number of ophthalmic, surgical, and pharmaceutical companies.

Ratnasingham Sooryakumar received the M.S. and Ph.D. degrees in Physics from the University of Illinois, Champaign-Urbana in 1976 and 1980 respectively. Following his Ph.D. degree, he was the recipient of an Alexander von Humboldt Fellowship to conduct research at the Max Planck Institute in Stuttgart, Germany where he remained until 1983. After spending a year at AT&T Bell Laboratories, in Holmdel, New Jersey, USA, he joined department of Physics at The Ohio State University in 1984 where he is currently a Professor of Physics. Dr. Sooryakumar's research interests have largely been in the application of Raman and Brillouin scattering to probe the electronic, magnetic and elastic properties of a broad class of condensed matter systems. In addition, his current research activities include development of mobile magnetic tweezers for biological and engineering applications at the micro and nano-scales.