Kinetics of protein-ligand unbinding via smoothed potential molecular dynamics simulations

Abstract

Drug discovery is expensive and high-risk. Its main reasons of failure are lack of efficacy and toxicity of a drug candidate. Binding affinity for the biological target has been usually considered one of the most relevant figures of merit to judge a drug candidate along with bioavailability, selectivity and metabolic properties, which could depend on off-target interactions. Nevertheless, affinity does not always satisfactorily correlate with in vivo drug efficacy. It is indeed becoming increasingly evident that the time a drug spends in contact with its target (aka residence time) can be a more reliable figure of merit. Experimental kinetic measurements are operatively limited by the cost and the time needed to synthesize compounds to be tested, to express and purify the target, and to setup the assays. We present here a simple and efficient molecular-dynamics-based computational approach to prioritize compounds according to their residence time. We devised a multiple-replica scaled molecular dynamics protocol with suitably defined harmonic restraints to accelerate the unbinding events while preserving the native fold. Ligands are ranked according to the mean observed scaled unbinding time. The approach, trivially parallel and easily implementable, was validated against experimental information available on biological systems of pharmacological relevance.

In vivo drug-target interactions may occur far from the thermodynamic equilibrium, and therefore steady drug concentration cannot always be reached or maintained. Binding and unbinding kinetics are thus emerging as being even more relevant than binding thermodynamics for predicting drug efficacy in living organisms¹,². This observation led to an increasing interest from both pharmaceutical companies and institutional funding agencies, as testified by the K4DD Innovative Medicines Initiative of 2012 ( http://www.imi.europa.eu/content/k4dd). Despite several experimental techniques (e.g., SPR, stopped-flow CD, fluorescence spectroscopy, etc.) for studying (un)binding kinetics exist, efficient computational approaches to the prediction of kinetic parameters are presently missing. There are a few attempts reported in the literature, based on brute-force molecular dynamics (MD) simulations, that are however very highly demanding in terms of time and computational power, and unsuitable for the industrial use, where dozens of compounds need to be prioritized in the hit-to-lead and the lead optimization phases³,⁴,⁵. Importantly, (un)binding rates cannot be directly computable in pharmacologically relevant systems – even considering the most advanced and specialized computational architectures⁶ – as the residence time (t_r) of molecules can be of the order of seconds, minutes or even hours. This unavoidably calls for smarter algorithms and effective practical solutions for tackling the problem of kinetic rate estimation. Very recently, a detailed computational study of the protein-ligand dissociation process was reported⁷, demonstrating the possibility of studying the mechanisms governing unbinding events, and of disclosing the pathways, the rates and the rate-limiting steps of the process. However, despite the useful information it provides, the practical effectiveness of this methodology is limited by the high amount of computational resources (i.e. many weeks on a huge computational infrastructure), which are required to evaluate every single binding and unbinding kinetic constant pair (k_on and k_off). Moreover, while the prediction of the k_on was pretty close to the experimental data, the value of the k_off turned out to be one order of magnitude smaller than the experimental value, pointing to the intrinsic difficulties in estimating k_off from theory and simulation. A possible alternative could be the combination of the k_on obtained from unbiased simulations with the binding free energy estimated using free energy methods⁵; despite being promising, this method is not yet mature and still too computationally demanding for any high-throughput screening purpose.

Here, we report on a novel computational method that addresses the challenge of unbinding kinetics usually optimized in the hit-to-lead and lead optimization phases of the drug discovery process. Rather than trying to predict the absolute off-rate value, k_off = t_r⁻¹, on individual complexes, we aim at an efficient procedure to identify the correct k_off-based ordering relationship among congeneric compounds, which bind to a given target using possibly limited computational resources. Our solution is rooted in the enhancement of the transition probability between different free energy minima during MD simulations by means of scaled potentials⁸,⁹,¹⁰. We use this methodology in a statistical framework that combines a regressive predictive model and a bootstrap-based analysis for establishing the confidence of the predictions. The underlying rationale is that simulating a protein-ligand complex under scaled potential energy conditions facilitates the rupture of the key physical interactions that confer stability to the complex, leading to unbinding in much shorter simulation timescales. The scaling has however some unavoidable consequences, mainly related to the loss of detail on the actual energetic landscape that is explored, and to the fact that other interactions are weakened, besides those between the protein and the ligand. Among them are the forces that contribute to the overall structure of the protein system. While the former aspect is intrinsic to the scaling, a countermeasure to the latter issue can be taken; here we do this by applying proper harmonic restraints that preserve the overall correct fold, while leaving unrestrained the regions involved in the binding process.

Basically, the overall protocol consists of the following phases: i) an initial model for each protein-ligand complex is built, starting from available crystallographic information; ii) multiple replicas of scaled molecular dynamics of the partially restrained system are performed and stopped when the ligand unbinds; iii) the ratios of the simulated unbinding times of the congeneric ligands with respect to a reference complex are converted to the “unscaled” domain via an Arrhenius-like¹¹ exponential relationship; iv) a bootstrap analysis on the simulated unbinding times per target is done in order to assess the statistical significance of the observations and to possibly decide whether to increase the number of replicas per complex. This protocol is used to analyze the structure kinetics relationships (SKRs) of three systems of pharmacological interest.

Results

Our goal was to assess the ability of the approach to correctly rank and estimate k_off ratios with respect to a reference complex in a series. The capability to estimate k_off ratios was evaluated via the correlation coefficient of a linear regression. The method was applied to three systems of pharmacological interest (Fig. 1), for which consistent experimental data were available in the literature. The scaling factor was λ = 0.4 and the number of replicas were set to a minimum of 20 (see the Methods section for further details). In all of the cases, the ranking provided by the mean simulated unbinding times per complex was in agreement with the experimental data. Finally, the bootstrap analysis was used to quantify the effects of the small sample regime. In this respect, a few more simulations were performed in the HSP90 case to explore the dependence on the sample size.

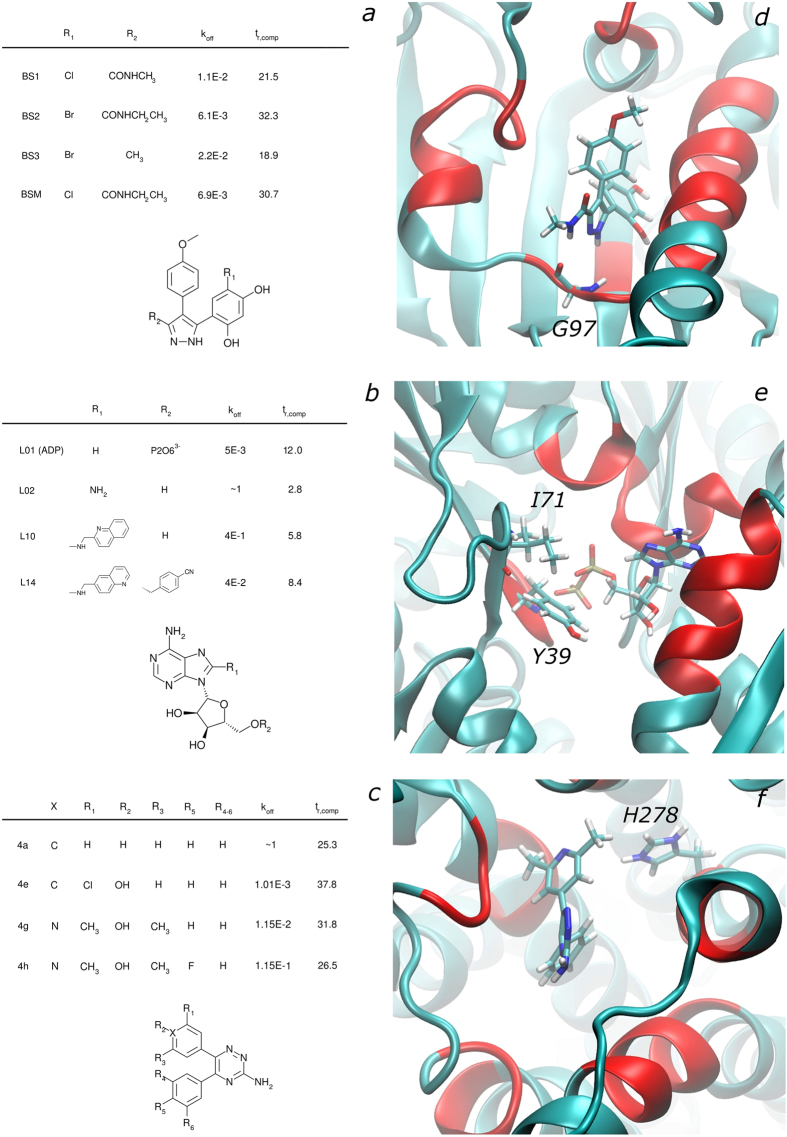
Figure 1. HSP90, Grp78, and A2A binding sites and ligands.

Molecular systems investigated in this work: both ligands (1a for HSP90, 1b for Grp78, 1c for A_2A) and binding sites (1d for HSP90, 1e for Grp78, 1f for A_2A) are reported. The red colored regions of the protein structures correspond to the unrestrained residues, as described in the main text and in the Methods. Residues represented in sticks are the ones that are reported as relevant for the physiological function of the protein: G97 is fundamental for the HSP90 binding to the investigated ligands¹³; Y39 and I71 are highly conserved residues in the binding sites of proteins belonging to the Grp78 family¹⁴; H278 is considered to be one of the most fundamental residues in harboring interactions between the A_2A binding site and the most favorable ligands belonging to the triazine series¹⁵. Together with the ligands’ scaffolds and their substituents, simulated residence times (expressed in ns) and experimental k_off from the literature¹³,¹⁴,¹⁵ have been reported. As explained in the main text, these times are not a direct estimate of their experimental counterpart but just a figure that is used for the ranking and to build the regressive model.

Heat Shock Protein 90

First, we focused on the HSP90 protein in complex with pyrazole-derived ligands, exemplified by NVP-AUY92225, currently in phase I and II of clinical trials for hematologic malignancies and solid tumors¹² (Fig. 1a,d). The fastest unbinders BS1 and BS3 were clearly separated from the slowest ones (BSM and BS2), with the longest and the shortest simulated unbinding times of about 30 ns and 20 ns, respectively. The correlation between experimental and calculated residence times was quite good with a Pearson’s coefficient r of 0.95 (see Fig. 2a). From a chemical standpoint, an ethyl to methyl substitution in the first series (compare BS2 to BS1; see also Fig. 1a) could generate an enthalpic penalty (see Supplementary Table 1) leading to the observed faster unbinding. Conversely, the replacement of the methyl (BS3) with the ethanol-amide (BSM) allowed the formation of a new hydrogen bond, resulting in a much slower unbinding.

Figure 2. Estimated vs. experimental residence times.

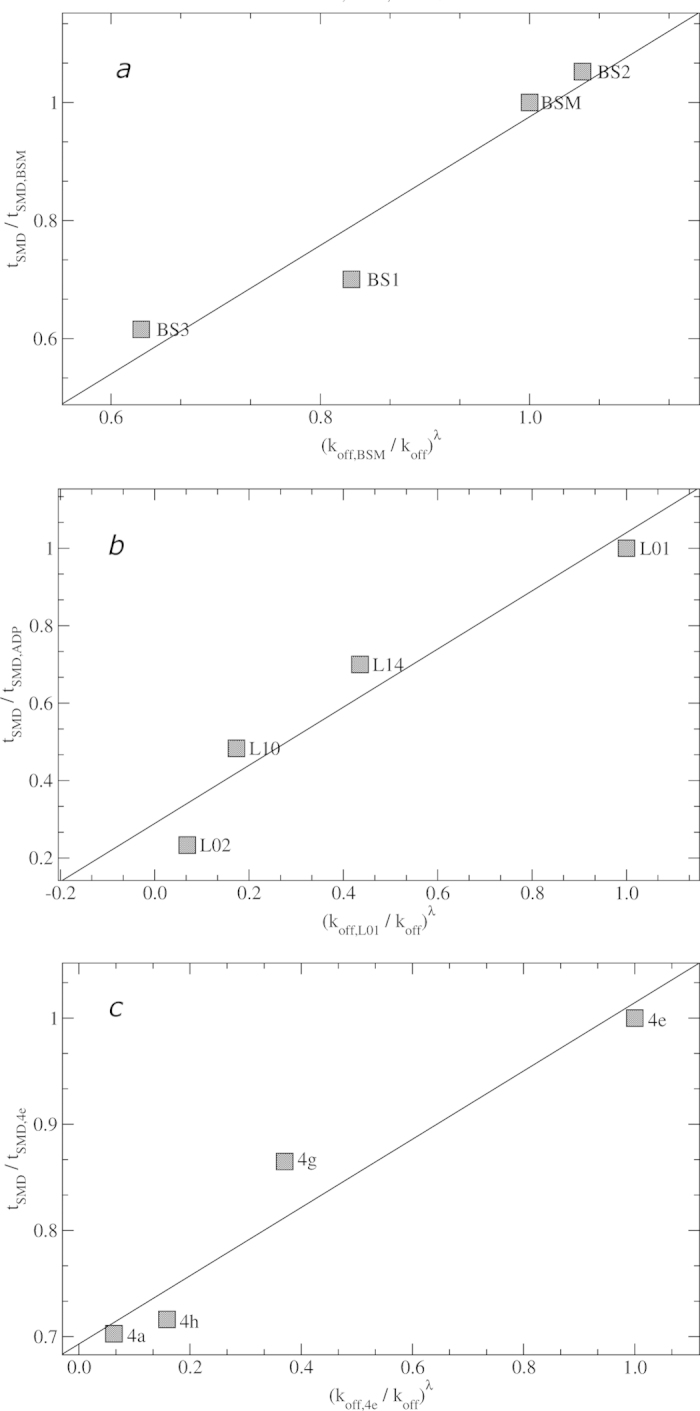
Estimated vs. experimentally measured residence times for HSP90 (2a), Grp78 (2b) and A_2A (2c). For sake of clarity, unbinding kinetic rates have been normalized with respect to the corresponding figure of reference ligands, i.e. BSM, L01 and 4e, respectively. Estimation was done by exponential scaling of simulated unbinding rates (see SI for more details) according to the potential smoothing factor adopted for SMD simulations (i.e., λ = 0.4). Linear regression correlation coefficients are 0.95 (2a), 0.85 (2b), and 0.95 (2c).

78 kDa Glucose-Regulated Protein

Then, we focused on the Grp78 protein in complex with purine-based inhibitors¹³ (Fig. 1b,e). From a chemical standpoint, this series is much less homogenous than that of the HSP90 inhibitors. Significant variations can be observed both in the molecular volume and in the net charge, which amounts to –3 e.s.u. in L01, while the other compounds are globally neutral. Moreover, calorimetric data¹³ (Table 1) suggest that the four ligands can be grouped in two categories based on their thermodynamic behavior. As reported in the literature, binding of L01 has a particularly high entropic contribution and the rest of the series shows rather uniform enthalpic contributions¹³. Also in this case, the correlation between calculated and experimental residence times was fairly good (r = 0.85, see Fig. 2b), allowing a clear separation between slow and fast binders. As it could be expected from the peculiarities of the L01 ligand with respect to the rest of the series, the correlation obtained excluding it from the series improves and becomes similar to that observed in HSP90.

Table 1. Summary of computed residence times and experimental kinetic/thermodynamic data for HSP90, Grp78, and A2A.

HSP90	BS2	BSM	BS1	BS3
Exp. tr [s]	163.9	144.9	90.9	45.5
ΔH [kcal mol−1]13	−2.7	−3.7	−3.8	−1.5
TΔS [kcal mol−1]13	−7.6	−6.7	−6.4	−7.5
Comp. Avg. tr ± σ [ns]	32.8 ± 17.5	30.7 ± 24.7	21.5 ± 13.8	19.1 ± 11.4
Comp. Avg. tr ± σe [ns]	32.8 ± 1.8	30.7 ± 2.5	21.5 ± 1.4	19.1 ± 1.1
Comp. Avg. tr ± σBS [ns]	32.3 ± 3.5	30.7 ± 4.5	21.5 ± 2.6	18.9 ± 2.2
Estimated koff [s−1]	6.6 × 10−3	reference	9.9 × 10−3	1.1 × 10−2
Grp78	L01	L14	L10	L02
Exp. tr [s]	200.0	25.0	2.5	1.0
ΔH [kcal mol−1]14	−1.3	−17.5	n.a.	−13.2
TΔS [kcal mol-1]14	0.5	−0.6	n.a.	−0.7
Comp. Avg. tr ± σ [ns]	11.3 ± 9.0	8.4 ± 6.7	5.9 ± 3.8	2.8 ± 1.6
Comp. Avg. tr ± σe [ns]	11.3 ± 1.0	8.4 ± 0.8	5.9 ± 0.4	2.8 ± 0.2
Comp. Avg. tr ± σBS [ns]	12.0 ± 2.2	8.4 ± 1.4	5.8 ± 0.8	2.8 ± 0.4
Estimated koff [s−1]	reference	7.1 × 10−3	1.0 × 10−2	2.1 × 10−2
A2A	4e	4g	4h	4a
Exp. tr [s]	990.1	90.0	8.7	~ 1
Comp. Avg. tr ± σ [ns]	37.8 ± 25.5	31.8 ± 20.2	26.5 ± 22.6	25.3 ± 18.9
Comp. Avg. tr ± σe [ns]	37.8 ± 5.7	31.8 ± 4.5	26.5 ± 5.1	25.3 ± 4.1
Comp. Avg. tr ± σBS [ns]	37.2 ± 5.1	30.4 ± 4.4	26.6 ± 4.2	25.2 ± 4.1
Estimated koff [s−1]	reference	1.2 × 10−3	1.4 × 10−3	1.4 × 10−2

Experimental residence times (Exp. t_r) were obtained by inversion of the reported k_off values and are reported in seconds, whereas computational residence times (Comp. Avg. t_r) averaged over replicas are reported in nanoseconds; ΔH and TΔS are expressed in kcal mol⁻¹. Residence times are reported together with standard deviation, σ, and standard error of the mean over n samples²⁷, 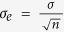. Moreover, data statistics analyzed by means of the bootstrapping (BS) method is also reported.

Adenosine A2A receptor

Finally, the new method was challenged with a representative of a large family of pharmaceutical targets, the adenosine A_2A G-protein-coupled receptor (GPCR) in complex with a series of congeneric triazine-based antagonists¹⁴(Fig. 1c,f). The A_2A receptor is widely investigated for different pathological conditions (e.g., Parkinson’s disease¹⁵). As reported in Table 1, here too we were able to correctly rank the ligands, and to achieve a correlation coefficient of 0.95 (see Figs 1c, 1f and 2c).

Statistical significance of the results

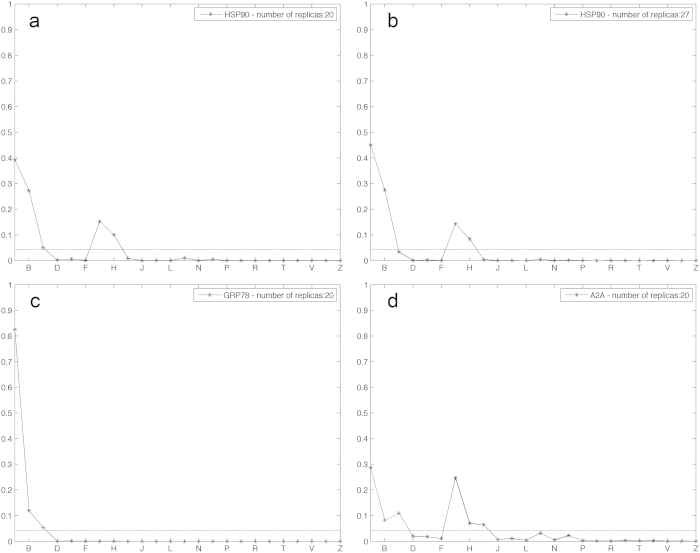
We then investigated whether the approach could provide useful information in the context of limited amount of computation, due to either computational resources or time constraints. In order to accomplish this task, we processed our data by means of the bootstrap analysis¹⁶, which does not require further simulations and is quite inexpensive from the computational standpoint. In the bootstrap technique, the observed unbinding times are extracted, with replacement, until convergence of the estimate is reached. This technique was used to estimate both the deviation of the mean unbinding times (Table 1) and the probability of every single ranking for different number of replicas (Fig. 3 and Supplementary Movies 1, 2 and 3). This analysis, based on all of our observations, is confirming that 20 replicas per complex can provide the correct ranking, but, as expected, the confidence of this result is system dependent. In the series studied here, for instance, the analysis showed that the outcome on the GRP78 system was statistically the most reliable, while for HSP90 and, especially, A_2A alternative rankings could not be completely ruled out. In this regard, a few more replicas per complex have been run for the HSP90 target, confirming that the probability of the experimentally validated ranking increases with the size of the samples.

Figure 3. Ranking probability estimates obtained via the bootstrap procedure.

Ranking probability estimates are presented for the three systems. In the abscissae, all the 24 possible rankings have been coded with an alphabet letter (Table 2), where the first, ‘A’, position corresponds to the experimentally validated ranking. The horizontal dashed lines correspond to 1/24, i.e. the probability or randomly drawing one out of the 24 possible rankings. a) HSP90 ranking probabilities with 20 replicas. b) HSP90 ranking probabilities with 27 replicas. c) Grp78 ranking probabilities with 20 replicas. d) A_2A ranking probabilities with 20 replicas. As expected, increasing the number of replicas, as done for the HSP90 case, corresponded to an increment of the probability of the ‘A’ ranking at the expense of its competitors ‘B’,’G’, and ‘H’. Data for different values of number of replicas are shown in the Supplementary movies 1, 2 and 3 for HSP90, GRP78 and A_2A, respectively.

Discussion and Conclusions

We presented here a computational method for estimating the unbinding kinetics of protein-ligand complexes, which represents a compromise between the complete information that would be achieved by the full exploration of the phase space (i.e. Boltzmann sampling) related to the unbinding process and the computational feasibility in a drug discovery context. The major strengths of the method are the relatively low computational cost, the easiness of implementation, and the fact that accuracy scales linearly with the availability of computational resources. Indeed, the method is trivially parallel with respect to the number of simulated replicas, and, in addition, each individual simulation can benefit of the availability and the performance of GPU-based MD engines¹⁷,¹⁸,¹⁹. A further key value lays in its simplicity and in the fact that it does not require any specific a priori knowledge of the reaction coordinate(s) associated with the process under investigation. A choice has however to be made, namely the portion of the protein that should be restrained. This is an important step for the success of the protocol, but the exact knowledge of the degrees of freedom involved in unbinding is however not essential, since a superset of them can be used, provided that it is the same for all the simulations performed within a series of congeneric compounds. In the test cases presented here, our method proved able to predict k_off ratios with respect to a reference complex with remarkable accuracy (r ranging between 0.85 and 0.95). Since no dramatic conformational changes are expected to occur upon ligand unbinding, the choice of letting unrestrained all the residues within a given distance from the ligand in the bound conformation seemed to be a natural choice, systematically applicable to many other cases. Another important aspect is the initial structure, the crystal of the complex is evidently the best choice, but in the case of congeneric series, as those discussed here and often considered in the hit-to-lead campaigns, one crystal per series may be enough to be used as a reliable structural model. Alternatively, molecular docking tools can be used.

Due to the loss of detail in the explored energetic landscape induced by the scaling, the presented method is not best suited for investigating the unbinding path at the atomic level. However, in the vicinity of the energetic minimum corresponding to the bound state it is still a valid tool for determining the mechanistic features of the protein-ligand complex dissociation.

The distributions of unbinding times for the 12 complexes present much larger standard deviations (see Table 1 and Supplementary Note) relative to those coming from a series of repeated experimental measures. This aspect requires considering that an experimental measurement is a macroscopic observation over an Avogadro-like number of microscopic events, each of them potentially following different underlying routes with different kinetic rates, which mix in a non-separable way. In contrast, each MD run represents, with some approximation, a single microscopic event, and inherently distinguishes between different possible mechanisms with different kinetics. This remarkably reduces the homogeneity of the outcome, leading to larger deviations, but with the advantage of providing detailed atomistic information, which is missing at a macroscopic level. Along the same line, smoothing the potentials also results in a broadening of the energetic basins width and therefore in larger thermal variations. Therefore, the variance of computational estimations of residence time should not be considered as a mere figure of error, and it is not expected to go to zero even by remarkably increasing the number of replicas. For example, if a multi-path unbinding is observed, then a multi-modal distribution is expected.

In this framework, we propose that the quantities that should be most reasonably compared are rather the experimental and estimated rankings. In particular, to assess the repeatability and robustness of our estimation procedure, we adopted a bootstrap-based approach. This analysis, which provides the probability estimate of each ranking and therefore also the confidence of the most likely ranking obtained by averaging simulated unbinding times, has shown that the estimates on the three considered systems had different degrees of confidence. This can be due to different factors, namely the number of replicas per complex, which still resides in the small sample regime, the possible restraining of degrees of freedom involved in the unbinding, or the fact that the different series exhibit a different proximity of the residence times, and therefore a different level of discrimination is achievable. This information supports the user in setting the desired threshold between accuracy and computational demand.

In conclusion, to the best of our knowledge, this is the first viable method for predicting the unbinding kinetics of protein-ligand complexes for a set of congeneric lead candidates, thus leading to a significant progress in the computationally driven discovery of both small organic molecules and biological compounds, improving early-stage predictions of drug efficacy and toxicity in academic and industrial settings. The next step could be combining the present approach with other theoretical and computational methods (e.g. those using Markov State models, Milestoning, Metadynamics, Transition State Theory, String method) that aim at a more quantitative description of the dynamical properties of protein-ligand interactions and related thermodynamic and kinetic factors.

Methods

Choice of the test systems

The developed method has been applied to three recently published targets, chosen because of the availability of crystal structures and experimental k_off values (by surface plasmon resonance) (Fig. 1):

1. HSP90 complexes with ligands belonging to the resorcinol series (exemplified by NVP-AUY92225, currently in phase I and II of clinical trial for hematologic malignancies and solid tumors)

2. Grp78 complexes with adenosine-derived inhibitors of its glucose related catalytic activity, a vital process for tumor metabolism the control of which is of paramount importance for the development of new anticancer drugs;

3. adenosine A_2A receptor complexes with antagonists that result to be effective in animal models of Parkinson’s disease, ranging from the reversal of haloperidol-induced catalepsy to efficacy in more disease-relevant models such as 6-hydroxydopamine lesioned rats and MPTP-lesioned primates and now successfully used in on-going phase II clinical trials.

The choice of such systems was driven by several reasons. For the first case, four compounds were investigated starting from the structure of HSP90 in complex with one member of the series (VER49009; PDB ID: 2BSM, hence the usage of the ligand name BSM in this work) and editing the ligand substituents R1 and R2 accordingly. The four chosen ligands display a common scaffold with only minor steric and chemical modifications that preserve the charge of the system: moreover, the k_off (Table 1) values are very close to each other, hence representing a perfect test set for understanding the “resolution” of the methodology in terms of k_off based ranking of ligands. On the other hand, the Grp78 case presents four ligands (PDB IDs: 3LDN (ADPnP), 3LDP (L10)) that offer the opportunity to test the robustness of the method when the ligands belong to the same chemical family (i.e., purines) but the substituents are varied from small groups or even single atoms to larger groups (such as heterocyclic aromatic rings), also varying the ligand net charge according to the nature of the substitution. Finally, the third system, the A_2A GPCR, (PDB ID: 3UZC) was chosen because it offers the opportunity to test the method against a system that belongs to a different and very relevant protein family (as well as a third new class of ligands), GPCR, which represents more than 20% of pharmaceutical targets.

Computational setup

Each compound was geometrically optimized via a quantum mechanical approach: electron density calculations were performed in Gaussian 09 [Frisch, M.J., et al. Gaussian 09, Revision D01, Gaussian, Inc, Wallingford CT, 2009] using the basis sets 6-31G* or 6-31g++ at the Hartree-Fock level of theory. Partial charges were derived using RESP method²⁰ in Antechamber, leading via a GAFF parameterization to a complete topological description of each ligand to be used for classical simulations. When the experimental complex structure was not available, the ligand was placed in the binding site according to the best superimposition of its scaffold with the experimental structure of the corresponding moiety.

The protein-ligand complexes were then used as a starting point for molecular dynamics simulations performed in a customized GROMACS 4.6.1 version that was made able to perform scaled molecular dynamics (SMD)⁹ implemented as recently described¹⁰.

The HSP90 and GRP78 complexes were placed in the geometrical center of parallelepiped-shaped boxes of volume equal to 400 nm3 and 650 nm³, respectively. For the A_2A system an 850 nm³ triclinic (dodecahedral) unit cell was used. The simulation boxes were then solvated using teLeap, with a number of TIP3P water molecules²¹ comprised between 27,000 (A_2A) and 60,000 (Grp78). Some water molecules were replaced with sodium ions in order to preserve the electro-neutrality of the system according to the need (8 Na⁺ ions for all the HSP90 simulations; 3 Na⁺ for all the Grp78 simulations with uncharged ligands and 6 Na⁺ ions for the simulations of ADP-Grp78 complex; 10 Na⁺ ions for all the A_2A simulations). The system was minimized with the steepest descent method, followed by equilibration of the restrained protein (isotropic 1000 kJ mol⁻¹ nm⁻¹ force applied to each heavy atom of the protein backbone) in NPT (up to 400 ps, pressure = 1 atm) and NVT (up to 400 ps) ensembles at 300 K via a standard MD procedure. Electrostatics was treated with the cutoff method for short-range interactions and with the Particle Mesh Ewald method for the long-range ones (rlist = 1 nm, cutoff distance = 0.9 nm, VdW distance = 0.9 nm, PME order = 4)²². The constant temperature conditions were provided by using V-rescale thermostat²³, which is a modification from Berendsen’s coupling algorithm.

A series of partially unrestrained (see further) SMD production runs were performed for each complex until the occurrence of the unbinding event, defined as the situation where no longer interactions between the ligand and the binding site are present (i.e., no hydrogen bonds; negligible interaction energy, corresponding, approximately, to a distance between the ligand-site centers of mass of 30 Å for the HSP90 and Grp78 systems and of 25 Å for A_2A). A total number of 108 simulations were performed for HSP90, 84 for Grp78 and 80 for A_2A.

All the HSP90 and Grp78 simulations were performed on a couple of in-house machines equipped with two esacore Intel Xeon processors and 2 NVIDIA GTX 780 GPUs, for a total of 1120 CPU days, whereas test simulations were performed on Fermi CINECA supercomputer (IBM-BlueGene /Q; IBM PowerA2, 1.6 GHz) using the hours allocated for the grant Pra07_1565. A_2A simulations have been all performed in Eurora CINECA supercomputer (Linux Infiniband Cluster; Intel Xeon processors + 64 NVIDIA K20 GPUs).

Choice of the scaling parameter

All the simulations were performed with a smoothing coefficient λ = 0.4. This value was chosen as the best compromise between a reasonable computing CPU time (see also the table reported in the Supplementary Information) and unbinding times ranging from few nanoseconds to tens of nanoseconds. In order to tune the exact λ value, we performed for the fastest and slowest ligands of each system a series of simulations with decreasing λ value between 0.7 and 0.3 and thereafter decided to adopt the value reported in the present work.

Application of the restraints

The overall method must preserve the protein fold and, at the same time, allow the complex dissociation in a reasonable time, considering also the need of achieving good statistics via a number of simulations. In order to prevent the protein unfolding, we adopted a set of weak restraints (50 kJ mol⁻¹ nm⁻¹) on the whole backbone heavy atoms with the exception of the ones of the residues having at least one atom (either of the backbone or of the side chain) composing the binding site and being within 6 Å of distance from the surface of the ligand computed on the starting crystal structure (without hydrogen atoms). This distance value in particular has been chosen considering the sum of: a. the maximal length of hydrogen bonds (4 Å in the case of weak hydrogen bonds²⁴), b. the C-H bond length (1 Å), c. the error associated to the experimental determination of crystallographic structures, that as a “rule of thumb”²⁵ is considered to be one sixth of the crystal resolution (i.e., in our cases between 2.0¹² and 3.3 Ź⁴, leading to an average error of 0.5 Å for the atomic positions and of 1 Å for a heavy atoms distance).

The set of unrestrained residues was expanded including also residues adjacent to those directly in contact with the ligand in order to allow longer-range motions. Moreover, this limits numerical instabilities of the restraining algorithm (in our case LINCS²⁶) during the simulations. In this way, the overall protein secondary and tertiary structure are preserved while the binding site is allowed to sample the rearrangements that allow the unbinding of the ligand and that would naturally occur at much longer timescales.

The list of the unrestrained residues for the three systems follows:

HSP90: L48-A55, I91-D93, G95-I99, D102-L107, G135-F138, K185-I187;

Grp78: G36-S40, L225-G228, G254-D259, E293-S301, G363-I368, P390-E392;

A2A: V84, L85, F168, E169, M174, M177, N181, W246, L249, H250, N253, H264, M270, I274, S277, H278.

Simulation stability check

The RMSD of the protein backbone was monitored in each simulation in order to check the overall system stability and the impact of the enhanced mobility of the ligand binding site on the protein structure: the backbone RMSD of the bound system is always below or equal to 1.5 Å and it displays a sudden increase up to 3-4 Å during the transition toward the unbound state (see Supplementary Figure 2). As a positive check of the course of the simulation, we verified that the RMSD of the protein after the unbinding goes back to the original values.

Additional Information

How to cite this article: Mollica, L. et al. Kinetics of protein-ligand unbinding via smoothed potential molecular dynamics simulations. Sci. Rep. 5, 11539; doi: 10.1038/srep11539 (2015).

Table 2. Alphabetical letter coding for all the possible rankings.

A	1 2 3 4	I	2 3 1 4	Q	3 4 1 2
B	1 2 4 3	J	2 3 4 1	R	3 4 2 1
C	1 3 2 4	K	2 4 1 3	S	4 1 2 3
D	1 3 4 2	L	2 4 3 1	T	4 1 3 2
E	1 4 2 3	M	3 1 2 4	U	4 2 1 3
F	1 4 3 2	N	3 1 4 2	V	4 2 3 1
G	2 1 3 4	O	3 2 1 4	W	4 3 1 2
H	2 1 4 3	P	3 2 4 1	Z	4 3 2 1

The 4 different ligands here are named ‘1’, ‘2’,‘3’ and ‘4’ according to their experimental residence time, in increasing order. Therefore, the ‘A’ ranking is the experimentally validated one.