Non-locking Tetrahedral Finite Element for Surgical Simulation

Abstract

To obtain a very fast solution for finite element models used in surgical simulations low order elements such as the linear tetrahedron or the linear under-integrated hexahedron must be used. Automatic hexahedral mesh generation for complex geometries remains a challenging problem, and therefore tetrahedral or mixed meshes are often necessary. Unfortunately the standard formulation of the linear tetrahedral element exhibits volumetric locking in case of almost incompressible materials. In this paper we extend the average nodal pressure tetrahedral element proposed by Bonet and Burton for a better handling of multiple material interfaces. The new formulation can handle multiple materials in a uniform way, with better accuracy, while requiring only a small additional computation effort. We discuss some implementation issues and show how easy an existing TLED (Total Lagrangian Explicit Dynamics) algorithm can be modified in order to support the new element formulation. The performance evaluation of the new element shows the clear improvement in reaction forces and displacements predictions compared to the average nodal pressure element in case of models consisting of multiple materials.

1 Introduction

Finite element models needed in surgical simulation must be both fast and accurate. In order to be fast, they must use low order elements that are not computationally intensive, such as the linear tetrahedron or the linear under-integrated hexahedron. In order to be accurate, the generated mesh should approximate well the real geometry, so that the boundary conditions can be imposed accurately. Many algorithms are now available for fast and accurate automatic mesh generation using tetrahedral elements, but not for automatic hexahedral mesh generation [1–3]. Therefore, in order to automate the simulation process, tetrahedral or mixed meshes are more convenient. Unfortunately, the standard formulation of the tetrahedral element exhibits volumetric locking, especially in case of soft tissues such as the brain, that are modeled as almost incompressible materials [4–10].

There are a number of improved linear tetrahedral elements already proposed by different authors [11–14]. The average nodal pressure (ANP) tetrahedral element proposed by Bonet and Burton in [11] is computationally inexpensive and provides much better results for nearly incompressible materials than the standard tetrahedral element. Nevertheless, one problem with the ANP element and its implementation in a finite element code is the handling of interfaces between different materials. In this paper we extend the formulation of the ANP element so that all elements in a mesh are treated in a similar way, requiring no special handling of the interface elements.

When organs such as the brain are meshed using a mixed mesh, most of the tetrahedral elements are situated at the interface between the different parts of the brain (ventricle, tumor, white matter, gray matter), as these irregular sections are harder to mesh using only hexahedral elements. Therefore the correct handling of the interface between different materials is very important.

We will show how this element formulation can be easily programmed in an existing finite element code [15] and present a deformation example that proves the increased performances of this element over the standard linear tetrahedron and the ANP elements.

The paper is organized as follows: the new element formulation is presented in Section 2, the integration in an existing finite element code is presented in Section 3, a computational example demonstrates the efficiency of the improved element in Section 4 and the conclusions are presented in Section 5.

2 Improved Average Nodal Pressure Element Formulation

2.1 Existing ANP Formulation

We will start the development of the improved ANP (IANP) element by briefly presenting the standard ANP formulation developed in [11]. The volume attached to a node a is computed by adding the contributions from elements e = 1,…, m_a surrounding node a:

$$V_a=\sum _{e=1}^{m_a}{V}_a^{(e)}{V}_a^{(e)}=\frac{V^{(e)}}{4}$$ (1)

The Jacobian over an element e is the ratio between the current and initial element volumes, and also represents the volumetric part of the deformation gradient F:

$$J^{(e)}=\frac{v^{(e)}}{V^{(e)}}=det(\mathbf{F})$$ (2)

The isochoric component of the deformation gradient is therefore given by:

$$\widehat{\mathbf{F}}=J^{-1/3}\mathbf{F}$$ (3)

The existence of a total elastic energy function is assumed, given as:

$$\mathrm{\Pi }(\mathbf{x})={\int }_V\mathrm{\Psi }(\mathbf{F})dV={\int }_V\widehat{\mathrm{\Psi }}(\widehat{\mathbf{F}})dV+{\int }_{V}U(J)dV$$ (4)

where Ψ is the strain energy density function with an isochoric component Ψ̂ and a volumetric component U. The volumetric component U can only be a function of the volumetric ratio J, with the simplest and most commonly used form incorporating the bulk modulus κ of the material:

$$U(J)=\frac{\kappa }{2}{(J-1)}^2$$ (5)

The element pressure is defined as:

$$p^{(e)}={\frac{dU}{dJ}|}_{J=J^{(e)}}=\kappa (J^{(e)}-1)$$ (6)

The volumetric virtual work for the standard linear tetrahedron is expressed as:

$$\delta W_{\mathit{vol}}=\sum _{e=1}^m{p}^{(e)}{v}^{(e)}\mathit{div}\delta {\mathbf{v}}^{(e)}$$ (7)

where δv are the virtual velocities and m is the number of elements in the mesh.

The volumetric components of the element internal nodal forces can be derived from the volumetric virtual work as:

$${\mathbf{T}}_{\mathit{vol}}^{(e)}=p^{(e)}{v}^{(e)}\nabla {\mathbf{N}}_a^{(e)}$$ (8)

with N_a the shape functions of the element.

The ANP formulation is obtained by assuming that the volume ratio J remains constant over the volume attached to each node, therefore reducing the number of incompressibility constraints. The average nodal volumetric ratio is defined in terms of the current and initial nodal volumes, given by (1), as:

$$J_a=\frac{v_a}{V_a}$$ (9)

and the volumetric strain energy is approximated by summing the contribution of all the n nodes in the mesh:

$${\mathrm{\Pi }}_{\mathit{vol}}(\mathbf{x})=\sum _{a=1}^{n}U(J_a)V_a$$ (10)

If only one material is considered, the average nodal pressure can be defined as:

$$p_a={\frac{dU}{dJ}|}_{J=J_a}=\kappa (J_a-1)$$ (11)

By differentiating the volumetric strain energy given by (10) in the direction of the virtual velocities, the volumetric internal virtual work is obtained:

$$\delta W_{\mathit{vol}}=\sum _{a=1}^n\sum _{e=1}^{m_a}\frac{1}{4}{p}_a{v}^{(e)}\mathit{div}\delta {\mathbf{v}}^{(e)}=\sum _{e=1}^m{\overline{p}}^{(e)}{v}^{(e)}\mathit{div}\delta {\mathbf{v}}^{(e)}$$ (12)

Therefore the average element pressure can be defined as:

$${\overline{p}}^{(e)}=\frac{1}{4}\sum _{a=1}^4{p}_a^{(e)}$$ (13)

The difference between the ANP element and the standard linear tetrahedral element is the usage of the average nodal pressure (13) instead of the element pressure (6) in the expression of the volumetric internal virtual work (and therefore in the computation of the volumetric components of the internal nodal forces).

In case of multiple material interfaces, the nodal pressure can not be computed using (11), as it is not clear what bulk modulus κ should be used. For each material type i converging at node a, a different nodal volume is defined as:

$$V_a^{(i)}=\sum _{e=1}^{m_a^{(i)}}\frac{1}{4}{v}^{(e)}$$ (14)

where m_a⁽ⁱ⁾ represents the number of elements of material type i sharing node a. A different nodal pressure is then evaluated for each material as:

$$p_a^{(i)}={\kappa }^{(i)}(J_a^{(i)}-1)$$ (15)

When the pressures are averaged over an element, only those corresponding to the right element material are used.

2.2 Improved ANP Formulation

The different treatment of elements having different material types at the interface nodes leads to:

• implementation problems, as not all elements in the mesh are treated in the same manner;

• a weaker enforcement of the incompressibility constraints for the nodes belonging to material interfaces (the elements of different material type are treated separately).

We will now demonstrate how both these problems can be eliminated. We start with the definition of the volumetric strain energy for one of the nodes a belonging to an interface between multiple materials:

$${\mathrm{\Pi }}_{\mathit{vol}}^a(\mathbf{x})=\sum _{i=1}^{k_a}U(J_a^{(i)})V_a^{(i)}$$ (16)

where k_a represents the number of different material types converging to node a.

Instead of considering different nodal pressure for the different material types, as given by (15), we will make the assumption that the nodal pressure is constant over the nodal volume. This assumption derives from the relation that exists between pressure and stress (p = −σ_ii/3) [16] and from the fact that at the interface between two different materials the stress in the materials should be the same.

Therefore, the nodal pressure for such a node is expressed as:

$$p_a={\kappa }^{(1)}(J_a^{(1)}-1)=\dots ={\kappa }^{(k_a)}(J_a^{(k_a)}-1)$$ (17)

This can be transformed to:

$$\begin{array}{l}{p}_a={\kappa }^{(1)}\frac{v_a^{(1)}-V_a^{(1)}}{V_a^{(1)}}=\dots ={\kappa }^{(k_a)}\frac{v_a^{(k_a)}-V_a^{(k_a)}}{V_a^{(k_a)}}\\ =\frac{{\displaystyle \sum _{i=1}^{k_a}}{\kappa }^{(i)}(v_a^{(i)}-V_a^{(i)})}{{\displaystyle \sum _{i=1}^{k_a}}{V}_a^{(i)}}=\frac{{\displaystyle \sum _{i=1}^{k_a}}{\kappa }^{(i)}\frac{1}{4}{\displaystyle \sum _{e=1}^{m_a^i}}(v^{(e)}-V^{(e)})}{{\displaystyle \sum _{i=1}^{k_a}}\frac{1}{4}{\displaystyle \sum _{e=1}^{m_a^i}}{V}^{(e)}}\\ =\frac{{\displaystyle \sum _{i=1}^{k_a}}{\displaystyle \sum _{e=1}^{m_a^i}}{\kappa }^{(i)}(v^{(e)}-V^{(e)})}{{\displaystyle \sum _{e=1}^{m_a}}{V}^{(e)}}=\frac{{\displaystyle \sum _{e=1}^{m_a}}{p}^{(e)}{V}^{(e)}}{{\displaystyle \sum _{e=1}^{m_a}}{V}^{(e)}}=\frac{{\displaystyle \sum _{e=1}^{m_a}}{p}^{(e)}{V}^{(e)}}{4V_a}\end{array}$$ (18)

The volumetric internal virtual work for node a will be given by:

$$\begin{array}{l}\delta W_{\mathit{vol}}^a=D{\mathrm{\Pi }}_{\mathit{vol}}^a[\delta \mathbf{v}]=\sum _{i=1}^{k_a}{\frac{dU}{dJ}|}_{J=J_a^{(i)}}{V}_a^{(i)}{DJ}_a^{(i)}[\delta \mathbf{v}]\\ =\sum _{i=1}^{k_a}{p}_a{V}_a^{(i)}{DJ}_a^{(i)}[\delta \mathbf{v}]=\sum _{i=1}^{k_a}{p}_a{V}_a^{(i)}\frac{1}{V_a^{(i)}}{Dv}_a^{(i)}[\delta \mathbf{v}]\\ =\sum _{i=1}^{k_a}{p}_a{Dv}_a^{(i)}[\delta \mathbf{v}]\end{array}$$ (19)

By replacing (14) in (19), and considering, from [12], that:

$${DJ}^{(e)}[\delta \mathbf{v}]=J^{(e)}\mathit{div}\delta {\mathbf{v}}^{(e)}$$ (20)

we obtain:

$$\begin{array}{l}\delta W_{\mathit{vol}}^a=\sum _{i=1}^{k_a}{p}_a\frac{1}{4}\sum _{e=1}^{m_a^{(i)}}{Dv}^{(e)}[\delta \mathbf{v}]=\sum _{e=1}^{m_a}{p}_a\frac{1}{4}{Dv}^{(e)}[\delta \mathbf{v}]\\ =\sum _{e=1}^{m_a}{p}_a\frac{1}{4}{V}^{(e)}{DJ}^{(e)}[\delta \mathbf{v}]=\sum _{e=1}^{m_a}\frac{1}{4}{p}_a{v}^{(e)}\mathit{div}\delta {\mathbf{v}}^{(e)}\end{array}$$ (21)

Comparing (21) with (12) we observe that the volumetric internal virtual work for node a is computed in the same manner, and therefore the element pressure will be defined by relation (13). The only difference between the standard ANP element and the improved ANP element consists in the computation of nodal pressure.

In case of a node surrounded by elements made of the same material, the nodal pressure given by (18) can be reduced to:

$$\begin{array}{l}{p}_a=\frac{{\displaystyle \sum _{e=1}^{m_a}}{p}^{(e)}{V}^{(e)}}{{\displaystyle \sum _{e=1}^{m_a}}{V}^{(e)}}=\frac{{\displaystyle \sum _{e=1}^{m_a}}\frac{1}{4}\kappa (v^{(e)}-V^{(e)})}{{\displaystyle \sum _{e=1}^{m_a}}\frac{1}{4}{V}^{(e)}}\\ =\kappa \frac{v_a-V_a}{V_a}=\kappa (J_a-1)\end{array}$$ (22)

and the pressure for the standard ANP element is obtained. Therefore, the standard and the improved ANP elements behave differently only for elements situated at an interface between different materials.

3 Implementation Considerations

3.1 The modified deformation gradient

The only difference between the (standard or improved) ANP element and the linear tetrahedral element consists in the way the pressure is computed. The internal forces derived from the isochoric component of the strain energy are the same for all these elements. These forces depend only on the isochoric part of the deformation gradient.

The volumetric components of the internal forces depend on the element pressure, as given by (8), while the element pressure depends only on the volumetric part of the deformation gradient (6).

We consider an existing implementation for a linear tetrahedral element, with the internal forces computed based on the volumetric and isochoric components of the deformation gradient. In order to obtain the internal forces corresponding to the ANP elements, the volumetric part of the deformation gradient can be modified in such a way that the desired pressure (corresponding to the ANP elements) is obtained. This pressure, given by (13), can therefore be replaced in (6) to obtain the modified volumetric part for the deformation gradient:

$${\overline{J}}^{(e)}=\frac{{\overline{p}}^{(e)}}{\kappa }+1$$ (23)

The modified deformation gradient:

$${\overline{\mathbf{X}}}^{(e)}={\left({\overline{J}}^{(e)}\right)}^{1/3}\widehat{\mathbf{X}}={\left({\overline{J}}^{(e)}\right)}^{1/3}{\left(J^{(e)}\right)}^{-1/3}\mathbf{X}$$ (24)

has the same isochoric part as the deformation gradient of the element, but the volumetric part is modified in such a way that the pressure computed from it will correspond to the ANP element.

The computation of the internal nodal forces (or stiffness matrix) can now be done in the usual manner, but using the modified deformation gradient instead of the normal deformation gradient for defining the strains. This way the existing material law implementation can be used, as demonstrated in the next section.

It is worth noting that if the standard ANP element is used, the modified volumetric part for the deformation gradient becomes, after replacing in (23) the average element pressure from (13) and the average nodal pressure from (11):

$${\overline{J}}^{(e)}=\frac{1}{4}\sum _{a=1}^4{J}_a$$ (25)

Therefore the computation of pressure is no longer needed for such an implementation.

3.2 Integration in the Total Lagrangian Explicit Dynamic (TLED) Algorithm

The TLED algorithm is a very efficient explicit algorithm based on the Total Lagrangian formulation that can be used for surgical simulation. The basic algorithm is presented in [17]. The modified algorithm that can use the IANP element presented in this paper is presented bellow. The additional steps required are marked with a (+).

Pre-computation stage

1. Load mesh and boundary conditions

2. For each element compute the determinant of the Jacobian det(J) and the spatial derivatives of shape functions ∂h (notation from [18] is used, where the left superscript represents the current time and the left subscript represents the time of the reference configuration - 0 when Total Lagrangian formulation is used).

3. Compute the diagonal (constant) mass matrix ⁰M.

4. (+) Compute the initial volumes associated with each node V_a using (1).

Initialization

1. Initialize nodal displacement ⁰u = 0,^−Δt u = 0, apply load for the first time step: forces or/and prescribed displacements: ${{}^{\mathrm{\Delta }t}R}_i^{(k)}\leftarrow R^{(k)}(\mathrm{\Delta }t)$ or/and ${{}^{\mathrm{\Delta }t}u}_i^{(k)}\leftarrow d(\mathrm{\Delta }t)$

Time stepping

Loop over elements

1. Take element nodal displacements from the previous time step

2. Compute deformation gradient ${}_t{}^0\mathbf{X}$ and its determinant J

3. (+) Compute current element pressure using (6).

   (+) Compute nodal pressure using (18).

Loop over elements

1. (+) Compute the average nodal pressure using (13).

2. (+) Compute the modified deformation gradient using (23) and (24).

3. Compute the 2^nd Piola-Kirchoff stress (vector) ${}_t{}^0\overline{\mathbf{S}}$ using the given material law (based on the modified deformation gradient).

4. Compute the element nodal reaction forces using Gaussian quadrature

Making a (time) step

1. Obtain net nodal reaction forces at time t, ^tT.

2. Explicitly compute displacements using central difference formula

   $${{}^{t+\mathrm{\Delta }t}u}_i^{(k)}=\frac{\mathrm{\Delta }{t}^2}{M_k}{}^t({{}^{t}R}_i-{{}^{t}T}_i^{(k)})+2^t{u}_i^{(k)}-{{}^{t-\mathrm{\Delta }t}u}_i^{(k)}$$ (26)

   where M_k is a diagonal entry in k-th row of the diagonalized mass matrix, R_i is an external nodal force, and Δt is the time step.

3. Apply load for next step: ${{}^{t+\mathrm{\Delta }t}R}_i^{(k)}\leftarrow R^{(k)}(t+\mathrm{\Delta }t)$ or/and ${{}^{t+\mathrm{\Delta }t}u}_i^{(k)}\leftarrow d(t+\mathrm{\Delta }t)$.

The needed modifications are easy to implement and do not require major changes in the existing algorithm. The performances of the modified algorithm will be presented in the next section.

4 Simulation Results

Because the only difference between the IANP element proposed in this paper and the standard ANP element consists in the way interfaces between different materials are handled, we designed a simulation experiment that highlights these differences. We considered a cylinder with a diameter of 0.1 m and a height of 0.2 m made out of alternating sections with two different material properties, as shown in Table 1. We used a neo-Hookean material model for both materials.

Table 1.

Material properties

Property	Material 1	Material 2
Young’s modulus E [Pa]	3 000	30 000
Poisson ratio ν	0.49	0.48
Density ρ [kg/m3]	1 000	1 000

Half of the nodes on the upper face of the cylinder were displaced in order to create a complex deformation field at the different material interfaces (Fig. 1.a).

Figure 1.

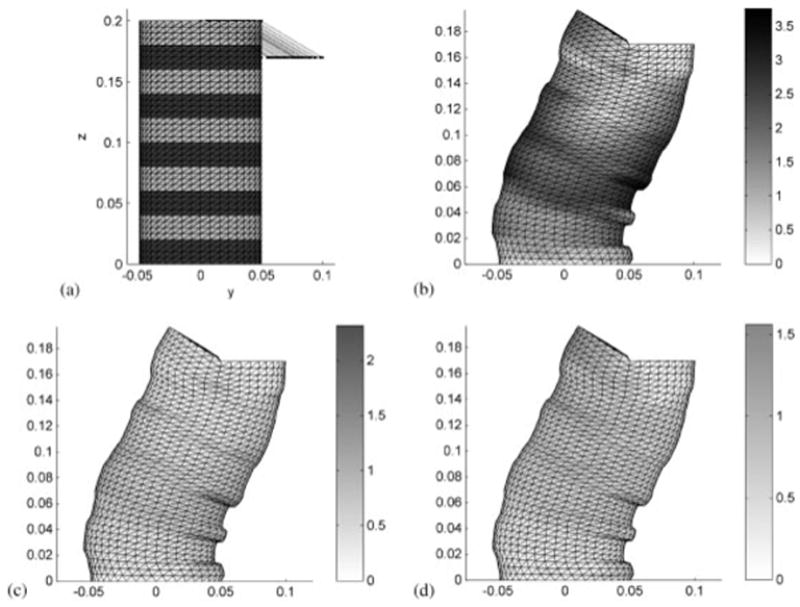
Deformation of a cylinder made out of section with different material properties: (a) the un-deformed configuration and the nodal displacements are applied. The color bars show the difference in positions of the surface nodes, in mm, between models using hexahedral elements and models using; (b) locking tetrahedral elements; (c) ANP elements; and (d) IANP elements.

Using the cylinder geometry we created a hexahedral mesh (13161 nodes and 12000 elements) and a tetrahedral mesh (11153 nodes and 60030 elements). The behavior of the following elements was compared:

1. Fully integrated linear hexahedra, with selectively reduced integration of the volumetric term (Hexa), which should offer a benchmark solution [19];

2. Standard Average Nodal Pressure elements (ANP);

3. Improved Average Nodal Pressure elements (IANP), as developed in this paper;

4. Linear standard tetrahedron (Tetra).

All the computations were done using the TLED algorithm. Based on the displacement differences presented in Fig. 1 we note the fact that the usage of standard locking tetrahedral elements can lead to errors of up to 3.8 mm in the deformation field. The use of ANP elements reduces the maximum error to 2.3 mm while the use of IANP elements leads to a maximum error of 1.5 mm (all errors are considered relative to the results of the model that uses Hexa elements).

The reaction forces computed on the displaced face are presented in Fig. 2. The results obtained using the IANP elements are the closest to the benchmark results given by the Hexa elements. Therefore, the IANP elements offer the best performances both in terms of displacements and reaction forces.

Figure 2.

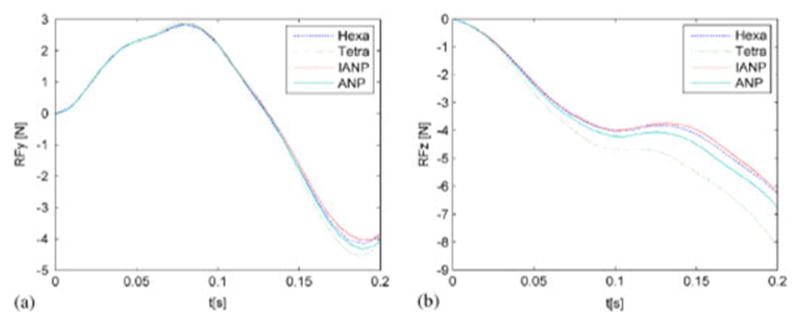
Reaction forces on the displaced face: (a) in the y direction and (b) in the z direction.

5 Discussions and Conclusions

An improvement of the ANP element is presented in this paper. This improved formulation handles all the elements of the mesh in the same manner (regardless of the fact they may be at an interface between materials) and therefore the use of different materials and the implementation in an existing finite element code can be made without difficulties.

The performance of the proposed IANP element is evaluated using the TLED algorithm against the standard tetrahedral element and the ANP element. The IANP element offered the best performances both in terms of displacements and reaction forces.

In an explicit code, the critical time step value for the ANP element is double compared to the critical time step for the standard locking tetrahedron in the one-dimensional case [20]. We observed a similar behavior for the ANP and IANP elements in the three-dimensional simulations. This means that we can use higher values for the time step in an explicit simulation using a mixed mesh, as the tetrahedral elements are usually the ones that impose the value of the critical time step. A higher critical time step leads to a reduction of the overall computation time.