Mechanical Loading of Cartilage Explants with Compression and Sliding Motion Modulates Gene Expression of Lubricin and Catabolic Enzymes

Abstract

Objective

Translation of the contact zone in articulating joints is an important component of joint kinematics, yet rarely investigated in a biological context. This study was designed to investigate how sliding contact areas affect cartilage mechanobiology. We hypothesized that higher sliding speeds would lead to increased extracellular matrix mechanical stress and the expression of catabolic genes.

Design

A cylindrical Teflon indenter was used to apply 50 or 100 N normal forces at 10, 40, or 70 mm/s sliding speed. Mechanical parameters were correlated with gene expressions using a multiple linear regression model.

Results

In both loading groups there was no significant effect of sliding speed on any of the mechanical parameters (strain, stress, modulus, tangential force). However, an increase in vertical force (from 50 to 100 N) led to a significant increase in extracellular matrix strain and stress. For 100 N, significant correlations between gene expression and mechanical parameters were found for TIMP-3 (r² = 0.89), ADAMTS-5 (r² = 0.73), and lubricin (r² = 0.73).

Conclusions

The sliding speeds applied do not have an effect on the mechanical response of the cartilage, this could be explained by a partial attainment of the “elastic limit” at and above a sliding speed of 10 mm/s. Nevertheless, we still found a relationship between sliding speed and gene expression when the tissue was loaded with 100 N normal force. Thus despite the absence of speed-dependent mechanical changes (strain, stress, modulus, tangential force), the sliding speed had an influence on gene expression.

Introduction

Articular cartilage is responsible for the low friction, reduced wear, and redistribution of complex mechanical loads for millions of cycles during one’s lifetime. These outstanding functional properties are based on a highly specialized extracellular matrix (ECM), which can be divided into a solid phase and a fluid phase.¹ The solid phase is primarily composed of collagen fibers, proteoglycans, and cells. The fluid phase contains interstitial water and mobile ions. During mechanical compression, the porous solid matrix hinders interstitial fluid escape, creating an internal pressure to resist the applied load and shield the cells within the solid matrix. The importance of this mechanism during physiological joint function has been previously investigated, both theoretically and experimentally.^2-5

When a static load is applied, fluid exudes from the loaded area to adjacent areas, resulting in a decrease in interstitial fluid pressure, a transition of the load from the fluid component to the solid matrix, and an elevated coefficient of friction. During physiological joint motion, loads are applied intermittently and result in multidirectional sliding of the joint surfaces and varied contact areas between cartilage surfaces.^6,7 This results in fluid flow between high- and low-pressure regions of the ECM and a continuous rehydration of the previously loaded areas. As a consequence, high fluid pressurization (and therefore high fluid load support) and a low coefficient of friction can be sustained over hours of loading under continuously changing contact locations.⁸ The influence of different loading parameters on the mechanical response of cartilage has already been extensively explored.^9-13 However, little is known about the effect of migrating contacts on the biological response of cartilage. It is known that the biological response of chondrocytes to mechanical forces depends on the magnitude of the force, where high forces cause an upregulation of catabolic genes, such as collagen- or proteoglycan-degrading enzymes.^14-17 However, these studies applied relatively simple loading regimens, typically uniaxial compressive and/or shear forces alone or in combination. A previous study from our laboratory found that increasing tractional forces, induced by sliding and plowing, induced catabolic changes within the cartilage.¹⁸

This study was designed to explore the influence of sliding on the biological response of cartilage. The mechanical response of the cartilage was measured during the application of 2 physiological sliding loads of 50 and 100 N for 2 hours. Mechanical parameters were then correlated with the cellular expression of catabolic genes. We hypothesized that increased sliding speeds would result in elevated stresses and regulate the expression of catabolic marker genes.

Methods

Unless otherwise indicated, all chemicals were purchased from Life Technologies, CH-6300 Zug, Switzerland.

Cartilage Explants

Cartilage was obtained from bovine nasal septum (BNS) of 20 young calves (12-18 months) provided by a local abattoir within 4 hours of slaughter. BNS is a homogenous and isotropic hyaline cartilage containing chondrocytes in their natural environment, which was easily cut into a rectangular shape for mounting onto our test apparatus.

Cartilage was explanted under sterile conditions by first removing the perichondrium and then cutting into experimental (70 × 17 × 2 mm³) and control (70 × 12 × 2 mm³) (L × W × H) sizes from the same nasal septum using a custom designed cutter. The specimens were washed in phosphate buffered saline (PBS), transferred to culture medium (Dulbecco’s modified eagle’s medium [DMEM] supplemented with 10% fetal bovine serum, 4 mM l-glutamine, 10 mM Hepes buffer, 100 units/mL penicillin, 100 µg/mL streptomycin, 1 mM sodium pyruvate, and 0.25 µg/mL amphotericin B) and equilibrated for 72 hours before sliding tests were performed.

Cell viability of explanted constructs was assessed immediately before loading using an inclusion/exclusion double-label assay kit containing calcein-acetoxymethyl ester (CAM) and propidium iodide (PI) (Fluka, Buchs, Switzerland). CAM passes through membranes of viable cells and emits a strong green fluorescence once it enters the cell nucleus. PI can only pass through damaged cell membranes (i.e., dead cells) and in combination with the DNA double helix emits a red fluorescence. Cartilage sections (~1 mm thick) were manually cut with a microtome blade, washed in PBS (2 × 5 minutes), and incubated in both stains for 15 minutes at 37 °C. After incubation, the cartilage sections were washed in PBS for another 3 minutes before imaging using a fluorescent microscope.

Mechanical Loading

Ten millimeters of the cartilage specimen were attached to a Plexiglas plate (130 × 34 × 1.5 mm³) with cyanoacrylate glue (Renfert, Hilzingen, Germany) as shown in Figure 1. The rest of the cartilage was free to move. The plate and cartilage were placed into a tank filled with culture medium at 37 °C. Control specimens were free and allowed to swell in culture medium at 37 °C.

Figure 1.

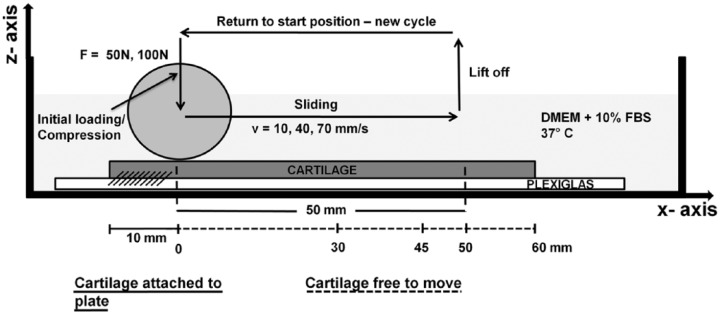
Illustration of the loading setup. The experimental cartilage strip is glued to the Plexiglas plate that is fixed to a Teflon tank filled with culture medium. The entire setup is placed in a flow hood to guarantee sterile conditions. Arrows show the unidirectional motion of the indenter in z- and x-directions. The first 10 mm of the cartilage strip are attached to the Plexiglas by medical glue. The biological sampling area is between x = 30 mm and x = 45 mm.

A cylindrical, nonrotating Teflon indenter (25 mm diameter by 50 mm length) was used to apply a normal force of 50 or 100 N to the cartilage. On reaching the target force, the force was held constant while the indenter slid over the cartilage for 50 mm at a constant speed of 10, 40, or 70 mm/s. After 50 mm translation, the indenter lifted off and returned to the start position to begin another load-sliding cycle (Fig. 1). The load was cycled for 120 minutes and the positions and forces of the indenter in the horizontal (x-) and vertical (z-) directions recorded at 100 Hz (minutes 0-5 and minutes 115-120) or 20 Hz (minutes 5-115) using linear variable differential transducers (LVDTs) and load sensors, respectively. The combination of 2 normal forces and 3 sliding speeds resulted in a total of 6 different experimental groups. For each group, at least 3 specimens were tested and for each loading condition a separate cartilage strip (and corresponding control) was used. For detailed information on the loading apparatus see previous work.¹⁹

Calculations

The strain, stress, and elastic modulus of the cartilage were continually calculated along the sliding path. Strain (ε) was calculated as a change in thickness (Δl), as measured by the LVDTs, divided by the initial thickness (l₀) of the cartilage specimen

$$\epsilon =\frac{\Delta l}{l_0}$$

The contact area and stress were calculated using the Hertzian theory of elastic deformation. The semicontact width a of the contact rectangle was calculated using

$$a=\sqrt{r^2-{(r-\delta )}^2}$$

where r is the radius of the indenter (12.5 mm) and δ the depth of indentation.

The modulus of the cartilage (E_carticlage) was calculated from

$$E_{\mathrm{cartilage}}=\frac{1-{\nu }_{\mathrm{cartilage}}^2}{\frac{1}{E^{\prime }}-\left(\frac{1-{\nu }_{\mathrm{Teflon}}^2}{E_{\mathrm{Teflon}}}\right)}$$

where the reduced modulus (E′) is

$$E^{\prime }=\frac{4\times F\times r}{a^2\times \pi \times L}$$

where F is the normal force and L the width of the cartilage strip (17 mm). The Poisson’s ratio for BNS cartilage (ν_cartilage) was 0.24 (Colombo et al.²⁰) and for the Teflon indenter (ν_Teflon) was 0.45. The elastic modulus for Teflon (E_Teflon) is 500 MPa. The cartilage modulus during sliding will subsequently be referred to as an “apparent modulus” since it may not represent the true compressive elastic modulus of cartilage. The maximum stress under the indenter was then calculated from

$${\sigma }_{\max }=\sqrt{\frac{F\times E_{\mathrm{cartilage}}}{L\times \pi \times r}}$$

Gene Expression Analysis

After loading for 2 hours, a 15 mm wide region (30-45 mm from the starting point of the indenter) was removed from the loaded and control specimens for analyses (Figs. 1 and 2). Three specimens were taken from this area. One specimen was immediately analyzed for gene expression after loading and the other 2 specimens after 4 and 8 hours in culture media at 37 °C. The samples were snap frozen in liquid nitrogen and stored at −80 °C until RNA extraction. Frozen specimens were pulverized using a biopulverizer (Biospec, Bartlesville, OK, USA), transferred into 1 mL Trizol reagent, centrifuged at 12,000 × g for 10 minutes at 4 °C, supernatant collected, 200 µL chloroform added, vigorously shaken and centrifuged at 12,000 × g for 15 minutes at 4 °C. The aqueous layers were then extracted with 200 µL chloroform (as described above), 500 µL isopropanol added and further centrifugation at 12,000 × g for 10 minutes at 4 °C formed RNA pellets. The pellets were washed with 75% ethanol and resuspended in RNase-free water. RNA was purified using RNeasy mini kit (Qiagen GmbH, CH-8634 Hombrechtikon, Switzerland) and reverse transcribed with QuantiTect Reverse Transcription Kit (Qiagen GmbH, Hombrechtikon, Switzerland) according to the manufacturer’s instructions. Real-time quantitative polymerase chain reaction (RT-PCR) was performed on an iCycler detection system (iQ5, BioRad Laboratories, Inc, Hercules, CA, USA) on 96-well plates with a QuantiFast SYBR Green RT-PCR Kit (Qiagen GmbH, Hombrechtikon, Switzerland).

Figure 2.

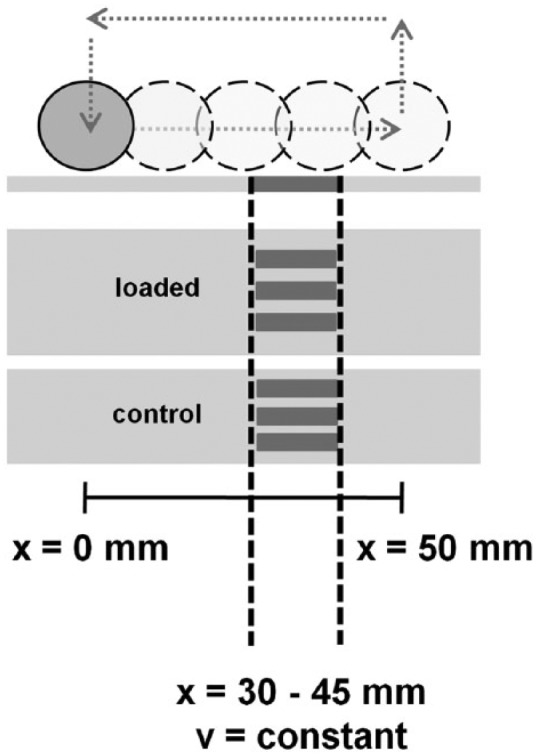
The area between x-position 30 to 45 mm was used for harvesting cartilage to analyze gene expression by means of polymerase chain reaction (PCR) analysis. The sampled strips are shown in dark gray. The indenter speed in the chosen area is constant.

Genes, commonly associated with degenerative states of cartilage, were analyzed and divided in 3 groups: genes degrading collagens and proteoglycans (MMP-3, MMP-13, ADAMTS-4, ADAMTS-5), genes inhibiting the degrading enzymes (TIMP-1, TIMP-3), and the gene for Lubricin, a surface protein, known to be upregulated with sliding motion and in degenerated states of cartilage. Glyceraldehyde-3-phospahte dehydrogenase (GAPDH) was used as a housekeeping gene (previously verified using a published algorithm²¹). Forward and reverse primers for each gene can be found in Table 1. Delta-delta Ct (ΔΔCt) values were calculated for each gene followed by the fold change in expression with the formula 2^−ΔΔCt. Primers for MMP-3, TIMP-1, GAPDH, and Lubricin were taken from the literature.^15,22 Primer sequences for MMP-13, ADAMTS-4/-5, and TIMP-3 were designed using GeneBank database.

Table 1.

Forward and Reverse Primers.^a

Gene	Forward Primer	Reverse Primer
MMP-3	CACTCAACCGAACGTGAAGCT	CGTACAGGAACTGAATGCCGT
MMP-13	TCCAGGAGATGAAGACCCCT	CAGCCGCCAGAAGAATCTGT
ADAMTS-4	CATCCTACGCCGGAAGAGTC	CATGGAATGCCGCCATCTTG
ADAMTS-5	CCTGCCCAGCTAACGGTAAA	GGGCAGGACACCAGCATATT
TIMP-1	TCCCTGGAACAGCATGAGTTC	TGTCGCTCTGCAGTTTGCA
TIMP-3	ACTTTGGAGACTCGAGCAGC	CTTGGCTCGGATCACGATGT
Lubricin	GAGCAGACCTGAATCCGTGTATT	GGTGGGTTCCTGTTTGTAAGTGTA
GAPDH	ATCAAGAAGGTGGTGAAGCAGG	TGAGTGTCGCTGTTGAAGTCG

^aForward and reverse primer sequences (bovine) used for gene expression analysis with real-time polymerase chain reaction (annealing temperature ~60 °C).

Statistics

A multiple linear regression model was used to express the mRNA regulation as a function of 8 experimental parameters. The linear regression equation for each gene was modeled by

$$\mathrm{gene}\mathrm{expression}={\displaystyle \sum _{i=1}^9{b}_{i-1}{x}_{i-1}}$$

and the following experimental parameters: sliding speed (b₁), sampling time point (b₂), cycle number (b₃), strain (b₄), x-force (b₅), z-force (b₆), modulus (b₇), and maximum stress (b₈). The values for each time step were averaged for the biological sampling area for the 2-hour loading period. The experimental parameters were treated as independent variables and plotted against the gene expression. The influence of each factor was determined from the r² and P values with a significance level of α = 0.05. A Kolmogorov-Smirnov test was used to determine if the residuals were equally distributed and the Durbin-Watson test to check for autocorrelations. An analysis of variance (ANOVA) was also performed to assess the gene expression changes with regard to the main controlled input variables: z-force, sliding speed, and sampling time. Differences between individual groups were determined with the Fisher’s least significant difference (LSD) test at α-level = 0.05. A total of 20 BNS were tested with N ≥ 3 for each experimental group.

Results

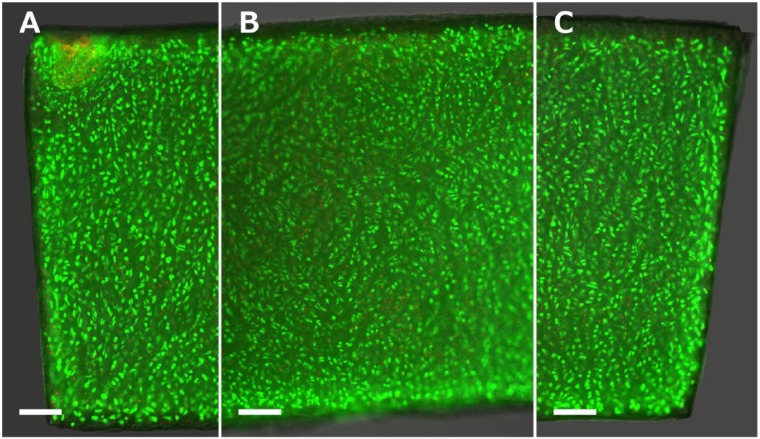
Viability assays showed that cell viability is generally very high and dead cells are only sparsely located throughout the tissue section. A roughly 75 µm thick, acellular outer layer can be found (Fig. 3).

Figure 3.

Calcein-acetoxymethyl ester and propidium iodide (CAM–PI) staining of a representative cartilage section before the load is applied. The image shows the left border (A), middle section (B), and right border of the cartilage strip (C). The nuclei of live and dead cells are stained green and red, respectively. Scale bar = 250 µm.

Each cartilage specimen was subjected to a sliding load of 50 or 100 N at a constant speed of 10, 40, or 70 mm/s for 2 hours. Table 2 illustrates how differences in sliding speed resulted in different cycle times and number of cycles (or impacts) over the 2-hour loading period. For a speed of 10 mm/s, there were 425 cycles; 40 mm/s had a total of 539 cycles or 26.8 % more impacts. At 70 mm/s sliding speed, there were 585 cycles and an increase of 37.6 % and 8.5 % impacts compared with 10 and 40 mm/s, respectively.

Table 2.

Duration of Individual Phases of the Loading/Unloading Cycle.

Sliding Speed (mm/s)	Total Cycle (seconds)	Sliding Phase (seconds)	Sampling Region (seconds)	Unloading (seconds)	Total Cycle No.a
10	16.71 ± 0.84	5.06 ± 0.05	1.530	11.60 ± 0.02	425
40	13.16 ± 0.72	1.33 ± 0.02	0.399	11.82 ± 0.05	539
70	12.13 ± 1.17	0.76 ± 0.04	0.228	11.29 ± 0.09	585

^aCycle No. refers to the number of cycles during the 2-hour loading time.

Initial Loading Phase

Before every sliding cycle, the target load was applied to the edge of the glued cartilage region (x-position = 0 mm, Fig. 1) and a stress–strain curve obtained. This provided an estimate of the initial mechanical properties of the cartilage and any changes during the 2-hour loading time. Figure 4 shows typical stress-strain curves (cycles 100, 200 and 400) for the 50 N and 100 N loads at 10 mm/s. Notice that on unloading, the cartilage regained its initial height after each loading cycle while the stress-strain curve continuously shifted to the right, the latter an indication of ECM softening.

Figure 4.

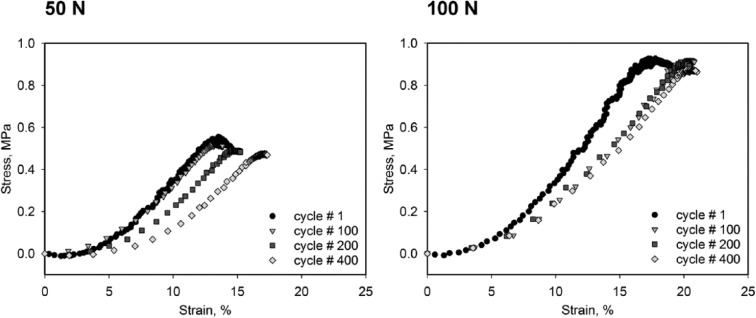
Typical stress–strain diagrams of the initial loading/compression phase. Graphs are displayed for sliding speed = 10 mm/s. Curves for ongoing cycle numbers are shown and reveal a shift to the right and flattening of the curve.

Mechanical Parameters During Sliding Phase

All mechanical parameters investigated are summarized in Table 3. The numbers represent averaged values for the biological sampling area (x-position: 30-45 mm) for the total number of cycles over the entire 2-hour loading period. Significantly higher (P ≤ 0.05) strains and maximum stresses were found for samples loaded with 100 N compared with 50 N. No significant differences were observed for apparent moduli and tangential (shear) forces between 50 and 100 N. No significant differences in any parameters were found between different sliding speeds at the same normal force.

Table 3.

Mechanical Parameters.^a

	50 N			100 N
Mechanical Parameter	10 mm/s	40 mm/s	70 mm/s	10 mm/s	40 mm/s	70 mm/s
z-force (N)	55.03 ± 2.9	63.66 ± 7.8	61.28 ± 6.1	102.55 ± 1.1*	111.87 ± 6.0*	107.93 ± 4.8*
x-force (N)	1.36 ± 0.8	2.12 ± 0.9	2.11 ± 0.9	1.9 ± 0.6	3.02 ± 0.9	3.01 ± 0.5
Strain (%)	28.11 ± 3.1	28.10 ± 5.2	28.60 ± 1.7	39.97 ± 4.9*	35.49 ± 2.6*	41.07 ± 5.1*
Stress (MPa)	0.51 ± 0.04	0.61 ± 0.14	0.58 ± 0.09	0.80 ± 0.07*	0.98 ± 0.10*	0.87 ± 0.10*
Modulus (MPa)	3.16 ± 0.4	4.16 ± 1.7	3.45 ± 0.7	4.01 ± 0.7	5.47 ± 0.9	4.55 ± 1.0

^aTable presents mean values ± standard deviation for the calculated mechanical parameters for the biological sampling area averaged over the 2-hour loading period.

^*P < 0.05 as compared with the same sliding speed loaded with 50 N.

Correlative Analysis

Analysis of variance between all controlled input parameters (z-force, sliding speed, and sampling time) and gene expression showed no significant differences. However, when the 50 N load data was removed and the ANOVA performed for cartilage loaded with 100 N, ANOVA revealed significant differences between 10 and 70 mm/s sliding speed for Lubricin (P = 0.012) and ADAMTS-5 (P = 0.049). No significant differences were found for different time points with all genes.

Linear correlations with 50 N revealed low r² values for all gene expressions and mechanical parameters, and thus only the results for the 100 N normal force are given in Tables 4 and 5. Significant correlations between mechanical parameters and gene expression were found for TIMP-3 (r² = 0.89), ADAMTS-5 (r² = 0.73), and Lubricin (r² = 0.73). Positive and negative correlations of experimental parameters varied with different genes. All residuals for each gene were normally distributed and the Durbin-Watson test did not reveal any autocorrelation between the mechanical parameters.

Table 4.

Multiple Linear Regression: Coefficients.^a

Gene	b0: Intercept	b1: Sliding Speed (mm/s)	b2: Time Point (hr)	b3: Cycle No.b	b4: Strain (%)	b5: x-force (N)	b6: z-force (N)	b7: Modulus (MPa)	b8: Maximum Stress (MPa)
Lubricin	−10.14	0.47	0.25	0.26	18.10	4.11	0.38	31.81	339.88
MMP-3	316.29	−2.06	−3.76	1.20	−597.98	−61.16	2.41	82.18	−1205.99
MMP-13	20.12	−0.05	−0.33	0.04	−70.53	−5.57	0.55	3.46	−74.81
ADAMTS-4	15.48	0.04	−0.11	−0.01	−64.12	−1.93	0.88	9.58	−135.14
ADAMTS-5	12.56	−0.03	0.16	0.03	−38.06	−3.19	0.07	−2.52	3.09
TIMP-1	9.24	0.04	−0.04	−0.02	−20.31	−0.92	−0.03	−5.49	44.33
TIMP-3	3.82	0.15	0.05	−0.07	−19.58	−1.37	−0.45	−21.55	210.40

^aGene expression = b₀ + b₁x₁ + b₂x₂ + b₃x₃ + b₄x₄ + b₅x₅ + b₆x₆ + b₇x₇ + b₈x₈. Table presents values representing the correlation coefficients for each experimental parameter.

^bCycle No. refers to the number of cycles during the 2-hour loading time.

Table 5.

Multiple Linear Regression: Significances.^a

Gene	r2	Sliding Speed (mm/s)	Time Point (hr)	Cycle No.b	Strain (%)	x-force (N)	z-force (N)	Modulus (MPa)	Maximum Stress (MPa)
Lubricin	0.73	0.011	0.012	0.005	0.479	0.029	0.425	0.029	0.031
MMP-3	0.52	0.610	0.097	0.546	0.337	0.158	0.834	0.799	0.732
MMP-13	0.45	0.905	0.163	0.866	0.287	0.221	0.651	0.919	0.841
ADAMTS-4	0.29	0.891	0.446	0.955	0.118	0.475	0.243	0.644	0.551
ADAMTS-5	0.73	0.772	0.021	0.618	0.047	0.018	0.835	0.789	0.976
TIMP-1	0.69	0.541	0.263	0.580	0.072	0.219	0.888	0.336	0.473
TIMP-3	0.89	0.033	0.146	0.050	0.060	0.054	0.025	0.001	0.002

^ar² values indicate the fit of the regression equation to explain the change in gene expression. The numbers below the mechanical parameters represent P values for each regression coefficient (Table 4).

^bCycle No. refers to the number of cycles during the 2-hour loading time.

Discussion

Cartilaginous surfaces of human joints, such as the knee or temporomandibular joint (TMJ), spend most of their time in relative motion with a continuous translation of the contact zone.^7,23 Several research groups have investigated joint tribology from a purely mechanical point of view.^8-13 Mechanobiological studies do not incorporate such migrating contacts into their loading regimens, however they do approximate the in vivo joint with compressive and/or shear forces. Dependent variables usually include strain rate and stress^14,24,25 as well as temporal patterns.¹⁶ By allowing the contact area to migrate over the cartilage surface, new variables such as sliding speed, cycle number, and tangential force are introduced. Thus, strain and stress become dynamic parameters depending on the speed applied. Our mechanobiological study was designed to address the complexity and multiaxial nature of joint motion with the goal to investigate the biological response in terms of catabolic gene expression. Lubricin was included into the study since it is considered a joint lubricant and its gene expression has been shown to increase with surface motion^22,26 as well as being increased in patients with degenerated joint diseases.²⁷

We used a mechanical test system capable of simultaneously applying a normal force and tangential sliding velocity, as previously described.¹⁹ Physiological loading conditions were established by combining 50 and 100 N normal forces with previously reported functional sliding speeds of 10, 40, and 70 mm/s.^7,28 Since most biomaterials, such as hydrogels, are mechanically weak and unable to resist physiological sliding/shear loads, a cell-scaffold system could not be used. In addition, the isolation of chondrocytes prior to adding them to a scaffold makes them prone to dedifferentiation, which can change the biological response.²⁹ Because of its size and availability, BNS was found to be a suitable hyaline cartilage model to investigate the response of chondrocytes to such mechanical forces. Most important, BNS incorporates the chondrocytes within their natural ECM environment. BNS can be shaped into sufficiently large and flat specimens allowing the application of translations over large sliding paths. It is abundantly available and shown to have viscoelastic behavior, with similar mechanical properties to a variety of other cartilaginous tissues.²⁰ In addition, the alignment of collagen fibers provides homogeneity in the plane used for the experiments.³⁰

For this study, contact stress and apparent modulus were calculated from the Hertzian theory of elastic deformation. Since the indenter is moving along the horizontal plane, the point of contact is dynamic and changes with time. To calculate contact stress and modulus, values for each time step were calculated and averaged over the biological sampling area. While these values do not necessarily represent the true elastic properties of the material, they are representative of the mechanical response and present a valid tool to compare relative changes with other sliding speeds and normal forces. Moore and Burris³¹ recently developed an analytical model to determine functional parameters, such as contact area and stress under migrating contact conditions. However, their approach is limited to small contacts of a sphere on a plane surface and is therefore not directly applicable to our study.

After each loading cycle, the initially loaded cartilage region (at x = 0) recovered to its initial thickness whereas the deformation in the sampled sliding region (x = 30-45 mm) continually increased. With the assumption of a recovery to its initial thickness after each loading cycle in the sliding region, the increasing deformation indicates a softening of the cartilage with increasing sliding load duration. However, the fact that the tissue is not attached and gets temporarily stretched during loading could lead to a different response. Because of the averaging of the mechanical values (for the 2-hour load) used in the regression model, this information was not taken into account when analyzing the gene response.

As expected, there was increased strain, contact stress, apparent modulus, and tangential force with 100 N compared with 50 N. However, sliding speed did not significantly affect the response of these mechanical parameters, which could be explained by a partial attainment of the “elastic limit” at and above 10 mm/s sliding speed. The finding of a slight increase in some of the experimental parameters between 10 and 40 mm/s, but not between 40 and 70 mm/s, further supports this and indicates that the cartilage is in transition from a viscoelastic to an elastic regime. This is in agreement with Bonnevie et al.,⁹ who found that sliding speeds greater than 1 mm/s did not cause changes in cartilage deformation.

In the present study, sliding contact stresses were in the order of 0.6 MPa (50 N) and 0.9 MPa (100 N) as calculated from Equation (5). Compared with physiological stresses in cartilage, these levels are on the lower limit. The lack of significant changes in gene expression for the 50 N specimens could be regarded as a low-stress response similar to no loading, and less as a metabolic response due to the applied loading regimen. However, by analyzing only the 100 N loaded cartilage, we found several significant correlations for Lubricin, ADAMTS-5, and TIMP-3. Lubricin gene expression was significantly influenced by sliding speed, time point, cycle number, horizontal (shear) force, modulus, and maximum stress, though all these parameters are not completely independent (Table 5). The absence of gene expression changes with strain may be due to the small number and range of sliding speeds and normal loads used. ANOVA with the 100 N samples did show significantly higher Lubricin and ADAMTS-5 gene expression between the 10 and 70 mm/s groups, which further emphasizes the results from the regression analysis and highlights the importance of sliding speed. Also, finite element analysis has shown that different sliding speeds result in dissimilar patterns of fluid flow.³² This is likely to affect the micro- and nano-environment of the chondrocytes. Ateshian et al.³³ calculated that fluid shear stresses acting on the chondrocyte surface differ by several orders of magnitude from the shear stresses in the solid matrix. Thus, differences in interstitial hydrostatic pressures and osmotic changes might account for an alteration in gene expression, as already proposed in other studies.^34-36

Finally, different sliding speeds obviously changed the number of cycles and therefore, these 2 factors seem to be inherently correlated with each other. However, for TIMP-3 gene expression, we found a positive correlation with sliding speed but a negative correlation with cycle number. It is also important to keep in mind that an up/downregulation of genes does not necessarily imply an up/downregulation of proteins. The fact that BNS is not a loaded tissue and does not have the zonal arrangement present in articular cartilage could be regarded as a potential limitation of the study. Therefore it is reasonable to assume that articular cartilage would react slightly different under the same loads.

In conclusion, this study demonstrates the importance of applying migrating contact loads to cartilage explants for studying the biological responses of the tissue. Even though we found no obvious macroscopic changes in the mechanical variables by comparing different sliding speeds, changes in the mRNA expression pattern still occur, possibly evoked by the migrating contact points. Therefore, applying such multiaxial forces is important when simulating joint kinematics in mechanobiological studies. In a first step a profound mechanical analysis of the behavior of the tissue under the applied mechanical stimuli is vital. Second, the mechanical parameters need to be directly linked to the biological response. This will improve our understanding of how chondrocytes react to such dynamic and multi axial forces during articulation.