Abstract
Motivation: Discovering and understanding patterns in networks of protein–protein interactions (PPIs) is a central problem in systems biology. Alignments between these networks aid functional understanding as they uncover important information, such as evolutionary conserved pathways, protein complexes and functional orthologs. A few methods have been proposed for global PPI network alignments, but because of NP-completeness of underlying sub-graph isomorphism problem, producing topologically and biologically accurate alignments remains a challenge.
Results: We introduce a novel global network alignment tool, Lagrangian GRAphlet-based ALigner (L-GRAAL), which directly optimizes both the protein and the interaction functional conservations, using a novel alignment search heuristic based on integer programming and Lagrangian relaxation. We compare L-GRAAL with the state-of-the-art network aligners on the largest available PPI networks from BioGRID and observe that L-GRAAL uncovers the largest common sub-graphs between the networks, as measured by edge-correctness and symmetric sub-structures scores, which allow transferring more functional information across networks. We assess the biological quality of the protein mappings using the semantic similarity of their Gene Ontology annotations and observe that L-GRAAL best uncovers functionally conserved proteins. Furthermore, we introduce for the first time a measure of the semantic similarity of the mapped interactions and show that L-GRAAL also uncovers best functionally conserved interactions. In addition, we illustrate on the PPI networks of baker's yeast and human the ability of L-GRAAL to predict new PPIs. Finally, L-GRAAL's results are the first to show that topological information is more important than sequence information for uncovering functionally conserved interactions.
Availability and implementation: L-GRAAL is coded in C++. Software is available at: http://bio-nets.doc.ic.ac.uk/L-GRAAL/.
Contact: n.malod-dognin@imperial.ac.uk
Supplementary information: Supplementary data are available at Bioinformatics online.
1 Introduction
Understanding the patterns in molecular interactions is of foremost importance in systems biology, as it is instrumental to understanding the functioning of the cell (Ryan et al., 2013). Because molecular interactions are often modeled by networks, a large number of studies focused on understanding the topology of these networks (Nepusz and Paccanaro, 2014; Pržulj, 2011). In the case of protein–protein interaction (PPI) networks, where nodes represent proteins and edges connect proteins that interact, comparative studies based on network alignments were particularly successful. Given two networks, aligning them means finding a node-to-node mapping (also called an alignment) between the networks that optimizes two objectives: (i) maximizing the number of mapped proteins (nodes) that are evolutionarily or functionally related and (ii) maximizing the number of common interactions (edges) between the networks. Network alignment uncovers valuable information, such as evolutionarily conserved pathways and protein complexes (Kelley et al., 2003; Kuchaiev et al., 2010) or functional orthologs (Bandyopadhyay et al., 2006). Finding these allows transfer of information across species, such as performing Herpes viral experiments in yeast or fly and then applying the insights toward understanding the mechanisms of human diseases (Uetz et al., 2006).
Network alignment problem is computationally intractable due to NP-completeness of the underlying sub-graph isomorphism problem (Cook, 1971). Hence, several network alignment heuristics (i.e. approximate aligners) have been proposed. Earlier methods, called local network aligners, search for small but highly conserved sub-networks called motifs (Flannick et al., 2006; Kelley et al., 2004; Koyutürk et al., 2006). As motifs can be duplicated, local network aligners often produce one-to-many or many-to-many mappings, in which a node from a given network can be mapped to several nodes of the other network. Although these multiple mappings can indicate gene duplications, they are often biologically implausible (Singh et al., 2007). Hence, global network aligners, which perform an overall comparison of the input networks and produce one-to-one mappings between the nodes of the two networks have been introduced. Several heuristics have been proposed for solving the global alignment problem.
The first one is ISORANK (Singh et al., 2007), which rephrases aligning networks as an eigenvalue problem, mimicking Google's Pagerank algorithm. HOPEMAP (Tian and Samatova, 2009) iteratively constructs the alignment between two networks by searching for a common maximally connected component. PATH and GA algorithms (Zaslavskiy et al., 2009) optimize the same objective function, which balances between mapping similar proteins and increasing the number of mapped interactions. The GRAAL family (Kuchaiev and Pržulj, 2011; Kuchaiev et al., 2010; Memišević and Pržulj, 2012; Milenković et al., 2010) is a set of network aligners, which are based on the idea that mapping together nodes that are involved in similar local wiring patterns (as measured by the statistics of small induced sub-graph called graphlets) will result in a large number of shared interactions. As newer GRAAL aligners use improved alignment heuristic strategies, using C-GRAAL or MI-GRAAL is recommended. Also, these two methods allow using additional node scores, such as sequence similarity. NATALIE (El-Kebir et al., 2011) is a combinatorial optimization method based on Lagrangian relaxation, which searches for top scoring network alignments over the biologically plausible node mappings obtained by sequence alignment. GHOST (Patro and Kingsford, 2012) is a spectral approach, where nodes are mapped according to the similarity of their spectral signatures. NETAL (Neyshabur et al., 2013) is a fast greedy heuristic that constructs an alignment by iteratively inserting the node mapping with the highest probability to induce common edges, where the probabilities are recomputed at each iteration. SPINAL (Aladağ and Erten, 2013) is a two-step approach, which first computes coarse-grained node similarity scores, and then based on these scores, iteratively grows a seed solution. PISWAP (Chindelevitch et al., 2013) optimizes global alignments using a derivative of the local 3-opt heuristic, which is originally used for solving the traveling salesman problem. MAGNA (Saraph and Milenković, 2014) uses a genetic algorithm to maximize the edge conservation between the aligned networks. HUBALIGN (Hashemifar and Xu, 2014) uses a minimum-degree heuristic to align ‘important’ proteins first and then gradually extends the alignment to the whole networks. Although all the above methods align networks to derive additional biological knowledge (e.g. orthology group and functional annotations), DUALALIGNER (Seah et al., 2014) does the opposite and uses biological knowledge to produce network alignments.
The number of known molecular interactions has increased tremendously during the last decade due to the technological advances in high-throughput interaction detection techniques such as yeast two-hybrid (Fields and Song, 1989) and affinity purification coupled to mass spectrometry (Ho et al., 2002). Because of the increasing amount of available interaction data, coupled with the computational hardness of the network alignment problem, producing topologically and biologically accurate alignments is still challenging.
In this article, we introduce a novel global network alignment tool that we call Lagrangian GRAphlet-based ALigner (L-GRAAL). Unlike previous aligners, which either do not take into account the mapped interactions (e.g. the previous GRAAL aligners and ISORANK) or use naive interaction mapping scoring schemes (e.g. NATALIE), L-GRAAL optimizes a novel objective function that takes into account both sequence-based protein conservation and graphlet-based interaction conservation, by using a novel alignment search heuristic based on integer programming and Lagrangian relaxation. We compare L-GRAAL with the state-of-the-art network aligners on the largest available PPI networks from BioGRID and observe that L-GRAAL uncovers the largest overlaps between the networks, as measured with edge-correctness (EC) and symmetric sub-structure scores. These largest overlaps are key for transferring annotations between networks. Using semantic similarity, we observe that L-GRAAL's protein mappings and interaction mappings are in better agreement with Gene Ontology (GO) (Ashburner et al., 2000) than any other network aligners. By aligning the PPI networks of baker's yeast and human, we additionally show that the results of L-GRAAL can be used to predict new PPIs. Finally, using our novel semantic similarity measure of the interaction mappings and the ability of L-GRAAL to produce alignments by using both topological and sequence similarity, we observe for the first time that topological similarity plays a more important role than sequence similarity in uncovering functionally conserved interactions, a result that escaped all previous approaches.
2 Materials and methods
2.1 Definitions and notations
2.1.1 PPI network
The PPIs of a given organism are represented by a PPI network, , where nodes in V represent proteins and two nodes u and v are connected by an edge (u, v) in E if the corresponding proteins are known to interact.
2.1.2 Global network alignment
Given two PPI networks, and , for which , a global alignment, f: , is a 1-to-1 mapping of the nodes in V1 to the nodes in V2. Formally, global alignment is assigned a real-valued score S:
| (1) |
where is the score of mapping a node of V1 to a node in V2, and is the score of mapping an edge of E1 to an edge of E2. The Global Network Alignment problem aims to find a global alignment that maximizes S.
2.1.3 Graphlets and orbits
Graphlets are small, connected, non-isomorphic, induced sub-graphs of a larger graph (denoted by in Fig. 1) (Pržulj et al., 2004). Within each graphlet, some nodes are topologically identical with others: such identical nodes are said to belong to the same automorphism orbit (denoted by in Fig. 1) (Pržulj, 2007). Graphlets generalize the notion of node degree: the graphlet degree of node v, denoted by , is the number of times node v touches a graphlet at orbit i (Pržulj, 2007). Graphlet degrees are successfully used for measuring the distance between two networks (Pržulj, 2007), as well as measuring the topological similarities among nodes in networks (Milenković and Pržulj, 2008), which are further applied for guiding the network alignment process in the GRAAL family of network aligners, and for comparing protein structures (Malod-Dognin and Pržulj, 2014).
Fig. 1.
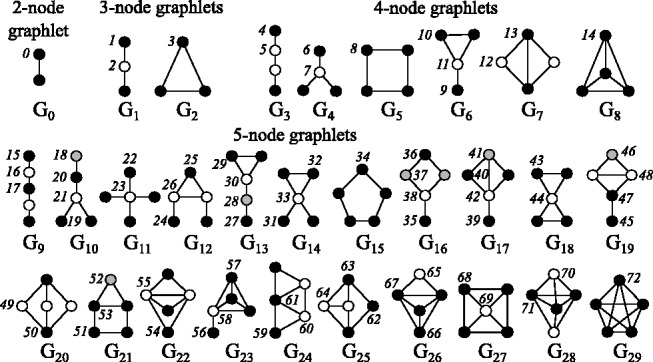
The 2- to 5-node graphlets and their automorphism orbits (Pržulj, 2007)
2.2 L-GRAAL method
2.2.1 Similarity scores and objective function
In L-GRAAL, we measure the evolutionary relationship between two mapped proteins u and f(u) according to their BLAST sequence alignment:
where seqsim can be any sequence-based similarity score (in this article, we use both log of BLAST's e-values and BLAST's bit-scores).
We measure the topological similarity between two mapped proteins u and f(u) using their 2- to 4-node graphlet degree similarity t:
We measure the topological similarity between two mapped interactions (edges), (u, v) and , according to the graphlet degree similarity of their mapped end nodes:
This score is in [0, 1] and it rewards mapping edges that are involved in similar local wiring patterns. Note that we also use all 2- to 5-node graphlet degrees, but it only resulted in larger running times, without improving the quality of the alignments.
L-GRAAL's objective function, S, either favors the evolutionary relationships between the mapped proteins or the topological similarity between the mapped interactions, according to a balancing parameter :
| (2) |
2.2.2 Two-step alignment search strategy
Because of the large sizes of PPI networks, solving the network alignment problem when considering all possible node mappings is computationally intractable.
In a first step, we use sequence and graphlet degree similarities to select a subset of the node mappings on which L-GRAAL will optimize seed alignments; namely, we only consider the node mappings , such that . We term the mapping that satisfy this criteria selected node mappings. In a second step, a greedy heuristic extends the seed alignments using all possible node mappings, i.e. without being restricted to selected node mappings anymore.
Because both L-GRAAL's and NATALIE's alignment search algorithms are based on integer programming and Lagrangian relaxation, Supplementary Section 1.4 presents the differences between the two approaches.
2.2.3 Generating seed alignments using integer programming
First, to each selected node mapping, , we associate a binary variable xik, such that xik = 1 if the node mapping is in the alignment and 0 otherwise. Similarly, we associate to each edge mapping between selected node mappings, , a binary variable yijkl, such that yijkl = 1 if the edge mapping is in the alignment and 0 otherwise. For brevity, henceforth, we ensure that each edge mapping is only considered once by enforcing k < l. This allows us to differentiate the two end-node mappings that result from an edge mapping : we term a tail-node mapping and a head-node mapping.
The network alignment problem can now be expressed with the following integer program (IP):
| (3) |
subject to:
| (4) |
| (5) |
| (6) |
| (7) |
where constraints (4, 5) enforce that a node from V1 is mapped to at most one node from V2 and vice versa and constraints (6, 7) enforce that the selected edge mappings must have their end-nodes mapped as: and .
Because of the 1-to-1 mapping constraints (4,5), the relations between the edge mappings and their head-node mappings can be rewritten in a compact form. Given a node mapping and any node , such that edge , then at most one edge mapping can be selected by choosing a node mapping . Constraint (6) can then be replaced by the following two set of constraints:
| (8) |
| (9) |
In IP, when all the constraints between the node mappings and the edge mappings are considered, the head-node mappings also respect the 1-to-1 matching constraints. To keep this property in our relaxed model, we add the following constraints into LR:
| (10) |
| (11) |
2.2.4 Lagrangian relaxation
To solve IP, we apply Lagrangian relaxation (Held and Karp, 1970), by relaxing constraints (8, 9), i.e. disconnecting the edge mappings from their head nodes. Relaxed constraints are added as penalties into the objective function, associated with Lagrangian multipliers ( for each constraint 8 and for each constraint 9). Because relaxed constraints are inequalities, the Lagrangian multipliers must be non-negative real numbers (i.e. ). This gives us the relaxed problem (LR):
| (12) |
subject to (4, 5, 7 and 10, 11), where and are the new node and edge scores after adding the penalties from the relaxed constraints.
We developed a double bipartite matching algorithm, detailed in the Supplementary Material, Section 1.1, for solving LR in time, where is the number of nodes in the networks and d is the largest degree of a node. Solving LR generates a relaxed solution . This relaxed solution is an upper bound on IP, as its score is greater than or equal to the one of IP, but it is often infeasible, as chosen edge mappings (the components of that are set to 1) may not coincide with chosen node mappings (the components of that are set to 1). However, any relaxed solution can be repaired into a feasible solution of IP by selecting the edge mappings corresponding to the selected node mappings. Such feasible solution is a lower bound on IP, as its score is smaller than or equal to the one of IP.
To solve IP, we solve its Lagrangian dual problem, which is a minimization of LR over λ. Many methods have been proposed so far for solving Lagrangian dual problem (Guignard, 2003). Here, we choose the sub-gradient descent method (Held et al., 1974) because of our large number of relaxed constraints. The sub-gradient descent is an iterative method that generates a sequence of Lagrangian multipliers , starting from , where aims to fix the broken relaxed constraints in the solution of LR(), by making a step along its sub-gradient vector. Details on our implementation are given in the Supplementary Material, Section 1.2. Unfortunately, the Lagrangian dual problem is also NP-complete, and thus one could not expect to solve it in a reasonable time.
In practice, the process of solving the Lagrangian dual is used for generating a sequence of seed solutions , until a given time limit or an iteration number limit is reached (we use 1 h and 1000 iterations as default).
2.2.5 Heuristically extending seed alignments
At each iteration of the sub-gradient descent, the seed alignment is extended to include all node mappings with a three-step greedy heuristic (see Algorithm 1 in Supplementary Material, Section 1.3). All node mappings that do not positively contribute to the score of the alignment are removed. The alignment is then maximally extended by sequentially visiting the yet unaligned nodes in V1 and mapping them to the yet unaligned nodes in V2, so that the score of the alignment is maximized. Then, a greedy local search sequentially visits V1 and tries inserting or exchanging node mapping to improve the score of the alignment. Note that the extended alignments are not returned to the dual solver, since they are not computed on the same search space (seed alignments are restricted to selected node mappings, whereas the extended alignments are not), so they would invalidate the sub-gradient descent scheme if included. When these computations end, L-GRAAL returns the extended alignment with the best score.
2.3 Datasets
From the manually curated BioGRID database (v3.2.101, June 2013) (Chatr-Aryamontri et al., 2013), we obtained PPI networks of eight organisms that have the largest number of known physical interactions: Homo sapiens (HS, 13 276 nodes and 110 528 edges), Saccharomyces cerevisiae (SC, 5831 nodes and 77 149 edges), Drosophila melanogaster (DM, 7937 nodes and 34 753 edges), Arabidopsis thaliana (AT, 5897 nodes and 13 381 edges), Mus musculus (MM, 4370 nodes and 9116 edges), Caenorhabditis elegans (CE, 3134 nodes and 5428 edges), Schizosaccharomyces pombe (SP, 1911 nodes and 4711 edges) and Rattus norvegicus (RN, 1657 nodes and 2330 edges). Note that physical interactions in BioGRID include both direct (e.g. from yeast-two-hybrid) and indirect (e.g. from affinity capture) interactions, so edges in our PPI networks connect proteins that either directly interact or that co-exist in stable complexes. We retrieved the corresponding protein sequences and GO annotations from NCBI's Entrez Gene database (Maglott et al., 2005). Note that we only retrieved experimentally validated GO annotations, from which we further removed the annotations inferred from PPIs (code IPI). L-GRAAL is one of the few methods that can align even the largest of the networks presented above. As already reported by Clark and Kalita (2014), many of the other aligners have memory issues when handling the two largest networks of yeast and human. Thus, the comparisons presented in sections 3.1 and 3.2 are based on the pairs of networks that involve DM, AT, MM, CE, SP and RN, which can be solved by all methods. L-GRAAL's alignments of yeast and human PPI networks are presented in Section 3.3. In the Supplementary Material, we also assess the robustness of our results by comparing the performance of network aligners on two more datasets. First, we create the binary PPI networks by restricting our BioGRID networks to the yeast-two-hybrid captured interactions only. Second, we use the synthetic random networks from the NAPA benchmark (Sahraeian and Yoon, 2012).
2.4 Evaluation
We compare the alignments of L-GRAAL to those of HUBALIGN, MAGNA, PISWAP, SPINAL, NETAL, GHOST, NATALIE, MI-GRAAL and ISORANK. We set MI-GRAAL to use graphlet degree vector similarity (GDS) alone, as well as to use GDS coupled with sequence similarity (GDS+SEQ); since it is a randomized algorithm, we repeat each alignment process 15 times for GDS and 15 times for GDS+SEQ, to find alignments of the best topological and biological quality. We set SPINAL to use mode II, as recommended in the corresponding paper. For all aligners that can produce alignments using pure topology or pure sequence information by balancing parameters varying in [0,1] (e.g. parameter α for L-GRAAL), we sample the balancing parameters from 0 to 1 in increments of 0.1. We set the time limits of both L-GRAAL and NATALIE to 1 h per alignment. We set MAGNA to optimize S3 score, on a population size of 2000, over 15 000 generations, setting that is recommended in the corresponding paper. For all network aligners, we leave other parameters at their default values. All computations are done on a desktop computer with an Intel Core I7–2600 CPU at 3.40 GHz with 64 GB of memory. For all these aligners, we report the results of their best alignments, according to the following measures.
2.4.1 Topological quality
Network aligners are first compared by their ability to map proteins that are similarly connected in both PPI networks. First, the size of the alignment is measured by EC, which is the percentage of interactions from the smaller network that are mapped to interactions from the other network (Kuchaiev et al., 2010). Because large EC can be achieved by mapping sparse regions of the smaller network to densely connected regions of the larger one, we also measure how topologically similar are the mapped regions using the symmetric sub-structure score (S3), which is the percentage of the conserved edges between the smaller network and the sub-network from the larger network that is induced by the alignment (Saraph and Milenković, 2014). Finally, we use the size of the largest connected component (LCC) to ensure that the alignments correspond to large common connected sub-structure, instead of several small disconnected ones (Kuchaiev et al., 2010).
2.4.2 Biological quality
It is not known which proteins from one PPI network should be mapped to which ones in the other PPI network. Biological similarity of two mapped proteins can be measured by the semantic similarity of their GO term annotations. We compute the semantic similarity using Resnik semantic similarity (Resnik, 1995) with best-match average mixing strategy. Then, we measure the biological quality of the entire alignment by the sum of the semantic similarities of the mapped proteins, divided by the smaller number of annotated proteins in the two networks.
3 Results and discussion
Here, we present the results achieved by network aligners on the real PPI networks from BioGRID.
3.1 Topological analysis
First, L-GRAAL, HUBALIGN and GHOST produce the largest alignments, with EC of 52.2% for L-GRAAL, 52.1% for HUBALIGN and 42.7% for GHOST (see the left panel of Fig. 2). These large alignments are key, as they allow transferring more information across networks. We also measure the statistical significance of the obtained EC scores using the standard model of sampling without replacement, as proposed by Kuchaiev et al. (2010) (the formula is presented in the Supplementary Material). All are statistically significant, as the probability of obtaining similar or higher values by chance is always smaller than 0.05. We test whether L-GRAAL achieves larger EC by mapping the smaller network to the densest regions of the larger network (the dense regions corresponding to, e.g. large complexes captured by affinity capture-based methods). This is not the case, since L-GRAAL, NETAL and MAGNA best map sparse regions with sparse regions and dense regions with dense regions, with symmetric sub-structures score = 31.1% for L-GRAAL, 29.3% for NETAL and 26.4% for MAGNA (see the middle panel of Fig. 2). In other word, L-GRAAL is less biased toward cliquish structures than other aligners. On the opposite, while HUBALIGN achieves EC that is comparable to the one of L-GRAAL, it achieves smaller S3 score. This is not surprising as HUBALIGN favors mapping densely connected proteins. Finally, HUBALIGN, L-GRAAL and MI-GRAAL produce the least fragmented network alignments, with LCC = 74.6% for HUBALIGN, 71.5% for L-GRAAL and 67.7% for MI-GRAAL (see the right panel of Fig. 2).
Fig. 2.
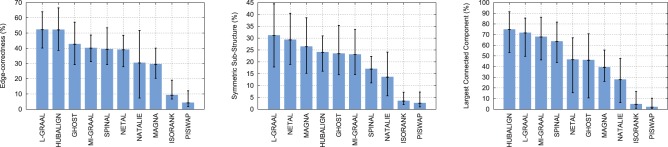
Topological comparisons of aligners. Methods (x axis) are compared according to the minimum, average and maximum of the best topological scores (the error bars on y axis) that they obtain when aligning PPI networks. Left: Methods are compared according to EC. Middle: Methods are compared according to symmetric sub-structure score (S3). Right: Methods are compared according to the size of the LCC in their alignments
Overall, L-GRAAL and HUBALIGN outperform all other aligners in terms of the topological quality of their alignments on the real networks from BioGRID (we also observe similar results when aligning binary PPIs only, see Supplementary Fig. S4). However, although L-GRAAL also achieves good performances when aligning the synthetic networks from the NAPA benchmark, HUBALIGN does not, which shows the higher robustness of L-GRAAL (see Supplementary Fig. S5).
3.2 Biological analysis
As presented in the left panel of Figure 3, L-GRAAL, HUBALIGN and GHOST map proteins that are involved in similar GO biological processes (GO-BPs) best, with average semantic similarity of the protein mappings of 1.09 for L-GRAAL, 1.08 for HUBALIGN and 1.04 for GHOST. Similar holds for GO molecular functions (GO-MFs) and GO cellular component annotations (GO-CC), as presented in the middle and right panels of Fig. 3).
Fig. 3.
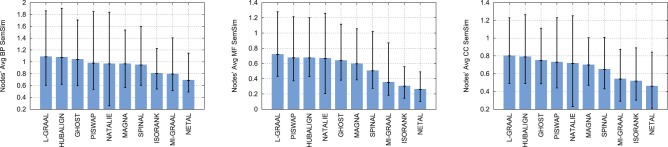
Biological comparison of network aligners. Methods (x axis) are compared according to the minimum, average and maximum semantic similarity of their aligned proteins (the error bars on y axis), when semantic similarity is measured using GO-BP (left), GO-MF (middle) or GO-CC (right)
Large semantic similarities of the protein mappings indicate that the alignments map functionally conserved proteins, but it does not mean that these functions are performed through conserved interaction patterns between the two PPI networks. Although functionally conserved interactions may highlight fundamental mechanisms (e.g. key binary interactions or complexes that must be conserved), network aligners are never compared in this respect. To measure the functional conservation of the mapped interactions, we define the semantic similarity of two mapped interactions as the average of the semantic similarities of the corresponding pairs of mapped proteins. Then, we measure the biological quality of the whole interaction mapping as the sum of all the interaction semantic similarities divided by the smaller number of interactions between annotated proteins in the two networks. To the best of our knowledge, this is the first time that the biological quality of the interaction mapping is considered.
As presented in Supplementary Figure S1, HUBALIGN, L-GRAAL and SPINAL are the best in mapping interactions that are involved in similar BPs, in similar MFs, and that are localized in similar cellular regions. Overall, L-GRAAL and HUBALIGN outperform all other aligners in terms of the biological quality of their alignments when aligning real networks from BioGRID (we also observe similar results when aligning binary PPIs only, see Supplementary Fig. S4) and again L-GRAAL shows higher robustness than HUBALIGN when aligning synthetic networks from the NAPA benchmark (see Supplementary Fig. S5).
3.3 Predicting protein interactions
Although a good network alignment should map together functionally related proteins that interact in similar ways, alignments are also composed of edge-mismatches, where interacting proteins are mapped to non-interacting proteins.
To illustrate this phenomenon, we first investigate the largest shared pathway between Saccharomyces cerevisiae and Homo sapiens PPI networks that is found in L-GRAAL's alignment, which is the ribosome pathway (KEGG Id 3010) that contains 105 proteins and 862 interactions.
This alignment, illustrated in the left panel of Figure 4, correctly aligns the dense sub-network from yeast to the dense sub-network of human. However, it also aligns interacting proteins to non-interacting ones. For example, it aligns yeast's MRPS5 and MRP17, which interact according to BioGRID's data, with human's MRPS5 and MRPS6, which are not reported to interact in BioGRID (see the inset of Fig. 4). Further investigation shows that these two protein mappings are biologically relevant. First, the proteins are evolutionarily related: human's and yeast's MRPS5 share 33.6% of sequence identity, and human's MRPS6 and yeast's MRP17 share 29.3% of sequence identity. Second, human's MRPS5 and MRPS6 are known to interact, as captured by anti tag coimmunoprecipitation assay (Richter et al., 2010). Therefore, L-GRAAL's alignment of yeast edge (MRPS5, MRP17) predicted the missing interaction in human data from BioGRID.
Fig. 4.
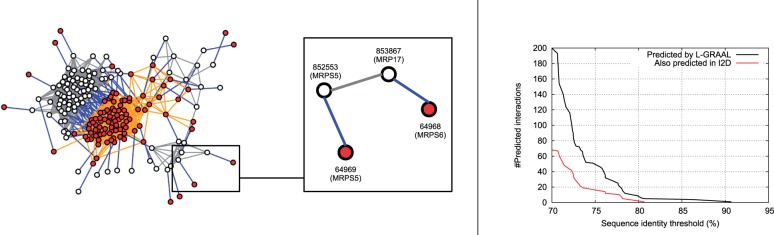
Predicting new protein interactions. Left: Part of L-GRAAL's alignment that aligns human and yeast ribosome pathways. The PPI sub-network of yeast (white nodes and gray edges) is mapped to the PPI sub-network of human (red nodes and orange edges) as indicated by the blue edges. The inset highlights a predicted interaction: Proteins MRPS5 and MRP17, which are interacting in the yeast PPI network, are aligned to proteins MRPS5 and MRPS6, which are not interacting in the human PPI network. Right: Using the whole L-GRAAL's alignment between yeast and human PPI networks, we plot in black the number of predicted interactions (y axis) as a function of the minimum sequence identity between the aligned yeast-human proteins (x axis). We add in red the number of these predicted interactions that are also predicted in I2D database
Building upon this insight, we measure how many potential interactions can be predicted by L-GRAAL's alignment, by counting the number of edge-mismatches whose node mappings involve proteins with high sequence identity. In this way, we show that L-GRAAL's alignment can predict 200 potential interactions for which the sequence identity between the mapped proteins is ≥70%, threshold for which the mapped proteins are expected to share the same functions (Rost, 2002), see the right panel of Figure 4. Supplementary Figure S3 presents the number of predictions that are obtained when using less stringent sequence identity thresholds (the list of all predicted interactions is available in the Supplementary Excel Table).
We find that 34% of these predicted interactions are also predicted in the Interologous Interaction Database (I2D ver. 2.3) (Brown and Jurisica, 2007), which is statistically significant since the probability to obtain better or equal overlaps by chance is less than (using sampling without replacement, as detailed in the Supplementary Material, Section 1.5). This result suggests that network aligners such as L-GRAAL can be used as alternative protein interaction predictors.
3.4 Balancing sequence and topological information
L-GRAAL can produce alignments from topology and sequence information when the balancing parameter, α, varies from 0 to 1. In the previous experiments, we report the best scores (EC, S3, semantic similarities of protein and interaction mappings) that are obtained when α varies from 0 to 1 using a step size of 0.1. Here, we report the effect of α on each of these scores. The corresponding plots are presented in Supplementary Figure S2.
First, all topological scores reach their maximum values when using topological information only (α = 0), with EC = 51.5%, S3 = 30.9% and LCC = 68.1% on average. It is also important to notice that using sequence information only (α = 1) results in alignment having almost no common interactions (EC = 2.0%, on average). Second, the semantic similarities of the aligned proteins either reach their maximum when using both topological and sequence information or when using sequence similarity only, for BP and cellular component and α = 1 for MF. In contrast, the semantic similarities of the aligned interactions reach their maximum when using topological information only (α = 0).
These results show again the complementarity of the two sources of information. Also, the comparison between the interactions’ semantic similarities that are obtained when using topological information only with the ones that are obtained when using sequence information only suggests that topology plays a more important role than sequence for uncovering functionally conserved interactions. To the best of our knowledge, this is the first time that this is observed. The importance of topology may be due to the concept of function itself, which implies interactions with some part of the cell or the environment (Hartwell et al., 1999) and these interactions are captured by the topology of the PPI networks. Also, sequence similarity may fail at identifying the correct one-to-one relationships between genes when their homology relationships are not straightforward. Such difficult cases where topology is required include finding the relationships between a set of paralogous genes in a given species and its set of co-ortholog genes in another species.
4 Concluding remarks
First, we propose a global network alignment method called L-GRAAL, which combines a novel objective function where the topological similarity of the mapped interaction is based on graphlet degree, with an efficient network alignment search algorithm based on integer programming and Lagrangian relaxation. Using the largest PPI networks from BioGRID, we show that L-GRAAL's alignments outperform other network alignments: they uncover the largest common sub-networks between aligned networks, as measured by EC and symmetric sub-structure scores.
Second, as measured by the average semantic similarity of the mapped proteins, we observe that L-GRAAL best uncovers functionally conserved proteins. Because the objective of network aligners is not only to uncover functionally conserved proteins but also functionally conserved interactions among these proteins, we propose a novel way of measuring the semantic similarity of the mapped interactions and observe that L-GRAAL is among the best aligners for uncovering functionally conserved interactions.
Third, on a case study of aligning human and yeast PPI networks, we show that L-GRAAL can be used to predict new interactions. Designing a whole benchmarking and validation strategy needed for finding which network aligners best predict protein interactions and for precisely comparing such predictions with the ones of traditional predictors are out of scope of this study.
Fourth, using the ability of L-GRAAL to produce alignments using topological and sequence similarity, we observe that topological similarity plays a more important role than sequence similarity for uncovering functionally conserved interactions. To the best of our knowledge, this is the first time that this has been observed.
Finally, L-GRAAL's computations can be easily speed up by using parallel programming. In each iteration of the Lagrangian dual solver, i.e. when solving LR for a given λ, each local bipartite matching for finding the best set of outgoing edges from a given node is an independent task. In addition, each bipartite matching problem, local and global, can be solved with parallel versions of the successive shortest paths algorithm (Storøy and Sørevik, 1997). This high level of parallelism for speeding up L-GRAAL's computations is very promising as it allows it to scale with the future growth of the interaction data.
Supplementary Material
Acknowledgements
We wish to thank Mr M. El-Kebir and Dr G.W. Klau for sharing with us their C++ implementation of the maximum weighted bipartite matching solver based on successive shortest paths. We also thank the anonymous reviewers for their helpful comments and ideas.
Funding
This work was supported by the European Research Council (ERC) Starting Independent Researcher Grant [278212], the National Science Foundation (NSF) Cyber-Enabled Discovery and Innovation (CDI) [OIA-1028394], the ARRS project [J1-5454] and the Serbian Ministry of Education and Science Project [III44006].
Conflict of Interest: none declared.
References
- Aladağ A.E., Erten C. (2013) Spinal: scalable protein interaction network alignment. Bioinformatics , 29, 917–924. [DOI] [PubMed] [Google Scholar]
- Ashburner M., et al. (2000) Gene ontology: tool for the unification of biology. Nat. Genet. , 25, 25–29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bandyopadhyay S., et al. (2006) Systematic identification of functional orthologs based on protein network comparison. Genome Res. , 16, 428–435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown K.R., Jurisica I. (2007) Unequal evolutionary conservation of human protein interactions in interologous networks. Genome Biol. , 8, R95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chatr-Aryamontri A., et al. (2013) The BioGRID interaction database: 2013 update. Nucleic Acids Res. , 41, D816–D823. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chindelevitch L., et al. (2013) Optimizing a global alignment of protein interaction networks. Bioinformatics , 29, 2765–2773. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clark C., Kalita J. (2014) A comparison of algorithms for the pairwise alignment of biological networks. Bioinformatics, 30, 2351–2359. [DOI] [PubMed] [Google Scholar]
- Cook S.A. (1971) The complexity of theorem-proving procedures. In: Proceedings of the Third Annual ACM Symposium on Theory of Computing , STOC '71, Shaker Heights, Ohio, USA. ACM, New York, NY, pp. 151–158. [Google Scholar]
- El-Kebir M., et al. (2011) Lagrangian relaxation applied to sparse global network alignment. In: Loog M., et al. (eds.) Pattern Recognition in Bioinformatics, volume 7036 of Lecture Notes in Computer Science. Springer Berlin Heidelberg, Berlin, Germany, pp. 225–236. [Google Scholar]
- Fields S., Song O.K. (1989) A novel genetic system to detect protein-protein interactions. Nature , 340, 245–246. [DOI] [PubMed] [Google Scholar]
- Flannick J., et al. (2006) Graelin: general and robust alignment of multiple large interaction networks. Genome Res. , 16, 1169–1181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guignard M. (2003) Lagrangean relaxation. TOP , 11, 151–200. [Google Scholar]
- Hartwell L.H., et al. (1999) From molecular to modular cell biology. Nature , 402, C47–C52. [DOI] [PubMed] [Google Scholar]
- Hashemifar S., Xu J. (2014) Hubalign: an accurate and efficient method for global alignment of protein–protein interaction networks. Bioinformatics , 30, i438–i444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Held M., Karp R.M. (1970) The traveling-salesman problem and minimum spanning trees. Oper. Res. , 18, 1138–1162. [Google Scholar]
- Held M., et al. (1974) Validation of subgradient optimization. Math. Programming , 6, 62–88. [Google Scholar]
- Ho Y., et al. (2002) Systematic identification of protein complexes in Saccharomyces cerevisiae by mass spectrometry. Nature , 415, 180–183. [DOI] [PubMed] [Google Scholar]
- Kelley B.P., et al. (2003) Conserved pathways within bacteria and yeast as revealed by global protein network alignment. Proc. Natl Acad. Sci. USA , 100, 11394–11399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kelley B.P., et al. (2004) PathBLAST: a tool for alignment of protein interaction networks. Nucleic Acids Res. , 32(Suppl. 2), W83–W88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koyutürk M., et al. (2006) Pairwise alignment of protein interaction networks. J. Comput. Biol. , 13, 182–199. [DOI] [PubMed] [Google Scholar]
- Kuchaiev O., Pržulj N. (2011) Integrative network alignment reveals large regions of global network similarity in yeast and human. Bioinformatics , 27, 1390–1396. [DOI] [PubMed] [Google Scholar]
- Kuchaiev O., et al. (2010) Topological network alignment uncovers biological function and phylogeny. J. R. Soc. Interface , 7, 1341–1354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maglott D., et al. (2005) Entrez gene: gene-centered information at NCBI. Nucleic Acids Res. , 33(Suppl. 1), D54–D58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malod-Dognin N., Pržulj N. (2014) GR-align: fast and flexible alignment of protein 3D structures using graphlet degree similarity. Bioinformatics, 30, 1259–1265. [DOI] [PubMed] [Google Scholar]
- Memišević V., Pržulj N. (2012) C-GRAAL: Common-neighbors-based global GRAph ALignment of biological networks. Integr. Biol. , 4, 734–743. [DOI] [PubMed] [Google Scholar]
- Milenković T., Pržulj N. (2008) Uncovering biological network function via graphlet degree signatures. Cancer Inform. , 6, 257. [PMC free article] [PubMed] [Google Scholar]
- Milenković T., et al. (2010) Optimal network alignment with graphlet degree vectors. Cancer Inform. , 9, 121–137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nepusz T., Paccanaro A. (2014) Structural pattern discovery in protein–protein interaction networks. In: Kasabov N. (ed.) Springer Handbook of Bio-/Neuroinformatics. Springer Berlin Heidelberg, Berlin, Germany, pp. 375–398. [Google Scholar]
- Neyshabur B., et al. (2013) NETAl: a new graph-based method for global alignment of protein-protein interaction networks. Bioinformatics , 29, 1654–1662. [DOI] [PubMed] [Google Scholar]
- Patro R., Kingsford C. (2012) Global network alignment using multiscale spectral signatures. Bioinformatics , 28, 3105–3114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pržulj N. (2007) Biological network comparison using graphlet degree distribution. Bioinformatics , 23, 177–183. [DOI] [PubMed] [Google Scholar]
- Pržulj N. (2011) Protein-protein interactions: making sense of networks via graph-theoretic modeling. Bioessays , 33, 115–123. [DOI] [PubMed] [Google Scholar]
- Pržulj N., et al. (2004) Modeling interactome: scale-free or geometric? Bioinformatics , 20, 3508–3515. [DOI] [PubMed] [Google Scholar]
- Resnik P. (1995) Using information content to evaluate semantic similarity in a taxonomy, Journal: arXiv preprint cmp-lg/9511007. [Google Scholar]
- Richter R., et al. (2010) A functional peptidyl-tRNA hydrolase, ict1, has been recruited into the human mitochondrial ribosome. EMBO J. , 29, 1116–1125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rost B. (2002) Enzyme function less conserved than anticipated. J. Mol. Biol. , 318, 595–608. [DOI] [PubMed] [Google Scholar]
- Ryan C.J., et al. (2013) High-resolution network biology: connecting sequence with function. Nat. Rev. Genet., 14, 865–879 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sahraeian S.M.E., Yoon B.-J. (2012). A network synthesis model for generating protein interaction network families. PLoS One , 7, e41474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saraph V., Milenković T. (2014) Magna: Maximizing accuracy in global network alignment. Bioinformatics , 30, 2931–2940. [DOI] [PubMed] [Google Scholar]
- Seah B.-S., et al. (2014). Dualaligner: a dual alignment-based strategy to align protein interaction networks. Bioinformatics, 30, 2619–2626. [DOI] [PubMed] [Google Scholar]
- Singh R., et al. (2007) Pairwise global alignment of protein interaction networks by matching neighborhood topology. In: Speed T., Huang H. (eds.), Research in Computational Molecular Biology, volume 4453 of Lecture Notes in Computer Science. Springer Berlin Heidelberg, Berlin, Germany, pp. 16–31. [Google Scholar]
- Storøy S., Sørevik T. (1997) Massively parallel augmenting path algorithms for the assignment problem. Computing , 59, 1–16. [Google Scholar]
- Tian W., Samatova N. (2009) Pairwise alignment of interaction networks by fast identification of maximal conserved patterns. In: Pacific Symposium on Biocomputing , Vol. 14, pp. 99–110. [PubMed] [Google Scholar]
- Uetz P., et al. (2006) Herpesviral protein networks and their interaction with the human proteome. Science , 311, 239–242. [DOI] [PubMed] [Google Scholar]
- Zaslavskiy M., et al. (2009) Global alignment of protein-protein interaction networks by graph matching methods. Bioinformatics , 25, i259–i1267. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


