Abstract
This review describes the diffusion model for light transport in tissues and the medical applications of diffuse light. Diffuse optics is particularly useful for measurement of tissue hemodynamics, wherein quantitative assessment of oxy- and deoxy-hemoglobin concentrations and blood flow are desired. The theoretical basis for near-infrared or diffuse optical spectroscopy (NIRS or DOS, respectively) is developed, and the basic elements of diffuse optical tomography (DOT) are outlined. We also discuss diffuse correlation spectroscopy (DCS), a technique whereby temporal correlation functions of diffusing light are transported through tissue and are used to measure blood flow. Essential instrumentation is described, and representative brain and breast functional imaging and monitoring results illustrate the workings of these new tissue diagnostics.
1. Introduction
More than 80 years ago [1] light was employed to “see” tumors in thick tissues. Basic ideas from those measurements still survive today. Optical methods offer a range of sensitivities useful for characterization of a wide variety of samples. The simplest of these methods is light absorption, whereby attenuation in signal intensity occurs whenever the light wavelength coincides with a material resonance. This effect permits quantitative identification of the molecules present in a sample, their concentration, and their local environment. In a different vein, light scattering provides information about micron-size objects (e.g. molecular weight, particle diameter) that scatter light in the sample, and dynamic or quasi-elastic light scattering (DLS or QELS, respectively) provides information about the motions of those objects. Generally, these traditional optical techniques are rigorous and are well established in simple, homogeneous, optically thin samples.
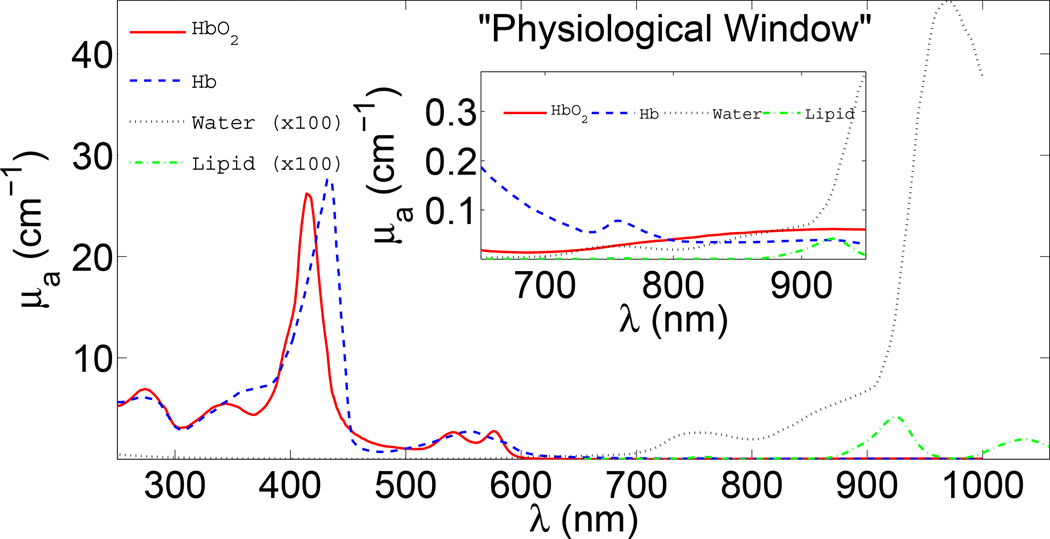
In order to use these schemes to study biological tissues, however, a physical understanding of photon propagation in highly scattering media is required. Otherwise the traditional techniques remain qualitative (at best) or are fraught with systematic errors (at worst). A key contribution to optical studies of tissue was made by Jöbsis in the late 1970s [2–4]. Jöbsis observed a spectral window in the near-infrared (NIR, ~650–950 nm) wherein photons could travel deep in tissue, as a result of the relatively reduced absorption of water and hemoglobin (see Figure 1). Of course this penetrating light was also scattered in tissue and more physics insight was required for better quantification of detected signals. Since the early work, arguably the most critical advance in the field was the recognition and widespread acceptance that light transport over long distances in tissues is well approximated as a diffusive process [5,6]. Using this physical model it is possible to quantitatively separate tissue scattering from tissue absorption, and to accurately incorporate the influence of boundaries and heterogeneities [5, 7–22]. These models for light propagation formalized the field and paved the way for a large variety of applications ranging from imaging breast tumors (“optical mammography”) to functional imaging of brain [23].
Figure 1.
Absorption (μa) spectra of main tissue chromophores over a large wavelength range. The inset shows the so-called “physiological window” in the near-infrared where water and hemoglobin absorption are relatively low. In this part of the spectrum, light can penetrate several centimeters into tissue. Furthermore, there are clear features in the spectra which enable estimation of chromophore concentration from diffuse optical measurements at several wavelengths.
Generally, the propagation of light through tissues is profoundly affected by scattering. Two length scales are important in this context: a rather short “scattering length” which corresponds to the typical distance traveled by photons before they scatter, and a longer “transport mean-free path” or “random walk step” which corresponds to the typical distance traveled by photons before their direction is randomized. The reciprocal of the photon transport mean free path is called the reduced scattering coefficient; it is wavelength-dependent and is denoted by , where λ is the wavelength of light. Light transport in tissue is also affected by a relatively smaller absorption. The wavelength dependent absorption length in tissue corresponds to the typical distance traveled by a photon before it is absorbed; its reciprocal, the absorption coefficient, is denoted by μa(λ).
In order to sort scattering from absorption in tissue, a model that separates the effects of tissue scattering from tissue absorption is required. The diffusion model provides a formal mathematical basis for this separation, and as a result of this approximation, experimenters can directly measure oxy- and deoxy-hemoglobin (HbO2,Hbr/Hb), water, and lipid concentrations using the well known spectra (Figure 1) of these molecules in the inverse analysis [5, 23]. From the scattering coefficient, experimenters gain access to information about cells, cell nuclei, cell organelles and surrounding fluids as well. Herein, we will refer to this measurement technique which uses diffuse near-infrared light to infer scattering and absorption, as “diffuse optical spectroscopy” (DOS) or “near-infrared spectroscopy” (NIRS). The imaging analog of DOS is called diffuse optical tomography (DOT); DOT provides a means to assign tissue optical and physiological properties independently to many volume elements within the tissue sample. Here we use “tomography” to refer to both “topographic” (2D) and “tomographic” (3D) approaches because they share similar formalism.
The diffusion approach is quite versatile and can be adapted to measure the concentrations and lifetimes of exogenous contrast agents such as dyes which may improve tumor contrast or specificity [24, 25]. A recent example of this application is fluorescence diffuse optical tomography wherein the fluorescent emission of a FDA approved contrast agent, Indocyanine Green (ICG), was used to identify breast cancer [26]. Other uses include the measurement of the concentration of oxidized cytochrome c-oxidase [2, 27] and the measurement of very fast changes in scattering related to neuronal swelling during neuronal activity [28, 29]. To learn more about these and other applications, readers can consult other recent reviews [23, 24, 30–35].
More information is available from diffusing light in tissues. Speckle fluctuations of light scattered by tissues are sensitive to the motions of scatterers such as red blood cells (RBCs). The traditional, single-scattering version of this optical technique is well known and has appeared with numerous names [36–50] over the years. In most of these experiments the temporal auto-correlation function of the scattered electric field (or its Fourier Transform) is measured and is explicitly related to the motions of scatterers within the samples. The most significant tissue signal derived from the temporal auto-correlation function is from blood flow. Early physiological work utilized single-scattering theory to analyze data derived from pairs of very closely separated (~0.25 mm) optodes, e.g. Laser Doppler and CCD-based speckle devices [41–43, 50–59]. Therefore, most of these early methods probed superficial tissue (< 1 mm). In the low signal limit, the photon correlation technique has an advantage over its Fourier counterpart because photon correlation instruments are essentially single photon counting devices. This advantage enables experimenters to probe more deeply into tissue samples, and begs for theoretical models to understand similar signals from deep tissues.
The multiple scattering analog of these dynamic light scattering measurements is called “diffuse correlation spectroscopy” (DCS) [60, 61] (Note, the technique called “diffusing wave spectroscopy” (DWS) [62–64] was introduced before DCS. DWS is essentially an integral formulation of DCS; the name DCS, however, has been adopted in the biomedical optics field because “DWS” had connotations for both absorption spectroscopy and fluctuation spectroscopy). Formally, DCS relies on the fact that diffusing temporal correlation also obeys a diffusion equation, albeit a slightly different one than is used for absorption spectroscopy. It shares the light penetration advantages of NIRS/DOS, but, since DCS explicitly measures cell movement, it provides a direct measure of quantities such as cerebral blood flow (CBF) [65–67]. Compared to NIRS/DOS and DOT, DCS is a relatively new methodology. DCS has been extensively validated in vivo in tissues, including comparisons with laser Doppler flowmetry (LDF) [65], Doppler ultrasound (DU) [65, 68–71], arterial-spin labeled MRI (ASL-MRI) [65,66,72,73], Xenon-CT [74], fluorescent microsphere measurement of CBF [75], and against expectations from invasive and non-invasive measures of tissue physiology [65–67,76–78]. In total, these and other [65,66,68–71,73–90] studies have shown that DCS can reliably provide a blood flow index (BFI) proportional to relative changes of tissue blood flow, and that the combination of DCS and DOS/DOT hold potential for continuous non-invasive estimation of metabolic rate of oxygen extraction that relies on fewer approximations than DOS/DOT alone, hence improving the quality of the estimates [71].
The remainder of this review outlines the fundamentals of diffuse optics in tutorial fashion. Towards the end of this review we illustrate the utility of diffuse optics with recent examples from optical mammography and cerebral monitoring. A glossary of terms and symbols is provided at the end of this document.
2. Theoretical Background
2.1. Photon Diffusion Formalism
Transport theory is the starting point for most theoretical formulations of diffuse optics. The key quantity in this formulation is the light radiance, L(r, Ω̂, t) (W/cm2sr), defined as the light power per unit area traveling in the Ω̂ direction at position r and time t. The light radiance is related to the light electric field; L ~ |E(r, Ω̂, t)|2, where E(r, Ω̂, t) is the electric field at (r, t) traveling in the Ω̂ direction. L(r, Ω̂, t) is governed by the radiation transport equation (RTE), which is a conservation equation for the radiance in each infinitesimal volume element within the sample [91–93], i.e.,
| (1) |
f(Ω̂, Ω̂′) is the normalized differential cross-section for single light scattering events in the medium; it essentially gives the probability that scattered light is scattered into the direction Ω̂′, given its incident direction was Ω̂. Q(r, Ω̂, t) (W/cm3sr) is the power per volume emitted by sources at position r and time t in the Ω̂ direction. The loss of radiance out of each infinitesimal volume element depends on the absorption and scattering coefficients in the volume and is formally characterized by the coefficient μt = μa + μs. Here μs (cm−1) is the light scattering coefficient, i.e., the reciprocal of the ‘scattering length’ (note, μs is different from ), and μa (cm−1) is the light absorption coefficient, i.e., the reciprocal of the ‘absorption length’. υ is the speed of light in the medium. The left-hand side of Equation (1) is a convective time derivative of the radiance in the infinitesimal volume element about r at time t travelling in direction Ω̂. This convective derivative of the radiance must equal the losses due to absorption and scattering (first term, right-hand side) plus the gains from radiance scattered into Ω̂ (third term, right-hand side), and gains from sources (second term, right-hand side). In most cases of interest, the RTE must be solved numerically.
To reduce the complexity of the RTE, we employ a standard method for approximating Equation (1) called the PN approximation. In this method, L is written as a series expansion of spherical harmonics, Yℓm (with coefficients ϕℓm), truncated at ℓ = N [91–94]:
| (2) |
We also assume that the normalized differential scattering cross-section, f, depends only on the the angle between incident and outgoing scattering wavevectors, i.e., f(Ω̂, Ω̂′) = f(Ω̂·Ω̂′). When L(r, Ω̂, t) is nearly isotropic, the so-called P1 approximation (wherein the series expansion in Equation (2) is truncated at N = 1) is valid, and we have [91–94]
| (3) |
Equation (3) introduces two important quantities. The photon fluence rate, Φ(r, t) (W/cm2), is defined as the total power per area moving radially outward from the infinitesimal volume element at position r and time t ‡. More explicitly,
| (4) |
The photon flux J(r, t) (W/cm2) is a vector sum of the radiance emerging from the infinitesimal volume, i.e.,
| (5) |
Thus, J(r, t) · Ω̂ is the power per area travelling in the Ω̂ direction at position r and time t.
The photon fluence rate and flux are related by a continuity equation obtained from integrating Equation (1) over all solid angles:
| (6) |
Here, S(r, t) (W/cm3) is the total power per volume emitted radially outward from position r at time t, i.e., S(r, t) ≡ ∫4π Q(r, Ω̂, t)dΩ.
In the P1 approximation, another relation between Φ and J is obtained by substituting Equation (3) into Equation (1); we then multiply the resulting P1 transport equation by Ω̂ and integrate over all solid angles to obtain §
| (7) |
The anisotropy factor g, which emerges from the differential scattering integral in Equation (1), is the ensemble average of the cosine of the scattering angle θ, i.e., g ≡ ∫4π f(Ω̂ · Ω̂′)Ω̂ · Ω̂′dΩ′ = 〈cos θ〉. The closer g is to unity, the more probable it is for a photon to be scattered in the forward direction. In soft mammalian tissue, typical values for g range between 0.8 and 0.98 [95].
Assuming isotropic sources (Q(r, Ω̂, t) = Q(r, t)), the integral over Q in Equation (7) is zero. Furthermore, if we also assume slow temporal variations in the photon flux J, then (1/υ)∂J/∂t in Equation (7) can be neglected compared to (μt − μsg)J. With these two assumptions, Equation (7) simplifies to Fick’s law of diffusion, i.e.,
| (8) |
is called the reduced scattering coefficient.
Substituting Equation (8) into Equation (6) results in the photon diffusion equation for the photon fluence rate [20, 96, 97]:
| (9) |
Here we have defined the photon diffusion coefficient .
Microscopically, within this P1 picture, photons travel through the medium along random walk pathways. Each photon is visualized to travel in straight-line segments with sudden interruptions wherein either the propagation direction is randomly changed or the photon is absorbed. The average length of the straight-line segments is the photon random walk step or the transport mean free path, ℓtr, which is approximately .
The validity of the photon diffusion model (Equation (9)) rests on the validity of the P1 approximation (Equation (3)), which requires the radiance to be nearly isotropic (Φ ≫ |J|). This isotropy is achieved when , and when photon propagation distances within the medium are large relative to ℓtr. As a rough rule of thumb, should exceed 10 to accurately apply the diffusion model [98]. Additional assumptions, noted above, include source isotropy, slow temporal flux variations, and rotational symmetry (i.e., f(Ω̂, Ω̂′) = f(Ω̂ · Ω̂′)). Near a boundary such as an air-tissue interface, the radiance will no longer be nearly isotropic. In Section 2.5, we will show how the diffusion model can be applied near the surface with additional boundary conditions at the interface. For anisotropic tissues, such as axon fiber bundles where the rotational symmetry assumption may no longer be reasonable, slightly more complicated anisotropic diffusion models [99] are necessary for data fitting. For complex tissues that contain “non-diffusing” domains such as (arguably) cerebral spinal fluid inside the head [100,101], or that contain very high concentrations of blood, as in the liver, optimal data analysis requires approximations beyond P1. In applications wherein photon propagation distances are comparable to ℓtr, the photon propagation directions do not fully randomize. Thus, approximations beyond the P1 are needed here as well. We will discuss various schemes that extend beyond the diffusion (i.e. P1) approximation in Section 2.10.
2.2. Source Types
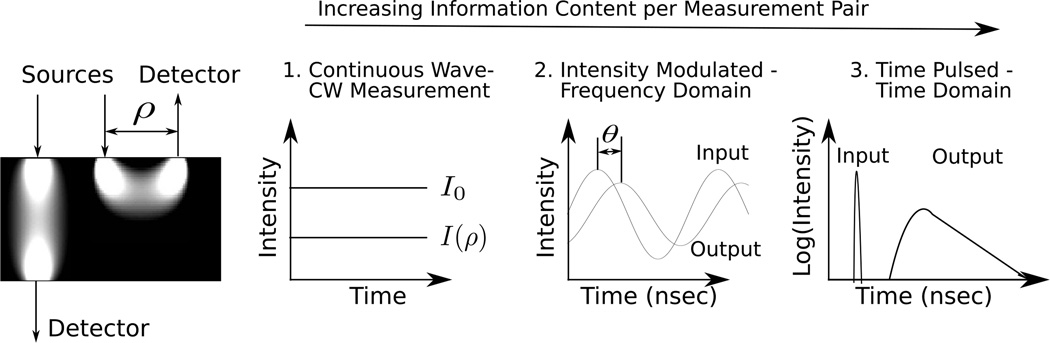
To apply the diffusion model, one typically detects light at known distances from point sources. Figure 2 shows two source-detector pairs; one in the reflection geometry and the other in the transmission geometry. In the reflection geometry, light injected into the tissue by a source fiber (usually coupled to a laser) is detected a distance ρ away with another fiber (usually coupled to a photo-multiplier tube or avalanche photo-diode). In the transmission geometry, light detection is facilitated using either a fiber or a lens/CCD camera system. At first glance, the directional light from a fiber violates the isotropic source assumption for the diffusion model. This light, however, can be very well approximated by an isotropic light source at depth ℓtr inside the tissue [97]. In practice, source-detector separation should exceed 3ℓtr to apply the diffusion model and expect accurate (~5%) results [102].
Figure 2.
Three common types of sources are employed. On the far left are schematic “banana patterns” showing the sampled volumes in the reflection and transmission geometries. As a rough rule of thumb, the mean light penetration depth in the reflection geometry is ρ/2 (for a more precise relation, see [498]). For continuous wave (CW), intensity modulated (FD) and time-resolved (TR) sources, the detected light intensity over time resembles (1), (2), and (3) respectively.
Three types of light sources commonly used in diffuse optics are (see Figure 2): continuous wave (CW), intensity modulated (FD), and time pulsed (TRS). The simplest source type is CW light, where the intensity remains constant over time [103–106]. This enables fast data acquisition and the use of simple detectors and detection electronics, but as we will discuss further, μa and D cannot be determined simultaneously from a single measurement.
Intensity modulated sources (the frequency-domain technique, FD) are more complex but also give more information about the medium [9, 15, 107, 108]. Here, the light intensity of the source at position rs is sinusoidally modulated with angular frequency ω (of order approximately 100 MHz or larger, up to ~1 GHz), producing a diffusive wave in the medium oscillating at the same frequency. At a given source-detector separation, both the amplitude and phase of the diffusing wave are measured. The additional information from the phase, in principle, permits simultaneous determination of μa and D.
Time pulsed light (the time-domain technique, TRS) is related to intensity modulated light via a Fourier transform, and it contains the same information content as intensity modulated sources scanned over the wide range of modulation frequencies present in the pulse [8, 12, 109–112]. Specifically, a short light pulse (< 100 ps) is delivered to the medium at position rs and time ts. The pulse temporally broadens as it propagates through the medium. At the detector, the pulse shape contains the necessary information to determine D and μa from a single source-detector pair. Also, by employing time-gating and moments analysis at the detection end, it is possible to pathlength resolve the detected light in order to reject contributions from superficial tissue layers [113, 114].
2.3. Diffuse Photon Density Waves
Most of the following theoretical discussion will be given in the frequency-domain, with the time-domain solution given for a common case. Frequency-domain sources induce fluence rate disturbances that behave in many ways like overdamped waves. To appreciate this point, we start with the diffusion equation for the fluence rate (Equation (9)) and assume the source term has DC and AC parts and can be written in the form S(r, t) = SDC(r) + SAC(r)e−iωt. Then we look for the solutions that oscillate at the same angular frequency as the source. These AC solutions will have the following general form
| (10) |
Substituting ΦAC into Equation (9), we see that U(r) is described by
| (11) |
which for homogeneous media gives
| (12) |
with k2 = (υμa−iω)/D. The general solution of Equation (12) is an overdamped wavelike fluence rate ‘disturbance’ in the turbid medium. Note, slightly different definitions for k2, e.g. k2 = (−υμa + iω)/D or k2 = −(υμa + iω)/D with ΦAC(r, t) = U(r)eiωt, enable us to write Equation (12) in a Helmholtz form. This approach was used early on and had the advantage of more obvious analogies with waves. Of course, regardless of the way terms are defined in Equation (12), the solutions are the same.
2.4. Solutions in Infinite, Homogeneous Turbid Media
The simplest geometry to consider is the infinite, homogeneous medium with a single intensity modulated point source at the origin (SAC(r) = SACδ(r)). In this case, the main boundary condition is that the fluence rate falls to zero at infinity. The solution to Equation (12) in this geometry is well known. It has the form of a simple overdamped spherical wave with complex wave vector k = kr + iki:
| (13) |
Here, r = |r|,
| (14) |
| (15) |
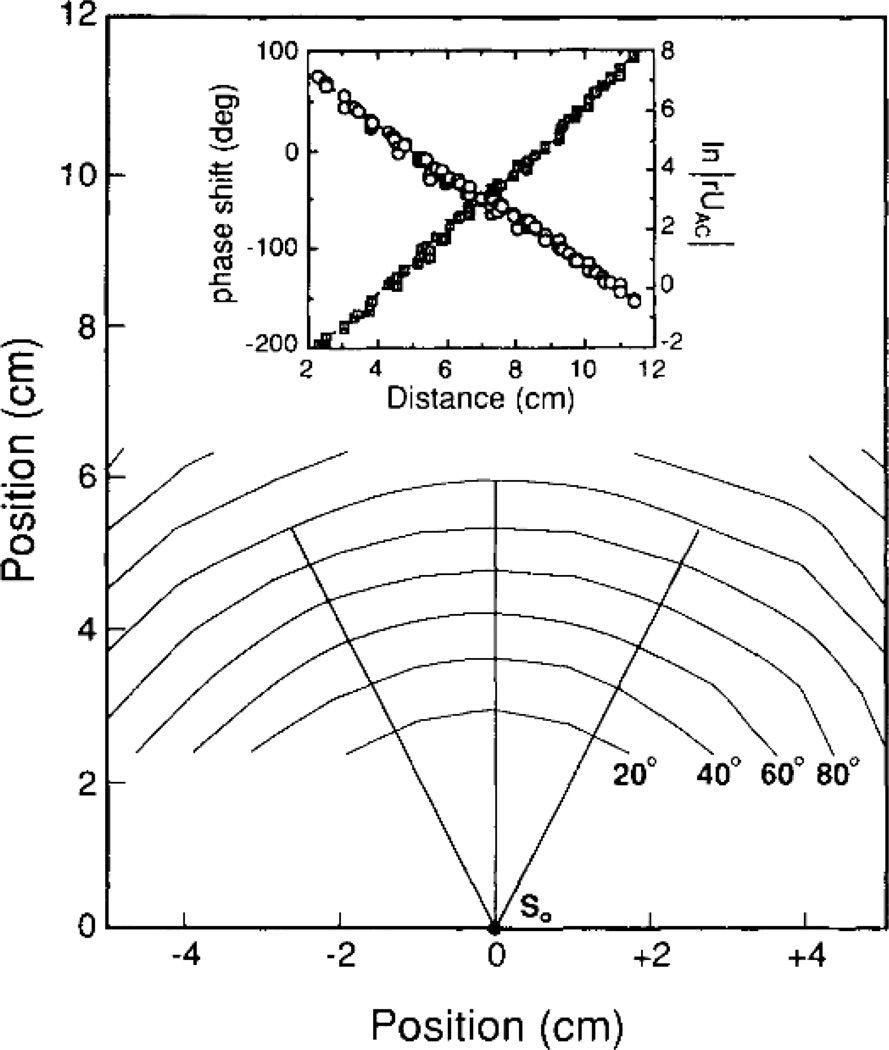
Writing the fluence rate in the form U(r) = Aeiθ, the determination of the change in wave amplitude, A, and wave phase, θ, with distance from the source enables experimenters to extract the absorption and reduced scattering factors of the turbid medium. In Figure 3 we show a measurement [13] of the amplitude and phase of such a diffuse photon density wave (DPDW).
Figure 3.
Constant phase contours shown as a function of position for homogeneous, 0.5% Intralipid solution filling a large aquarium (30 × 30 × 60 cm). At the origin (roughly the middle of the aquarium) is the source (3-mW laser diode operating at 816 nm and modulated at 200 MHz), resulting in a geometry that very well approximates a homogeneous infinite medium. The contours are shown in 20° intervals. Inset: The measured phase shift (squares) and ln |rU(r)| (circles) are plotted as a function of radial distance from the source. The slopes reveal −ki and kr, from which μa and D can be calculated using Equation (15) and Equation (14). Figure taken from O’Leary et al. [13, Fig. 2].
In tissue measurements, a typical set of parameters are , μa = 0.025 cm−1, ω = 2π × (70 MHz), and an index of refraction n = 1.4. In this case the DPDW wavelength (2π/ki ~ 19 cm) is roughly a factor of 20 greater than the attenuation length (1/kr ~ 1 cm). In the near-field, DPDWs have been demonstrated to exhibit several familiar wave-like properties including diffraction [14], refraction [13], interference [16], and dispersion [17].
The time-domain and frequency-domain solutions to Equation (9) are Fourier transform pairs. Therefore, if the solution in one domain is known, then it is straightforward to determine the solution in the other domain. The Fourier transform of Equation (13) gives the fluence rate solution in the presence of a pulsed point source of the form, S(r, t) = S0δ(r)δ(t), in the homogeneous infinite medium. The resulting fluence rate is
| (16) |
Here, to derive optical properties, one performs a nonlinear fit comparing Equation (16) to the measured fluence rate temporal arrival distribution at the detector (using only a single source-detector separation). The fitting determines D and μa. Alternatively, if it is only necessary to determine μa, the nonlinear fit can be avoided by noting that ∂ ln Φ(r, t)/∂t → −μaυ as t → ∞. Thus, μa is given by the slope of the natural log of the fluence rate at long times (i.e. typically only a few nanoseconds).
2.5. Boundary Conditions
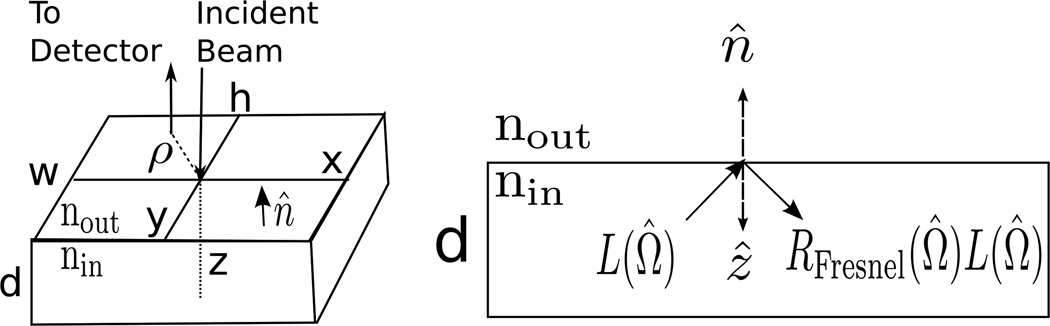
While conceptually useful, the infinite homogeneous medium is not a good approximation for practical tissue geometries. Most realistic geometries have interfaces. A particularly useful geometry is the planar interface wherein a semi-infinite turbid tissue is bounded in the other half-space by air. To derive boundary conditions for the light diffusion problem, it is necessary to consider the radiance again. Typically, photons escaping from the tissue into air will never re-enter the tissue medium. Thus, the incoming irradiance (i.e., total light power per area traveling into the diffuse medium at the boundary), 𝖩in, is due to Fresnel reflections of the radiance in the diffuse medium that travels out towards the interface (see Figure 4):
| (17) |
RFresnel(Ω̂) is the familiar Fresnel reflection coefficient for light incident upon the boundary in a direction Ω̂ from within the medium.
Figure 4.
Common geometry used to model tissue. In the semi-infinite geometry, w, h, and d all go to infinity, while in the infinite slab geometry, w and h are infinite but d is finite. Both geometries have azimuthal symmetry about the z-axis, meaning the photon fluence rate only depends on the radial and axial cylindrical coordinates ρ and z. The unit vector n̂ points from inside the tissue to outside. On the left, a single source-detector pair (with separation ρ) in the reflection geometry is shown. Note that for the slab geometry, detectors can also be used for transmission measurements by being placed on the z = d plane. On the right is a cross-section showing that the radiance moving into the turbid medium at the boundary is due to the Fresnel reflection of the radiance incident on the boundary.
Using the diffusion model, i.e., substituting the P1 approximation (Equation (3)) in for L, and an appropriate form for RFresnel(Ω̂), one readily obtains the so-called partial-flux boundary condition (also known as the Robin boundary condition) which relates the fluence rate to its gradient at the boundary [115, 116]:
| (18) |
Here, zb = 2ℓtr(1+Reff)/3(1−Reff), where Reff is the effective reflection coefficient to account for the index mismatch between tissue and air: Reff ≈ −1.440n−2 + 0.710n−1 + 0.668 + 0.0636n (Reff is defined exactly in Table 1). n = nin/nout is the ratio of the index of refraction “inside” and “outside” the diffusing medium.
Table 1.
Frequency-domain Green’s functions for Equation (12) in several homogeneous geometries subject to the extrapolated-zero boundary condition (Equation (19)). rs is the position of a normalized isotropic point source. With the exception of the infinite case, cylindrical coordinates are used explicitly to specify position, i.e. r = (ρ, z). Notation is defined in the lower part of the Table. In practice, the infinite sums are truncated after a desired accuracy has been reached.
| Case | Green’s function (frequency-domain) | ||
|---|---|---|---|
| Infinite | |||
| Semi-infinite | |||
| Infinite Slab |
|
||
| Infinite Cylindrical |
|
||
| Jm(z) mth order Bessel function, 1st kind | |||
| a, cylinder radius | |||
| z+,m ≡ 2m(d + 2zb) + ℓtr | ab = a + zb, i.e. extrapolated-zero boundary (cylinder) | ||
| z−,m ≡ 2m(d + 2zb) − 2zb − ℓtr | βm, a positive root of Jm(βmab) = 0 | ||
| ρ, radial cylindrical coordinate | |||
|
|
|||
| m, an integer | d, slab thickness (Figure 4) | ||
| cos ϑ = Ω̂ · n̂ Figure 4) | RFresnel(ϑ), Fresnel reflection coefficient | ||
| ϑ, angle of incidence in RFresnel(ϑ) | φ, angle between input/output light beams (cylinder) | ||
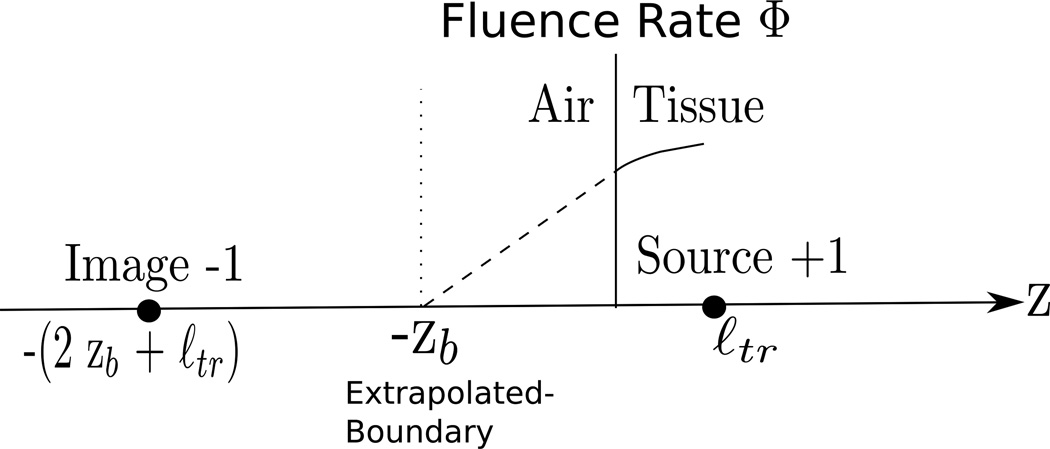
The partial-flux boundary condition is exact, but it is relatively difficult to use, especially if analytical solutions to the diffusion equation with interfaces are desired. In this case, a simpler boundary condition is usually made as an approximation to the more fundamental result. In particular, the fluence rate is Taylor expanded to first order around the boundary, with the first-derivative term taken from the partial-flux boundary condition. The treatment gives a zero-crossing point for the fluence rate at a distance, zb, outside (i.e. on the air-side) of the tissue (Figure 5):
| (19) |
Equation (19) is called the extrapolated zero boundary condition. It approximates the exact partial-flux boundary condition quite well (see [115, 116] for details). With this ‘new’ zero fluence rate interface, it is readily possible to use the method of images to obtain analytic solutions in a variety of geometries. Many researchers employ numerical methods to solve these and other problems; in such cases the partial-flux boundary condition is often directly incorporated into the numerical codes rather than the extrapolated zero boundary condition (for example, see [117]).
Figure 5.
The fluence rate curve is approximated by its tangent line at z = 0, and the Φ = 0 intercept of this curve is found to occur z = −zb (zb is defined exactly in Table 1).
2.6. Green’s Function Solutions
An age old strategy [118, 119] employed to solve the time-domain and frequency-domain diffusion equations (Equation (9) and Equation (11)) is to first find their respective Green’s functions, and then to use these Green’s functions to construct more general solutions. In diffuse optical spectroscopy, the usual assumption is to treat tissues as homogeneous media. For homogeneous media, Equation (9) can be written in the form ÂΦ(r, t) = −υS(r, t)/D, where  ≡ ∇2 − ∂/∂t − υμa. The time-domain Green’s function G0(r, rs, t, ts) then satisfies ÂG0(r, rs, t, ts) = −δ(r−rs)δ(t−ts) and the boundary conditions for the geometry of interest. Similarly, Equation (12) can be written in the form B̂U(r) = −υSAC(r)/D, where B̂ ≡ ∇2 − k2. The frequency domain Green’s function G0(r, rs) then satisfies B̂G0(r, rs) = −δ(r − rs) and the relevant boundary conditions. The full fluence rate solution in homogeneous media will be the convolution of these Green’s functions with the source term υS/D.
2.7. Solutions for Semi-infinite Media and Other Simple Geometries
In NIRS/DOS, the most commonly used models approximate tissue either as a homogeneous semi-infinite medium or as a homogeneous infinite slab (Figure 4). In both geometries, the method of images can be employed to find the diffusion equation Green’s functions, subject to the extrapolated-zero boundary condition (Equation (19)) [120, 121]. For example, consider a single normalized isotropic point source at position (in cylindrical coordinates) rs = (ρs = 0, zs = ℓtr) in the semi-infinite geometry. Recall from Section 2.2 that this source is a good approximation for light injected into the tissue by a fiber at r = (ρ = 0, z = 0). The extrapolated zero boundary condition is satisfied by introducing a negative image point source at zs = −(2zb + ℓtr) (Figure 5). Superposition of the infinite medium solutions (Equation (13)) from each (positive and negative) point source yields the homogeneous semi-infinite Green’s function. In the frequency domain,
| (20) |
where
| (21) |
| (22) |
Let us now consider a NIRS/DOS measurement in reflection on a tissue sample, using a frequency domain source (Figure 4). Assuming the tissue is well modeled by a homogeneous semi-infinite geometry, the fluence rate along the tissue surface is S0υG0([ρ, z = 0], [ρs = 0, zs = ℓtr])/D, where G0 is given by Equation (20) and S0 is the strength of the source. This solution contains two independent equations: one for the fluence rate amplitude, A(ρ), and the other for the phase, θ(ρ). Thus, as with the infinite medium (Section 2.4), by measuring A(ρ) and θ(ρ), one can solve the system of equations from the semi-infinite solution for D and μa.
We note that the detected light signal is the radiance integrated over the collection solid angle, which in the diffusion model is proportional to the fluence rate near the detector [115, 122]. It is difficult to predict this proportionality constant theoretically. Thus, in practice additional amplitude and phase-shift unknowns are usually incorporated into the solutions. Multiple source-detector separations are preferred to minimize this uncertainty and enable calibration.
Equation (20) can be fit exactly, but in the limit, ρ ≫ (ℓtr + 2zb), the solution simplifies considerably to
| (23) |
Note that in this limit, ln[ρ2A(ρ)] and θ(ρ) depend linearly on ρ,
| (24) |
| (25) |
making it particularly simple to fit for ki and kr, which in turn permits calculation of μa and D.
The method of images can also be used to compute the frequency domain Green’s functions for a homogeneous turbid medium in other geometries [120, 121]. Table 1 shows the frequency-domain Green’s functions subject to the extrapolated-zero boundary condition for several simple geometries. Similarly, analytic solutions exist for heterogeneities such as spherical [123] and cylindrical [124] inclusions in homogeneous media as well as for multi-layer media [125–129].
2.8. Spectroscopy for Determination of Tissue Chromophore Concentrations
The tissue absorption depends linearly on the concentrations of tissue chromophores. In particular, the wavelength-dependent absorption coefficient is given by
| (26) |
Here εi(λ) is the wavelength-dependent extinction coefficient (usually known for typical tissue chromophores), and ci represents the concentration of the ith chromophore. We have seen above (Section 2.4 and Section 2.7) that the diffusion approximation enables us to separate the scattering and absorption contributions in the detected light signals. Thus, by measuring μa at multiple optical wavelengths, we generate a system of coupled equations (Equation (26)) that can be solved to yield the unknown chromophore concentrations. Generally, to estimate the concentrations of N chromophores, one must determine μa at N or more wavelengths.
NIRS/DOS is most typically employed to measure oxygenated and de-oxygenated hemoglobin; thus a bare minimum of phase and amplitude measurements at two wavelengths are required. Use of more wavelengths permits inclusion of other tissue chromophores such as water and lipid, and also improves the accuracy of the hemoglobin measurements because measurement redundancy reduces systematic errors. Of course, more wavelengths increase the cost and complexity of the instrument and require longer data acquisition times.
The most common NIRS/DOS configuration is the reflection geometry, which employs the homogeneous semi-infinite medium analysis described above (Section 2.7) to derive μa(λ). However, other geometries are sometimes used to obtain bulk tissue properties; in this case the derived phase-shift and amplitude as a function of source-detector separation are usually more complex than the simple linear functions outlined above, and the fitting is correspondingly more tricky (but still possible). Imaging schemes employ essentially the same ideas on a volume-element-by-volume-element basis to assign chromophore concentrations to particular voxels in the sample (see Section 2.10).
NIRS/DOS provides quick estimates of bulk chromophore concentrations in large tissue volumes. These estimates are often accurate enough to be useful in many monitoring applications (see Section 4).
One technical problem associated with the multi-source/detector, multi-wavelength approach arises because each source and each detector has a different light coupling coefficient to tissue. This “coupling coefficient” (generally, a complex number in the frequency domain) is a parameter that combines many factors such as the wavelength-dependent fiber transmission, different source and detector optics, differences in the physical properties of sources and detectors, electronics, and tissue-fiber interfaces. The measured fluence rate for a given source-detector pair is thus equal to a product of the true fluence rate with the pair’s coupling coefficients. The light coupling coefficients for each source-detector pair will be additional unknowns in the inverse problem. If the coupling coefficients for different source-detector pairs are significantly different, then the NIRS/DOS inverse problem is harder with added variables [130]. Several methods are commonly employed to address this problem. One approach uses calibration phantoms with known optical properties to determine the coupling coefficients before and after each experiment (see [131]). A second approach employs self-calibrating probes (see [81]). The first method assumes the coupling will be the same for tissue and phantom; the second method assumes tissue homogeneity. In the case of tomography (Section 2.10), it is often assumed that the reference measurement cancels out these coupling coefficients [132]. A more rigorous approach is to consider the coupling coefficients as unknowns and explicitly reconstruct them [130].
2.8.1. Optimal Wavelengths
Determination of tissue chromophore concentrations requires the separation of tissue absorption from tissue scattering at more than one optical wavelength. The optimal choice of wavelengths for chromophore concentration determination is an important topic in its own right, with an interesting history that involved careful consideration of measurement type, i.e. frequency-, time-domain, CW, and measurement signal-to-noise. For simple, two-wavelength time- and frequency-domain instruments, early experimenters wondered about which wavelengths to choose to minimize cross-talk between chromophores when inverting Equation (26). Superficially, one might expect that at least one wavelength within the NIR window should be below the isosbestic point of hemoglobin and one should be above this isosbestic point. The isosbestic point is the wavelength wherein the extinction coefficients of oxygenated and de-oxygenated hemoglobin are the same (~800 nm, see Figure 1); wavelengths below the isosbestic point are thus more sensitive to deoxy-hemoglobin, while wavelengths above are more sensitive to oxy-hemoglobin. However, such wavelength selection processes are limited. Yamashita et al [133], Strangman et al [134], and Boas et al [135] have shown theoretically and experimentally that when using only two wavelengths, a pair at 660 – 760 nm and 830 nm provides superior oxy- and deoxy- hemoglobin separation by comparison to what was the more commonly used choice of 780 nm and 830 nm.
A formal evaluation of the optimum wavelength selection for an arbitrary number of wavelengths was carried out by Corlu et al [136, 137]; they introduced a general procedure for finding those wavelengths which best differentiate tissue chromophores using CW and frequency-domain light. These results built on a theoretical approach developed in a classic paper by Lionheart and Arridge [138]. That paper [138] theoretically proved that it is impossible to uniquely separate scattering from absorption in a diffuse optical imaging experiment employing CW light. In an attempt to circumvent this uniqueness problem for CW imaging, Corlu et al demonstrated that a multi-spectral approach can be employed to uniquely reconstruct the chromophore concentrations, ci. In a key advance, Corlu et al [136,137] abandoned the two-step approach of determining μa at each wavelength first and then inverting Equation (26). Instead, they introduced a multi-spectral approach that exploits known spectral properties of the medium a priori to directly reconstruct chromophore concentrations with better fidelity than the traditional two-step method. Specifically, a priori assumptions about the form of the scattering (e.g., ) and wavelength-dependent absorption extinction factors (i.e., Equation (26)) are used, and the wavelength independent variables ci, A, and b are reconstructed directly from all of the data simultaneously. Because the data from all wavelengths are simulataneously used, the inverse problem is better-constrained than the traditional approach (see [137] for details). The multi-spectral technique is now commonly used, and has been extended for frequency domain sources [139], for including uncertainties in the hemoglobin extinction coefficients [140], and for spectral window optimization when using broadband sources [141].
2.8.2. The Differential Pathlength (DPF) Approach
In many situations, we are interested in the temporal variation of quantities such as hemoglobin concentration or oxygenation with respect to some perturbation. In such cases, one need only measure ‘changes’ in tissue optical properties, i.e., Δμa and . If Δμa and are small relative to their baseline values, and , respectively, and if they are homogeneously distributed across the sample, then a much simpler differential pathlength method can be employed using only the intensity of the detected light. Specifically, this method relates temporal changes in the optical density, OD ≡ − ln(A(rd, t)/A(rs)), to changes in chromophore concentrations [10,120,134,142–146]. Here A(r, t) is the fluence rate amplitude. Furthermore, only one source-detector separation is needed to estimate these concentration changes.
The differential pathlength method is derived by truncating the Taylor series expansion of the optical density for a given source-detector separation ρ to first order in μa and :
| (27) |
Substituting Equation (26) into Equation (27), we see that temporal changes in the detected optical density, i.e.,
| (28) |
may be related to changes in tissue chromophore concentrations and scattering through a modified Beer-Lambert law:
| (29) |
Here, da ≡ ∂OD(λ, t = 0, ρ)/∂μa and are called the differential absorption and scattering pathlengths respectively for wavelength λ (or baseline values and ) and source-detector separation ρ [120]. The last step in Equation (29) is an approximation that is utilized widely in studies of brain hemodynamics (see Section 4). This approximation assumes that scattering is unchanged (i.e., ) and that da(ρ, λ) = DPF(λ)ρ, where DPF is a ‘normalized’ ρ-independent differential pathlength factor usually obtained from the literature.
Thus, by measuring ΔOD at multiple wavelengths, we can invert Equation (29) to determine the changes in chromophore concentrations Δci. Again, in addition to assuming small absorption and scattering changes, Equation (29) assumes homogeneously distributed changes for Δμa and . If the changes are localized, the modified Beer Lambert law leads to systematic underestimations of the chromophore concentration changes (i.e., the partial volume effect) [145].
The parameters da and ds depend on source-detector separation, tissue geometry, and the baseline optical properties of the underlying tissue, which in turn depend on the wavelength used. The parameters can be estimated analytically with a diffusion model, numerically using the Monte Carlo method [146], or measured using pulse-time methods in a sample of statistically similar tissue-types [10]. Pulse-time methods are relevant for a differential pathlength analysis involving light intensity only, because here the differential pathlength factors are related to the photon mean time of flight in tissue, 〈t〉, determined by pulse-time methods [120], i.e.,
| (30) |
| (31) |
The differential pathlength approach essentially makes a best estimate for the actual light pathlength in the tissue. Although it is clearly a very approximate method, it has been employed extensively in the biomedical optics community (see [35,147–150], and many others).
2.9. Diffuse Correlation Spectroscopy
2.9.1. Dynamic Light Scattering in the Single-scattering Limit
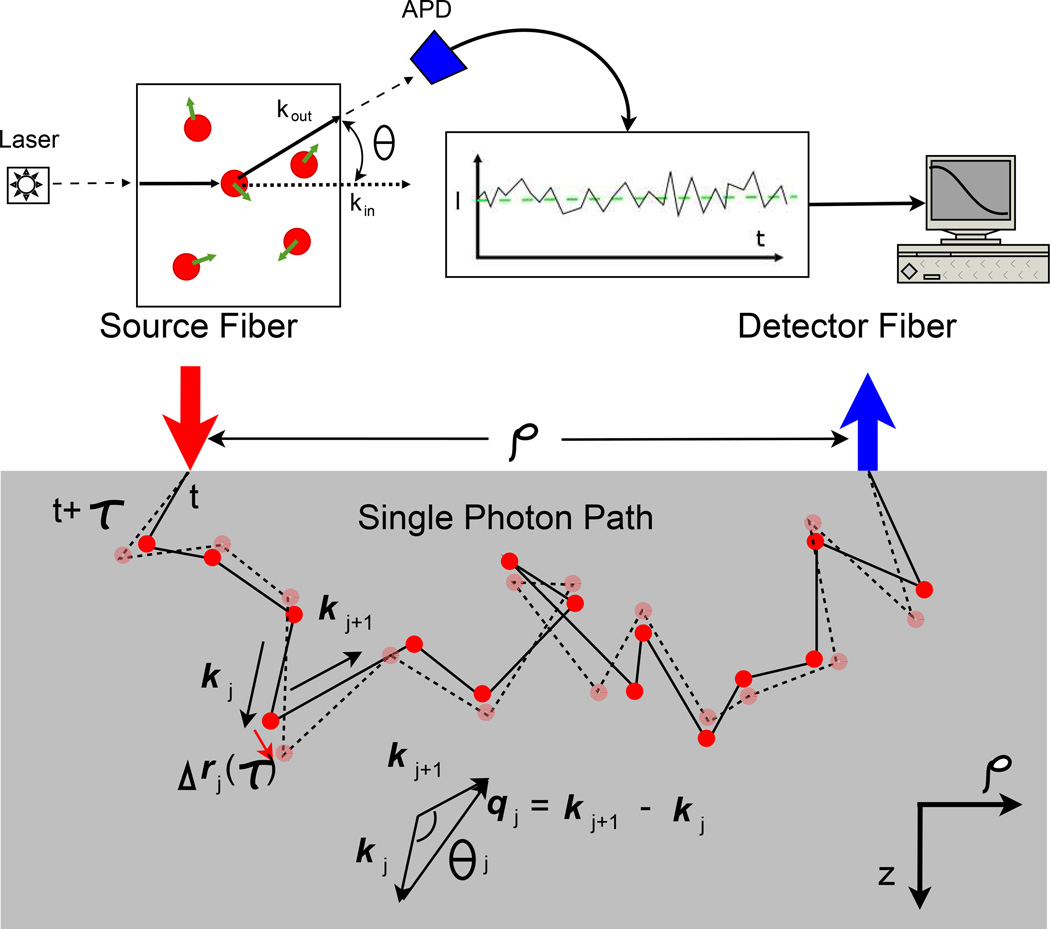
The Dynamic Light Scattering (DLS) (sometimes called Quasi-elastic Light Scattering (QELS)) technique is a well known optical method for measuring the motions of scatterers such as particles in suspension [45,46,151]. In the experiment (Figure 6(Top)), a light beam illuminates a sample. To be concrete, let us assume that the sample is composed of a dilute solution of particles or macro-molecules; dilute in the sense that light is scattered once or not at all as it traverses the sample. Each of the particles develops an induced dipole moment in the presence of the incident light, and these oscillating dipoles, in turn, emit scattered light fields into all directions. The scattered light electric field at the detector, E(t), is thus built from a superposition of these dipole contributions. Because the particles move, the relative phases of the scattered dipole fields change and the light field (and light intensity) at the detector fluctuates in time.
Figure 6.
Illustration of a single scattering DLS experiment (Top) and of multiple scattering (Bottom) along a single photon path in turbid media. kj and kj+1 are the wavevectors before and after the jth scattering event, respectively. qj = kj+1 − kj is the momentum transfer and θj is the scattering angle of the jth scattering event. The solid line represents the photon path at time t, while the dotted line represents the photon path at time t + τ. During the delay time τ, the jth scatterer moves Δrj(τ). Courtesy of C Zhou [499].
It is straightforward to show [45, 46, 151] that for independent particles with isotropic dynamics, the normalized electric field temporal auto-correlation function (g1) at the detector is
| (32) |
Here, f is the frequency of the incident light, q is the scattered wave-vector representing the difference between output and input beam wave-vectors, and 〈Δr2(τ)〉 is the mean-square particle displacement in time τ. The brackets 〈〉 represent time-averages (for experiments) or ensemble averages (for calculations). Thus by measuring the temporal fluctuations of scattered light, one obtains quantitative information about the particle motions. For the case of Brownian motion, 〈Δr2(τ)〉 = 6Dbτ; for the case of random flow, 〈Δr2(τ)〉 = 〈V2〉τ2. Here, Db is the particle diffusion coefficient and 〈V2〉 is the second moment of the particle speed distribution. Of course there are other types of motions (e.g. rotation) which affect these signals, but we will restrict our discussion to these two types of particle motion.
In practice, experimenters often measure the scattered, normalized intensity temporal auto-correlation function (g2); 𝗀2(τ) ≡ 〈I(t)I(t + τ)〉/〈I(t)〉2, with the intensity I(t) = |E(t)|2. The Siegert relation [152],
| (33) |
is then used to extract the electric field auto-correlation function from the intensity data. β is a constant determined primarily by the collection optics of the experiment, and is equal to one for an ideal experiment setup.
2.9.2. Dynamic Light Scattering in the Multiple Light Scattering Limit
In samples such as tissue or more concentrated colloidal supsensions, the incident light field is multiply scattered. As with light diffusion, one can envision the electric field temporal auto-correlation function propagating ballistically, then scattering from small volume elements within the sample, and then propagating ballistically again in a random manner as the light makes its way from one side of the sample to the other side. Each of these ‘single’ dynamic light scattering events, from a volume element within the sample, contributes to the detected correlation function. This is illustrated in Figure 6(Bottom). It is thus apparent that the detected field auto-correlation function is also related to motions of the scatterers within the medium, albeit in a more complex way. There has been elegant research on this multiple ‘dynamic light scattering’ problem over the years (for example, see [61–63, 153–155]). In the late 1980s the Diffusing Wave Spectroscopy (DWS) technique was formulated [62,63,156]. In DWS, the phase of the various photon random-walk paths through the sample is computed at time τ = 0 and then recomputed at time τ. When the scattering events within each path are uncorrelated, and when the diffusion approximation is valid, one finds that the detected field autocorelation function is then essentially equal to the angle-averaged DLS signal due to a typical single scattering event in the random walk sequence raised to the power N (where N is the number of random walk steps in the photon path). The detected signal is the integral of these single-path signals over all allowed photon paths. Another approach, which we will discuss in detail below, employs correlation transport theory to derive a diffusion equation for the field auto-correlation function. The correlation transport equation and the resultant correlation diffusion equation are particularly attractive in the context of tissues, because they share a formal similarity with the results we have presented already about diffuse photon density waves.
2.9.3. Diffusion of Temporal Correlation Functions
Temporal fluctuations in the sample are characterized by an unnormalized electric field auto-correlation function, , where the brackets 〈〉 denote the usual time and/or ensemble averages, and as mentioned earlier, E(r, Ω̂, t) is the electric field at position r and time t propagating in the Ω̂ direction. Ackerson and co-workers first suggested that is analogous to the radiance L and should be governed by a correlation transport equation [154, 155]:
| (34) |
Here is the normalized temporal field auto-correlation function for single scattering (see Equation (32)), f(Ω̂, Ω̂′) is the normalized differential single scattering cross-section, Q(r, Ω̂) is the light source distribution, and μt = μa + μs. Equation (34) is a steady-state equation independent of time, meaning it is applicable for CW sources and systems in equilibrium.
Given Equation (34), one can implement a set of steps formally identical to the steps used to derive the diffusion equation for photon fluence rate from the radiative transport equation. That is, using a P1 approximation for , the correlation transport equation reduces to the correlation diffusion equation for correlation ‘fluence rate’ [60, 61]:
| (35) |
Here, 𝖦1(r, τ) is the correlation fluence rate, i.e.,
| (36) |
where E(r, t) is the total light electric field at (r, t), and S(r) is an isotropic source term:
| (37) |
α represents the fraction of photon scattering events that occur from moving particles in the medium, 〈Δr2(τ)〉 is the usual mean square displacement in time τ of the scattering particles (e.g., blood cells), κ0 = 2π/λ is the wavenumber of the CW light diffusing through the medium, and D, μa, and υ are the same optical properties that arise in the photon diffusion equation (Equation (9)). Furthermore, a set of analogous correlation diffusion boundary conditions arise for 𝖦1(r, τ):
| (38) |
| (39) |
Diffuse correlation spectroscopy (DCS) refers to the measurement of the temporal diffusing field auto-correlation function to obtain information about tissue dynamics. Equation (35) is essentially a differential equation formulation of diffusing wave spectroscopy (DWS). It is better suited than DWS for handling point sources, heterogeneous media, and tomography. Notice also that if we take the τ = 0 limit of the correlation diffusion equation, then we obtain the CW diffusion equation for photon fluence rate.
Since Equation (35) with its boundary conditions has the same form as the photon diffusion equation (Equation (9)) for CW sources, the Green’s function solutions of the correlation diffusion equation will also have the same form. For example, in a homogeneous semi-infinite medium, the solution to Equation (35) is (see Equation (20)),
| (40) |
where , and r1 and rb are given by Equation (21) and Equation (22), respectively. The new feature is that the decay constant, K(τ), also depends on the correlation time τ; of course that is where the dynamical information resides.
As in the case of DLS, the quantity measured in practice is usually not 𝖦1, but is instead proportional to the intensity auto-correlation function 𝖦2(r, τ) = 〈I(r, t)I(r, t + τ)〉, where I(r, t) = |E(r, t)|2. Again, the Siegert relation (Equation (33)) may be used to relate the intensity and field auto-correlation functions.
Thus, 𝖦1 is derived from the experimentally measured 𝖦2, and K2 is determined by fitting to the temporal decay of 𝖦1 (for a given source-detector separation). This information plus optical property information permit determination of α〈Δr2(τ)〉.
Strictly speaking, the Siegert relation is fully valid if the electric field, E(r, t), is a Gaussian variable in time with zero mean [152]. For samples such as tissue, wherein some scatterers are static and some scatterers move, the total electric field will have static and dynamic components and can be written as E(r, t) = Ec(r) + Ef (r, t). Here, Ec is a time-independent contribution to the total field from photons that have experienced only static scattering on their path from source to detector. Ef is the field due to photons that have experienced at least one dynamic scattering event between source and detector; this field will fluctuate in time. Application of the Siegert relation in such cases requires careful consideration of the interference terms involving Ec and Ef. To date, a few methods for circumventing this problem have been developed [157–159], e.g., moving the sample (or detector) to induce fluctuations in Ec [157] or choosing speckles wherein Ec is small. We have conducted experiments in tissue phantoms and tissues to explore this further. In most practical tissue geometries we have found that the intensity auto-correlation functions decay to unity (typical field auto-correlation measurements are shown in Figure 8); collectively these measurements indicate that Ec is small, perhaps because most of the detected photon paths involve at least one moving red blood cell or another slow moving tissue scatterer (e.g., due to subtle vibrations or other effects). More work remains to clarify this observation. Nevertheless, it appears that one can routinely employ the Siegert relation in most tissue dynamics experiments, except perhaps those wherein the subject is exercising.
Figure 8.
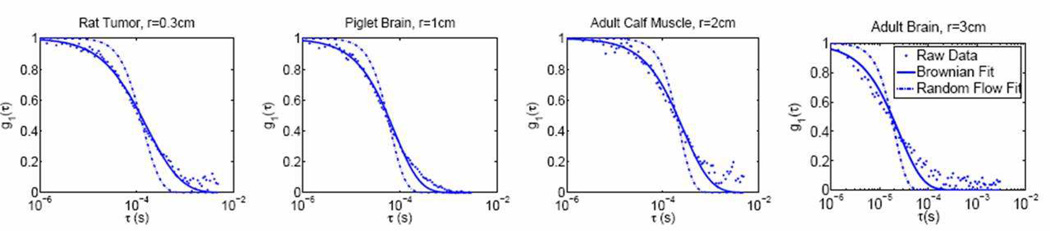
Data from a mouse tumor, a piglet brain, a human calf muscle and adult human brain. Dots show the experimental data, the dashed line is a fit with 〈Δr2〉 ~ τ2 (random flow), and the solid line is a fit with 〈Δr2〉 ~ τ2 (Brownian motion). Note how the accuracy of the fits vary depending on the delay time (τ) and the longer delays tend to deviate further from the fits for brain measurements. This is mainly because later delays correspond to photons that probe more superficial tissues and presence of the skull alters this part of the curves. Note, r in the figure titles is the source-detector separation on the tissue surface.
2.9.4. Blood Flow Indices from Diffuse Correlation Spectroscopy
DCS is most sensitive to the motion of blood cells in the microvasculature (i.e. capillaries, arterioles, venules), since the diffusing light is mostly absorbed when traversing large arteries and veins. Typical detected photons experience scattering events from static (or very slow moving) scatterers in biological tissue (e.g. organelles and interfaces), in addition to the dynamic scattering from moving RBCs (see previous section for details) [153].
Since the microvasculature is convoluted, we may expect that the distribution of the directions of velocities of the sampled RBCs is more or less isotropic. Thus, the random ballistic flow model is sometimes a first “guess” as a choice for the dynamics of RBCs, where 〈Δr2(τ)〉 = 〈V2〉τ2 (see Section 2.9.1). In practice, however, we and others [65, 66, 68–90] have found that the Brownian model, 〈Δr2(τ)〉 = 6Dbτ, fits the observed correlation decay curves better over a wide range of tissue types including rat brain [77, 78]; mouse tumors [68]; piglet brain [75]; and human skeletal muscle [81], tumors [83,84], and brain [66,69,71,74,80] (see Figure 8). In these cases, Db is an effective diffusion coefficient obtained from fitting to correlation data; it is a few orders of magnitude larger than the traditional thermal Brownian diffusion coefficient of RBCs in the blood given by the Einstein-Smoluchowski relation [160]. Upon reflection, it should not be too surprising that the random flow model does not fit the data well. RBCs in the microvasculature do not move ballistically; they experience position-dependent shear stresses, they roll, they tumble, and they translate in the vasculature.
Clearly, the final cumulative effect of photon-RBC interactions on the measured auto-correlation function will depend on both the nature of the microscopic motions and on the spatial distribution of moving particles in tissue. In the vasculature, both of these factors can be quite complex [161, 162], and, in fact, their affects on light signals are not fully understood. The situation is further complicated by the nontrivial distribution of photon paths in tissue; for example, contributions from the largest vessels tend to be small, since photons that interact with RBCs in an artery are mostly absorbed and do not reach the detector.
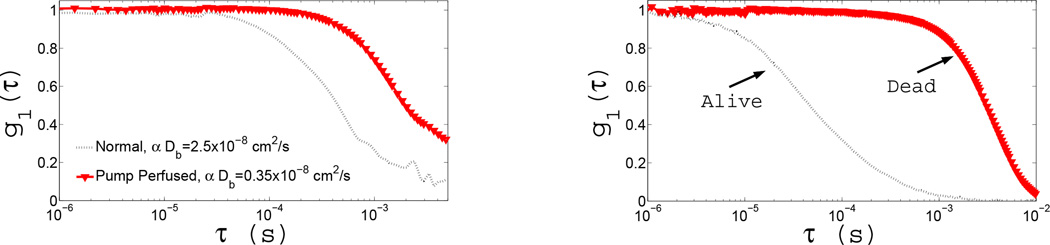
Despite these apparent difficulties, we (and others) have worked to elucidate DCS measurement sensitivity. For example, we have carried out isolated limb perfusion measurements in rats (see Figure 7(Left)). The figure shows two correlation decay curves, one from the limb with normal circulation and the other due to controlled circulation (of roughly the same speed) of an external suspension of RBCs (with ~10 times reduced concentration) through the same vasculature. The measurement clearly demonstrates that our signal is due to RBC motion. Variation of RBC concentration in suspension decreased the measured αDB in a proportional manner (~7.2 times). When healthy flow is compared to that from a dead limb the residual decay is < 3% of the baseline (see Figure 7(Right)). In the latter state, we altered and monitored the temperature of the limb while continuing to measure the correlation decay. Fitted αDB was dependent linearly on the temperature, as expected for true Brownian motion of the scatterers, which has a linear temperature dependence.
Figure 7.
The measured intensity auto-correlation curves from two experiments on isolated limb preparations on rats; (Left) Shows the electric field correlation functions during healthy circulation and under artificial perfusion with a pump. (Right) Shows the electric field auto-correlation functions from a rat before/after death.
Furthermore, we (and others) have found that the fitted parameter αDb (from the Brownian model) correlates well with other blood flow measurement modalities. As a result, it is natural to identify the αDB parameter as a blood flow index (BFI). The BFI is not a measure of absolute blood flow in the strict sense (e.g., it has the wrong units), but the relative change in BFI has been repeatedly shown to be a quantitative measure of relative change in blood flow. In particular, it has been shown that under well controlled circumstances, αDb is proportional to the absolute blood flow measured by ASL-MRI [73] and transcranial Doppler ultrasound [69,71]. Similar sorts of ambiguities are well known in the Laser Doppler literature, and in general, calibration and empirical modeling are used to estimate absolute values of blood flow velocity [43,153,163]. Calibration methods similar to those utilized by laser Doppler, e.g., to calibrate for “biological zero”, are also applicable for DCS [164–167]. We also note that it is possible (but difficult without constraints) to measure absorption and even scattering with DCS [168].
2.10. Tomography with Diffuse Photon Density Waves
Many of the simplifying assumptions used in spectroscopy, such as homogeneity and a semi-infinite or infinite slab geometry, are relaxed when imaging with diffusing waves. By using a more realistic model of tissue, diffuse optical tomography (DOT) improves the accuracy of the measured optical properties. Tomography is also critical for identification of localized heterogeneities such as tumors in tissue. The goal of DOT is to reconstruct the spatial distribution of optical/physiological properties at each point (or volume element) in the tissue from measurements of fluence rate on the tissue surface. This problem is typically called the ‘inverse problem’, whereas ‘forward problem’ refers to the calculation of the fluence rate on the tissue surface given a particular spatial distribution of optical/physiological properties. The transport/diffusion equations provide a tractable mathematical basis for tomographic image reconstruction [30].
Unfortunately, the dominance of scattering in light propagation makes each fluence rate measurement sensitive to a relatively large tissue volume compared, for example, to X-ray CT wherein scattering is minimal. The inverse problem in diffuse optical imaging is thus much more difficult than standard X-ray CT. The DOT inverse problem is also intrinsically nonlinear with respect to the tissue optical properties. As a result, it is computationally intensive to arrive at the inverse solutions, though as we will discuss, for some applications the problem can be linearized.
Despite these difficulties, several approaches have been developed and successfully applied for diffuse optical tomography (DOT) [30, 34, 169–171]. These include: backprojection methods [172, 173], diffraction tomography in k-space and variants [174–177], perturbation approaches [178–182], the Taylor series expansion approach [183–188], gradient based iterative techniques [189,190], elliptic systems methods [191, 192], truncated Newton schemes [193–196], multigrid inversion algorithms [197], and Bayesian conditioning [198–205]. Other important and related theoretical advances include the development of analytic inversion formalisms [206–209], development and clarification of differencing [210] and differential [211] methodologies, and advances in the use of a priori information [212, 213]. Experimentally, different schemes such as the use of spatially structured/modulated illumination [214–216] and phased-arrays of sources [217, 218] were also considered to improve localization. For other recent reviews on image reconstruction, see [23, 30, 31, 98, 219–221].
As mentioned before, though the diffusion model is adequate for light transport in most tissues, many biomedical applications involve tissues with “non-diffusing domains” and/or tissue volumes which are smaller than a few scattering lengths. To handle these cases, more complex (and more computationally intensive) models are needed. These models are summarized in recent reviews [30, 220]. One approach consists of schemes based on the full radiative transport equation [30, 190, 222–224], which have recently been reviewed by Klose and Hielscher [225]. This approach has been especially successful for imaging small tissue volumes such as the finger [226]. Another approach is to use higher order PN approximations of the transport equation [227–230]. If DOT is combined with an anatomical MRI, then it is possible to segment tissue into diffusive and non-diffusive regions. In this case, a hybrid model can be applied where light transport is modelled by diffusion in the diffusive regions and by radiosity theory [30, 231–233] or Monte Carlo [234] in the non-diffusive regions. The disadvantage of the hybrid model is that the boundaries between the diffusive and non-diffusive regions must be known. That said, many researchers are combining DOT with other imaging methods such as MRI in order to have more prior information to constrain the inverse problem. The incorporation of prior information improves the resolution and accuracy of the reconstructed images with DOT. A comprehensive review focusing on the incorporation of prior information into DOT has been recently published by Dehghani et al [235].
In the following sections, some common tomography approaches are outlined. Forward problem computations are an essential part of most of the methods used to solve the inverse problem. For simple geometries (e.g. Table 1), analytic solutions to the forward problem are quite useful. However, for complex geometries and/or heterogeneous optical property distributions, the forward problem is sometimes solved using numerical finite difference methods (FDM), finite element methods (FEM), boundary element methods (BEM), or Monte Carlo [30, 181, 182, 190, 236, 237]. Tomography approaches can be classified as linear or nonlinear. As mentioned above, the tomography inverse problem is nonlinear, but in the limit that the volume element optical properties are close to a specified background, the inverse problem is approximately linear (Section 2.10.1). This is usually the case for imaging differences in optical properties. For example, in a functional brain activation experiment, the perturbations in optical properties due to the brain stimulation are small compared with the background resting state of the brain (i.e., no stimulus). However, if the goal is to measure absolute optical properties, the full nonlinear problem should be tackled. Here, we focus the discussion on frequency-domain single-wavelength data; one can readily expand these ideas to continuous-wave and time-domain sources, as well as multi-spectral data (section 2.8.1).
2.10.1. Linear Numerical Inversion using the Perturbation Approach
To start, we write the optical properties at position r as
| (41) |
| (42) |
where δμa(r) and δD(r) can be regarded as perturbations from a homogeneous “background” medium with optical properties and D(0). Here, and D(0) are estimated from a tissue spectroscopy measurement or from values reported in the literature for similar tissue samples. Thus, the inverse problem utilizes measurements of fluence rate on the tissue surface to determine δμa(r) and δD(r), given some and D(0).
Two common forms are used for U(r) to set up the inverse problem [238]. The Born approach writes U(r) = U0(r) + Usc(r), while the Rytov approach writes . In both cases, U0 is the spatial part of the frequency-domain fluence rate in the homogeneous background medium, which can be calculated theoretically given and D(0), and is the correction to U0 as a result of the heterogeneities. Note that Usc has units of power per area, but is dimensionless. For more detail on both approaches see [238].
Let us focus on the Born approach. Corresponding Rytov results will also be given. In the linear perturbative approach, U(r) is set equal to its first-order Taylor series expansion about U0, i.e., U = U0 + (∂U0/∂μa)δμa + (∂U0/∂D)δD. This defines a simple linear problem for δμa and δD:
| (43) |
where [J] = [Ja,ij, Js,ij] = [∂U0(rj)/∂μa, ∂U0(rj)/∂D] is the Jacobian. The index i refers to the source-detector pair and the index j refers to the position within the sample. Equation (43) is derived from an expansion of U to first order, whose accuracy depends on δμa and δD being small. We note that the terminology weight matrix, sensitivity matrix, and Jacobian are often used interchangeably in the literature to refer to the matrix in Equation (43).
One could potentially calculate the Jacobian directly using numerical methods, but the perturbation approach lets one derive an analytic expression for the Jacobian. Substituting U(r) = U0+Usc, Equation (41), and Equation (42) into the heterogeneous diffusion equation (Equation (11)) gives a differential equation for Usc:
| (44) |
As before, . The integral solution for Usc(rd, rs), at detector position rd given source position rs, is given by the convolution of the homogeneous Green’s function G0(rd, r) (for the geometry of interest) with the right-hand side of Equation (44) (see Ch. 5 of [239]):
| (45) |
Equation (45) is intrinsically nonlinear in δμa(r) and δD(r) because U(r, rs) on the right-hand side also depends on δμa(r) and δD(r).
If we assume that U0 ≫ Usc, Equation (44) is readily linearized, i.e., U is replaced with U0 in the integrals (U0 is independent of the perturbations δμa and δD). Discretization of the integral in Equation (45) leads to a sum over NV elements (or voxels) of size ΔV:
| (46) |
where Wa,j = −υΔVG0(rd, rj)U0(rj, rs)/D0 and Ws,j = ΔV∇G0(rd, rj) · ∇U0(rj, rs)/D0.
In tomography problems, many source-detector pairs are typically spread out over the sample surface. Given N M source-detector pairs, Equation (46) is most easily expressed as a matrix equation that relates a vector of source-detector measurements to a vector of absorption and diffusion coefficient variations at voxels within the sample. Note that Equation (46) and Equation (43) are identical (i.e., [J] = [W]), so that
| (47) |
| (48) |
The matrix [J] has dimensions N M × (2NV), the measurement vector Usc = U − U0 has length N M, and the perturbation vector {δμa, δD} has length 2NV. Note, in most practical cases in the frequency domain, amplitude and phase data are further split in the matrix. Finally, the measurement vector Usc is obtained from measurements of the fluence rate U; but as we discussed in Section 2.7, the intensity measured in practice for a given source-detector pair, I(rd, rs), is proportional to the fluence rate U(rd, rs). Thus, as with spectroscopy (see earlier discussion on “coupling coefficients” in Section 2.8), a calibration scheme or explicit reconstruction of these unknowns should be employed [130].
The linearized Rytov approach (i.e., ) leads to a matrix equation of the same form as Equation (43), except that the measurement vector and the Jacobian terms are
| (49) |
| (50) |
Note, the Rytov approximation requires that the scattered field varies comparatively slowly (i.e. is small relative to υδμa/D(0) and (δD/D(0))(∇G0/G0)2).
The construction and the inversion of Equation (43) is generally the computationally most expensive step in the tomography problem. Because the Jacobian is almost always a nonsquare matrix (N M × 2NV), one often multiplies Equation (43) by the transpose of the Jacobian to create a square matrix for the inversion, i.e.,
| (51) |
[J]T [J] is usually singular, or close to singular, and is thus difficult to invert directly. Furthermore, experimental noise in the data tends to produce artifacts when explicitly solving Equation (51). To convert Equation (51) into a more readily solvable problem, a regularization parameter is usually introduced into the inverse problem. The regularization parameter is employed to suppress effects of measurement noise and model errors,
| (52) |
where 𝖱g is a regularization scalar that weights a regularization operator [C] [188, 240–243]. Regularization is a theoretical knob that can be adjusted to smooth image artifacts from experimental noise and other errors at the cost of decreasing the spatial resolution [244, 245].
Let us review the steps for this inversion approach. The linearized inversion problem constructs a suitable “perturbed” fluence rate, often within Born or Rytov approximations. The so-called “background”, “baseline,” or “homogeneous” field, U0, is either measured (e.g., using a homogeneous phantom before the breast scan, or during a “rest” period in case of functional studies of the brain) or calculated using a forward solver. The second step is the construction of the appropriate Jacobian (or weight matrix), which is derived from analytic solutions, numerical solutions (such as finite-element or finite-difference forward solutions of the photon diffusion equation), or a combination thereof. Then, typically, some sort of a regularization is applied to the Jacobian. Thus, up to this point, the steps are cumbersome but straightforward. The next step is to invert the often ill-posed Jacobian. Many strategies can be employed for this purpose, including “standard” singular value decomposition (SVD), algebraic reconstruction technique (ART) or simultaneous iterative reconstruction technique (SIRT), and k-space expansions [30, 170, 175, 179, 206, 208, 220, 239, 246, 247]. Despite the well known [30,170,220,239,246] limitations of linearized methods, these methods are employed for many applications including functional brain imaging, wherein well-defined and often localized optical property changes occur in response to neuronal stimulation (see Section 4), and optical mammography, wherin optical properties change in response to stimuli such as compression (see Section 3). Furthermore, in applications that involve many time points and near real-time feedback, such as the case of bed-side monitoring of brain function, the linearized inversion is attractive as a feasible option given the current state of portable computational power and speed.
2.10.2. Linear Analytical Inversion with Assumed Symmetry
For simple geometries such as semi-infinite, infinite slab, infinite cylindrical, and spherical, Schotland and colleagues have developed a fast alternative method for solving the inverse problem. Essentially, this method exploits the symmetry of the geometry to avoid constructing and inverting the entire weight matrix in Equation (43) [174, 206–208, 248]. Here, we will outline the method for the infinite-slab geometry using the Rytov approach.
The geometry is as defined in Figure 4 where ρ is the position vector on the plane where there is symmetry. By exploiting this symmetry, the Green’s function (G0) can be expanded in plane waves along ρ [175, 249], i.e.,
| (53) |
where ζ(q; z, zs) gives the amplitude and phase of the plane wave with wave-vector q = (qx, qy) in the plane z due to a source in the plane zs. Analytic expressions for ζ(q; z, zs) are given in [208].
Substituting Equation (53) into the linearized Rytov solution (Section 2.10.1) and then taking a four-dimensional (two each for the source and detector coordinates ρs and ρd) spatial Fourier transform, we obtain
| (54) |
Both κA and κD are known since we have analytic expressions for the coefficients defined in Equation (53) and are given by
| (55) |
| (56) |
These steps, collectively, reduce the original inverse problem to a linear one-dimensional integral equation which can be inverted in a manner similar to those mentioned in Section 2.10.1 to obtain δμ̃a(q, z) and δD̃(q, z), which are the spatial Fourier transforms of the “images” we seek to reconstruct (see [208] for details). Performing an inverse Fourier transform on δμ̃a(q, z) and δD̃(q, z) gives the desired images. Exploiting the planar symmetry this way dramatically decreases the computation time relative to constructing the inverse for the entire Jacobian numerically (Equation (43)).
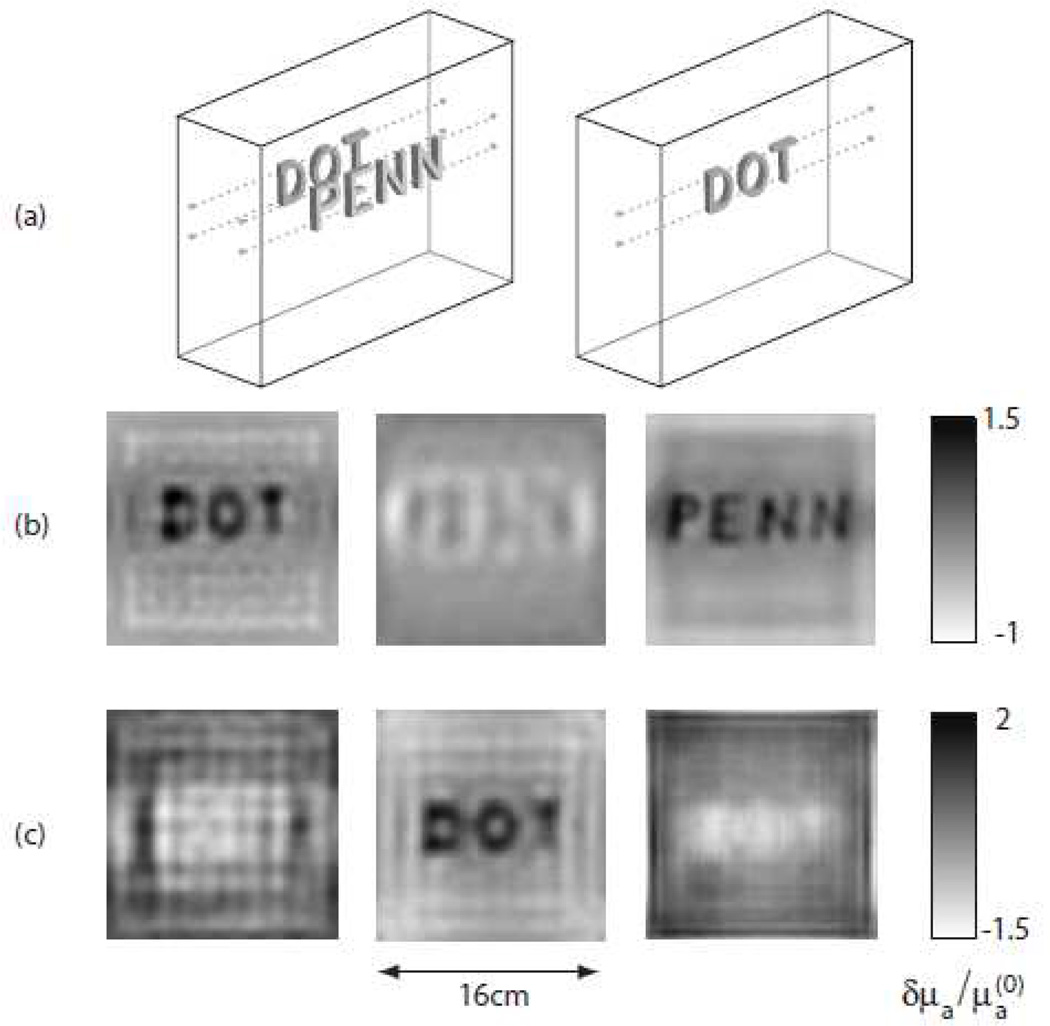
For example, Konecky et al. [250] used the Rytov linearized analytic inversion method to reconstruct objects of a complex structure (i.e. letters made from silicone rubber) with optical properties comparable to those of tissue embedded in an optically thick medium. In this study, reconstructions utilizing data sets of 107 source-detector pairs obtained with a CW instrument only required a minute of CPU time on a 1.3 GHz workstation. In addition to identifying the location and spatial extent of the heterogeneities, the resulting images contained spatially-resolved features on the sub-centimeter scale at varying depths inside the optically thick medium (see Figure 9).
Figure 9.
Slices from three dimensional image reconstructions of the relative absorption coefficient for targets suspended in a 6 cm thick slab filled with highly scattering fluid. The Rytov linearized analytic inversion was used for this reconstruction. The three slices shown for each reconstruction correspond to depths of 1 cm (left), 3 cm (middle), and 5 cm (right) from the source plane. (a) Schematics of the positions of the letters during the experiments. Left: The target consists of letters “DOT” and “PENN” suspended 1 cm and 5 cm from the source plane, respectively. Right: The target consists only of the letters “DOT” suspended 3 cm from the source plane. (b) Reconstructed image of the letters “DOT” and “PENN” (c) Reconstructed image of the letters “DOT”. This figure is reproduced from Konecky et al. [250, Figure 1].
2.10.3. Nonlinear Numerical Inversion (Jacobian- and Gradient-based Methods)
Linearized approaches are useful for generating images, but if the tissue optical properties are significantly different from those of a specified background, then the accuracy of the linear image reconstruction will be compromised. In Section 2.10.1, we showed that the linearized inverse problem in the Born approach (U = U0+Usc) is valid if the magnitude of the fluence rate correction Usc is small relative to the background U0. In the Rytov approach , the linearized inverse problem is valid if the fluence rate correction is slowly varying, i.e., . In general, both of these linearized approaches break down when optical property perturbations are large. With the Born approach, this can easily be seen by noting that the derivation of Equation (43) assumed small optical property perturbations. [246]. When attempting to measure absolute optical properties of tissue, the specified background is an initial guess of these properties, which is often significantly different from the true properties. To improve image reconstruction, nonlinear approaches for the inverse problem are required. Jacobian-based nonlinear schemes in essence solve linear problems again and again, updating the perturbations δμa and δD iteratively, and then comparing calculated fluence rates with the measured fluence rates until they become sufficiently close.
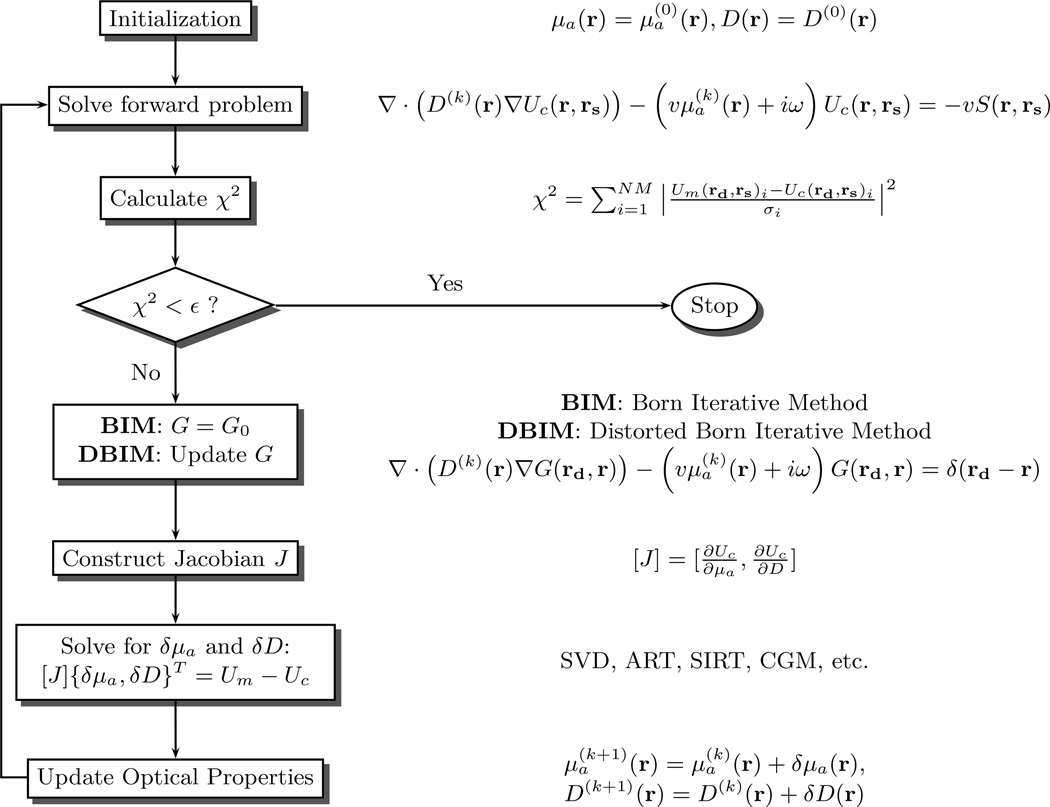
Here, we will discuss a Born iterative method (BIM) and a Distorted Born iterative method (DBIM) presented by Yao et al [182]. Figure 10 is a schematic illustrating the steps for these two methods. First, μa and D are initialized, and the corresponding Green’s function, G0, for the photon diffusion equation (Equation (44)) is determined. The forward problem is then solved; typically by using finite elements or finite difference numerical methods. To quantify the agreement between calculated fluence rate Uc(rd) and the measured fluence rate Um(rd), an objective function χ2 is constructed:
| (57) |
Here N M is the number of measurements and σi is the measurement error for the ith source-detector pair. When χ2 falls below some pre-defined convergence criterion ε, the iteration procedure is stopped. If the iteration procedure is not stopped, then the optical properties are updated. Updated optical properties are derived via the solution to an inverse problem which has been outlined already for the linearized prolem in Section 2.10.1 (i.e., Equation (52)).
Figure 10.
Flow chart of Born and Distorted Born iterative methods. A linear inverse problem of the form Jδx = y is solved for each iteration. Both the fluence rate and Green’s function are updated in the Distorted Born method, but only the fluence rate is updated in the Born iterative method (see text for details). The iterations continue until χ2 has reached the desired tolerance.
The difference between the two methods is that the DBIM method calculates a new Green’s function at every iteration, while the BIM method always uses the same Green’s function (see Figure 10). The DBIM usually converges faster than the BIM, but it is also less robust to noise than the BIM [182]. Equivalent methods using the Rytov approach, i.e., Rytov iterative method and Distorted Rytov iterative method, are also utilized.
Another useful nonlinear reconstruction approach employs a gradient-based iterative scheme rather than explicitly building the Jacobian and solving Equation (52) [171, 189, 190]; in this case, the gradient of the objective function χ2 (Equation (57)) with respect to μa and D (e.g. ) is determined to establish a search direction to minimize χ2 directly. A line search is performed to find the optical properties that minimize χ2 along this search direction, and these new optical properties are then used for the next iteration. The search direction is established using the nonlinear conjugate gradient method (see [171] for details). This process repeats until χ2 has converged within a desired tolerance. Since the gradient-based approach does not involve direct inversion of the Jacobian matrix (time- and memory-consuming computational process), it is computationally less intensive than the Jacobian-based iterative methods under many conditions.
Public software packages are available that utilize the iterative methods described above for image reconstruction. Both the gradient-based and Jacobian-based approaches can be employed in the well known DOT reconstruction package Time-Resolved Optical Absorption and Scattering Tomography (TOAST) [171]. NIRFAST is another software package written in the MATLAB environment that uses the Jacobian-based approach [117].
2.10.4. Nonlinear Analytical Inversion
The exact fluence rate solution to Equation (11) can be written as an infinite series. For example, taking the Born approach, the series is generated by replacing U with U0+Usc in Equation (45) and then substituting Equation (45) in for Usc in an interative fashion:
| (58) |
Here, F(r) ≡ (−υδμa(r) + δD(r)∇rG0(rd, r) · ∇r)/D0.
Equation (58) truncated at first order is the Born approximation. Inclusion of higher order terms in the series leads to more accurate results, but numerically evaluating the higher order terms is more computationally expensive [246]. However, for special geometries, symmetry properties of the fluence rate can be exploited for all of the higher order terms in a similar manner to the method described for the linear term in Section 2.10.2. This scheme speeds up the reconstruction with higher order terms. Schotland and co-workers have derived an exact analytic inversion formula for the fluence rate written as an infinite series. For details about this approach, see references [209, 251].
2.11. Fluorescence Diffuse Optical Spectroscopy and Tomography
The use of extrinsic near-infrared fluorescent dyes has gained attention recently, in part because of their potential to target specific tissues and in part because of their potential to provide information about tissue type and tissue microenvironment. Some researchers in the biomedical optics field recognized the potential of fluorescence early on [14, 252–267] and set about developing theoretical formalisms to understand these fluorescence signals in the multiple scattering limit; these theories have provided a framework to quantitatively assess the potential of fluorescent contrast agents and to use fluorescence for diagnosis. Proper inversion of flurescent data to derive contrast agent concentration (or fluorophore life time information), however, is more complication than DOS/DOT. It requires an understanding of the transport of excitation light and the transport of fluorescent light. Thus, most generally, a set of coupled equations for both diffuse light waves must be set up and solved.
Fluorescence diffuse optical spectroscopy (FDOS) is a fluorescence analog of NIRS/DOS. Much of the theory for this relatively simple problem is fully developed (see, for example, references [254, 256, 260]), and these theories have been applied in contexts such as photodynamic therapy [268, 269]. Similarly, the potential for contrast agents has stimulated the development and use of fluorescence diffuse optical tomography (FDOT) for imaging molecular-targeting probes in small animals [270–272], for sentinel lymph node tracking in animals and humans [273, 274], for imaging tumors in human breast [26, 275, 276], and for monitoring blood flow in human brain [277–280]. The feasibility of FDOS and FDOT in humans has thus been demonstrated.
In a related vein, phosphorescence lifetime spectroscopy and tomography has been introduced as a unique means to measure tissue parameters such as the partial pressure of oxygen [281–283]. Bioluminescence tomography of tagged molecules has been utilized to track physiological processes such as gene expression [284], and the autofluorescence from various components of tissue components has been studied in oncological contexts [285–288] and in neuro-imaging [289]. All of these applications require knowledge of the diffuse light transport problem.
2.12. Diffuse Correlation Tomography
Image reconstruction with temporal correlation functions, i.e., diffuse correlation tomography (DCT), employs essentially the same theoretical techniques as DOT for CW light, because the underlying mathematical models are formally similar. In general, such reconstruction schemes permit imaging of spatially heterogeneous dynamics. The inverse problem, in this case, must reconstruct the homogeneous and spatially varying blood flow index, BFI(r) = BFI0 + δBFI(r), absorption, μa(r) = μa0 + δμa(r), and scattering, D(r) = D0 + δD(r). Quite often the changes in BFI dominate the problem, making it reasonable to assume that δμa(r) = δD(r) = 0 or in case of hybrid instrumentation [76] to include them as inputs for the reconstructions.
The key difference between reconstruction with correlation functions versus reconstruction with the CW photon fluence rate is the correlation-time-dependence of 𝖦1. A simple practical approach selects a particular time τ = τ* for reconstruction of BFI from measured 𝖦1. Zhou et al. developed a model for estimating the reconstructed image noise in DCT from the DCS noise information at each source-detector pair; it was found that the time τ* that minimizes the DCT noise satisfies the relation 𝖦1(r, τ*) = 𝖦1(r, 0)e−1 [78]. This approach thus optimized data selection for DCT by considering both the experimental noise and ill-posedness of the tomographic problem.
2.13. Metabolic Rate of Oxygen Extraction
An important physiological parameter to monitor is the local metabolic rate of oxygen extraction. This quantity depends on the oxygen extraction fraction, i.e. the difference in oxygen saturation between the arterial and venous ends, and blood flow. The cerebral metabolic rate of oxygen extraction (CMRO2) has been studied extensively in the context of the brain and a wide range of models have been developed to estimate CMRO2 from measurable quantities under different regimes [290–293].
A relatively simple model permits changes in CMRO2 (rCMRO2) to be calculated using a synthesis of rCBF, ΔHb and ΔTHC [76, 291–293]. In this case, a compartmentalized model of the vasculature is assumed and an equation that relates the measurable quantities is derived using Fick’s law: CMRO2 = OEF × CBF × Ca [294]. OEF is the normalized oxygen extraction fraction, i.e. the difference between oxygen concentrations in arterial (Ca) and venous ends of the vasculature. Our goal is to estimate OEF (or changes thereof) with optical data. Since NIRS/DOS measures a mixture of arteriole, capillary and venuole blood oxygen saturation and does not separate venous from arterial saturations, this task is non-trivial. We refer to this mixed signal as “tissue blood oxygen saturation” (StO2).
A compartmental model relates microvascular blood oxygen saturation to the percentage of blood in the venous and arterial components of the vasculature [77,295]. We write StO2 as a mixture StO2 = k1 × SaO2 + k2 × ScO2 + k3 × SυO2. Here, SaO2, ScO2, and SυO2 are the arteriolar, capillary, and venous saturations, respectively, and k1, k2, and k3 are the respective weights of each compartment to the total blood volume (k1+k2+k3 = 1). A standard simplification is to represent ScO2 as a weighted average of the arterial and venous saturations; ScO2 = k4 × SaO2 + k5× SυO2 where k4+k5 = 1. The system can then be reduced to a two-compartment model [65, 66, 76, 77, 296] to estimate rCMRO2:
| (59) |
StO2 = HbO2/(THC) is the microvascular blood oxygen saturation measured by NIRS/DOS. Sub-script “bl” (bl) is used to indicate baseline values of a parameter. Baseline StO2 (StO2bl) and THCbl are ideally measured but are often estimated from the literature values. Here γ is the percentage of blood in the venous compartment and if we assume that it remains constant over time, it divides out of our measures of rOEF. Thus, rCMRO2 can be directly calculated from optical measurements of rOEF and rCBF.
3. Breast Cancer Imaging & Spectroscopy
Approximately one in eight women in the United States will develop breast cancer, and, about 30% of these women will ultimately die of the disease [297]. Thus even modest improvements in breast cancer screening (detection), diagnosis, and therapy monitoring can have huge impact in women’s health. While existing clinical modalities have reduced the morbidity and mortality rates of breast cancer, no single diagnostic modality is suitable for the plethora of management problems that arise in the clinic. For example, accurate detection and characterization of tumors is required for screening and diagnosis, whereas predictions about treatment efficacy are important for therapy monitoring. X-ray mammography, a routine screening modality, has high false negative rate (i.e. missing cancers) in women under 50 years of age [298] and cannot be used too frequently due to the ionizing nature of X-ray radiation. Techniques such as ultrasound and magnetic resonance imaging (MRI) are sometimes employed in addition to X-ray mammography, but they have limitations such as high cost, low throughput, limited specificity (MRI) and low sensitivity (ultrasound). Most of these imaging modalities rely on the anatomical differences between cancer and healthy tissues. On the other hand, positron emission tomography (PET) relies on functional tumor contrast such as glucose metabolism and is recommended for assessing metastatic status. However, frequent measurements with PET pose problems due to its expense and the requirement of radioactive isotope injection. Thus new methods are needed to detect cancers earlier for treatment, to detect cancers missed by mammography [299–301], to reduce the false-positive rate [302,303], and to monitor tumor progression during cancer therapy.
Near-infrared diffuse optical tomography and spectroscopy are tools that rely on functional processes for contrast and therefore have potential to enhance sensitivity and specificity of breast cancer detection/diagnosis. Diffuse optical techniques are attractive, because they provide physiological information directly related to tumor vascularity and oxygenation, while utilizing inexpensive, non-ionizing, rapid, portable, and non-invasive instrumentation.
A variety of instrumentation and algorithmic strategies have been developed for optical mammography and tumor monitoring. Instruments range from handheld remission systems [304–309], to tandem-scanning systems [310–315] to full three-dimensional tomographic systems [106, 111, 316–321]. These instruments generally differ with respect to measurement geometry (e.g. remission, parallel-plate, ring/cone), detection type (e.g. CW, FD, TD), wavelength implementation (e.g. broadband vs discrete wavelengths), and source/detector numbers. Analysis algorithms vary too, ranging from analytic solutions in the homogeneous semi-infinite geometry to full fledged 3D tomographic reconstruction; algorithm choices must carefully consider clinical trade-offs in time and space against increased spectral- and spatial-content, and detection complexity for improved data fidelity.
3.1. Diffuse Optical Mammography Based on Endogenous Contrast
3.1.1. Endogenous Properties of Normal Breast Tissue
An understanding of normal breast optical properties is desirable, even if one’s ultimate goal is to probe cancer. Recent diffuse optical spectroscopic research on normal tissues has demonstrated sensitivity to tissue composition [322–329], which can change significantly with age or hormonal status. The subcutaneous breast tissues consist of adipose, glandular and fibrous stroma, and the blood supply is typically richest in the glandular areas [330]. Total hemoglobin concentration is thus expected to be larger in breasts with high glandular content and smaller in breasts with high adipose content. Since verification of actual breast composition for individual subject is difficult, we rely on surrogate markers such as body mass index (BMI) or mammographic parenchymal patterns for consistency checks. A significant inverse correlation between THC and BMI has been found, wherein high BMI is an indication of high adipose tissue content [321,322,324,331]. Mammographic parenchymal patterns can be derived from the X-ray attenuation characteristics of fat (radiolucent) and epithelial and stromal tissues (radiodense) [332]. Cubeddu and co-workers have found that water and lipid content correlated well with the mammographic parenchymal pattern, which is an indicator of the composition of adipose and fibrous tissue content [331].
The observation that optical measurements of absorption and scattering can provide physiologically relevant information about breast tissue composition [324] has been extended in a new direction by Lilge and co-workers. Based on parenchymal pattern classification studies of X-ray mammography, it was found that women with dense tissue in more than 60–75% of the breast are at 4–6 times greater risk of breast cancer than others [332]. Using a principal components analysis of a broadband optical spectroscopy measurement, Lilge and co-workers have found agreement between the mammographic assessment of tissue density (high vs low) and optical measurements with 90% accuracy [333–335].
3.1.2. Breast Cancer Detection and Characterization
Tissue properties accessible to DOT and DOS techniques are demonstrably different in tumors compared to normal tissues [213,306,310,314,316,319,321,325,326,336–344]. Among various physiological parameters available to DOT and DOS, most groups have reported high THC contrast in malignant tumors [321, 325, 337, 338, 340, 344–348]. Since the malignant growth of tumors is often accompanied by sustained angiogenesis to supply oxygen and nutrient [349], THC might reasonably be expected to be higher in the cancers compared to normal tissues. Indeed, a positive correlation between microvessel density and THC has been found, providing further insight about the microscopic origin of THC contrast [337, 348, 350]. The rapid growth of many tumor cells can also give rise to an increase in number density of subcellular organelles (e.g. mitochondria, nucleolus), which in turn affect tissue light scattering coefficients. Mean size and volume fraction of the nucleus and nucleolus measured by microscopy have indeed been correlated with light scattering observations by DOT [351], and some groups have reported tumor-to-normal contrast in tissue scattering parameters [122, 342, 345, 346,348, 351].
Information about tumor oxygenation status is important, especially for predicting the efficacy of cancer therapies [352–354]. However, while it has been hypothesized that malignant cancer would exhibit low oxygenation due to hypermetabolism [306], its manifestation in macroscopic DOT measurements has not been apparent. Some groups have observed a decrease of StO2 in the tumor [306, 344, 355–358], whereas others observed no difference [122, 321, 341–343, 359, 360] or even an increase [345]. This discrepancy may be due to dependency of cancer oxygen metabolism on the cancer stage, type, biochemical pathways, or differences in oxygenation accuracy sensitivity among systems.
The spatial locations of tumors based on optical contrast have been compared with X-ray mammograms/ultrasound [314, 321, 337, 351, 361, 362], and MRI [122, 363, 364]. Since optical and other imaging measurements were performed with different compression geometries, new image coregistration schemes [365] and algorithms [341, 366, 367] have been developed for quantitative comparisons between different imaging modalities. It was demonstrated that the spatial locations of optical tumor contrast agree with those identified by MRI and/or PET, and the extracted tumor physiological contrast parameters from optics have been shown to be correlated with PET parameters [367].
Ultimately, characterization of a new imaging modality can be established through computation of Receiver Operating Characteristic (ROC) curve [368, 369]. Let us suppose that there is a parameter (X) from new imaging modality whose value seems to be higher for malignant lesions and lower for benign lesions. (Note: depending on the test, one can easily substitute ‘healthy’ or ‘non-diseased’ state to ‘benign’.) For each value of the threshold value (Xthreshold), all the lesions under consideration can be grouped into the following four categories. Some lesions are indeed maligant and correctly predicted to be malignant by the new modality (true positive; TP); some lesions are malignant, but incorrectly predicted to be healthy (false negative; FN); some lesions are benign, and correctly predicted to be benign (true negative, TN); and some lesions are benign, but incorrectly predicted to be malignant (false positive; FP). These quantities can be expressed as rates by dividing by the total number of true malignant lesions or true benign lesions: for example, true positive rate TPR = TP/(TP+FN) and false positive rate FPR = FP/(TN+FP). The ROC curve is constructed by plotting true positive rate on the horizontal axis and false positive rate on the vertical axis at different Xthreshold. A perfect test establishes a threshold which separates diseased and non-diseased subjects completely, i.e. the true positive rate is 1 and the false positive rate is 0. A useless test is one in which diseased and non-diseased states have the same probability (i.e. 50/50 chance) regardless of the threshold; in this case the ROC curve has slope of unity. Thus, a larger ‘Area under ROC curve’ (AUC) implies a better test/method. AUC of 50% corresponds to an ROC slope of unity (i.e. a useless test). Chance et al [306] used a threshold based on a combination of relative THC and StO2 (derived by DOS) of tumors compared to the tissue from the contralateral breast and obtained 95% AUC to discern cancer from normal tissue. Poplack et al [370] achieved 88% AUC for differentiating cancer from normal tissue, and 76% AUC for differentiating malignant cancer from benign lesions using rTHC derived from 3D DOT images for a subset of subjects with lesions larger than 6 mm; their AUC decreased when smaller lesions were included in the data set. In recent work from our laboratory [122], we have extracted the optical parameters from 3D reconstructed images based on MRI-guided region-of-interest selection. As seen in Figure 11, there is a clear distinction between benign and malignant lesions in tumor-to-normal ratio of THC with AUC higher than 90%. Similar trends were seen in tumor-to-normal contrast of HbO2 and the tissue scattering coefficient. While AUCs of DOS/DOT are relatively high, showing the potential of DOS/DOT for differentiating malignant tumors from healthy or even benign tumors, it needs more assessment since the number of subjects are still low compared to other imaging modalities.
Figure 11.
(a)Tumor-to-normal ratio of total hemoglobin concentration (rTHC) of 10 benign and 41 malignant lesions. (b) Receiver-operating-characteristic curve for rTHC showing true positive rate for malignant lesions versus false positive rate for benign lesions.(Reprinted with permission from Ref. [122].)
At this point in time, these findings do not represent a final assessment of DOT performance. Most often, each study focused on demonstration of a particular methodology. Discrepancies among groups can be a function of method, subject groups (e.g. lesion size, percentage of benign and malignant lesions, etc) and lack of large-scale, blinded clinical trials. Clearly much work remains, but promise has been demonstrated.
3.2. Optical Mammography Based on Exogenous Contrast
DOT can be conducted concurrently with injection of exogenous contrast agents. With use of exogenous contrast dyes tumor contrast can be improved as a result of tissue-dependent spatial distributions of the dyes and dye lifetimes [24, 25]. Currently, ICG is the only FDA-approved compound suitable for DOT, having an absorption and fluorescence spectra in the NIR window. ICG has been demonstrated to enhance absorption of human breast cancer in vivo [336, 371, 372].
In principle, fluorescence signals can provide greater detection sensitivity and specificity compared to absorption signals, as well as access to new information about tissue micro-environment, such as pO2, pH, and intracellular calcium concentration [373, 374].
Sevick-Muraca and co-workers have demonstrated fluorescence imaging using ICG in canine breast cancer [375] and in realistic breast phantoms [376]. In our laboratory, we have recently demonstrated the first 3D fluorescence diffuse optical tomography (FDOT) of in vivo human breasts and breast cancer [26]. In Figure 12, one example of FDOT is given. Endogenous optical signals and fluorescence signals from ICG injection were measured from a 46-year-old pre-menopausal female diagnosed with invasive ductal carcinoma. Selected slices from 3D DOT reconstructions of endogenous optical properties (i.e. THC, StO2, ) and 3D FDOT reconstruction of ICG concentration exhibit large contrast. In a volume that was confirmed to be the tumor region by Gd uptake and radiology reports, the reconstructed THC, and ICG concentrations were higher and StO2 somewhat lower than the surrounding tissue. When we take 3D iso-surface images of THC, and ICG concentration contrast with iso-values set to three standard deviations above their means. The iso-surfaces of the three contrasts overlay quite well, and the volumetric differences may be due to real tissue physiology variation. Other groups have now started to report more cases of in vivo FDOT in human patients with enhancement of tumor contrast [275, 276].
Figure 12.
A case of 3D optical tomography of breast with maligant cancer is shown with both endogenous (relative total hemoglobin, relative blood oxygen saturation and relative tissue scattering) and exogeneous contrast images (relative Indocyanine Green concentration measured from fluorescence) (left). On the top right, a parallel-plane DOT instrument and measurement geometry is illustrated. The isosurface diagram on the bottom right shows the volumetric extent of the observed tumor for each optically derived parameter. (Reprinted with permission from Ref. [26].)
3.3. Therapy Monitoring
Neoadjuvant (i.e. pre-surgical) chemotherapy is an important therapeutic approach for women with locally advanced breast cancer that can increase long-term survival. Typically, such breast cancers are large (e.g. larger than 5 cm) and many anticipated responses to drugs are vascular in nature. For treatment optimization, it is desirable to monitor tumor responses during this process. For example, alterations in tumor biology and physiology can be seen early following cytotoxic chemotherapy and can be a marker of tumor response. Dynamic contrast enhanced MRI (DCE-MRI) has been used to monitor the change in both tumor size and vascularity following preoperative (neoadjuvant) chemotherapy in patients with locally advanced breast cancer [377–379]. Results demonstrate that even before clinical or imaging evidence of tumor shrinkage are measurable, changes in tumor vascularity can be seen through blunting of the dynamic enhancement curve following intravenous administration of gadolinium contrast agents. Furthermore, Positron Emission Tomography (PET) has found that metabolic changes of cancer due to cancer therapy can precede morphological changes by up to eight days [380, 381]. DCE-MRI and PET, however, are expensive and are not practical for frequent monitoring.
The feasibility of applying diffuse optical techniques in the context of cancer therapy monitoring has been demonstrated successfully in imaging instruments [341, 350, 382, 383] and with hand-held probes [84, 325, 384]. Thus far, tumor size and/or properties (e.g. THC, HbO2, water) detected by diffuse optical methods have correlated well with patient response to chemotherapy (i.e. complete, partial or none) [382–384].
3.4. Outlook: Optical Mammography
The field of diffuse optics, as applied to breast cancer imaging and monitoring, is rapidly evolving. Innovative instrumentation and reconstruction algorithms have been developed and combined to improve image fidelity, and these factors continue to improve over time. In addition, more statistics from in vivo breast cancer data provide insight into the biological issues and guidance for more directed instrumentation and algorithm development.
Spatial resolution and detectability are two major concerns about optical mammography. In general, these factors depend on the size and contrast of the heterogeneities we investigate. To date, a few groups have demonstrated that the tumors of order 1 cm are readily detectable with excellent sensitivity and specificity based on, for example, total hemoglobin concentration contrast [122,306,370]. Tumor sensitivity and specificity decreases as the lesion size becomes smaller [370], with 4–7 mm being the state-of-the art resolution demonstrated in tissue phantoms at tumor-to-normal ratios of 2× to 4× [250]. The resolution of a DOT system depends on the many factors, such as the number of sources and detectors, the field of view covered by the optodes and optode spacings, the tissue volume to be reconstructed, the depth of target (e.g. tumor), the target-to-background contrast, the presence of a priori spatial or spectral information, and fundamentally on the physics of photon propagation in tissues [229]. While the current level of DOT resolution poses some barriers for its use as a stand-alone imaging modality for cancer screening, cancer detectability is not necessarily limited by resolution and can be utilized in complementary fashion with other imaging modalities in tumor detection and diagnosis. Strategies to further improve detectability and/or resolution are (1) to find other optical contrast related to tumoral physiological changes, (which may even occur before angiogenic changes) (2) to use anatomical constraints given by other imaging modalities to improve DOT resolution, and (3) to enhance tumor-to-normal contrast based on molecular-targeted (fluorescent/absorption) probes.
In the search for optical contrast to enhance differentiation between tumor and normal tissues, research groups are employing broader wavelength ranges to explore water, lipid and collagen concentrations, bound water fraction, and refractive index [312, 313, 348, 358, 360, 385–387]. Some of the most recent investigations have found that water concentration is higher in tumors compared to normal tissues [312,313,348,358,360], that lipid concentration is lower in tumors compared to normal tissues [312, 360], that the bound water fraction [385] and refractive indices [387] may provide novel tumor contrast as well. In addition, using diffuse correlation spectroscopy, experimenters have found that blood flow in breast cancer is larger than in normal breast tissues [84, 86].
Several groups have incorporated concurrent optical measurements with other imaging modalities. The multi-modal approach can potentially overcome structural resolution limitations of DOT, using the spatial information provided by other imaging modalities to constrain the DOT inverse problem. This multi-modal approach also provides extra physiological information for the other imaging modalities. Thus far advances have been made in three fronts: concurrent measurements with MRI [336, 371, 388–392], 3D X-ray mammography [213, 393, 394], and ultrasound [340, 347, 350, 383, 395–397].
The most effective clinical role for diffuse optical tomography in the screening, diagnosis, and treatment monitoring of breast cancer has yet to be determined. It is clear, however, that DOT and DOS provide exquisite functional information directly related to tumor patho-physiology (e.g. metabolic activity, angiogenesis, and blood flow/concentration), and complementary to structural and functional information provided by conventional imaging. Furthermore, advances in diffuse optical tomography of breast are critical for exploitation of the advances of molecular imaging [24, 270, 398], an emerging field of medicine with promise of new generation optical contrast agents. Photo-acoustic, optical mammography was also recently reported [399].
4. Optical Monitoring of Cerebral Hemodynamics
4.1. Clinical Relevance of Diffuse Optics for Cerebral Hemodynamics
The ability to measure cerebral hemodynamic responses to stimuli has important implications in fundamental neuroscience, clinical modeling and the clinic. A key concept in the field concerns the coupling between functional stimulation and regional changes in cerebral blood flow (CBF). This phenomenon is often referred to as activation flow coupling (AFC). AFC has been known for over a century but is still poorly understood [400–403]. Since most neuroimaging methods rely on AFC as an indicator of neuronal activity, a detailed characterization of AFC under normal conditions improves understanding of normal as well as pathological brain physiology, and it permits us to relate hemodynamic quantities to neuronal activity.
Hemodynamics play other crucial roles in the brain. Cerebral well-being is dependent on adequate and continuous delivery of oxygen and on the clearance of the by-products of oxygen consumption, e.g. carbon dioxide. In a simplistic picture, oxygen-saturated red blood cells (RBCs) are pumped through the arterial network to smaller vessels and into the microvasculature. Tissues are perfused by the microvasculature. Oxygen exchange occurs by diffusion at the microvascular level and the by-products are cleared, along with oxygen depleted RBCs, on the venous side (see Section 2.13). In general, this phenomena is tightly autoregulated by a variety of processes, including changes in the vascular resistance [404], to maintain constant blood perfusion in spite of changes in local pressures and other factors (see Figure 15 inset). In brain, local perfusion pressure (i.e. “cerebral perfusion pressure” (CPP)) is defined as the difference between the mean-arterial pressure (MAP) and the intracranial pressure (ICP). It is very difficult to monitor cerebral autoregulation in clinical settings. ICP can be monitored by invasive probes [405], but in many populations, clinicians prefer not to accept the risks of invasive probes; in this case MAP and neurologic signs are utilized as surrogate markers for ICP.
Figure 15.
(Top) Cerebral autoregulation implies a range of cerebral perfusion pressure (CPP) values where CBF is kept constant. As shown in the inset, impairment causes CBF to depend passively on CPP. Head-of-bed positioning was used to induce orthostatic changes in CPP. Schematic showing placement of probes where one is placed on the infarcted hemisphere and the other on contralateral, ‘healthy’ hemisphere. (Bottom) Changes in ΔTHC and rCBF are significantly larger on the infarcted hemisphere (right) which is presumably due to impaired cerebral autoregulation.
Microvascular CBF is particularly difficult to measure at the bed-side. To date many attempts have been made to measure CBF, all with unique advantages and disadvantages. Below, we list some of the major modalities employed in the clinic; research only modalities, which are very promising but not yet widely utilized are not included in the list [406]:
Laser speckle techniques such as Laser Doppler Flowmetry (LDF) rely on physical principles similar to those of DCS [50]. These techniques can measure microvascular CBF. However, practical problems in detection and overly simplified modeling largely restrict the use of LDF to the single scattering and limit its uses to about ~ 0.5 mm below the tissue surface (see Section 1). Therefore, the skull must be removed to access the brain, and clinical applications are limited to intraoperative measurements [407–409]. Recent, developments now permit penetration up to ~ 5 mm in skeletal muscles [410], but the technology is not yet useful for non-invasive, transcranial monitoring. Another variant of the method, laser speckle flowmetry (LSF) using a CCD camera, has recently been introduced to examine cerebral hemodynamics in rodents [411, 412]. It has not yet been widely commercialized, however, and its application in humans is limited to measurements during open-skull surgery [409].
Doppler ultrasound uses the frequency shifts in an ultrasound beam to image blood flow. However, due to technical issues only the proximal portions of the intracranial arteries can be insonated. Thus far the ultrasound method has only been used to measure blood flow velocity through large vessels, i.e. macrovascular blood flow velocity [413, 414]. Furthermore, since velocity changes predict CBF variation only if vessel diameters do not change, transcranical Doppler ultrasound (TCD) has limited utility in important clinical applications such as stroke evaluation [415], with its success arising in patients with proximal arterial occlusions [416]. Nevertheless, TCD remains a primary clinical modality for serial monitoring of CBF at the bedside.
Arterial Spin Labeling MRI (ASL) [417–419] and Flow-Sensitive Alternating Inversion Recovery MRI (FAIR) [420, 421] are two modalities of magnetic resonance imaging (MRI) sensitive to perfusion/flow that have been used extensively in the brain. Additional MRI modalities are available for perfusion measurements, but they require bolus injections. Although these MRI methods offer a “full-head” imaging capability and can readily be co-registered with the high-resolution anatomical information of MRI and other functional MRI modalities (e.g blood oxygen level dependent, BOLD), their use in clinical settings is limited. For example, the presence of strong magnetic fields makes them difficult to use in intensive care units, and their low through-put relegates their use to a single-shot measurement where the patients are transferred into the magnet for one ~ 30 – 60 minute observation. Furthermore, the instruments and instrument-time are expensive. Some difficulties also arise from patient specific problems; for example, it is sometimes difficult to hold infants still, and some patients are claustrophobic.
Xenon Computed Tomography (Xenon CT) is used in the clinic for measurements of “full-head” maps of cerebral blood flow [422, 423]. The modality dynamically scans the head using a CT system while the patient inhales Xenon gas. The method is gaining acceptance as a complementary modality in some intensive care units, i.e., in preference over MRI and PET modalities. As in the case of MRI, however, the use of Xenon-CT is limited to few time-points, even though quasi-portable variants are available to reduce patient transport issues. Finally, the instrument and the xenon gas are quite expensive, and xenon gas is also known to alter CBF which makes quantification more difficult.
Positron Emission Tomography (PET) is a diagnostic modality that offers direct measurements of a variety of physiological parameters including blood flow [424], glucose metabolism [425] and oxygen metabolism [424]. However, use of radioactive materials limits its applicability in many clinical settings such as the intensive care unit [426]. PET shares problems with MRI and Xenon CT as per expense, availability, patient discomfort and limitations for long-term monitoring. Finally, PET requires injection and/or inhalation of chemicals and uses radioactive materials.
Clearly, an optimal method for hemodynamic monitoring has yet to be developed. A strong need exists for an inexpensive, continuous, non-invasive instrument for measurement of CBF, and the technologies described in this review offer a great deal of promise along these lines. Diffuse optical tomographic and spectroscopy (i.e. DOT and DOS) methods have been demonstrated to measure blood volume, blood oxygenation and changes thereof, in research and clinical settings; in addition, through some maneuvers, it is also possible to employ DOS/DOT for the measurement of blood flow. DOS/DOT have been particularly successful in infants [144, 427–433]. The development of DCS has had even more impact, however, because it permits clinicians to measure several hemodynamic parameters independently with non-invasive probes (i.e. the hemoglobin concentrations and the blood flow), thus permitting estimation of changes in oxygen metabolism.
The primary advantages of diffuse optics for monitoring cerebral hemodynamics in the clinic are as follows:
The technique is non-invasive and involves no risk to the patient (e.g. no ionizing radiation, no gases to be inhaled or drugs to be injected).
The technique samples and reports results in real-time.
The technique can track changes over long periods (hours to days), in contrast to single-time-point modalities (e.g MRI, PET, Xenon-CT).
The technique can sample more than one spatial location, permitting examination of regional differences in the brain.
The technique can be employed at the bedside; critically ill patients need not be moved.
The technique is applicable to measurements patients of all ages, from pre-mature born infants to adults.
The instrumentation is relatively inexpensive and the per-measurement costs are minimal.
Diffuse optical measurements also have limitations: relatively short penetration beyond the skull/scalp, relatively coarse spatial resolution, limited structural/morphological information which makes partial volume effects more difficult to account for, and difficulties with the assignment of absolute optical properties. Furthermore, as with any new modality proposed for clinical use, diffuse optical monitors must demonstrate clinical utility in large, controlled trials before mainstream acceptance is assured. For applications in neurology, portable devices that monitor hemodynamics in large tissue volumes are popular due to the relative simplicity of the instrumentation and analysis algorithms, and due to simple, comfortable probe-heads. Several topographic (2D) and tomographic (3D) imagers are used now to map hemodynamic changes locally or globally [434, 435], and various approaches ranging from dense probe designs to utilization of secondary data have been considered to optimize the spatial resolution [135, 436]. Given these pros and cons, we now consider clinical applications at the present state of diffuse optics technology.
4.2. Selected Translational Results
Optical imaging – ranging from microscopy methods to diffuse optics – has found a myriad of applications in brain imaging [434,435]. It is beyond the scope of this review to describe this wide-ranging field. Here we limit our discussion to those translational applications wherein diffuse optical methods are used in the clinic.
Broadly speaking, two groups of studies have been employed: (1) Those using commercial devices [435], and (2) those using state-of-the-art research devices and algorithms [435].
Thousands of commercial instruments are currently in use with a rapidly increasing number of studies being published as a result [435]. Unfortunately, some of these studies have been done without state-of-the-art instrumentation and/or algorithms, and over the years, the lack of optimized methodology has led to some debate over the utility of (particularly) NIRS/DOS [437–439]. We believe that NIRS/DOS and related techniques offer a great deal of promise and with improvements in technology and improvements in physical understanding about photon propagation through tissues and its modeling, the utility of NIRS/DOS will rapidly become more apparent. Commercial systems are, indeed, crucial for the clinical penetration of the technology, but until large-scale clinical trials have been performed, instrumentation needs to be handled as research tools. At this point, at least three [435] devices have the USA Food and Drug Administration’s approval for use in patient populations.
Amongst many potential applications, NIRS/DOS has been utilized for cerebral monitoring of adults with traumatic brain injury (TBI) and subarachnoid hemorrhage (SAH) [440–445], ischemic stroke [80, 277–280, 446–453], sleep apnea and other sleep disorders [454–457], intraoperative brain monitoring [458, 459] and in neonates and children [433, 460–462]. This list is not exhaustive; it is meant to give a “flavor” of the field. Over the years, NIRS/DOS has been utilized for a very wide-range of applications, but unfortunately largely for feasibility demonstrations.
4.2.1. Hemodynamics of Healthy Brain
Figure 13(a) shows a schematic and data from two studies conducted in our laboratory [65, 66]. Here we have combined NIRS/DOS and DCS methods in a hybrid instrument [65, 77]. For NIRS/DOS, three, amplitude modulated (70 MHz, “frequency-domain”) lasers operating at 690nm, 785nm and 830nm were employed as light sources. A photomultiplier tube (PMT) was used as a detector and its output was fed to a radio-frequency, homodyne, I&Q demodulation electronics box which calculated the relative amplitude and phase [463]. NIRS/DOS data was analyzed using the “differential pathlength factor” (DPF, see Section 2.8.2) formulation [143]. For DCS, a long coherence length, continuous wave laser was used as a source. Eight photon-counting, fast avalanche-photodiodes (APDs) and a multi-channel autocorrelator board was used. DCS data was analyzed using a semi-infinite medium solution (see Section 2.9.3) [65,76,77]. The fiber optics from the two devices were mounted on the same probe and were time shared; data was acquired in an interlaced sequence by utilizing optical switches.
Figure 13.
(a) Schematic showing placement of probes used for hypercapnia (frontal) and sensorimotor (side) studies. For the frontal probe, a laser Doppler flowmetry (LDF) probe was placed mid-way the source and detector fibers to record scalp blood flow. (b) Increased CO2 breathing (hypercapnia) results in significant increases in end-tidal CO2 (EtCO2) and blood-flow in brain (rCBF(DCS)) but only a negligible amount in scalp blood-flow (rCBF(LDF)). (c–d) Hemodynamic response to finger-tapping when the probe is placed (c) away from the contralateral sensorimotor cortex and (d) when its placed on the contralateral sensorimotor cortex.
Figure 13(b) shows data from a hypercapnia experiment wherein we have measured the CBF response to increased carbon dioxide (CO2) breathing. We measured CBF in five subjects at rest, and during 4–6 minute periods of increased cerebral carbon dioxide induced by breathing a 6% CO2 gas mixture. In healthy subjects, hypercapnia causes a well-defined increases in CBF [464]. We observed a sustained increase of mean CBF of 35.4± 9.6%, and an accompanying increase in EtCO2 of 14.7±4.7 mmHg. This relative rate corresponds to a 2.4± 0.4% CBF increase per mmHg of EtCO2, a number well within the literature values (i.e. 2–3.6%/mmHg). During this investigation we also placed a laser Doppler probe on the scalps of a subset of volunteers. The probe enabled us to directly compare CBF measured by DCS to scalp flow measured by laser Doppler flowmetry (LDF) during activation. Figure 13(b) shows these measurements for one subject, along with measured EtCO2. Notice the scalp flow signal is small compared to CBF measured by DCS and largely unchanged with changes in EtCO2 (right vertical axis). These studies demonstrate the DCS signal does not arise from changes in scalp blood flow, but some contamination is inevitable.
Figure 13(c–d) show data from an experiment where the subject was asked to carry out a task that would stimulate the sensorimotor cortex [66]. First, we localized the hand sensorimotor cortical area contralateral to the dominant hand according to the 10–20 system [465]. The probe (Figure 13(a)) was placed and secured over this region. For the activation period, the subject was instructed to tap index and middle fingers against the thumb at 3 Hz. A blocked design of fifteen such stimuli was used. In order to illustrate the local nature of the observed response, we have also taken data where the whole process was repeated with probe placed ~2 cm frontal to the sensorimotor cortex. Figure 13(c) shows the results of one such study. None of the observed quantities show any changes that are correlated with the stimuli despite the fact that stimuli were presented during the time period shown by vertical bars. Figure 13(d) shows the population averaged results from seven subjects; a robust change correlated with the activation was observed in all quantities. Mean changes observed were 39±10% for rCBF, 12.5±2.8µM for ΔHbO2, −3.8±0.8µM for ΔHb, 8.3±2.3µM for ΔTHC and 10.1±4.4% for rCMRO2. rCBF changes are well within the range of values determined by MRI [466, 467], [H2 15O] PET [468], [133Xe] [469] and [11CH3] PET [470] for similar measurement stimuli, i.e. 21% – 60%. Mean oxy-, deoxy- and total-hemoglobin changes agree quantitatively with increases reported by BOLD of 2 – 4% [466, 471]. The increase in CMRO2 is within the range of values (9% to 29%) from hybrid MRI measurements [466]. The ratio of rCBF to rCMRO2 is also agreement with data reported by hybrid MRI techniques [466, 472] which range from two to four.
Overall, these results demonstrate the ability of NIRS/DOS and DCS to probe local changes in cerebral hemodynamics.
4.2.2. Diffuse Optics versus fMRI
Since NIRS/DOS and DCS both employ fiber-optics to deliver and detect light, they are readily adaptable for use concurrently in the MRI-magnet using MRI compatible probes and long optical fibers. This permits cross-validation studies, as well as utilization of MRI derived spatial information for diffuse optical data analysis. In a series of papers, Boas and coworkers have compared NIRS/DOS with BOLD and ASL MRI; in so doing, they have also developed models to describe the physiological origin of the BOLD signal, to account for partial volume effects in NIRS/DOS signals and to derive composite models to estimate rCMRO2 [473–478].
Here we highlight one study [474] that compares the temporal properties of NIRS/DOS signals with BOLD and ASL-MRI. As shown in Figure 14, the temporal evolution of NIRS/DOS determined ΔTHC and ΔHbO2 agree with ASL-MRI and ΔHb agrees with BOLD. Notice how ASL-MRI derived CBF, ΔTHC and ΔHbO2 maxima arise earlier than BOLD and ΔHb maxima. ΔHb and BOLD are strongly correlated while ΔTHC and BOLD exhibit a weaker correlation, in agreement with biophysical models for the BOLD signals. It has long been assumed that NIRS/DOS measures of ΔTHC (or blood volume) would correlate with CBF under many circumstances. These results explicitly demonstrate strong correlation between these signals.
Figure 14.
(a–b) Morphological MRI scans showing location of fiducial markers indicating the location of NIRS/DOS probe which is then overlaid onto BOLD and ASL scans to define ROIs. As shown in (c), an MRI compatible NIRS/DOS probe was used for simultaneous data acquisition. (d) Group averaged responses from simultaneous ASL, BOLD and NIRS/DOS studies. Temporal evolution of NIRS/DOS measures of ΔTHC and ΔHbO2 agree with ASL and ΔHb agrees with BOLD. Notice how ASL, ΔTHC and ΔHbO2 maxima are earlier than BOLD and ΔHb maxima. ΔHb curve is shown inverted. Figure courtesy of D. A. Boas [474]).
4.2.3. Longitudinal Bed-Side Monitoring
One of the most promising applications of diffuse optics is at the bed-side for longitudinal monitoring of cerebral hemodynamics. To demonstrate this idea and to test the feasibility of hybrid NIRS/DOS-DCS measurements on a critically ill population of acute, ischemic stroke patients, we have induced orthostatic stress by changes in head-of-bed positioning as shown in Figure 15 [80]. Our hypothesis was that in response to this challenge, the impaired cerebral autoregulation would lead to larger changes in cerebral hemodynamics in the infarcted hemisphere by comparison to the “healthy”, contralateral hemisphere.
To this end, diffuse optical measurements were obtained from patients with acute hemispheric ischemic stroke (n=17, mean age 65 years) with probes placed on the forehead near the frontal poles (Figure 15 (Top, right)). CBF and hemoglobin concentrations were measured sequentially for 5 min each at HOB positions: 30, 15, 0, −5 and 0 degrees and normalized to their values at 30 degrees. Figure 15(bottom) shows continuous CBF data taken over 25 minutes from a representative subject with acute ischemic stroke. A clear differentiation is observed between two hemispheres; this differentiation was statistically significant over the whole population. In contrast, when an age-matched group with “vascular risk factors” was studied, i.e. risk factors such as cigarette smoking, high blood pressure etc, we did not observe any hemispherical differentiation. Interestingly, in ~25% of subjects, we have observed that CBF was not maximized at −5 degrees; rather it was minimized at this HOB angle. This paradoxical response was observed in traumatic brain injury patients [479]. The effect was likely a result of a substantial increase in intra-cranial pressure, a parameter that is not routinely monitored in ischemic stroke patients.
This example illustrates that diffuse optical instrumentation can be deployed at the bed-side of critically ill-patients, and that it may be promising for use as a tool to optimize patient care based on cerebral hemodynamic measurements in real-time.
4.2.4. Full Head, 3D tomography in Neonates
Amongst numerous applications of NIRS/DOS to neonatal studies, few groups have reported three-dimensional, tomographic imaging of the whole head [460, 480–484]. As discussed in previous sections, 3D tomography with NIRS/DOS has mostly been limited to less absorbing tissues such as the breast. New results, while still very preliminary, demonstrate the feasibility of whole-head imaging in neonates by taking advantage of their smaller head circumferences and thinner skulls. When combined with other modalities such as Ultrasound, MRI or CT, this approach could provide valuable physiologic information in addition to the mostly morphological information available via other modalities. Figure 16 (from Ref [480]) shows a photo of the probe on a subject and coronal sections of images of blood volume and blood oxygen saturation as it compares to an ultrasound image from a 34-week gestational age infant. In general, 3D scans such as this one show a left/right symmetry between hemispheres, except in the presence of a condition such as a hemorrhage. The images shown are from an infant who was diagnosed with a left-sided intraventricular hemorrhage which is also visible on the ultrasound image. A clear increase in blood volume is evident on the left hemisphere, consistent with the presence of the hemorrhage. In the blood oxygen saturation image, a small region of significantly low oxygen saturation (10% vs 62% on the contralateral side) that is apparent; it is more lateral and superficial than both the ultrasound and blood volume images. This observation may be attributed to the presence of an ischemic penumbra surrounding hemorrhagic lesions, or it may be due to issues with optical image reconstruction. Nevertheless, the authors reported data from ~40 infants showing the feasibility of 3D tomography in neonates. This type of approach may become more common in the future with improved probe designs, detectors and newer reconstruction algorithms.
Figure 16.
(Left) Placement of probes on an infant. (Right) Coronal sections showing (a) blood volume, (b) blood oxygen saturation and (c) the corresponding ultrasound image. Figure courtesy of J. C. Hebden [480].
5. Other Applications
Due to space constraints, we have chosen to focus on breast and brain applications. Other applications include, but are not limited to, imaging and monitoring in preclinical and clinical oncology [485], monitoring of muscle diseases and physiology [435, 486], photo-dynamic therapy planning [487, 488], in-surgery monitoring [458] and guidance [273, 489], dermatology [490] and tomography of finger joint physiology and disease [491, 492]. The biomedical optics field has, more broadly, also been branching into many other clinically exciting directions with tools ranging from optical coherence tomography to photo-acoustic tomography and microscopy to optical projection tomography. Interested readers will find more information about these subjects in references [493–497].
6. Conclusion
In this review, we have outlined the physical and algorithmic foundations of near-infrared (NIRS) or diffuse optical (DOS) spectroscopy, diffuse correlation spectroscopy (DCS), and diffuse optical tomography (DOT). We have showcased their applications in two sub-fields: optical mammography and cerebral hemodynamics. These subfields were chosen because they are, arguably, the two areas with the largest amount of diffuse optics research activity. The field has now evolved to a point wherein substantial effort is oriented towards clinical application. In the near future, improved understanding of photon propagation in tissues, better access to algorithms and computational resources, new developments in laser and detector technologies, and increasing amounts of clinical data will enable these developments.
Acknowledgments
This work was partially funded by NIH-grants HL-57835, NS-60653, RR-02305, EB-07610, NS-45839, CA-126187, Thrasher Research Fund (NR 0016) and Fundació Cellex Barcelona. The authors gratefully acknowledge many fruitful discussions and interactions over the years with colleagues from the biomedical optics community at the University of Pennsylvania and, indeed, throughout the world. At UPenn, much of the research in this review was facilitated by sustained collaborations over many years with Britton Chance, Mitchell Schnall, Joel Greenberg, John Detre, Daniel Licht, Theresa Busch, Mark Rosen, Joseph Culver, Guoqiang Yu, and David Boas.
Glossary
- α
Fraction of dynamic photon scattering events in medium
- g
Scattering anisotropy factor
- G0
Homogeneous Green’s Function
- ci
Concentration of the ith chromophore
- g1
Normalized electric field temporal auto-correlation function, g1(r, τ, t) = G1(r, τ, t)/ < E(r, t)E*(r, t) >
- g2
Normalized intensity auto-correlation function, g2(r, τ, t) = G2(r, τ, t)/ < I(t) >2
- 𝖦1
Electric field temporal auto-correlation function, G1(r, τ, t) = 〈E*(r, t)E(r, t + τ)〉
- 𝖦2
Intensity auto-correlation function, G2(r, τ, t) = 〈I(r, t)I(r, t + τ)〉
- D
Photon Diffusion Coefficient, D = υℓtr/3
- Db
Brownian Diffusion Coefficient
- ε
Extinction coefficient
- λ
Wavelength of Light (nm)
- L(r, Ω̂, t)
Radiance; power per unit area per unit angle traveling in Ω̂ direction at position r and time t
- E(r, Ω̂, t)
Light electric field traveling in Ω̂ direction at position r and time t
- ℓtr
Transport mean free path,
- E(r, t)
Total light electric field at position r and time t
- I(r, t)
Light field intensity (i.e., |E(r, t)|2) at position r and time t
Reduced Scattering Coefficient,
- μa
Absorption Coefficient
- μs
Scattering Coefficient
- υ
Speed of light in tissue
- 〈Δr2(τ)〉
The mean-square displacement in time τ of the scattering particles (e.g. red blood cells)
- Φ(r, t)
Photon-Fluence Rate at position r and time t
- U(r)
Photon-Fluence Rate; expressed in the frequency domain, Φ(r, t) = U(r)e−iωt
- ω
Laser/Source Modulation Frequency
- BFI
Blood Flow Index estimated by DCS (i.e., αDb)
- CBF
Cerebral Blood Flow
- CMRO2
Cerebral Metabolic Rate of Oxygen
- CT
Computed Tomography
- CW
Continuous Wave
- DCS
Diffuse Correlation Spectroscopy
- DOS
Diffuse Optical Spectroscopy
- DOT
Diffuse Optical Tomography
- FD
Frequency Domain
- HbO2
Oxy-Hemoglobin Concentration
- Hbr/Hb
De-oxy Hemoglobin Concentration
- ICG
Indocyanine Green
- MRI
Magnetic Resonance Imaging
- NIRS
Near Infrared Spectroscopy
- PET
Positron Emission Tomography
- RBCs
Red Blood Cells
- StO2
Tissue Blood Oxygen Saturation
- THC
Total Hemoglobin Concentration
- TRS
Time Domain Spectroscopy
Footnotes
Some authors prefer to use the photon energy concentration, Γ(r, t) (J/cm3), which is directly proportional to the fluence rate: Γ = υΦ.
For any vector A, , and ∫4π Ω̂[Ω̂ · ∇(A · Ω̂)]dΩ = 0. Also, and ∫4π f (Ω̂ · Ω̂′)J · Ω̂′dΩ̂′ = J · Ω̂ ∫4πf (Ω̂ · Ω̂′)Ω̂ · Ω̂′dΩ̂′.
References
- 1.Cutler M. Transillumination of the breast. Surg Gynecol Obstet. 1929;48:721–727. [Google Scholar]
- 2.Jobsis FF. Noninvasive infrared monitoring of cerebral and myocardial sufficiency and circulatory parameters. Science. 1977;198:1264–1267. doi: 10.1126/science.929199. [DOI] [PubMed] [Google Scholar]
- 3.Jobsis-vanderVliet FF, Jobsis PD. Biochemical and physiological basis of medical near-infrared spectroscopy. Journal of Biomedical Optics. 1999;4:397. doi: 10.1117/1.429953. [DOI] [PubMed] [Google Scholar]
- 4.Jöbsis-vanderVliet FF. Discovery of the near-infrared window into the body and the early development of near-infrared spectroscopy. Journal of Biomedical Optics. 1999;4:392. doi: 10.1117/1.429952. [DOI] [PubMed] [Google Scholar]
- 5.Yodh A, Chance B. Spectroscopy and imaging with diffusing light. Physics Today. 1995;48(3):34–40. [Google Scholar]
- 6.Chance B, Alfano R. Proceedings of Optical Tomography, Photon Migration, and Spectroscopy of Tissue and Model Media: Theory, Human Studies, and Instrumentation. SPIE; 1995. p. 2389. [Google Scholar]
- 7.Patterson MS, Moulton JD, Wilson BC, Berndt KW, Lakowicz JR. Frequency-Domain reflectance for the determination of the scattering and absorption properties of tissue. Appl Opt. 1991;30(31):4474–4476. doi: 10.1364/AO.30.004474. [DOI] [PubMed] [Google Scholar]
- 8.Patterson MS, Chance B, Wilson BC. Time resolved reflectance and transmittance for the non-invasive measurement of tissue optical properties. Appl Opt. 1989;28:2331–2336. doi: 10.1364/AO.28.002331. [DOI] [PubMed] [Google Scholar]
- 9.Gratton E, Mantulin W, Ven MJ, van de Ven M, Fishkin J, Maris M, Chance B. The possibility of a near-infrared imaging system using frequency-domain methods. Japan: Hamamatsu; 1990. pp. 183–189. [Google Scholar]
- 10.Delpy DT, Cope M, van der Zee P, Arridge S, Wray S, Wyatt J. Estimation of optical pathlength through tissue from direct time of flight measurement. Phys Med Biol. 1988;33:1433–1442. doi: 10.1088/0031-9155/33/12/008. [DOI] [PubMed] [Google Scholar]
- 11.Jacques SL. Time resolved propagation of ultrashort laser pulses within turbid tissues. Appl Opt. 1989;28:2223–2229. doi: 10.1364/AO.28.002223. [DOI] [PubMed] [Google Scholar]
- 12.Benaron DA, Stevenson DK. Optical time-of-flight and absorbance imaging of biologic media. Science. 1993;259(5100):1463–1466. doi: 10.1126/science.8451643. [DOI] [PubMed] [Google Scholar]
- 13.O’Leary MA, Boas DA, Chance B, Yodh AG. Refraction of diffuse photon density waves. Phy Rev Lett. 1992;69(18):2658–2661. doi: 10.1103/PhysRevLett.69.2658. [DOI] [PubMed] [Google Scholar]
- 14.Boas DA, O’Leary MA, Chance B, Yodh AG. Scattering and wavelength transduction of diffuse photon density waves. Phys Rev E. 1993;47(5):R2999–R3002. doi: 10.1103/physreve.47.r2999. [DOI] [PubMed] [Google Scholar]
- 15.Fishkin JB, Gratton E. Propagation of photon density waves in strongly scattering media containing an absorbing ’semi-infinite’ plane bounded by a straight edge. J Opt. Soc. Am. A. 1993;10:127–140. doi: 10.1364/josaa.10.000127. [DOI] [PubMed] [Google Scholar]
- 16.Schmitt JM, Knuttel A, Knutson JR. Interference of diffusive light waves. J Opt. Soc. Am. A. 1992;9:1832. doi: 10.1364/josaa.9.001832. [DOI] [PubMed] [Google Scholar]
- 17.Tromberg BJ, Svaasand LO, Tsay T, Haskell RC. Properties of photon density waves in multiple-scattering media. Appl Opt. 1993;32:607–616. doi: 10.1364/AO.32.000607. [DOI] [PubMed] [Google Scholar]
- 18.Sevick EM, Lakowicz JR, Szmacinski H, Nowaczyk K, Johnson ML. Frequency domain imaging of absorbers obscured by scattering. J.Photochem.Photobiol.B: Biol. 1992;16:169–185. doi: 10.1016/1011-1344(92)80007-i. [DOI] [PubMed] [Google Scholar]
- 19.Johnson CC. Optical diffusion in blood. IEEE Transactions on Biomedical Engineering. 1970;BME17:129–133. doi: 10.1109/tbme.1970.4502711. [DOI] [PubMed] [Google Scholar]
- 20.Ishimaru A. Wave Propagation and Scattering in Random Media. San Diego: Academic Press, Inc.; 1978. [Google Scholar]
- 21.Furutsu K. On the diffusion equation derived from the space-time transport equation. J Opt. Soc. Am. A. 1980;70:360. [Google Scholar]
- 22.Groenhuis RAJ, Ferwerda HA, Bosch TJJ. Scattering and absorption of turbid materials determined from reflection measurements, I. theory. Appl Opt. 1983;22:2456–2462. doi: 10.1364/ao.22.002456. [DOI] [PubMed] [Google Scholar]
- 23.Yodh AG, Boas DA. chapter Functional Imaging with Diffusing Light. CRC Press; 2003. Biomedical Photonics; pp. 21pp. 1–45. [Google Scholar]
- 24.Ntziachristos V, Chance B. Probing physiology and molecular function using optical imaging: applications to breast cancer. Breast Cancer Res. 2001;3(1):41–46. doi: 10.1186/bcr269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Hawrysz DJ, Sevick-Muraca EM. Developments toward diagnostic breast cancer imaging using near-infrared optical measurements and fluorescent contrast agents. Neoplasia. 2000;2(5):388–417. doi: 10.1038/sj.neo.7900118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Corlu A, Choe R, Durduran T, Rosen MA, Schweiger M, Arridge SR, Schnall MD, Yodh AG. Three-dimensional in vivo fluorescence diffuse optical tomography of breast cancer in humans. Optics Express. 2007;15(11):6696–6716. doi: 10.1364/oe.15.006696. [DOI] [PubMed] [Google Scholar]
- 27.Ferrari M, Hanley DF, Wilson DA, Traystman RJ. Redox changes in cat brain cytochrome-c oxidase after blood-fluorocarbon exchange. American Journal of Physiology-Heart and Circulatory Physiology. 1990;258(6):1706–1713. doi: 10.1152/ajpheart.1990.258.6.H1706. [DOI] [PubMed] [Google Scholar]
- 28.Gratton G, Corballis PM, Cho E, Fabiani M, Hood DC. Shades of gray matter: noninvasive optical images of human brain responses during visual stimulation. Psychophysiology. 1995;32:505–509. doi: 10.1111/j.1469-8986.1995.tb02102.x. [DOI] [PubMed] [Google Scholar]
- 29.Gratton G, Fabiani M, Friedman D, Franceschini MA, Fantini S, Corballis PM, Gratton E. Rapid changes of optical parameters in the human brain during a tapping task. J Cogn Neuroscience. 1995;7:446–456. doi: 10.1162/jocn.1995.7.4.446. [DOI] [PubMed] [Google Scholar]
- 30.Arridge SR, Schotland JC. Optical tomography: forward and inverse problems. Inverse Problems. 2009;25(12):123010. [Google Scholar]
- 31.Boas DA, Brooks DH, Miller EL, DiMarzio CA, Kilmer M, Gaudette RJ, Zhang Q. Imaging the body with diffuse optical tomography. IEEE Signal Processing Magazine. 2001;18:57–75. [Google Scholar]
- 32.Hebden JC, Arridge SR, Delpy DT. Optical imaging in medicine: I. experimental techniques. Phys Med Biol. 1997;42:825–840. doi: 10.1088/0031-9155/42/5/007. [DOI] [PubMed] [Google Scholar]
- 33.Hebden JC, Delpy DT. Diagnostic imaging with light. Br J Radiol. 1997;70 Spec No:S206–S214. doi: 10.1259/bjr.1997.0026. [DOI] [PubMed] [Google Scholar]
- 34.Arridge SR, Hebden JC. Optical imaging in medicine: II. modelling and reconstruction. Phys. Med. Biol. 1997;42(5):841–854. doi: 10.1088/0031-9155/42/5/008. [DOI] [PubMed] [Google Scholar]
- 35.Villringer A, Chance B. Non-invasive optical spectroscopy and imaging of human brain function. Trends Neurosci. 1997;20:435–442. doi: 10.1016/s0166-2236(97)01132-6. [DOI] [PubMed] [Google Scholar]
- 36.Clark NA, Lunacek JH, Benedek GB. A study of brownian motion using light scattering. Am J Phys. 1970;38:575–585. [Google Scholar]
- 37.Fuller GG, Rallison JM, Schmidt RL, Leal LG. The measurement of velocity gradients in laminar flow by homodyne light-scattering spectroscopy. J.Fluid Mech. 1980;100:555–575. [Google Scholar]
- 38.Tong P, Goldburg WI, Chan CK, Sirivat A. Turbulent transition by photon-correlation spectroscopy. Phys. Rev. A. 1988;37:2125–2133. doi: 10.1103/physreva.37.2125. [DOI] [PubMed] [Google Scholar]
- 39.Bertolotti M, Crosignani B, Di Porto P, Sette D. Light scattering by particles suspended in a turbulent fluid. J Phys. A. 1969;2:126–128. [Google Scholar]
- 40.Bourke PJ, Butterworth J, Drain LE, Egelstaff PA, Jakeman E, Pike ER. A study of the spatial structure of turbulent flow by intensity-fluctuation spectroscopy. J.Phys.A. 1970;3:216–228. [Google Scholar]
- 41.Tanaka T, Riva C, Ben-Sira I. Blood velocity measurements in human retinal vessels. Science. 1974;186:830–831. doi: 10.1126/science.186.4166.830. [DOI] [PubMed] [Google Scholar]
- 42.Stern MD. In vivo evaluation of microcirculation by coherent light scattering. Nature. 1975;254:56–58. doi: 10.1038/254056a0. [DOI] [PubMed] [Google Scholar]
- 43.Bonner RF, Nossal R. chapter Principles of laser-Doppler flowmetry. Vol. 107. Boston: Kluwer Academic Publishers; 1990. Laser-Doppler blood flowmetry; pp. 17–45. [Google Scholar]
- 44.Pusey PN, Vaughan JM. chapter Light Scattering and Intensity Fluctuation Spectroscopy. Vol. 2. London: The Chemical Society; 1975. Dielectric and Related Molecular Processes X - Ed. M. D. Specialist Periodical Report. [Google Scholar]
- 45.Berne BJ, Pecora R. Dynamic Light Scattering with Applications to Chemistry, Biology, and Physics. Malabar, FL: Krieger; 1990. [Google Scholar]
- 46.Brown W. Dynamic Light Scattering: The Method and Some Applications. New York: Clarendon; 1993. [Google Scholar]
- 47.Cummings HZ, Pike ER. Photon Correlation and Light-Beating Spectroscopy. New York: Plenum; 1974. Vol. 3 of NATO Advanced Study Institute Series B: Physics. [Google Scholar]
- 48.Cummings HZ, Swinney HL. Light beating spectroscopy. Prog. Opt. 1970;8:133–200. [Google Scholar]
- 49.Valkov AY, Romanov VP. Characteristics of propagation and scattering of light in nematic liquid crystals. Sov. Phys. JETP. 1986;63:737–743. [Google Scholar]
- 50.Briers JD. Laser doppler, speckle and related techniques for blood perfusion mapping and imaging. Physiol. Meas. 2001;22:R35–R66. doi: 10.1088/0967-3334/22/4/201. [DOI] [PubMed] [Google Scholar]
- 51.Riva CE, Ross B, Benedek GB. Laser doppler measurements of blood flow in capillary tubes and retinal arteries. Invest. Ophthalmol. 1972;11:936–944. [PubMed] [Google Scholar]
- 52.Tanaka T, Benedek GB. Measurement of the velocity of blood flow (in vivo) using a fiber optic catheter and optical mixing spectroscopy. Appl Opt. 1975;14:189–196. doi: 10.1364/AO.14.000189. [DOI] [PubMed] [Google Scholar]
- 53.Stern MD, Bowen PD, Parma R, Osgood RW, Bowman RL, Stein JH. Measurements of renal cortical and medullary blood flow by laser-doppler spectroscopy in the rat. Am. J. Physiol. 1979;236:F80–F87. doi: 10.1152/ajprenal.1979.236.1.F80. [DOI] [PubMed] [Google Scholar]
- 54.Stern MD, Lappe DL, Bowen PD, Chimosky JE. Continuous measurements of tissue blood flow by laser-doppler spectroscopy. Am. J. Physiol. 1977;232:H441–H448. doi: 10.1152/ajpheart.1977.232.4.H441. [DOI] [PubMed] [Google Scholar]
- 55.Oberg PA, Nilsson GE, Tenland T, Holmstrom A, Lewis DH. Use of a new laser doppler flowmeter for measurements of capillary blood flow in skeletal muscle after bullet wounding. Acta Chir Scand Suppl. 1979;489:145–150. [PubMed] [Google Scholar]
- 56.Kiel JW, Riedel GL, DiResta GR, Shepherd AP. Gastric mucosal blood flow measured by laser-doppler velocimetry. Am. J. Physiol. 1985;249:G539–G545. doi: 10.1152/ajpgi.1985.249.4.G539. [DOI] [PubMed] [Google Scholar]
- 57.Hellem S, Jacobsson LS, Nilsson GE, Lewis DH. Measurements of microvascular blood flow in cancellous bone using laser doppler flowmetry and 133Xe-clearance. Int. J. Oral Surg. 1983;12:165–177. doi: 10.1016/s0300-9785(83)80063-5. [DOI] [PubMed] [Google Scholar]
- 58.Williams PC, Stern MD, Bowen PD, Brooks RA, Hammock MK, Bowman RL, Chiro G. Mapping of cerebral cortical strokes in rhesus monkeys by laser doppler spectroscopy. Med. Res. Eng. 1980;13:3–5. [PubMed] [Google Scholar]
- 59.Shepherd AP, Riedel GL. Continuous measurements of intestinal mucosal blood flow by laser-doppler velocimetry. Am. J. Physiol. 1982;242:G668–G672. doi: 10.1152/ajpgi.1982.242.6.G668. [DOI] [PubMed] [Google Scholar]
- 60.Boas DA, Campbell LE, Yodh AG. Scattering and imaging with diffusing temporal field correlations. Phys Rev Lett. 1995;75(9):1855–1858. doi: 10.1103/PhysRevLett.75.1855. [DOI] [PubMed] [Google Scholar]
- 61.Boas DA, Yodh AG. Spatially varying dynamical properties of turbid media probed with diffusing temporal light correlation. J Opt. Soc. Am. A. 1997;14(1):192–215. [Google Scholar]
- 62.Pine DJ, Weitz DA, Chaikin PM, Herbolzheimer Diffusing-wave spectroscopy. Phys. Rev. Lett. 1988;60:1134–1137. doi: 10.1103/PhysRevLett.60.1134. [DOI] [PubMed] [Google Scholar]
- 63.Maret G, Wolf PE. Multiple light scattering from disordered media. the effect of brownian motion of scatterers. Z Phys. B. 1987;65:409–413. [Google Scholar]
- 64.Stephen MJ. Temporal fluctuations in wave propagation in random media. Phys. Rev. B. 1988;37:1–5. doi: 10.1103/physrevb.37.1. [DOI] [PubMed] [Google Scholar]
- 65.Durduran T. Ph.D. Dissertation. University of Pennsylvania; 2004. Non-Invasive Measurements of Tissue Hemodynamics with Hybrid Diffuse Optical Methods. [Google Scholar]
- 66.Durduran T, Yu G, Burnett MG, Detre JA, Greenberg JH, Wang J, Zhou C, Yodh AG. Diffuse optical measurements of blood flow, blood oxygenation and metabolism in human brain during sensorimotor cortex activation. Opt Lett. 2004;29:1766–1768. doi: 10.1364/ol.29.001766. [DOI] [PubMed] [Google Scholar]
- 67.Li J, Dietsche G, Iftime D, Skipetrov SE, Maret G, Elbert T, Rockstroh B, Gisler T. Noninvasive detection of functional brain activity with near-infrared diffusing-wave spectroscopy. J Biomed Opt. 2005 Jul-Aug;10(4):044002–1–044002–12. doi: 10.1117/1.2007987. [DOI] [PubMed] [Google Scholar]
- 68.Yu G, Durduran T, Zhou C, Wang HW, Putt ME, Saunders M, Seghal CM, Glatstein E, Yodh AG, Busch TM. Noninvasive monitoring of murine tumor blood flow during and after photodynamic therapy provides early assessment of therapeutic efficacy. Clin. Cancer Res. 2005;11:3543–3552. doi: 10.1158/1078-0432.CCR-04-2582. [DOI] [PubMed] [Google Scholar]
- 69.Buckley EM, Cook NM, Durduran T, Kim MN, Zhou C, Choe R, Yu Guoqiang, Shultz S, Sehgal CM, Licht DJ, Arger PH, Putt ME, Hurt HH, Yodh AG. Cerebral hemodynamics in preterm infants during positional intervention measured with diffuse correlation spectroscopy and transcranial doppler ultrasound. Optics Express. 2009;17:12571–12581. doi: 10.1364/oe.17.012571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Menon C, Polin GM, Prabakaran I, Hs A, Cheung C, Culver JP, Pingpank J, Sehgal CS, Yodh AG, Buerk DG, Fraker DL. An integrated approach to measuring tumor oxygen status using human melanoma xenografts as a model. Cancer Res. 2003;63:7232–7240. [PubMed] [Google Scholar]
- 71.Roche-Labarbe N, Carp SA, Surova A, Patel M, Boas DA, Grant PE, Franceschini MA. Noninvasive optical measures of cbv, sto2, cbf index, and rcmro2 in human premature neonates’ brains in the first six weeks of life (p na) Human Brain Mapping. 2009 doi: 10.1002/hbm.20868. advance online. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Durduran T, Zhou C, Buckley EM, Kim MN, Yu G, Choe R, Gaynor WJ, Spray TL, Durning SM, Mason SE, Montenegro LM, Nicolson SC, Zimmerman RA, Putt ME, Wang JJ, Greenberg JH, Detre JA, Yodh AG, Licht DJ. Optical measurement of cerebral hemodynamics and oxygen metabolism in neonates with congenital heart defects. J Biomed Opt. 2009 doi: 10.1117/1.3425884. accepted. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Yu G, Floyd T, Durduran T, Zhou C, Wang JJ, Detre JA, Yodh AG. Validation of diffuse correlation spectroscopy for muscle blood flow with concurrent arterial-spin-labeling perfusion. Opt Exp. 2007;15:1064–1075. doi: 10.1364/oe.15.001064. [DOI] [PubMed] [Google Scholar]
- 74.Kim MN, Durduran T, Frangos S, Edlow BL, Buckley EM, Heather EM, Zhou C, Yu G, Choe R, Maloney-Wilensky E, Wolf RL, Woo JH, Grady MS, Greenberg JH, Levine JM, Yodh AG, Detre JA, Kofke WA. Noninvasive measurement of cerebral blood flow and blood oxygenation using near-infrared and diffuse correlation spectroscopies in critically brain-injured adults. Neurocritical Care. 2009 doi: 10.1007/s12028-009-9305-x. advance online. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Zhou C, Eucker S, Durduran T, Yu G, Ralston J, Friess SH, Ichord RN, Margulies SS, Yodh AG. Diffuse optical monitoring of hemodynamic changes in piglet brain with closed head injury. Journal of Biomedical Optics. 2009;14:034015. doi: 10.1117/1.3146814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Culver JP, Durduran T, Furuya D, Cheung C, Greenberg JH, Yodh AG. Diffuse optical tomography of cerebral blood flow, oxygenation and metabolism in rat during focal ischemia. J Cereb. Blood Flow Metab. 2003;23:911–924. doi: 10.1097/01.WCB.0000076703.71231.BB. [DOI] [PubMed] [Google Scholar]
- 77.Cheung C, Culver JP, Takahashi K, Greenberg JH, Yodh AG. In vivo cerebrovascular measurement combining diffuse near-infrared absorption and correlation spectroscopies. Phys. Med. and Biol. 2001;46(8):2053–2065. doi: 10.1088/0031-9155/46/8/302. [DOI] [PubMed] [Google Scholar]
- 78.Zhou C, Yu G, Furuya D, Greenberg JH, Yodh AG, Durduran T. Diffuse optical correlation tomography of cerebral blood flow during cortical spreading depression in rat brain. Opt. Exp. 2006;14:1125–1144. doi: 10.1364/oe.14.001125. [DOI] [PubMed] [Google Scholar]
- 79.Durduran T, Zhou C, Yu G, Edlow B, Choe R, Shah Q, Kasner SE, Cucchiara BL, Yodh AG, Greenberg JH, Detre JA. International Stroke Conference. P37. American Heart Association; 2007. Bed-side monitoring of cerebral blood flow (CBF) in acute stroke patients during changes in head of bed position. [Google Scholar]
- 80.Durduran T, Zhou C, Edlow BL, Yu G, Choe R, Kim MN, Cucchiara BL, Putt ME, Shah Q, Kasner SE, Greenberg JH, Yodh AG, Detre JA. Transcranial optical monitoring of cerebrovascular hemodynamics in acute stroke patients. Optics Express. 2009;17(5):3884–3902. doi: 10.1364/oe.17.003884. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Yu G, Durduran T, Lech G, Zhou C, Chance B, Mohler ER, Yodh AG. Time-dependent blood flow and oxygenation in human skeletal muscle measured with noninvasive near-infrared diffuse optical spectroscopies. J Biomed Opt. 2005;10(3):024027–1–024027–12. doi: 10.1117/1.1884603. [DOI] [PubMed] [Google Scholar]
- 82.Yu G, Durduran T, Zhou C, Zhu TC, Finlay JC, Busch TM, Malkowicz SB, Hahn SM, Yodh AG. Real-time in situ monitoring of human prostate photodynamic therapy with diffuse light. Photochem Photobiol. 2006;82:1279–1284. doi: 10.1562/2005-10-19-RA-721. [DOI] [PubMed] [Google Scholar]
- 83.Sunar U, Quon H, Durduran T, Zhang J, Du J, Zhou C, Yu G, Choe R, Kilger A, Lustig R, Loevner L, Nioka S, Chance B, Yodh AG. Non-invasive diffuse optical measurement of blood flow and blood oxygenation for monitoring radiation therapy in patients with head and neck tumors: a pilot study. J Biomed Opt. 2006;11:064021. doi: 10.1117/1.2397548. [DOI] [PubMed] [Google Scholar]
- 84.Zhou C, Choe R, Shah N, Durduran T, Yu Guoqiang, Durkin A, Hsiang D, Mehta R, Butler J, Cerussi A, Tromberg BJ, Yodh AG. Diffuse optical monitoring of blood flow and oxygenation in human breast cancer during early stages of neoadjuvant chemotherapy. J Biomed Opt. 2007 Oct-Sep;12(5):051903. doi: 10.1117/1.2798595. [DOI] [PubMed] [Google Scholar]
- 85.Sunar U, Makonnen S, Zhou C, Durduran T, Yu Guoqiang, Wang HW, Lee WM, Yodh AG. Hemodynamic responses to antivascular therapy and ionizing radiation assessed by diffuse optical spectroscopies. Opt. Express. 2007 Nov;15(23):15507–15516. doi: 10.1364/oe.15.015507. [DOI] [PubMed] [Google Scholar]
- 86.Durduran T, Choe R, Yu G, Zhou C, Tchou JC, Czerniecki BJ, Yodh AG. Diffuse optical measurement of blood flow in breast tumors. Opt Lett. 2005 Nov;30:2915–2917. doi: 10.1364/ol.30.002915. [DOI] [PubMed] [Google Scholar]
- 87.Li J, Ninck M, Koban L, Elbert T, Kissler J, Gisler T. Transient functional blood flow change in the human brain measured noninvasively by diffusing-wave spectroscopy. Optics Letters. 2008;33(19):2233–2235. doi: 10.1364/ol.33.002233. [DOI] [PubMed] [Google Scholar]
- 88.Dietsche G, Ninck M, Ortolf C, Li J, Jaillon F, Gisler T. Fiber-based multispeckle detection for time-resolved diffusing-wave spectroscopy: characterization and application to blood flow detection in deep tissue. Applied Optics. 2007;46(35):8506–8514. doi: 10.1364/ao.46.008506. [DOI] [PubMed] [Google Scholar]
- 89.Jaillon F, Li J, Dietsche G, Elbert T, Gisler T. Activity of the human visual cortex measured non-invasively by diffusing-wave spectroscopy. Optics Express. 2007;15(11):6643–6650. doi: 10.1364/oe.15.006643. [DOI] [PubMed] [Google Scholar]
- 90.Jaillon F, Skipetrov SE, Li J, Dietsche G, Maret G, Gisler T. Diffusing-wave spectroscopy from head-like tissue phantoms : influence of a non-scattering layer. Optics Express. 2006;14(22):10181–10194. doi: 10.1364/oe.14.010181. [DOI] [PubMed] [Google Scholar]
- 91.Case KM, Zweifel PF. Linear Transport Theory. Boston: Addison-Wesley; 1967. [Google Scholar]
- 92.Davidson B. Neutron Transport Theory. Oxford: Clarendon; 1957. [Google Scholar]
- 93.Glasstone S, Edlund MC. The Elements of Nuclear Reactor Theory. New York: Van Nostrand; 1952. [Google Scholar]
- 94.Chandrasekhar S. Radiative Transfer. Dover: 1960. [Google Scholar]
- 95.Cheong WF, Prahl SA, Welch AJ. A review of the optical properties of biological tissues. IEEE J. Quantum Electron. 1990;QE-26:2166–2185. [Google Scholar]
- 96.Ripoll J. Ph.D. Dissertation. Universidad Autonoma de Madrid; 2000. Ligth Diffusion in Turbid Media With Biomedical Applications. [Google Scholar]
- 97.Farrell TJ, Patterson MS, Wilson B. A diffusion theory model of spatially resolved, steady-state diffuse reflectance for the noninvasive determination of tissue optical properties in vivo. Medical Physics. 1992;19(4):879–888. doi: 10.1118/1.596777. [DOI] [PubMed] [Google Scholar]
- 98.Jacques SL, Pogue BW. Tutorial on diffuse light transport. J Biomed. Opt. 2008;13(4):041302. doi: 10.1117/1.2967535. [DOI] [PubMed] [Google Scholar]
- 99.Heino J, Arridge S, Sikora J, Somersalo E. Anisotropic effects in highly scattering media. Phys. Rev. E. 2003;68:031908. doi: 10.1103/PhysRevE.68.031908. [DOI] [PubMed] [Google Scholar]
- 100.Custo A, Wells WM, III, Barnett AH, Hillman EMC, Boas DA. Effective scattering coefficient of the cerebral spinal fluid in adult head models for diffuse optical imaging. Appl. Opt. 2006;45(19):4747–4755. doi: 10.1364/ao.45.004747. [DOI] [PubMed] [Google Scholar]
- 101.Okada E, Delpy DT. Near-infrared light propagation in an adult head model. I. modeling of low-level scattering in the cerebrospinal fluid layer. Appl. Opt. 2003;42:2906–2914. doi: 10.1364/ao.42.002906. [DOI] [PubMed] [Google Scholar]
- 102.Kaplan PD, Kao MH, Yodh AG, Pine DJ. Geometric constraints for the design of diffusing-wave spectroscopy experiments. Appl Opt. 1993;32(21):3828–3836. doi: 10.1364/AO.32.003828. [DOI] [PubMed] [Google Scholar]
- 103.Siegel AM, Marota JA, Boas DA. Design and evaluation of a continuous-wave diffuse optical tomography system. Optics Express. 1999;4:287–298. doi: 10.1364/oe.4.000287. [DOI] [PubMed] [Google Scholar]
- 104.Nioka S, Luo Q, Chance B. Human brain functional imaging with reflectance CWS. Oxygen Transport to Tissue XIX. 1997;428:237–242. doi: 10.1007/978-1-4615-5399-1_33. [DOI] [PubMed] [Google Scholar]
- 105.Colier W, van der Sluijs MC, Menssen J, Oeseburg B. A new and highly sensitive optical brain imager with 50 Hz sample rate. NeuroImage. 2000;11:542. [Google Scholar]
- 106.Culver JP, Choe R, Holboke MJ, Zubkov L, Durduran T, Slemp A, Ntziachristos V, Pattanayak DN, Chance B, Yodh AG. Three-dimensional diffuse optical tomography in the plane parallel transmission geometry: Evaluation of a hybrid frequency domain/continuous wave clinical system for breast imaging. Med Phys. 2003;30:235–247. doi: 10.1118/1.1534109. [DOI] [PubMed] [Google Scholar]
- 107.Chance B, Cope M, Gratton E, Ramanujam N, Tromberg B. Phase measurement of light absorption and scattering in human tissues. Rev. Sci. Instru. 1998;689:3457–3481. [Google Scholar]
- 108.Pogue BW, Patterson MS. Frequency-domain optical-absorption spectroscopy of finite tissue volumes using diffusion-theory. Phys. Med. Biol. 1994;39:1157–1180. doi: 10.1088/0031-9155/39/7/008. [DOI] [PubMed] [Google Scholar]
- 109.Andersson-Engels S, Berg R, Svanberg S, Jarlman O. Time-resolved transillumination for medical diagnostics. Optics Letters. 1990;15(21):1179–1181. doi: 10.1364/ol.15.001179. [DOI] [PubMed] [Google Scholar]
- 110.Jacques SL. Time-resolved reflectance spectroscopy in turbid tissues. IEEE Transactions on Biomedical Engineering. 1989;36:1155–1161. doi: 10.1109/10.42109. [DOI] [PubMed] [Google Scholar]
- 111.Schmidt FEW, Fry ME, Hillman EMC, Hebden JC, Delpy DT. A 32-channel time-resolved instrument for medical optical tomography. Rev. Sci. Instrum. 2000;71:256–265. [Google Scholar]
- 112.Ntziachristos V, Ma XH, Chance B. Time-correlated single photon counting imager for simultaneous magnetic resonance and near-infrared mammography. Rev. Sci. Instru. 1998;69:4221–4233. [Google Scholar]
- 113.Selb J, Stott JJ, Franceschini MA, Sorensen AG, Boas DA. Improved sensitivity to cerebral hemodynamics during brain activation with a time-gated optical system: analytical model and experimental validation. J Biomed. Opt. 2005;10(1):011013. doi: 10.1117/1.1852553. [DOI] [PubMed] [Google Scholar]
- 114.Liebert A, Wabnitz H, Steinbrink J, Obrig H, Moller M, Macdonald R, Villringer A, Rinneberg H. Time-resolved multidistance near-infrared spectroscopy of the adult head: intracerebral and extracerebral absorption changes from moments of distribution of times of flight of photons. Appl Opt. 2004;43:3037–3047. doi: 10.1364/ao.43.003037. [DOI] [PubMed] [Google Scholar]
- 115.Haskell RC, Svaasand LO, Tsay T, Feng T, McAdams MS, Tromberg BJ. Boundary conditions for the diffusion equation in radiative transfer. J Opt Soc Am A. 1994;11:2727–2741. doi: 10.1364/josaa.11.002727. [DOI] [PubMed] [Google Scholar]
- 116.Aronson R. Boundary conditions for diffusion of light. J.Opt.Soc.of Am.A. 1995;12:2532–2539. doi: 10.1364/josaa.12.002532. [DOI] [PubMed] [Google Scholar]
- 117.Dehghani H, Eames ME, Yalavarthy PK, Davis SC, Srinivasan S, Carpenter CM, Pogue BW, Paulsen KD. Near infrared optical tomography using nirfast: algorithm for numerical model and image reconstruction. Commun. Numer. Meth. Engng. 2008 doi: 10.1002/cnm.1162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 118.Arfken G. Mathematical Methods for Physicists. second edition. Academic; 1970. [Google Scholar]
- 119.Barton G. Elements of Green’s Functions and Propagation: Potentials, Diffusion, and Waves. Vol. 7. USA: Oxford University Press; 1989. [Google Scholar]
- 120.Arridge SR, Cope M, Delpy DT. The theoretical basis for the determination of optical pathlengths in tissue: temporal and frequency analysis. Phys Med Biol. 1992;37(7):1531–1560. doi: 10.1088/0031-9155/37/7/005. [DOI] [PubMed] [Google Scholar]
- 121.Carslaw HS, Jaeger J. Conduction of heat in solids. New York: Oxford University Press; 1986. [Google Scholar]
- 122.Choe R, Konecky SD, Corlu A, Lee K, Durduran T, Busch DR, Pathak S, Czerniecki BJ, Tchou J, Fraker DL, DeMichele A, Chance B, Arridge SR, Schweiger M, Culver JP, Schnall MD, Putt ME, Rosen MA, Yodh AG. Differentiation of benign and malignant breast tumors by in-vivo three-dimensional parallel-plate diffuse optical tomography. J Biomed. Opt. 2009;14(2):024020. doi: 10.1117/1.3103325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 123.Boas DA, O’Leary MA, Chance B, Yodh AG. Scattering of diffuse photon density waves by spherical inhomogeneities within turbid media - analytic solution and applications. Proceedings of the National Academy of Sciences of the United States of America. 1994;91(11):4887–4891. doi: 10.1073/pnas.91.11.4887. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 124.Walker SA, Boas DA, Gratton E. Photon density waves scattered from cylindrical inhomogeneities: Theory and experiments. Appl Opt. 1998;37:1935–1944. doi: 10.1364/ao.37.001935. [DOI] [PubMed] [Google Scholar]
- 125.Ripoll J, Ntziachristos V, Culver JP, Pattanayak DN, Yodh AG, Nieto-Vesperinas M. Recovery of optical parameters in multiple-layered diffusive media: theory and experiments. J Opt. Soc. A. 2001;18(4):821–830. doi: 10.1364/josaa.18.000821. [DOI] [PubMed] [Google Scholar]
- 126.Farrell TJ, Patterson MS, Essenpreis M. Influence of layered tissue architecture on estimates of tissue optical properties obtained from spatially resolved diffuse reflectometry. Appl Opt. 1998;37(10):1958–1972. doi: 10.1364/ao.37.001958. [DOI] [PubMed] [Google Scholar]
- 127.Hielscher AH, Liu HL, Chance B, Tittel FK, Jacques SL. Time-resolved photon emission from layered turbid media. Appl Opt. 1996;35(4):719–728. doi: 10.1364/AO.35.000719. [DOI] [PubMed] [Google Scholar]
- 128.Alexandrakis G, Busch DR, Faris GW, Patterson MS. Determination of the optical properties of two-layer turbid media by use of a frequency-domain hybrid monte carlo diffusion model. Appl Opt. 2001;40(22):3810–3821. doi: 10.1364/ao.40.003810. [DOI] [PubMed] [Google Scholar]
- 129.Alexandrakis G, Farrell TJ, Patterson MS. Accuracy of the diffusion approximation in determining the optical properties of a two-layer turbid medium. Appl Opt. 1998;37(31):7401–7409. doi: 10.1364/ao.37.007401. [DOI] [PubMed] [Google Scholar]
- 130.Schweiger M, Nissilä I, Boas DA, Arridge SR. Image reconstruction in optical tomography in the presence of coupling errors. Applied optics. 2007;46(14):2743–2756. doi: 10.1364/ao.46.002743. [DOI] [PubMed] [Google Scholar]
- 131.Hueber DM, Franceschini MA, Ma HY, Zhang Q, Ballesteros JR, Fantini S, Wallace D, Ntziachristos V, Chance B. Non-invasive and quantitative near-infrared haemoglobin spectrometry in the piglet brain during hypoxic stress, using a frequency-domain multidistance instrument. Phys Med Biol. 2001;46(1):41–62. doi: 10.1088/0031-9155/46/1/304. [DOI] [PubMed] [Google Scholar]
- 132.Nissilä I, Noponen T, Kotilahti K, Katila T, Lipiainen L, Tarvainen T, Schweiger S, Arridge S. Instrumentation and calibration methods for the multichannel measurement of phase and amplitude in optical tomography. Review of Scientific Instruments. 2005;76(4):044302. [Google Scholar]
- 133.Yamashita Y, Maki A, Koizumi H. Wavelength dependence of the precision of noninvasive optical measurement of oxy-, deoxy-, and total-hemoglobin concentration. Med Phys. 2001;28(6):1108–1114. doi: 10.1118/1.1373401. [DOI] [PubMed] [Google Scholar]
- 134.Strangman G, Franceschini MA, Boas DA. Factors affecting the accuracy of near-infrared spectroscopy concentration calculations for focal changes in oxygenation parameters. NeuroImage. 2003;18:865–879. doi: 10.1016/s1053-8119(03)00021-1. [DOI] [PubMed] [Google Scholar]
- 135.Boas DA, Dale AM, Franceschini MA. Diffuse optical imaging of brain activation: approaches to optimizing image sensitivity, resolution, and accuracy. Neuroimage. 2004;23:275–288. doi: 10.1016/j.neuroimage.2004.07.011. [DOI] [PubMed] [Google Scholar]
- 136.Corlu A, Durduran T, Choe R, Schweiger M, Hillman EMC, Arridge SR, Yodh AG. Uniqueness and wavelength optimization in continous-wave multispectral diffuse optical tomography. Opt. Lett. 2003;28:2339–2341. doi: 10.1364/ol.28.002339. [DOI] [PubMed] [Google Scholar]
- 137.Corlu A, Choe R, Durduran T, Lee K, Schweiger M, Hillman EMC, Arridge SR, Yodh AG. Diffuse optical tomography with spectral constraints and wavelength optimization. Appl Opt. 2005;44:2082–2093. doi: 10.1364/ao.44.002082. [DOI] [PubMed] [Google Scholar]
- 138.Arridge SR, Lionheart WRB. Nonuniqueness in diffusion-based optical tomography. Opt Lett. 1998;23:882–884. doi: 10.1364/ol.23.000882. [DOI] [PubMed] [Google Scholar]
- 139.Srinivasan S, Pogue BW, Jiang S, Dehghani H, Paulsen KD. Spectrally constrained chromophore and scattering near-infrared tomography provides quantitative and robust reconstruction. Appl. Opt. 2005;44(10):1858–1869. doi: 10.1364/ao.44.001858. [DOI] [PubMed] [Google Scholar]
- 140.Brendel B, Nielsen T. Selection of optimal wavelengths for spectral reconstruction in diffuse optical tomography. J Biomed. Opt. 2009;14(3):034041. doi: 10.1117/1.3156823. [DOI] [PubMed] [Google Scholar]
- 141.Eames ME, Wange J, Pogue BW, Dehghani H. Wavelength band optimization in spectral near-infrared optical tomography improves accuracy while reducing data acquisition and computational burden. J Biomed. Opt. 2008;13(5):054037. doi: 10.1117/1.2976425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 142.van der Zee P, Cope M, Arridge SR, Essenpreis M, Potter LA, Edwards AD, Wyatt JS, McCormick DC, Toth SC, Reynolds EOR, Delpy DT. Experimentally measured optical pathlengths for the adult’s head, calf and forearm and the head of the newborn infant asa function of interoptode spacing. Adv. Exp. Med. Biol. 1992;316:143–153. doi: 10.1007/978-1-4615-3404-4_17. [DOI] [PubMed] [Google Scholar]
- 143.Duncan A, Meek JH, Clemence M, Elwell CE, Tyszczuk L, Cope M, Delpy DT. Optical pathlength measurements on adult head, calf and forearm and the head of the newborn infant using phase resolved optical spectroscopy. Phys. Med. Biol. 1995;40(2):295–304. doi: 10.1088/0031-9155/40/2/007. [DOI] [PubMed] [Google Scholar]
- 144.Cope M, Delpy DT. System for long-term measurement of cerebral blood flow and tissue oxygenation on newborn infants by infra-red transillumination. Med Biol Eng Comput. 1988;26:289–294. doi: 10.1007/BF02447083. [DOI] [PubMed] [Google Scholar]
- 145.Boas DA, Gaudette T, Strangman G, Cheng X, Marota JJA, Mandeville JB. The accuracy of near infrared spectroscopy and imaging during focal changes in cerebral hemodynamics. NeuroImage. 2001;13:76–90. doi: 10.1006/nimg.2000.0674. [DOI] [PubMed] [Google Scholar]
- 146.Kohl M, Lindauer U, Royl G, Kuhl M, Gold L, Villringer A, Dirnagl U. Physical model for the spectroscopic analysis of cortical intrinsic optical signals. Phys. Med. Biol. 2000;45:3749–3764. doi: 10.1088/0031-9155/45/12/317. [DOI] [PubMed] [Google Scholar]
- 147.Franceschini MA, Toronov V, Filiaci ME, Gratton E, Fantini S. On-line optical imaging of the human brain with 160-ms temporal resolution. Optics Express. 2000;6(3):49–57. doi: 10.1364/oe.6.000049. [DOI] [PubMed] [Google Scholar]
- 148.Tamura M, Hoshi Y, Okada F. Localized near-infrared spectroscopy and functional optical imaging of brain activity. Philos. Trans. R. Soc. Lond. B. Biol. Sci. 1997;352:737–742. doi: 10.1098/rstb.1997.0056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 149.Nollert G, Jonas RA, Reichart B. Optimizing cerebral oxygenation during cardiac surgery: a review of experimental and clinical investigations with near infrared spectrophotometry. Thorac. Cardiovasc. Surg. 2000;48:247–253. doi: 10.1055/s-2000-6895. [DOI] [PubMed] [Google Scholar]
- 150.Fantini S, Hueber D, Franceschini MA, Gratton E, Rosenfeld W, Stubblefield PG, Maulik D, Stankovic MR. Non-invasive optical monitoring of the newborn piglet brain using continuous-wave and frequency-domain spectroscopy. Phys Med Biol. 1999;44(6):1543–1563. doi: 10.1088/0031-9155/44/6/308. [DOI] [PubMed] [Google Scholar]
- 151.Chu B. Laser Light Scattering, Basic Principles and Practice. New York: Academic; 1991. [Google Scholar]
- 152.Lemieux PA, Durian DJ. Investigating non-gaussian scattering processes by using nth-order intensity correlation functions. J Opt. Soc. Am. A. 1999;16(7):1651–1664. [Google Scholar]
- 153.Bonner R, Nossal R. Model for laser doppler measurements of blood flow in tissue. Appl Opt. 1981;20:2097–2107. doi: 10.1364/AO.20.002097. [DOI] [PubMed] [Google Scholar]
- 154.Ackerson BJ, Dougherty RL, Reguigui NM, Nobbman U. Correlation transfer: Application of radiative transfer solution methods to photon correlation problems. J. Thermophys. and Heat Trans. 1992;6:577–588. [Google Scholar]
- 155.Dougherty RL, Ackerson BJ, Reguigui NM, Dorri-Nowkoorani F, Nobbmann U. Correlation transfer: Development and application. J Quant Spectrosc Radiat Transfer. 1994;52:713–727. [Google Scholar]
- 156.Weitz DA, Pine DJ. chapter Diffusing-wave Spectroscopy. Oxford Science Publications; 1993. Dynamic Light Scattering The Method and Some Applications. [Google Scholar]
- 157.Xue JZ, Pine DJ, Milner ST, Wu XL, Chaikin PM. Nonergodicity and light scattering from polymer gels. Phys. Rev. A. 1992;46:6550–6563. doi: 10.1103/physreva.46.6550. [DOI] [PubMed] [Google Scholar]
- 158.Schatzel K. Accuracy of photon correlation measurements on nonergodic samples. Appl Opt. 1993;32:3880–3885. doi: 10.1364/AO.32.003880. [DOI] [PubMed] [Google Scholar]
- 159.Pusey PN, Van Megen W. Dynamic light scattering by non-ergodic media. Physica A. 1989;157:705–742. [Google Scholar]
- 160.Einstein A. On the motion of small particles suspended in liquids at rest required by the molecular-kinetic theory of heat. Annalen der Physik. 1905;17:549–560. [Google Scholar]
- 161.Bishop JJ, Popel AS, Intaglietta M, Johnson PC. Effect of aggregation and shear rate on the dispersion of red blood cells flowing in venules. Am J Physiol Heart Circ Physiol. 2002 Nov;283(5):1985–1996. doi: 10.1152/ajpheart.00888.2001. [DOI] [PubMed] [Google Scholar]
- 162.Boryczko K, Dzwinel W, Yuen DA. Dynamical clustering of red blood cells in capillary vessels. J Mol Model (Online) 2003 Feb;9(1):16–33. doi: 10.1007/s00894-002-0105-x. [DOI] [PubMed] [Google Scholar]
- 163.Binzoni T, Leung TS, Seghier ML, Delpy DT. Translational and brownian motion in laser-doppler flowmetry of large tissue volumes. Phys Med Biol. 2004 Dec;49(24):5445–5458. doi: 10.1088/0031-9155/49/24/004. [DOI] [PubMed] [Google Scholar]
- 164.Abbot NC, Beck JS. Biological zero in laser doppler measurements in normal ischemic and inflamed human skin. International Journal of Microcirculation - Clinical and Experimental. 1993;12:89–98. [PubMed] [Google Scholar]
- 165.Kernick DP, Tooke JE, Shore AC. The biological zero signal in laser doppler fluximetry - origins and practical implications. Pflugers Arch. 1999 Mar;437(4):624–631. doi: 10.1007/s004240050826. [DOI] [PubMed] [Google Scholar]
- 166.Caspary L, Creutzig A, Alexander K. Biological zero in laser doppler fluxmetry. Int J Microcirc Clin Exp. 1988 Nov;7(4):367–371. [PubMed] [Google Scholar]
- 167.Liebert A, Leahy M, Maniewski R. A calibration standard for laser-doppler perfusion measurements. Review of Scientific Instruments. 1995;66(11):5169–5173. [Google Scholar]
- 168.Katayama K, Nishimura G, Kinjo M, Tamura M. Absorbance measurements in turbid media by the photon correlation method. Appl.Optics. 1995;34:7419–7427. doi: 10.1364/AO.34.007419. [DOI] [PubMed] [Google Scholar]
- 169.Arridge SR, Schweiger M. Inverse methods for optical tomography. Information Processing in Medical Imaging (IPMI’93 Proceedings), Lecture Notes in Computer Science; Springer-Verlag; 1993. pp. 259–277. [Google Scholar]
- 170.Arridge SR, Schweiger M. Image reconstruction in optical tomography. Philosophical Transactions of the Royal Society of London Series B-Biological Sciences. 1997;352(1354):717– 726. doi: 10.1098/rstb.1997.0054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 171.Arridge SR. Optical tomography in medical imaging. Inverse Problems. 1999;15:R41–R93. [Google Scholar]
- 172.Walker SA, Fantini S, Gratton E. Image reconstruction by backprojection from frequency-domain optical measurements in highly scattering media. Appl. Opt. 1997;36(1):170–179. doi: 10.1364/ao.36.000170. [DOI] [PubMed] [Google Scholar]
- 173.Colak SB, Papaioannou DG, W’t Hooft G, van der Mark MB, Schomberg H, Paasschens JCJ, Melissen JBM, van Asten NAAJ. Tomographic image reconstruction from optical projections in light-diffusing media. Appl. Opt. 1997;36(1):180–213. doi: 10.1364/ao.36.000180. [DOI] [PubMed] [Google Scholar]
- 174.Schotland JC. Continuous-wave diffusion imaging. J. Opt. Soc. Am. A. 1997;14(1):275–279. [Google Scholar]
- 175.Li XD, Durduran T, Chance B, Yodh AG, Pattanayak DN. Diffraction tomography for biochemical imaging with diffuse-photon density waves. Opt Lett. 1997;22(8):573–575. doi: 10.1364/ol.22.000573. errata: p 1198. [DOI] [PubMed] [Google Scholar]
- 176.Cheng X, Boas DA. Diffuse optical reflectance tomography with continuous-wave illumination. Opt. Express. 1998;3:118–123. doi: 10.1364/oe.3.000118. [DOI] [PubMed] [Google Scholar]
- 177.Matson CL, Liu HL. Analysis of the forward problem with diffuse photon density waves in turbid media by use of a diffraction tomography model. J. Opt. Soc. Am A. 1999;16:455–466. [Google Scholar]
- 178.Schotland JC, Haselgrove JC, Leigh JS. Photon hitting density. Appl. Opt. 1993;32:448–453. doi: 10.1364/AO.32.000448. [DOI] [PubMed] [Google Scholar]
- 179.O’Leary MA, Boas DA, Chance B, Yodh AG. Experimental images of heterogeneous turbid media by frequency-domain diffusing-photon tomography. Opt Lett. 1995;20(5):426–428. doi: 10.1364/ol.20.000426. [DOI] [PubMed] [Google Scholar]
- 180.Arridge SR. Photon-measurement density functions. Part 1: Analytical forms. Appl. Opt. 1995;34(31):7395–7409. doi: 10.1364/AO.34.007395. [DOI] [PubMed] [Google Scholar]
- 181.Arridge SR, Schweiger M. Photon-measurement density functions. Part 2: Finite-element-method calculations. Appl. Opt. 1995;34(34):8026–8036. doi: 10.1364/AO.34.008026. [DOI] [PubMed] [Google Scholar]
- 182.Yao Y, Wang Y, Pei Y, Zhu W, Barbour RL. Frequency-domain optical imaging of absorption and scattering distributions using a born iterative method. J. Opt. Soc. Am. A. 1997;14:325–342. doi: 10.1364/josaa.14.000325. [DOI] [PubMed] [Google Scholar]
- 183.Paulsen KD, Jiang H. Spatially varying optical property reconstruction using a finite element diffusion equation approximation. Med. Phys. 1995;22(6):691–701. doi: 10.1118/1.597488. [DOI] [PubMed] [Google Scholar]
- 184.Jiang H, Paulsen KD, Osterberg UL. Optical image reconstruction using DC data: simulations and experiments. Phys. Med. Biol. 1996;41:1483–1498. doi: 10.1088/0031-9155/41/8/015. [DOI] [PubMed] [Google Scholar]
- 185.Paulsen KD, Jiang H. Enhanced frequency-domain optical image reconstruction in tissues through total variation minimization. Appl. Opt. 1996;35:3447–3458. doi: 10.1364/AO.35.003447. [DOI] [PubMed] [Google Scholar]
- 186.Jiang H, Paulsen KD, Oesterberg UL, Patterson MS. Frequency-domain optical image reconstruction in turbid media: an experimental study of single-target detectability. Appl. Opt. 1997;36(1):52–63. doi: 10.1364/ao.36.000052. [DOI] [PubMed] [Google Scholar]
- 187.Jiang H, Paulsen KD, Osterberg UL, Patterson MS. Improved continuous light diffusion imaging in single- and multi-target tissue-like phantoms. Phys. Med. Biol. 1998;43(3):675–693. doi: 10.1088/0031-9155/43/3/018. [DOI] [PubMed] [Google Scholar]
- 188.Pogue BW, McBride TO, Prewitt J, Osterberg UL, Paulsen KD. Spatially variant regularization improves diffuse optical tomography. Appl Opt. 1999;38(13):2950–2961. doi: 10.1364/ao.38.002950. [DOI] [PubMed] [Google Scholar]
- 189.Arridge SR, Schweiger M. A gradient-based optimisation scheme for optical tomography. Optics Express. 1998;2(6):213–226. doi: 10.1364/oe.2.000213. [DOI] [PubMed] [Google Scholar]
- 190.Hielscher AH, Klose AD, Hanson KM. Gradient-based iterative image reconstruction scheme for time-resolved optical tomography. IEEE Trans. Med. Imaging. 1999;18:262–271. doi: 10.1109/42.764902. [DOI] [PubMed] [Google Scholar]
- 191.Klibanov MV, Lucas TR, Frank RM. A fast and accurate imaging algorithm in optical /diffusion tomography. Inverse Problems. 1997;13:1341–1361. [Google Scholar]
- 192.Gryazin YA, Klibanov MV, Lucas TR. Imaging the diffusion coefficient in a parabolic inverse problem in optical tomography. Inverse Problems. 1999;1:373–397. [Google Scholar]
- 193.Roy R, Sevick-Muraca EM. Truncated newton’s optimization scheme for absorption and fluorescence optical tomography: Part I Theory and formulation. Opt. Express. 1999;4:353–371. doi: 10.1364/oe.4.000353. [DOI] [PubMed] [Google Scholar]
- 194.Roy R, Sevick-Muraca EM. Truncated newton’s optimization scheme for absorption and fluorescence optical tomography: Part II Reconstruction from synthetic measurements. Opt. Express. 1999;4:372–382. doi: 10.1364/oe.4.000372. [DOI] [PubMed] [Google Scholar]
- 195.Roy R, Sevick-Muraca EM. Active constrained truncated newton method for simple-bound optical tomography. J. Opt. Soc. Am. A. 2000;17:1627–1641. doi: 10.1364/josaa.17.001627. [DOI] [PubMed] [Google Scholar]
- 196.Roy R, Sevick-Muraca EM. Three-dimensional unconstrained and constrained image-reconstruction techniques applied to fluorescence, frequency-domain photon migration. Appl. Opt. 2001;40:2206–2215. doi: 10.1364/ao.40.002206. [DOI] [PubMed] [Google Scholar]
- 197.Oh S, Milstein AB, Bouman CA, Webb KJ. A general framework for nonlinear multigrid inversion. IEEE Trans. Image Processing. 2005;14:125–140. doi: 10.1109/tip.2004.837555. [DOI] [PubMed] [Google Scholar]
- 198.Eppstein MJ, Dougherty DE, Troy TL, Sevick-Muraca EM. Biomedical optical tomography using dynamic parameterization and Bayesian conditioning on photon migration measurements. Appl. Opt. 1999;38:2138–2150. doi: 10.1364/ao.38.002138. [DOI] [PubMed] [Google Scholar]
- 199.Eppstein MJ, Dougherty DE, Hawrysz DJ, Sevick-Muraca EM. Three-dimensional Bayesian optical image reconstruction with domain decomposition. IEEE Trans. Med. Imaging. 2001;20:147–163. doi: 10.1109/42.918467. [DOI] [PubMed] [Google Scholar]
- 200.Eppstein MJ, Hawrysz DJ, Godavarty A, Sevick-Muraca EM. Three-dimensional, Bayesian image reconstruction from sparse and noisy data sets: Near-infrared fluorescence tomography. Proc. Natl. Acad. Sci. U. S. A. 2002;99:9619–9624. doi: 10.1073/pnas.112217899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 201.Ye JC, Webb KJ, Bouman CA, Millane RP. Optical diffusion tomography using iterative coordinate descent optimization in a Bayesian framework. J. Opt. Soc. Am. A. 1999;16:2400–2412. [Google Scholar]
- 202.Ye JC, Bouman CA, Webb KJ, Millane RP. Nonlinear multigrid algorithms for Bayesian optical diffusion tomography. IEEE Trans. Image Processing. 2001;10:909–922. [Google Scholar]
- 203.Milstein AB, Oh S, Reynolds JS, Webb KJ, Bouman CA, Millane RP. Three-dimenstional Bayesian optical diffusion imaging using experimental data. Opt. Lett. 2002;27:95– 97. doi: 10.1364/ol.27.000095. [DOI] [PubMed] [Google Scholar]
- 204.Milstein AB, Oh S, Webb KJ, Bouman CA, Zhang Q, Boas DA, Millane RP. Fluorescence optical diffusion tomography. Appl. Opt. 2003;42:3081–3094. doi: 10.1364/ao.42.003081. [DOI] [PubMed] [Google Scholar]
- 205.Milstein AB, Stott JJ, Oh S, Boas DA, Millane RP, Bourman CA, Webb KJ. Fluorescence optical diffusion tomography using multiple frequency data. J. Opt. Soc. Am. A. 2004;21:1035–1049. doi: 10.1364/josaa.21.001035. [DOI] [PubMed] [Google Scholar]
- 206.Markel VA, Schotland JC. Inverse problem in optical diffusion tomography: I. Fourier-Laplace inversion formulas. J. Opt. Soc. Am. A. 2001;18:1336–1347. doi: 10.1364/josaa.18.001336. [DOI] [PubMed] [Google Scholar]
- 207.Markel VA, Schotland JC. Inverse problem in optical diffusion tomography. II. role of boundary conditions. J. Opt. Soc. Am. A. 2002;19:558–66. doi: 10.1364/josaa.19.000558. [DOI] [PubMed] [Google Scholar]
- 208.Markel VA, Mital V, Schotland JC. Inverse problem in optical diffusion tomography. III. inversion formulas and singular-value decomposition. J. Opt. Soc. Am. A. 2003;20:890–902. doi: 10.1364/josaa.20.000890. [DOI] [PubMed] [Google Scholar]
- 209.Markel VA, O’Sullivan JA, Schotland JC. Inverse problem in optical diffusion tomography. iv. nonlinear inversion formulas. J. Opt. Soc. Am. A. 2003;20:903–912. doi: 10.1364/josaa.20.000903. [DOI] [PubMed] [Google Scholar]
- 210.Pei Y, Graber HL, Barbour RL. Influence of systematic error in reference states on image quiality and on stability of derived information for DC optical imaging. Appl. Opt. 2001;40:5755–5769. doi: 10.1364/ao.40.005755. [DOI] [PubMed] [Google Scholar]
- 211.Ntziachristos V, Chance B, Yodh AG. Differential diffuse optical tomography. Opt. Express. 1999;5:230–242. doi: 10.1364/oe.5.000230. [DOI] [PubMed] [Google Scholar]
- 212.Kilmer ME, Miller EL, Barbaro A, Boas D. Three-dimensional shape-based imaging of absorption perturbation for diffuse optical tomography. Appl. Opt. 2003;42:3129–3144. doi: 10.1364/ao.42.003129. [DOI] [PubMed] [Google Scholar]
- 213.Li A, Miller EL, Kilmer ME, Brukilacchio TJ, Chaves T, Stott J, Zhang Q, Wu T, Chorlton M, Moore RH, Kopans DB, Boas DA. Tomographic optical breast imaging guided by three-dimensional mammography. Appl. Opt. 2003;42:5181–5190. doi: 10.1364/ao.42.005181. [DOI] [PubMed] [Google Scholar]
- 214.Cuccia DJ, Bevilacqua F, Durkin AJ, Tromberg BJ. Modulated imaging: quantitative analysis and tomography of turbid media in the spatial-frequency domain. Optics letters. 2005;30(11):1354–1356. doi: 10.1364/ol.30.001354. [DOI] [PubMed] [Google Scholar]
- 215.Joshi A, Bangerth W, Hwang K, Rasmussen JC, Sevick-Muraca EM. Fully adaptive fem based fluorescence optical tomography from time-dependent measurements with area illumination and detection. Medical Physics. 2006;33:1299. doi: 10.1118/1.2190330. [DOI] [PubMed] [Google Scholar]
- 216.Bassi A, D’Andrea C, Valentini G, Cubeddu R, Arridge S. Temporal propagation of spatial information in turbid media. Optics Letters. 2008;33(23):2836–2838. doi: 10.1364/ol.33.002836. [DOI] [PubMed] [Google Scholar]
- 217.Knuttel A, Schmitt JM, Knutson JR. Spatial localization of absorbing bodies by interfering diffusive photon density waves. Appl Opt. 1993;32:381–389. doi: 10.1364/AO.32.000381. [DOI] [PubMed] [Google Scholar]
- 218.Chance B, Kang K, He L, Weng J, Sevick EM. Highly sensitive object location in tissue models with linear in-phase and anti-phase multi-element optical arrays in one and two dimensions. Proc. Natl. Acad. Sci. USA. 1993;90:3423–3427. doi: 10.1073/pnas.90.8.3423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 219.Gibson A, Dehghani H. Diffuse optical imaging. Phil. Trans. R. Soc. A. 2009;367:3055–3072. doi: 10.1098/rsta.2009.0080. [DOI] [PubMed] [Google Scholar]
- 220.Gibson AB, Hebden JC, Arridge SR. Recent advances in diffuse optical imaging. Phys Med Biol. 2005;50:R1–R43. doi: 10.1088/0031-9155/50/4/r01. [DOI] [PubMed] [Google Scholar]
- 221.Dunsby C, French PMW. Techniques for depth-resolved imaging through turbid media including coherence gated imaging. J. Phys. D: Appl. Phys. 2003;36:R207–R227. [Google Scholar]
- 222.Schulz RB, Ripoll J, Ntziachristos V. Noncontact optical tomography of turbid media. Opt. Lett. 2003;28(18):1701–1703. doi: 10.1364/ol.28.001701. [DOI] [PubMed] [Google Scholar]
- 223.Ripoll J, Ntziachristos V. Iterative boundary method for diffuse optical tomography. J. Opt. Soc. Am. A. 2003;20(6):1103–1110. doi: 10.1364/josaa.20.001103. [DOI] [PubMed] [Google Scholar]
- 224.Ripoll J, Schulz RB, Ntziachristos V. Free-space propagation of diffuse light: Theory and experiments. Phys. Rev. Lett. 2003;91(10):1039011–1039014. doi: 10.1103/PhysRevLett.91.103901. [DOI] [PubMed] [Google Scholar]
- 225.Klose AD, Hielscher AH. Optical tomography with the equation of radiative transfer. Methods for Heat and Fluid Flow. 2008;18:443–464. [Google Scholar]
- 226.Hielscher AH, Klose AD, Scheel AK, Moa-Anderson B, Backhaus M, Netz U, Beuthan J. Sagittal laser optical tomography for imaging of rheumatoid finger joints. Phys. Med. Biol. 2004;49:1147–1163. doi: 10.1088/0031-9155/49/7/005. [DOI] [PubMed] [Google Scholar]
- 227.Wright S, Schweiger M, Arridge SR. Reconstruction in optical tomography using the pn approximations. Meas. Sci. Technol. 2007;18:79–86. [Google Scholar]
- 228.Aydin ED, de Oliveira CRE, Goddard AJH. A comparison between transport and diffusion calculations using a finite element-spherical harmonics radiation transport method. Med. Phys. 2002;2:2013–2023. doi: 10.1118/1.1500404. 2003. [DOI] [PubMed] [Google Scholar]
- 229.Boas DA. Ph.D. Dissertation. University of Pennsylvania; 1996. Diffuse Photon Probes of Structural and Dynamical Properties of Turbid Media: Theory and Biomedical Applications. [Google Scholar]
- 230.Hull EL, Foster TH. Steady-state reflectance spectrsocopy in the P 3 approximation. J. Opt. Soc. Am. A. 2001;18(3):584–599. [Google Scholar]
- 231.Firbank M, Arridge SR, Schweiger M, Delpy DT. An investigation of light transport through scattering bodies with non-scattering regions. Phys Med Biol. 1996;41(4):767–783. doi: 10.1088/0031-9155/41/4/012. [DOI] [PubMed] [Google Scholar]
- 232.Arridge SR, Dehghani H, Schweiger M, Okada E. The finite element model for the propagation of light in scattering media: A direct method for domains with nonscattering regions. Med Phys. 2000;27(1):252–264. doi: 10.1118/1.598868. [DOI] [PubMed] [Google Scholar]
- 233.Riley J, Dehghani H, Schweiger M, Arridge SR, Ripoll J, Nieto-Vesperinas M. 3d optical tomography in the presence of void regions. Optics Express. 2000;7(13):462–467. doi: 10.1364/oe.7.000462. [DOI] [PubMed] [Google Scholar]
- 234.Hayashi T, Kashio Y, Okada E. Hybrid monte carlo-diffusion method for light propagation in tissue with a low-scattering region. Appl. Opt. 2003;42(16):2888–2896. doi: 10.1364/ao.42.002888. [DOI] [PubMed] [Google Scholar]
- 235.Dehghani H, Srinivasan S, Pogue BW, Gibson A. Numerical modelling and image reconstruction in diffuse optical tomography. Phil. Trans. R. Soc. A. 2009;367:3073–3093. doi: 10.1098/rsta.2009.0090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 236.Srinivasan S, Pogue BW, Carpenter C, Yalavarthy PK, Paulsen K. A boundary element approach for image-guided near-infrared absorption and scatter estimation. Med. Phys. 2007;34:4545–4557. doi: 10.1118/1.2795832. [DOI] [PubMed] [Google Scholar]
- 237.Wang LV, Jacques SL. Hybrid model of Monte Carlo simulation diffusion theory for light reflectance by turbid media. J. Opt. Soc. Am. A. 1993;10:1746–1752. doi: 10.1364/josaa.10.001746. [DOI] [PubMed] [Google Scholar]
- 238.Kak AC, Slaney M. Principles of Computerized Tomographic Imaging. New York: IEEE Press; 1988. [Google Scholar]
- 239.O’Leary MA. Ph.D. Dissertation. Unversity of Pennsylvania; 1996. Imaging with diffuse photon density waves. [Google Scholar]
- 240.Lagendijk A, Biemond J. Iterative Identification and Restoration of Images. Kluwer Academic Publishers; 1991. [Google Scholar]
- 241.Hansen Per Christian. Rank-Deficient and Discrete Ill-Posed Problems. SIAM, Philadelphia; 1998. [Google Scholar]
- 242.Tikhonov AN. Regularization of mathematically incorrectly posed problems. Sov. Math. 1963;4:1624. [Google Scholar]
- 243.Douiri A, Schweiger M, Riley J, Arridge S. Local diffusion regularization method for optical tomography reconstruction by using robust statistics. Opt Lett. 2005;30:2439–2441. doi: 10.1364/ol.30.002439. [DOI] [PubMed] [Google Scholar]
- 244.Hansen P, O’Leary D. The use of the L-curve in the regularization of discrete ill-posed problems. SIAM J. Sci. Comput. 1993;14:1487–1503. [Google Scholar]
- 245.Hansen P. Analysis of discrete ill-power problems by means of the L-curve. SIAM Rev. 1992;34:561–580. [Google Scholar]
- 246.Boas DA. A fundamental limitation of linearized algorithms for diffuse optical tomography. Opt. Expr. 1997;1:404–413. doi: 10.1364/oe.1.000404. [DOI] [PubMed] [Google Scholar]
- 247.Li XD, Pattanayak DN, Durduran T, Culver JP, Chance B, Yodh AG. Near-field diffraction tomography with diffuse photon density waves. Phys Rev E. 2000;61(4):4295–4309. doi: 10.1103/physreve.61.4295. [DOI] [PubMed] [Google Scholar]
- 248.Schotland JC, Markel VA. Inverse scattering with diffusing waves. J. Opt. Soc. Am. A. 2001;18(11):2767–2777. doi: 10.1364/josaa.18.002767. [DOI] [PubMed] [Google Scholar]
- 249.Matson CL. A diffraction tomographic model of the forward problem using diffuse photon density waves. Optics Express. 1997;1:6–11. doi: 10.1364/oe.1.000006. [DOI] [PubMed] [Google Scholar]
- 250.Konecky SD, Panasyuk GY, Lee K, Markel VA, Yodh AG, Schotland JC. Imaging complex structures with diffuse light. Opt Expr. 2008;16(7):5048–5060. doi: 10.1364/oe.16.005048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 251.Moskow S, Schotland JC. Convergence and stability of the inverse scattering series for diffuse waves. Inverse Problems. 2008;24(6):065005. [Google Scholar]
- 252.O’Leary MA, Boas DA, Chance B, Yodh AG. Reradiation and imaging of diffuse photon density waves using fluorescent inhomogeneities. Journal of Luminescence. 1994;60-1:281–286. [Google Scholar]
- 253.O’Leary MA, Boas DA, Li XD, Chance B, Yodh AG. Fluorescence lifetime imaging in turbid media. Opt Lett. 1996;21(2):158–160. doi: 10.1364/ol.21.000158. [DOI] [PubMed] [Google Scholar]
- 254.Li XD, O’Leary MA, Boas DA, Chance B, Yodh AG. Fluorescent diffuse photon: Density waves in homogeneous and heterogeneous turbid media: Analytic solutions and applications. Appl Opt. 1996;35(19):3746–3758. doi: 10.1364/AO.35.003746. [DOI] [PubMed] [Google Scholar]
- 255.Li XD, Chance B, Yodh AG. Fluorescent heterogeneities in turbid media: limits for detection, characterization, and comparison with absorption. Appl Opt. 1998;37(28):6833–6844. doi: 10.1364/ao.37.006833. [DOI] [PubMed] [Google Scholar]
- 256.Patterson MS, Pogue BW. Mathematical-model for time-resolved and frequency-domain fluorescence spectroscopy in biological tissue. Appl Opt. 1994;33(10):1963–1974. doi: 10.1364/AO.33.001963. [DOI] [PubMed] [Google Scholar]
- 257.Sevick-Muraca EM, Burch CL. The origin of phosphorescence signals re-emitted from tissues. Opt Lett. 1994;19:1928–1930. doi: 10.1364/ol.19.001928. [DOI] [PubMed] [Google Scholar]
- 258.Reynolds JS, Troy TL, Mayer RH, Thompson AB, Waters DJ, Cornell KK, Snyder PW, Sevick-Muraca EM. Imaging of spontaneous canine mammary tumors using fluorescent contrast agents. Photochem Photobiol. 1999;70(1):87–94. [PubMed] [Google Scholar]
- 259.Sevick-Muraca EM, Lopez G, Reynolds JS, Troy TL, Hutchinson CL. fluorescence and absorption contrast mechanisms for biomedical optical imaging using frequency-domain techniques. Photochemistry and Photobiology. 1997;66(1):55–64. doi: 10.1111/j.1751-1097.1997.tb03138.x. [DOI] [PubMed] [Google Scholar]
- 260.Wu J, Feld MS, Rava RP. Analytical model for extracting intrinsic fluorescence in turbid media. Appl Opt. 1993;32:3585–3595. doi: 10.1364/AO.32.003585. [DOI] [PubMed] [Google Scholar]
- 261.Wu J, Wang Y, Perelman L, Itzkan I, Dasari RR, Feld MS. Time-resolved multichannel imaging of fluorescent objects embedded in turbid media. 1995;20:489–491. doi: 10.1364/ol.20.000489. 1997. [DOI] [PubMed] [Google Scholar]
- 262.Durkin AJ, Jaikumar S, Ramanujam N, Richards-Kortum R. Relation between fluorescence spectra of dilute and turbid samples. Applied Optics. 1994;33(3):414–423. doi: 10.1364/AO.33.000414. [DOI] [PubMed] [Google Scholar]
- 263.Chang JW, Graber HL, Barbour RL. Luminescence optical tomography of dense scattering media. J. Opt. Soc. Am. A. 1997;14(1):288–299. doi: 10.1364/josaa.14.000288. [DOI] [PubMed] [Google Scholar]
- 264.Paithankar DY, Chen AU, Pogue BW, Patterson MS, Sevick-Muraca EM. Imaging of fluorescent yield and lifetime from multiply scattered light reemitted from random media. Appl Opt. 1997;36(10):2260–2272. doi: 10.1364/ao.36.002260. [DOI] [PubMed] [Google Scholar]
- 265.Jiang H. Frequency-domain fluorescent diffusion tomography: a finite-element-based algorithm and simulations. Applied optics. 1998;37:5337–5343. doi: 10.1364/ao.37.005337. [DOI] [PubMed] [Google Scholar]
- 266.Ntziachristos V, Weissleder R. Experimental three-dimensional fluorescence reconstruction of diffuse media by use of a normalized born approximation. Optics Letters. 2001;26(12):893–895. doi: 10.1364/ol.26.000893. [DOI] [PubMed] [Google Scholar]
- 267.Milstein AB, Oh S, Webb KJ, Bouman CA, Zhang Q, Boas DA, Millane RP. Fluorescence optical diffusion tomography. Applied Optics. 2003;42(16):3081–3094. doi: 10.1364/ao.42.003081. [DOI] [PubMed] [Google Scholar]
- 268.Wilson BC, Patterson MS, Lilge L. Implicit and explicit dosimetry in photodynamic therapy: a new paradigm. Las. Med. Sci. 1997;12:182–192. doi: 10.1007/BF02765099. [DOI] [PubMed] [Google Scholar]
- 269.Cottrell WJ, Oseroff AR, Foster TH. A portable instrument that integrates irradiation with fluorescence and reflectance spectroscopies during clinical photodynamic therapy of cutaneous disease. Rev. Sci. Instrum. 2006;77:064302. [Google Scholar]
- 270.Ntziachristos V, Bremer C, Graves EE, Ripoll J, Weissleder R. In vivo tomographic imaging of near-infrared fluorescent probes. Mol. Imaging. 2002;1(2):82–88. doi: 10.1162/15353500200201121. [DOI] [PubMed] [Google Scholar]
- 271.Weissleder R, Ntziachristos V. Shredding light onto live molecular targets. Nat. Med. 2003;9(1):123–128. doi: 10.1038/nm0103-123. [DOI] [PubMed] [Google Scholar]
- 272.Ntziachristos V, Ripoll J, Wang LV, Weissleder R. Looking and listening to light: the evolution of whole-body photonic imaging. Nature Biotechnology. 2005;23(3):313–320. doi: 10.1038/nbt1074. [DOI] [PubMed] [Google Scholar]
- 273.Tanaka E, Choi HS, Fujii H, Bawendi MG, Frangioni JV. Image-guided oncologic surgery using invisible light: completed pre-clinical development for sentinel lymph node mapping. Annals of Surgical Oncology. 2006;13:1671–1681. doi: 10.1245/s10434-006-9194-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 274.Sevick-Muraca EM, Sharma R, Rasmussen JC, Marshall MV, Wendt JA, Pham HQ, Bonefas E, Houston JP, Sampath L, Adams KE, Blanchard DK, Fisher RE, Chiang SB, Elledge R, Mawad ME. Imaging of lymph flow in breast cancer patients after microdose administration of a near-infrared fluorophore: Feasibility study. Radiology. 2008;246:734–741. doi: 10.1148/radiol.2463070962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 275.Hagen AJ, Grosenick D, Pöllinger A, Burock S, Warnick P, Macdonald R, Rinneberg HH, Schlag PM. SPIE Photonics West. San Jose, CA: 2009. In-vivo fluorescence imaging of breast cancer; pp. 7174–7138. [Google Scholar]
- 276.Leproux A, van der Voort M, Harberts R, Verhaegh W, Bakker L, Nielsen T, Brendel BJ, van der Mark MB. SPIE Photonics West. San Jose, CA: 2009. Optical mammography: improved sensitivity by combined absorption and fluorescence analysis; pp. 7174–7137. [Google Scholar]
- 277.Kuebler WM. How NIR is the future in blood flow monitoring? J Appl Physiol. 2008;104(4):905–906. doi: 10.1152/japplphysiol.00106.2008. [DOI] [PubMed] [Google Scholar]
- 278.Terborg C, Bramer S, Harscher S, Simon M, Witte OW. Bedside assessment of cerebral perfusion reductions in patients with acute ischaemic stroke by near-infrared spectroscopy and indocyanine green. J Neurol Neurosurg Psychiatry. 2004;75(1):38–42. [PMC free article] [PubMed] [Google Scholar]
- 279.Liebert A, Wabnitz H, Steinbrink J, Moller M, Macdonald R, Rinneberg H, Villringer A, Obrig H. Bed-side assessment of cerebral perfusion in stroke patients based on optical monitoring of a dye bolus by time-resolved diffuse reflectance. Neuroimage. 2005;24:426–435. doi: 10.1016/j.neuroimage.2004.08.046. [DOI] [PubMed] [Google Scholar]
- 280.Keller E, Wietasch G, Ringleb P, Scholz M, Schwarz S, Stingele R, Schwab S, Hanley D, Hacke W. Bedside monitoring of cerebral blood flow in patients with acute hemispheric stroke. Crit Care Med. 2000;28(2):511–516. doi: 10.1097/00003246-200002000-00037. [DOI] [PubMed] [Google Scholar]
- 281.Apreleva SV, Wilson DF, Vinogradov SA. Tomographic imaging of oxygen by phosphorescence lifetime. Appl. Opt. 2006;45:8547–8559. doi: 10.1364/ao.45.008547. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 282.Vinogradov SA, Lo LW, Jenkins WT, Evans SM, Koch C, Wilson DF. Noninvasive imaging of the distribution of oxygen in tissue in vivo using infrared phosphors. Biophys J. 1996;70:1609. doi: 10.1016/S0006-3495(96)79764-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 283.Sakadžić S, Yuan S, Dilekoz E, Ruvinskaya S, Vinogradov SA, Ayata C, Boas DA. Simultaneous imaging of cerebral partial pressure of oxygen and blood flow during functional activation and cortical spreading depression. Applied Optics. 2009;48(10):169–177. doi: 10.1364/ao.48.00d169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 284.Wang G, Cong W, Durairaj K, Qian X, Shen H, Sinn P, Hoffman E, McLennan G, Henry M. In vivo mouse studies with bioluminescence tomography. Biomed. Eng. 2002;4:235–260. doi: 10.1364/oe.14.007801. [DOI] [PubMed] [Google Scholar]
- 285.Quistorff B, Haselgrove JC, Chance B. High spatial resolution readout of 3-D metabolic organ structure: An automated, low-temperature redox ratio-scanning instrument. Analytical Biochemistry. 1985;148:389–400. doi: 10.1016/0003-2697(85)90244-1. [DOI] [PubMed] [Google Scholar]
- 286.Ramanujam N. Encyclopedia of Analytical Chemistry. Wiley; 2000. Fluorescence spectroscopy in vivo; pp. 20–56. [Google Scholar]
- 287.Bigio IJ, Mourant JR. Encyclopedia of Optical Engineering. Marcel Dekker Press; 2003. Optical biopsy. [Google Scholar]
- 288.Bigio IJ, Bown SG. Spectroscopic sensing of cancer and cancer chemotherapy, current status of translational research. Cancer Biology and Therapy. 2004;3:259–267. doi: 10.4161/cbt.3.3.694. [DOI] [PubMed] [Google Scholar]
- 289.Ji S, Chance B, Stuart BH, Nathan R. Two-dimensional analysis of the redox state of the rat cerebral cortex in vivo by NADH fluorescence photography. Brain Research. 1977;119:357–373. doi: 10.1016/0006-8993(77)90316-x. [DOI] [PubMed] [Google Scholar]
- 290.Siesjo BK. Brain Energy Metabolism. Vol. 4. John Wiley & Sons Ltd; 1978. [Google Scholar]
- 291.Buxton RB, Frank LR. A model for the coupling between cerebral blood flow and oxygen metabolism during neural stimulation. J. Cereb. Blood Flow Metab. 1997;17:64–72. doi: 10.1097/00004647-199701000-00009. [DOI] [PubMed] [Google Scholar]
- 292.Friston KJ, Mechelli A, Turner R, Price CJ. Nonlinear responses in fMRI: the balloon model, volterra kernels, and other hemodynamics. NeuroImage. 2000;12(4):466–477. doi: 10.1006/nimg.2000.0630. [DOI] [PubMed] [Google Scholar]
- 293.Gjedde A. Cerebrovascular disease, chapter on The relation between brain function and cerebral blood flow and metabolism. Philadelphia: Lippincott-Raven; 1997. pp. 23–40. [Google Scholar]
- 294.Kety SS, Schmidt CF. The nitrous oxide method for the quantitative determination of cerebral blood flow in man; theory, procedure and normal values. J Clin Invest. 1948 Jul;27(4):476–483. doi: 10.1172/JCI101994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 295.Gesztelyi G, Finnegan W, DeMaro JA, Wang JY, Chen JL. Parenchymal microvascular systems and cerebral atrophy in spontaneously hypertensive rats. Brain Research. 1993;611:249–257. doi: 10.1016/0006-8993(93)90510-t. [DOI] [PubMed] [Google Scholar]
- 296.Boas DA, Strangman G, Culver JP, Hoge RD, Jasdzewski G, Poldrack RA, Rosen BR, Mandeville JB. Can the cerebral metabolic rate of oxygen be estimated with near-infrared spectroscopy? Phys Med Biol. 2003;48:2405–2418. doi: 10.1088/0031-9155/48/15/311. [DOI] [PubMed] [Google Scholar]
- 297.American cancer society, statistics for 2007 : Cancer facts & figures 2007. [accessed July 8, 2007]; http://www.cancer.org/docroot/STT/stt_0.asp. [Google Scholar]
- 298.Kerlikowske K, Barclay J, Grady D, Sickles EA, Ernster V. Comparison of risk factors for ductal carcinoma in situ and invasive breast cancer. J. Natl. Cancer Inst. 1997;89(1):76–82. doi: 10.1093/jnci/89.1.76. [DOI] [PubMed] [Google Scholar]
- 299.Goergen SK, Evans J, Cohen GPB, MacMillan JH. Characteristics of breast carcinomas missed by screening radiologists. Radiology. 1997;204:131–135. doi: 10.1148/radiology.204.1.9205234. [DOI] [PubMed] [Google Scholar]
- 300.Birdwell RL, Ikeda DM, O’Shaughnessy KF, Sickles EA. Mammographic characteristics of 115 missed cancers later detected with screening mammography and the potential utility of computer-aided detection. Radiology. 2001;219(1):192–202. doi: 10.1148/radiology.219.1.r01ap16192. [DOI] [PubMed] [Google Scholar]
- 301.Wang J, Shih TT, Hsu JC, Li YW. The evaluation of false negative mammography from malignant and benign breast lesions. J. Clin. Imaging. 2000;24:96–103. doi: 10.1016/s0899-7071(00)00184-4. [DOI] [PubMed] [Google Scholar]
- 302.Fletcher SW. Breast cancer screening among women in their forties: an overview of the issues. J. Natl. Cancer Inst. Monogr. 1997;22:5–9. doi: 10.1093/jncimono/1997.22.5. [DOI] [PubMed] [Google Scholar]
- 303.Elmore JG, Barton MB, Moceri VM, Polk S, Arena PJ, Fletcher SW. Ten-year risk of false positive screening mammograms and clinical breast examinations. New Engl. J. Med. 1998;338:1089–1096. doi: 10.1056/NEJM199804163381601. [DOI] [PubMed] [Google Scholar]
- 304.Bevilacqua F, Berger AJ, Cerussi AE, Jakubowski D, Tromberg BJ. Broadband absorption spectroscopy in turbid media by combined frequency-domain and steady-state methods. Appl. Opt. 2000;39:6498–6507. doi: 10.1364/ao.39.006498. [DOI] [PubMed] [Google Scholar]
- 305.Cheng X, Mao J, Bush R, Kopans DB, Moore RH, Chorlton M. Breast cancer detection by mapping hemoglobin concentration and oxygen saturation. Appl. Opt. 2003;42:6412–6421. doi: 10.1364/ao.42.006412. [DOI] [PubMed] [Google Scholar]
- 306.Chance B, Nioka S, Zhang J, Conant EF, Hwang E, Briest S, Orel SG, Schnall MD, Czerniecki BJ. Breast cancer detection based on incremental biochemical and physiological properties of breast cancers: A six-year, two-site study. Acad. Radiol. 2005;12:925–933. doi: 10.1016/j.acra.2005.04.016. [DOI] [PubMed] [Google Scholar]
- 307.Simick MK, Jong R, Wilson B, Lilge L. Non-ionizing near-infrared radiation transillumination spectroscopy for breast tissue density and assessment of breast cancer risk. J. Biomed. Opt. 2004;9:794–803. doi: 10.1117/1.1758269. [DOI] [PubMed] [Google Scholar]
- 308.Xu RX, Quang B, Mao JJ, Povoski SP. Development of a handheld near-infrared imager for dynamic characterization of in vivo biological tissue systems. Appl. Opt. 2007;46:7442–7451. doi: 10.1364/ao.46.007442. [DOI] [PubMed] [Google Scholar]
- 309.Chen NG, Guo PY, Yan SK, Piao DQ, Zhu Q. Simultaneous near-infrared diffusive light and ultrasound imaging. Appl. Opt. 2001;40:6367–6380. doi: 10.1364/ao.40.006367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 310.Franceschini MA, Moesta KT, Fantini S, Gaida G, Gratton E, Jess H, Mantulin WW, Seeber M, Schlag PM, Kaschke M. Frequency-domain techniques enhance optical mammography: Initial clinical results. Proc. Natl. Acad. Sci. U. S. A. 1997;94:6468–6473. doi: 10.1073/pnas.94.12.6468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 311.Pera VE, Heffer EL, Siebold H, Schutz O, Heywang-Kobrunner S, Gotz L, Heinig A, Fantini S. Spatial second-derivative image processing: an application to optical mammography to enhance the detection of breast tumors. J. Biomed. Opt. 2003;8:517–524. doi: 10.1117/1.1578496. [DOI] [PubMed] [Google Scholar]
- 312.Torricelli A, Spinelli L, Pifferi A, Taroni P, Cubeddu R, Danesini GM. Use of a nonlinear perturbation approach for in vivo breast lesion characterization by multi-wavelength time-resolved optical mammography. Opt Express. 2003;11:853–867. doi: 10.1364/oe.11.000853. [DOI] [PubMed] [Google Scholar]
- 313.Bassi A, Spinelli L, D’Andrea C, Guisto A, Swartling J, Pifferi A, Torricelli A, Cubeddu R. Feasibility of white-light time-resolved optical mammography. J. Biomed. Opt. 2006;11:054035. doi: 10.1117/1.2355663. [DOI] [PubMed] [Google Scholar]
- 314.Grosenick D, Moesta KT, Möller M, Mucke J, Wabnitz H, Gebauer B, Stroszczynski C, Wassermann B, Schlag PM, Rinneberg H. Time-domain scanning optical mammography: I. Recording and assessment of mammograms of 154 patients. Phys. Med. Biol. 2005;50(11):2429–2450. doi: 10.1088/0031-9155/50/11/001. [DOI] [PubMed] [Google Scholar]
- 315.Dierkes T, Grosenick D, Moesta KT, Möller M, Schlag PM, Rinneberg H, Arridge S. Reconstruction of optical properties of phantom and breast lesion in vivo from paraxial scanning data. Phys. Med. Biol. 2005;50(11):2519–2542. doi: 10.1088/0031-9155/50/11/006. [DOI] [PubMed] [Google Scholar]
- 316.Colak SB, van der Mark MB, Hooft GW, Hoogenraad JH, van der Linden ES, Kuijpers FA. Clinical optical tomography and NIR spectroscopy for breast cancer detection. IEEE J. Quantum Electron. 1999;5(4):1143–1158. [Google Scholar]
- 317.Iftimia N, Gu XJ, Xu Y, Jiang HB. A compact, parallel-detection diffuse optical mammography system. Rev. Sci. Instrum. 2003;74:2836–2842. [Google Scholar]
- 318.Li C, Zhao H, Anderson B, Jiang H. Multispectral breast imaging using a ten-wavelength 64×64 source/detector channels silicon photodiode-based diffuse optical tomography system. Med. Phys. 2006;33:627–636. doi: 10.1118/1.2171508. [DOI] [PubMed] [Google Scholar]
- 319.Schmitz CH, Klemer DP, Hardin R, Katz MS, Pei Y, Graber HL, Levin MB, Levina RD, Fraco NA, Solomon WB, Barbour RL. Design and implementation of dynamic near-infrared optical tomographic imaging instrumentation for simultaneous dual-breast measurements. Appl. Opt. 2005;44:2140–2153. doi: 10.1364/ao.44.002140. [DOI] [PubMed] [Google Scholar]
- 320.McBride TO, Pogue BW, Jiang S, Osterberg UL, Paulsen KD. A parallel-detection frequency-domain near-infrared tomography system for hemoglobin imaging of the breast in vivo. Rev. Sci. Instrum. 2001;72:1817–1824. [Google Scholar]
- 321.Intes X, Djeziri S, Ichalalene Z, Mincu N, Wang Y, St-Jean P, Lesage F, Hall D, Boas D, Polyzos M, Fleiszer D, Mesurolle B. Time-domain optical mammography SoftScan: Initial results. Acad. Radiol. 2005;12:934–947. doi: 10.1016/j.acra.2005.05.006. [DOI] [PubMed] [Google Scholar]
- 322.Durduran T, Choe R, Culver JP, Zubkov L, Holboke MJ, Giammarco J, Chance B, Yodh AG. Bulk optical properties of healthy female breast tissue. Phys. Med. Biol. 2002;47:2847–2861. doi: 10.1088/0031-9155/47/16/302. [DOI] [PubMed] [Google Scholar]
- 323.Jiang SD, Pogue BW, Paulsen KD, Kogel C, Poplack SP. In vivo near-infrared spectral detection of pressure-induced changes in breast tissue. Opt. Lett. 2003;28:1212–1214. doi: 10.1364/ol.28.001212. [DOI] [PubMed] [Google Scholar]
- 324.Srinivasan S, Pogue BW, Jiang SD, Dehghani H, Kogel C, Soho S, Gibson JJ, Tosteson TD, Poplack SP, Paulsen KD. Interpreting hemoglobin and water concentration, oxygen saturation, and scattering measured in vivo by near-infrared breast tomography. Proc. Natl. Acad. Sci. U. S. A. 2003;100:12349–12354. doi: 10.1073/pnas.2032822100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 325.Jakubowski DB, Cerussi AE, Bevilacqua F, Shah N, Hsiang D, Butler J, Tromberg BJ. Monitoring neoadjuvant chemotherapy in breast cancer using quantitative diffuse optical spectroscopy: a case study. J. Biomed. Opt. 2004;9:230–238. doi: 10.1117/1.1629681. [DOI] [PubMed] [Google Scholar]
- 326.Tromberg BJ, Shah N, Lanning R, Cerussi A, Espinoza J, Pham T, Svaasand L, Butler J. Non-invasive in vivo characterization of breast tumors using photon migration spectroscopy. Neoplasia. 2000;2:26–40. doi: 10.1038/sj.neo.7900082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 327.Painchaud Y, Mailloux A, Harvey E, Verreault S, Frechette J, Gilbert C, Vernon ML, Beaudry P. Multi-port time-domain laser mammography: results on solid phantom and volunteers. International Symposium of Biomedical Optics. 1999;3597:548–555. [Google Scholar]
- 328.Chance B. Near-infrared images using continuous, phase-modulated, and pulsed light with quantitation of blood and blood oxygenation. Ann. N. Y. Acad. Sci. 1998;838:19–45. doi: 10.1111/j.1749-6632.1998.tb08185.x. [DOI] [PubMed] [Google Scholar]
- 329.Suzuki K, Yamashita Y, Ohta K, Kaneko M, Yoshida M, Chance B. Quantitative mesurement of optical parameters in normal breasts using time-resolved spectroscopy: In vivo results of 30 Japanese women. J. Biomed. Opt. 1996;1:330–334. doi: 10.1117/12.239902. [DOI] [PubMed] [Google Scholar]
- 330.Thomsen S, Tatman D. Physiological and pathological factors of human breast disease that can influence optical diagnosis. Ann. N. Y. Acad. Sci. 1998;838:171–193. doi: 10.1111/j.1749-6632.1998.tb08197.x. [DOI] [PubMed] [Google Scholar]
- 331.Spinelli L, Torricelli A, Pifferi A, Taroni P, Danesini GM, Cubeddu R. Bulk optical properties and tissue components in the female breast from multiwavelength time-resolved optical mammography. J. Biomed. Opt. 2004;9:1137–1142. doi: 10.1117/1.1803546. [DOI] [PubMed] [Google Scholar]
- 332.Boyd NF, Lockwood GA, Byng JW, Tritchler DL, Yaffe MJ. Mammographic densities and breast cancer risk. Cancer Epidemiol. Biomarkers Prevent. 1998;7:1133–1144. [PubMed] [Google Scholar]
- 333.Blyschak K, Simick M, Jong R, Lilge L. Classification of breast tissue density by optical transillumination spectroscopy: Optical and physiological effects governing predictive value. Med. Phys. 2004;31:1398–1414. doi: 10.1118/1.1738191. [DOI] [PubMed] [Google Scholar]
- 334.Blackmore KM, Knight JA, Jong R, Lilge L. Assessing breast tissue density by transillumination breast spectroscopy (tibs): an intermediate indicator of cancer risk. British Journal Of Radiology. 2007;80:545–556. doi: 10.1259/bjr/26858614. [DOI] [PubMed] [Google Scholar]
- 335.Blackmore KM, Knight JA, Lilge L. Association between transillumination breast spectroscopy and quantitative mammographic features of the breast. Cancer Epidemiology Biomarkers & Prevention. 2008;17:1043–1050. doi: 10.1158/1055-9965.EPI-07-2658. [DOI] [PubMed] [Google Scholar]
- 336.Ntziachristos V, Yodh AG, Schnall M, Chance B. Concurrent MRI and diffuse optical tomography of breast after indocyanine green enhancement. Proc. Natl. Acad. Sci. U. S. A. 2000;97:2767–2772. doi: 10.1073/pnas.040570597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 337.Pogue BW, Poplack SP, McBride TO, Wells WA, Osterman KS, Osterberg UL, Paulsen KD. Quantitative hemoglobin tomography with diffuse near-infrared spectroscopy: Pilot results in the breast. Radiology. 2001;218:261–266. doi: 10.1148/radiology.218.1.r01ja51261. [DOI] [PubMed] [Google Scholar]
- 338.Jiang H, Xu Y, Ifitimia N, Eggert J, Klove K, Baron L, Fajardo L. Three-dimensional optical tomographic imaging of breast in a human subject. IEEE Trans. Med. imaging. 2001;20:1334–1340. doi: 10.1109/42.974928. [DOI] [PubMed] [Google Scholar]
- 339.Dehghani H, Pogue BW, Jiang SD, Brooksby B, Paulsen KD. Three-dimensional optical tomography: resolution in small-object imaging. Appl. Opt. 2003;42:3117–3128. doi: 10.1364/ao.42.003117. [DOI] [PubMed] [Google Scholar]
- 340.Zhu QI, Huang MM, Chen NG, Zarfos K, Jagjivan B, Kane M, Hedge P, Kurtzman SH. Ultrasound-guided optical tomographic imaging of malignant and benign breast lesions: Initial clinical results of 19 cases. Neoplasia. 2003;5:379–388. doi: 10.1016/s1476-5586(03)80040-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 341.Choe R, Corlu A, Lee K, Durduran T, Konecky SD, Grosicka-Koptyra M, Arridge SR, Czerniecki BJ, Fraker DL, DeMichele A, Chance B, Rosen MA, Yodh AG. Diffuse optical tomography of breast cancer during neoadjuvant chemotherapy: a case study with comparison to MRI. Med. Phys. 2005;32(4):1128–1139. doi: 10.1118/1.1869612. [DOI] [PubMed] [Google Scholar]
- 342.Grosenick D, Wabnitz H, Moesta KT, Mucke J, Schlag PM, Rinneberg H. Time-domain scanning optical mammography: II. Optical properties and tissue parameters of 87 carcinomas. Phys. Med. Biol. 2005;50(11):2451–2468. doi: 10.1088/0031-9155/50/11/002. [DOI] [PubMed] [Google Scholar]
- 343.Spinelli L, Torricelli A, Pifferi A, Taroni P, Danesini G, Cubeddu R. Characterization of female breast lesions from multi-wavelength time-resolved optical mammography. Phys. Med. Biol. 2005;50(11):2489–2502. doi: 10.1088/0031-9155/50/11/004. [DOI] [PubMed] [Google Scholar]
- 344.Enfield LC, Gibson AP, Everdell NL, Delpy DT, Schweiger M, Arridge SR, Richardson C, Keshtgar M, Douek M, Hebden JC. Three-dimensional time-resolved optical mammography of the uncompressed breast. Appl. Opt. 2007;46:3628–3638. doi: 10.1364/ao.46.003628. [DOI] [PubMed] [Google Scholar]
- 345.Dehghani H, Pogue BW, Poplack SP, Paulsen KD. Multiwavelength three-dimensional near-infrared tomography of the breast: initial simulation, phantom, and clinical results. Appl. Opt. 2003;42:135–145. doi: 10.1364/ao.42.000135. [DOI] [PubMed] [Google Scholar]
- 346.Jiang HB, Iftimia NV, Xu Y, Eggert JA, Fajardo LL, Klove KL. Near-infrared optical imaging of the breast with model-based reconstruction. Acad. Radiol. 2002;9:186–194. doi: 10.1016/s1076-6332(03)80169-1. [DOI] [PubMed] [Google Scholar]
- 347.Zhu Q, Chen N, Kurtzman SH. Imaging tumor angiogenesis by use of combined near-infrared diffusive light and ultrasound. Opt. Lett. 2003;28:337–339. doi: 10.1364/ol.28.000337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 348.Srinivasan S, Pogue BW, Brooksby B, Jiang S, Dehghani H, Kogel C, Wells WA, Poplack SP, Paulsen KD. Near-infrared characterization of breast tumors in vivo using spectrally-constrained reconstruction. Tech. Cancer Res. Treat. 2005;4:513–526. doi: 10.1177/153303460500400505. [DOI] [PubMed] [Google Scholar]
- 349.Hanahan D, Weinberg RA. The hallmarks of cancer. Cell. 2000;100:57–70. doi: 10.1016/s0092-8674(00)81683-9. [DOI] [PubMed] [Google Scholar]
- 350.Zhu Q, Kurtzma SH, Hegde P, Tannenbaum S, Kane M, Huang M, Chen NG, Jagjivan B, Zarfos K. Utilizing optical tomography with ultrasound localization to image heterogeneous hemoglobin distribution in large breast cancers. Neoplasia. 2005;7(3):263–270. doi: 10.1593/neo.04526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 351.Li C, Grobmyer SR, Massol N, Liang X, Zhang Q, Chen L, Fajardo LL, Jiang H. Noninvasive in vivo tomographic optical imaging of cellular morphology in the breast: Possible convergence of microscopic pathology and macroscopic radiology. Med. Phys. 2008;35:2493–2501. doi: 10.1118/1.2921129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 352.Brown JM. Tumor hypoxia in cancer therapy. Methods Enzymol. 2007;435:297–321. doi: 10.1016/S0076-6879(07)35015-5. [DOI] [PubMed] [Google Scholar]
- 353.Hockel M, Vaupel P. Tumor hypoxia: Definitions and current clinical, biologic, and molecular aspects. J. Natl. Cancer Inst. 2001;93:266–276. doi: 10.1093/jnci/93.4.266. [DOI] [PubMed] [Google Scholar]
- 354.Evans SM, Koch CJ. Prognostic significance of tumor oxygenation in humans. Cancer Lett. 2003;195:1–16. doi: 10.1016/s0304-3835(03)00012-0. [DOI] [PubMed] [Google Scholar]
- 355.Fantini S, Walker SA, Franceschini MA, Kaschke M, Schlag PM, Moesta KT. Assessment of the size, position, and optical properties of breast tumors in vivo by noninvasive optical methods. Appl. Opt. 1998;37:1982–1989. doi: 10.1364/ao.37.001982. [DOI] [PubMed] [Google Scholar]
- 356.Chernomordik V, Hattery DW, Grosenick D, Wabnitz H, Rinneberg H, Moesta KT, Schlag PM, Gandjbakhche A. Quantification of optical properties of a breast tumor using random walk theory. J. Biomed. Opt. 2002;7:80–87. doi: 10.1117/1.1427049. [DOI] [PubMed] [Google Scholar]
- 357.Heffer E, Pera V, Schutz O, Siebold H, Fantini S. Near-infrared imaging of the human breast: complementing hemoglobin concentration maps with oxygenation images. J. Biomed. Opt. 2004;9:1152–1160. doi: 10.1117/1.1805552. [DOI] [PubMed] [Google Scholar]
- 358.Srinivasan S, Pogue BW, Carpenter C, Jiang S, Wells WA, Poplack SP, Kaufman PA, Paulsen KD. Developments in quantitative oxygen-saturation imaging of breast tissue in vivo using multispectral near-infrared tomography. Antioxidants & Redox Signaling. 2007;9:1143–1156. doi: 10.1089/ars.2007.1643. [DOI] [PubMed] [Google Scholar]
- 359.McBride TO, Pogue BW, Poplack S, Soho S, Wells WA, Jiang SD, Osterberg UL, Paulsen KD. Multispectral near-infrared tomography: a case study in compensating for water and lipid content in hemoglobin imaging of the breast. J. Biomed. Opt. 2002;7:72–79. doi: 10.1117/1.1428290. [DOI] [PubMed] [Google Scholar]
- 360.Cerussi A, Shah N, Hsiang D, Durkin A, Butler J, Tromberg BJ. In vivo absorption, scattering, and physiologic properties of 58 malignant breast tumors determined by broadband diffuse optical spectroscopy. J. Biomed. Opt. 2006;11:044005. doi: 10.1117/1.2337546. [DOI] [PubMed] [Google Scholar]
- 361.Gu XJ, Zhang QZ, Bartlett M, Schutz L, Fajardo LL, Jiang HB. Differentiation of cysts from solid tumors in the breast with diffuse optical tomography. Acad. Radiol. 2004;11:53–60. doi: 10.1016/s1076-6332(03)00562-2. [DOI] [PubMed] [Google Scholar]
- 362.Taroni P, Torricelli A, Spinelli L, Pifferi A, Arpaia F, Danesini G, Cubeddu R. Time-resolved optical mammography between 637 and 985 nm: clinical study on the detection and identification of breast lesions. Phys. Med. Biol. 2005;50(11):2469–2488. doi: 10.1088/0031-9155/50/11/003. [DOI] [PubMed] [Google Scholar]
- 363.Yates T, Hebden JC, Gibson A, Everdell N, Arridge SR, Douek M. Optical tomography of the breast using a multi-channel time-resolved imager. Phys. Med. Biol. 2005;50(11):2503–2518. doi: 10.1088/0031-9155/50/11/005. [DOI] [PubMed] [Google Scholar]
- 364.Shah N, Gibbs J, Wolverton D, Cerussi A, Hylton N, Tromberg BJ. Combined diffuse optical spectroscopy and contrast-enhanced magnetic resonance imaging for monitoring breast cancer neoadjuvant chemotherapy: a case study. J. Biomed. Opt. 2005;10:051503. doi: 10.1117/1.2070147. [DOI] [PubMed] [Google Scholar]
- 365.Tromberg BJ, Cerussi AE, Shah N, Hsiang D, Butler JA, Du T, Compton M, Fedyk A. Predicting response to breast cancer neoadjuvant chemotherapy using diffuse optical opectroscopy. In: Chance B, Alfano RR, Tromberg BJ, Tamura M, Sevick-Muraca EM, editors. Optical Tomography and Spectroscopy of Tissue VI. Vol. 5693. Bellingham, WA: SPIE; 2005. [Google Scholar]
- 366.Azar FS, Lee K, Khamene A, Choe R, Corlu A, Konecky SD, Sauer F, Yodh AG. Standardized platform for coregistration of non-concurrent diffuse optical and magnetic resonance breast images obtained in different geometries. J. Biomed. Opt. 2007;12:051902. doi: 10.1117/1.2798630. [DOI] [PubMed] [Google Scholar]
- 367.Konecky SD, Choe R, Corlu A, Lee K, Wiener R, Srinivas SM, Saffer JR, Freifelder R, Karp JS, Hajjioui N, Azar F, Yodh AG. Comparison of diffuse optical tomography of human breast with whole-body and breast-only positron emission tomography. Med. Phys. 2008;35:446–455. doi: 10.1118/1.2826560. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 368.Breslow NE, Day NE, Davis W. Statistical methods in cancer research. International Agency for Research on Cancer; 1980. [Google Scholar]
- 369.Pepe MS. The Statistical Evaluation of Medical Tests for Classification and Prediction. Oxford University Press; 2003. [Google Scholar]
- 370.Poplack SP, Tosteson TD, Wells WA, Pogue BW, Meaney PM, Hartov A, Kogel CA, Soho SK, Gibson JJ, Paulsen KD. Electromagnetic breast imaging: Results of a pilot study in women with abnormal mammograms. Radiology. 2007;243(2):350–359. doi: 10.1148/radiol.2432060286. [DOI] [PubMed] [Google Scholar]
- 371.Ntziachristos V, Yodh AG, Schnall MD, Chance B. MRI-guided diffuse optical spectroscopy of malignant and benign breast lesions. Neoplasia. 2002;4:347–354. doi: 10.1038/sj.neo.7900244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 372.Intes X, Ripoll J, Chen Y, Nioka S, Yodh AG, Chance B. In vivo continuous-wave optical breast imaging enhanced with indocyanine green. Med. Phys. 2003;30:1039–1047. doi: 10.1118/1.1573791. [DOI] [PubMed] [Google Scholar]
- 373.Bastiaens PI, Squire A. Fluorescence lifetime imaging microscopy: spatial resolution of biochemical processes in the cell. Trends Cell Biol. 1999;9:48–52. doi: 10.1016/s0962-8924(98)01410-x. [DOI] [PubMed] [Google Scholar]
- 374.Kuwana E, Sevick-Muraca EM. Fluorescence lifetime spectroscopy for pH sensing in scattering media. Anal. Chem. 2003;75:4325–4329. doi: 10.1021/ac034059a. [DOI] [PubMed] [Google Scholar]
- 375.Reynolds JS, Troy TL, Mayer RH, Thompson AB, Waters DJ, Cornell KK, Snyder PW, Sevick-Muraca EM. Imaging of spontaneous canine mammary tumors using fluorescent contrast agents. Photochem. Photobiol. 1999;70:87–94. [PubMed] [Google Scholar]
- 376.Godavarty A, Eppstein MJ, Zhang CY, Theru S, Thompson AB, Gurfinkel M, Sevick-Muraca EM. Fluorescence-enhanced optical imaging in large tissue volumes using a gain-modulated iccd camera. Phys. Med. Biol. 2003;48:1701–1720. doi: 10.1088/0031-9155/48/12/303. [DOI] [PubMed] [Google Scholar]
- 377.Knopp MV, Brix G, Zeger SL. MR mammography with pharmacokinetic mapping for monitoring of breast cancer treatment during neoadjuvant therapy. Magn. Reson. Imaging Clin. N. Am. 1994;2(4):633–658. [PubMed] [Google Scholar]
- 378.Tsuboi N, Ogawa Y, Inomata T, Yoshida D, Yoshida S, Moriki T, Kumon M. Changes in the findings of dynamic MRI by preoperative CAF chemotherapy for patients with breast cancer of stage II and III: pathologic correlation. Oncol. Rep. 1999;6(4):727–732. doi: 10.3892/or.6.4.727. [DOI] [PubMed] [Google Scholar]
- 379.Drew PJ, Kerin MJ, Mahapatra T, Malone C, Monson JRT, Turnbull LW, Fox JN. Evaluation of response to neoadjuvant chemoradiotherapy for locally advanced breast cancer with dynamic contrast-enhanced MRI of the breast. Eur. J. Surg. Oncol. 2001;27:617–620. doi: 10.1053/ejso.2001.1194. [DOI] [PubMed] [Google Scholar]
- 380.Wahl RL. Overview of the current status of PET in breast cancer imaging. Q. J. Nucl. Med. 1998;42:1–7. [PubMed] [Google Scholar]
- 381.Tiling R, Linke R, Untch M, Richter A, Fieber S, Brinkbaumer K, Tatsch K, Hahn K. F-18-FDG PET and tc-99m-sestamibi scintimammography for monitoring breast cancer response to neoadjuvant chemotherapy: a comparative study. Eur. J. Nucl. Med. 2001;28:711–720. doi: 10.1007/s002590100539. [DOI] [PubMed] [Google Scholar]
- 382.Jiang S, Pogue BW, Carpenter CM, Poplack SP, Wells WA, Kogel CA, Forero JA, Muffly LS, Schwartz GN, Paulsen KD, Kaufman PA. Evaluation of breast tumor response to neoadjuvant chemotherapy with tomographic diffuse optical spectroscopy: Case studies of tumor region-of-interest changes. Radiology. 2009;252:551–560. doi: 10.1148/radiol.2522081202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 383.Zhu Q, Tannenbaum S, Hegde P, Kane M, Xu C, Kurtzman SH. Noninvasive monitoring of breast cancer during neoadjuvant chemotherapy using optical tomography with ultrasound localization. Neoplasia. 2008;10:1028–1040. doi: 10.1593/neo.08602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 384.Cerussi A, Hsiang D, Shah N, Mehta R, Durkin A, Butler J, Tromberg BJ. Predicting response to breast cancer neoadjuvant chemotherapy using diffuse optical spectroscopy. Proc. Natl. Acad. Sci. U. S. A. 2007;104:4014–4019. doi: 10.1073/pnas.0611058104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 385.Chung SH, Cerussi AE, Klifa C, Baek HM, Birgul O, Gulsen G, Merritt SI, Hsiang D, Tromberg BJ. In vivo water state measurements in breast cancer using broadband diffuse optical spectroscopy. Phys. Med. Biol. 2008;53:6713–6727. doi: 10.1088/0031-9155/53/23/005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 386.Taroni P, Comelli D, Pifferi A, Torricelli A, Cubeddu R. Absorption of collagen: effects on the estimate of breast composition and related diagnostic implications. J. Biomed. Opt. 2007;12:014021. doi: 10.1117/1.2699170. [DOI] [PubMed] [Google Scholar]
- 387.Liang X, Zhang Q, Li C, Grobmyer SR, Fajardo LL, Jiang H. Phase-contrast diffuse optical tomography: Pilot results in the breast. Acad. Radiol. 2008;15:859–866. doi: 10.1016/j.acra.2008.01.028. [DOI] [PubMed] [Google Scholar]
- 388.Brooksby B, Jiang SD, Dehghani H, Pogue BW, Paulsen KD, Kogel C, Doyley M, Weaver JB, Poplack SP. Magnetic resonance-guided near-infrared tomography of the breast. Rev. Sci. Instrum. 2004;75(12):5262–5270. [Google Scholar]
- 389.Brooksby B, Jiang S, Dehghani H, Pogue BW, Paulsen KD, Weaver J, Kogel C, Poplack SP. Combining near-infrared tomography and magnetic resonance imaging to study in vivo breast tissue: implementation of a Laplacian-type regularization to incorporate magnetic resonance structure. J. Biomed. Opt. 2005;10:051504. doi: 10.1117/1.2098627. [DOI] [PubMed] [Google Scholar]
- 390.Boverman G, Miller EL, Li A, Zhang Q, Chaves T, Brooks DH, Boas DA. Quantitative spectroscopic diffuse optical tomography of the breast guided by imperfect a priori structural information. Phys. Med. Biol. 2005;50:3941–3956. doi: 10.1088/0031-9155/50/17/002. [DOI] [PubMed] [Google Scholar]
- 391.Carpenter CM, Pogue BW, Jiang S, Dehghani H, Wang X, Paulsen KD, Wells WA, Forero J, Kogel C, Weaver JB, Poplack SP, Kaufman PA. Image-guided optical spectroscopy provides molecular-specific information in vivo: MRI-guided spectroscopy of breast cancer hemoglobin, water, and scatterer size. Optics Letters. 2007;32(8):933–935. doi: 10.1364/ol.32.000933. [DOI] [PubMed] [Google Scholar]
- 392.Carpenter CM, Srinivasan S, Pogue BW, Paulsen KD. Methodology development for three-dimensional MR-guided near infrared spectroscopy of breast tumors. Opt. Express. 2008;16:17903–17914. doi: 10.1364/oe.16.17903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 393.Zhang Q, Brukilacchio TJ, Li A, Stott JJ, Chaves T, Hillman E, Wu T, Chorlton A, Rafferty E, Moore RH, Kopans DB, Boas DA. Coregistered tomographic x-ray and optical breast imaging: initial results. J. Biomed. Opt. 2005;10(2):024033. doi: 10.1117/1.1899183. [DOI] [PubMed] [Google Scholar]
- 394.Fang Q, Carp SA, Selb J, Boverman G, Zhang Q, Kopans DB, Moore RH, Miller EL, Brooks DH, Boas DA. Combined optical imaging and mammography of the healthy breast: optical contrast derived from breast structure and compression. IEEE Trans. Med. Imaging. 2009;28:30–42. doi: 10.1109/TMI.2008.925082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 395.Zhu Q, Durduran T, Ntziachristos V, Holboke M, Yodh AG. Imager that combines near-infrared diffusive light and ultrasound. Opt. Lett. 1999;24:1050–1052. doi: 10.1364/ol.24.001050. [DOI] [PubMed] [Google Scholar]
- 396.Holboke MJ, Tromberg BJ, Li X, Shah N, Fishkin J, Kidney D, Butler J, Chance B, Yodh AG. Three-dimensional diffuse optical mammography with ultrasound localization in a human subject. J. Biomed. Opt. 2000;5:237–247. doi: 10.1117/1.429992. [DOI] [PubMed] [Google Scholar]
- 397.Zhu Q, Conant E, Chance B. Optical imaging as an adjunct to sonograph in differentiating benign from malignant breast lesions. J. Biomed. Opt. 2000;5:229–236. doi: 10.1117/1.429991. [DOI] [PubMed] [Google Scholar]
- 398.Weissleder R, Ntziachristos V. Shedding light onto live molecular targets. Nat Med. 2003;9:123–128. doi: 10.1038/nm0103-123. [DOI] [PubMed] [Google Scholar]
- 399.Ermilov SA, Khamapirad T, Conjusteau A, Leonard MH, Lacewell R, Megta K, Miller T, Oraevsky AA. Laser optoacoustic imaging system for detection of breast cancer. J. Biomed. Opt. 2009;14:024007. doi: 10.1117/1.3086616. [DOI] [PubMed] [Google Scholar]
- 400.Roy CS, Sherrington CS. On the regulation of the blood-supply of the brain. The Journal of Physiology. 1890;11(1–2):85. doi: 10.1113/jphysiol.1890.sp000321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 401.Mosso A. Ueber den Kreislauf des Blutes im menschlichen Gehirn. Veit, Leipzig: 1881. [Google Scholar]
- 402.Lou HC, Edvinsson L, Mackenzie ET. The concept of coupling blood-flow to brain-function - revision required. An. of Neurol. 1987;22(3):289–297. doi: 10.1002/ana.410220302. [DOI] [PubMed] [Google Scholar]
- 403.Villringer A, Dirnagl U. Coupling of brain activity and cerebral blood flow: basis of functional neuroimaging. Cereb. Brain. Metab. Rev. 1995;7:240–276. [PubMed] [Google Scholar]
- 404.Paulson OB, Strandgaard S, Edvinsson L. Cerebral autoregulation. Cerebrovasc Brain Metab Rev. 1990;2(2):161–192. [PubMed] [Google Scholar]
- 405.Smith M. Monitoring intracranial pressure in traumatic brain injury. Anesth Analg. 2008;106(1):240–248. doi: 10.1213/01.ane.0000297296.52006.8e. [DOI] [PubMed] [Google Scholar]
- 406.Wintermark M, Sesay M, Barbier E, Borbely K, Dillon WP, Eastwood JD, Glenn TC, Grandin CB, Pedraza S, Soustiel JF, Nariai T, Zaharchuk G, Caille JM, Dousset V, Yonas H. Comparative overview of brain perfusion imaging techniques. Stroke. 2005;36(9):83–99. doi: 10.1161/01.STR.0000177884.72657.8b. [DOI] [PubMed] [Google Scholar]
- 407.Rosenblum BR, Bonner RF, Oldfield EH. Intraoperative measurement of cortical blood flow adjacent to cerebral AVM using laser doppler velocimetry. Journal of neurosurgery. 1987;66(3):396–399. doi: 10.3171/jns.1987.66.3.0396. [DOI] [PubMed] [Google Scholar]
- 408.Fasano VA, Urciuoli R, Bolognese P, Mostert Intraoperative use of laser doppler in the study of cerebral microvascular circulation. Acta neurochirurgica. 1988;95(1):40–48. doi: 10.1007/BF01793081. [DOI] [PubMed] [Google Scholar]
- 409.Prakash N, Uhleman F, Sheth SA, Bookheimer S, Martin N, Toga AW. Current trends in intraoperative optical imaging for functional brain mapping and delineation of lesions of language cortex. NeuroImage. 2008;47:T116–T126. doi: 10.1016/j.neuroimage.2008.07.066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 410.Binzoni T, Leung TS, Boggett D, Delpy DT. Non-invasive laser Doppler perfusion measurements of large tissue volumes and human skeletal muscle blood RMS velocity. Phys Med Biol. 2003;48:2527–2549. doi: 10.1088/0031-9155/48/15/318. [DOI] [PubMed] [Google Scholar]
- 411.Dunn AK, Bolay T, Moskowitz MA, Boas DA. Dynamic imaging of cerebral blood flow using laser speckle. J. Cereb. Blood Flow Metab. 2001;21(3):195–201. doi: 10.1097/00004647-200103000-00002. [DOI] [PubMed] [Google Scholar]
- 412.Durduran T, Burnett MG, Yu G, Zhou C, Furuya D, Yodh AG, Detre JA, Greenberg JH. Spatio-temporal quantification of cerebral blood flow during functional activation in rat somatosensory cortex using laser speckle flowmetry. J. Cereb. Blood Flow Metab. 2004;24:518–525. doi: 10.1097/00004647-200405000-00005. [DOI] [PubMed] [Google Scholar]
- 413.Kirkham FJ, Padayachee TS, Parsons S, Seargeant LS, House FR, Gosling RG. Transcranial measurement of blood velocities in the basal cerebral arteries using pulsed doppler ultrasound: velocity as an index of flow. Ultrasound Med Biol. 1986;12:15–21. doi: 10.1016/0301-5629(86)90139-0. [DOI] [PubMed] [Google Scholar]
- 414.Bishop CC, Powell S, Rutt D, Browse NL. Transcranial doppler measurement of middle cerebral artery blood flow velocity: a validation study. Stroke. 1986;17:913–915. doi: 10.1161/01.str.17.5.913. [DOI] [PubMed] [Google Scholar]
- 415.Pindzola RR, Balzer JR, Nemoto EM, Goldstein S, Yonas H. Cerebrovascular reserve in patients with carotid occlusive disease assessed by stable xenon-enhanced ct cerebral blood flow and transcranial Doppler. Stroke. 2001 Aug;32(8):1811–1817. doi: 10.1161/01.str.32.8.1811. [DOI] [PubMed] [Google Scholar]
- 416.Alexandrov AV, Demchuk AM, Wein TH, Grotta JC. Yield of transcranial Doppler in acute cerebral ischemia. Stroke. 1999 Aug;30(8):1604–1609. doi: 10.1161/01.str.30.8.1604. [DOI] [PubMed] [Google Scholar]
- 417.Detre JA, Alsop DC. Perfusion magnetic resonance imaging with continuous arterial spin labeling: methods and clinical applications in the central nervous system. Euro J Rad. 1999;30(2):115–124. doi: 10.1016/s0720-048x(99)00050-9. [DOI] [PubMed] [Google Scholar]
- 418.Barbier EL, Silva AC, Kim SG, Koretsky AP. Perfusion imaging using dynamic arterial spin labeling (DASL) Mag Res Med. 2001;45:1021–1029. doi: 10.1002/mrm.1136. [DOI] [PubMed] [Google Scholar]
- 419.Detre JA, Zhang W, Roberts DA, Silva AC, Williams DS, Grandis DJ, Koretsky AP, Leigh JS. Tissue specific perfusion imaging using arterial spin labeling. NMR in Biomedicine. 1994;7:75–82. doi: 10.1002/nbm.1940070112. [DOI] [PubMed] [Google Scholar]
- 420.Kim SG. Quantification of relative cerebral blood flow change by flow-sensitive alternating inversion recovery (FAIR) technique: application to functional mapping. Mag. Res. Med. 1995;34:293–301. doi: 10.1002/mrm.1910340303. [DOI] [PubMed] [Google Scholar]
- 421.Kwong KK, Belliveau JW, Chesler DA, Goldberg IE, Weisskoff RM, Poncelet BP, Kennedy DN, Hoppel BE, Cohen MS, Turner R, Cheng H-M, Brady TJ, Rosen BR. Dynamic magnetic resonance imaging of human brain activity during primary sensory stimulation. Proc. Natl. Acad. Sci. USA. 1992;89(12):5675–5679. doi: 10.1073/pnas.89.12.5675. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 422.Pindzola RR, Yonas H. The xenon-enhanced computed tomography cerebral blood flow method. Neurosurgery. 1998;43:1488–1492. doi: 10.1097/00006123-199812000-00147. [DOI] [PubMed] [Google Scholar]
- 423.Yonas RP, Pindzola H, Johnson DW. Xenon/computed tomography cerebral blood flow and its use in clinical management. Neurosurg Clin N Am. 1996;7:605–616. [PubMed] [Google Scholar]
- 424.Frackowiak RS, Lenzi GL, Jones T, Heather JD. Quantitative measurement of regional cerebral blood flow and oxygen metabolism in man using 150 and positron emission tomography: theory, procedure, and normal values. J. Comput. Assit. Tomogr. 1980;4:727–736. doi: 10.1097/00004728-198012000-00001. [DOI] [PubMed] [Google Scholar]
- 425.Reivich M, Kuhl D, Wolf A, Greenberg JH, Phelps M, Ido T, Casella V, Fowler J, Hoffman E, Alavi A, Som P, Sokoloff L. The [18F] fluorodeoxyglucose method for the measurement of local cerebral glucose utilization in man. Circ Res. 1979;44:127–137. doi: 10.1161/01.res.44.1.127. [DOI] [PubMed] [Google Scholar]
- 426.Phelps ME, Mazziotta JC, Schelbert HR, Hawkins RA, Engel J. Clinical PET - what are the issues. J Nucl Med. 1985;26(12):1353–1358. [Google Scholar]
- 427.Brazy JE, Lewis DV, Mitnick MH, Jobsis FF. Noninvasive monitoring of cerebral oxygenation in preterm infants: preliminary observations. Pediatrics. 1985;75:217–225. [PubMed] [Google Scholar]
- 428.Brazy JE, Lewis DV. Changes in cerebral blood volume and cytochrome AA3 during hypertensive peaks in preterm infants. J Pediatr. 1986;108:983–987. doi: 10.1016/s0022-3476(86)80944-1. [DOI] [PubMed] [Google Scholar]
- 429.Bucher HU, Edwards AD, Lipp AE, Duc G. Comparison between near infrared spectroscopy and 133xenon clearance for estimation of cerebral blood flow in critically ill preterm infants. Pediatric Research. 1993;33:56–59. doi: 10.1203/00006450-199301000-00012. [DOI] [PubMed] [Google Scholar]
- 430.Cope M. The Development of a Near-Infrared Spectroscopy System and Its Application for Noninvasive Monitoring of Cerebral Blood and Tissue Oxygenation in the Newborn Infant. London: University College London; 1991. [Google Scholar]
- 431.Delpy DT, Cope MC, Cady EB, Wyatt JS, Hamilton PA, Hope PL, Wray S, Reynolds EO. Cerebral monitoring in newborn infants by magentic resonance and near infrared spectroscopy. Scand. J. Clin. Lab. Invest. Suppl. 1987;188:9–17. [PubMed] [Google Scholar]
- 432.Hintz SR, Benaron DA, Siegel AM, Stevenson DK, Boas DA. Bedside functional imaging of the premature infant brain during passive motor activation. Journal of Investigative Medicine. 1999;47(2):60a–60a. doi: 10.1515/JPM.2001.048. [DOI] [PubMed] [Google Scholar]
- 433.Hebden JC. Advances in optical imaging of the newborn infant brain. Psychophysiol. 2003;40:501–510. doi: 10.1111/1469-8986.00052. [DOI] [PubMed] [Google Scholar]
- 434.Hillman EMC. Optical brain imaging in vivo: techniques and applications from animal to man. Journal of Biomedical Optics. 2007;12(5) doi: 10.1117/1.2789693. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 435.Wolf M, Ferrari M, Quaresima V. Progress of near-infrared spectroscopy and topography for brain and muscle clinical applications. Journal of Biomedical Optics. 2007;12(6):062104. doi: 10.1117/1.2804899. [DOI] [PubMed] [Google Scholar]
- 436.Dehghani H, White BR, Zeff BW, Tizzard A, Culver JP. Depth sensitivity and image reconstruction analysis of dense imaging arrays for mapping brain function with diffuse optical tomography. Applied Optics. 2009;48(10):137–143. doi: 10.1364/ao.48.00d137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 437.Gomersall CD, Joynt GM, Gin T, Freebairn RC, Stewart IE. Failure of the INVOS3100 cerebral oximeter to detect complete absence of cerebral blood flow. Crit. Care. Med. 1997;25:1252–1254. doi: 10.1097/00003246-199707000-00031. [DOI] [PubMed] [Google Scholar]
- 438.Schwarz G, Litscher G, Kleinert R, Jobstmann R. Cerebral oximetry in dead subjects. J Neurosurg. Anesthesiol. 1996;8:189–193. doi: 10.1097/00008506-199607000-00001. [DOI] [PubMed] [Google Scholar]
- 439.Nicklin SE, Hassan IAA, Wickramasinghe YA, Spencer SA. The light still shines, but not that brightly? the current status of perinatal near infrared spectroscopy. Archives of Disease in Childhood Fetal & Neonatal Edition. 2003;88(4):F263. doi: 10.1136/fn.88.4.F263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 440.Al-Rawi PG. Near infrared spectroscopy in brain injury: today’s perspective. Acta Neurochirurgica-Supplementum. 2005;95:453. doi: 10.1007/3-211-32318-x_93. [DOI] [PubMed] [Google Scholar]
- 441.Kirkpatrick PJ, Smielewski P, Czosnyka M, Menon DK, Pickard JD. Near-infrared spectroscopy use in patients with head injury. Journal of Neurosurgery. 1995;83(6):963–970. doi: 10.3171/jns.1995.83.6.0963. [DOI] [PubMed] [Google Scholar]
- 442.Gopinath SP, Robertson CS, Contant CF, Narayan RK, Grossman RG, Chance B. Early detection of delayed traumatic intracranial hematomas using near-infrared spectroscopy. J Neurosurg. 1995;83:438–444. doi: 10.3171/jns.1995.83.3.0438. [DOI] [PubMed] [Google Scholar]
- 443.Gopinath SP, Robertson CS, Grossman RG, Chance B. Near-infrared spectroscopic localization of intracranial hematomas. J Neurosurg. 1993;79:43–47. doi: 10.3171/jns.1993.79.1.0043. [DOI] [PubMed] [Google Scholar]
- 444.Lewis SB, Myburgh JA, Thornton EL, Reilly PL. Cerebral oxygenation monitoring by near-infrared spectroscopy is not clinically useful in patients with severe closed-head injury: A comparison with jugular venous bulb oximetry. Crit. Care. Med. 1996;24:1334–1338. doi: 10.1097/00003246-199608000-00011. [DOI] [PubMed] [Google Scholar]
- 445.Keller E, Nadler A, Imhof HG, Niederer P, Roth P, Yonekawa Y. New methods for monitoring cerebral oxygenation and hemodynamics in patients with subarachnoid hemorrhage. Acta neurochirurgica. Supplement. 2002;82:87. doi: 10.1007/978-3-7091-6736-6_16. [DOI] [PubMed] [Google Scholar]
- 446.Carandang R, Krieger DW. Near infrared spectroscopy: finding utility in malignant hemispheric stroke. Neurocritical Care. 2007;6(3):161–164. doi: 10.1007/s12028-007-0023-y. [DOI] [PubMed] [Google Scholar]
- 447.Bönöczk P, Panczel G, Nagy Z. Vinpocetine increases cerebral blood flow and oxygenation in stroke patients: a near infrared spectroscopy and transcranial doppler study. European Journal of Ultrasound. 2002;15(1–2):85–91. doi: 10.1016/s0929-8266(02)00006-x. [DOI] [PubMed] [Google Scholar]
- 448.Sakatani K, Xie Y, Lichty W, Li S, Zuo H. Language-activated cerebral blood oxygenation and hemodynamic changes of the left prefrontal cortex in poststroke aphasic patients : A near-infrared spectroscopy study. Stroke. 1998;29(7):1299–1304. doi: 10.1161/01.str.29.7.1299. [DOI] [PubMed] [Google Scholar]
- 449.Kato H, Izumiyama M, Koizumi H, Takahashi A, Itoyama Y. Near-infrared spectroscopic topography as a tool to monitor motor reorganization after hemiparetic stroke: A comparison with functional MRI. Stroke. 2002;33(8):2032–2036. doi: 10.1161/01.str.0000021903.52901.97. [DOI] [PubMed] [Google Scholar]
- 450.Miyai I, Yagura H, Hatakenaka M, Oda I, Konishi I, Kubota K. Longitudinal optical imaging study for locomotor recovery after stroke. Stroke. 2003;34(12):2866–2870. doi: 10.1161/01.STR.0000100166.81077.8A. [DOI] [PubMed] [Google Scholar]
- 451.Damian MS, Schlosser R. Bilateral near infrared spectroscopy in space-occupying middle cerebral artery stroke. Neurocritical Care. 2007;6(3):165–173. doi: 10.1007/s12028-007-0010-3. [DOI] [PubMed] [Google Scholar]
- 452.Vernieri F, Rosato N, Pauri F, Tibuzzi F, Passarelli F, Rossini PM. Near infrared spectroscopy and transcranial doppler in monohemispheric stroke. Eur Neurol. 1999;41(3):159–162. doi: 10.1159/000008041. [DOI] [PubMed] [Google Scholar]
- 453.Hargroves D, Tallis R, Pomeroy V, Bhalla A. The influence of positioning upon cerebral oxygenation after acute stroke: a pilot study. Age Ageing. 2008;37(5):581–585. doi: 10.1093/ageing/afn143. [DOI] [PubMed] [Google Scholar]
- 454.Hayakawa T, Terashima M, Kayukawa Y, Ohta T, Okada T. Changes in cerebral oxygenation and hemodynamics during obstructive sleep apneas. Chest. 1996;109(4):916–921. doi: 10.1378/chest.109.4.916. [DOI] [PubMed] [Google Scholar]
- 455.McGown AD, Makker H, Elwell C, Al Rawi PG, Valipour A, Spiro SG. Measurement of changes in cytochrome oxidase redox state during obstructive sleep apnea using near-infrared spectroscopy. Sleep. 2003;26(6):710–716. doi: 10.1093/sleep/26.6.710. [DOI] [PubMed] [Google Scholar]
- 456.Spielman AJ, Zhang G, Yang CM, D’Ambrosio P, Serizawa S, Nagata M, von Gizycki H, Alfano RR. Intracerebral hemodynamics probed by near infrared spectroscopy in the transition between wakefulness and sleep. Brain research. 2000;866(1–2):313–325. doi: 10.1016/s0006-8993(00)02320-9. [DOI] [PubMed] [Google Scholar]
- 457.Michalos A, Safonova LP, Wolf U, Wolf M, Choi JH, Gupta R, Mantulin WW, Hueber DM, Barbieri B, Gratton E. Obstructive sleep apnea: Evaluation of brain oxygenation and hemodynamics by near-infrared spectroscopy. Sleep. 2002;25:547. [Google Scholar]
- 458.Taillefer MC, Denault AY. Cerebral near-infrared spectroscopy in adult heart surgery: systematic review of its clinical efficacy. Canadian Journal of Anesthesia. 2005;52(1):79–87. doi: 10.1007/BF03018586. [DOI] [PubMed] [Google Scholar]
- 459.Al-Rawi PG, Kirkpatrick PJ. Tissue oxygen index: Thresholds for cerebral ischemia using near-infrared spectroscopy. Stroke. 2006;37(11):2720. doi: 10.1161/01.STR.0000244807.99073.ae. [DOI] [PubMed] [Google Scholar]
- 460.Benaron DA, Hintz SR, Villringer A, Boas D, Kleinschmidt A, Frahm J, Hirth C, Obrig H, van Houten JC, Kermit EL, Cheong WF, Stevenson DK. Noninvasive functional imaging of human brain using light. J Cereb Blood Flow Metab. 2000;20(3):469–477. doi: 10.1097/00004647-200003000-00005. [DOI] [PubMed] [Google Scholar]
- 461.Wolfberg AJ, du Plessis AJ. Near-infrared spectroscopy in the fetus and neonate. Clinics in Perinatology. 2006;33(3):707–728. doi: 10.1016/j.clp.2006.06.010. [DOI] [PubMed] [Google Scholar]
- 462.Minagawa-Kawai Y, Mori K, Hebden J, Dupoux E. Optical imaging of infants’ neurocognitive development: Recent advances and perspectives. Developmental Neurobiology. 2008;68(6):712–728. doi: 10.1002/dneu.20618. [DOI] [PubMed] [Google Scholar]
- 463.Yang Y, Liu HL, Li XD, Chance B. Low cost frequency-domain photon migration instrument for tissue spectroscopy, oximetry, and imaging. Opt. Eng. 1997;36950:1562–1569. [Google Scholar]
- 464.Sokoloff L. The effects of carbon dioxide on the cerebral circulation. Anesthesiology. 1960;21:664–673. [Google Scholar]
- 465.Jasper H. Report of the committe on methods of clinical examination in electroencephalography. Clin. Neurophysiol. 1958;10:370–375. [Google Scholar]
- 466.Kastrup A, Kruger G, Neumann-Haefelin T, Glover GH, Moseley ME. Changes of cerebral blood flow, oxygenation, and oxidative metabolism during graded motor activation. NeuroImage. 2002:74–82. doi: 10.1006/nimg.2001.0916. [DOI] [PubMed] [Google Scholar]
- 467.Ye FQ, Smith AM, Yang Y, Duyn J, Mattay VS, Ruttimann UE, Frank JA, Weinberger DR, McLaughlin AC. Quantitation of regional cerebral blood flow increases during motor activation: A steady-state arterial spin tagging study. Mag Res Med. 1999;42:404–407. doi: 10.1002/(sici)1522-2594(199908)42:2<404::aid-mrm23>3.0.co;2-0. [DOI] [PubMed] [Google Scholar]
- 468.Colebatch JG, Deiber MP, Passingham RE, Friston KJ, Frackowiak RS. Regional cerebral blood flow during voluntary arm and hand movements in human subjects. J Neurophysiol. 1991;65:1392–1401. doi: 10.1152/jn.1991.65.6.1392. [DOI] [PubMed] [Google Scholar]
- 469.Roland PE, Larsen B, Lassen NA, Skinhoj E. Supplementarymclaughlinfinger motor area and other cortical areas in organization of voluntary movements in man. J. Neurophysiol. 1980;43:118–136. doi: 10.1152/jn.1980.43.1.118. [DOI] [PubMed] [Google Scholar]
- 470.Seitz RJ, Roland PE. Learning of sequential finger movements in man: a combined kinematic and positron emission tomography (pet) study. Eur. J. Neurosci. 1992;4:154–165. doi: 10.1111/j.1460-9568.1992.tb00862.x. [DOI] [PubMed] [Google Scholar]
- 471.Mehagnoul-Schipper DJ, van der Kallen BFW, Colier WNJM, van der Sluijs MC, van Erning LJTO, Thijssen HOM, Oeseburg B, Hoefnagels WHL, Jansen RWMM. Simultaneous measurements of cerebral oxygenation changes during brain activation by near-infrared spectroscopy and functional magnetic resonance imaging in healthy young and elderly subjects. Human Brain Mapping. 2002;16:14–23. doi: 10.1002/hbm.10026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 472.Hoge RD, Atkinson J, Gill B, Crelier GR, Marrett S, Pike GB. Linear coupling between cerebral blood flow and oxygen consumption in activated human cortex. Proc Natl Acad Sci U S A. 1999;96(16):9403–9408. doi: 10.1073/pnas.96.16.9403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 473.Hoge RD, Franceschini MA, Covolan RJM, Huppert T, Mandeville JB, Boas DA. Simultaneous recording of task-induced changes in blood oxygenation, volume, and flow using diffuse optical imaging and arterial spin-labeling MRI. Neuroimage. 2005;25(3):701–707. doi: 10.1016/j.neuroimage.2004.12.032. [DOI] [PubMed] [Google Scholar]
- 474.Huppert TJ, Hoge RD, Diamond SG, Franceschini MA, Boas DA. A temporal comparison of BOLD, ASL, and NIRS hemodynamic responses to motor stimuli in adult humans. Neuroimage. 2006 Jan;29(2):368–382. doi: 10.1016/j.neuroimage.2005.08.065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 475.Diamond SG, Huppert TJ, Kolehmainen V, Franceschini MA, Kaipio JP, Arridge SR, Boas DA. Dynamic physiological modeling for functional diffuse optical tomography. Neuroimage. 2006;30(1):88–101. doi: 10.1016/j.neuroimage.2005.09.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 476.Joseph DK, Huppert TJ, Franceschini MA, Boas DA. Diffuse optical tomography system to image brain activation with improved spatial resolution and validation with functional magnetic resonance imaging. Applied optics. 2006;45(31):8142–8151. doi: 10.1364/ao.45.008142. [DOI] [PubMed] [Google Scholar]
- 477.Huppert TJ, Hoge RD, Dale AM, Franceschini MA, Boas DA. Quantitative spatial comparison of diffuse optical imaging with blood oxygen level-dependent and arterial spin labeling-based functional magnetic resonance imaging. Journal of biomedical optics. 2006;11:064018. doi: 10.1117/1.2400910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 478.Huppert TJ, Allen MS, Diamond SG, Boas DA. Estimating cerebral oxygen metabolism from fmri with a dynamic multi-compartment windkessel model. Human brain mapping. 2009;30(5):1548. doi: 10.1002/hbm.20628. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 479.Kim MN, Durduran T, Frangos S, Buckley EM, Zhou C, Yu G, Moss H, Edlow BL, Maloney-Wilensky E, Detre JA, Greenberg JH, Kofke WA, Yodh AG, Grady MS, Woo JH, Wolf RL, Levine J. SPIE Photonics West. San Jose, CA: 2009. Diffuse optical measurements of cerebral blood flow and oxygenation in patients after traumatic brain injury or subarachnoid hemorrhage. [Google Scholar]
- 480.Hebden JC, Austin T. Optical tomography of the neonatal brain. European Radiology. 2007;17(11):2926–2933. doi: 10.1007/s00330-007-0659-1. [DOI] [PubMed] [Google Scholar]
- 481.Hintz SR, Benaron DA, Houten JP, Duckworth JL, Liu FWH, Spilman SD, Stevenson DK, Cheong WF. Stationary headband for clinical time-of-flight optical imaging at the bedside. Photochemistry and photobiology. 1998;68(3):361–369. [PubMed] [Google Scholar]
- 482.Hintz SR, Cheong WF, van Houten JP, Stevenson DK, Benaron DA. Bedside imaging of intracranial hemorrhage in the neonate using light: Comparison with ultrasound, computed tomography, and magnetic resonance imaging. Pediatric research. 1999;45(1):54. doi: 10.1203/00006450-199901000-00009. [DOI] [PubMed] [Google Scholar]
- 483.Hebden JC, Gibson A, Yusof RM, Everdell N, Hillman EMC, Delpy DT, Arridge SR, Austin T, Meek JH, Wyatt JS. Three-dimensional optical tomography of the premature infant brain. Physics in Medicine and Biology. 2002;47(23):4155–4166. doi: 10.1088/0031-9155/47/23/303. [DOI] [PubMed] [Google Scholar]
- 484.Hebden JC, Gibson A, Austin T, Yusof RM, Everdell N, Delpy DT, Arridge SR, Meek JH, Wyatt JS. Imaging changes in blood volume and oxygenation in the newborn infant brain using three-dimensional optical tomography. Physics in Medicine and Biology. 2004;49(7):1117–1130. doi: 10.1088/0031-9155/49/7/003. [DOI] [PubMed] [Google Scholar]
- 485.Kondepati VR, Heise HM, Backhaus J. Recent applications of near-infrared spectroscopy in cancer diagnosis and therapy. Analytical and Bioanalytical Chemistry. 2008;390(1):125–139. doi: 10.1007/s00216-007-1651-y. [DOI] [PubMed] [Google Scholar]
- 486.Vardi M, Nini A. Near-infrared spectroscopy for evaluation of peripheral vascular disease. a systematic review of literature. Eur J Vasc Endovasc Surg. 2008;35:68–74. doi: 10.1016/j.ejvs.2007.07.015. [DOI] [PubMed] [Google Scholar]
- 487.Luksiene Z. Photodynamic therapy: mechanism of action and ways to improve the efficiency of treatment. Medicina (Kaunas) 2003;39:1137–1150. [PubMed] [Google Scholar]
- 488.Dougherty TJ, Gomer CJ, Henderson BW, Jori G, Kessel D, Korbelik M, Moan J, Peng Q. Photodynamic therapy. J. Nat. Cancer Inst. 1998;90:889–905. doi: 10.1093/jnci/90.12.889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 489.De Grand AM, Frangioni JV. An operational near-infrared fluorescence imaging system prototype for large animal surgery. Tech Cancer Res & Treat. 2003;2(6):553–562. doi: 10.1177/153303460300200607. [DOI] [PubMed] [Google Scholar]
- 490.Marghoob AA, Swindle LD, Moricz CZM, Negron FAS, Slue B, Halpern ACH, Kopf AW. Instruments and new technologies for the in vivo diagnosis of melanoma. Journal of the American Academy of Dermatology. 2003;49(5):777–797. doi: 10.1016/s0190-9622(03)02470-8. [DOI] [PubMed] [Google Scholar]
- 491.Xu Y, Iftimia N, Jiang HB, Key LL, Bolster MB. Imaging of in vitro and in vivo bones and joints with continuous-wave diffuse optical tomography. Optics Express. 2001;8(7):447–451. doi: 10.1364/oe.8.000447. [DOI] [PubMed] [Google Scholar]
- 492.Lasker JM, Fong CJ, Ginat DT, Dwyer E, Hielscher AH. Dynamic optical imaging of vascular and metabolic reactivity in rheumatoid joints. Journal of Biomedical Optics. 2007;12:052001. doi: 10.1117/1.2798757. [DOI] [PubMed] [Google Scholar]
- 493.Wang LV, Wu HI. Biomedical Optics: Principles and Imaging. 1 edition. Wiley-Interscience; 2007. p. 5. [Google Scholar]
- 494.Vo-Dinh T, editor. Biomedical Photonics Handbook. CRC Press; 2003. [Google Scholar]
- 495.Bouma BE, Tearney GJ. Handbook of Optical Coherence Tomography. 1st edition. Informa HealthCare; 2001. p. 11. [Google Scholar]
- 496.Sharpe J. Optical projection tomography. Annual Review of Biomedical Engineering. 2004;6(1):209–228. doi: 10.1146/annurev.bioeng.6.040803.140210. [DOI] [PubMed] [Google Scholar]
- 497.Johansson A, Katharina K, Ronald S, Herbert S. Clinical optical diagnostics - status and perspectives. Medical Laser Application. 2008;23(4):155–174. [Google Scholar]
- 498.Patterson MS, Andersson-Engels S, Wilson BC, Osei EK. Absorption spectroscopy in tissue-simulating materials: a theoretical and experimental study of photon paths. Appl. Opt. 1995;34(1):22–30. doi: 10.1364/AO.34.000022. [DOI] [PubMed] [Google Scholar]
- 499.Zhou C. Ph.D. Dissertation. University of Pennsylvania; 2007. In-Vivo Optical Imaging and Spectroscopy of Cerebral Hemodynamics. [Google Scholar]