CHARMM Drude Polarizable Force Field for Aldopentofuranoses and Methyl-aldopentofuranosides

Abstract

An empirical all-atom CHARMM polarizable force filed for aldopentofuranoses and methyl-aldopentofuranosides based on the classical Drude oscillator is presented. A single electrostatic model is developed for eight different diastereoisomers of aldopentofuranoses by optimizing the existing electrostatic and bonded parameters as transferred from ethers, alcohols and hexopyranoses to reproduce quantum mechanical (QM) dipole moments, furanose-water interaction energies and conformational energies. Optimization of selected electrostatic and dihedral parameters was performed to generate a model for methyl-aldopentofuranosides. Accuracy of the model was tested by reproducing experimental data for crystal intramolecular geometries and lattice unit cell parameters, aqueous phase densities, and ring pucker and exocyclic rotamer populations as obtained from NMR experiments. In most cases the model is found to reproduce both QM data and experimental observables in an excellent manner, while for the remainder the level of agreement is in the satisfactory regimen. In aqueous phase simulations the monosaccharides have significantly enhanced dipoles as compared to the gas phase. The final model from this study is transferrable for future studies on carbohydrates and can be used with the existing CHARMM Drude polarizable force field for biomolecules.

Introduction

Carbohydrates are one of the essential classes of biomolecules and, in the context of poly- or oligosaccharides, are comprised of monosaccharides linked through a variety of different types of glycosidic linkages and decorated with a range of functional groups in addition to the common hydroxyl groups. Of the monosaccharides, the furanoses are an important class that contain five-membered rings formed from the cyclization of various aldoses or ketoses. Furanoses are hemiacetals or hemiketals and can be formed from pentose, hexose or heptose sugars. Due to the presence of the three chiral ring carbon centers eight different stereoisomers of aldopentofuranoses are found, as shown in Figure 1.

Figure 1.

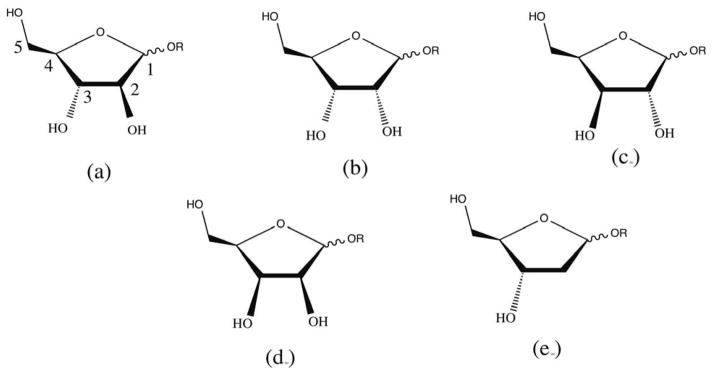
Schematic representation of (a) Arabinofuranose, (b) Ribofuranose, (c) Lyxofuranose, (d) Xylofuranose and (e) deoxyribofuranose where R= H/CH_3.

Furanoses are important constituents of a number of biologically important molecules, including nucleic acids.¹ In nucleic acids the furanose rings are either ribose or deoxy-ribose and these ring moieties contribute to the conformations of DNA and RNA by means of changing their own conformations.² Furanoses are also found in bacterial cell walls, including in Mycobacterium tuberculosis as well as in a number of microorganisms, fungi, parasites and plants.^3–6 In glycan containing cell walls the furanose rings are mostly D-galactofuranose or D-arabinofuranose.⁷ In addition, furanose containing polysaccharides are used as targets for various therapeutic agents.^8–10 For example, the increase in drug-resistant bacteria requires the development of novel vaccines and antibiotics,^11–12 with the latter often targeting the biosynthesis of cell walls. In this context, the cell wall in mycobacteria includes two furanoses, arabinogalactan (AG) and lipoarabinomannan (LAM), such that compounds that contain furanoses may be used in the development of new antibiotics.^13–14

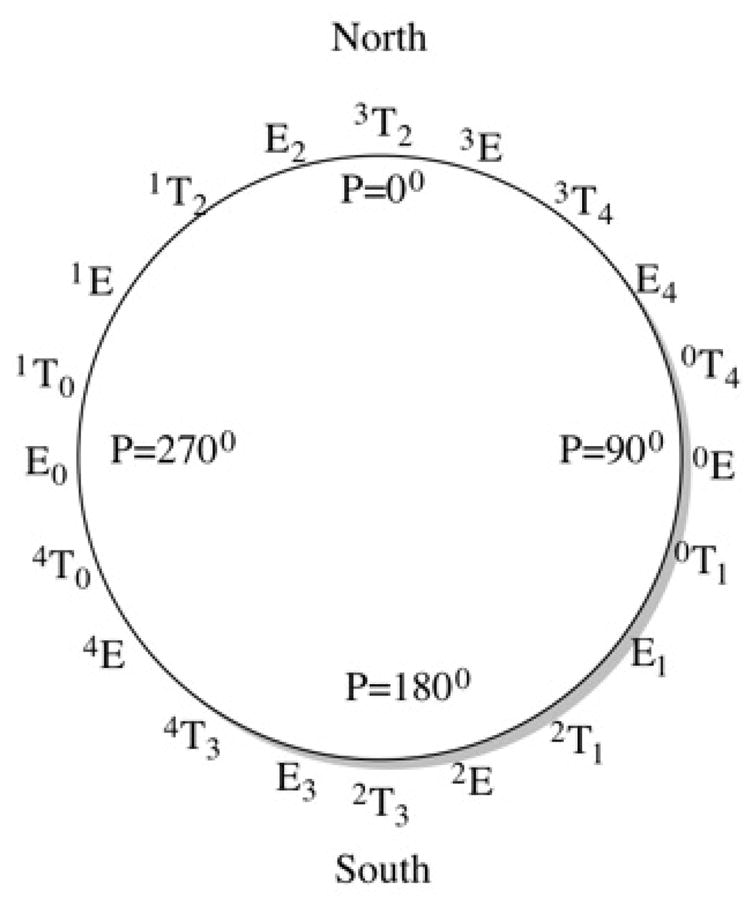
As compared to pyranoses the furanoses are thermodynamically less favorable due to additional ring strain. In aqueous solution many hemiacetal or hemiketal furanoses readily interconvert into their lower energy isomeric pyranose forms.^15–16 In addition, the ring strain allows furanoses to adopt several conformational states, which are generally separated by low energy barriers.^17–18 This flexibility leads to difficulty in assigning their most preferable conformation. Based on the analysis of a large number of crystallographic structures Altona and Sundaralingam developed a pseudorotation wheel model that can describe the conformations of furanoses.^19–20 According to the model (Figure 2) the conformations can be subdivided into 20 ideal twist (T) and envelope (E) forms, with the low-energy furanose conformational states classified into two categories namely, North (N) and South (S). The conformational states can be described by two parameters, pseudorotation phase angle, P, and puckering amplitude, Φ_m. When P falls in the northern hemisphere of the wheel the state is designated as N versus S when it falls in the southern hemisphere. The flexibility of the furanoses allows the N and S states to remain in equilibrium via pseudorotation.

Figure 2.

Pseudorotation wheel model^19–20 for D-aldopentofuranoses

Experimental and computational studies were carried out over the last few decades to probe the conformational flexibility of furanose rings.^{17, 21–33} Experimental studies generally involve NMR and interpretation of those data through Karplus equations.^21–24 Analysis of the data is generally done with either the PSEUROT computer program,³⁴ based on the definitions presented in Figure 2, or based on a continuous probability distribution (CUPID) approach.^26–28 Beside experimental approaches theoretical studies based on molecular mechanics (MM), molecule dynamics (MD), quantum mechanics (QM), or combinations thereof can provide a wealth of information.^{17, 29–33} Empirical force fields (FF) including CHARMM,^{33, 35–40} GLYCAM,⁴¹ GROMOS,⁴² and OPLS⁴³ are available for carbohydrates. These models are based on fixed partial atomic charges centered on atoms, referred to as additive FFs, that do not explicitly account for the phenomenon of electronic polarization. Incorporation of electrostatic induction as a function of the polarity of the environment is an important advancement over additive FFs.^44–47 For example, in condensed-phase simulations where the high dielectric medium polarizes the molecular charge distribution changes in the geometry and conformational energetics of molecules can occur.^{44, 48} Thus, a number of polarizable FFs are being developed,^44–45 based on various models including inducible point dipoles,^49–51 fluctuating charges (FQ) or electronegativity equalization,^52–56 inducible point dipole with fluctuating and fixed charges,⁵⁷ Gaussian polarization model,⁵⁸ and classical Drude oscillators.^{46, 59}

The classical Drude oscillator model involves a point charge (Drude particle) attached to the nucleus of each non-hydrogen atom via a harmonic spring and, hence, it preserves the simple Coulomb electrostatic interactions as employed in additive FFs.⁶⁰ Notably, shifting a portion of the mass of the parent atom to the Drude particle allows for efficient MD simulations using an extended Lagrangian^{59, 61} in which the polarizability approaches the self-consistent field (SCF) limit in the context of computationally efficient MD simulations. Drude FF parameters have been successfully developed for a range of molecular entities including water,^62–64 alkanes,⁶⁵ amides,⁶⁶ ethers,^67–68 alcohols,⁶⁹ sulphur and nitrogen containing compounds.^70–72 Further, a first generation Drude model has been implemented for proteins,^73–74 selected lipids,⁷⁵ and DNA.⁷⁶ Importantly, the explicit inclusion of electronic polarizability via the Drude model has been found to improve the condense phase properties for these classes of molecules. Notably, the Drude model is now available in NAMD,⁷⁷ ChemShell QM/MM ⁷⁸ and Gromacs⁷⁹ and MD simulations on the microsecond time scale have been reported.⁷⁴

In this work we present an extension of the Drude polarizable FF^80–81 to aldopentofuranoses, deoxy-ribofuranoses and methyl-aldopenrofuranoses (Figure 1). For convenience in the rest of our study we have designated the α-forms of arabinofuranose, ribofuranose, lyxofuranose, xylofuranose and deoxyribofuranose compounds as aarb, arib, alyf, axyf and adeo and the β-forms of these compounds as barb, brib, blyf, bxyf and bdeo, respectively.

Computational Details

Quantum mechanical (QM) calculations were carried out with the Gaussian03,⁸² PSI4,⁸³ or QCHEM programs.⁸⁴ QM optimization of the geometries, dipole moments and potential energy scans (PES) for model compounds were performed using the MP2/6-31G(d) model chemistry. Final energy surfaces were obtained by single point calculations at the RIMP2/cc-pVQZ level. QM calculations to determine gas phase molecular polarizabilities were carried out at the B3LYP/aug-cc-pVDZ//MP2/6-31G(d) model chemistry. The model compounds are the same as used in the previous development of the additive CHARMM force field for furanoses.³³ QM interaction energies for furanoses and water were obtained at the RIMP2/cc-pVQZ//MP2/6-31G(d) model chemistry with correction made for the basis set super-imposition error (BSSE).⁸⁵

Empirical force field calculations were carried out using the CHARMM⁸⁶ program. The water model used in this study is the four-site SWM4-NDP model.⁶³ Gas phase minimizations were carried out with steepest-descent (SD) algorithm where all the Drude particles were allowed to relax while other atoms were kept restrained using an harmonic force constant of 1000 kcal/mol/Å. This was followed by minimizations of all particles using the adopted-basis Newton-Rapson (ABNR) algorithm. PESs were performed with a harmonic restraint of 10,000 kcal/mol/radian applied to the targeted dihedrals while all other degrees of freedom were allowed to relax. Atomic charges, atomic polarizabilities (ie. alpha) and the atom-based Thole scale factors were optimized targeting QM dipole moments by using a Monte Carlo Simulated Annealing (MCSA) approach.^{62, 73, 80, 87} In the MCSA the initial temperature was set at 500 K which was gradually reduced by a factor 0.75 after every 1600 steps until it approached 0 K. The final parameters were obtained by averaging over the last 20 MCSA steps of the optimization.

Except as otherwise specified, all the condensed-phase MD simulations were performed at constant temperature (298K) and pressure (1 atm) (NPT) using the velocity-Verlet integrator that approximates the self-consistent field (SCF) motion of the Drude particles via an extended Lagrangian multiple thermostat formalism.⁵⁹ A mass of 0.4 amu was transferred from the real atoms to the corresponding Drude particles. A separate low-temperature thermostat (at T = 1.0 K) was used to control the temperature of the Drude particles to ensure that their time course approximates the SCF regimen. A 1 fs integration time step with a relaxation time of 0.1 ps applied to all real atoms was used in the MD simulations. The long-range electrostatic interactions were treated with the Particle-Mesh Ewald (PME)⁸⁸ method using a real-space cutoff of 16 Å, a kappa value of 0.34, and a 6th-order spline and the Lennard-Jones (LJ) interactions⁸⁹ were truncated via a switching function over 10–12 Å with an isotropic long range LJ correction.⁹⁰ All the covalent bonds involving hydrogens were constrained using the SHAKE algorithm.⁹¹ The Drude Hardwall constraint was applied in all simulations with a distance of 0.2 Å.⁷⁵ MD simulations of the crystals were performed with the complete crystal unit cells retrieved from the Cambridge Structural Database⁹² at the experimental temperatures. Due to the unavailability of furanose monosaccharide crystals, all the crystal simulations were performed with methyl-furanosides. All the crystal simulations involved a 100 ps equilibration followed by a 10 ns production run. The trajectories were saved during production run with a time resolution of 1 ps.

To compare the solution densities of the furanoses with experimentally available data, aqueous phase MD simulations were performed at various concentrations of the compounds. Simulations were carried out with 1:1 mixtures of alpha and beta forms of the furanose in a cubic box of 1100 water molecules. Each system was equilibrated for 500 ps followed by a 10 ns production run. Aqueous phase MD simulations were also carried out for all the α- and β-methyl-furanosides separately in a cubic box of 1100 water molecules at various concentrations to obtain NMR observables. All the simulations involving the aqueous phase methyl-furanosides were carried out for 10 ns.

The ring pucker conformations for methyl-furanosides in terms of N and S conformations were calculated from the 10 ns aqueous phase MD simulation by determining pseudorotation angle (P) that corresponds to the appropriate region of the pseudorotation wheel (Figure 2). According to the nomenclature¹⁹ a furanose conformation that has P value smaller than 90° and greater than 270° is designated as N conformer whereas if the P value falls between 90° and 270⁰ then the conformer is S.¹⁹ The P and amplitude Φ_m were calculated using the following expressions^19–20

$$\mathit{tan}P=\frac{({\vartheta }_4+{\vartheta }_1)-({\vartheta }_3+{\vartheta }_0)}{2{\vartheta }_2(sin{36}^0+sin{72}^0)}$$ (1)

and

$${\mathrm{\Phi }}_m=\frac{{\vartheta }_2}{cosP}$$ (2)

where ϑ₀ =C4-O4-C1-C2, ϑ₁ =O4-C1-C2-C3, ϑ₂ =C1-C2-C3-C4, ϑ₃ =C2-C3-C4-O4, and ϑ₄ =C3-C4-O4-C1. Population of the N and S conformers and their percentage distributions were calculated using 2° bin widths. Values were calculated every 1 ps over the production trajectories.

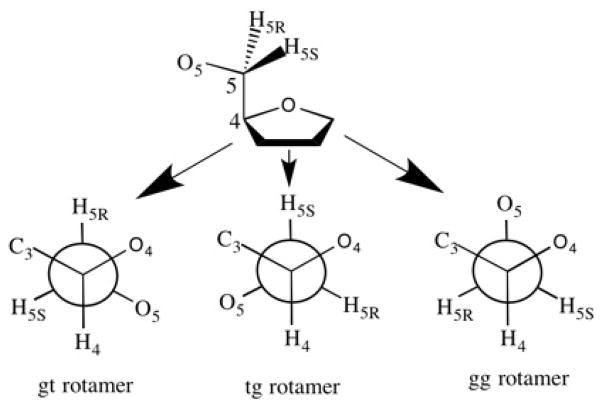
The distribution of the exocyclic rotamer about the C4-C5 bond of furanose rings were also calculated from the 10 ns aqueous phase simulation by measuring O4-C4-C5-O5 torsion over the trajectory. The C4-C5 bond conformation can be depicted by three staggered rotamers, namely gg (gauche, gauche), gt (gauche, trans) and tg (trans, gauche), as shown in Figure 3. The populations of the three rotamers were calculated from the corresponding probability distributions.

Figure 3.

Definition of the three staggered rotamers about the C4–C5 bond in furanoses.

Results and Discussion

Optimization of electrostatic parameters for aldopentofuranoses

Development of Drude polarizable parameters for furanoses involved a hierarchical process. Initially electrostatic, bonded and nonbonded parameters were transferred from the existing tetrahydrofuran (THF),⁶⁸ ethanol,⁶⁹ glycerol,⁸¹ and hexopyranose⁸⁰ parameters. In particular, the electrostatic parameters involving the ring hydroxyl and exocyclic hydroxyl moieties were transferred from the recently developed hexopyranoses whereas parameters for the ring O4 oxygen were from THF and the charge on the C1 atom was adjusted to achieve electrostatic neutrality. Initial analyses indicated the need for optimization of electrostatic parameters along with several dihedral angles, while the other bonded parameters, including the bond and valance angle terms and the Lennard-Jones parameters were found to be completely transferrable.

The general procedure adapted for parameter optimization of the furanoses closely followed that previously reported for the Drude hexapyranose model⁸⁰ to maintain compatibility of the parameters among different class of monosaccharides. Due to availability of crystallographic and condensed phase data for methyl-furanosides versus the furanoses alone the extent of the parametrization included the methyl-furanosides. Parametrization of methyl-furanosides involved transfer of all the optimized electrostatic, bonded and nonbonded parameters from aldopentofuranoses and only the parameters in the glycosidic bond associated with the –OMe functional group were subjected to further optimization.

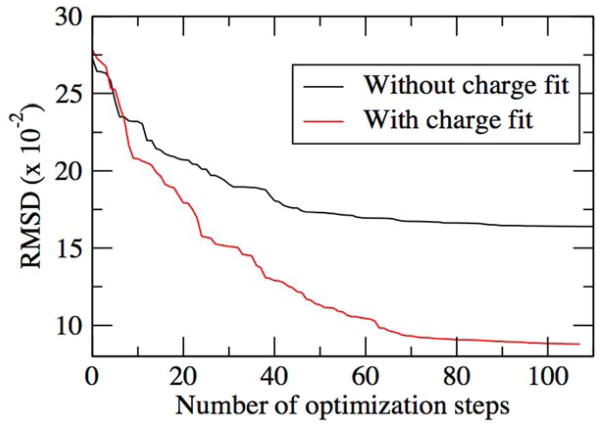
Directly transferred electrostatic parameters were initially used to calculate the dipole moments of 60 furanose conformers for comparison with QM RIMP2/cc-pVQZ//MP2/6-31G(d) dipole moments. Although the results were found to be good as compared to the CHARMM36 additive FF (Table 1), additional optimization was undertaken. The initial optimization included only the alphas and Thole scale factors. This lead to only a small improvement in the agreement with the QM data. Additional optimization included the partial atomic charges along with the alpha and Thole terms (Table S1) leading to significant improvement as shown in a plot of the root mean square difference (RMSD) between the MM and QM dipoles as a function of MCSA steps (Figure 4) for the Global Fit approach described below.

Table 1.

RMSDs calculated between MM and QM molecular dipole moments (Debye) over 60 different conformations of the aldopentofuranoses for different electrostatic models.

Compound	No of confs	RMSD
		Isomerfit	Anomerfit	Globalfit	Direct	Additive
arib	15	0.036	0.074	0.120	0.358	1.269
brib	15	0.023	0.057	0.089	0.308	0.832
aarb	15	0.015	0.031	0.083	0.195	0.743
barb	15	0.020	0.044	0.068	0.277	0.712

Figure 4.

Convergence of the RMSD between MM and QM total dipole moments for Globalfit MCSA approach with a) only the alpha and Thole terms optimized (Without charge fit) and with the b) alpha, Thole and charge terms optimized (With charge fit)..

Due to the omission of the hydroxyl on the C2 in the deoxyaldopentose compounds, which is adjacent to anomeric carbon, the optimization procedure involved a multistep process, as performed during optimization of the CHARMM additive FF for furanoses.³³ Different conformations of arabinofuranose and ribofuranose compounds were used as the training set for the electrostatic optimization. Next, several conformations of xylofuranose and lyxofuranose were chosen to validate the optimized electrostatic parameters. Once the validation was done in a satisfactory manner the parameters were transferred to model deoxyribofuranose. For deoxyribofuranose the electrostatic parameters for the -CH₂- at C2 were transferred from THF. The resulting model was then checked for accuracy based on QM dipole moments. The same strategy was followed to optimize bonded parameters with validation based on geometric target data.

Optimization of the electrostatic parameters in the aldopentoses was carried out using the MCSA technique. A total of 31 variables were subjected to the optimization. To assure that the values of the parameters did not vary significantly during the MCSA optimization predefined upper and lower boundaries were set for the different electrostatic terms. Table S1 of the supporting information shows the values of the predefined bounds for the electrostatic parameters for the different atom types. The MCSA runs were considered converged when the change in the RMSD between two MCSA steps was less than 0.001.

Fifteen different conformations of each arabinofuranose and ribofuranose, yielding a total of 60 conformations, were used to fit the molecular dipole moments as obtained from the MP2/cc-pVQZ//MP2-6-31G(d) model chemistry. Following the earlier study on hexapyranoses⁸⁰ the optimization strategy involves Isomerfit, Anomerfit and Globalfit procedures. The Isomerfit strategy involves fitting of dipole moments with individual MCSA runs for each furanose isomer, yielding 4 sets of electrostatic parameters. In the Anomerfit strategy the two anomers of each diastereomer were considered to be identical, yielding two sets of the electrostatic parameters. The Globalfit strategy involved a single MCSA run yielding a single set of partial atomic charge, alpha and Thole terms. RMS differences (RMSD) between MM and QM total dipole moments for each case are shown in Table 1.

All the fitting approaches showed significant improvements over the directly transferred electrostatic parameters (Table 1). As expected the Globalfit approach yields larger RMSDs than the Isomerfit and Anomerfit. To determine if the degradation of the quality of the fit with Globalfit was acceptable, allowing use of the fully transferable electrostatic parameters, additional validation was undertaken. This involved the ability of the three electrostatic models to reproduce QM interaction energies and distances of the model compounds with the individual water molecules^{80, 93} as compared to QM MP2/cc-pVQZ//MP2/6-31G(d) model chemistry with BSSE correction.

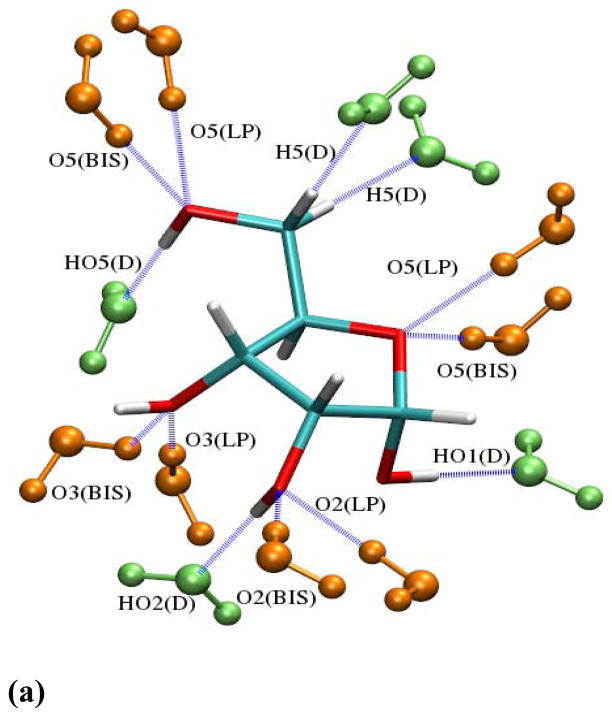
Figure 5 shows the interactions of representative conformations of α-D-ribofuranose (ARIB) and β-D-ribofuranose (BRIB) with water in different orientations. Both the in- and out-of-plane orientations of water, acting as both a hydrogen bond donor and acceptor with the hydroxyls, the methylene hydrogens and the ring ether oxygen were analyzed. The results obtained for ARIB-water and BRIB-water interactions using the different electrostatic models are summarized in Table 2, with individual minimum interaction energies and distances included in Table S2 – S5. Direct transfer of the parameters yielded improvements over the additive FF, which is expected given that scaled HF/6-31G* energies were targeted in the development of that model. Importantly, additional fitting targeting the dipole moments lead to improvements over the directly transferred parameters for the interactions with water. Of note is that the Isomerfit results are not better than the Anomerfit or Globalfit results, actually being in poorer agreement in the majority of cases with the Anomerfit or Globalfit results having a similar level of agreement. Such a result is not unexpected as the original nonbonded parameters, including the LJ terms, were based, in part, on interactions of small alcohols and THF with water, where the LJ terms were balanced with the electrostatic parameters. Thus, when performing optimization targeting dipole moments alone and allowing for the electrostatic parameters to adjust for all the isomers individually the balance between the electrostatic and LJ parameters is partially lost. The problem is limited due to the inherent restraints in the Anomerfit and Globalfit approaches. Therefore, the Globalfit model was selected for the final FF considering the transferability in which a single set of electrostatic parameters is used for all the aldopentofuranoses, the reasonable agreement with the QM dipole moments (Table 1) and the agreement with the interactions with water (Table 2).

Figure 5.

Interaction geometries of (a) α-D-ribofuranose-water and (b) β-D-ribofuranose–water. Both acceptor (LP/BIS) and donor (D) type interactions are shown. LP represents lone pair direction and BIS represents bisector angle based interactions with water oxygen. For clarification water molecules as acceptor type have been shown in green and those as donor type have been shown in orange.

Table 2.

Average and RMS differences with respect to QM data for ARIB-water and BRIB-water interaction energies (kcal/mol) with the Drude FF and the CHARMM additive FF.

Compound	Energy	Isomerfit	Anomerfit	Globalfit	Direct	Additive
arib	Avg difference	−0.105	−0.040	−0.157	−0.324	−0.483
	RMSD	1.152	0.768	0.789	1.210	1.040
	Avg abs difference	0.900	0.587	0.580	1.013	0.937
brib	Avg difference	−0.149	−0.060	−0.163	−0.243	−0.391
	RMSD	0.830	0.570	0.559	0.961	0.753
	Avg abs difference	0.725	0.515	0.546	0.803	0.587

Water interaction energies and distances obtained from QM, Globalfit and additive models are shown in supporting information Tables S2–S5.

An additional check of the quality of newly developed Globalfit model was the reproduction of QM gas phase molecular polarizability tensors. Shown in Table 3 are the QM and MM results for two conformers of α-arabinofuranose and β-arabinofuranose. As the Drude polarizabilities have been systemically scaled targeting dielectric constants of pure liquids, QM values scaled by 0.75 are included in the table. This scaling was 0.7 for the original alcohol model⁶⁹ and 0.71⁶⁴ for the SWM4-NDP model. In general, the Globalfit electrostatic model reproduces the magnitude and relative values of the scaled QM values in a satisfactory manner, indicating that fitting targeting the dipole moments did not negatively impact the molecular polarizabilities.

Table 3.

QM and Globalfit components of gas phase molecular polarizability tensors of α-arabinofuranose and β-arabinofuranose.

Compound	Component	QM	QM*0.75	Drude
AARB	XX	11.89	8.92	9.78
	YY	12.13	9.10	9.95
	ZZ	12.33	9.25	8.98
	Total	36.36	27.27	28.71
BARB	XX	12.50	9.38	9.52
	YY	13.11	9.83	11.07
	ZZ	11.18	8.38	8.15
	Total	36.79	27.59	28.75

Dihedral parameter optimization

Due to highly flexible nature of the furanoses most of the dihedrals that involve the ring, exocyclic and hydroxyl atoms were optimized. Dihedral parameters that were not included in the fit were those terminated with aliphatic hydrogen atoms. All the considered dihedrals were fitted simultaneously, with the fit targeting the same collection of conformations used for the development of the additive force field.³³ This included a total of 1096 conformations of the aldopentofuranoses, with conformations whose relative QM energy was 12 kcal/mol or greater above the global minimum discarded. Dihedral parameter optimization involves minimizing the targeted RMSD between QM and MM energies using an in-house least square fitting approach.⁹⁴ During fitting the phases of targeted dihedrals were fixed either at 0° or 180° with multiplicities 1, 2 and 3 considered. The use of 0° or 180° for the phase assures that the parameters are applicable for both diastereomers about the respective chiral centers. A detailed list of targeted dihedrals is given in Table S6 and S6b of the supporting information.

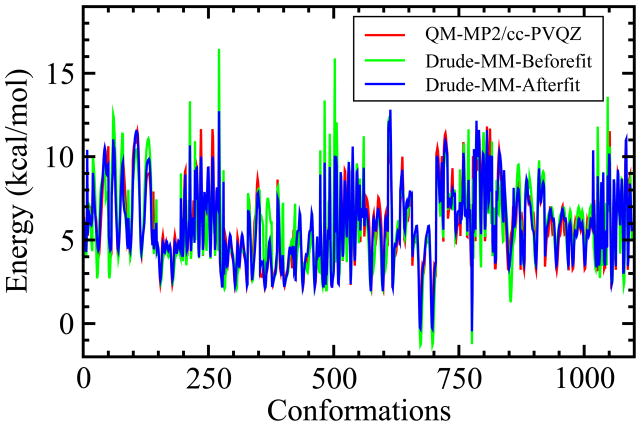
Presented in Figure 6 are the QM and MM relative conformational energies of all the 1096 conformations, with MM results from both before and after optimization shown. The RMSD calculated from the direct transfer model was 1.97 kcal/mol, which is improved over the RMSD of 2.18 kcal/mol obtained with the additive force field. When the Globalfit electrostatic parameters are used with the directly transferred dihedral parameters the RMSD becomes 1.31 kcal/mol, indicating the importance of the polarizable electrostatic model in improving the treatment of the conformational energies. Least square fitting of the dihedral parameters yields an RMSD value of 0.59 kcal/mol. These results clearly indicate that the optimization of dihedral parameters combined with the improved electrostatic model significantly improve the ability of the FF to reproduce QM conformational energies as compared to the additive C36 FF.

Figure 6.

Relative QM (red) and Drude MM energies before (green) and after (blue) dihedral fit of AARB, BARB, ARIB and BRIB conformations.

Xylofuranose and lyxofuranose

Transferability and validation of the final set of parameters optimized targeting arabinofuranose and ribofuranose were carried out by reproducing QM conformational energies and dipole moments for selected conformations of xylofuranose and lyxofuranose. Figure 7 shows the QM and MM dipole moments and relative conformational energies for the studied conformations. The results obtained from the Drude Globalfit model are in good agreement with the QM data and show an improvement over the additive FF. The additive model systematically overestimates the QM dipole moments consistent with the overestimation of the partial atomic changes as required to model the condensed phase environment in a fixed charge model.^{48, 69} The overall level of agreement based on average RMSDs of QM and MM dipole moments and conformational energies for the conformations of xylofuranose and lyxofuranose shown in Table 4 is similar to that for the directly targeted arabinofuranose and ribofuranose monosaccharides.

Figure 7.

Dipole moments (left panel) and conformational energies (right panel) of α-lyxofuranose (alyf), α-xylofuranose (axyf) and β-xylofuranose (bxyf) as obtained from QM calculation (red), Drude Globalfit model (blue), and additive model (green).

Table 4.

RMSDs between MM and QM molecular dipole moments and conformational energies for the selected conformations of α-lyxofuranose, α-xylofuranose, and β-xylofuranose compounds.

Compounds	RMSD
	Dipole moment (Debye)		Energy (Kcal/mol)
	Globalfit	Additive	Globalfit	Additive
alyf	0.132	0.425	0.747	1.293
axyf	0.099	0.485	1.166	1.573
bxyf	0.190	1.082	0.724	1.127

Parametrization of Deoxyribofuranose

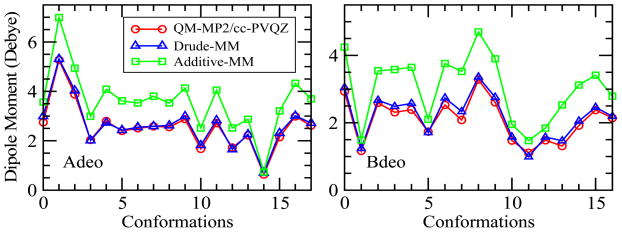
The electrostatic parameters as obtained from the Globalfit model and the dihedral parameters as obtained from the least square fitting approach were transferred to α- and β-deoxyribofuranoses. Only the electrostatic parameters involving the C2 atom and attached hydrogens in the deoxy-sugars are different from the aldopentofuranoses, with those parameters transferred directly from THF. The accuracy of the model was checked by comparing QM and Drude MM dipole moments (Figure 8), showing good agreement for the Drude model. RMSDs obtained for the 18 conformations of α-deoxyribofuranose from Drude Globalfit, direct transfer and additive models were 0.106, 0.381 and 0.914, respectively, whereas for the 17 different β-deoxyribofuranose conformations the values were 0.136, 0.263, and 0.928, respectively. The results obtained from Drude Globalfit model were found to be highly satisfactory as compared to the additive model.

Figure 8.

Dipole moments of α-deoxyribofuranose (Adeo), and β-deoxyribofuranse (Bdeo) as obtained from QM calculation (red), Drude Globalfit model (blue), and additive model (green).

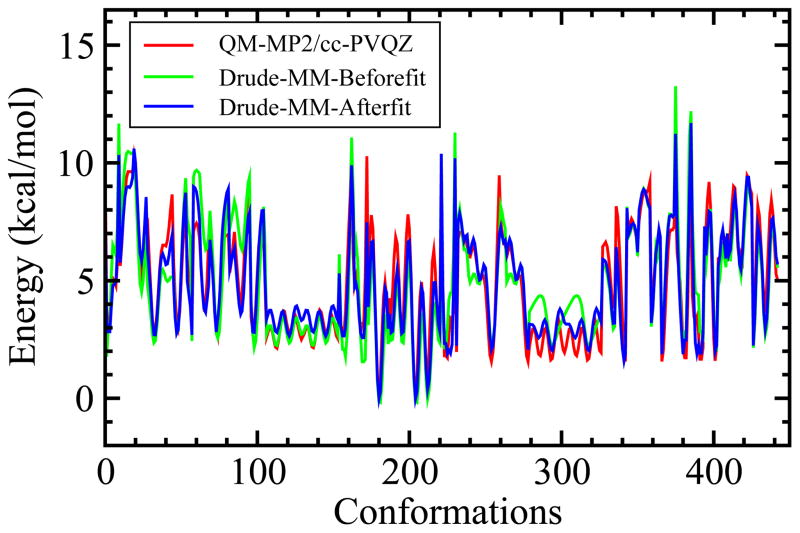
Due to the lack of a hydroxyl group on the C2 of deoxyribofuranoses the dihedrals involving the C2 atom required additional optimization. 450 different conformations of α- and β-deoxyribofuranoses with relative QM conformational energies less than 12 kcal/mol were targeted to fit the selected dihedrals. The QM and Drude MM potential energies before and after fitting are shown in Figure 9. Following dihedral fitting the RMSD was improved from 1.325 kcal/mol to 0.827 kcal/mol.

Figure 9.

Relative QM (red) and Drude MM energies before (green) and after (blue) dihedral fit of ADEO and BDEO conformations.

Parametrization of Methyl-aldopentofuranoses

Parametrization of methyl-aldopentofuranoses involved optimization of selected electrostatic and dihedral parameters associated with the –OCH₃ group attached to the C1 atom via a glycosidic linkage. Replacement of the –OH group by –OCH₃ was assumed to change the electrostatic properties of the anomeric carbon atom (C1) and hence optimization of the electrostatic parameters involving the C1, C4, and O4 atoms along with the non-hydrogen atoms of –OCH₃ group was performed. As depicted above, the optimization of electrostatic parameters (total of 15 for each methyl-furanoside) to fit the target MP2/cc-pVQZ//MP2/6-31G(d) dipole moments of 150 different conformations of α-methyl-arabinofuranoside, β-methyl-arabinofuranoside, and α-methyl-lyxofuranoside was done using the MCSA approach. Figure S1 (supporting information) shows the convergence behavior of the RMSD between MM and QM total dipole moments for the MCSA run. The calculated RMSD obtained after electrostatic fitting was 0.134 versus an RMSD of 0.307 before fitting. Figure S2 shows the results for the dihedral optimization for methyl-furanosides. Prior to dihedral optimization the RMSD was 2.12 kcal/mol improving to 1.22 kcal/mol.

Validation of optimized methyl-aldopentofuranose parameters was done by comparing the Drude minimum interaction energies and distances to QM results for α-methyl-arabinofuranose-water and β-methyl-arabinofuranose-water interacting pairs. The interacting pairs are shown in Figure S3 of the supporting information. A comparison of QM and Drude AARB-water and BARB-water interaction energies and distances are shown in Table S7 of the supporting information. Once again the Drude FF was found to reproduce QM energies and distances in a satisfactory manner, with RMSD values of 0.49 and 0.50 kcal/mol for α and β anomers of the methyl-D-arabinofuranosides, respectively.

Crystal Simulations

Crystal simulations were performed to test the accuracy of the optimized Drude parameters based on their ability to reproduce the crystal lattice parameters and intramolecular geometries. Due to the lack of availability of crystal data for pure furanoses the crystal simulations were performed for five different methyl-furanosides, namely methyl-α-arabinofuranoside (JUQSET), methyl-β-arabinofuranoside (QIBTIE), methyl-α-lyxofuranoside (JUQSOD), methyl-β-ribofuranoside (ZOWJAW) and methyl-α-xylofuranoside (JUQSUJ) as obtained from the CSD.⁹² All the simulations were carried out at the experimental temperatures with the number of molecules present in the experimental unit cell.

The crystal lattice parameters are shown in Table 5. For the Drude model the total average percent difference in the crystal volume shows the model to yield values slightly larger than the experimental values, though the values are in better agreement than with the additive FF. Similar trends were obtained with the Drude hexopyranose⁸⁰ and polyol⁸¹ model, where an improvement over the overestimation of the crystal parameters with the additive FF^{33, 48} was also observed. The average percent difference in a, b and c unit cell parameters are all approximately 0.6 % with the Drude model versus the variations obtained with the additive FF as a function of unit cell parameter. This was also observed in the hexopyranose and polyol studies and indicates that the overall balance of nonbond model in the Drude polarizable force field is an improvement over the additive FF.

Table 5.

Crystal lattice parameters and volumes as obtained from crystal simulations

compounds	CSD ID	Method	a (Å)	%diff	b (Å)	%diff	c (Å)	%diff	volume	%diff
methyl-α-arabinofuranoside	JUQSET	Expt	12.26		6.83		4.60		378.17
		Drude	12.31	0.41	6.91	0.43	4.66	0.42	383.04	1.29
		Adda	12.92	5.41	6.79	−0.62	4.60	−0.08	390.62	3.29
methyl-β-arabinofuranoside	QIBTIE	Expt	5.90		10.79		12.15		773.75
		Drude	5.88	−0.38	10.75	−0.37	12.11	−0.37	765.09	−1.12
		Adda	6.71	13.68	9.41	−12.78	12.42	2.23	783.66	1.28
methyl-α-lyxofuranoside	JUQSOD	Expt	10.34		15.50		4.63		741.18
		Drude	10.35	0.10	15.50	0.05	4.63	0.16	743.54	0.32
		Adda	10.49	1.45	15.83	2.10	4.59	−0.78	762.54	2.88
methyl-β-ribofuranoside	ZOWJAW	Expt	4.86		24.16		12.88		1511.84
		Drude	4.93	1.52	24.53	1.50	13.07	1.54	1582.16	4.65
		Adda	4.78	−1.59	25.82	6.88	12.99	0.88	1603.90	6.09
methyl-α-xylofuranoside	JUQSUJ	Expt	6.22		8.14		7.42		369.11
		Drude	6.32	1.48	8.27	1.53	7.54	1.56	386.25	4.64
		Adda	6.50	4.53	8.20	0.72	7.49	1.00	389.82	5.61
Average %difference		Drude	0.63		0.63		0.66		1.96
Average %difference		Adda	4.70		−0.74		0.65		3.83

^aref from Hatcher et.al³³ additive force field

The intramolecular geometries were calculated from the crystal simulations of the methyl-furanosides and were compared with the experimental crystal data. The differences in the calculated average bond, angle and dihedrals from the crystal simulations are shown in Table 6. The differences obtained for the internal parameters of all the compounds are shown in Table S8 of supporting information. It can be noted that on average the Drude bond lengths, angles and dihedral angles are not higher or lower than 0.03 Å, 2° and 4°, respectively of the experimental values. Hence, direct transfer of the bond, valence angle and a number of the dihedral angle parameters from the existing Drude force field was found to reproduce intramolecular geometries in a satisfactory manner. Further, as shown in Table 7, the average pseudorotation angles and amplitudes from crystal simulations, obtained using equations 1 and 2, show good agreement with the experimental data. The computed P values are within 10° of the experimental values. Accordingly, the Drude model satisfactorily reproduces the experimental intramolecular geometries.

Table 6.

Differences in average internal geometries of all the aldopentofuranoses as calculated from simulations of infinite crystals and experimental crystal data

Bonds	Average difference	Angles	Average difference	Dihedrals	Average difference
O4-C1	0.02	O4-C1-C2	−0.77	C4-O4-C1-C2	−1.53
C1-C2	0.00	C2-C1-O1	1.68	O4-C1-C2-C3	−0.61
C2-C3	0.00	C1-C2-C3	−0.08	C1-C2-C3-C4	2.34
C3-C4	0.00	C2-C3-C4	−0.61	C2-C3-C4-O4	−3.15
O1-CM	−0.01	O4-C4-C5	−1.38	C3-C4-O4-C1	2.93
C2-O2	0.03	C1-O1-CM	−1.82	C2-C1-O1-CM	4.19
C3-O3	0.03	C3-C2-O2	−2.05	C3-C2-O2-HO2	−1.74
C4-C5	0.01	C4-C3-O3	0.48	C4-C3-O3-HO3	−0.87
C5-O5	0.00	C4-C5-O5	0.30	O4-C4-C5-O5	2.00
C4-O4	−0.02	C3-C4-O4	−0.17	C4-C5-O5-HO5	−0.30
C1-O1	0.03	C4-O4-C1	0.05	C1-O4-C4-C5	−0.08
		O4-C1-O1	−0.53

Table 7.

Experimental and calculated average pseudorotation angles and amplitudes as obtained from crystal simulations.

Compound	P expt	P calc	Φexpt	Φcalc
Me-aarb	61	57	41	45
Me-barb	322	332	40	42
Me-alyf	28	31	44	45
Me-brib	350	343	38	37
Me-axyf	156	157	40	40

Density of furanose monosaccharide solutions

Further validation of the final optimized Drude model was performed by calculating solution densities of furanose monosaccharides at various concentrations. Aqueous phase simulations at ambient condition (T= 298K and P=1 atm)⁹⁵ and at varying concentrations show an excellent agreement between calculated and experimental solution densities (Table 8). The difference found for all the solutions are 0.4 % or less, which is an improvement of the maximum difference of 1.3 % obtained with the additive FF.³³ On average the difference in calculated solution densities using the Drude FF are within 0.26 % of experimental values. These results are consistent with the crystal simulations results clearly indicating the ability of the Drude model to reproduce condense phase properties in an excellent manner.

Table 8.

Experimental and calculated solution densities of furanose monosaccharides with varying concentrations at 298K temperature and 1 atm pressure

Compounds	Molality (mol/kg)	ρcxpt (gm/cc)	ρDrude (gm/cc)	ρAddl33(gm/cc)	% difference (Drude)	% difference (Addl33)
Arabinofuranose	0.2	1.008	1.011	1.021	0.35	1.29
	0.3	1.014	1.017	1.025	0.28	1.08
Lyxofuranose	0.2	1.008	1.012	1.021	0.39	1.29
	0.3	1.013	1.017	1.025	0.42	1.18
Ribofuranose	0.2	1.008	1.012	1.021	0.40	1.29
	0.3	1.013	1.017	1.025	0.41	1.18
Xylofuranose	0.2	1.013	1.012	1.021	−0.12	0.79
	0.3	1.017	1.017	1.025	−0.03	0.79
Average difference					0.26	1.11

Conformational flexibility of furanoses in aqueous solution: ring pucker and exocyclic group rotation

Aqueous phase MD simulations were performed on methyl-aldopentofuranosides to study their conformational flexibilities associated with the ring pucker dynamics. The puckering time evolution and distribution plots of P for all the methyl-furanosides studied in this work are shown in Figures S4 and S5 of the supporting information. Due to low energy barriers between the conformations of the furanose rings the time evolution plot of P shows rapid interconversion between the N and S conformation for all the furanoses. Notably, the pucker populations differ significantly for the different monosaccharides. Convergence of the simulations was verified by calculating the average pseudorotation angle and the N-S populations for the two halves of the trajectories, with the results obtained from the two halves found to be the same as those obtained from the full trajectory.

Average Φ_m values were computed for all the compounds along with separate P values for the N and S hemispheres for all the methyl-furanosides. Table 9 shows the average results from the aqueous phase simulations and from experiments calculated using the PSEUROT program and NMR analysis.^{18,34, 96–98} Deviations in the average P values for N and S conformers for the furanosides are present with respect to the experimental data. However, given the significant variations in the experimental estimates (see following paragraph) the Drude results are found to be satisfactory. For example with Me-arb, Me-rib and Me-xyf the β anomer is seen to sample more N than Σ in the experimental studies, a trend reproduced by the Drude model while the N sampling of Me-lyf is similar, which is also reproduced by the Drude model.

Table 9.

Population of N and S conformers of furanoses as obtained from the aqueous phase simulations. The Experimental results³⁴ as obtained from NMR and PSEUROT analysis are also included for comparison.

Compound	North state			South state			<Φm >
		Expt	Calc		Expt	Calc
Me-aarb	PN	44/70	72	PS	123/238	156	37
	%N	39/67	47	%S	61/33	53
Me-barb	PN	353/352	331	PS	162/187	230	38
	%N	86/87	63	%S	14/13	37
Me-arib	PN	119/37	55	PS	125/278	209	42
	%N	4/29	47	%S	96/71	53
Me-brib	PN	338/28	231	PS	85/219	220	40
	%N	86/73	70	%S	14/27	30
Me-alyf	PN	24/20	65	PS	145/219	136	41
	%N	71/65	55	%S	29/35	45
Me-blyf	PN	36/349/345	336	PS	139/305/95	239	39
	%N	60/77/74	56	%S	40/23/26	44
Me-axyf	PN	114/309/324	49	PS	122/188/124	137	43
	%N	11/39/8	48	%S	89/61/92	52
Me-bxyf	PN	348/27	154	PS	265/267	174	38
	%N	66/45	78	%S	34/55	22

The multiple sets of experimental values for some furanosides included in Table 9 is due to more than one conformer being able to reproduce the experimentally measured ³J_H,H values, as examined from 4 sets of PSEUROT runs with different initial P_N and P_S values.³⁴ In most cases the results obtained from the aqueous phase simulations are in good agreement with at least one of the experimental values. However, in many cases the computed P_N and P_S values are in poor agreement with the experimental data. This occurs due to the presence of very weakly populated puckering angles (Figure S5). While calculating the average P values for N and S conformers of the furanoses we have considered the full range of P values (ie. N is from 270 through 0 to 90°), which may be a poor approximation and hence can affect the average values of P_N and P_S. Similar poor agreement of P values for furanoses was found in the CHARMM additive FF³³ as well as in GLYCAM FF.^{41, 98} Notably, there are cases where the experimental values are in contradiction with the definition of pseudorotation wheel, such as P = 119° of methyl-α-lyxofuranoside being reported as a N conformer and P = 278^° and 305^° of methyl-α-ribofuranoside and methyl-β-lyxofuranoside, respectively, as S conformers. However, it should be noted that the P values obtained from the crystal simulations are in good agreement with the experimental crystal values as shown in Table 7, indicating the satisfactory nature of the final Drude model.

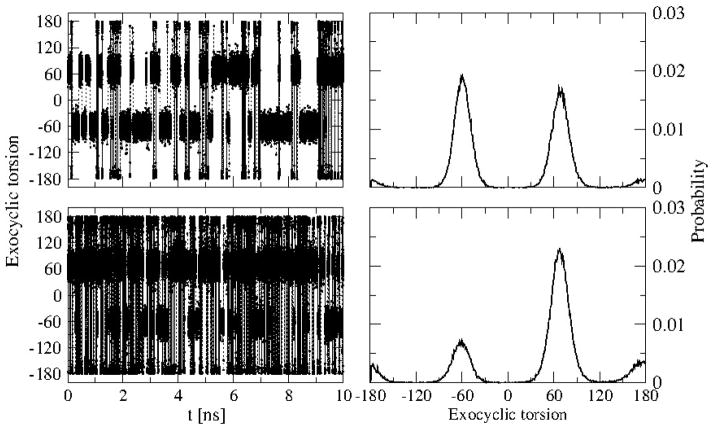
Sampling of the exocyclic torsion angle O4-C4-C5-O5 was computed from aqueous phase simulations of methyl-α- and β-arabinofuranosides. The time evolution plot of the exocyclic torsion and its distribution for the two sugars are shown in Figure 10. From the simulations the percentage of gg, gt and tg rotamer populations were calculated as shown in Table 10 along with the NMR experimental values.^18,97–98 Although deviations are present, the calculated rotamer populations are found to be in good agreement with the NMR data. This is true for both the α- and β anomers. Consistent with experimental data the highly populated rotamer as observed for methyl-α-arabinofuranoside is gg whereas for methyl-β-arabinofuranoside it is gt and the population follow the order gg>gt>tg for methyl-α-arabinofuranoside and is gt>gg>tg for methyl-β-arabinofuranoside. It is clear from the results that the calculated data can reproduce the trend of rotamer populations in a satisfactory manner.

Figure 10.

Time evolution (left panels) and probability of the exocyclic torsion (right panels) of methyl-α-arabinofuranoside (top) and methyl-β-arabinofuranoside (bottom).

Table 10.

Experimental^{18, 97–98} and computed population of exocyclic rotamer

Compound	Method	% gg	% gt	% tg
Me-aarb	Expt	48	38	14
	Calc	50	45	5
Me-barb	Expt	35	57	8
	Calc	21	67	12

Variability of furanose dipole moments in aqueous solution

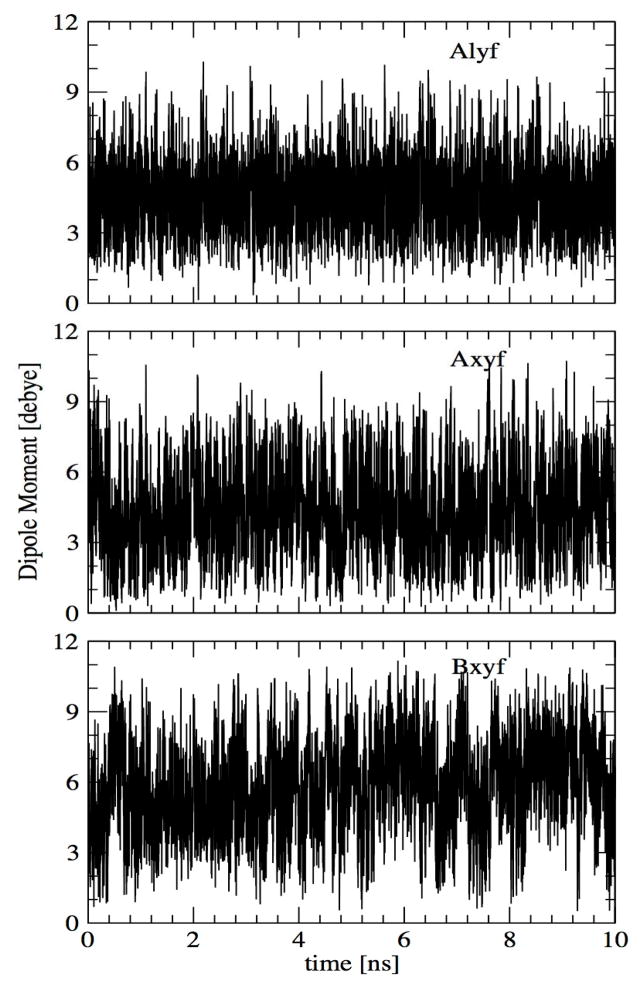
As the central strength of a polarizable force field is the ability of the dipole moments to vary as a function of environment we undertook analysis of the dipole moments of the xylofuranose and lyxofuranose monosaccharides from the MD simulations used to calculate the solution densities of the furanose monosaccharides. The time evolution plots of the dipole moments of these molecules in solution phase are shown in Figure 11. Those results may be compared with the gas phase dipole moments for different conformations of those sugars shown in Figure 7. As is evident, there is wide variability of the dipole moments in aqueous solution. Notably, the dipole moments in solution are much higher than in the gas phase, with the former sampling values of 9 or more, while with the latter the values were all less than 6. The average gas phase minimized dipole moments of alyf, axyf and bxyf are 2.16, 1.85, and 3.67 D for the studied conformations whereas the values in aqueous solution averaged over the MD simulations are 4.61 D, 4.43 D and 5.83 D.

Figure 11.

Time evolution of dipole moments of α-lyxofuranose (Alyf), α-xylofuranose (Axyf) and β-xylofuranose (Bxyf) as obtained from the aqueous solution simulations

To better understand the origin of the larger dipole moments in aqueous solution for the full monosaccharides the dipole moments of several hydroxyl groups present in alyf were analyzed. Figure 12 shows the gas phase dipole moments of the hydroxyl groups for the conformations of alyf included in Figure 7 along with their time evolution as obtained from the aqueous solution simulation. Large fluctuations in solution are observed with the values typically larger than the gas phase dipoles. The average gas phase dipole moments of CH₂OH and the two CHOH groups are 1.57 D, 1.50 D and 1.58 D whereas those in aqueous solution are 2.60 D, 2.06 D and 2.23 Thus, increases in the local dipoles of the hydroxyl groups in aqueous solution combine to yield larger increases in the dipole moments of the full furanose monosaccharides. It is anticipated that variability of the dipole moments in different environments will contribute to the physical properties of this class of molecules.

Figure 12.

Gas phase dipole moments for different conformations (left panel) and the time evolution (right panel) of aqueous solution dipole moments of the C5, C2 and C3 hydroxyl groups of α-lyxofuranose (Alyf). Dipole moments are calculation for the hydroxyl and the covalently bound CH₍₂₎ atoms thereby yielding a neutral charge group.

Conclusions

In this work an empirical all-atom polarizable force filed for aldopentofuranoses, deoxy-aldopentofuranose and methyl-aldopentofuranosides based on the classical Drude oscillator is presented. Initially, all the electrostatic, bonded and nonbonded parameters for the furanoses were transferred from the existing ether, alcohols and hexopyranose monosaccharide parameters. The parametrization then involved a multistep process. First, an electrostatic model was developed for the aldopentofuranoses and subsequently the bonded parameters were optimized. Once the model was found to reproduce target data in satisfactory manner further parametrizations were carried out for the deoxy-ribofuranose and methyl-aldopentofuranoside compounds.

Optimization of the partial atomic charges, atomic polarizabilities and Thole scale factors was performed using an MCSA approach based on three different strategies namely, Anomerfit, Isomerfit and Globalfit. The optimization targeted QM total dipole moments for a number of selected conformers of several aldopentofuranoses. Final selection of the electrostatic model involved consideration of the transferability of the model and the ability to reproduce QM furanose-water interactions. This criteria lead to selection of the Drude Globalfit model, which was shown to satisfactorily reproduce QM molecular polarizability tensors. Thus, the same electrostatic parameters are applied to all the furanoses, a goal that was also achieved with the polarizabile hexopyranose model⁸⁰, indicating the ability of a model that includes electronic polarizability to be transferrable across all diastereomers of a given class of monosaccharide, a goal that was not achieved with the additive CHARMM and GLYCAM carbohydrate FFs. In addition, the inclusion of polarizability in the model also allows for significant improvement over the additive force field in the reproduction of QM relative energies for a large number of furanose conformations.

Validation of the parameters included reproduction of additional QM conformational energies and dipole moments, experimentally obtained crystal geometries and unit cell parameters, aqueous phase densities and NMR data based on pseudorotation angle, puckering amplitude and exocylic rotamer populations. For most of these observables, the Drude force field was found to reproduce the experimental observables in a more satisfactory manner as compared to the CHARMM additive force field. Although the present as well as a previous studies^80–81 made by our group showed both the Drude and additive force fields to overestimate the crystal volume, the extent of overestimation is significantly reduced in the Drude model with the shifts in the individual unit cell parameters more balanced versus the additive FF. Further, aqueous phase density calculations using the Drude FF are in very good agreement with the experimental densities with an average difference of 0.26 % as compared to the average difference of 1.11% from the additive FF.³³ Pseudorotation angle populations and amplitudes of puckering from the aqueous phase simulations are in satisfactory agreement with the experimental data. It is noted that the experimental data as obtained from the combination of NMR coupling and PSEUROT program³⁴ has potential limitations with respect to assignment of the N and S conformers. The populations of the exocyclic rotamers, as computed using Drude force field, agrees well with the experimental data, reproducing the qualitative populations of the gg, gt and tg rotamers in a satisfactory manner. Thus, the reported Drude polarizable model for furanoses may be used to study their structural, dynamical and thermodynamical properties as well as be part of more complex polysaccharides and more heterogeneous systems in conjunction with the Drude polarizable parameters for hexapyranoses, polyols, lipids, DNA and proteins.^{69, 73–74, 76, 80}

The final parameters are reported in Table S9 of the supporting information. They may also be obtained from the MacKerell website at http://mackerell.umaryland.edu/ and via the Drude Prepper utility in the CHARMM-Gui.⁹⁹