Membrane potential and Ca²⁺ concentration dependence on pressure and vasoactive agents in arterial smooth muscle: A model

A mathematical model incorporating junctional and stretch-activated microdomains and 37 protein components describes the myogenic response in arterial smooth muscle cells.

Abstract

Arterial smooth muscle (SM) cells respond autonomously to changes in intravascular pressure, adjusting tension to maintain vessel diameter. The values of membrane potential (V_m) and sarcoplasmic Ca²⁺ concentration (Ca_in) within minutes of a change in pressure are the results of two opposing pathways, both of which use Ca²⁺ as a signal. This works because the two Ca²⁺-signaling pathways are confined to distinct microdomains in which the Ca²⁺ concentrations needed to activate key channels are transiently higher than Ca_in. A mathematical model of an isolated arterial SM cell is presented that incorporates the two types of microdomains. The first type consists of junctions between cisternae of the peripheral sarcoplasmic reticulum (SR), containing ryanodine receptors (RyRs), and the sarcolemma, containing voltage- and Ca²⁺-activated K⁺ (BK) channels. These junctional microdomains promote hyperpolarization, reduced Ca_in, and relaxation. The second type is postulated to form around stretch-activated nonspecific cation channels and neighboring Ca²⁺-activated Cl⁻ channels, and promotes the opposite (depolarization, increased Ca_in, and contraction). The model includes three additional compartments: the sarcoplasm, the central SR lumen, and the peripheral SR lumen. It incorporates 37 protein components. In addition to pressure, the model accommodates inputs of α- and β-adrenergic agonists, ATP, 11,12-epoxyeicosatrienoic acid, and nitric oxide (NO). The parameters of the equations were adjusted to obtain a close fit to reported V_m and Ca_in as functions of pressure, which have been determined in cerebral arteries. The simulations were insensitive to ±10% changes in most of the parameters. The model also simulated the effects of inhibiting RyR, BK, or voltage-activated Ca²⁺ channels on V_m and Ca_in. Deletion of BK β1 subunits is known to increase arterial–SM tension. In the model, deletion of β1 raised Ca_in at all pressures, and these increases were reversed by NO.

INTRODUCTION

Arteries are lined by endothelial cells and are wrapped by one or more layers of smooth muscle (SM) cells. There are electrical coupling and chemical signaling between SM cells and between SM cells and endothelial cells, and SM cells receive numerous neurotransmitter, endocrine, and paracrine signals that promote either contraction or relaxation. Independently of these signals, arterial SM cells respond autonomously to changes in sarcolemmal stretch caused by changes in intravascular pressure (McCarron et al., 1989). This phenomenon is called “myogenic reactivity.” It has an early phase called the “myogenic response” and a sustained phase called “myogenic tone.” The overall effect is to control luminal diameter in the face of changing luminal pressure. It is a vital background activity on top of which the many other stimuli have their effects.

The myogenic response is regulated by opposing circuits: one promoting an increase in sarcoplasmic Ca²⁺ concentration (Ca_in) and thereby an increase in tension and one promoting the opposite. Both circuits use Ca²⁺ (Ca) as a signal (Hill-Eubanks et al., 2011). The dual roles of Ca as a signal both for contraction and relaxation depend on the physical separation of opposing pathways afforded both by SM cellular architecture (Moore et al., 2004; van Breemen et al., 2013) and the widely different Ca sensitivities of the circuit-specific components. In the SM sarcoplasm, Ca_in varies between ∼100 and ∼400 nM, over which range myosin light chain kinase activity goes from low to half-maximal (Stull et al., 1998), and tension from low to maximal (Hill-Eubanks et al., 2011). The stretch-induced rise in Ca_in depends on the activity of voltage-dependent Ca (CaV) channels, principally those containing CaV1.2 (Moosmang et al., 2003; Navedo et al., 2007).

The activation of CaV channels is opposed by the hyperpolarizing activity of large-conductance, voltage- and Ca²⁺-activated K⁺ (BK) channels. In the range of membrane potential (V_m) in SM cells, half-maximal activity of BK channels requires tens of micromolar Ca (Jaggar et al., 2000), which is obtained in narrow junctions between the peripheral SR and the sarcolemma (Moore et al., 2004; van Breemen et al., 2013). In these junctions, clusters of ryanodine receptors (RyRs) in the peripheral SR membrane are apposed to clusters of BK channels in the sarcolemma (Lifshitz et al., 2011). RyR releases Ca into the junctional gap, transiently raising the Ca concentration 10–100 times higher than that in the sarcoplasm (Jaggar et al., 2000), recruiting additional RyR activity and activating the apposed BK channels (Nelson et al., 1995). The junction is a microdomain, in which signaling is directed by proximity and the signal intensity is tailored to the sensitivities of the target components (Neher, 1998; Berridge et al., 2003; Rizzuto and Pozzan, 2006; Neves and Iyengar, 2009; Santana and Navedo, 2009; van Breemen et al., 2013).

The initiation of the myogenic response requires its own microdomain, albeit one that does not, at least to date, have a defined subcellular structure. Stretch-activated sarcolemmal cation–conducting channels have not been definitively identified. In the current model, they are taken to be transient receptor potential (TRP) channels (Earley et al., 2004; Sharif-Naeini et al., 2009; Earley and Brayden, 2010). These deliver Ca to neighboring Ca-activated Cl (ClA) channels formed by TMEM16A, of which the half-maximal activation occurs at micromolar Ca (Bulley et al., 2012; Jin et al., 2014). The ClA channel current depolarizes the SM cell, activating CaV channels.

I present a model of the short-term, pressure-induced responses of an isolated arterial SM cell. In small arteries, removal of the endothelium did not affect either pressure-induced responses or the block of key components (Knot and Nelson, 1998). The model SM cell contains five interconnected compartments for Ca: the sarcoplasm, the central SR, the peripheral SR, the combined junctional microdomains, and the combined stretch-transducing microdomains (Fig. 1). The model includes 37 protein components located within the compartments or embedded in their bounding membranes. The experimental evidence for the assigned roles and locations of the components is stronger for some than for others. The current model builds on previous models, none of which, however, included the junctional and the stretch-transducing microdomains or dealt with the myogenic response (Bennett et al., 2005; Yang et al., 2005; Kapela et al., 2008). The current model has a large number of parameters (number of molecules of each component, rate constants, dissociation constants, permeabilities, etc.), of which only some were constrained by experimental results. Most of the unconstrained “local” parameters were adjusted to give plausible properties to the individual components. The model was closely fit to V_m and Ca_in as functions of intravascular pressure, determined in cerebral arteries by Knot and Nelson (1998). The fit was achieved mainly by adjusting the numbers of molecules of each of the components, considered “global” parameters. There were not enough data to determine uniquely even the subset of parameters adjusted to obtain this fit, and given the complexity of the mechanism, a unique set of fitting parameters might not be obtainable (e.g., Hines et al., 2014). Nevertheless, the model simulated experimental data beyond those used to find the set of close-fit parameters, such as the effects of the block of key components on the relationships of V_m and Ca_in to pressure (Knot and Nelson, 1998; Knot et al., 1998) and the effects of the knockout of the BK β1 subunit (Brenner et al., 2000; Dong et al., 2008; Sachse et al., 2014). It also predicted the effects of selected vasoactive agents on the responses to pressure of an arterial SM cell after knockout of BK β1. In addition, the fit with plausible parameters of the model to experimental data demonstrated the feasibility of its speculative components as, for example, stretch-transducing microdomains.

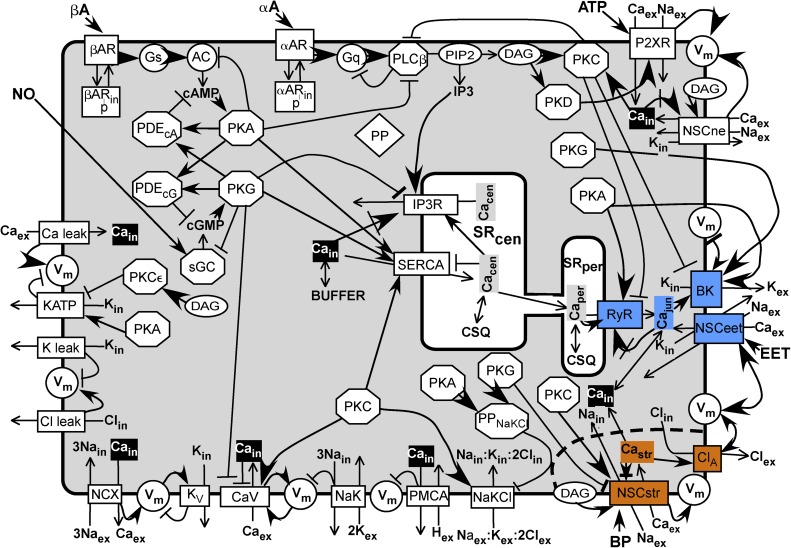
Figure 1.

Scheme of model. A SM cell sarcolemma contains channels, receptors, and transporters shown as rectangles spanning the membrane. Enzymes are represented as circles or octagons. Membrane-bound substrate PIP2 and effector DAG are shown as ovals. A common Ca buffer (BUFFER) is uniformly distributed throughout the cell except in the central SR (SR_cen) and the peripheral SR (SR_per), in which the Ca buffer is uniformly CSQ. Inorganic ions are shown without their charges and subscripted to indicate their compartment. Subscript “ex” refers to the extracellular milieu, “in” refers to the sarcoplasm, “jun” refers to the junction between the SRper and the sarcolemma, “str” refers to the postulated Ca microdomain around the stretch-activated channel (NSCstr), “cen” refers to the central SR, and “per” refers to the peripheral SR. (The longer subscripts NSCstr, SRper, and SRcen are used in the text and in the program.) The components associated with the junction are highlighted in blue, and those associated with the stretch microdomain are highlighted in orange. Ca_in, considered uniformly distributed in the sarcoplasm except for the microdomains, is highlighted in black. Other soluble components and effectors are shown in bold lettering. Most components are shown once. The kinases are repeated to be close to their targets, and the inorganic ions are repeated to be close to their sources and sinks. All abbreviations are defined in Materials and methods. A line ending in a closed arrowhead indicates activation; a line ending in a bar indicates inhibition. A closed arrow head pointing at an encircled V_m indicates depolarization, and a barred line indicates hyperpolarization. A line ending in a closed arrow crossed by a bar indicates activation followed by inhibition. A line ending in an open arrowhead indicates a flux between compartments or an enzyme reaction.

MATERIALS AND METHODS

Physical model.

The model of an arterial SM cell (Fig. 1) includes compartments and components relevant to the control of V_m and Ca_in by intravascular pressure. It also includes the targets for a few exemplary endocrine and paracrine inputs to SM. The compartments are the sarcoplasm (subscript “in”), the central SR (SR_cen), the peripheral SR (SR_per), the junctional microdomain (subscript “jun”), and the postulated stretch-transducing microdomain (subscript “str”). There are hundreds of junctional microdomains per SM cell (Moore et al., 2004) between the sarcolemma and apposing peripheral SR cisternae. I assume that there are also a similar number of stretch-transducing microdomains. In my initial estimates of the rate constants for the relaxation by diffusion of concentration differences between these microdomains and the domains to which they are connected, their approximate dimensions were taken into account. Otherwise, they were treated as single composite compartments with uniform concentrations and with volumes that are the sums of the individual microdomains.

Inorganic ions and second messengers.

The key ion is Ca. Its concentrations in the different domains are Ca_in, Ca_jun, Ca_SRcen, Ca_SRper, and Ca_NSCstr. The microdomains are relatively small volumes into which Ca influxes are transiently greater than Ca effluxes (Sobie et al., 2002). Both the stretch microdomains and the junctional microdomains have paths to the cytoplasm, and Ca in these domains equilibrates by diffusion with Ca in the sarcoplasm (see supplementary equations Seqs. D1 and D3). Similarly, Ca in the SR_cen equilibrates with Ca in the SR_per by diffusion (Seq. D2). The cytoplasmic concentrations of Na, K, and Cl, designated “Na_in,” “K_in,” and “Cl_in,” are also taken to be the concentrations in the other intracellular domains. All of the intracellular ion concentrations are functions of time (Seqs. J31 and J36–J41). The extracellular ion concentrations, Ca_ex, Na_ex, K_ex, and Cl_ex, are fixed. The diffusible second messengers, cAMP, cGMP, and IP3, are distributed uniformly in the cytoplasm and in the stretch and junctional microdomains. Diacylglycerol (DAG), no doubt almost completely confined to lipid membranes, for simplicity is also treated as if it were soluble and uniformly distributed in all domains. The concentrations of the second messengers vary with time (Seqs. J2, J10, J21, and J29).

Protein components

αAR (α1-adrenergic receptor).

αAR binds α-adrenergic agonist reversibly, activates Gα_qβγ, and is phosphorylated, internalized, and recycled (Schöfl et al., 1993; Bennett et al., 2005). These processes are represented as simplified reactions (see supplementary reaction schemes), the time courses of which are determined by Seqs. J11–J15 and J25.

AC (adenylate cyclase).

AC6 is the major subtype involved in β-adrenergic vasodilator signaling in arterial SM cells (Nelson et al., 2011). AC is activated by Gα_{s_GTP} and converts ATP to cAMP (Dessauer and Gilman, 1997) (see supplementary reaction schemes), as governed by Seqs. J9, J10, and J46–J49. In the model, PKA inactivates AC, representing feedback inhibition (Vandamme et al., 2012). The time courses of the phosphorylated and dephosphorylated states are determined by Seqs. J8 and J49.

βAR (β-adrenergic receptor).

β1AR is the predominant subtype in small resistance arteries (Garland et al., 2011). The reaction scheme (see supplementary reaction schemes) mirrors that for αAR, except that βAR activates Gα_sβγ. The time courses are determined by Seqs. J42–J45.

BK channel.

BK channel consists of four pore-forming α subunits and four modulatory β1 subunits (Butler et al., 1993; Knaus et al., 1994; Wang et al., 2002). The steady-state dependence of P_BK on V_m (“v” in steady-state equations) and Ca_in (“c” in steady-state equations) (Seqs. E1–E3) is based on the model of Horrigan et al. (1999) as modified for the complex with β1 (Bao and Cox, 2005). The complex enhancement of BK channel activity by PKA and PKG and its suppression by PKC (Zhou et al., 2008, 2010) are represented simply by changes in L_BK (Seqs. E6, E9, and E12). In the model, BK channel phosphorylation by one kinase blocks phosphorylation by another. The time courses of the phosphorylated states are governed by Seqs. J22–J24 and J27. The potentiation of BK channels by PKG and PKA via enhanced trafficking of β1 to the sarcolemma (Leo et al., 2014) is not included: the BK complex is assumed to contain a full complement of four β1 subunits.

BUFFER.

BUFFER stands in for all protein and nonprotein Ca buffers in the sarcoplasm, junctions, and the stretch-transducing microdomains, and is assumed to be uniformly distributed.

CaV channel (voltage-activated Ca channel containing the CaV1.2 α subunit together with additional subunits).

CaV1.2-containing CaV channel plays a dominant role in SM control of Ca and of tension (Moosmang et al., 2003). Steady-state P_open for CaV channel, called P_CaV, increases with increasing V_m (Rubart et al., 1996) and decreases with increasing Ca_in (Zühlke et al., 1999) (Seqs. E17–E19). Potentiation of CaV channel activity by PKC phosphorylation (Navedo et al., 2006) is modeled as a negative shift in the midpoint of the dependence of P_CaV on V_m, from V_CaV for the dephosphorylated channel to V_{CaV_PKC} (Seqs. E22 and E23). Suppression of CaV channel activity by PKG phosphorylation (Yang et al., 2007) is modeled as a positive shift from V_CaV to V_{CaV_PKG} (Seqs. E26 and E27). The time courses of the phosphorylated states are governed by Seqs. J57–J59. The steady-state Ca flux and current are given by Seqs. E20 and E21, E24 and E25, and E28–E30.

ClA channel (TMEM16A).

ClA channel contributes to the myogenic response in resistance-size cerebral arteries (Bulley et al., 2012). Furthermore, ClA channel is activated by locally elevated Ca_in conducted by nearby nonspecific cation channels (Bulley et al., 2012), which are designated here as “NSCstr channels” and share the stretch-transducing microdomain with ClA channel in the model (Fig. 1). The EC50 for Ca decreases with depolarization, and the channel is inhibited by high Ca_in (Yang et al., 2008). These characteristics are represented by the steady-state equations for P_ClA (Seqs. E31–33). The steady-state Cl flux and current are given by Seqs. E34–E36.

CSQ (calsequestrin).

CSQ stands in for all Ca buffers in the central and peripheral SR.

G_q (Gα_qβγ).

G_q is primed by αAR to exchange GTP for GDP. Gα_{q_GTP} activates PLC and slowly hydrolyzes bound GTP, a reaction accelerated by PLC (Waldo et al., 2010) (supplementary reaction schemes). Time courses of G_q forms are determined by Seqs. J14, J15, J17–J21, J25, J26, and J28.

G_s (Gα_sβγ).

G_s is primed by βAR to exchange GTP for GDP. Gα_{s_GTP} activates AC and slowly hydrolyzes bound GTP (supplementary reaction schemes), as governed by Seqs. J9, J42, and J45–J49.

IP3R (IP3 receptor, Ca release channel).

These tetrameric Ca release channels are located principally in the SR_cen membrane (Fig. 1) (Narayanan et al., 2012). IP3R contains stimulatory sarcoplasmic Ca sites, inhibitory sarcoplasmic Ca sites (Seq. F5), and stimulatory luminal Ca sites (Seq. F6) (Bezprozvanny et al., 1991). Binding of IP3 increases the affinity of the stimulatory sarcoplasmic Ca sites (Seqs. F1 and F3) and may also decrease the Ca affinity of the inhibitory sites (Taylor and Prole, 2012), although the latter effect is neglected here. ATP is a coregulator of the Ca affinity of the stimulatory sites (Mak et al., 2001), but because sarcoplasmic ATP concentration is assumed here to be constant, its effect on IP3R is implicit. PKG phosphorylation is modeled as suppressing IP3R activity by lowering its affinity for IP3 (Seqs. F2 and F4) (Desch et al., 2010). The time courses of the phosphorylated states are governed by Seqs. J50 and J51.The steady-state Ca flux and current are given by Seqs. F9–F12.

KATP (Kir6/SUR).

KATP channels in resistance artery SM are activated by PKA, causing hyperpolarization and vasodilation, and inhibited by PKCε, causing depolarization and vasoconstriction (Quayle et al., 1997; Aziz et al., 2012). Sarcoplasmic ATP, the concentration of which is assumed to be constant, acts as a low-affinity inhibitor. In the model, the open probability, P_{KATP_PKA}, of PKA-phosphorylated KATP is greater than P_KATP of dephosphorylated KATP; P_open of PKCε-phosphorylated KATP is assumed to be zero. Furthermore, phosphorylation by PKA and phosphorylation by PKCε are assumed to be mutually exclusive. The time courses of the phosphorylated states are governed by Seq. J73-J75. The steady-state K flux and current are given by Seq. E37-E42.

K_V (voltage-dependent K) channels.

One type of voltage-dependent K channel, with the properties of Kv1.5, is incorporated in the model (McGahon et al., 2007; Kapela et al., 2008; Hald et al., 2012). The steady-state K flux and current are given by Seqs. E44 and E45.

Leak channels Ca_leak, Cl_leak, and K_leak.

These are postulated conductors of background Ca, K, and Cl currents. The model has equations for a Na leak (Seqs. E50 and E51), but this leak was set to zero in all simulations presented here. The steady-state fluxes and currents are given by Seqs. E46–E54.

NaK (Na, K-ATPase).

The relative driving force for transport is taken as the electrochemical free energy change for the transport of 3 mol of Na outward plus 2 mol of K inward plus the free energy change caused by the hydrolysis of 1 mol of ATP (Δµ_ATP), all normalized by Δµ_ATP (Seq. G1). The net current depends on Hill functions of Na_in and K_ex (Kapela et al., 2008) multiplied by the relative driving force and by the maximum NaK current per cell (Seq. G2).

NaKCl (Na-K-Cl cotransporter NKCC1).

NaKCl is essential for the maintenance of the relatively high Cl_in in SM cells (Chipperfield and Harper, 2000). It is modeled as containing four ion-binding sites: one for Na, one for K, and two for Cl (supplementary reaction schemes). There are two accessibility states: all sites facing outward and all sites facing inward. Isomerization between these states occurs only when all sites are empty or when all sites are occupied. These isomerizations are governed by rate constants. Ion binding to the sites is ordered in single file (first on, first off) (Lytle et al., 1998) and is governed by three equilibrium-binding constants. These are unchanged by changes in site accessibility. The steady-state net inward flux of the fully occupied transporter is given by Seq. G7 (derivation not shown). This model is based on that of Benjamin and Johnson (1997) but with fewer parameters. Because the binding constants are the same in the two conformations, the isomerization rate constants are constrained by microscopic reversibility, as shown in Seq. G3. NaKCl transport is potentiated by PKC (Chipperfield and Harper, 2000), and in the model the rate constants for the isomerization of the occupied, phosphorylated NaKCl are multiplied by an enhancement factor (Seq. G8). The transport is suppressed by both PKA and PKG (Chipperfield and Harper, 2000), and in the model these kinases activate a hypothetical protein phosphatase specific for PKC-phosphorylated NaKCl. (This is a simplifying logical device permitting just one NaKCl phosphorylation site.) The time courses of phosphorylation and dephosphorylation are governed by Seqs. J66 and J67. The net inward fluxes of Cl, Na, and K are given by Seqs. G10–G13. Notwithstanding that the sum of the Cl, Na, and K currents via NaKCl is zero, the Cl flux is also expressed as current (Seq. G13) for convenient comparison with other currents.

NCX (Na–Ca exchanger).

In one of three possible functional modes, NCX exchanges three Na for one Ca (Kang and Hilgemann, 2004). In a relatively simple model of this major mode (supplementary reaction schemes), NCX is activated by Ca_in binding cooperatively to regulatory sites (Seq. G15) (Reeves and Condrescu, 2008). Furthermore, NCX has one transport site for Ca and three transport sites for Na. The transport Ca site and the Na sites are simultaneously accessible only on opposite sides of the membrane. Association and dissociation are ordered: the three Na associate before the Ca and dissociate after the Ca. Binding is always at equilibrium. Only NCX with empty transport sites or with fully occupied transport sites can switch the accessibilities of the transport sites. In the model, unoccupied NCX has two net negative charges in its Ca transport site and three net negative charges in its three Na transport sites. When these unoccupied sites switch their accessibilities to opposite sides of the membrane, the equivalent of one negative charge crosses the membrane, and the free energy changes by ±FV_m, depending on the direction of transport. No net charge is transported when the fully loaded sites switch their accessibilities. It is assumed that the effect of V_m is on the rate constants for switching accessibilities and that the transition state is halfway through the potential drop; thus, the rate constant for the isomerization for Na sites–out and Ca site–in to Na sites–in and Ca site–out, α′_{NCX_0}, contains the factor exp[F*V_m/(2RT)], and the rate constant for the opposite isomerization, β′_{NCX_0}, contains the factor exp[−F*V_m/(2RT)] (supplementary reaction schemes; Seq. G16). Microscopic reversibility applies to the isomerization rate constants at V_m = 0 (Seq. G14). In the steady state, the total fluxes of Na sites, both empty and occupied, in the two directions must be equal. This and the equilibrium-binding equations yield the steady-state transport rate of three Na outward and one Ca inward minus three Na inward and one Ca outward (Seq. G19) and the net current (Seq. G20).

NSCeet (nonspecific cation channels activated by 11,12-epoxyeicosatrienoic acid [EET], an endothelium-derived hyperpolarizing factor).

NSCeet includes TRPV4, which acts as an EET receptor in a signaling microdomain with BK channel and RyR (Earley et al., 2005, 2009). In the model, NSCeet is located in the junctional microdomains. EET binding activates NSCeet (Seq. E56). When activated, it increases Ca_jun, activating BK channel and RyR. TRPV4 is also activated by depolarization in the absence of ligand, but nP_o is low at V_m of less than −40 mV (Loukin et al., 2010). One way to simulate both the V dependence of TRPV4 in the absence of EET and its significant activation by EET in the physiologically relevant range of V_m of less than −40 mV is to allow EET binding to shift the V₅₀ to the left (Seq. E55). The steady-state Na, K, and Ca fluxes and currents are given by Seqs. E57–E63.

NSCne (receptor-activated nonspecific cation) channels.

In mesenteric artery SM, NSCne channel is close to α1-adrenergic receptors and activated by phenylephrine and by DAG, but not by PKC (Hill et al., 2006). NSCne channel is composed of TRPC6 and possibly TRPC3 or TRPC1 (Saleh et al., 2006). NSCne channel open probability is modeled as activated by DAG and both activated and inhibited by Ca_in (Seq. E64). The steady-state Na, K, and Ca fluxes and currents are given by Seqs. E65–E71.

NSCstr (stretch-activated nonspecific cation) channels.

These channels share the stretch-transducing microdomains with ClA channels (see above). Several types of TRP channels, including TRPM4, are candidates for roles in the myogenic response to intramural pressure (Sharif-Naeini et al., 2009; Earley and Brayden, 2010), and the NSCstr channels might be hetero-oligomeric complexes of TRP types (Earley et al., 2004). Because TRPM4 alone does not conduct Ca, it is unlikely to be the sole component of NSCstr channels. Piezo1 and Piezo2 are unlikely candidates for stretch-activated channels in SM: Piezo 1, half-maximally activated at 28 mm Hg and maximally activated at 60 mm Hg, is too sensitive, and Piezo 2 desensitizes too quickly (Coste et al., 2010). NSCstr channels are modeled as activated by stretch and DAG (Seq. E72), and both are activated (Seqs. E73–E75) and inhibited (Seq. E76) by Ca_NSCstr. P_open for NSCstr, called “P_NSCstr,” is a product of these factors (Seqs. E77–E79). Potentiation by PKC (Earley et al., 2007) is modeled as a decreased EC50 (K.NSCstr_PKC_Ca_act) for activation by Ca (Seq. E74), and suppression by PKG (Takahashi et al., 2008) is modeled as an increased EC50 (K.NSCstr_PKG_Ca_act) for Ca (Seq. E75). The time courses of the phosphorylated states are determined by Seqs. J70–J72. The steady-state Na, K, and Ca fluxes and currents are given by Seqs. E80–E105.

PDE_cA and PDE_cG (generic phosphodiesterases specific for cAMP and cGMP, respectively).

These are modeled as activated by binding of their cognate substrate at an allosteric site, as described by equilibrium Hill functions (Seqs. H1–H4) (Francis et al., 2011). They can be potentiated by both PKA and PKG (Vandamme et al., 2012). In the model, they each can be phosphorylated at a single site by either PKA or PKG (Fig. 1), and this phosphorylation increases the affinities of their allosteric sites. The time courses of phosphorylation are determined by Seqs. J62–J65. The cAMP and cGMP hydrolysis reactions are modeled as second order (Seqs. J2 and J10), i.e., at low extents of saturation of the catalytic sites, as opposed to the allosteric sites.

PKA.

The allosteric activation of PKA by cAMP is modeled as a Hill function with a Hill coefficient >1 (Herberg et al., 1994; Boettcher et al., 2011) (Seq. H5). In the model, all kinases are assumed to be in one-to-one complexes with their targets (Santana and Navedo, 2009; Kholodenko et al., 2010; Gold et al., 2011; Schlossmann and Desch, 2011), with reaction rate constants specific for these targets.

PKC.

This is a generic, conventional PKC requiring both DAG and Ca for activity (Nishizuka, 1995). The relative activity is modeled as a product of two Hill functions (Seq. H6).

PKCε.

PKCε is a DAG-dependent, Ca-independent subtype, which targets KATP (Aziz et al., 2012). Its relative activity is given by Seq. H7.

PKD.

PKD is another DAG-dependent, Ca-independent subtype, which targets P2XR (Ase et al., 2005). Its relative activity is given by Seq. H8.

PKG.

PKG is activated by cGMP, as given by Seq. H9.

PLC (PLCβ).

PLC is activated by G_{αq_GTP} and hydrolyzes PIP2 to DAG and IP3. In the model, PLC has low basal activity. PLC acts as a GAP and hastens the hydrolysis of GTP by G_{αq_GTP} (Waldo et al., 2010). PLC activity is suppressed by both PKA and PKC (Yue et al., 2000; Huang et al., 2007), which is simplified in the model as direct phosphorylation of PLC resulting in the lowering of its affinity for G_{αq_GTP}. These reactions are shown in supplementary reaction schemes (α-Adrenergic signaling), and the time courses are governed by Seqs. J16–J21.

PMCA (sarcolemmal Ca-ATPase).

PMCA exchanges one Ca for one or more protons with the hydrolysis of one ATP (Brini and Carafoli, 2011). In the model, it is assumed that Ca/H is 1:1, so that the 1 net charge is transferred per cycle (Seq. G21). PMCA is disinhibited by Ca-calmodulin at K_d < 1 µM for Ca. This is simplified in the model as a dependence of activity on a Hill function in Ca (Seq. G22).

PP (generic protein phosphatase).

PP is modeled to be in a complex with each component that is a target of a kinase and to be constitutively active.

PP_NaKCl.

This is a hypothetical protein phosphatase specific for NaKCl. PP_NaKCl is modeled as activated by PKA and PKC. This is a simple mechanism for the suppression of NaKCl activity by these kinases (Chipperfield and Harper, 2000). The time courses of PP_NaKCl and of PP_NaKCl_P are determined by Seqs. J68 and J69.

P2XR (P2X1 receptor).

This receptor is activated by ATP coreleased with norepinephrine in pulses from proximal sympathetic nerve varicosities (Nausch et al., 2012) (see supplementary reaction schemes). The rate constants of the upper cycle are constrained by microscopic reversibility. Desensitization is from the open state (Kaczmarek-Hájek et al., 2012), and PKD potentiation is modeled as increasing the rate of recovery from desensitization (Ase et al., 2005). The time courses of all forms are governed by Seqs. J76–J82. The steady-state Na, K, and Ca fluxes and currents are given by Seqs. E106–E112.

RyR (Ca release channel type 2).

In the model, only RyR channels located in the peripheral SR are considered. RyR is both activated and inhibited (Seqs. F15 and F16) by Ca_jun binding to separate junctional sites (Bezprozvanny et al., 1991). Significant binding of Ca in the physiological range to the latter site likely involves calmodulin (Xu and Meissner, 2004), which is implicit in the model. RyR is potentiated by Ca_SRper binding to an SR-luminal site (Sobie et al., 2002; Launikonis et al., 2006). This potentiation is modeled as Ca_SRper lowering the dissociation constant of the activating junctional site (Seqs. F13 and F14). In the model, PKA potentiates RyR (Shan et al., 2010) by increasing the affinity of the activating site (Seqs. F17–F19). In contrast, PKC suppresses RyR (Liu et al., 2009; Peng et al., 2010) by decreasing the affinity for Ca_jun (Seqs. F20–F22). PKA and PKC phosphorylation are modeled as mutually exclusive. The time courses of the phosphorylated states are determined by Seqs. J54–J56. The steady-state Ca flux and current are given by Seqs. F23–F27.

SERCA (Sarcoplasmic/endoplasmic reticulum Ca²⁺-ATPase).

SERCA is restricted in the model to the central SR. It is activated by Ca_in and inhibited by Ca_SRcen (Wray and Burdyga, 2010) (Seq. G23). PKA, PKG, and PKC phosphorylate phospholamban causing disinhibition, thereby increasing the apparent affinity of SERCA for Ca_in (Colyer, 1998; Wray and Burdyga, 2010). These modulations are simplified in the model, in which direct phosphorylation of SERCA by these kinases increases the affinity for Ca_in (Seq. G24). Two Ca are transported and approximately two protons are counter-transported per ATP hydrolyzed (Tran et al., 2009) (Seqs. G25–G29). Because the SR V_m and the proton concentration gradient are both assumed zero, the energy cost of transport is the result of the Ca concentration gradient alone. The time courses of the phosphorylated forms are governed by Seqs. J60 and J61.

sGC (soluble guanylate cyclase).

sGC is the target for nitric oxide (NO), modeled as in supplementary reaction schemes. The binding of one NO activates sGC; the binding of a second NO accelerates this activation (Yang et al., 2005). Feedback inhibition of sGC by PKG (Murthy, 2004) is modeled as exclusive phosphorylation of the active state to yield an inactive state incapable of binding NO. Seqs. J2–J7 govern the time courses of the sGC states and the concentration of cGMP.

Mathematical representation

The core of the program is a solve block of 63 nonlinear ordinary differential equations and 18 algebraic equations (Seqs. J2–J82) that generate the time courses of 81 variables. These include V_m; the concentrations of Ca in all compartments; the concentrations of Na, K, Cl, cAMP, cGMP, IP3, and DAG; the states of occupation and activity of receptors for αA, ATP, βA, and NO; the states of AC, G_s, G_q, sGC, and PLC; the states of phosphorylation of all modulated components; and the states of occupation of Ca buffers. The equations in the solve block call 180 steady-state equations (in which time is not an explicit argument) that determine for all channels and transporters their open-state probabilities or activities and the currents and fluxes conducted or transported by them and, in addition, the relative activities of all kinases and phosphodiesterases. The time courses of the applications of effectors are described by functions (Seqs. C1–C16), the parameters of which are given in Table S1.

The equations were written and solved in PTC Mathcad 15.0 M010. The differential equations and algebraic equations in the solve block were solved with the radau option for stiff differential equations. In a typical run with the normal parameter set (Table S6), the time courses over 300 s of 81 variables, and of additional functions of these variables, were solved at 6 values of intravascular pressure. For each variable (and functions of variables like fluxes and currents) at each intravascular pressure, 12,000 points were retained for the calculation of mean values of the variables and for plotting. On a computer with an Intel Core i7-3770K cpu, calculations and plotting were completed in ∼35 min.

Parameters

The equations of the model involved a large number of adjustable parameters (Table S6). Parameters that determined the behavior of the individual components were considered local; the parameters specifying the total numbers of molecules, or concentrations, or maximum currents of the components were considered global. Parameter values were (a) experimentally determined; (b) adjusted to give local model output that approximated the observed behavior of individual components; or (c) biochemically reasonable guesses calculated to give behavior of the components consistent with their expected roles and, if rate constants, to give steady states within a few minutes. In case (a), the local models and their parameters were taken from the literature. Local models were extended to simulate the reported qualitative effects of phosphorylation. In case (b), the local model was different from any published model, and its parameters could not have been obtained previously even if the experimental data existed. For some of these components, there are experimentally derived composite parameters such as EC50s, desensitization rates, and so on. For this subset of components, parameter values were initially adjusted to simulate the observed properties. These values, however, were often ballpark approximations because, for example, arterial constriction might have been determined experimentally, whereas the ultimate outputs of the model are Ca_in and V_m; furthermore, these outputs are not determined by a single component. Also, published experiments were performed with a variety of species, cell types, and conditions, and different values have been reported for the same composite parameter.

Many of the parameters, excluding the few well-established ones, were adjusted to achieve a close simulation of the primary experimental targets, V_m and Ca_in, as functions of intravascular pressure (Knot and Nelson, 1998). Because the number of adjustable parameters relevant just to the fit of the Knot and Nelson data was very large (189), it was impractical to search for the best fit over all parameters simultaneously. Instead, the fit was selective and iterative. The parameters of the components with the largest impacts (identified below) were adjusted one at a time, first to improve the global fit while maintaining realistic local properties. The fit was quantified separately for V_m and for Ca_in by calculating, first, the difference between the simulated value and experimental value for each of six pressures; second, each difference divided by the experimental value to get the relative difference; and, finally, the square root of the mean of the squares of the relative differences (rmsRelErr). The primary goal was to minimize rmsRelErr_Ca_in. With a few exceptions, the parameter values were determined to only one or two significant places. This was justified by the shallowness of the minimum (see Robustness below). A parameter set, called the “normal” parameter set (Table S6), minimized rmsRelErr_Ca_in and, within a small margin, rmsRelErr_V_m as well.

The sensitivity of the fit to changes in 24 global parameters was quantified as rmsRelErr_V_m and rmsRelErr_Ca_in after changing each parameter, one at a time, to 0.8, 0.9, 1.1, and 1.2 times their normal values. These were in all cases compared with the rmsRelErrs after elimination of the component. In addition, the sensitivities of the simulations of V_m and Ca_in and the output of the individual components to changes in 97 local parameters were calculated based on the differences between perturbed simulated values and normal simulated values (for details see legends of Figs. S8–S10).

Online supplemental material

Model equations (Mathcad program) are available in a PDF file. A PDF file of reaction schemes for α-adrenergic signaling, β-adrenergic signaling, NaKCl cotransporter, NCX exchanger, and P2XR is also available. Figs. S1–S10 and Tables S1–S6 are part of the online supplemental material. Figs. S1–S5 show the time courses of 15 variables, each at 20, 60, and 100 mm Hg. Figs. S6 and S7 show the sensitivities to variations in the global parameters of the fit of simulated <V_m> to V_exp and of simulated <Ca_in> to Ca_exp. Figs. S8–S10 show the sensitivities of <V_m>, <Ca_in>, and the outputs of individual components to variations in 97 global and local parameters. Table S1 shows the set of parameters determining the application of intravascular pressure and concentrations of chemical effectors. Table S2 shows the values of selected variables from a run with the normal set of parameters. Table S3 shows the effects of varying and/or holding constant key variables and parameters on the output oscillations. Table S4 shows the fractional changes in <V_m>, <Ca_in>, and the local component output per millivolt change in additive parameters that set the midpoints of voltage dependence. Table S5 shows the dose–response parameters characterizing the simulated responses to chemical effectors. Table S6 gives the values of the normal set of parameters and their derivations. The online supplemental material is available at http://www.jgp.org/cgi/content/full/jgp.201511380/DC1.

RESULTS

Simulations of V_m and Ca_in as functions of intravascular pressure

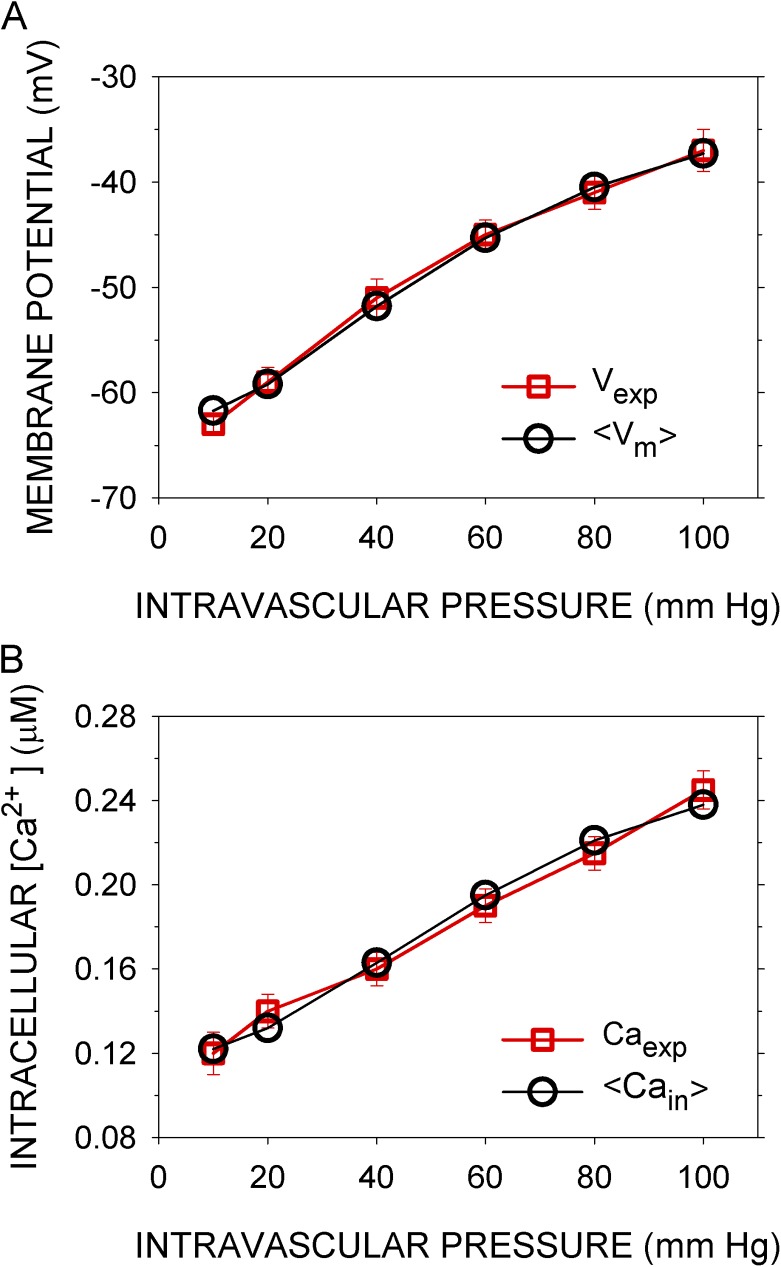
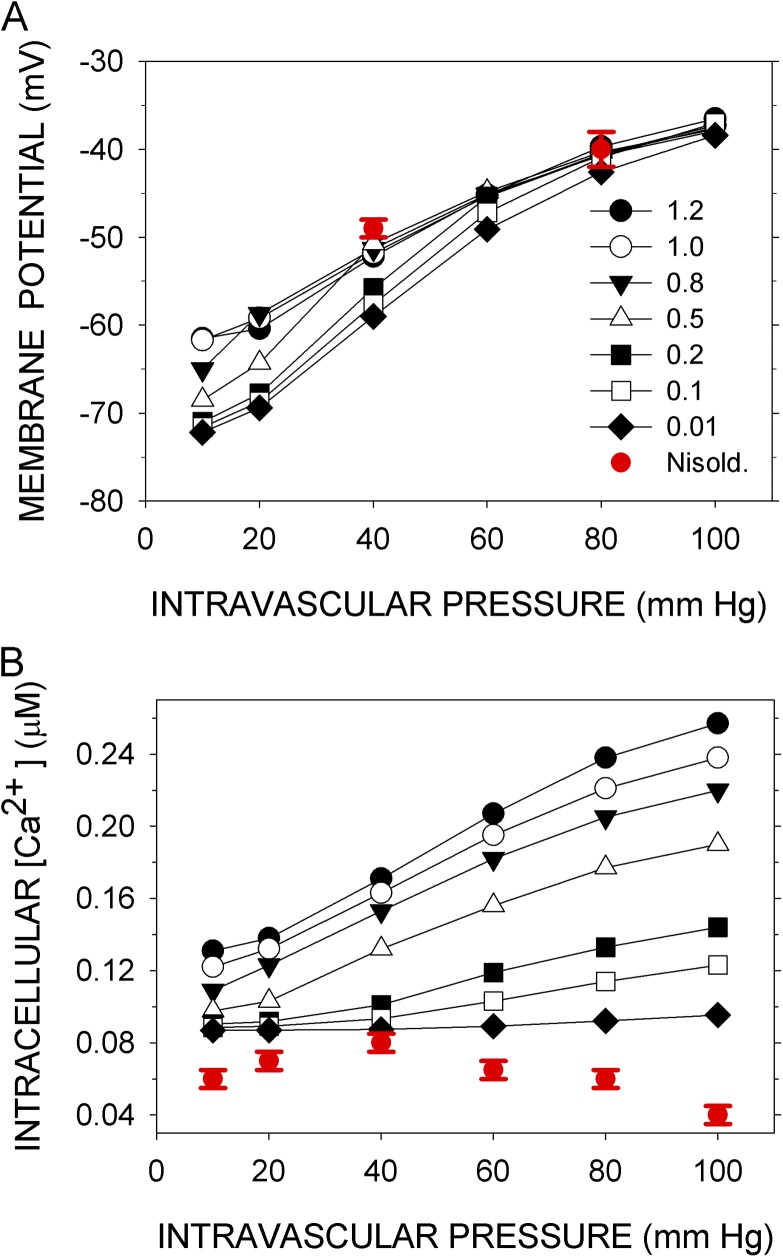
Simulations were run for 300 s, with pressure applied gradually starting at 10 s, reaching a steady value by 15 s, and sustained to 300 s. With most sets of parameter values tested, the simulated variables oscillated (Figs. S1–S5). To compare the simulated V_m and Ca_in with the experimentally determined V_exp and Ca_exp (Knot and Nelson, 1998), I took as the responses to pressure the means <V_m> and <Ca_in> over the last 50 s of the 300-s simulation. The means changed little over this last 50 s. A set of parameters that gave a close fit (see Materials and methods) of <V_m> and <Ca_in> to V_exp and Ca_exp (Fig. 2) was designated the normal set (Table S6). The root mean square (rms)-relative differences over the six experimentally tested intravascular pressures were 1.25% for V_m and 3.21% for Ca_in. Variations of most of the parameters by ±10% had little effect on the rms errors of the fits (see Robustness below).

Figure 2.

Simulated and experimental V_m and sarcoplasmic Ca concentration as functions of intramural pressure. (A) V_exp (red squares) are the means over 30 s of the observed V_ms after steady-state responses to the indicated intramural pressures were reached, recorded in rat cerebral arteries (Knot and Nelson, 1998). <V_m> (black circles) are the means of V_m over the last 50 s of a 300-s simulation with the normal parameter set (Table S6). In the simulations, the indicated intramural pressures were applied starting at 10 s. (B) Ca_exp (red squares) are the mean Ca concentrations recorded under the conditions in A, and <Ca_in> (black circles) are the means of Ca_in calculated as in A. Error bars represent standard deviations of the experimental data.

Means were also calculated for all other variables and for all fluxes or currents. For each trial run, automatic plots of the means as functions of intravascular pressure provided insight into the effects of changing parameter values. The means of the salient variables and currents from a run with the normal parameters, in the absence of all effectors except intravascular pressure, are shown in Table S2. In many cases, for example Ca_jun and I_{BK_ALL}, the means are much smaller than the peak values (Figs. S4 H, inset, and S5 E, inset; the peaks are sharper in the insets than in the main panel because the plotting density is greater). In the absence of chemical effectors, the concentrations of second messengers and the activities of phosphodiesterases and kinases remain at their basal levels. Even in the absence of chemical effectors, however, PKC activity changes with Ca_in.

Simulations of the effects of inhibiting BK, RyR, and CaV channels

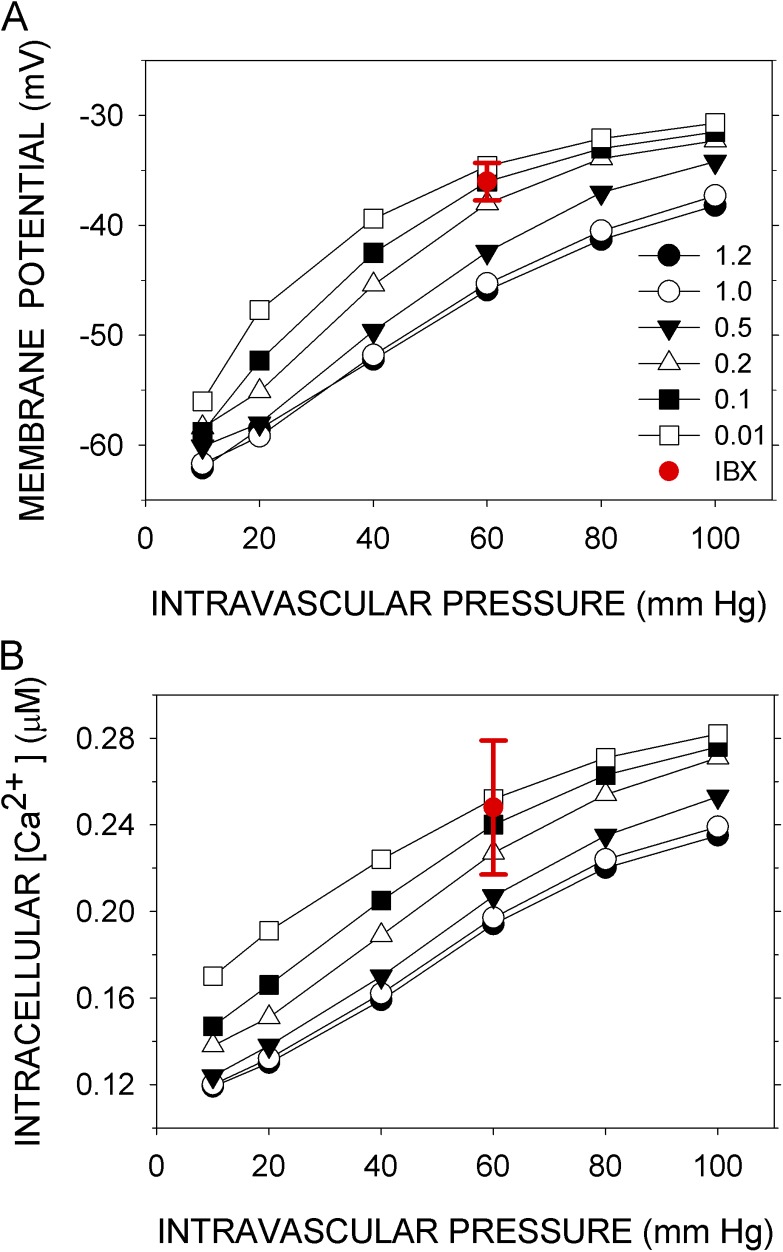
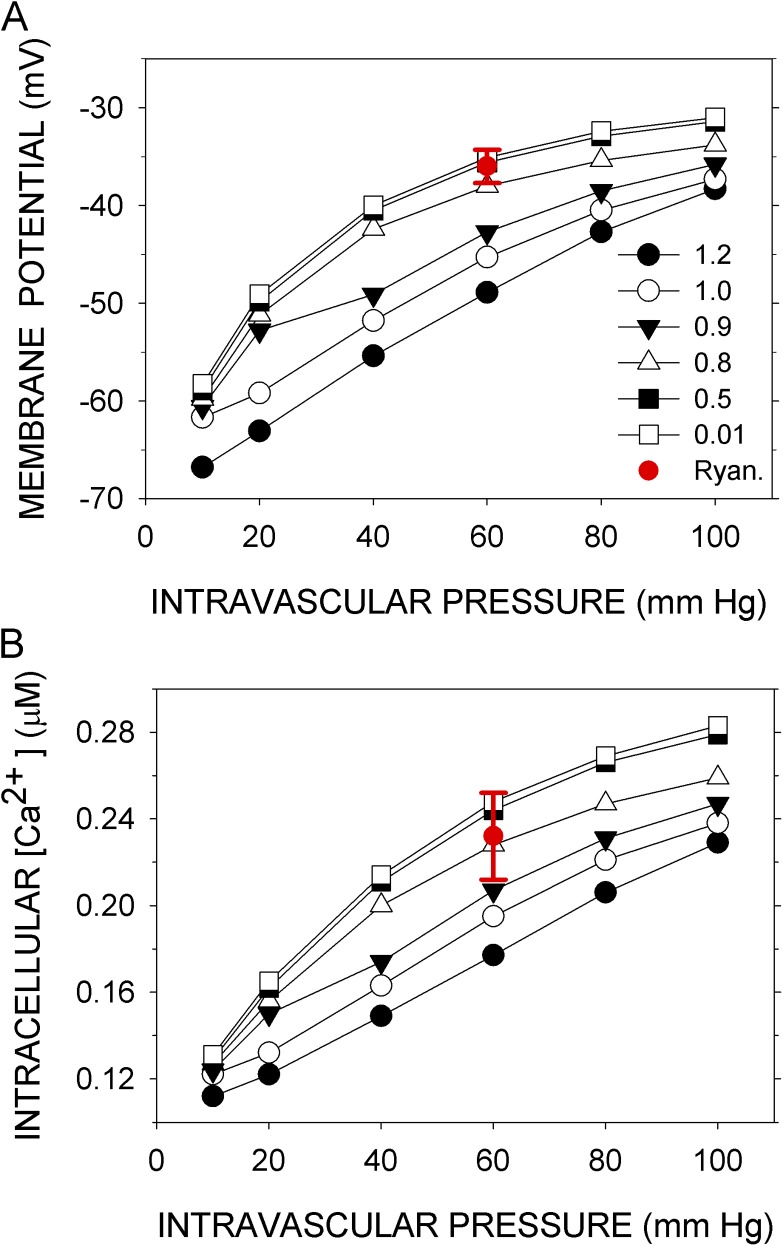
Knot et al. (1998) determined the effects on V_exp and Ca_exp of the inhibition of three key components: BK channels by iberiotoxin, RyR channels by ryanodine, and CaV channels by nisoldipine. In the model, reduction of the number of BK channels (BK_T) to between 1 and 10% of the normal value simulated the effects of 100 nM iberiotoxin on V_exp and Ca_exp at 60 mm Hg (Fig. 3, A and B). In the model, reducing the number of RyR channels (RyR_T) to 50% of the normal value and reducing it to 1% had nearly the same effect on <V_m>, and both overlap with V_exp at 60 mm Hg in the presence of 10 µM ryanodine (Fig. 4 A). (There may be three distinct ryanodine-binding sites on RyR2, binding to each of which promotes a distinct state of the channel [Bidasee et al., 2003]. At 10 µM ryanodine, however, the “shut” state predominates.) The mean effect of ryanodine on Ca_exp was simulated by the reduction of RyR_T to between 80 and 50% of the normal value, but 1% of the normal value gave <Ca_in> within the experimental error in Ca_exp (Fig. 4 B). Finally, reduction of CaV_T to 1% of the normal value simulated the small effect of 10 nM nisoldipine on V_m at 80 mm Hg but not at 40 mm Hg, where the reduction of CaV_T generated a hyperpolarization not observed experimentally (Fig. 5 A). Reduction of CaV_T to 1% or to 0.1% of its normal value simulated, at least qualitatively, the effect of nisoldipine on Ca_exp; namely, the increase in Ca_in with pressure is completely abrogated over the entire pressure range (Fig. 5 B).

Figure 3.

Simulation of the effects of inhibiting BK. (A) V_exp and (B) Ca_exp (red circles with error bars) were recorded at 60 mm Hg in the presence of 100 nM iberiotoxin (Knot et al., 1998). V_m and Ca_in were simulated with the number of BK molecules (BK_T) set at the indicated multiples (1–120%) of its normal value. <V_m> and <Ca_in> are the means over the last 50 s of a 300-s simulation (black symbols). Except for BK_T, the parameters were normal. Error bars represent standard deviations of the experimental data.

Figure 4.

Simulation of the effects of inhibiting RyR. (A) V_exp and (B) Ca_exp (red circles with error bars) were recorded at 60 mm Hg in the presence of 10 µM ryanodine (Knot et al., 1998). V_m and Ca_in were simulated with RyR_T set at the indicated multiples (1–120%) of its normal value. <V_m> and <Ca_in> are the means over the last 50 s of a 300-s simulation (black symbols). Except for RyR_T, the parameters were normal. Error bars represent standard deviations of the experimental data.

Figure 5.

Simulation of the effects of inhibiting CaV channels. (A) V_exp and (B) Ca_exp (red circles with error bars) were recorded at various intravascular pressures in the presence of 10 nM nisoldipine (Knot and Nelson, 1998). V_m and Ca_in were simulated with CaV_T set at the indicated multiples (1–120%) of its normal value. <V_m> and <Ca_in> are the means over the last 50 s of a 300-s simulation (black symbols). Except for CaV_T, the parameters were normal. Error bars represent standard deviations of the experimental data.

Ca concentrations in different compartments

The Ca concentrations in the five compartments included in the model spanned three orders of magnitude. For example, during the interval from 250 to 300 s at 60 mm Hg, the mean concentrations (µM) are 0.195 <Ca_in>, 108 <Ca_SRcen>, 82.3 <Ca_SRper>, 0.7 <Ca_jun>, and 0.53 <Ca_NSCstr>, and the peak values in the smaller compartments (microdomains), namely of Ca_SRper, Ca_jun, and Ca_NSCstr, were considerably higher than their means. These concentrations were in the ranges of activation of compartment-specific targets or functions; e.g., Ca_in activates myosin light chain kinase, Ca_NSCstr activates ClA, Ca_jun activates RyR and BK, Ca_SRcen is a reservoir for IP3R and replenishes Ca_SRper, and Ca_SRper both sensitizes RyR and feeds Ca_jun (Fig. 1).

Oscillations

V_m, Ca_in, and other of the simulated variables showed sustained, synchronous oscillations (Figs. S1–S5). Such synchronous oscillations, however, are not seen experimentally. Rather, there are sporadic, localized spikes in Ca (“sparks”) and, imperfectly correlated with them, spontaneous, transient outward currents (“STOCs”) (Nelson et al., 1995; Lifshitz et al., 2011). Sparks and STOCs result from the activation of RyR and BK channels, respectively. Sparks and the correlated STOCs occur at individual junctions and are stochastic. Their properties depend on the gating kinetics and spatial distributions of RyR and BK channels (Lifshitz et al., 2011), on the diffusion of Ca, and on the electrotonic spread of changes in V_m. In the model, however, all individual channels of a type were simultaneously in the same state determined by the steady-state equation for P_open. There were no delays in the transitions between steady states. Nonetheless, the underlying mechanism driving the irregular spikes of experimentally observed sparks and STOCs and of the regular oscillations in the simulation are likely the same.

The mechanism as it applies to RyR and sparks is analogous to the flushing of a toilet. The flapper stays up (i.e., RyR continues to open) until the tank (SRper) nearly empties (but see Sobie et al., 2002). This toilet analogy needs the refinement that the filling of the tank beyond a certain level promotes the opening of the flapper (RyR), and the filling of the bowl (junctional domain) keeps the flapper up (RyR open). The spikes in Ca_jun drive the spikes in I_BK, i.e., the STOCs (Hill-Eubanks et al., 2011). Although this mechanism for sparks and STOCs is too simple, because not all sparks result in STOCs, and not all STOCs are correlated with sparks (Lifshitz et al., 2011), it should suffice for the correlated sparks and STOCs.

The mechanisms promoting and sustaining the oscillations in the model are illuminated by the effects of changes in component parameters on the frequency of oscillations (Table S3). In the model with the normal set of parameters, all variables oscillated synchronously, albeit with widely different amplitudes (Figs. S1–S5). During the interval from 150 to 155 s (for illustration) and at an intravascular pressure of 60 mm Hg, the common frequency was 2.9 Hz. The rate of refilling of SRper depended on the rate of SERCA pumping Ca into the SRcen: the frequency decreased to 2.2 Hz when I_{SERCA_MAX} was set at 80% of its normal value and increased to 3.3 Hz when I_{SERCA_MAX} was set at 120% of its normal value. It has been observed that inhibition of SERCA decreases the frequency of sparks (Vandier et al., 1998).

The refilling also depended directly on the Ca gradient between SRcen and SRper. Although normally Ca_SRcen oscillated with a small amplitude (Fig. S4, A–C), this oscillation was not required for oscillation in Ca_SRper and Ca_jun. Fixing Ca_SRcen at 108 µM, its normal mean value at 60 mm Hg, yielded a frequency of 3.0 Hz in the other variables. Fixing Ca_SRcen at 97.2 µM, 90% of its normal value, eliminated the oscillations. Fixing Ca_NSCcen at 110% of its normal value, 118.8 µM, however, increased the frequency to 5.3 Hz, consistent with the more rapid refilling of SRper. At 129.6 µM Ca_NSCcen, 120% of its normal value, there was again no oscillation, and the rate of refilling of SRper equaled the rate of its emptying via RyR.

Consistent with the idea that the periodic drop in Ca_SRper drives the oscillation, fixing Ca_SRper either at its normal mean value (82.3 µM) or at 65.8 µM (80% of normal) or at 98.8 µM (120% of normal) eliminated all oscillations. It follows that the frequency should increase as the rates of emptying and refilling of SRper increases, and these will increase as VOL_SRper decreases, and vice versa. In the simulation, the frequency increased when VOL_SRper was decreased to 80% of normal, and the frequency decreased when VOL_SRper was increased to 120% of normal.

The drop in Ca_SRper and the rise in Ca_jun depend on Ca flux through the open RyR channel, the opening of which depends on both of these concentrations. Decreased numbers of RyR compared with normal resulted in decreased Ca flux and decreased frequency, whereas increased numbers of RyR resulted in increased frequency. In the model, Ca_SRper binding promotes RyR activity by decreasing the dissociation constant, K_{RyR_Ca_act}, from K_{RyR_Ca_max} toward K_{RyR_Ca_min}. With these three parameters fixed at a low value of 6.0 µM, promoting RyR activity, the frequency was 5.4 Hz. At an intermediate value of 7.5 µM, the frequency was 2.2 Hz, and at a high value of 9.0 µM (low RyR activity), there was no sustained oscillation; rather, a steady state was reached.

The oscillation of Ca_jun was necessary but not sufficient for all other oscillations. Both RyR and BK channels are activated by Ca_jun. Allowing Ca_jun to oscillate as usual but fixing just the input to RyR of Ca_jun at its normal mean value, 0.7 µM, or at 80% (0.56 µM) or 120% (0.84 µM) of its mean value eliminated all oscillations. It follows that there are no other oscillations without oscillation in RyR activity. On the other hand, if Ca_jun input to RyR was allowed to vary with time as usual and only the input to BK channels was fixed (Table S3, bottom), oscillations in I_RyR__ALL, Ca_SRper, and Ca_jun continued, albeit with frequencies changed as expected, but there was no oscillation in I_{BK_ALL}, V_m, or in any sarcolemmal currents. These last currents are all dependent on the electrochemical potential, and some are also carried by voltage-activated channels. RyR oscillations entrain BK channels, and BK channel oscillations entrain V_m. There is also strong negative feedback on BK channel activity of the hyperpolarization caused by I_BK, which contributes to the sharpness of the spikes of simulated I_BK and also of experimentally observed STOCs.

Robustness

Robustness is the insensitivity of the output of a mechanism to changes in its components. The mathematical model of a mechanism is robust to the extent that its output is insensitive to changes in the parameters of its governing equations. As in the well-known case of bacterial chemotaxis, in which adaptation was insensitive to parameter changes but tumbling rate was not (Alon et al., 1999), a mechanism and a model can have both robust and sensitive outputs. Also, of course, a model is likely to be more sensitive to changes in some parameters than in others.

Sensitivity was examined in two ways. In the first, the effects of changes in parameters on the rms-relative differences between V_exp and <V_m> (Fig. S6) and between Ca_exp and <Ca_in> (Fig. S7) were determined at six intramural pressures (Materials and methods). The parameters changed were the numbers of functional molecules of each component. These numbers represent the expression levels, which are likely to vary among cells. The parameters were changed, one at a time, to 0.8, 0.9, 1.1, and 1.2 times their normal values. In addition, they were set to zero. The model lacks redundancy, so that insensitivity of the simulations to 10 and 20% changes in expression levels is pertinent to robustness only if complete removal of the component has a significant effect on the fit.

The perturbed rms-relative errors are also compared with the normal rms-relative errors, rmsRelErr_V_m and rmsRelErr_Ca_in, which were 1.25 and 3.21%, respectively, and indicated by dashed red lines in Figs. S6 and S7. Also shown as reference lines for a moderately perturbed state are the rms-relative errors simulated with the parameters for the channel composed of BK channel α subunits alone, i.e., in the absence of β1 subunits (Bao and Cox, 2005). These are 16.7 and 21.0%, respectively.

The rms-relative errors were obtained for perturbed expression levels of 24 components. The model has 37 protein components, but some are not active in these simulations because chemical effectors are absent, and some are enzymes assumed to be in 1:1 complexes with their targets and, hence, with no separate parameter for expression. The rms-relative errors were insensitive to the total elimination of AC, KATP, and sGC because, in the absence of chemical effectors, these components were active only at a basal level. There were 14 components, of which the elimination of any one resulted in an rms-relative error in either V_m or Ca_in >10%. For eight of these (BK, Ca_leak, Cl_A, Cl_leak, IP3R, NaK, NSCne, and BUF_jun), altering the number per cell by ±20% yielded rms-relative errors in V_m and Ca_in <5%. These components play significant roles in the model, and yet <V_m> and <Ca_in> were relatively insensitive to their expression levels. The simulations of V_exp and Ca_exp were more sensitive to changes in the numbers of CaV, NSCstr, PLC, PMCA, RyR, and SERCA; altering the number of any one of them by ±20% yielded an rms-relative error in V_m or Ca_in >5%. Only for PLC, however, did the rms-relative errors exceed those obtained in the absence of BK β1. Sensitivity to variation in PLC_T is caused by the dependence of NSCstr, NSCne, and PKC on the basal level of DAG, the regulation of which in the model is highly simplified. Overall, the rms-relative errors in the simulations were moderately insensitive to changes in the expression levels of most of the components.

In a second approach, I looked at the sensitivity of the simulations to changes by ±10% of 97 parameters, including the expression levels and the kinetic parameters of the components (Figs. S8–S10). I calculated global sensitivities as the absolute values of the relative changes |(<V_m>_norm − <V_m>_perturbed)/ε<V_m>_norm| and |(<Ca_in>_norm − <Ca_in>_perturbed)/ε<Ca_in>_norm|, where ε is 0.1, the fractional change in the parameter, and averaged these over six intramural pressures. In addition, I calculated the fractional change in the output of the cognate component (e.g., I_BK for BK channel parameters, I_CaV for CaV channel parameters, etc.) per fractional change in each parameter. These were the local sensitivities. Calculated this way, sensitivity approximates the mean of the absolute value of the partial derivative ∂[ln(Z)]/∂[ln(parameter)], where Z is <V_m>, <Ca_in>, or the mean output of the cognate component. A sensitivity of 1 indicates, for example, that a 10% change in a given parameter results in a 10% change in output.

For most of the 97 parameters considered, the global sensitivities are far <1 and also less than the sensitivities of the cognate components (Figs. S8–S10). For <V_m> and <Ca_in>, the sensitivities are ≤0.1 for 54 and 53 parameters, respectively, whereas the component sensitivities are ≥0.4 for 65 parameters. Five additional parameters, V_x (where x is the relevant component), appear as the expression (V_m − V_x) in exponentials. These were perturbed by ±2 mV, and a modified sensitivity was calculated (Table S4). Except for the sensitivity of <Ca_in> to V_{CaV_act}, the sensitivities of <V_m> and <Ca_in> were far less than the component sensitivities. Thus, at least in the vicinity of the normal set, the effects of most parameter changes on <V_m> and <Ca_in> are small both absolutely and relatively compared with their effects on the outputs of their cognate components. The model is buffered against changes in many of its parameters and can be considered robust.

Chemical effectors

α-adrenergic input.

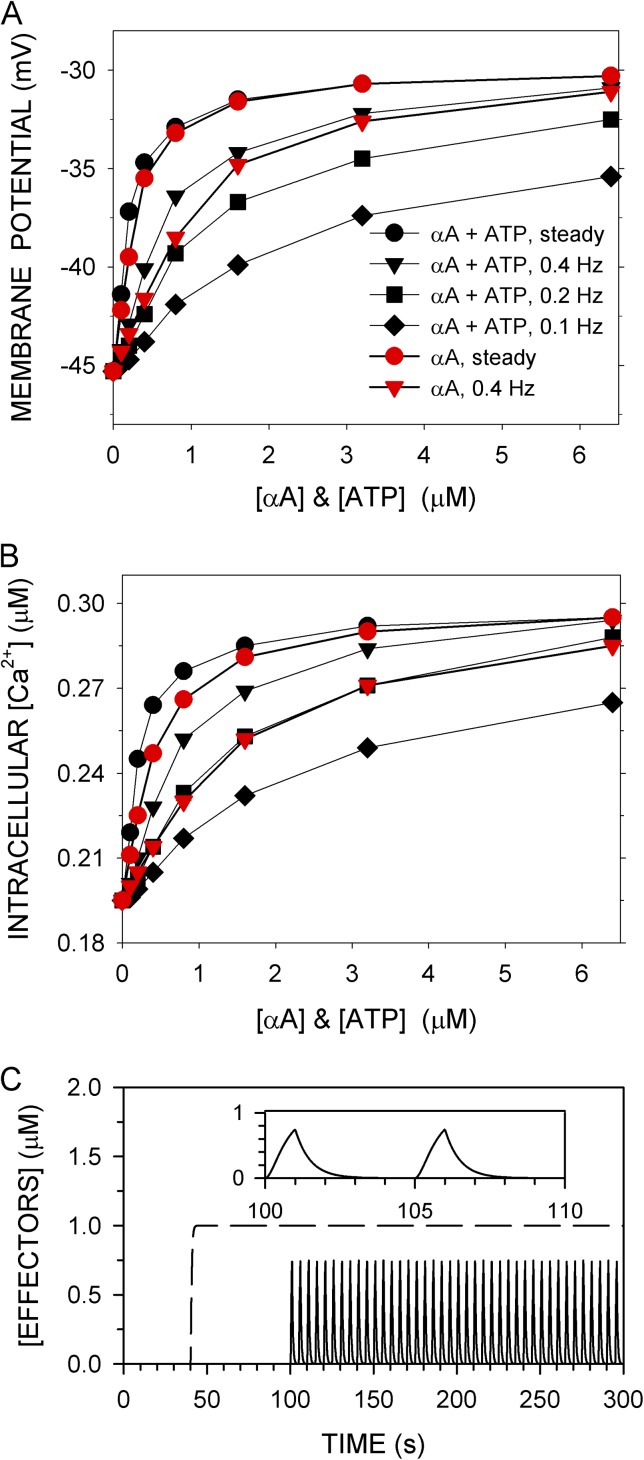
The effects on <V_m> and <Ca_in> of an α-adrenergic agonist (αA) were simulated at 60–mm Hg intravascular pressure and normal parameters (Fig. 6, A and B). The association and dissociation rate constants of αA were selected so that its equilibrium dissociation constant was 10 µM, characteristic of norepinephrine (see Table S6). αA was added alone or simultaneously with the same concentration of extracellular ATP. Also, the addition was either steady or pulsatile (Fig. 6 C), with the latter simulating release from sympathetic neurovascular junctions (Todorov et al., 1999). The EC50 for the increase in <Ca_in> caused by the steady application of αA was 0.41 µM (Table S5). The EC50 for norepinephrine-induced contraction of isolated rat mesenteric arteries pressurized to 60 mm Hg was 0.25 µM (Enouri et al., 2011). The EC50 for the effects of the steady application of αA plus ATP was lower than that for αA alone, more so for the effects on <Ca_in> than on <V_m> (Table S5). The maximum depolarizations and maximum increases in Ca_in, however, were nearly identical for αA alone and αA plus ATP. Thus, ATP enhanced the effects of αA more at lower than at higher concentrations. With pulsatile application, the EC50s for the effects of αA plus ATP were also lower than the EC50s for the effects of αA alone.

Figure 6.

Effects of α-adreneric agonist (αA) and ATP on <V_m> and <Ca_in> at 60 mm Hg. (A) <V_m> and (B) <Ca_in> are the means over the last 50 s of a 300-s simulation computed with normal parameters. αA alone (red symbols) or αA and ATP together at the same concentration (black symbols) were added either steadily from t = 40–300 s (C; dashed line) or in pulses from t = 100–300 s (C; solid line). Pulses were on for 1 s and were off for 1.5 s (0.4 Hz), 4 s (0.2 Hz), or 9 s (0.1 Hz). The rate constant for both the rise and fall of a pulse was 2/s. (C) Nominally 1-µM pulses at 0.2 Hz and (inset) two cycles on expanded scale (solid line) are shown, at a steady application of 1 µM (dashed line).

Pulsatile application was both effective and economical. For example, 80 1-s pulses over 200 s (i.e., at 0.4 Hz) of nominally 3.2 µM αA plus ATP increased <Ca_in> by 89 µM, whereas steady application of 3.2 µM αA plus ATP increased <Ca_in> by 97 µM. The quantity of αA added in pulses, however, was cumulatively only 15% of that added during steady application. Note that the effector concentration in a pulse reached only ∼75% of the nominal concentration after 1 s, when the pulse turned off (Fig. 6 C).

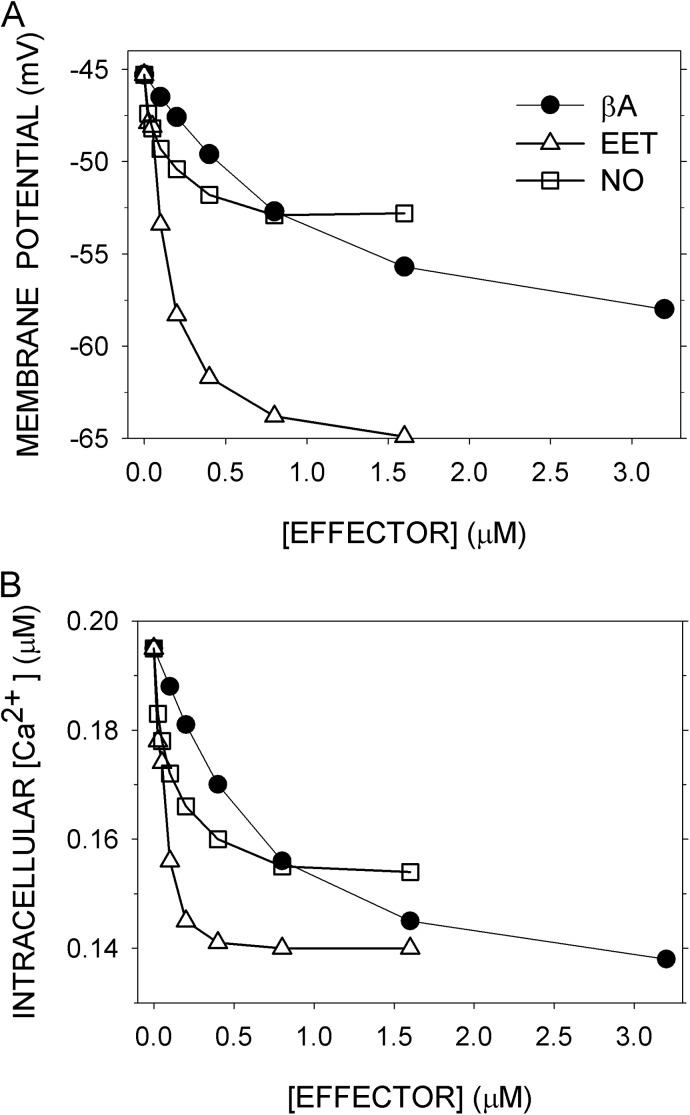
βA, EET, and NO input.

These three effectors hyperpolarize V_m and lower Ca_in by overlapping pathways. They all promote BK channel activity, among other channels that are modulated (Fig. 1). The effects of their steady application on <V_m> and <Ca_in> were simulated at 60–mm Hg intravascular pressure and normal parameters (Fig. 7, A and B). For βA, the EC50s for the two variables (Table S5) were similar to the EC50s for epinephrine determined in rat mesenteric arteries in the presence of the αAR blocker prazocin at ∼60 mm Hg, namely, 0.79 µM for hyperpolarization and 0.25 µM for relaxation (Garland et al., 2011). In the model, elimination of KATP suppressed the βA-induced hyperpolarization, simulating the observed effect of the KATP inhibitor glibenclamide (Garland et al., 2011). In the model, however, elimination of KATP suppressed the βA-induced decrease in <Ca_in>, counter to the observed lack of effect of glibenclamide on relaxation (Garland et al., 2011). The model lacks additional significant pathways for the lowering of tension by PKA.

Figure 7.

Effects of β-adrenergic agonist (βA), EET, and NO on <V_m> and <Ca_in> at 60 mm Hg. (A) <V_m> and (B) <Ca_in> were computed as before with normal parameters. Effectors were added steadily from t = 40–300 s.

For EET, the EC50s for <V_m> and <Ca_in> from the simulation were 0.54 and 0.24 µM (Table S5). The EC50 for 11,12-EET–induced vasodilation of pressurized mesenteric arteries, however, was far lower, in the range of 1 to 10 nM (Earley et al., 2005). For NO, the EC50s for <V_m> and <Ca_in> were 0.46 and 0.40 µM (Table S5). The observed EC50s for relaxation were higher, ∼8 µM for aorta and ∼5 µM for femoral artery (Nimmegeers et al., 2007). Roles for sGC-independent NO effects (Nimmegeers et al., 2007; Yuill et al., 2010) were not considered in the model.

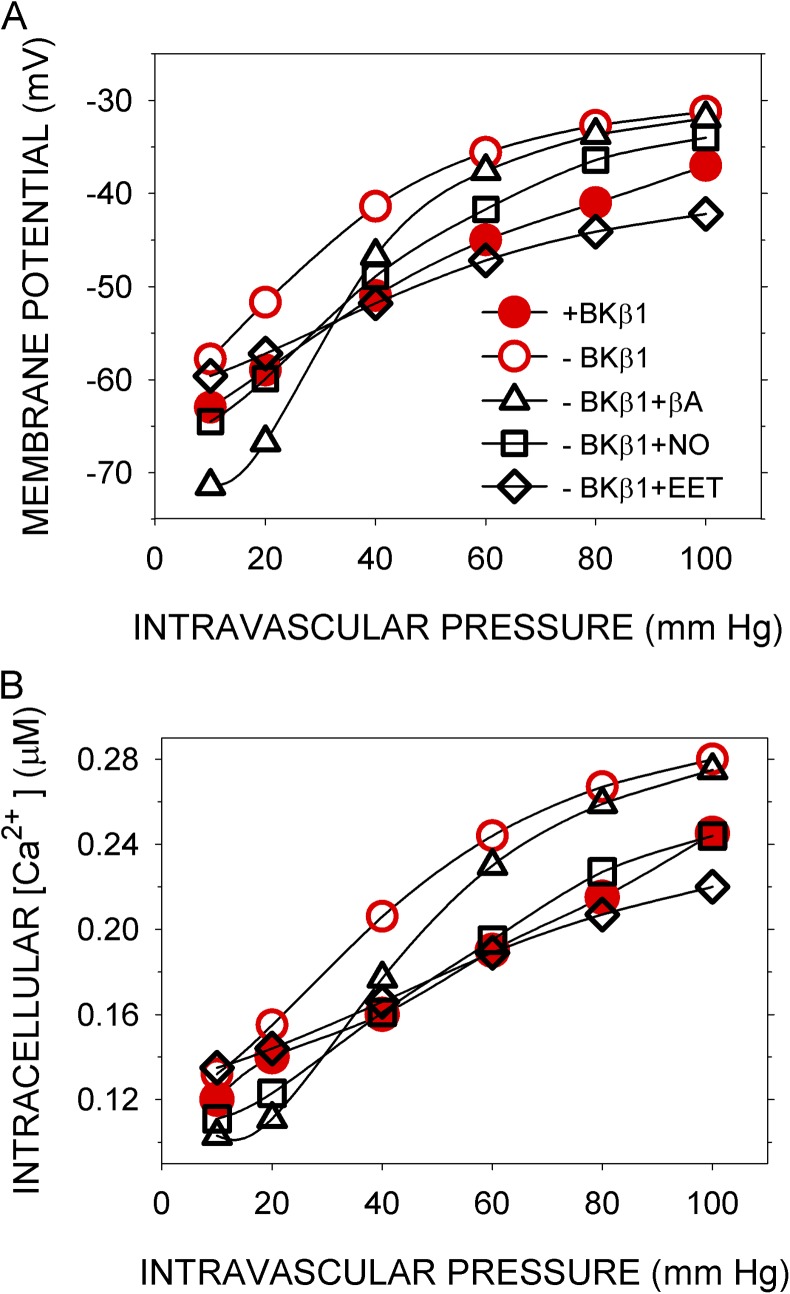
Mitigating the effects of the loss of BK β1

In mice, knockout of BK β1 subunit reduces the Ca sensitivity and shifts the G-V curve of the BK channel to the right so that STOCs are less efficiently activated by Ca sparks (Brenner et al., 2000; Bao and Cox, 2005). Low expression of BK β1 results in increased arterial SM tone and increased blood pressure (Brenner et al., 2000), although the latter effect depends on the mouse strain (Sachse et al., 2014). In the simulation with BK channel parameters appropriate for channels composed of α alone (Horrigan and Aldrich, 2002), <V_m> and <Ca_in> are higher at all pressures than <V_m> and <Ca_in> simulated with the normal parameters, which include those for BK α in complex with β1 (Bao and Cox, 2005) (Fig. 8). SM tension is directly related to <Ca_in>, and thus the myogenic response is predicted to be abnormal in the absence of β1.

Figure 8.

Effects of intravascular pressure and vasorelaxants on <V_m> and <Ca_in> in the absence of BK β1. (A) <V_m> and (B) <Ca_in> were computed as before either with normal parameters (closed red circles), which include those appropriate for the BK channel containing both α and β1 subunits (+BKβ1) (Bao and Cox, 2005), or with parameters appropriate for BK α alone (−BKβ1) (Horrigan and Aldrich, 2002), in the absence (open red circles) or presence (open black symbols) of effectors. 0.1 µM βA (open black triangles), 0.4 µM NO (open black squares), or 0.2 µM EET (open black diamonds) was added steadily from t = 40–300 s.

βA, EET, and NO all brought <V_m> and <Ca_in> closer to their normal values and hence should have a normalizing effect on the myogenic response. At least in the simulation, one vasorelaxant is more effective than the others (Fig. 8). For effector concentrations approximately optimal for shifting the BK β1 knockout curves toward the normal curve, the mean over six intramural pressures of |(<Ca_in> − <Ca_in,norm>)/<Ca_in,norm>| for the β1 knockout with no effector was 19.3%, with 0.1 µM βA it was 15.1%, with 0.2 µM EET it was 6.4%, and with 0.4 µM NO it was 3.7%. Among these vasorelaxants, NO is the most effective in restoring global Ca concentrations to near-normal over the tested range of intramural pressure.

DISCUSSION

The model should be evaluated based on whether it simulates experimental data, whether it does so with credible mechanisms and parameters, whether it incorporates all components known to be significant in the short-term control of V_m and Ca_in in arterial SM cells (and excludes components not present in these cells), and whether the architecture of an arterial SM cell and the distribution of components in this architecture are adequately represented. Obviously, the equations should represent the model adequately and should be solvable over the relevant ranges of inputs and time. These criteria concern the testability and conformity of the model to properties of arterial SM inferred from experiments. If the model satisfies these criteria, it consolidates and tests the consistency of these inferences. Where the model fills in or goes beyond previously proposed mechanisms, it predicts that these mechanisms will be verified experimentally.

A set of parameters (the “normal” set) was obtained that resulted in a close fit of the model-generated V_m and Ca_in to the experimentally determined V_exp and Ca_exp as functions of intravascular pressure (Knot and Nelson, 1998) (Fig. 2). With the same normal parameters, except that the number of molecules of the target component was progressively decreased, the model also simulated, at least qualitatively, the experimentally determined effects of inhibiting, one at a time, RyR, BK, and CaV channels (Knot et al., 1998) (Figs. 3–5). This conformity of the model to experimental data beyond those used to derive the normal parameters is, at the very least, the absence of its invalidation; i.e., the model is possibly a valid mathematical representation. Nevertheless, the normal set of parameter values cannot be considered well determined or providing a unique fit to the limited experimental data available. Even if there were more data, unique best-fit parameter values for the complex of mechanisms constituting the model would be elusive (Hines et al., 2014). The existence of even one set of normal parameters, however, confirms that the combination of reasonably behaving components as in the model can result in global behavior that simulates experimentally observed behavior. Again, the model is possibly a valid representation of arterial SM cell function in the limited range of the myogenic response.

The activities of all channels, transporters, kinases, phosphatases, and phosphodiesterases are represented by steady-state equations (not explicitly dependent on time). These include all of the components involved in the control of V_m and Ca_in by pressure in the absence of other effectors. The steady-state equations are called by the differential equations that determine as functions of time V_m and all ion concentrations, among other variables. In this approach, the faster processes are governed by steady-state equations, and the slower processes are governed by differential equations (Saucerman and McCulloch, 2004). For most components, the steady-state equations differ from those used in previously published models of SM. Here, all fluxes and currents through channels are driven by the Goldman–Hodgkin–Katz constant-field integral of the Nernst–Planck equation, which is at least a thermodynamically consistent simplification. Primary transporters are driven by the negative free energy change per mole of the overall reaction, including hydrolysis of ATP (Δµ_ATP). Cotransporters, NCX and NaKCl, are modeled with thermodynamically valid reaction schemes and parameters. The model here for NCX, in particular, is more complicated than that in Kapela et al. (2008) and less complicated than that in Kang and Hilgemann (2004). The equations for the open probability of BK channels are taken from Horrigan and Aldrich (2002), and those for CaV channels are from Rubart et al. (1996). For other channels, the local mechanisms incorporated the reported qualitative effects of V_m, Ca, and DAG on open probabilities. Similarly, for all modulated channels and transporters, the reported qualitative effects of phosphorylation were represented quantitatively. The data did not exist to train these local models and to obtain local best-fit parameters. At most, a partial set of related parameters was available (Table S6). For rate constants unconstrained by experiment, I used values within the range of biochemical reaction rate constants and also consistent with the reactions reaching a steady state within ∼200 s.

The disparate signaling roles of Ca require separate microdomains (see Introduction). The model contains two types: the junctional microdomains and the stretch-transducing microdomains. Junctions between the peripheral SR and the sarcolemma were identified in electron micrographs of urinary bladder SM, where they contain RyR and CaV channels and promote contraction (Moore et al., 2004). In the model, I have assumed that similar subcellular structures exist in arterial SM but that their role is to promote relaxation. There is close apposition of the peripheral SR and caveolae in arterial SM (Shaw et al., 2006). One role suggested for such structures is the direct coupling, independent of Ca release, of IP3R and TRPC3 (Adebiyi et al., 2010). Thus, physically restricted spaces that could serve as microdomains for Ca exist in arterial SM. Furthermore, at least in airway myocytes, arrays of RyR in SR and arrays of BK channels in the sarcolemma are close, although not overlapping (Lifshitz et al., 2011).

There is no evidence for stretch-transducing microdomains formed by apposing membranes, but this arrangement is not required for a Ca microdomain. NSCstr and ClA channels are in the same membrane, with 1 NSCstr channel per approximately 10 ClA channels according to the fitted normal set of parameters. If the ClA channels were arrayed in close proximity to the NSCstr channel, the local Ca concentration could be transiently elevated enough (Rizzuto and Pozzan, 2006) to activate the ClA channel sufficiently to depolarize V_m. If instead ClA channels were sensing Ca delivered directly into the global sarcoplasmic pool, the Ca concentration needed to activate ClA channels sufficiently would also strongly activate myosin light chain kinase and cause maximum contraction. Furthermore, experimentally, the Ca current via NSCstr channels does not contribute significantly to Ca_in, which is almost entirely caused by influx via CaV channels, as seen in Fig. 5 B. Thus, if Ca influx via NSCstr channels need be limited and yet achieve concentrations greater than Ca_in, NSCstr channels must release this Ca signal into a restricted volume, a microdomain, also containing the ClA channels.

A simplification of the model is that each channel and transporter is found only in the membrane bounding one compartment; e.g., RyR is exclusively in the peripheral SR membrane bounding the junctional microdomain, and IP3R is exclusively in the central SR membrane (c.f. Kapela et al., 2008). In arterial SM, however, RyR is also found in the central SR, and IP3R is likely also in the peripheral SR membrane (Adebiyi et al., 2010). Moreover, not all BK channels are directly apposed to RyR (Lifshitz et al., 2011). Would the output of the model differ significantly if it included more realistic distributions of components? BK channels outside the junctions exposed to global Ca_in would have very low open probabilities. Active RyR channels in the central SR would raise Ca_in, opposing the lowering of Ca_in by junctional RyR acting through BK and CaV channels. Given that inhibiting RyR with 10 µM ryanodine raised Ca_in (Fig. 4), RyR must be active predominantly in junctions in arterial SM.

In the model, NCX is in the sarcolemma facing the sarcoplasm. Given the simulated values of Na_in, Ca_in, and V_m, NCX transports Na inward and Ca outward. NCX makes small contributions to the control of V_m and Ca_in (Table S2 and Figs. S6 and S7). There is, however, evidence that NCX makes a significant contribution to the maintenance of arterial SM tone (Zhang, 2013). To do so, NCX would need to run in reverse mode, transporting Na outward and Ca inward. In the range of V_m in the SM cell and if Ca_in were 0.2–1 µM, Na_in would need to be >16–25 mM to drive influx of Ca. More relevant to the control of Ca_in by pressure is the possibility that NCX is present in the stretch-transducing microdomains, amplifying the activation of NSCstr channels and the resulting influx of Na by increasing Ca_NSCstr. In that case, Ca_NSCstr would be ∼0.5 µM, and Na_NSCstr would need to be >20 mM to get influx of Ca via NCX. I have simulated the addition of NCX to the NSCstr microdomain and found that with reasonable rates of diffusive equilibration of Na_NSCstr with Na_in and plausible VOL_NSCstr, the I_NSCstr needed to obtain Na_NSCstr of >20 mM would in itself depolarize V_m to approximately −30 mV and raise Ca_in to ∼300 nM without much contribution from NCX. A major role of NCX in the short-term myogenic response seems unlikely. There is, however, evidence that NCX runs in reverse mode in a microdomain shared with NSCne (Zhang, 2013), which I have not explored in the current model.

The model incorporates only pared-down versions of signaling via α- and β-adrenergic receptors and G proteins. Cyclic nucleotide–independent effects via Gβγ, which can promote vasoconstriction (Zhou et al., 2008) or vasorelaxation (Meens et al., 2012), depending on the terminal components of the circuits, are neglected. Including Gβγ effects would require a fine-grained approach beyond the scope of the present model.

The model makes two types of predictions. The first type is explicit, and such predictions can be tested by straightforward experiments. For example, the model predicts the sensitivities of V_m and Ca_in as functions of pressure to partial block of components (Figs. S6 and S7). These predictions can be tested by measurements of V_exp and Ca_exp in pressurized arteries over a range of concentrations of specific inhibitors, combined with assays for the residual activities of the target components. It also predicts that observables, such as V_exp and Ca_exp, will be buffered against modest changes in the properties of components (Figs. S8–S10); i.e., like the model, SM cell responses to perturbations are predicted to be robust. It predicts the effects of changes in the activities and properties of SERCA, RyR, and BK channels on the frequency of sparks and STOCs. It predicts the effects of the knockout of the BK β1 subunit (Brenner et al., 2000; Dong et al., 2008; Sachse et al., 2014) on the myogenic response as reflected in V_m and Ca_in and the effects of selected vasoactive agents on the myogenic response after knockout of BK β1. Among these vasoactive agents, it predicts that NO will be most effective in restoring the normal functional relationship between Ca_in and pressure over its entire range.

The second type of prediction is implicit in the postulated mechanisms included in the model. Two of these are the pressure-transducing microdomains containing NSCstr and ClA channels and the core mechanism of spiking Ca concentrations (sparks) and spiking V_m (STOCs). These predictions are just a short step beyond what others have observed and inferred, made concrete by their mathematical expression.